1 Introduction

It is well known that the observed physical parameters of the low energy theory differ by many orders of magnitude. Otherwise, no complex structures would be formed. At the same time a future theory should not contain very big/small physical parameters. The fine tuning (FT) of observable parameters makes the situation much more challenging. Indeed the most probable basis of FT, the multiverse idea, implies the existence of a huge variety of universes with different properties. At first glance the multiverse cannot be obtained having a fixed set of initial parameters of the future theory. There are a lot of attempts to explain the observable Universe with moderate success [1, 2]. One of the best-known ways is based on the idea of extra space and more specifically on 4-dim branes embedded in n-dim extra space [3, 4].

The physical parameters of a primary theory are not the only ones which influence the low energy physics. The initial conditions of formation of the universe play a significant role also. The well-known idea of the creation of the universe from a space-time foam presumes randomly distributed initial conditions. The accidental formation of manifolds with various metrics and topologies may be considered as a source of different universes whose variety is connected with the huge number of stationary metrics of the extra space [5, 6]. Even if the parameters of the primary Lagrangian are fixed we still have a set of initial conditions provided by the space-time foam. It could resolve the FT and hierarchy problems.

The probability of the birth of the universe was calculated via numerous approaches with radically different results [7]. This is not surprising due to the absence of the theory of quantum gravity. In this study it will be sufficient to assume a non-zero probability of any metric originating from a space-time foam. Some of these metrics evolve classically to stationary states; see e.g. [8].

The idea of random initial conditions originating from the space-time foam are used in this paper to explain the smallness of the cosmological constant, the prominent example of the fine tuning.

The extra spaces with point-like defects [9] underlie this research. It is shown that a scalar field is localized on the point-like defects of the 2-dim metric of extra space while its distribution in ordinary space is assumed to be uniform. In its turn, the back reaction of the trapped scalar field on the extra space metric appears to be significant. It deepens the “gravitational well” as it occurs in the case of Einstein gravity.

The point-like defects being uniformly distributed in our space form a brane embedded in \((4+n)\)-dim space. Brane solutions with various ways of matter localization have been widely investigated in the literature where the existence of a brane is usually postulated [10, 11]. Another widely used way to form a brane in noncompact extra spaces is to involve scalar fields with a complex potential [12]. Matter fields are trapped by such branes and deform their shape. This result may be obtained in the simplest version of f(R) gravity; see e.g. [13]. Branes embedded in 6-dim space are also the subjects of wide discussion [14–17].

In this paper the smallness of the \(\Lambda \) term produced by the brane is explained without fine tuning of the physical parameters. It means that all physical parameters of the Lagrangian are chosen within the interval \(10^{-3}<\xi <10^3\) if it is a dimensionless unit, or it lies within the interval \((10^{-3}m_D)^n<\xi <(10^3 m_D)^n\) if its dimensionality is \([m_D]^n\).

The general basis of the present study is f(R) gravity. The interest in f(R) theories is motivated by inflationary scenarios starting with the pioneering work of Starobinsky [18]. A number of viable f(R) models in 4-dim space that satisfy the observable constraints were proposed in Refs. [19–21].

Nonlinear Lagrangians depending on the Ricci invariants inevitably appear if one takes into account quantum phenomena [22–26]. At first sight there are no reasons to set \(f(R)=R\) if it does not contradict the observations. However, a more thorough analysis indicates serious internal problems. They include negative metric states, unitarity violation, and the instability of flat space. However, Simon [27, 28] has shown that these problems do not appear when the theory is treated as an effective field theory. In the low energy limit the effect of nonlinearity is a small correction to the pure Einstein–Hilbert action and no bad behavior is revealed. This particularly relates to the Kaluza–Klein f(R) gravity where the small parameter—the ratio of curvature in our 4-dim space and the curvature of compact extra space—arises naturally.

The following sections are devoted to the mechanism of the formation of point-like defects.

2 Setup

From now on, it is assumed that the characteristic scale of the extra space is small and its geometry has been stabilized shortly after the creation of the universe. The stabilization issue is discussed in [29, 30].

As a common basis, consider a Riemannian manifold with metric

$$\begin{aligned} \mathrm{d}s^2\!=\!\mathfrak {G}_{AB}\mathrm{d}Z^A \mathrm{d}Z^B \!=\! g_{\mu \nu }(x)\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }+G_{ab}(x,y)\mathrm{d}y^a\mathrm{d}y^b.\nonumber \\ \end{aligned}$$
(1)

Here M, \(M'\) are the manifolds with metrics \(g_{mn}(x)\) and \(G_{ab}(x,y)\), respectively. x and y are the coordinates of the subspaces M and \(M'\). We will refer to 4-dim space M and n-dim compact space \(M'\) as the main space and the extra space, respectively. Here the metric has the signature (\(+\) \(-\) \(-\) \(-\) \(\cdots \)), the Greek indices \(\mu , \nu =0,1,2,3\), refer to 4-dimensional coordinates). Latin indices run over \(a,b,\ldots = 4, 5,\ldots \)

The time behavior of the metric tensor \(G_{ab}(x,y)\) is governed by the classical equations of motion and changes under variations of initial conditions. As was shown in [30] the energy dissipation into the main space M leads to an entropy decrease of the manifold \(M'\). This explains the emergence of a friction term in the classical equations for the extra metric \(G_{ab}(x,y)\). This term stabilizes the extra metric. Finally the inflationary process strongly smooths out a space inhomogeneity so that

$$\begin{aligned} G_{ab}(x,y) \xrightarrow {t\rightarrow \infty }G_{ab} (t,y) \end{aligned}$$
(2)

at the modern epoch. The time dependence of the external metric was discussed within the framework of the Kaluza–Klein cosmology and Einstein’s gravity [31]. If a gravitational Lagrangian contains terms nonlinear in the Ricci scalar the extra metric \(G_{ab}\) could have asymptotically stationary states [8, 30]

$$\begin{aligned} G_{ab}(t,y)\rightarrow G_{ab}(y), \end{aligned}$$
(3)

see also [32, 33] for a discussion.

Let us estimate the rate of stabilization of the extra space. Weak deviations of the geometry from the equilibrium configuration can be interpreted as excited states with the mass \(m_{KK}\) (see, for example, [34]). Since it is the only scale, the decay probability is expected to satisfy the relationship \(\Gamma \sim m_{KK}\sim 1/L_n\), where \(L_n\) is the characteristic size of the n-dim extra space. According to observations \(L_n \le 10^{-18}\) cm, so that the lifetime of the excited state is \(t_1 \sim L_n \le 10^{-28}\) s. Therefore, the extra space reaches a stationary state long before the onset of the primordial nucleosynthesis but, possibly, after completion of the inflationary stage.

According to (1) and (3), the Ricci scalar represents a simple sum of the Ricci scalar of the main space and the Ricci scalar of the extra space

$$\begin{aligned} R=R_4 + R_n. \end{aligned}$$
(4)

In the following, the natural inequality

$$\begin{aligned} R_4 \ll R_n \end{aligned}$$
(5)

is assumed. This suggestion looks natural for an extra space size of \(L_n < 10^{-18}\) cm as compared to the Schwarzschild radius \(L_n \ll r_g \sim 10^6\) cm of a stellar mass black hole where the largest curvature in the modern universe exists.

Consider gravity with higher order derivatives and the action in the form

$$\begin{aligned}&S=\frac{m_D ^{D-2}}{2}\int \mathrm{d}^{D}Z \sqrt{|\mathfrak {G}|}[f(R)+L_m];\\&f(R) = \sum \limits _k {a_k R^k }\nonumber \end{aligned}$$
(6)

with arbitrary parameters \(a_k,\, k\ne 1\) and \(a_1 = 1\). Here \(D=n+4\) and \(L_m\) is the Lagrangian of matter.

Using inequality (5) the Taylor expansion of f(R) in Eq. 6 gives

$$\begin{aligned} S= & {} \frac{m_D^{D-2}}{2}\int \mathrm{d}^4x\mathrm{d}^n y \sqrt{|g(x)|} \sqrt{|G(y)|}\left[ f(R_4 \!+\! R_n) \!+\!L_m \right] \nonumber \\\simeq & {} \frac{m_D ^{D-2}}{2}\int \mathrm{d}^4 x \mathrm{d}^n y\sqrt{|g(x)|} \sqrt{|G(y)|}[ R_4(x) f' (R_n (y))\nonumber \\&+ f(R_n (y))+L_m]. \end{aligned}$$
(7)

The prime denotes the derivation of functions with respect to the argument. Thus, \(f'(R)\) stands for \(\mathrm{d}f/\mathrm{d}R\) in the formula written above. In this paper the stationary and uniform distribution of the matter fields is taken into account. The comparison of the second line in expression (7) with the Einstein–Hilbert action

$$\begin{aligned} S_{\mathrm{EH}}=\frac{M^2_{\mathrm{Pl}}}{2}\int \mathrm{d}^4x \sqrt{|g(x)|}(R-2\Lambda ) \end{aligned}$$
(8)

gives the expression

$$\begin{aligned} M^2_{\mathrm{Pl}}=m_{D}^{D-2}\int \mathrm{d}^n y \sqrt{|G(y)|}f' (R_n (y)) \end{aligned}$$
(9)

for the Planck mass. According to the effective action (7) the term

$$\begin{aligned} \Lambda \equiv -\frac{m_D^{D-2}}{2M^2_{\mathrm{Pl}}}\int \mathrm{d}^n y \sqrt{|G(y)|} [f(R_n) + L_m (y)] \end{aligned}$$
(10)

represents the cosmological \(\Lambda \) term. Both the Planck mass and the \(\Lambda \) term depend on the stationary geometry \(G_{ab} (y)\). As shown below, the physical parameters \(\{a_k\}\) are not necessarily fine tuned in order to make the \(\Lambda \) term small.

3 Deformed extra space and boundary conditions

Let us find the 2-dim metric disregarding the influence of scalar field and keeping in mind (5). In this work, the metric formalism is used, which consists of varying the action with respect to \(G^{ab}\). Note that the r.h.s. of the expression (7) consists of three terms. The first term is much smaller than the second one according to (5); accordingly, a stationary configuration \(G_{ab} (y)\) is determined by static classical equations

$$\begin{aligned}&\frac{\delta S}{\delta G^{ab} (y)}\simeq \frac{\delta S_{\mathrm{extra}}}{\delta G^{ab} (y)}=0,\nonumber \\&S_{\mathrm{extra}} = \frac{m_D^{D-2}}{2}v_4 \int \mathrm{d}^ny\sqrt{|G|}[ f(R_n)+L_m], \end{aligned}$$
(11)

where \(v_4 =\int \mathrm{d}^4x \sqrt{g(x)}\), or in more explicit form

$$\begin{aligned} R_{ab} f' -\frac{1}{2}f(R)G_{ab} - \nabla _a\nabla _b f_R + G_{ab} \square f' = \frac{1}{m_D^{D-2}}T_{ab}.\nonumber \\ \end{aligned}$$
(12)

Here \(\square \) stands by the d’Alembert operator

$$\begin{aligned} \square =\square _n =\frac{1}{\sqrt{|G|}}\partial _a ( {G}^{ab}\sqrt{|G|}\partial _b),\quad a,b=1,2. \end{aligned}$$
(13)

Here, the term proportional to \(R_4\) is omitted; see (5). The smallness of the Lambda term (10) is the additional condition that will be proven later.

Evidently, there is a continuum set of solutions to system (12) depending on the boundary conditions. Maximally symmetrical extra spaces, which are used in the great majority of the literature, represent a small subset of the continuum set. The relationship of the extra metric and boundary conditions is studied below. We will see that such nontrivial metrics lead to interesting results.

The trace of (12) can be written in the form

$$\begin{aligned} f'(R_n)R_n-\frac{n}{2} f(R_n)+(n-1)\square _n f'(R_n)=T, \end{aligned}$$
(14)

which will be used below. From now on we will use the units \(m_D = 1\).

In order to perform numerical analysis in the first order approximation let us disregard the matter contribution and choose \(n=2\), which strongly facilitates the analysis. Indeed, if the extra space is 2-dimensional, only one equation in system (12) remains independent. Let it be Eq. (14).

The compact 2-dim manifold is supposed to be parameterized by the two spherical angles \(\theta \) and \(\phi \) \((0 \le \theta \le \pi , 0 \le \phi \le 2\pi )\). The choice of the metric

$$\begin{aligned} G_{\theta \theta } = -r(\theta )^2;\quad G_{\phi \phi } = -r(\theta )^2 \sin ^2(\theta ) \end{aligned}$$
(15)

leads to the Ricci scalar expressed in terms of the radius \(r(\theta )\),

$$\begin{aligned} R= & {} \frac{2}{r(\theta )^4\sin (\theta )}(-r'r\cos (\theta )+r^2 \sin (\theta )\nonumber \\&+r'^2 \sin (\theta )-\sin (\theta )rr''), \end{aligned}$$
(16)

where the prime means \(\mathrm{d}/\mathrm{d}\theta \).

If a brane is artificially attached to a point \(\theta =0\) the 2-dim metric acquires the form

$$\begin{aligned} r_0^2(\mathrm{d}\theta ^2+\alpha ^2 \sin ^2\theta \mathrm{d}\phi ^2). \end{aligned}$$
(17)

The effect of the brane causes a deficit angle \(\delta = 2\pi (1-\alpha )\) in a bulk with flat 4-dim metric. The cost is a strict connection between the parameters of the model; see e.g. [11, 16] and for a review [35], where the pros and cons of this approach are discussed.

The metric (15) has a more general form, which causes a thick brane formation—a solution to Eq. (14). This equation leads to the trivial equality, if the function f is a linear function of R. The solutions are much more promising if the function f has a more complex form. So suppose that

$$\begin{aligned} f(R)=u_1 (R-R_0)^2. \end{aligned}$$
(18)

As a result the explicit form of Eq. (14) to be solved numerically is

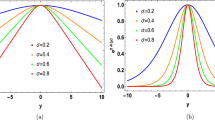
$$\begin{aligned} \partial ^2_{\theta }R+\cot \theta \partial _{\theta } R =- \frac{1}{2}r(\theta )^2 (R_0^2 - R^2 ) - \frac{r(\theta )^2}{2u_1} T. \end{aligned}$$
(19)

The solutions \(r_b (\theta )\) for \(T=0\) are represented in Figs. 1 and 2 (solid lines). Their features are discussed in [36]. Due to the high nonlinearity of the equation, the gravity is able to trap itself in a small region around \(\theta =0 \).

Fig. 1
figure 1

Radius \(r(\theta )\) as a function of the angle \(\theta \). Solid line matter is absent \((C=0)\), see (25), dotted line small density of the scalar field \((C<1)\), dashed line moderate density of the scalar field \((C\simeq 1)\). Boundary conditions: \(r(\pi ) = 447, r'(\pi ) = 0, R(\pi ) =2/r(\pi )^2, R'(\pi ) = 0\), and the parameters \(R_0 = 10^{-5}; u_1 = 100;m=0.15\)

Full size image
Fig. 2
figure 2

Radius \(r(\theta )\) as a function of the angle \(\theta \). Boundary conditions and the parameters the same as in Fig. 1 except \(r(\pi ) = 448\)

Full size image

The variation of the boundary value \(r(\pi )\) reveals two classes of the metric. They are separated by the boundary value \(r_* =\sqrt{2/R_0}\), which gives a maximally symmetrical stable 2-metric as a particular solution of Eq. (19) (\(r_* = 447.2\) for the parameters written in the capture of Fig. 1). Two representatives of these classes are shown in Figs. 1 and 2 by solid lines. Apple-like configurations are formed if \(r(\pi )< r_*\), while onion-like configurations appear if \(r(\pi )> r_*\). One can smoothly vary the form of the 2-dim extra space by variation of the boundary condition \(r(\pi )\). The physical parameters, like the Planck mass and the cosmological constant, depend on the geometry of the extra space and hence on the specific value of \(r(\pi )\). As was shown below, it leads to a set of different universes which has the cardinality of the continuum. The matter contribution—dotted and dashed lines in Figs. 1 and 2—is discussed in Sect. 4.2.

It is important to notice that in the framework of ordinary gravity the scale of classical region is about \(l_c \ge 1/M_{\mathrm{Pl}}\). In our case with D-dim space and multidimensional Planck mass \(m_D\) the situation is not so evident. The main difference is found in hyperbolic extra spaces [9]. For a space with positive curvature (like in our case), the result coincides in order of magnitude with the expected one—\(l_c \ge 1/m_D ({=}1 \text { in } m_D \text { units})\). This means that the classical solutions represented in Figs. 1 and 2 are valid at \(\theta \sim l_c/r(\theta ) \ge 1/r(\theta )\sim 1/400\). Therefore, the quantum effects invalidate our classical results only in the close vicinity of the point-like defect at \(\theta =0\).

The 2-dim metric depends on the internal coordinates only. Thus, it may be interpreted as a thick 4-dim brane embedded into 6-dim space \(M_4 \times M_2\). In the framework of Einstein–Hilbert gravity the brane must include matter to avoid singularities [7]. In our case of unavailability of matter the brane has a predictable structure in classical region and fails near the brane. The latter should be true not only for the model in question.

Let us discuss the mechanism of matter concentration inside a small volume of compact manifold with “apple”-type metric represented in Fig. 1.

4 Localization of scalar field

4.1 Field trapping by point-like defects of the 2-dim metric

Consider the influence of a deformed extra geometry represented by a solid line in Fig. 1 on a scalar field distribution. As is shown in this section, the scalar field with the Lagrangian

$$\begin{aligned} L_m =\frac{1}{2} \partial _a \varphi G^{ab}\partial _b \varphi - \frac{m^2}{2}\varphi ^2 \end{aligned}$$
(20)

is localized in the vicinity of such defect.

The field is assumed to be uniformly distributed in our 4-dim space,

$$\begin{aligned} \varphi (x,y) = Y(y), \end{aligned}$$
(21)

so that the classical equation of motion is

$$\begin{aligned} \square _n Y(y) +m^2 Y(y) =0. \end{aligned}$$
(22)

With the metric (15) it may be written in the following form:

$$\begin{aligned} \cot (\theta )\partial _{\theta }Y(\theta ) + \partial ^2 _{\theta }Y(\theta ) - m^2 r_b (\theta )^2Y(\theta ) =0. \end{aligned}$$
(23)

This equation can be simplified to obtain an analytical solution. For that purpose recall that the characteristic size \(\bar{r}\) of an extra space must satisfy the condition

$$\begin{aligned} \bar{r}\gg 1/m_D, \end{aligned}$$
(24)

which is a necessary condition for the extra space to be considered classically. For the particular case represented in Figs. 1 and 2, \(\bar{r}\sim \bar{r_b}\simeq 400/m_D\), and the inequality (24) holds. Let us define the “potential” \(v(\theta )\equiv m^2 r_b(\theta )^2 \epsilon ^2\) where the small parameter

$$\begin{aligned} \epsilon =1/(\bar{r}m_D)\ll 1 \end{aligned}$$

was introduced.

In the spirit of WKB a solution to (23) may be found in the form

$$\begin{aligned} Y(\theta ) = C\mathrm{e}^{S/\epsilon }. \end{aligned}$$
(25)

Here C is an arbitrary constant. The equation acquires the form

$$\begin{aligned} \epsilon \cot (\theta )S'_{\theta } + \epsilon S^{\prime \prime } + S'{}^2_\theta -v(\theta )=0. \end{aligned}$$
(26)

The first and the second terms are proportional to the small parameter \(\epsilon \) and therefore may be omitted as compared to \(S'{}^2_\theta \).

The first term tends to infinity for \(\theta \rightarrow 0\) and some speculations are necessary to demonstrate that it is nevertheless small in the classical region where quantum fluctuations are negligible. Indeed, a necessary condition for the classical description of an area of a size l reads \(l\gg 1/m_D\). In angular units it means that \(\theta \simeq l/r_b (\theta )>l/ \bar{r}_b\gg 1/m_D\bar{r}_b\) (\(\theta \ll 1\) is assumed). The first inequality is true in a close vicinity to \(\theta = 0\), where the condition \(r_b(\theta )<\bar{r}_b\) holds, as can be seen from Fig. 1. Hence the classical description is valid if \(\theta \) satisfies the inequality

$$\begin{aligned} \theta \gg \frac{1}{\bar{r}m_D}=\epsilon . \end{aligned}$$
(27)

This condition is equivalent to the condition \(\epsilon \cot (\theta ) \ll 1\) at small angles. It means that the first term is also small in comparison with the term \(S'{}^2_\theta \) and the classical solution to (25) has the following form:

$$\begin{aligned} Y(\theta )= C\exp \left\{ -m\int ^{\theta }_0 \mathrm{d}\theta ' r_b (\theta ')\right\} . \end{aligned}$$
(28)

If the radius \(r_b (\theta )\) is growing monotonically as in Fig. 1 (solid line) the scalar field density has a sharp peak, as is seen from Fig. 3.

Fig. 3
figure 3

Typical distribution of the energy-momentum tensor trace of the scalar field

Full size image

As a result, the matter is concentrated near point-like defects of the extra space metric. At the same time it is uniformly distributed throughout our 4-dim space \(M_4\). The effect of fermion trapping on the apple-like brane is discussed in [37] on the basis of Einstein–Hilbert gravity.

4.2 Back reaction of the scalar field to the metric

Let us study the influence of a scalar field on the metric of 2-dim manifold. Suppose that the trace of energy-momentum tensor has a sharp peak near \(\theta =0\) as in Fig. 3. An origin of such peak does not matter. It could be a result of metric influence as was discussed above or an accidental fluctuation.

The energy-momentum tensor

$$\begin{aligned} T_{ab}(\varphi (\theta )))=\partial _a \varphi \partial _b \varphi -G_{ab}\left[ \frac{1}{2}\partial _c \varphi G^{cd}\partial _d\varphi -U(\varphi )\right] \quad \end{aligned}$$
(29)

should show a sharp maximum as well.

For the 2-dim extra space we have

$$\begin{aligned} T= & {} G^{ab}T_{ab}=2U(\varphi )= m^2 \varphi ^2\nonumber \\= & {} C^2 m^2 Y^2 = C^2 m^2 \exp \left\{ -2m\int ^{\theta }_0 \mathrm{d}\theta ' r_b (\theta ')\right\} . \end{aligned}$$
(30)

The abundance of matter is ruled by the arbitrary parameter C. Numerical calculations with the help of the same Eq. (14) and the trace in the r.h.s. of Eq. (30) are presented in Fig. 1. It can be seen that the local matter distribution strongly influences the 2-dim metric making the wall deeper (dotted and dashed lines). It can be concluded from Fig. 2 that a matter clump is able to form a gravitational well. The more densely the matter is concentrated near a point, the deeper the gravitational well. This coincides with our physical intuition.

5 Self-fitting of the cosmological \(\Lambda \) term and the Planck mass

The approach developed above is based on the approximation (5). Let us check its validity. To be more precise, and keeping in mind the connection \(R_4 \sim \Lambda \) we must obtain the smallness of the \(\Lambda \) term, \(\Lambda \ll R_n\); see (10).

The main assumption of the developed approach is the formation of universes from space-time foam. Any initial conditions may occur with non-zero probability. In our case it relates both to a scalar field placed in the extra space and to the form of the extra space. The chosen physical parameter \(u_1 >0\) and the quadratic form of the function f(R) means that \(f(R)>0\) always. A simple analysis of expression (20) indicates that \(L_m <0\) for stationary solutions of the scalar field, so that these terms could annihilate each other. The matter distribution strongly depends on the initial conditions that can vary within a wide range. This observation is confirmed by the numerical calculations presented in Fig. 4. It is assumed that the trace of the energy-momentum tensor \(T(\theta =0)\) is also the result of the initial conditions.

Fig. 4
figure 4

The cosmological \(\Lambda \) term versus scalar density distributed on the extra space. T(0) is the trace of the energy-momentum tensor at \(\theta =0\), \(m_D=1\)

Full size image

Thus, the cosmological constant may vary from negative values (when matter is absent) to positive values (due to the matter contribution). The variety of universes differs due to their initial conditions. In particular there exist a set of universes with cosmological \(\Lambda \) terms being arbitrarily close to zero. According to Fig. 4 these universes are formed with a scalar field distribution such that \(T(0)\approx 0.00024\).

The Planck mass depends significantly on the metric of the extra space as shown on Fig. 5. Even if \(m_D =\hbox {const}\), the calculated Planck mass can be fitted to the observable one by a modification of the boundary conditions. Notice that some boundary conditions lead to negative values of the Planck mass and hence are unacceptable.

Fig. 5
figure 5

The Planck mass square versus boundary value \(r(\theta =\pi )\) normalized by the sphere metric at \(r(\pi )=r_*\)

Full size image

6 Conclusion

This paper discusses extra spaces with metrics that differ from the maximally symmetrical ones within the framework of f(R) gravity. The variety of initial conditions caused by the space-time foam leads to a continuous set of 2-dim metrics containing point-like defects of the extra space. The extra space metric is uniform in our 3-dim space and therefore may be responsible for the 4-dim brane formed in 6-dim space \(M_6 = M_2 \times M_4\). The extra space structure is determined everywhere except for the close vicinity of the brane where the quantum gravitational effects destroy the classical description.

A scalar field distributed in the extra space is localized within the vicinity of the point-like defect. Such a clump of scalar field, in its turn, makes the gravitational well of the point-like defect more prominent.

Both the metric and the scalar field contribute to the value of the cosmological \(\Lambda \) term. The signs of their contributions are opposite, so they could annihilate each other at some specific initial conditions. It is shown that the continuous set of 2-dim metrics contains a subset responsible for the range of \(\Lambda \) terms including the zero value. Consequently, this subset contains an extra space metric leading to an observable value of the cosmological constant.