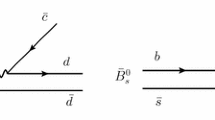The $B_c\rightarrow \psi (2S)\pi$, $\eta _c(2S)\pi$ decays in the perturbative QCD approach

Abstract

Nonleptonic two-body $B_c$ decays including radially excited $\psi (2S)$ or $\eta _c(2S)$ mesons in the final state are studied using the perturbative QCD approach based on $k_T$ factorization. The charmonium distribution amplitudes are extracted from the $n = 2, l = 0$ Schrödinger states for the harmonic oscillator potential. Utilizing these distribution amplitudes, we calculate the numerical results of the $B_c\rightarrow \psi (2S),\eta _c(2S)$ transition form factors and branching fractions of $B_c\rightarrow \psi (2S)\pi , \eta _c(2S)\pi$ decays. The ratio between two decay modes $B_c\rightarrow \psi (2S)\pi$ and $B_c\rightarrow J/\psi \pi$ is compatible with the experimental data within uncertainties, which indicates that the harmonic-oscillator wave functions for $\psi (2S)$ and $\eta _c(2S)$ work well. It is found that the branching fraction of $B_c\rightarrow \eta _c(2S)\pi$, which is dominated by the twist-3 charmonium distribution amplitude, can reach the order of $10^{-3}$. We hope it can be measured soon in the LHCb experiment.

1 Introduction

The meson $B_c$, a pseudoscalar ground state of b and c quarks, can only decay through weak interactions. Either of the heavy quarks (b or c) in it can decay individually, which makes it an ideal system to study weak decays of heavy quarks. Around $\mathcal {O}(10^{9})$ mesons can be anticipated with 1 fb$^{-1}$ of data at the LHC [1], which is sufficient for studying the $B_c$ meson family systematically. Up to now, several new decay channels of the $B_c$ meson [2–6] have been successfully observed by the LHCb Collaboration, while an excited $B_c$ meson state which is consistent with expectations of the $B_c(2S)$ has been found by the ATLAS detector [7].

Recently, the LHCb Collaboration observed the decay mode $B_c\rightarrow \psi (2S)\pi$ for the first time with the measured ratio of the branching fractions as [8]

$$\begin{aligned} \frac{\mathcal {B}(B_c\rightarrow \psi (2S)\pi )}{\mathcal {B}(B_c\rightarrow J/\psi \pi )}= & {} 0.250 \pm 0.068 (\text {stat})\nonumber \\&\pm \,0.014 (\text {syst})\pm 0.006(\mathcal {B}). \end{aligned}$$

(1)

The last term above accounts for the uncertainty on $\mathcal {B}(\psi (2S)\rightarrow \mu ^+\mu ^-)/\mathcal {B}(J/\psi \rightarrow \mu ^+\mu ^-)$. Although there is not much data for the $B_c$ meson decaying into two-body final states containing a radially excited charmonium such as $\psi (2S)$ or $\eta _c(2S)$ except the $B_c\rightarrow \psi (2S)\pi$ channel, many theoretical studies of nonleptonic $B_c$ decays with radially excited charmonium mesons in the final state have been performed by using various approaches. For example, in Ref. [9], the authors computed the branching ratios for $B_c\rightarrow \psi (2S)X$ decays with the modified harmonic-oscillator wave function in the light front quark model; in Ref. [10], the ISGW2 quark model was adopted to study the production of radially excited charmonium mesons in two-body nonleptonic $B_c$ decays; the relativistic (constituent) quark model, the potential model, the QCD relativistic potential model, and the improved instantaneous BS equation and Mandelstam approach were adopted in Refs. [11–15], respectively. However, all of these calculations are based on a naive factorization hypothesis, with various form factor inputs. There are uncontrolled large theoretical errors with quite different numerical results, and most of them cannot give any theoretical error estimates because of the unreliability of these models.

The perturbative QCD approach (pQCD) [16–19] based on $k_T$ factorization, which not only can deal with the emission diagrams corresponding to the naive factorization terms basically, but can also handle well the nonfactorizable diagrams by introducing the wave function of the light meson in the final states of the $B_c$ decay modes, is widely used in the nonleptonic two-body $B_c$ decays [20–31]. In our recent work [32], the pQCD approach was used successfully in describing the S-wave ground state charmonium decays of $B_c$ meson based on the harmonic-oscillator wave functions for the charmonium 1S states. In this work, we will use the harmonic-oscillator wave function as the approximate wave function of the 2S states and study the $B_c\rightarrow \psi (2S)\pi , \eta _c(2S)\pi$ decays in the pQCD approach to provide a ready reference to existing and forthcoming experiments.

The structure of this paper is organized as follows. After this Introduction, we describe the wave functions of radially excited charmonium mesons $\psi (2S),\eta _c(2S)$ in Sect. 2. We calculate and present the expressions for the $B_c\rightarrow \psi (2S),\eta _c(2S)$ transition form factors in the large-recoil regions and the $B_c\rightarrow \psi (2S)\pi ,\eta _c(2S)\pi$ decay amplitudes in Sect. 3. The numerical results and relevant discussions are given in Sect. 4, and Sect. 5 contains a brief summary.

2 Wave functions

In hadronic B decays, there are several energy scales involved. In the expansion of the inverse power of heavy quark mass, the hadronic matrix element can be factorized into perturbative and nonperturbative factors. In the pQCD approach, the decay amplitude $\mathcal{A}(B_c \rightarrow M_2 M_3)$ can be written conceptually as the convolution [16–19]

$$\begin{aligned}&\mathcal{A}(B_c \rightarrow M_2 M_3)\sim \int \!\! \mathrm{d}^4k_1 \mathrm{d}^4k_2 \mathrm{d}^4k_3\ \mathrm {Tr}\nonumber \\&\quad \times [ C(t) \Phi _{B_c}(k_1) \Phi _{M_2}(k_2) \Phi _{M_3}(k_3)H(k_1,k_2,k_3, t) ], \end{aligned}$$

(2)

where $k_i$’s are momenta of spectator quarks included in each meson, and “$\mathrm {Tr}$” denotes the trace over Dirac and color indices. In the above convolution, C(t) is the Wilson coefficient evaluated at scale t, the function $H(k_1,k_2,k_3,t)$ describes the four quark operator and the spectator quark connected by a hard gluon, which can be perturbatively calculated including all possible Feynman diagrams without end-point singularity. The wave functions $\Phi _{B_c}(k_1)$, $\Phi _{M_2}$ and $\Phi _{M_3}$ describe the hadronization of the quark and anti-quark in the $B_c$ meson, the charmonium meson $\psi (2S)$ or $\eta _c(2S)$, and the final state light meson pion, respectively.

As a heavy quarkonium discussed in Refs. [32, 33], the nonrelativistic QCD framework can be applied for the $B_c$ meson, which means its leading-order wave function should be just the zero-point wave function with the distribution amplitude

$$\begin{aligned} \phi _{B_c}(x)= \frac{f_{B_c}}{2\sqrt{2N_c}}\delta (x-m_c/m_{B_c}) \exp [-\omega ^2_{B_c}b^2/2]. \end{aligned}$$

(3)

For the light meson pion, we adopt the same distribution amplitudes $\phi _{\pi }^A(x)$ and $\phi _{\pi }^{P,T}(x)$ as defined in Refs. [34–37].

The harmonic-oscillator wave functions has been adopted to describe the 1S state mesons [38–40], and they can explain the experimental data well [32]. In the quark model, $\eta _c(2S)$ and $\psi (2S)$ are the first excited states of $\eta _c$ and $J/\psi$, respectively. The 2S means that for these states, the principal quantum number $n=2$ and the orbital angular momentum $l=0$. The definitions of the 2S state wave functions are similar to the 1S states via the nonlocal matrix elements [41]:

(4)

where P stands for the momentum of the charmonium meson $\eta _c(2S)$ or $\psi (2S)$ and m is its mass. The x represents the momentum fraction of the charm quark inside the charmonium, and b is the conjugate variable of the transverse momentum of the valence quark of the meson. The $\epsilon ^{L(T)}$ denotes its longitudinal (transverse) polarization vector. The asymptotic models for the twist-2 distribution amplitudes $\psi ^{L,T,v}$, and the twist-3 distribution amplitudes $\psi ^{t,V,s}$ will be derived following the prescription in [38].

First, we write down the Schrödinger equal-time wave function $\Psi _{\mathrm{Sch}}(\mathbf r )$ for the harmonic-oscillator potential. The radial wave function of the corresponding Schrödinger state is given by

$$\begin{aligned} \Psi _{(2S)}(\mathbf r )\propto \left( \frac{3}{2}-\alpha ^2r^2\right) \mathrm{e}^{-\frac{\alpha ^2r^2}{2}}, \end{aligned}$$

(5)

where $\alpha ^2=\frac{m\omega }{2}$ and $\omega$ is the frequency of oscillations or the quantum of energy. We perform the Fourier transformation to the momentum space to get $\Psi _{2S}(\mathbf{k})$:

$$\begin{aligned} \Psi _{(2S)}(\mathbf k )\propto (2k^2-3\alpha ^2)\mathrm{e}^{-\frac{k^2}{2\alpha ^2}}, \end{aligned}$$

(6)

with $k^2$ being the square of the three momentum. In terms of the substitution assumption,

$$\begin{aligned} \mathbf k _{\perp }\rightarrow \mathbf k _{\perp },\quad k_z\rightarrow \frac{m_0}{2}(x-\bar{x}), \quad m_0^2=\frac{m_c^2+\mathbf k ^2_{\perp }}{x\bar{x}}, \end{aligned}$$

(7)

with $m_c$ the c-quark mass and $\bar{x}=1-x$. We should make the following replacement as regards the variable $k^2$:

$$\begin{aligned} k^2\rightarrow \frac{\mathbf{k }^2_{\perp }+(x-\bar{x})^2m_c^2}{4x\bar{x}}. \end{aligned}$$

(8)

Then the wave function can be taken as

$$\begin{aligned}&\Psi _{(2S)}(\mathbf{k })\rightarrow \Psi _{(2S)}(x,\mathbf{k }_{\perp })\nonumber \\&\quad \propto \left( \frac{\mathbf{k }^2_{\perp }+ m_c^2(x-\bar{x})^2}{2x\bar{x}}-3\alpha ^2\right) \mathrm{e}^{-\frac{\mathbf{k }^2_{\perp }+ m_c^2(x-\bar{x})^2}{8x\bar{x}\alpha ^2}}. \end{aligned}$$

(9)

Applying the Fourier transform to replace the transverse momentum $\mathbf k _{\perp }$ with its conjugate variable b, the 2S oscillator wave function can be taken as

$$\begin{aligned} \Psi _{(2S)}(x,\mathbf b )\sim & {} \int \mathbf d ^2\mathbf k _{\perp }\mathrm{e}^{-i\mathbf k _{\perp } \cdot \mathbf b }\Psi _{(2S)}(x,\mathbf k _{\perp })\nonumber \\ \quad\propto & {} x\bar{x}\mathcal {T}(x) \mathrm{e}^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]}, \end{aligned}$$

(10)

with

$$\begin{aligned} \mathcal {T}(x)=1-4b^2m_c\omega x\bar{x}+\frac{m_c(x-\bar{x})^2}{\omega x\bar{x}}. \end{aligned}$$

(11)

We then propose the 2S states distribution amplitudes inferred from Eq. (10),

$$\begin{aligned} \Psi _{(2S)}(x,b) \propto \Phi ^{\mathrm{asy}}(x)\mathcal {T}(x) \mathrm{e}^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]}, \end{aligned}$$

(12)

with the $\Phi ^{\mathrm{asy}}(x)$ being the asymptotic models, which have been given in [42]. Therefore, we have the distribution amplitudes for the radially excited charmonium mesons $\eta _c(2S)$ and $\psi (2S)$

$$\begin{aligned}&\Psi ^{L,T,v}(x,b)=\frac{f_{2S}}{2\sqrt{2N_c}}N^{L,T,v} x\bar{x}\mathcal {T}(x) \mathrm{e}^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]},\nonumber \\&\Psi ^t(x,b)=\frac{f_{2S}}{2\sqrt{2N_c}}N^t (x-\bar{x})^2\mathcal {T}(x) \mathrm{e}^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]},\nonumber \\&\Psi ^V(x,b)=\frac{f_{2S}}{2\sqrt{2N_c}}N^V [1\!+\!(x\!-\!\bar{x})^2]\mathcal {T}(x) \mathrm{e}^{\!-\!x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2\!+\!(\frac{x\!-\!\bar{x}}{2x\bar{x}})^2]},\nonumber \\&\Psi ^s(x,b)=\frac{f_{2S}}{2\sqrt{2N_c}}N^s \mathcal {T}(x) \mathrm{e}^{-x\bar{x}\frac{m_c}{\omega }[\omega ^2b^2+(\frac{x-\bar{x}}{2x\bar{x}})^2]}, \end{aligned}$$

(13)

with the normalization conditions:

$$\begin{aligned} \int _0^1\Psi ^{i}(x,0)\mathrm{d} x= & {} \frac{f_{2S}}{2\sqrt{2N_c}}. \end{aligned}$$

(14)

$N_c$ above is the color number, $N^{i}(i=L,T,t,V,v,s)$ are the normalization constants, and $f_{2S}$ is the decay constant of the 2S state. All the distribution amplitudes in Eq. (13) are symmetric under $x\leftrightarrow \bar{x}$. Here we do not distinguish the leading twist distribution amplitude $\Psi ^v$ of the $\eta _c(2S)$ meson from $\Psi ^{L,T}$ of the $\psi (2S)$ meson, and the same decay constant has been assumed for the longitudinally and transversely polarized $\psi (2S)$ meson. To make things clearer, the shape of the distribution amplitude $\Psi ^{L}(x,0)$ is displayed in Fig. 1. The free parameter $\omega =0.2$ GeV is adopted, such that the valence charm quark, carrying the invariant mass $x^2P^2\approx m_c^2$, is almost on shell. It can be seen that the two maximum positions are near $x=0.35$ and $x=0.65$ and a larger value of parameter $\omega$ gives a wider shape. Note that the dip at $x=0.5$ is a consequence of the radial Schrödinger wave function of the $n=2,l=0$ state.

Fig. 1

The shape of the distribution amplitude for $\psi ^L(x)$ when $b=0$, with the solid (dashed) line for $\omega =0.2(0.3)$ GeV

Fig. 2

The leading-order Feynman diagrams for the $B_c\rightarrow (\psi (2S), \eta _c(2S))$ transitions

3 Form factors and decay amplitudes

In the pQCD approach, the $B_c\rightarrow \psi (2S),\eta _c(2S)$ transition form factors in the large-recoil limit ($q^2=0$), which are similar to that of $B_c\rightarrow J/\psi ,\eta _c$ [43], can be calculated from the above universal hadronic distribution amplitudes. The lowest-order diagrams are displayed in Fig. 2. The form factors $F_{+,0}(q^2)$, $V(q^2)$, and $A_{0,1,2}(q^2)$ are defined via the matrix element [44]

$$\begin{aligned}&\langle \eta _c(2S)(P_2)|\bar{c}\gamma ^{\mu }b|B_c(P_1)\rangle \nonumber \\&\quad =\left[ (P_1\!+\!P_2)^{\mu } \!-\!\frac{M^2\!-\!m^2}{q^2}q^{\mu }\right] F_+(q^2)\nonumber \\&\qquad + \frac{M^2-m^2}{q^2}q^{\mu }F_0(q^2), \end{aligned}$$

(15)

$$\begin{aligned} \langle \psi (2S)(P_2)|\bar{c}\gamma ^{\mu }b|B_c(P_1)\rangle =\frac{2iV(q^2)}{M+m} \epsilon ^{\mu \nu \rho \sigma }\epsilon ^*_{\nu }P_{2\rho }P_{1\sigma },\nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned}&\langle \psi (2S)(P_2)|\bar{c}\gamma ^{\mu }\gamma _5b|B_c(P_1)\rangle \nonumber \\&\quad =2mA_0(q^2) \frac{\epsilon ^*\cdot q}{q^2}q^{\mu }+(M+m)A_1(q^2)\left[ \epsilon ^{*\mu }- \frac{\epsilon ^*\cdot q}{q^2}q^{\mu }\right] \nonumber \\&\qquad - A_2(q^2)\frac{\epsilon ^*\cdot q}{M+m}\left[ (P_1+P_2)^{\mu }-\frac{M^2-m^2}{q^2}q^{\mu }\right] , \end{aligned}$$

(17)

where $q=P_1-P_2$ is the momentum transfer and $P_1(P_2)$ is the momentum of the initial (final) state meson. M is the mass of $B_c$ meson, and $\epsilon ^*$ is the polarization vector of the $\psi (2S)$ meson. In the large-recoil limit, say $q^2=0$, we have

$$\begin{aligned} F_0(0)=F_+(0),\quad A_0(0)=\frac{1+r}{2r}A_1(0)-\frac{1-r}{2r}A_2(0).\nonumber \\ \end{aligned}$$

(18)

It is straightforward to calculate the form factors $F_{0}(q^2)$, $V(q^2)$, and $A_{0,1}(q^2)$ at the tree level in the pQCD. They read

$$\begin{aligned} F_0= & {} 2 \sqrt{\frac{2}{3}} \pi M^2 f_B C_f\int _0^1\mathrm{d}x_2\nonumber \\&\times \int _0^{\infty }b_1b_2db_1db_2 \exp \left( -\frac{\omega _B^2 b_1^2}{2}\right) \nonumber \\&\times \,\{[\psi ^v(x_2,b_2) (x_2-2 r_b)-\psi ^s(x_2,b_2)r (2 x_2-r_b)]\nonumber \\&\times \, E_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_2)S_t(x_2)\nonumber \\&+\,[\psi ^v(x_2,b_2)(r_c+r^2(1-x_1))-\psi ^s(x_2,b_2)\nonumber \\&\times \,2r(1-x_1+r_c)] E_{ab}(t_b)h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1)\},\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} V= & {} 2 \sqrt{\frac{2}{3}}(1+r)\pi M^2 f_B C_f\int _0^1dx_2\nonumber \\&\times \int _0^{\infty }b_1b_2db_1db_2 \exp \left( -\frac{\omega _B^2 b_1^2}{2}\right) \nonumber \\&\times \,\{[\psi ^V(x_2,b_2) r(1-x_2)+\psi ^T(x_2,b_2)(r_b-2)]\nonumber \\&\times \, E_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_2) S_t(x_2)\nonumber \\&-\,\psi ^V(x_2,b_2)rE_{ab}(t_b)h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1)\}, \end{aligned}$$

(20)

$$\begin{aligned} A_0= & {} 2 \sqrt{\frac{2}{3}} \pi M^2 f_B C_f\int _0^1\mathrm{d}x_2\nonumber \\&\times \int _0^{\infty }b_1b_2\mathrm{d}b_1\mathrm{d}b_2 \exp \left( -\frac{\omega _B^2 b_1^2}{2}\right) \nonumber \\&\times \,\{[\psi ^L(x_2,b_2) (x_2-2 r_b)-\psi ^t(x_2,b_2)r (2 x_2-r_b)]\nonumber \\&\times \, E_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_2)S_t(x_2)\nonumber \\&-\,\psi ^L(x_2,b_2)[r_c+r^2(1-x_1)]E_{ab}(t_b)\nonumber \\&\times \, h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1)\}, \end{aligned}$$

(21)

$$\begin{aligned} A_1= & {} 2 \sqrt{\frac{2}{3}}\frac{r}{1+r} \pi M^2 f_B C_f\int _0^1\mathrm{d}x_2\nonumber \\&\times \int _0^{\infty }b_1b_2\mathrm{d}b_1\mathrm{d}b_2 \exp \left( -\frac{\omega _B^2 b_1^2}{2}\right) \nonumber \\&\times \bigg \{\bigg [\psi ^V(x_2,b_2) (1\!+\!x_2\!-\!r^2(1\!-\!x_2)\!-\!4r_b)\!+\!\psi ^T(x_2,b_2)\nonumber \\&\times \, \bigg [r(2-4x_2+r_b) +\frac{r_b-2}{r}\bigg ]\bigg ]\nonumber \\&\times \, E_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_2)S_t(x_2) -\psi ^V(x_2,b_2)\nonumber \\&\times \, [1-2x_1+2r_c+r^2]E_{ab}(t_b)h(\alpha _e,\beta _b,b_2,b_1)S_t(x_1)\bigg \},\nonumber \\ \end{aligned}$$

(22)

with $r=\frac{m}{M}$ and $r_{b,c}=\frac{m_{b,c}}{M}$. The functions $E_{ab}$, the scales $t_{a,b}$, and the hard functions h are given in Appendix B of Ref. [32].

Fig. 3

Feynman diagrams for $B_c\rightarrow \psi (2S)\pi ,\eta _c(2S)\pi$ decays

The quark diagrams contributing to the $B_c\rightarrow \psi (2S)\pi ,\eta _c(2S)\pi$ decays are displayed in Fig. 3, where (a) and (b) are for the factorizable topology, and (c) and (d) are for the nonfactorizable topology. The effective Hamiltonian relevant to the considered decays is written as [45]

$$\begin{aligned} \mathcal {H}_{\mathrm{eff}}=\frac{G_F}{\sqrt{2}}V^*_{cb}V_{ud}[C_1(\mu )O_1(\mu )+C_2(\mu )O_2(\mu )]+\text {h.c.},\nonumber \\ \end{aligned}$$

(23)

with $V^*_{cb}$ and $V_{ud}$ the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, $C_{1,2}(\mu )$ the Wilson coefficients, and $O_{1,2}(\mu )$ the effective four quark operators

$$\begin{aligned} O_{1}(\mu )= & {} \bar{b}_{\alpha }\gamma ^{\mu }(1-\gamma _5)c_{\beta } \otimes \bar{u_{\beta }}\gamma _{\mu } (1-\gamma _5)d_{\alpha },\nonumber \\ O_{2}(\mu )= & {} \bar{b}_{\alpha }\gamma ^{\mu }(1-\gamma _5)c_{\alpha }\otimes \bar{u}_{\beta }\gamma _{\mu } (1-\gamma _5)d_{\beta }, \end{aligned}$$

(24)

where $\alpha$ and $\beta$ are the color indices. Since the four quarks in the operators are different from each other, there is no penguin contribution. Therefore there will be no CP violation in the decays of $B_c\rightarrow \psi (2S)\pi ,\eta _c(2S)\pi$ within the standard model. After a straightforward calculation using the pQCD formalism of Eq. (2), we have the decay amplitudes

$$\begin{aligned}&\mathcal {A}(B_c\rightarrow (\psi (2S), \eta _c(2S))\pi )=V_{cb}^*V_{ud}\nonumber \\&\quad \times \left[ \left( C_2+\frac{1}{3}C_1\right) \mathcal {F}_{e}+C_1\mathcal {M}_{e}\right] . \end{aligned}$$

(25)

The detailed expressions of $\mathcal {F}_{e}$ and $\mathcal {M}_{e}$ are the same as the $B_c\rightarrow (J/\psi , \eta _c)\pi$ decay modes in Appendix A of Ref. [32], except for the replacements $J/\psi \rightarrow \psi (2S)$ and $\eta _c\rightarrow \eta _c(2S)$.

4 Numerical results and discussions

In the numerical calculations we need the following input parameters (in units of GeV) [46]:

$$\begin{aligned}&m_{c}=1.275,\;\; m_b=4.18,\;\; M_{B_c}=6.277,\;\;\nonumber \\&\quad m_{\psi (2S)}=3.686,\;\; m_{\eta _c(2S)}=3.639. \end{aligned}$$

(26)

For the relevant CKM matrix elements we use $V_{cb}=(40.9 \pm 1.1)\times 10^{-3}$ and $V_{ud}=0.97425\pm 0.00022$ [46].

The decay constant $f_{\psi (2S)}$ can be derived from the process $\psi (2S)\rightarrow e^+e^-$ by the relationship

$$\begin{aligned} f_{\psi (2S)}=\sqrt{\frac{3m_{\psi (2S)}\Gamma _{\psi (2S)\rightarrow e^+e^-}}{4\pi \alpha ^2Q_c^2}}, \end{aligned}$$

(27)

using the data given in [46]

$$\begin{aligned} \Gamma _{\psi (2S)\rightarrow e^+e^-}=(2.36\pm 0.04)\,\, \text {keV}. \end{aligned}$$

(28)

Then we have $f_{\psi (2S)}=296^{+3}_{-2}$ MeV. The decay constant $f_{\eta _c(2S)}$ can be determined by the double photon decay of $\eta _c(2S)$ as

$$\begin{aligned} f_{\eta _c(2S)}=\sqrt{\frac{81\pi m_{\eta _c(2S)}\Gamma _{\eta _c(2S)\rightarrow \gamma \gamma }}{4(4\pi \alpha )^2}}. \end{aligned}$$

(29)

Using the measured results of the branching fractions $\eta _c(2S)\rightarrow \gamma \gamma$ and the full width of $\eta _c(2S)$ [46],

$$\begin{aligned}&\mathcal {B}(\eta _c(2S)\rightarrow \gamma \gamma )=(1.9\pm 1.3)\times 10^{-4},\;\;\nonumber \\&\Gamma _{\eta _c(2S)}=11.3^{+3.2}_{-2.9}~\text {MeV}, \end{aligned}$$

(30)

we can get the decay constant $f_{\eta _c(2S)}=243^{+79}_{-111}$ MeV. As for the decay constant for $B_c$, we adopt $f_{B_c}=489$ MeV [47].

Table 1 The form factors for $F_0^{B_c\rightarrow \eta _c(2S)}$, $A^{B_c\rightarrow \psi (2S)}_{0,1,2}$ and $V^{B_c\rightarrow \psi (2S)}$ at $q^2=0$ evaluated by pQCD and by other methods in the literature. We also show theoretical uncertainties induced by the shape parameters, $m_c$, $f_{\psi (2s)}$ or $f_{\eta _c(2s)}$, and the hard scale t, respectively

Our numerical results for the form factors $F_0^{B_c\rightarrow \eta _c(2S)}$, $A^{B_c\rightarrow \psi (2S)}_{0,1,2}$ and $V^{B_c\rightarrow \psi (2S)}$ are listed in Table 1. We find that the form factors are close by different approaches within errors, except the results in Ref. [11], which are typically smaller. Some dominant uncertainties are considered in our numerical values: the first error comes from the shape parameters $\omega _B=0.6\pm 0.1$ ($\omega =0.2\pm 0.1$) GeV for the $B_c$($\psi (2S)/\eta _c(2S)$) meson, the second one is induced by $m_c=1.275\pm 0.025$ GeV, the third error comes from the decay constants of the $\psi (2S)$ or $\eta _c(2S)$ meson, and the last one is caused by the variation of the hard scale from 0.75t to 1.25t in Eq. (2), which characterizes the size of next-to-leading-order contribution. It is found that the main errors come from the uncertainties of the shape parameters and the charm-quark mass. Therefore, the decay of $B_c\rightarrow \psi (2S)(\eta _c(2S))$ provides a good platform to understand the wave function of the radially excited charmonium states and the constituent quark model. The uncertainty from the decay constant of $\eta _c(2S)$ meson is large due to the low accuracy measurement of the branching fraction in Eq. (30); the relevant uncertainty of $F_0$ is large, too. We expect that it could be measured precisely at LHCb and Super-B factories in the near future. We also noticed that the error from the uncertainty of the hard scale t is small, which means the next-to-leading-order contributions can be safely neglected. The errors from the uncertainty of the CKM matrix elements are very small, and they have been neglected.

Table 2 Branching ratios ($10^{-4}$) of the $B_c\rightarrow \eta _c(2S)\pi , \psi (2S)\pi$ decays. The errors are induced by the same sources as in Table 1

The branching fractions for the $B_c\rightarrow \eta _c(2S)\pi , \psi (2S)\pi$ decays in the $B_c$ meson rest frame can be written as

$$\begin{aligned} \mathcal {B}(B_c\rightarrow (\psi (2S), \eta _c(2S))\pi )=\frac{G_F^2\tau _{B_c}}{32\pi M_B}(1-r^2)| \mathcal {A}|^2,\nonumber \\ \end{aligned}$$

(31)

where the decay amplitudes $\mathcal {A}$ have been given explicitly in Eq. (25). In Table 2, we show the results of the branching fractions for the two-body nonleptonic $B_c\rightarrow \eta _c(2S)\pi , \psi (2S)\pi$ decays, where the sources of the errors in the numerical estimates have the same origin as in the discussion of the form factors in Table 1. It is easy to see that the most important theoretical uncertainties are caused by the nonperturbative shape parameters, the charm-quark mass, and the decay constant $f_{\eta _c(2S)}$, which can be improved by future experiments. It is found that the branching fractions of $B_c$ decays to the 2S state are smaller than those of the 1S state in our previous study [32] in the perturbative QCD approach. This phenomenon can be understood from the wave functions of the two states. The presence of the node in the 2S wave function, which can be seen in Fig. 1, causes the overlap between the initial and final state wave functions to become smaller. Besides, the tighter phase space and the smaller decay constants of 2S state also suppress their branching ratios.

We also make a comparison of our results with the previous studies. One can see that our results are comparable to those of [49] within the error bars, but larger than the results from other modes. This is because they have used the smaller form factors at maximum recoil. Regardless of this effect, our results are consistent with theirs. For example, as shown in Tables 1 and 2, our values of $A_0$ and $F_0$ are about 2.5 times the results of Ref. [11], and result in our branching ratios to be six times larger than theirs. For a more direct comparison with the available experimental data, we compare the present results in Table 2 with those for the decays of $B_c$ to S-wave charmonium states $J/\psi$ and $\eta _c$ (also based on the harmonic-oscillator wave functions), whose results can be found in Ref. [32], and we obtain the ratios $\mathcal {B}(B_c\rightarrow (\psi (2S) \pi ))/ \mathcal {B}(B_c\rightarrow (J/\psi \pi ))=0.29^{+0.17}_{-0.11}$ and $\mathcal {B}(B_c\rightarrow (\eta _c(2S) \pi ))/\mathcal {B}(B_c\rightarrow (\eta _c \pi )) =0.35^{+0.36}_{-0.29}$. The former is consistent with the data $0.25\pm 0.068\pm 0.014$ [8], and also comparable with the recent prediction of the Bethe–Salpeter relativistic quark model [15], 0.24. This fact may indicate that the harmonic-oscillator wave functions for radially excited states are reasonable and applicable. Although the $B_c\rightarrow \eta _c(2S)\pi$ decay has not yet been measured so far, the predicted large branching ratio ($10^{-3}$) makes it possible to measure it soon at the LHCb experiment or a future facility.

Table 3 The values of decay amplitude from twist-2 and twist-3 charmonium wave functions for $B_c\rightarrow \eta _c(2S)\pi , \psi (2S)\pi$ decays. The results are given in units of $\text {GeV}^3$

We now investigate the relative importance of the twist-2 and twist-3 contributions in Eq. (4) to the decay amplitude, whose results are displayed separately in Table 3, where the label “twist-2 (twist-3)” corresponds to the contribution of the twist-2 (twist-3) distribution amplitude only, while the label “total” corresponds to both of the contributions. It is found that the contribution of the twist-3 distribution amplitude is not power-suppressed for $B_c\rightarrow \eta _c(2S)\pi$ decay, whose contribution is 1.5 times larger than the twist-2 contribution. The reason is that the term $\psi ^s(x_2,b_2)2r$ in Eq. (19) from Fig. 3b gives the dominant contribution to the decay amplitude, since the asymptotic model of the twist-3 distribution amplitude in Eq. (13) for the $\eta _c(2S)$ meson has no factor like $x(1-x)$ to suppress its integral value in the end-point region, which leads to a large enhancement compared with the twist-2 contribution. However, because twist-3 terms of the $\psi (2S)$ meson distribution amplitude do not contribute to the $B_c\rightarrow \psi (2S)\pi$ decay amplitude from Fig. 3b, the contribution from other diagrams with the twist-3 distribution amplitude is only one-fifth smaller than that of the twist-2 contribution in this process. It is also found that there is a very strong interference between contributions of the twist-2 and twist-3 wave functions for both $B_c\rightarrow \psi (2S)\pi$ and $B_c\rightarrow \eta _c(2S)\pi$ decays. The numerical results show that the contributions from the twist-3 wave function have an opposite sign between the two channels. This results in constructive interference for the former, but destructive interference for the latter. The reason is that the amplitudes are different between the two decays at twist-3 level, which can be seen in Eqs. (A1) and (A4) of [32]. A similar situation also exists in $B_c\rightarrow D\pi ,D^*\pi$ [29] decays.

5 Conclusion

We calculated the form factors of the weak $B_c$ decays to radially excited charmonia and the branching ratios of the $B_c\rightarrow \psi (2S)\pi ,\eta _c(2S)\pi$ decays in the pQCD approach. The new charmonium distribution amplitudes based on the radial Schrödinger wave function of the $n=2,l=0$ state for the harmonic-oscillator potential are employed. We discussed theoretical uncertainties arising from the nonperturbative shape parameters, the charm-quark mass, the decay constants, and the scale dependence. It is found that the main uncertainties of the processes concerned come from the shape parameters and the charm-quark mass. The theoretically evaluated ratio $\mathcal {B}(B_c\rightarrow (\psi (2S) \pi )) /\mathcal {B}(B_c\rightarrow (J/\psi \pi ))=0.29^{+0.17}_{-0.11}$ is consistent with the data, which indicates that the harmonic-oscillator wave functions work well, not only for the ground state charmonium, but also for the radially excited charmonia. It is also found that the twist-3 charmonium distribution amplitude gives a large contribution, especially for $B_c\rightarrow \eta _c(2S)\pi$ decay, whose branching fraction is of the order of $10^{-3}$, which could be tested at the ongoing large hadron collider.