1 Introduction

The seminal works on traversable wormholes and thin shell wormholes (TSWs), respectively, by Morris and Thorne [1] and Visser [2] both employed spherical/cylindrical [3, 4] geometry at the throats. Besides instability of TSWs [5–20] and the wormholes supported by ghost scalar field [21, 22] one major problem in this venture is the violation of the null energy condition (NEC). Precisely, TSWs allow presence of exotic matter at the throat with \(\sigma <0\) in which \(\sigma \) is the energy density on the hypersurface of the throat. Several attempts have been made to introduce the TSWs supported by normal matter of the kind with \( \sigma >0\) in the framework of the Gauss–Bonnet theory of gravity [23–27]. We aim in this study to seek for \(\sigma >0\) against violation of NEC by changing the spherical/circular geometry to more general, angle dependent throats in the wormholes. That is, since NEC is violated a different choice of frame may account a negative energy density. Motivation for such a study originates from the consideration of Zipoy–Voorhees metrics which surpasses spherical symmetry with a quadrupole moment by employing a distortion parameter [28–30]. In brief, this amounts to compress a sphere into an ellipsoidal form through a distortion mechanism. This minor change contributes to the total energy and makes it positive in the static reference frame under certain conditions. In local angular intervals we confront still with negative energies in part but the integral of the total energy happens to be positive. We recall that any rotating system with spherical symmetry becomes axial in which by employing a similar refinement of the throat we may construct wormholes with a positive total energy. It is our belief that by this method of suitable choice of geometry at the throat and in a special frame we can measure a positive energy. Recently we have shown [31] that the flare-out conditions [32], which were thought to be unquestionable, can be reformulated. We must admit, however, that although geometry change has positive effects on the energy content this does not guarantee that the resulting wormhole becomes stable. For the particular case of counter-rotational effects in \(2+1\)-dimensional TSW we have shown that stability conditions are slightly improved [33]. That is, when the throat consists of counter-rotating rings in \(2+1\) dimensions the stability of the resulting TSW becomes stronger. This result has not been confirmed in \(3+1\)-dimensional TSWs yet. Arbitrary angle dependent throat geometries have also been considered by the same token recently in \(2+1\) dimensions [34]. Therein a large class of wormholes with non-circular throat shapes are pointed out in which positive energy supports the wormhole. In the same reference we explain also the distinctions (if any) by employing the ordinary time instead of the proper time. Extension of this result to the more realistic \(3+1\) dimensions makes the aim of the present study. Numerical computation of our chosen ansatzes yields a positive total energy, as promised from the outset.

We start with the \(3+1\)-dimensional flat, spherically symmetric line element in which a curved hypersurface is induced to act as our throat’s geometry. Such a hypersurface, \(\Sigma \left( t,r,\theta ,\varphi \right) =0\), has an induced metric satisfying the Einstein equations at the junction with the proper conditions, obeying the flare-out conditions. No doubt, such an ansatz is too general; for this reason they are restricted subsequently. The static case, for instance, eliminates the time dependence in \(\Sigma \left( t,r,\theta ,\varphi \right) =0\). We derive the general conditions for such throats and present particular ansatzes depending on \(\theta \) and \(\varphi \) angles alone that satisfy our constraint conditions.

The organization of the paper goes as follows. In Sect. 2 we present in brief the formalism for TSWs. Static TSWs follow in Sect. 3 where angle dependent constraint conditions are derived. (The details of computations can be found in Appendices A and B.) The paper ends with our conclusion in Sect. 4.

2 Formalism for TSWs

We start with a \(3+1\)-dimensional flat spacetime in spherical coordinates

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+\mathrm{d}r^{2}+r^{2}( \mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\varphi ^{2}) , \end{aligned}$$
(1)

and introduce a closed hypersurface defined by

$$\begin{aligned} \Sigma \left( t,r,\theta ,\varphi \right) =r-R\left( t,\theta ,\varphi \right) =0 \end{aligned}$$
(2)

such that the original spacetime is divided into two parts which will form the inside and outside of the given hypersurface in (2). Now, we get two copies of the outside manifold and glue them at the hypersurface \(\Sigma \left( t,r,\theta ,\varphi \right) =0.\) What is constructed by this procedure is a complete manifold and as introduced first by M. Visser it is called a TSW; its throat turns out to be the closed hypersurface \(r=R\left( t,\theta ,\varphi \right) \) [35–38]. Let us choose \(x^{\alpha }=\left( t,r,\theta ,\varphi \right) \) for the \(3+1\)-dimensional spacetime and \(\xi ^{i}=\left( t,\theta ,\varphi \right) \) for the \(2+1\)-dimensional hypersurface \(\Sigma \left( t,r,\theta ,\varphi \right) =0\). The induced metric tensor of the hypersurface \(h_{ij}\) is defined by

$$\begin{aligned} h_{ij}=\frac{\partial x^{\alpha }}{\partial \xi ^{i}}\frac{\partial x^{\beta }}{\partial \xi ^{j}}g_{\alpha \beta }, \end{aligned}$$
(3)

which yields

$$\begin{aligned} \mathrm{d}s_{\Sigma }^{2}= & {} -( 1-R_{,t}^{2}) \mathrm{d}t^{2}+( R^{2}+R_{,\theta }^{2}) \mathrm{d}\theta ^{2}\nonumber \\&+( R^{2}\sin ^{2}\theta +R_{,\varphi }^{2}) \mathrm{d}\varphi ^{2}+2R_{,t}R_{,\theta }\mathrm{d}t\mathrm{d}\theta \nonumber \\&+2R_{,t}R_{,\varphi }\mathrm{d}t\mathrm{d}\varphi +2R_{,\theta }R_{,\varphi }\mathrm{d}\theta \mathrm{d}\varphi . \end{aligned}$$
(4)

Note that our notation \(R_{,i}\) means partial derivative with respect to \( x^{i}.\) Next, we apply the Einstein equations on the shell, also called the Israel junction conditions [39–43], which are

$$\begin{aligned} k_{i}^{j}-k\delta _{i}^{j}=-8\pi S_{i}^{j}, \end{aligned}$$
(5)

where \(k_{i}^{j}=K_{i}^{j+}-K_{i}^{j-},\) \(k=\mathrm{trace}\left( k_{i}^{j}\right) ,\) \( K_{i}^{j\pm }\) are the extrinsic curvatures of the hypersurface in either sides. \(S_{i}^{j}\) is the energy–momentum tensor on the shell with the components

$$\begin{aligned} S_{i}^{j}=\left( \begin{array}{c@{\quad }c@{\quad }c} -\sigma &{} S_{t}^{\theta } &{} S_{t}^{\varphi } \\ S_{\theta }^{t} &{} p_{\theta }^{\theta } &{} S_{\theta }^{\varphi } \\ S_{t}^{\varphi } &{} S_{\varphi }^{\theta } &{} p_{\varphi }^{\varphi } \end{array} \right) \end{aligned}$$
(6)

where \(\sigma \) is the energy density on the surface and \(S_{i}^{j}\) are the appropriate energy–momentum flux and momentum densities, respectively. Our explicit calculations reveal (see Appendix A)

$$\begin{aligned} k_{tt}&=-\frac{2}{\sqrt{\Delta }}R_{,t,t}\end{aligned}$$
(7)
$$\begin{aligned} k_{\theta \theta }&=-\frac{2}{\sqrt{\Delta }}\left( R_{,\theta ,\theta }-R- \frac{2R_{,\theta }^{2}}{R}\right) \end{aligned}$$
(8)
$$\begin{aligned} k_{\varphi \varphi }&=-\frac{2}{\sqrt{\Delta }} \left( R_{,\varphi ,\varphi }\!-\!R\sin ^{2}\theta \!+\!R_{,\theta }\sin \theta \cos \theta -\frac{2R_{,\varphi }^{2}}{R}\right) ,\end{aligned}$$
(9)
$$\begin{aligned} k_{t\theta }&=-\frac{2}{\sqrt{\Delta }}\left( R_{,t,\theta }-\frac{R_{,\theta }R_{,t}}{R}\right) ,\end{aligned}$$
(10)
$$\begin{aligned} k_{t\varphi }&=-\frac{2}{\sqrt{\Delta }}\left( R_{,t,\varphi }-\frac{ R_{,\varphi }R_{,t}}{R}\right) , \end{aligned}$$
(11)

and

$$\begin{aligned} k_{\theta \varphi }=-\frac{2}{\sqrt{\Delta }}\left( R_{,\theta ,\varphi }- \frac{2R_{,\theta }R_{,\varphi }}{R}-R_{,\varphi }\cot \theta \right) . \end{aligned}$$
(12)

In Appendix B we give the mixed tensor \(k_{i}^{j}\) in closed forms which are also used to determine explicit expressions for the energy–momentum tensor.

3 Static TSWs

Using the general formalism given above and in Appendices A and B we may consider some specific cases. First of all we consider the case in which the throat is static. This means \(R\left( t,\theta ,\varphi \right) =\mathcal {R} \left( \theta ,\varphi \right) \) and consequently the line element on the shell/TSW becomes

$$\begin{aligned} \mathrm{d}s_{\Sigma }^{2}= & {} -\mathrm{d}t^{2}+( \mathcal {R}^{2}+\mathcal {R}_{,\theta }^{2}) \mathrm{d}\theta ^{2} \nonumber \\&+( \mathcal {R}^{2}\sin ^{2}\theta +\mathcal {R}_{,\varphi }^{2}) \mathrm{d}\varphi ^{2}+2\mathcal {R}_{,\theta }\mathcal {R}_{,\varphi }\mathrm{d}\theta \mathrm{d}\varphi . \end{aligned}$$
(13)

The non-zero components of the effective extrinsic curvature tensor are then given as

$$\begin{aligned} k_{\theta \theta }=-\frac{2}{\sqrt{\Delta }}\left( \mathcal {R}_{,\theta ,\theta }-\mathcal {R}-\frac{2\mathcal {R}_{,\theta }^{2}}{\mathcal {R}}\right) , \end{aligned}$$
(14)
$$\begin{aligned} k_{\varphi \varphi }\!=\!-\frac{2}{\sqrt{\Delta }}\left( \mathcal {R}_{,\varphi ,\varphi }-\mathcal {R}\sin ^{2}\theta \!+\!\mathcal { R}_{,\theta }\sin \theta \cos \theta \!-\!\frac{2\mathcal {R}_{,\varphi }^{2}}{ \mathcal {R}}\right) ,\nonumber \\ \end{aligned}$$
(15)

and

$$\begin{aligned} k_{\theta \varphi }=-\frac{2}{\sqrt{\Delta }}\left( \mathcal {R}_{,\theta ,\varphi }-\frac{2\mathcal {R}_{,\theta }\mathcal {R}_{,\varphi }}{\mathcal {R}} -\mathcal {R}_{,\varphi }\cot \theta \right) . \end{aligned}$$
(16)

Finally, in the static configuration, one finds

$$\begin{aligned}&-8\pi \sigma _{0}=\frac{2\left( \mathcal {R}^{2}\sin ^{2}\theta +\mathcal {R} _{,\varphi }^{2}\right) \left( \mathcal {R}_{,\theta ,\theta }-\mathcal {R}- \frac{2\mathcal {R}_{,\theta }^{2}}{\mathcal {R}}\right) }{h\sqrt{\Delta }} \nonumber \\&\quad -\frac{4\mathcal {R}_{,\theta }\mathcal {R}_{,\varphi }\left( \mathcal {R} _{,\theta ,\varphi }-\frac{2\mathcal {R}_{,\theta }\mathcal {R}_{,\varphi }}{ \mathcal {R}}-\mathcal {R}_{,\varphi }\cot \theta \right) }{h\sqrt{\Delta }} \nonumber \\&\quad +\frac{2( \mathcal {R}^{2}+\mathcal {R}_{,\theta }^{2}) }{h\sqrt{ \Delta }} \nonumber \\&\quad \times \left( \mathcal {R}_{,\varphi ,\varphi }-\mathcal {R}\sin ^{2}\theta +\mathcal { R}_{,\theta }\sin \theta \cos \theta -\frac{2\mathcal {R}_{,\varphi }^{2}}{ \mathcal {R}}\right) ,\nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned} 8\pi p_{\theta }^{\theta }= & {} k_{t}^{t}+k_{\varphi }^{\varphi }=\frac{2( \mathcal {R}^{2}+\mathcal {R}_{,\theta }^{2}) }{h\sqrt{\Delta }} \nonumber \\&\times \left( \mathcal {R}_{,\varphi ,\varphi }-\mathcal {R}\sin ^{2}\theta +\mathcal { R}_{,\theta }\sin \theta \cos \theta -\frac{2\mathcal {R}_{,\varphi }^{2}}{ \mathcal {R}}\right) \nonumber \\&-\frac{2\mathcal {R}_{,\theta }\mathcal {R}_{,\varphi }}{h\sqrt{\Delta }} \left( \mathcal {R}_{,\theta ,\varphi }-\frac{2\mathcal {R}_{,\theta }\mathcal { R}_{,\varphi }}{\mathcal {R}}-\mathcal {R}_{,\varphi }\cot \theta \right) ,\nonumber \\ \end{aligned}$$
(18)

an

$$\begin{aligned} 8\pi p_{\varphi }^{\varphi }= & {} k_{t}^{t}+k_{\theta }^{\theta } \nonumber \\= & {} \frac{2\left( \mathcal {R}^{2}\sin ^{2}\theta +\mathcal {R}_{,\varphi }^{2}\right) }{h\sqrt{\Delta }}\left( \mathcal {R}_{,\theta ,\theta }- \mathcal {R}-\frac{2\mathcal {R}_{,\theta }^{2}}{\mathcal {R}}\right) \nonumber \\&-\frac{2\mathcal {R}_{,\theta }\mathcal {R}_{,\varphi }}{h\sqrt{\Delta }} \left( \mathcal {R}_{,\theta ,\varphi }-\frac{2\mathcal {R}_{,\theta }\mathcal { R}_{,\varphi }}{\mathcal {R}}-\mathcal {R}_{,\varphi }\cot \theta \right) .\nonumber \\ \end{aligned}$$
(19)

We note that for the static TSW we have

$$\begin{aligned} \Delta =1+\frac{\mathcal {R}_{,\theta }^{2}}{\mathcal {R}^{2}}+\frac{\mathcal {R }_{,\varphi }^{2}}{\mathcal {R}^{2}\sin ^{2}\theta } \end{aligned}$$
(20)

and

$$\begin{aligned} h=-\mathcal {R}^{2}( \sin ^{2}\theta ( \mathcal {R}^{2}+\mathcal {R} _{,\theta }^{2}) +\mathcal {R}_{,\varphi }^{2}) . \end{aligned}$$
(21)

Having the exact form of \(\sigma _{0}\), we find the total energy which supports the static TSW. This can be done by using the following integral:

$$\begin{aligned} \Omega =\int _{0}^{2\pi }\int _{0}^{\pi }\int _{0}^{\infty }\sqrt{-g}\sigma \delta \left( r-\mathcal {R}\right) \mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi , \end{aligned}$$
(22)

which becomes

$$\begin{aligned} \Omega =\int _{0}^{2\pi }\int _{0}^{\pi }\sigma _{0}\mathcal {R}^{2}\sin \theta \mathrm{d}\theta \mathrm{d}\varphi \end{aligned}$$
(23)

upon using the property of the Dirac delta function \(\delta \left( r- \mathcal {R}\right) \). To make this energy positive we have to consider an appropriate function for \(\mathcal {R}\left( \theta ,\varphi \right) \) and calculate the total energy \(\Omega .\) Particular cases of \(\mathcal {R}\left( \theta ,\varphi \right) \) are considered in the sequel.

3.1 \(\mathcal {R}\left( \theta ,\varphi \right) \) function of \(\theta \) only

Let us make the simpler choice by considering \(\mathcal {R}\left( \theta ,\varphi \right) =\Theta \left( \theta \right) .\) Following this one gets

$$\begin{aligned} \mathrm{d}s_{\Sigma }^{2}=-\mathrm{d}t^{2}+( \Theta ^{2}+\Theta _{,\theta }^{2}) \mathrm{d}\theta ^{2}+\Theta ^{2}\sin ^{2}\theta \mathrm{d}\varphi ^{2}, \end{aligned}$$
(24)

where the only non-zero components of the extrinsic curvature are

$$\begin{aligned} k_{\theta \theta }=-\frac{2}{\sqrt{\Delta }}\left( \Theta _{,\theta ,\theta }-\Theta -\frac{2\Theta _{,\theta }^{2}}{\Theta }\right) \end{aligned}$$
(25)

and

$$\begin{aligned} k_{\varphi \varphi }=-\frac{2}{\sqrt{\Delta }}( -\Theta \sin ^{2}\theta +\Theta _{,\theta }\sin \theta \cos \theta ) . \end{aligned}$$
(26)

Consequently,

$$\begin{aligned} \tilde{\sigma }_{0}&=8\pi \sigma _{0}=\frac{2\left( \frac{\Theta _{,\theta ,\theta }-\Theta -\frac{2\Theta _{,\theta }^{2}}{\Theta }}{\Theta ^{2}+\Theta _{,\theta }^{2}}+\frac{\Theta _{,\theta }\cot \theta -\Theta }{ \Theta ^{2}}\right) }{\sqrt{1+\frac{\Theta _{,\theta }^{2}}{\Theta ^{2}}}},\end{aligned}$$
(27)
$$\begin{aligned} \tilde{p}_{0}&=8\pi p_{\theta }^{\theta }=k_{t}^{t}+k_{\varphi }^{\varphi }= \frac{2( \Theta -\Theta _{,\theta }\cot \theta ) }{\Theta ^{2} \sqrt{1+\frac{\Theta _{,\theta }^{2}}{\Theta ^{2}}}}, \end{aligned}$$
(28)

and

$$\begin{aligned} \tilde{q}_{0}=8\pi p_{\varphi }^{\varphi }=k_{t}^{t}+k_{\theta }^{\theta }=- \frac{2\left( \Theta _{,\theta ,\theta }-\Theta -\frac{2\Theta _{,\theta }^{2}}{\Theta }\right) }{( \Theta ^{2}+\Theta _{,\theta }^{2}) \sqrt{1+\frac{\Theta _{,\theta }^{2}}{\Theta ^{2}}}}. \end{aligned}$$
(29)

One must note that \(r=\Theta \left( \theta \right) \) is the hypersurface of the throat, therefore \(\Theta \left( \theta \right) \) must be chosen such that the surface remains closed. For instance, if we set \(\Theta \left( \theta \right) =a=\mathrm{const.}\) then the throat will be a spherical shell of radius a and \(8\pi \sigma _{0}=-\frac{4}{a}\), which is clearly negative and so is \(\Omega .\) Picking more complicated functions periodic in \(\theta \) is acceptable provided it makes the total energy positive. Here, having \(\sigma _{0}\ge 0\) is a sufficient condition to have \(\Omega \ge 0,\) but not necessary. Our main purpose as we stated in the Sect. 1 is to show that there is possibility of having a TSW supported by ordinary matter in the sense that \(\tilde{\sigma }_{0}\ge 0.\) This condition effectively reduces to

$$\begin{aligned} \frac{\Theta _{,\theta ,\theta }-\Theta -\frac{2\Theta _{,\theta }^{2}}{ \Theta }}{\Theta ^{2}+\Theta _{,\theta }^{2}}+\frac{\Theta _{,\theta }\cot \theta -\Theta }{\Theta ^{2}}\ge 0. \end{aligned}$$
(30)

At this stage we shall not pursue a \(\Theta \left( \theta \right) \) that satisfies this condition.

3.2 \(\mathcal {R}\left( \theta ,\varphi \right) \) function of \(\varphi \) only

As in the previous section, here we consider \(\mathcal {R}\left( \theta ,\varphi \right) =\Phi \left( \varphi \right) \), which yields

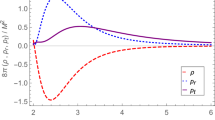
$$\begin{aligned} 8\pi \sigma _{0}=\frac{2\left( \Phi _{,\varphi ,\varphi }-2\Phi \sin ^{2}\theta -\frac{3\Phi _{,\varphi }^{2}}{\Phi }\right) }{( \Phi ^{2}\sin ^{2}\theta +\Phi _{,\varphi }^{2}) \sqrt{1+\frac{\Phi _{,\varphi }^{2}}{\Phi ^{2}\sin ^{2}\theta }}}. \end{aligned}$$
(31)

If we set \(\Phi =a,\) then \(8\pi \sigma _{0}=\frac{-4}{a}\) once more as it should be. It is observed that even with \(\mathcal {R}\left( \theta ,\varphi \right) =\Phi \left( \varphi \right) \) the energy density \(\sigma _{0}\) is a function of both \(\theta \) and \(\varphi .\) In Fig. 1 we plot

$$\begin{aligned} \Phi =\frac{1}{\sqrt{\left| \cos \left( 3\varphi \right) \right| }+1}, \end{aligned}$$
(32)

which implies that \(\sigma _{0}>0\) everywhere. This is what we were looking for, at least in this stage. We also note that the total energy through a numerical computation [given by Eq. (23)] is finite, and more importantly, positive i.e., \(\Omega =22.137.\) This shows that the turning/critical points on the throat do not demand infinite energy and therefore the model can be physically acceptable. This situation is similar to the \(2+1\)-dimensional case, studied in [34].

Fig. 1
figure 1

A plot (left) of a thin shell with the hyperplane equation \(\Phi = \frac{1}{\sqrt{\left| \cos \left( 3\varphi \right) \right| }+1}\), which admits the energy density on the shell to be positive everywhere. The right figure is the opening of the left which shows that the surface is concave out everywhere. It should be added that the sharp edges can be smoothed at the expense of adding negative energy. Since we refrain doing this we have to face differentiability problem at those edges. We note that the total energy is finite in these sharp edges

Full size image

3.3 \(\mathcal {R}\left( \theta ,\varphi \right) \) as a general periodic function

Now, we state the most general condition which is provided by a general periodic function for \(\mathcal {R}\left( \theta ,\varphi \right) .\) As a matter of fact, in (17) we gave in closed form such a \(\sigma _{0}\) and what is left is to provide a proper function for \(\mathcal {R}\left( \theta ,\varphi \right) \) such that \(\sigma _{0}\ge 0.\) Figure 2 is a typical example which admits the energy density \(\sigma _{0}\) positive. In this figure we set

$$\begin{aligned} \mathcal {R}\left( \theta ,\varphi \right) =\frac{1}{( \sqrt{\left| \cos \left( \theta \right) \right| }+1) ( \sqrt{\left| \cos \left( 4\varphi \right) \right| }+1) }, \end{aligned}$$
(33)

which is dependent on one of the two spherical angles. As in Fig. 1, our numerical calculation reveals that the total energy calculated by Eq. (23) is finite and positive i.e., \(\Omega =28.900.\) This shows that the edges of the throat are made of a finite amount of energy which is desired in a physical model.

Fig. 2
figure 2

A plot of a thin shell with the equation \(\mathcal {R}\left( \theta ,\varphi \right) =\frac{1}{\left( \sqrt{\left| \cos \left( \theta \right) \right| }+1\right) \left( \sqrt{\left| \cos \left( 4\varphi \right) \right| }+1\right) }\) in spherical coordinate system. This specific form of throat provides the energy density positive on the throat. Similar problems raised about sharp edges in caption of Fig. 1 are valid also here. The total energy which supports the throat is finite and positive even at the sharp edges energy does not diverge

Full size image

3.4 Existence of solution

In [44] we have shown that for the TSW in \(3+1\) dimensions, \( \sigma \) relates to the trace of extrinsic curvature of spatial part of the Gaussian line element which amounts to

$$\begin{aligned} -8\pi \sigma =k_{\theta }^{\theta }+k_{\varphi }^{\varphi }. \end{aligned}$$
(34)

Therefore for \(\sigma \ge 0\) the spatial extrinsic curvature must be negative, which is why for a positive curvature shape such as a sphere \( \sigma \) is negative. We note that an open surface with negative curvature cannot be an answer to our requirement, because the throat of a TSW is defined to be closed. To show that such shapes i.e., negatively curved but closed, exist, we refer to, for instance, a concave dodecahedron. This is defined as a surface whose faces are concave individually, like the cellular surface of a soccer ball with inside pressure less than outside. In such shapes, although the surface is closed, it consists of negatively curved individual patches in geometry with anti-de Sitter spacetime and hence makes \(\sigma \ge 0.\) Similar argument is also valid in \(2+1\) dimensions which we have considered in [34].

4 Conclusion

The throat geometry for TSWs is taken embedded in \(3+1\)-dimensional flat geometry in spherical coordinates. For static case we obtain the most general angle dependent constraints the functions have to satisfy in order to yield a positive total energy. We must admit that the positivity condition refers to a static frame in which the energy density becomes positive although the NEC remains violated. Specific reduction procedures are given dependent on both \(\varphi ,\) and \(\theta \) and \(\varphi \), which simplify the constraint conditions. Once these constraint conditions are satisfied we shall not be destined to confront exotic matter in TSWs. At least in particular, static frames two particular examples are given which yield positive total energy \(\Omega \), from Eq. (23). We admit also that finding analytically general integrals for functions to satisfy our differential equation constraints does not seem an easy task at all. The details of our technical part are given in the Appendix. The argument/method can naturally be extended to cover more general wormholes, not only the TSWs. One issue that remains open, in all this endeavor which we have not discussed, is the stability of such constructions. A final warning to the traveler who intends to cross the throat: The thin edges may give harmful tidal effects from geometrical point of view, so keep away from those edges if you dream to enjoy a journey at all.