Phenomenology of supersymmetric Z$'$ decays at the Large Hadron Collider

Abstract

I study the phenomenology of heavy neutral bosons $Z'$, predicted in GUT-inspired U(1)$'$ models, at the Large Hadron Collider. In particular, I investigate possible signatures due to $Z'$ decays into supersymmetric particles, such as chargino, neutralino, and sneutrino pairs, leading to final states with charged leptons and missing energy. The analysis is carried out at $\sqrt{s}=14$ TeV, for a few representative points of the parameter space of the Minimal Supersymmetric Standard Model, suitably modified to accommodate the extra $Z'$ boson and consistent with the discovery of a Higgs-like boson with mass around 125 GeV. Results are presented for several observables and compared with those obtained for direct $Z'$ decays into lepton pairs, as well as direct production of supersymmetric particles. For the sake of comparison, $Z'$ phenomenology in an effective supersymmetric extension of the Sequential Standard Model is also discussed.

1 Introduction

Searching for heavy neutral gauge bosons $Z'$ is one of the challenging goals of the experiments performed at the Large Hadron Collider (LHC). In fact, such bosons are predicted in extensions of the Standard Model involving an extra U(1)$'$ gauge group, inspired by Grand Unification Theories (GUTs) (see, e.g., [1, 2] for a review). Furthermore, $Z'$ bosons are also present in the so-called Sequential Standard Model (SSM), where the $Z'$ has the same couplings to fermions as the Standard Model (SM) Z boson. Though not being theoretically motivated, the SSM is often used as a benchmark for the experimental searches.

The LHC experiments have so far searched for high-mass neutral gauge bosons $Z'$ and have set exclusion limits on its mass $m_{Z'}$. In detail, the ATLAS Collaboration [3] set the limits in the range $m_{Z'}>$ 2.90 TeV for a SSM $Z'$ and $m_{Z'}>$ 2.51–2.62 TeV for GUT-inspired U(1)$'$ models. The same numbers for CMS [4] are instead $m_{Z'}>2.90~\hbox {TeV}$ for the SSM and $m_{Z'}> 2.57~\hbox {TeV}$ in U(1)$'$ models. However, such analyses were carried out looking for high-mass dilepton pairs ($e^+e^-$ or $\mu ^+\mu ^-$) and assuming that the $Z'$ has only Standard Model decay modes. Possible decays Beyond the Standard Model (BSM), e.g. in supersymmetric particles, were investigated first in [5] and lately reconsidered in [6–9] within the Minimal Supersymmetric Standard Model [10, 11]. Although SM decays are still dominant and the most promising for the searches, the opening of new channels decreases the branching ratios into electron and muon pairs and therefore the mass exclusion limits. Reference [12], using a representative point of the MSSM parameter space as in [8, 9], found that the LHC exclusion limits decrease by an amount $\Delta m_{Z'}\simeq$ 150–300 GeV, once accounting for BSM decay modes at $\sqrt{s}=8$ TeV.

From the viewpoint of supersymmetry, the lack of evidence of new particles in the LHC runs at 7 and 8 TeV, together with the discovery of a boson with mass $m_h=125.7\pm \,0.4$ GeV [13] and properties consistent with the Standard Model Higgs boson [14, 15], sets some tight constraints on the mass spectra and couplings of possible supersymmetric models. While awaiting the collisions at 13 and ultimately 14 TeV, it is therefore worthwhile thinking of scenarios, not yet excluded by the current searches and compatible with the Higgs discovery, which may deserve some specific analyses at high luminosity and energy. Extending the MSSM via a U(1)$'$ group presents some features which makes it a pretty interesting scenario, so that novel analyses, looking for signals of supersymmetric $Z'$ decays by using current and future data, may be well justified. Unlike direct sparticle production in $q\bar{q}$ or gg annihilation, the $Z'$ is colorless and its mass sets a constraint on the invariant mass of the sparticle pair. Therefore, if one had to discover a $Z'$, its decay modes would be an ideal environment to look for supersymmetry, as they would yield a somewhat cleaner signal, with respect to direct sparticle production. Supersymmetric $Z'$ decays would also be an excellent framework to study electroweak interactions in regions of the phase space which would not be accessible through other processes, such as Drell–Yan interactions. Moreover, possible decays into pairs of the lightest neutralinos of the MSSM would lead to mono-photon or mono-jet final states, like those which are investigated when looking for dark matter candidates.

The reference point of the parameter space chosen in Refs. [8, 9, 12] yielded substantial decay rates into supersymmetric particles and was consistent with the present exclusion limits, but did not take into account for the recent discovery of a Higgs-like boson. In this paper, I shall extend the work in [8, 9] giving some useful benchmarks for possible $Z'$ searches within supersymmetry. First, it will be chosen a set of points in the parameter space yielding a SM-like Higgs boson with a mass around 125 GeV. Then, thanks to the Monte Carlo implementation of the U(1)$'$ models along with the MSSM, a phenomenological analysis will be performed and a few final-state distributions in events with supersymmetric $Z'$ decays will be presented. On the contrary, Refs. [8, 9] only calculated total production cross sections and branching ratios and left the investigation of differential distributions as an open issue. Furthermore, I shall also account for an effective supersymmetric extension of the Sequential Standard Model, denoted by S-SSM hereafter, wherein the couplings of the Z and $Z'$ to supersymmetric particles are the same.

In detail, in Sect. 2 I will briefly review the theoretical framework of the investigation here undertaken, paying special attention to the new features of the MSSM once a $Z'$ boson is included. In Sect. 3 I shall discuss the practical implementation of supersymmetric $Z'$ decays in a few computing codes and Monte Carlo event generators. Sections 4, 5, and 6 will deal with the phenomenology of the $Z'$ in three scenarios, namely the $Z'_\psi$ and $Z'_\eta$ models, within U(1)$'$ gauge theories, and the S-SSM, respectively. Section 7 will contain some final remarks and comments on possible further developments of this work.

2 U(1)$'$ gauge group and minimal supersymmetric standard model

In this section, I shall discuss the theoretical framework of supersymmetric $Z'$ decays, already thoroughly reviewed in [5] and, more recently, in [8, 9]. As discussed in [1, 2], U(1)$'$ groups typically arise from the breaking of a Grand Unification gauge group E$_6$ of rank 6. The neutral boson $Z'_\psi$ is associated with U(1)$'_\psi$, coming from the breaking into SO(10) as follows:

$$\begin{aligned} \mathrm{E}_6\rightarrow \mathrm{SO}(10)\times \mathrm{U}(1)'_\psi . \end{aligned}$$

(1)

The $Z'_\chi$ is instead related to the subsequent breaking of SO(10) according to

$$\begin{aligned} \mathrm{SO}(10)\rightarrow \mathrm{SU}(5)\times \mathrm{U}(1)'_\chi . \end{aligned}$$

(2)

The $Z'_\psi$ and $Z'_\chi$ mix into a generic $Z'(\theta )$ depending on the mixing angle $\theta$:

$$\begin{aligned} Z'(\theta )=Z'_\psi \cos \theta -Z'_\chi \sin \theta . \end{aligned}$$

(3)

The $Z'_\psi$ and $Z'_\chi$ models correspond to $\theta =0$ and $\theta =-\pi /2$, respectively. Another scenario, which is often investigated from both theoretical and experimental viewpoints, is the one, characteristic of superstring theories, where E$_6$ breaks in the Standard Model (SU(2)$_\mathrm{L}\times$ U(1)$_\mathrm{Y}$) and an extra U(1)$'_\eta$:

$$\begin{aligned} \mathrm{E}_6\rightarrow \mathrm{SM}\times U(1)'_\eta . \end{aligned}$$

(4)

Equation (4) leads to a $Z'_\eta$ boson, with a mixing angle $\theta =\arccos \sqrt{5/8}$ in Eq. (3). One can anticipate that the following analysis will be performed for the $Z'_\psi$ and $Z'_\eta$ models, since other models like those leading to the $Z'_\chi$, as well as the $Z_\mathrm{I}$, $Z'_\mathrm{S}$, and $Z'_\mathrm{N}$, corresponding to the mixing angle $\theta$ described in [8, 9], are less interesting, as the $Z'$ branching ratios into supersymmetric final states are rather low.

As far as the MSSM is concerned, a few relevant features are inherited by the presence of the extra $Z'$ boson. In addition to the scalar Higgs doublets $H_d$ and $H_u$ of the MSSM, an extra neutral singlet S is necessary to break the U(1)$'$ gauge symmetry and give mass to the $Z'$. Hereafter, the Higgs bosons will be denoted as follows:

$$\begin{aligned} H_d=\left( \begin{array}{c} H_d^0 \\ H_d^- \end{array}\right) ,\quad H_u=\left( \begin{array}{c}H_u^+ \\ H_u^0 \end{array}\right) ,\quad S=S^0, \end{aligned}$$

(5)

and their vacuum expectation values like $v_d$, $v_u$, and $v_s$, respectively. The Higgs superfields will then contain a Higgsino component as well, i.e. $\tilde{H}_u$, $\tilde{H}_d$, and $\tilde{S}$ fields.

The superpotential of the MSSM, once it is extended by means of a U(1)$'$ group, is then given by [7, 16]

$$\begin{aligned} W=u^c y_u Q H_u-d^c y_d Q H_d-e^c y_e L H_d+\lambda H_uH_dS, \end{aligned}$$

(6)

where, following the notation in [5], $y_{u,d,e}$ are the Yukawa coupling matrices for up- and down-type quarks, Q, and L are the MSSM superfields containing left-handed (s)quarks and (s)leptons, $u^c$, $d^c$, and $e^c$ are the singlet fields of right-handed up-, down-type (s)quarks and (s)leptons, respectively. The trilinear term $\lambda H_uH_dS$ involving all three Higgs superfields, is a feature of the U(1)$'$ extension of the MSSM and gives rise to the well-known $\mu$ term, which can be expressed in terms of $\lambda$ and the vacuum expectation value of S as $\mu =\lambda v_s/\sqrt{2}$.¹

For the analysis which will be hereafter undertaken, the soft supersymmetry-breaking Lagrangian plays a crucial role. It is given by the following expression [5, 16]:

$$\begin{aligned} \mathcal{L}= & {} -\frac{1}{2}(M_3\tilde{g}\tilde{g}+M_2\tilde{W}\tilde{W}+ M_1\tilde{B}\tilde{B}+M'\tilde{B}'\tilde{B}'+\mathrm{h. c.})\nonumber \\&-\,(\tilde{u^c}A_u\tilde{Q} H_u-\tilde{d^c} A_d\tilde{Q}H_d-\tilde{e^c}A_e\tilde{L} H_d+\mathrm{h. c.}) \nonumber \\&-\,\tilde{Q}^\dagger (m^0_Q)^2\tilde{Q}-\tilde{L}^\dagger (m^0_L)^2\tilde{L} -\tilde{u^c}(m^0_{\tilde{u}})^2 {\tilde{u^c}}^\dagger \nonumber \\&-\,\tilde{d^c} (m^0_{\tilde{d}})^2 {\tilde{d^c}}^\dagger -\tilde{e^c}(m^0_e)^2 {\tilde{e^c}}^\dagger \nonumber \\&-\,m_{H_d}^2H_d^\dagger H_d-m_{H_u}^2{H_u}^\dagger H_u-m_S^2 S^\dagger S \nonumber \\&+\,\frac{i}{\sqrt{2}}\lambda A_\lambda (H_d^\dagger \sigma _2H_uS+\mathrm{h.c.}). \end{aligned}$$

(7)

In Eq. (7), $M_3$, $M_2$, and $M_1$ are the soft masses of gluino ($\tilde{g}$), wino ($\tilde{W}$) and bino ($\tilde{B}$) fields of the MSSM, while $M'$ is the mass of $\tilde{B}'$, the supersymmetric partner of $B'$, the gauge boson associated with the U(1)$'$ group. Moreover, $m_{H_u}$, $m_{H_d}$, and $m_S$ are the soft masses of $H_u$, $H_d$, and S in (5), $m^0_Q$, $m^0_L$ and $m^0_{\tilde{f}}$ are the soft masses of the left-handed superfields Q and L, and of the right-handed $\tilde{f}$, respectively. $A_u$, $A_d$, and $A_e$ are the soft trilinear couplings of squarks and sleptons with the Higgs fields, in one-to-one correspondence with the Yukawa couplings in the superpotential (6); one usually writes the trilinear couplings as $A_f=m_fA_{f,0}$, where $A_{f,0}$ is dimensionless. $A_\lambda$ is the soft Higgs trilinear coupling, with $\sigma _2$ being one of the Pauli matrices; the term $\sim \!\lambda A_\lambda H_d^\dagger \sigma _2 H_uS$ is the counterpart in the soft Lagrangian of the trilinear contribution $\lambda H_uH_dS$ in the superpotential. Also, in Eq. (7) $\tilde{Q}$, $\tilde{L}$, $\tilde{u}^c$, $\tilde{d}^c$, and $\tilde{e}^c$ are the squark/slepton components in the left- and right-handed superfields, already introduced in (6).

In the Higgs sector, after electroweak symmetry breaking and giving mass to W, Z, and $Z'$ bosons, one is left with two charged $H^\pm$ and four neutral Higgs bosons, namely one pseudoscalar A and three scalars h, H, and $H'$, where $H'$ is due to the U(1)$'$ gauge group and is typically much heavier than the $Z'$. Furthermore, with respect to the MSSM, two extra neutralinos are present, associated with the supersymmetric partners of $Z'$ and $H'$, for a total of six neutralinos: in [8, 9] it was nevertheless argued that these new neutralinos are typically too heavy to be significant in $Z'$ phenomenology.

In order to reliably compute the sfermion masses, one would need to perform this analysis in a specific scenario for supersymmetry breaking, such as gauge-, gravity- or anomaly-mediated mechanisms. Investigations of supersymmetry-breaking models are beyond the scopes of this paper; it is nevertheless mandatory to recall that supersymmetry can be spontaneously broken if the so-called D-term and/or the F-term in the scalar potential have non-zero vacuum expectation values. The contribution of D- and F-terms to the potential reads

$$\begin{aligned}&V_{D,F}(\phi ,\phi ^*)=F^{*i}F_i+\frac{1}{2}D^aD_a,\quad F_i=\frac{\delta W}{\delta \phi _i},\quad \nonumber \\&D_a=-g_a(\phi _i^*T^a\phi ^i), \end{aligned}$$

(8)

where W is the superpotential, $\phi _i$ are the scalar (Higgs) fields, $g_a$ and $T^a$ the coupling constant and the generators of the gauge groups of the theory. The F-terms are proportional to the particle masses, and therefore they are mostly important for stop quarks; the D-terms are relevant for both light and heavy sfermions and contain two contributions. The first one, already present in the MSSM, is related to the hyperfine splitting due to electroweak symmetry breaking: for a sfermion a, it depends on its weak isospin $T_{3,a}$, electric charge $Q_a$ and weak hypercharge $Y_a$, as well as on the vacuum expectation values of the two MSSM Higgs doublets ($v_1$ and $v_2$):

$$\begin{aligned} \Delta \tilde{m}_a^2= & {} (T_{3,a}g_1^2-Y_ag_2^2)(v_1^2-v_2^2)\nonumber \\= & {} (T_{3,a}-Q_a\sin ^2\theta _W)m_Z^2\cos 2\beta , \end{aligned}$$

(9)

where $g_1$ and $g_2$ are the coupling constants of U(1) and SU(2), respectively, and $\theta _W$ is the Weinberg angle. A second contribution is due to possible extensions of the MSSM, such as the U(1)$'$ group, and is related to the Higgs bosons which break the new symmetry:

$$\begin{aligned} \Delta {\tilde{m}}_a^{\prime 2}=\frac{g'^2}{2}Q'_a(Q_{H_u}'v_u^2+Q_{H_d}'v_{H_d}^2+Q_S'v_S^2), \end{aligned}$$

(10)

where $g'$ is the U(1)$'$ coupling, $Q'_{H_u}$, $Q'_{H_d}$, $Q'_S$ and $Q'_a$ are the U(1)$'$ charges of the Higgs fields $H_u$, $H_d$, and S, and of the sfermion a. As a result, the soft sfermion masses $m^0_f$ in (7) get F- and D-term corrections: as they are not positive definite, one may even be driven to unphysical scenarios, where the sfermion squared mass gets negative (see few examples in Refs. [8, 9]).

In general, sfermion mass eigenstates are obtained by diagonalizing the following mass matrix:

$$\begin{aligned} \mathcal{M}_{\tilde{f}}^2=\left( \begin{array} {c@{\quad }c} (M_{LL}^{\tilde{f}})^2 &{} (M_{LR}^{\tilde{f}})^2\\ (M_{LR}^{\tilde{f}})^2 &{} (M_{RR}^{\tilde{f}})^2 \end{array} \right) , \end{aligned}$$

(11)

where the matrix elements are obtained by summing the squared soft masses in (7) and the D- and F-term corrections. As an example, the matrix elements for down-type squarks are given by

$$\begin{aligned} ( M^{\tilde{d}}_{LL})^2= & {} (m^0_{\tilde{d}_{L}})^2 + m^2_d + \left( -\frac{1}{2}+\frac{1}{3}x_W \right) m_{Z'} ^2\ \cos 2\beta \nonumber \\&+\, \Delta {\tilde{m}}^{\prime 2}_{\tilde{d}_L} \end{aligned}$$

(12)

$$\begin{aligned} (M^{\tilde{d}}_{RR})^2= & {} (m^0_{\tilde{d}_R})^2 + m^2_d - \frac{1}{3} x_W m_{Z'}^2\ \cos 2\beta + \Delta {\tilde{m}}^{\prime 2}_{\tilde{d}_R} \end{aligned}$$

(13)

$$\begin{aligned} ( M^{\tilde{d}}_{LR})^2= & {} m_d\left( A_d - \mu \tan \beta \right) , \end{aligned}$$

(14)

where $x_W=\sin \theta _W^2$, $m^0_{\tilde{d}_{L,R}}$ is the $\tilde{u}_{L,R}$ soft mass at the $Z'$ energy scale and $A_d=m_dA_{d,0}$ is the coupling entering in the Higgs–sfermion interaction term in the soft supersymmetry-breaking Lagrangian. The mixing matrix element $M^{\tilde{d}}_{LR}$ is due to the F-term and, as anticipated, is proportional to the quark mass $m_d$; the expressions for the F- and D-term corrections to the soft mass of up-type squarks and sleptons can be found in [5].

In the following, besides GUT-inspired models, I will also account for the Sequential Standard Model; unlike the U(1)$'$ gauge groups, the SSM is not a real model, but nonetheless it is used by the experimental collaborations as a benchmark for the searches. In fact, if the $Z'$ has the same couplings to the fermions as the Z, the production cross section can be straightforwardly computed as a function of the $Z'$ mass. Following [7–9] I will consider an effective model, named S-SSM in the following, where the $\tilde{Z}'$ is too heavy to be visible at the LHC and the couplings of the $Z'$ to sfermions and gauginos are the same as the Z in the MSSM. In principle, a consistent SSM should be built up along the lines of [17], wherein it was explained that any sequential $Z'$ must be accompanied by another $Z'$ and a longitudinal $W'$. However, employing this improved formulation of the SSM goes beyond the goals of this paper and therefore I shall stick to the approximations in [7–9], with a $Z'_\text {S-SSM}$ coupled to SM and BSM particles like the Standard Model Z.

3 Framework for $Z'$ supersymmetric decays

Hereafter, I will present a phenomenological analysis of $Z'$ production and decay at the LHC, paying special attention to supersymmetric decay modes and comparing the results with those obtained in standard analyses, where only Standard Model channels are allowed. As discussed before, the investigation will be concentrated on the $Z'_\psi$ and $Z'_\eta$ models and, for each scenario, it will be chosen a point in the parameter space not yet excluded by the LHC searches and leading to an interesting phenomenology within supersymmetry. In all cases, I will set the $Z'$ mass to the value

$$\begin{aligned} m_{Z'}=2~\mathrm{TeV} \end{aligned}$$

(15)

and will use the following relation between U(1)$'$ and U(1)$_\mathrm{Y}$ coupling constants $g'$ and $g_1$, typical of GUTs:

$$\begin{aligned} g'=\sqrt{\frac{5}{3}}g_1. \end{aligned}$$

(16)

When dealing with the S-SSM, the $Z'$ coupling constant to fermions will be the same as the Z:

$$\begin{aligned} g_\text {S-SSM}=\frac{g_2}{2\cos \theta _W}. \end{aligned}$$

(17)

In [8, 9] the authors fixed the $Z'$ mass and the MSSM parameters and calculated, either analytically or numerically, particle masses and $Z'$ branching ratios into SM and MSSM final states. However, the computation was carried out at leading order (LO) in the couplings $g_1$, $g_2$, and $g'$; therefore the mass of the lightest MSSM neutral Higgs boson, which roughly plays the role of the Standard Model Higgs, was around the value of the Z mass, i.e. about 90 GeV. In this paper, I shall include higher-order corrections, especially top and stop loops, in such a way to recover a light Higgs mass about 125 GeV. For this purpose, I will make use of the Mathematica package SARAH [18] which calculates the mass matrices by using the renormalization group equations at one loop.² Among the implemented models, SARAH includes the so-called UMSSM, namely the extension of the MSSM through a U(1)$'$ gauge group: the output of SARAH is used as a source code for SPheno [20] to create a precision spectrum generator for the given scenario. Model files in the Universal FeynRules Output (UFO) format [21] are then used by the MadGraph code [22] to generate the hard-scattering process, with $Z'$ production, i.e. $q\bar{q}\rightarrow Z'$, and decay according to the chosen mode. The events are thus written in the Les Houches format and the HERWIG Monte Carlo event generator [23] can provide them with parton showers and hadronization, eventually leading to exclusive final states. The analysis within the S-SSM is somewhat different, since SARAH and SPheno do not contain this benchmark model. A straightforward implementation can nevertheless be achieved within the package FeynRules itself [21], by simply adding to the MSSM code a $Z'$ boson, coupled to SM and BSM particles as the Z in the Standard Model. FeynRules then constructs the UFO model files which can be read by MadGraph and HERWIG to simulate full hadron-level events.

In order to perform a consistent investigation and comparison with previous work in [5, 7–9], few further changes were implemented into SARAH and FeynRules. In SARAH, I added Dirac right-handed neutrinos and sneutrinos, not present in its default version, in order to allow $Z'$ decays into both left- and right-handed neutrino and sneutrino pairs. When modifying SARAH, the mass of the right-handed neutrino is set to zero by default. In the FeynRules implementation of the effective S-SSM, the $Z'WW$ coupling was suppressed: in fact, if one naively assumed that the $Z'$ couples to WW pairs like the Z, on the one hand the decay $Z'\rightarrow WW$ would largely dominate, on the other the unitarity of the theory would be in trouble, because of the enhancement of WW scattering mediated by a $Z'$. A consistent S-SSM, possibly built up along the lines of [17], would not suffer from this drawback.³

In the choice of the working reference point for this investigation, I will make use of the results in [24, 25], wherein the authors determined the regions of the supersymmetric phase space which are not yet excluded by the direct searches and are consistent with a Higgs of 125 GeV, taking care of the limits from flavor physics and Dark Matter searches. Strictly speaking, the results of [24, 25] are obtained for the so-called phenomenological MSSM (pMSSM), which makes a few simplifying assumptions in order to reduce the number of parameters. In detail, the pMSSM assumes that the soft supersymmetry-breaking terms are real, there is no new source of CP violation, we have diagonal matrices for the sfermion masses and trilinear couplings, i.e. no flavor change at tree level, and the same soft masses and trilinear couplings at least for the first two generations of squarks and sleptons at the electroweak scale. The leftover parameters are then the ratio of the MSSM neutral Higgs vacuum expectation values $\tan \beta =v_u/v_d$, the Higgs (higgsino) mass parameter $\mu$, the soft masses of bino and wino $M_1$ and $M_2$, the sfermion masses and the trilinear couplings. As in [5, 8, 9], because of the $Z'$, one has an extra gaugino $\tilde{B}'$, whose soft mass parameter is named $M'$.

For all the scenarios which will be studied, $M_1$, $M'$, $\tan \beta$, and $\mu$ will be set as follows:

$$\begin{aligned} M_1=400~\mathrm{GeV},\ M'=1~\mathrm{TeV},\ \tan \beta =30, \ \mu =200~\mathrm{GeV}. \end{aligned}$$

(18)

Given $M_1$, the wino mass $M_2$ can be obtained by using the relation $M_2=(3/5)\cot ^2\theta _W\simeq 827$ GeV.

Furthermore, in the Standard Model it is well known that bottom and especially top quarks play a fundamental role in Higgs phenomenology: in fact, heavy-quark loops give the highest corrections to the Higgs mass and the largest contribution to the Higgs production cross section in gluon fusion. It is therefore obvious that in the MSSM stops and sbottoms, the supersymmetric partners of top and bottom quarks, will deserve special attention and, although they have not been observed, the measured mass of the Higgs boson sets some constraints on their masses. In fact, they can be very heavy, i.e. their mass in the TeV range, but even quite light, say of the order of a few hundred GeV, provided that the mixing is large, i.e. the mixing parameter $A_t$ is about a few TeV (see, e.g., the discussion in [26]). The latter case is often chosen in the supersymmetry studies, namely the first two squark generations heavier than sbottoms and stops. In this paper, I shall consider both possibilities: all three squark generations heavy and degenerate, as well as the option of lighter stops and sbottoms. The authors of [24] define the mixing parameter:

$$\begin{aligned} x_t=A_t-\mu \cot \beta , \end{aligned}$$

(19)

which runs in the range $0<x_t<\sqrt{6}~M_S$, $M_S$ being the geometrical average of the stop masses, i.e. $M_S=\sqrt{m_{\tilde{t}_1}m_{\tilde{t}_2}}$, where $m_{\tilde{t}_1}$ and $m_{\tilde{t}_2}$ are obtained after adding to the soft mass $m_{\tilde{t}}^0$ the D-term (see [5]) and diagonalizing the stop mixing matrix.

In Eq. (19), $A_t$ is a dimensionful quantity related to the dimensionless trilinear coupling $A_{t,0}$ in [8, 9] via $A_t=A_{t,0} m_t$, where $m_t$ is the top quark mass, fixed to $m_t=173$ GeV. For $x_t=4$ TeV, one obtains that, using the numbers in (18), $A_t\simeq 4$ TeV and $A_{t,0}\simeq 23.2$. Later on, all the trilinear couplings, as well as $A_\lambda$, contained in the soft supersymmetry-breaking Lagrangian (7), will be set the same value:⁴

$$\begin{aligned} A_q=A_\ell =A_\lambda \simeq 4~\mathrm{TeV}. \end{aligned}$$

(20)

In the following sections, I shall present the results yielded at the LHC by the models U(1)$'_\psi$, U(1)$'_\eta$, and S-SSM. As in [8, 9], a few decay chains will be taken into account: they all start with a primary supersymmetric decay, e.g. into pairs of charged sleptons, sneutrinos, charginos or neutralinos, and eventually yield final states with two or four charged leptons and missing transverse energy (MET), associated with neutrinos or light neutralinos. For each model, I will consider a specific point in the parameter space, with the goal of maximizing the branching ratio in at least one of the supersymmetric modes. Then I shall present some leptonic final-state distributions, in the scenario which maximizes the BSM $Z'$ decay rate. Whenever it makes sense, the results will be confronted with those from the standard search strategies, where the $Z'$ decays into a SM charged-lepton pair and has no BSM decay width.

4 Phenomenology: U$(1)'_\psi$ model

The model U(1)$'_\psi$, leading to a heavy boson $Z'_\psi$, corresponds to a mixing angle $\theta =0$ in Eq. (3). In [8, 9], it was found that, in a reference point of the parameter space and for a $Z'_\psi$ mass between 1 and 5 TeV, about 35 % of the $Z'_\psi$ width is due to the supersymmetric modes. However, as discussed above, that scenario was not consistent with a Higgs mass of 125 GeV and the supersymmetric mass spectrum was computed only at tree level: such approximations will be relaxed in the present analysis.

Hereafter, the representative points of the parameter space will be chosen in order to satisfy the Higgs mass constraint and the supersymmetry exclusion limits. The quantities $M_1$, $M'$, $\mu$ and $\tan \beta$ are fixed as in Eq. (18); as for sfermions, I assume that sleptons, as well as the first two generations of squarks, are degenerate at the $Z'_\psi$ mass scale and have mass:⁵

$$\begin{aligned} m_{\tilde{\ell }}^0=m_{\tilde{\nu }_\ell }^0=1.2~\mathrm{TeV},\ m^0_{\tilde{q}}=5.5~\mathrm{TeV}, \end{aligned}$$

(21)

where $\ell =e,\mu ,\tau$, $\nu =\nu _e,\nu _\mu ,\nu _\tau$, and $q=u,d,c,s$. The soft masses of stops and sbottoms are instead fixed as follows:

$$\begin{aligned} m^0_{\tilde{t}}=m^0_{\tilde{b}}=2.2~\mathrm{TeV}. \end{aligned}$$

(22)

The sfermion masses at the $Z'_\psi$ mass scale are obtained after summing to the numbers in (21) and (22) the F- and D-terms due to U(1)$'$ and electroweak symmetry breaking; at leading order, the masses yielded by the SARAH code agree with those computed by using the expressions in [5]. For $m_{Z'}=2$ TeV, the sfermion masses are quoted in Tables 1 and 2, for squarks and sleptons, respectively. The notation $\tilde{q}_{1,2}$, $\tilde{\ell }_{1,2}$, and $\tilde{\nu }_{1,2}$ refers to the mass eigenstates, which differ from the gauge ones $\tilde{q}_{L,R}$, $\tilde{\ell }_{L,R}$, and $\tilde{\nu }_{L,R}$ because of the mixing; such mixing terms are proportional to the fermion squared masses, and therefore they are mostly relevant in the case of the stops. From such tables, one can learn that the impact of the D-term is about 100 GeV on squarks and even larger than 200 GeV on sleptons; also, in the chosen reference point, the D-term can be either positive or negative.

Table 1 Masses of squarks in the MSSM, for the chosen reference point and accounting for the U$(1)'_\psi$ modifications. The masses of $\tilde{q}_{1,2}$ differ from those of the gauge eigenstates $\tilde{q}_{L,R}$ because of the mixing contribution, relevant especially in the stop case. All numbers are expressed in GeV

Table 2 As in Table 1, but for charged sleptons ($\ell =e,\mu$) and sneutrinos

The Higgs masses, computed by SARAH to one-loop accuracy, are reported in Table 3: the lightest scalar h has roughly the same mass as the SM-like Higgs boson, H is approximately as heavy as the $Z'_\psi$, whereas $H'$, A, and the charged $H^\pm$ are above 4 TeV, and therefore too heavy to be significant for $Z'_\psi$ phenomenology. The $\lambda$ parameter, contained in the trilinear potential $V_\lambda$, is related to $\mu$ and the vacuum expectation value $v_S$ of the extra Higgs boson S via $\lambda =\sqrt{2}\mu /v_S\simeq 5.4\times 10^{-2}$. Table 4 contains the masses of the two charginos ($\tilde{\chi }^\pm _{1,2}$) and of the six neutralinos ($\tilde{\chi }^0_1,\dots ,\tilde{\chi }^0_6$): in principle, with the exception of $\tilde{\chi }^0_6$, whose mass is even above 6 TeV, several $Z'_\psi$ decay modes into pairs of charginos and neutralinos are kinematically permitted.

Table 3 Masses of neutral and charged Higgs bosons in GeV in the chosen point of the MSSM extended by means of the U$(1)'_\psi$ gauge model

Table 4 Masses of charginos and neutralinos in the reference point for the $Z'_\psi$ model

Given the numbers in Tables 1, 2, 3, and 4, one can calculate, by means of the SPheno program, the branching ratios of the $Z'_\psi$ into Standard Model and supersymmetric final states. At leading order in $g'$, i.e. $\mathcal{O}(g'^2)$, the main $Z'_\psi$ branching ratios are quoted in Table 5, for $m_{Z'}=2$ TeV and omitting decay rates which are below 0.1 %. The Standard Model decays are still the dominant ones, but one has an overall 28.3 % branching ratio into supersymmetric final states, which deserves further investigation. In particular, the decay into chargino pairs $\tilde{\chi }^+_1\tilde{\chi }^-_1$ accounts for about 10 %, whereas the ratios into neutralino pairs vary from 0.2 % ($\tilde{\chi }_1^0\tilde{\chi }_3^0$) to 8 % ($\tilde{\chi }_4^0\tilde{\chi }_4^0$). Decays into pairs of the lightest neutralinos, i.e. $\tilde{\chi }^0_1\tilde{\chi }^0_1$, possibly relevant for the searches for Dark Matter candidates, have non-negligible branching ratio, accounting for about 5 %.

Table 5 $Z'_\psi$ decay rates for $m_Z'=2$ TeV

Since the highest BSM rate is the one into chargino pairs, it is worthwhile carrying out the phenomenological analysis for final states originated from a $Z'_\psi \rightarrow \tilde{\chi }_1^+\tilde{\chi }_1^-$ process. As discussed in [8, 9], primary decays into chargino pairs can lead to a chain yielding charged leptons and missing energy in the final states. To gauge the rates of the different final states, one must compute the branching ratios of the 2- and 3-body decays of the charginos $\tilde{\chi }^\pm _1$: these numbers, calculated by means of SPheno, are quoted in Table 6.

Table 6 Chargino $\tilde{\chi }_1^+$ decay rates in the reference point for the $Z'_\psi$ model

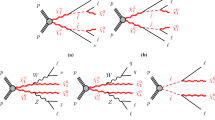
As hadronic final states are likely affected by large QCD backgrounds, I shall focus on the modes with neutralinos and leptons, which will eventually lead to the following decay chain:

$$\begin{aligned} pp\rightarrow Z'_\psi \rightarrow \tilde{\chi }_1^+\tilde{\chi }_1^-\rightarrow (\tilde{\chi }_1^0\ell ^+\nu _\ell )(\tilde{\chi }_1^0\ell ^-\bar{\nu }_\ell ), \end{aligned}$$

(23)

with $\ell =\mu ,e$. The neutrinos and neutralinos in (23) will give rise to some missing energy; the diagram of such a process is presented in Fig. 1. The U(1)$'_\psi$/MSSM masses and coupling constants, in the UFO format, can be used by MadGraph to generate parton-level events and then by HERWIG to simulate showers and hadronization. The cross section for the process $pp\rightarrow Z'_\psi$, computed by MadGraph at LO, by using the CTEQL1 set [27] for the initial-state parton distributions, is $\sigma (pp\rightarrow Z'_\psi )\simeq 0.13$ pb. The cross section for the decay chain (23) is then given by $\sigma (pp\rightarrow Z'_\psi \rightarrow \ell ^+\ell ^- +\mathrm {MET})\simeq 7.9\times 10^{-4}$ pb at 14 TeV. This means that such events can be, e.g., about 80 for a luminosity $\mathcal{L}\simeq 100~\mathrm{fb}^{-1}$, almost 240 at 300 fb$^{-1}$, and so on. Though being less likely than SM channels, supersymmetric decays are nevertheless pretty interesting, since, unlike direct production of squark, slepton, and gaugino pairs in pp collisions, the final state with two charginos decaying in two charged leptons and two neutrinos has a fixed invariant mass.

Fig. 1

Final state with two charged leptons and missing energy, due to neutrinos and neutralinos, through a primary decay of the $Z'$ into a chargino pair

In the following, I will present some relevant leptonic distributions and compare them with those from direct decays $Z'_\psi \rightarrow \ell ^+\ell ^-$, accounted in the LHC searches for $Z'$ bosons carried out so far. Furthermore, the final state in process (23) can even occur in events with direct chargino production, i.e.

$$\begin{aligned} pp\rightarrow \tilde{\chi }_1^+\tilde{\chi }_1^-\rightarrow (\tilde{\chi }_1^0\ell ^+\nu _\ell )(\tilde{\chi }_1^0\ell ^-\bar{\nu }_\ell ), \end{aligned}$$

(24)

which represent a sort of supersymmetric background for the events initiated by a $Z'_\psi$ decay. In the chosen reference point, the LO cross section for direct $\tilde{\chi }^+_1\tilde{\chi }^-_1$ production is $\sigma (pp\rightarrow \tilde{\chi }^+_1\tilde{\chi }^-_1)\simeq 0.2$ pb; accounting for the chargino branching ratios into neutralinos and leptons (muons and electrons), the rate of the process (24) is then given by $\sigma \simeq 1.15\times 10^{-2}$ pb, higher than in the chain (23). Before presenting some distributions and comparisons, one can anticipate that, while in processes like (23) the chargino-pair invariant mass is forced to reproduce $m_{Z'}$, in (24) the charginos do not have this constraint and can therefore be very soft: the kinematics of the leptons produced in chargino decays will in fact reflect this property.

Figure 2 presents the transverse momentum spectrum of leptons produced in all three processes: $Z'_\psi \rightarrow \ell ^+\ell ^-$ $Z'_\psi \rightarrow \tilde{\chi }^+_1\tilde{\chi }^-_1$, i.e. Eq. (23), and direct chargino-pair production, like in Eq. (24). Since the kinematics of $\ell ^+$ and $\ell ^-$ is symmetric, the histograms contain the $p_T$ of both leptons. For direct production (Fig. 2, left), the $p_T$ distribution starts to be non-negligible for $p_T>200$ GeV, i.e. about $m_{Z'}/10$, then increases and reaches a peak about $p_T\simeq m_{Z'}/2=1$ TeV; above 1 TeV the spectrum rapidly decreases. In the case of the decay chain (23), the lepton transverse momentum has a completely different behavior: there are nearly no events below $p_T\simeq 8$ GeV, then the spectrum increases, reaches its peak at $p_T\,\simeq 15$ GeV and smoothly decreases, being negligible for $p_T>60$ GeV. For direct chargino production, i.e. Eq. (24), the lepton $p_T$ distribution is mostly concentrated in the range $0<p_T<20$ GeV, exhibiting a sharp peak about 5 GeV. The observed $p_T$ spectra can easily be understood: for direct $Z'_\psi \rightarrow \ell ^+\ell ^-$, the two leptons get the full initial-state transverse momentum and therefore the $p_T$ spectrum is substantial at high values, whereas, in the case of the cascades (23) and (24), a consistent (missing) $p_T$ is lent to neutrinos and neutralinos, which significantly decreases the $p_T$ of $\ell ^+$ and $\ell ^-$. In particular, for direct charginos (24) there is no cutoff on the invariant mass of $\chi ^+_1\chi ^-_1$ pairs, which can therefore be very soft, thus yielding mostly low-$p_T$ leptons. When the charginos come from $Z'$ decays, $m_{Z'}$ is a constraint on their invariant mass, shifting the lepton transverse momentum to higher values with respect to those produced in (24).

Fig. 2

Lepton transverse momentum for the $Z'_\psi$ model at $\sqrt{s}=14$ TeV and $m_{Z'}=2$ TeV, for a direct $Z'_\psi \rightarrow \ell ^+\ell ^-$ decay (left) and chains initiated by $Z'_\psi \rightarrow \tilde{\chi }^+_1\chi ^-_1$ or direct chargino production processes (right)

In Fig. 3 one can instead find the $\ell ^+\ell ^-$ invariant mass $m_{\ell \ell }$ (left) and the angle $\theta$ between the two charged leptons in the laboratory frame (right). The invariant mass is plotted only for the cascades (23) and (24), since, for direct $Z'_\psi \rightarrow \ell ^+\ell ^-$, it would just be a narrow resonance with the same mass and width as the $Z'_\psi$. In the cascade (23), $m_{\ell \ell }$ varies essentially in the range 20 GeV $<m_{\ell \ell }<$ 100 GeV and has its maximum value about $m_{\ell \ell }\simeq 45$ GeV. For direct chargino production, $m_{\ell \ell }$ is peaked about 5 GeV and rapidly decreases, so that there are nearly no events for $m_{\ell \ell }> 30$ GeV: as observed before for the purpose of the $p_T$ distribution, processes like (24) are dominated by soft charginos and therefore $\ell ^\pm$ are substantially produced at small $m_{\ell \ell }$.

Fig. 3

Left $\ell ^+\ell ^-$ invariant-mass distribution of charged-lepton pairs in the events (23) and (24). Right angle between the two leptons $\ell ^\pm$ in the laboratory frame for direct $Z_\psi '\rightarrow \ell ^+\ell ^-$ production (dashes) and after the decay chains (23) (solid) and (24) (dots)

As for the $\theta$ spectrum (Fig. 3, right), for direct $Z'_\psi \rightarrow \ell ^+\ell ^-$ production it exhibits a maximum about $\theta \simeq 3$, a value close to back-to-back production, i.e. $\theta =\pi$. When the leptons are accompanied by missing energy in $Z'_\psi \rightarrow \tilde{\chi }^+_1\tilde{\chi }^-_1$ events, the $\theta$ distribution is broader; it lies above the direct-production spectrum at small and middle angles, below at high $\theta$, and is peaked at a lower $\theta \simeq 2.75$. The angular distribution of charged leptons in the chain (24) is instead completely different: since there is no cutoff imposed by the $Z'$ mass, $\ell ^+$ and $\ell ^-$ are essentially produced at small angles and the $\theta$ spectrum is pretty broad, being peaked about $\theta \simeq \pi /6$ and negligible for back-to-back leptons.

Figure 4 presents the $\ell ^\pm$ rapidity distributions: the $\eta$ spectrum for leptons originated from the supersymmetric cascade (23) has the highest fraction of leptons with $\eta \sim 0$, corresponding to production perpendicular to the beam axis, and the lowest at large $|\eta |$, i.e. small angles with respect to the beam. The $\eta$ distribution in direct chargino production, i.e. process (24), is instead the lowest at small $|\eta |$ and the highest at large $|\eta |$; for direct lepton production in $Z'_\psi$ decays, it lies between the other two distributions. As observed for the $\theta$ spectra, such a behavior can easily be understood in terms of the kinematics of the processes which have been investigated: in $Z'\rightarrow \ell ^+\ell ^-$ the production is dominantly back-to-back, whereas in Eq. (24) the leptons are substantially collinear to the beam axis.

Fig. 4

Lepton rapidity distributions for standard $Z'_\psi$ decays into lepton pairs (dashes) and in the supersymmetric cascades in Eqs. (23) (solid histogram) and (24) (dots)

Figure 5 presents the differential distributions of two observables which are typically studied in supersymmetry searches: the sum of the transverse momenta of ‘invisible’ particles like neutrinos and neutralinos, also called MET (missing transverse energy), and the transverse mass $m_T$ of all final-state particles (neutrinos, neutralinos, and charged leptons) in the decay chains (23) and (24). They are defined as follows:

$$\begin{aligned}&\mathrm{MET}=\sqrt{\left( \sum _i p_{x,i}\right) ^2+ \left( \sum _i p_{y,i}\right) ^2},\quad i=\nu ,\bar{\nu }, \tilde{\chi }^0_1; \nonumber \\&m_T=\sqrt{\left( \sum _jE_{T,j}\right) ^2-\left( \sum _j\mathbf {p}_{T,j}\right) ^2},\quad \nonumber \\&E_{T,j}=\sqrt{m_j^2+p_{T,j}^2} ,\, j=\ell ^+,\ell ^-,\nu ,\bar{\nu },\tilde{\chi }^0_1. \end{aligned}$$

(25)

In both processes (23) and (24), the MET spectrum is significant in the low range: in the chain (23), it is sharply peaked at MET $\simeq 20$ GeV and smoothly decreases, vanishing for MET $>300$ GeV. For direct chargino production, the MET exhibits an even sharper peak at MET $\simeq 10$ GeV and decreases very rapidly, so that it is negligible above 200 GeV.

Fig. 5

Left missing transverse energy due to the neutrinos and neutralinos in the cascade initiated by a primary $Z'_\psi \rightarrow \tilde{\chi }^+_1\tilde{\chi }^-_1$ decay (solid histogram) and for direct chargino production (dashes). Right transverse mass for the final-state particles (leptons, neutrinos and neutralinos) in the reactions (23) (solid) and (24) (dashes)

The transverse mass distribution exhibits instead a completely different behavior for processes (23) and (24). In (24), leptons and neutralinos are likely rather soft and collinear with respect to the beam and therefore the transverse mass of the final state is substantial only at small $m_T$: it is peaked around $m_T\simeq$ 500 GeV and vanishes above 1 TeV. The chain (23) is initiated by a $Z'_\psi$ with mass 2 TeV: the transverse mass is thus relevant in the range $m_{Z'}/2<m_T<m_{Z'}$ and maximum at $m_T\simeq 1.8$ TeV, just below the $Z'_\psi$ mass threshold.

Before moving to the investigation of direct decays into light neutralinos, I wish to point out that, as a result of the study so far carried out for a few observables, plotted in Figs. 2, 3, 4, and 5, final states initiated by $Z'_\psi$ decays into charginos can be safely discriminated from those coming from direct decays into lepton pairs, as well as from direct chargino production. The last finding is not trivial, since the final states of processes (23) and (24) are the same and, in principle, direct chargino production would have been a background for supersymmetric signals in $Z'_\psi$ decays.

Since the branching ratio into neutralino pairs $\tilde{\chi }^0_1\tilde{\chi }^0_1$ is almost 5 %, even the process

$$\begin{aligned} pp\rightarrow Z'_\psi \rightarrow \tilde{\chi }^0\tilde{\chi }^0_1 \end{aligned}$$

(26)

has a substantial cross section, i.e. $\sigma (pp\rightarrow Z'_\psi \rightarrow \tilde{\chi }^0_1\tilde{\chi }^0_1)\simeq 6.4\times 10^{-3}$ pb at $\sqrt{s}=14$ TeV, which yields about 640 events at $\mathcal{L}=100$ fb$^{-1}$ and up to almost $2\times 10^3$ at 300 fb$^{-1}$. In fact, unlike charginos, the lightest neutralinos are stable particles in the MSSM, and therefore the cross section of the process (26) does not get any further branching fraction which possibly dilutes the event rate. Therefore, the U(1)$'_\psi$ extension of the MSSM could be an interesting scenario to search for Dark Matter candidates in the 14 TeV run of the LHC. The typical signature is given by mono-photon or mono-jet final states, with the photon and jet being associated with initial-state radiation from the incoming quarks. The actual implementation of photon isolation criteria or jet-clustering algorithms goes beyond the scopes of this paper and will not debated here.

Competing processes, leading to final states with just missing energy, are $Z'_\psi$ decays into neutrino pairs, amounting to about $\sigma (pp\rightarrow Z'_\psi \rightarrow \nu \bar{\nu })\simeq 1.1\times 10^{-2}$ pb at 14 TeV, with $\mathcal{O}(10^3)$ events at 100 and 300 fb$^{-1}$. Figure 6 displays the total missing transverse energy (MET) spectrum and the contribution due to the neutrino and neutralino pairs in $Z'_\psi$ decays; unlike previous distributions, they are normalized to the total LO cross section and not to unity, in such a way to appreciate the discrepancy between the two subprocesses. All plots are peaked at $\mathrm{MET}\simeq 10$ GeV and smoothly decrease, up to the point of being quite negligible for $\mathrm{MET}> 300$ GeV. The shapes of both neutrino- and neutralino-induced spectra are very similar, which is quite reasonable since the $\tilde{\chi }^0_1$ particles, though being massive, are still much lighter than the decaying $Z'_\psi$. Nevertheless, the total number of events at any MET value is substantially higher, by about 60 %, if neutralinos contribute.

Fig. 6

Missing transverse energy in $Z'_\psi$ decays: plotted are the neutralino (dashes), neutrino (dots) and total (solid) contributions to the missing transverse energy

5 Phenomenology: U$(1)'_\eta$ model

The model U$(1)'_\eta$ corresponds to a mixing angle $\theta =\arccos {\sqrt{5/8}}$ and, even in the reference point considered in [8, 9], gives rise to an interesting $Z'_\eta$ phenomenology within supersymmetry, the BSM channels accounting for about 1/4 of the total width. In the following, though keeping the constraints due to the Higgs mass and direct supersymmetry searches, I shall choose a slightly different representative point of the parameter space, with respect to the previous U$(1)'_\psi$ model, in order to enhance supersymmetric decays. In particular, the $Z'_\eta$ will still have mass $m_{Z'}=2$ TeV, $M_1$, $M_2$, $M'$, $\tan \beta$, $\mu$, $A_q$, $A_\ell$, and $A_\lambda$ will be set to the values in Eqs. (18) and (20), like in the $Z'_\psi$ scenario, whereas all three generations of squarks and sleptons will be degenerate at the $Z'_\eta$ scale, with masses equal to the following values:

$$\begin{aligned} m_{\tilde{\ell }}^0=m_{\tilde{\nu }_\ell }^0=1.5~\mathrm{TeV},\quad m^0_{\tilde{q}}=3~\mathrm{TeV}, \end{aligned}$$

(27)

where $q=u,d,c,s,t,b$ and $\ell =e,\mu ,\tau$. After adding the D-term, the masses of squarks and sleptons are quoted in Tables 7 and 8, and exhibit a substantial impact of the D-term. The squark masses increase or decrease by few hundred GeV, whereas $\tilde{\ell }_2$ and $\tilde{\nu }_1$ get slightly heavier, $m_{\tilde{\ell }_2}$ a bit lower and $\tilde{\nu }_2$ considerably lighter, by about 850 GeV. This is therefore an example of negative D-term; in fact, in [8, 9], negative and large D-terms had even led to the exclusion of a few $Z'$ models, since some sfermion squared masses had become negative. Table 9 contains the masses of the Higgs bosons, which are rather similar to those obtained for the $Z'_\psi$ case: $m_h\simeq 125$ GeV, $m_H\simeq m_{Z'}$, with $H'$, A, and $H^+$ above 4 TeV. With those numbers for the Higgs boson, the $\lambda$ parameter in the trilinear potential $V_\lambda$ is now equal to $\lambda =\sqrt{2}\mu /v_3\simeq 4.3\times 10^{-2}$. Chargino and neutralino masses are reported in Table 10: $\tilde{\chi }^\pm _1$, $\tilde{\chi }^\pm _2$, and the first four neutralinos ($\tilde{\chi }^0_1\dots \tilde{\chi }^0_4$) are roughly as heavy as those in the $Z'_\psi$ model previously considered; $\tilde{\chi }^0_5$ and $\tilde{\chi }^0_6$ have masses above 1.5 and 2.5 TeV, respectively, and they are therefore negligible for $Z'_\eta$ phenomenology in this scenario.

Table 7 Masses in GeV of the squarks in the $Z'_\eta$ model in the representative point of the parameter space, for a soft mass $m^0_{\tilde{q}}=3$ TeV and $m_{Z'}=2$ TeV

Table 8 Masses of sleptons in the $Z'_\eta$ scenario, with a soft term $m^0_{\tilde{\ell }}=m_{\tilde{\nu }}=1.3$ TeV. All numbers are in GeV and $\ell =e,\mu$

Table 9 Higgs bosons in the $Z'_\eta$ model, with masses expressed in GeV

Table 10 Masses in GeV of charginos and neutralinos in the $Z'_\eta$ model

Table 11 presents the branching ratios of the $Z'_\eta$ into the most significant decay channels: the Standard Model modes are still the most relevant, with the supersymmetric channels accounting for about 21 % of the total width. Among the supersymmetric channels, sneutrino pairs $\tilde{\nu }_2\tilde{\nu }_2^*$ exhibit the highest rate, slightly below 10 % after adding up all three flavors; the decay into $\tilde{\chi }^+_1\tilde{\chi }^-_1$ accounts for about 6 %, into neutralino pairs for another 5 %.

Table 11 $Z'_\eta$ decay rates in the MSSM reference point for a mass $m_{Z'}=2$ TeV

As done for the previous model, the phenomenological analysis will be undertaken for the supersymmetric mode with the highest branching ratio, i.e. $Z'_\eta \rightarrow \tilde{\nu }_2\tilde{\nu }_2^*$. In the notation used in this paper, $\tilde{\nu }_2$ is the supersymmetric partner of the $\nu _2$, which, after the mixing, is mostly a right-handed neutrino. The sneutrinos decay into neutrinos $\nu _2$ and neutralinos, with branching ratios given in Table 12: the highest rates are into neutralino–neutrino pairs $\tilde{\chi }_3^0\nu _2$ and $\tilde{\chi }_2^0\nu _2$. In order to discriminate among the final states yielded by these two decay modes, one needs to evaluate, by using SPheno, the rates of the neutralinos $\tilde{\chi }^0_3$ and $\tilde{\chi }^0_2$: they are quoted in Tables 13 and 14, respectively.

Table 12 Sneutrino $\tilde{\nu }_2$ branching ratios, in the representative point of the $Z'_\eta$ model, where $m_{\tilde{\nu }_2}\simeq 456$ GeV

Table 13 Branching ratios of the neutralino $\tilde{\chi }^0_3$ in the representative point of the $Z'_\eta$ model

Table 14 As in Table 13, but for the lighter neutralino $\tilde{\chi }^0_2$

Because of its higher mass, the neutralino $\tilde{\chi }_3^0$ is capable of decaying according to $\tilde{\chi }^0_3\rightarrow \tilde{\chi }_1^\pm W^\mp$, with a branching fraction about 56 %; the other main channels are $\tilde{\chi }^0_{1,2}h$ and $\tilde{\chi }^0_{1,2}Z$ pairs, accounting for about 20 and 23 %, respectively. As for $\tilde{\chi }^0_2$, it undergoes decays into the lightest $\tilde{\chi }_1^0$ and a pair of quarks, charged leptons or neutrinos, through an intermediate charged slepton $\tilde{\ell }^\pm$, with branching ratios varying from about 63 to 13 %, as quoted in Table 14.

As a result, in order to end up with a final state with leptons and missing energy, and considering only electrons and muons, one has

$$\begin{aligned}&\mathrm{B}(\tilde{\nu }_2\rightarrow \tilde{\chi }^0_2\nu _2)\times \mathrm{B}(\tilde{\chi }^0_2\rightarrow \tilde{\chi }^0_1\ell ^+\ell ^-) \simeq 3.3\,\%,\\&\mathrm{B}(\tilde{\nu }_2\rightarrow \tilde{\chi }^0_3\nu _2)\times \mathrm{B}(\tilde{\chi }^0_3\rightarrow \tilde{\chi }_1^\pm W^\mp )\times \mathrm{B}(\tilde{\chi }_1^\pm \rightarrow \tilde{\chi }^0_1\ell ^\pm \nu _\ell )\nonumber \\&\qquad \times \, \mathrm{B}(W^\mp \rightarrow \ell ^\mp \nu _\ell ) \simeq 3.0\,\%.\nonumber \end{aligned}$$

(28)

From Eq. (28) one learns that, although the decay $\tilde{\nu }_2\rightarrow \tilde{\chi }^0_3\nu _2$ is more probable than $\tilde{\nu }_2\rightarrow \tilde{\chi }^0_2\nu _2$, after accounting for all the subprocesses, the overall branching ratios are comparable, with the one originated from a sneutrino decay into $\tilde{\chi }^0_2\nu _2$ being even slightly larger.

In this paper, I shall therefore investigate the following cascade, originating from a $\chi _2^0\nu _2$ pair, leaving the study of sneutrino decays into $\tilde{\chi }^0_3\nu _2$ to future work:

$$\begin{aligned} pp\rightarrow & {} Z'_\eta \rightarrow \tilde{\nu }_2\tilde{\nu }_2^*\rightarrow (\tilde{\chi }^0_2\nu _2) (\tilde{\chi }^0_2\bar{\nu }_2)\nonumber \\\rightarrow & {} (\ell ^+\ell ^-\tilde{\chi }^0_1\nu _2)(\ell ^+\ell ^-\tilde{\chi }^0_1\bar{\nu }_2). \end{aligned}$$

(29)

The final state is thus made of four charged leptons and missing energy, due to neutrinos $\nu _2$ and neutralinos $\tilde{\chi }^0_1$; the diagram for the process (29) is presented in Fig. 7.

Fig. 7

Final state with four charged leptons and missing energy, initiated by a $Z'$ decay into a sneutrino pair

The cross section for $Z'_\eta$ production in the above scenario at 14 TeV, computed by MadGraph, is $\sigma (pp\rightarrow Z'_\eta )\simeq 0.18$ pb. Given the numbers in Tables 12 and 14, and accounting only for $e^\pm$ and $\mu ^\pm$, the cross section of the cascade (29) is thus $\sigma (pp\rightarrow Z'_\eta \rightarrow 4\ell +\mathrm{MET})\simeq 1.90\times 10^{-4}$ pb, which yields about 20 events at $\mathcal{L}=100$ fb$^{-1}$ and 60 at 300 fb$^{-1}$.

In Fig. 8 the lepton transverse momenta in the decay chain (29) and in direct decays $Z'_\eta \rightarrow \ell ^+\ell ^-$ are plotted: unlike the $Z'_\psi$ case, where we had final states with two charged leptons, exhibiting roughly the same kinematic properties, the decay chain (29) presents four leptons, with different kinematics. Therefore, in Fig. 8, on the left-hand one has the spectra in $p_T$ of the hardest (solid) and softest (dashes) lepton in the cascade (29), on the right-hand side the lepton $p_T$ in $Z'_\eta \rightarrow \ell ^+\ell ^-$. In the cascade, the hardest lepton has a broad spectrum, relevant in the 10  GeV$<p_T<50$ GeV range and maximum around $p_T\simeq$ 20–25 GeV; the $p_T$ of the softest $\ell ^\pm$ is instead a narrow distribution, substantial only for 8 GeV$<p_T<20$ GeV and sharply peaked at $p_T\simeq 11$ GeV. The spectrum in the direct production $Z'_\eta \rightarrow \ell ^+\ell ^-$ is roughly the same as in the $Z'_\psi$ case: in fact, using normalized distributions like $(1/\sigma )~\mathrm{d}\sigma /\mathrm{d}p_T$ minimizes the impact of the value of the coupling.

Fig. 8

Left Transverse momentum of the hardest (solid) and softest (dashes) lepton in the cascade (29). Right Lepton transverse momentum in $Z'_\eta \rightarrow \ell ^+\ell ^-$ processes

In Fig. 9, I have instead included two invariant-mass spectra: $m_{4\ell }$, the invariant mass of the four charged leptons in (29), and $m_{\ell \ell }$, invariant mass of the $\ell ^+\ell ^-$ pairs in secondary $\chi ^0_2\rightarrow \chi ^0_1\ell ^+\ell ^-$ processes, assuming that one is ideally able to identify and reconstruct the leptons coming from each $\tilde{\chi }^0_2$ decay. The $m_{\ell \ell }$ spectrum is significant only in the range 4 GeV $<m_{\ell \ell }<$ 13 GeV and peaked around $m_{\ell \ell }\simeq 9$ GeV; $m_{4\ell }$ is relevant between 40 and 150 GeV and is maximum at $m_{4\ell }\simeq 70$ GeV.

Fig. 9

Invariant mass of the four leptons in the process $pp\rightarrow 4\ell +~\mathrm{MET}$ (left) and of the $\ell ^+\ell ^-$ pairs coming from each $\tilde{\chi }^0_2\rightarrow \tilde{\chi }^0_1\ell ^+\ell ^-$ decay in the cascade (29) (right)

Finally, Fig. 10 presents the spectrum of the missing transverse energy and transverse mass of the final states in the process in Fig. 7, defined as in Eq. (25). The MET distribution is similar to the $Z'_\psi$ one, peaked at 20 GeV and decreasing quite rapidly for larger MET values; the transverse mass is relevant in the range $m_{Z'}/2<m_T<m_{Z'}$ and is overall a broader and smoother distribution with respect to the previous model, with a peak still around $m_T\simeq 1.8$ TeV.

Fig. 10

Left transverse mass for the final state in the process described in Fig. 7. Right missing transverse energy due to neutrinos and neutralinos

6 Phenomenology: supersymmetric extension of the Sequential Standard Model

In this section, I briefly discuss possible analyses within the Sequential Standard Model (SSM): this is the simplest extension of the Standard Model, just containing $Z'$ and possibly $W'$ bosons, with the same couplings to fermions as the Standard Model Z and W. Although it does not have any strong theoretical motivation, as happens for GUT-inspired gauge symmetries, the SSM turns out to be very useful as a benchmark model, since, once the coupling to quarks is fixed, the production cross section can be computed. In principle, in order to fairly extend the SSM to include supersymmetry, one would also need to account for the $\tilde{Z}'$ and $\tilde{W}'$, the supersymmetric partners of the $Z'$ and $W'$, for the extra Higgs fields and D-term corrections to the sfermion masses. However, following [7] and the more recent study in [8, 9], for the sake of releasing some numbers which can be used as benchmarks in the experimental analyses, one can carry out the investigation in an effective theory, wherein the $\tilde{Z}'$, the $\tilde{W}'$, and extra Higgs degrees of freedom are too heavy to contribute to LHC phenomenology and the $Z'$ couples to MSSM sfermions and gauginos like the Standard Model Z. In this scenario, denoted by S-SSM, the coupling to WW pairs must be suppressed, otherwise the WW scattering cross section, mediated by a $Z'$, would diverge. In the representative point of Refs. [8, 9], the $Z'_\text {S-SSM}$ had substantial branching fractions in supersymmetric channels, yielding an overall contribution around 40 % to the total decay width.

In this effective model, I still set the $Z'_\text {S-SSM}$ mass to $m_{Z'}=2$ TeV and, in order to obtain a light Higgs consistent with the recent LHC observations, choose a reference point yielding squark, slepton, Higgs, and gaugino masses as in Tables 15, 16, 17, and 18. The first three squark generations are degenerate, while stops and sbottoms are considerably lighter. With the exception of $\tilde{\chi }^\pm _2$ and $\tilde{\chi }^0_4$, the gaugino masses are of the order of a few hundred GeV and therefore they are light enough to be capable of contributing to the width of a 2 TeV $Z'_\text {S-SSM}$. The branching ratios of the $Z'_\text {S-SSM}$ into Standard Model and supersymmetric channels are given in Table 19: the total rate into BSM final states is 27 %, with the highest fraction being into charginos $\tilde{\chi }^+_1\tilde{\chi }^-_1$, about 17 %; decays into neutralinos and sneutrinos account for about 10 %, whereas SM modes are the remaining 73 %.

Table 15 Squark masses in the S-SSM effective model, in GeV

Table 16 Slepton masses in the S-SSM reference point. Numbers are in GeV; all three generations are slightly degenerate

Table 17 Masses of the Higgs bosons in the $Z'_\text {S-SSM}$ model, for a $Z'$ mass equal to 2 TeV

Table 18 Masses of charginos and neutralinos in the reference point of the S-SSM

Table 19 $Z'_\text {S-SSM}$ decay rates for $m_Z'=2$ TeV

Within this effective S-SSM, $Z'$ decays into chargino pairs, possibly leading to final states with leptons and missing energy, like those in Fig. 1, are worthwhile to be investigated. The main chargino branching ratios are quoted in Table 20: the Cabibbo-favored decays into $\tilde{\chi }^0_1u\bar{d}$ and $\tilde{\chi }^0_1c\bar{s}$ are largely dominant, but even the decays into electrons and muons, i.e. $\tilde{\chi }^0_1 e^+\nu _e$ and $\tilde{\chi }^0_1\mu ^+\nu _\mu$ final states, are quite relevant, accounting for about 1/4 of the total $\tilde{\chi }^{+}_1$ rate.

Table 20 Chargino $\tilde{\chi }_1^+$ decay rates in the reference point for the $Z'_\text {S-SSM}$ model

Even in the S-SSM, an interesting decay chain is (23), with the obvious replacement of the $Z'_\psi$ with the $Z'_\text {S-SSM}$, leading to final states with two charged leptons and missing energy. At $\sqrt{s}=14$ TeV, the inclusive cross section reads $\sigma (pp\rightarrow Z'_\text {S-SSM})\simeq 0.63$ pb and the one of the chain (23) is $\sigma (pp\rightarrow Z'_\mathrm{S-SSM}\rightarrow \ell ^+\ell ^-+\mathrm{MET}) \simeq 6.18\times 10^{-3}$ pb, implying about 600 final states with $e^+e^-$ or $\mu ^+\mu ^-$ and missing energy in the phase $\mathcal{L}=100$ fb$^{-1}$ and even few thousands at 300 fb$^{-1}$. It is thus confirmed the finding of Refs. [8, 9], where it was observed that the S-SSM is the scenario which enhances both production cross section and rates into supersymmetric final states.

In principle, even in the S-SSM one may study leptonic observables like those investigated for the U(1)$'_\psi$ and U(1)$'_\eta$ models. Nevertheless, it was found that, especially if one plots normalized distributions like $(1/\sigma ) \mathrm{d}\sigma /\mathrm{d}p_T$, the impact of the coupling is mild and therefore the spectra are very similar to those obtained in Sect. 4 for the $Z'_\psi$. I shall not present such observables in the S-SSM for the sake of brevity.

7 Conclusions

I presented a phenomenological analysis of supersymmetric $Z'$ decays at the LHC, for $\sqrt{s}=14$ TeV and a few models, based on GUT-inspired U(1)$'$ symmetries. The MSSM was suitably extended, in order to accommodate the new features due to the U(1)$'$ group and the extra $Z'$ boson, and the reference points in the parameter space were chosen in such a way to recover a light Higgs with mass of 125 GeV and obtain substantial $Z'$ branching ratios in the supersymmetric channels.

The analysis was carried out for the so-called U(1)$'_\psi$ and U(1)$'_\eta$ groups, since, even in previous work on supersymmetric $Z'$ decays, they were the theoretical scenarios enhancing the supersymmetric signal. When fixing the soft squark masses, two options were considered, namely degenerate squarks for all three generations as well as lighter stops and sbottoms with respect to the first two generations. It was found that, in both U(1)$'$ models, for the chosen parameters and $m_{Z'}=2$ TeV, supersymmetric modes account for about 25–30 % of the $Z'$ width, with the decays into chargino and sneutrino pairs yielding the highest supersymmetric branching ratios for the $Z'_\psi$ and $Z'_\eta$ models, respectively. The $Z'_\psi$ scenario had also a visible rate into the lightest neutralinos $\tilde{\chi }^0_1$, which could be a useful channel to search for dark matter candidates.

In the $Z'_\psi$ case, it was then considered a decay chain, initiated by a $Z'_\psi \rightarrow \tilde{\chi }^+_1\tilde{\chi }^-_1$ process, leading to a final state with two charged leptons (electrons or muons) and missing transverse energy, due to the production of neutrinos and neutralinos. About $\mathcal{O}(100)$ of such events, for luminosities of 100 or 300 fb$^{-1}$, are expected in the 14 TeV LHC run. The decay into neutralinos $(\tilde{\chi }^0_1\tilde{\chi }^0_1)$ yields an even larger number of events, about $\mathcal{O}(10^3)$ at 14 TeV, and, although it will have to compete with the decay into neutrino pairs, it may deserve an appropriate analysis when looking for Dark Matter particles at the LHC. In the $Z'_\eta$ scenario, the $Z'_\eta \rightarrow \tilde{\nu }_2\tilde{\nu }^*_2$ process, where $\tilde{\nu }_2$ is mostly a right-handed sneutrino, can give rise to a chain yielding four charged leptons and missing energy. The expected rate of such events is lower than the $Z'_\psi$ scenario, but still a few dozens of events are expected for pp collisions at 14 TeV. In both U(1)$'$ models, observables like lepton transverse momentum, rapidity, opening angle and invariant mass, as well as missing transverse energy and transverse mass, are peculiar of supersymmetric decays; the spectra are rather different from those obtained in direct $Z'\rightarrow \ell ^+\ell ^-$ processes and, because of the $Z'$-mass constraint, even from supersymmetric backgrounds, such as direct chargino production. For the sake of comparison, even the Sequential Standard Model was extended to include supersymmetric particles, assuming that the $\tilde{Z}'$ is outside the LHC reach. In the chosen point of the parameter space, it is still the decay into charginos, leading to final states with two charged leptons and missing transverse energy, the most promising supersymmetric channel. Several hundreds of events are in fact foreseen in the high-energy LHC run and even $\mathcal{O}(10^3)$ for a luminosity of 300 fb$^{-1}$.

In summary, the expected rates and final-state observables make supersymmetric $Z'$ decays a rather interesting investigation to search for supersymmetry, once the $Z'$ mass were to be known. For the time being, opening the supersymmetric decay channels up will result in lowering the $Z'$ mass exclusion limits, since the expected rates in Standard Model dilepton pairs decrease. Therefore, although the presented analysis will be useful to search for supersymmetry only after the possible discovery of the $Z'$, it should be possibly taken into account when determining the $Z'$ mass exclusion limits. Once the data on high-mass leptons are available at $\sqrt{s}=14$ TeV, it will be very interesting comparing the data with the theory results on the product $\sigma (pp\rightarrow Z')\times \mathrm{BR}(Z'\rightarrow \ell ^+\ell ^-)$, as done in [12] for the analysis at 8 TeV, and determine the exclusion limits accounting for supersymmetric decays. However, a complete analysis should necessarily compare possible supersymmetric signals in $Z'$ decays with the backgrounds coming from the SM and other supersymmetric processes, as well as from non-supersymmetric $Z'$ decays, and include the detector simulation. The systematic computation of the backgrounds and the implementation of detector effects is presently in progress.

Another possible improvement of the analysis here presented consists of relaxing the approximation of neglecting the interference between Z and $Z'$ bosons. In fact, Ref. [28] compared a NLO + NLL resummed calculation, accounting for such an interference, with the standard analyses, which employ the PYTHIA [29] event generator and rescale the cross section to account for higher-order corrections [30]. The finding of [28] is that, after including resummed as well as interference effects, the $Z'$ mass exclusion bound may well vary by a few hundred GeV in both U(1)$'$ and SSM. It will be therefore worthwhile carrying out the study on supersymmetric $Z'$ decays along the lines of [28], especially once the first high-energy LHC data are available.

Furthermore, beyond the models here studied, which are among those accounted for in the experimental analyses, it may be worthwhile studying in the near future other scenarios, such as the leptophobic models (see, e.g., the pioneering work in [31] or late studies in [32]), wherein the $Z'$ does couple to quarks, thus allowing production via $q\bar{q}\rightarrow Z'$, but the coupling to leptons is suppressed. Within supersymmetry, the very fact that the $Z'$ is leptophobic necessarily decreases the SM rate and enhances the branching ratio in supersymmetric particles. Besides, since $Z'$ decays into charginos and neutralinos played a major role in the present work, a possible application of this work can also be achieved in the context of split supersymmetry [33–35], wherein the scalar particles are much heavier than the gauginos, which are therefore the only supersymmetric particles accessible at present colliders. Investigations of leptophobic $Z'$ models as well as of $Z'$ bosons in the framework of split supersymmetry are in progress as well.