Anisotropic models for compact stars

Abstract

In the present paper we obtain an anisotropic analog of the Durgapal and Fuloria (Gen Relativ Gravit 17:671, 1985) perfect fluid solution. The methodology consists of contraction of the anisotropic factor $\Delta$ with the help of both metric potentials $e^{\nu }$ and $e^{\lambda }$. Here we consider $e^{\lambda }$ the same as Durgapal and Fuloria (Gen Relativ Gravit 17:671, 1985) did, whereas $e^{\nu }$ is as given by Lake (Phys Rev D 67:104015, 2003). The field equations are solved by the change of dependent variable method. The solutions set mathematically thus obtained are compared with the physical properties of some of the compact stars, strange star as well as white dwarf. It is observed that all the expected physical features are available related to the stellar fluid distribution, which clearly indicates the validity of the model.

1 Introduction

A few decades ago a new analytic relativistic model was obtained by Durgapal and Fuloria [1] for superdense stars in the framework of Einstein’s General Theory of Relativity. They showed that the model in connection to the neutron star stands all physical tests with the maximum mass $4.17~M_{\odot }$ and the surface redshift $0.63$. Very recently, Gupta and Maurya [3] presented a class of charged analogs of the superdense star model due to Durgapal and Fuloria [1] with Einstein–Maxwell spacetimes. The members of this class have been shown to satisfy various physical conditions and exhibit these features: (a) a maximum mass $3.2860~M_{\odot }$ and a radius $18.3990$ km for a particular interval of the parameter: $1<K \le 1.7300$, and (b) a maximum mass $1.9672~M_{\odot }$ and a radius $15.9755$ km for another interval of the parameter: $1 <K \le 1.1021$. Later on, a family of well behaved charged analogs of the Durgapal and Fuloria [1] perfect fluid exact solution was also obtained by Murad and Fatema [4] where they have studied the Crab pulsar with radius $13.21$ km.

In a similar way we have considered a generalization of Durgapal and Fuloria [1] with an anisotropic fluid sphere such that $p_\mathrm{r} \ne p_\mathrm{t}$, where $p_\mathrm{r}$ and $p_\mathrm{t}$, respectively, are the radial and tangential pressures of the fluid distribution. The present work is a sequel of the paper [5] where we have developed a general algorithm in the form of the metric potential $\nu$ for all spherically symmetric charged anisotropic solutions in connection to compact stars. However, in the present study without considering any anisotropic function we can develop an algorithm with the help of the metric potentials only and herein lies the beauty of the investigation. Another point we would like to add here is that, till now, to the best of our knowledge, no alternative anisotropic analog of Duragapal and Fuloria [1] solution is available in the literature.

In connection to anisotropy we note that it was Ruderman [6] who argued that the nuclear matter may have anisotropic features at least in certain very high density ranges (>$10^{15}~\mathrm{gm}/\mathrm{cm}^3$), and thus the nuclear interaction can be treated under relativistic background. Later on Bowers and Liang [7] specifically investigated the non-negligible effects of anisotropy on the maximum equilibrium mass and surface redshift. There is an exhaustive review on the subject of anisotropic fluids by Herrera and Santos [8] which provides almost all references until 1997, as well as a detailed discussion of some of the issues analyzed in this article. More recently, a comprehensive work on the influence of local anisotropy on the structure and evolution of compact object has been published by Herrera et al. [9]. In this regard several recently performed anisotropic compact star models may be consulted for further reference [10–18]. We also note some particular work concerned with the anisotropic aspect in physical systems like Globular Clusters, Galactic Bulges, and Dark Halos in Refs. [19, 20].

As a special feature of anisotropy we note that for a small radial increase the anisotropic parameter increases. However, after reaching a maximum in the interior of the star it becomes a decreasing function of the radial distance as shown by Mak and Harko [21, 22]. Obviously at the center of the fluid sphere the anisotropy is expected to vanish.

We would like to mention that an algorithm for a perfect fluid and an anisotropic uncharged fluid is already available in the literature [2, 23, 24]. For example, we note that in his work Lake [2, 23] has considered an algorithm based on the choice of a single monotone function, which generates all regular static spherically symmetric perfect as well as anisotropic fluid solutions for the Einstein spacetimes. It is also observed that Herrera et al. [24] have extended the algorithm to the case of locally anisotropic fluids. Thus we opt for an algorithm applied to the more general case with an anisotropic fluid distribution. However, in this context it is to be noted that in Ref. [5] we developed an algorithm in the Einstein–Maxwell spacetimes.

The outline of the present paper is as follows: in Sect. 2 the Einstein field equations for an anisotropic stellar source are given, whereas the general solutions are shown in Sect. 3 along with the necessary matching condition. In Sect. 4 we represent interesting features of the physical parameters, which include density, pressure, stability, charge, anisotropy, and redshift. As a special study we provide several data sheets in connection to compact stars. Section 5 is used as a platform for some discussions and conclusions.

2 The Einstein field equations

In this work we intend to study a static and spherically symmetric matter distribution whose interior metric is given in Schwarzschild coordinates, $x^i=(r, \theta , \phi , t)$ [25, 26],

$$\begin{aligned} \mathrm{d}s^2 = - e^{\lambda (r)} \mathrm{d}r^2 - r^2(\mathrm{d}\theta ^2 + \mathrm{sin}^2\theta \mathrm{d}\phi ^2) + e^{\nu (r)} \mathrm{d}t^2. \end{aligned}$$

(1)

The functions $\nu$ and $\lambda$ satisfy the Einstein field equations,

$$\begin{aligned} \kappa {T^i}_j = {R^i}_j - \frac{1}{2} R {g^i}_j , \end{aligned}$$

(2)

where $\kappa = 8\pi$ is the Einstein constant with $G=1=c$ in relativistic geometrized units, $G$ and $c$, respectively, being the Newtonian gravitational constant and velocity of photons in vacuum.

The matter within the star is assumed to be locally anisotropic fluid in nature and consequently ${T^i}_j$ is the energy-momentum tensor of the fluid distribution defined by

$$\begin{aligned} {T^i}_j = [(\rho + p_\mathrm{r})v^iv_j - p_\mathrm{t}{\delta ^i}_j + (p_\mathrm{r} - p_\mathrm{t}) \theta ^i \theta _j], \end{aligned}$$

(3)

where $v^i$ is the four-velocity with $e^{\lambda (r)/2}v^i={\delta ^i}_4$, $\theta ^i$ is the unit space-like vector in the direction of radial vector, $\theta ^i = e^{\lambda (r)/2}{\delta ^i}_1$ is the energy density, $p_\mathrm{r}$ is the pressure in direction of $\theta ^i$ (normal pressure), and $p_\mathrm{t}$ is the pressure orthogonal to $\theta _i$ (transverse or tangential pressure).

For the spherically symmetric metric (1), the Einstein field equations may be expressed as the following system of ordinary differential equations [27]:

$$\begin{aligned} -\kappa {T^1}_1 = \frac{{\nu }^{\prime }}{r} e^{-\lambda } - \frac{(1 - e^{-\lambda })}{r^2} = \kappa p_\mathrm{r} , \end{aligned}$$

(4)

$$\begin{aligned} -\kappa {T^2}_2= & {} -\kappa {T^3}_3 = \left[ \frac{{\nu }^{\prime \prime }}{2} - \frac{{\lambda }^{\prime }{\nu }^{\prime }}{4} + \frac{{{\nu }^{\prime }}^2}{4} + \frac{{\nu }^{\prime } - {\lambda }^{\prime }}{2r}\right] e^{-\lambda }\nonumber \\= & {} \kappa p_\mathrm{t}, \end{aligned}$$

(5)

$$\begin{aligned} \kappa {T^4}_4 = \frac{{\lambda }^{\prime }}{r} e^{-\lambda } + \frac{(1 - e^{-\lambda })}{r^2} = \kappa \rho , \end{aligned}$$

(6)

where the prime denotes differentiation with respect to the radial coordinate $r$.

The pressure anisotropy condition for the system can be written

$$\begin{aligned} \Delta =\kappa \left( p_\mathrm{t}-p_\mathrm{r} \right)&=\left[ \frac{{\nu }^{\prime \prime }}{2} - \frac{{\lambda }^{\prime }{\nu }^{\prime }}{4} + \frac{{{\nu }^{\prime }}^2}{4} + \frac{{\nu }^{\prime } - {\lambda }^{\prime }}{2r}\right] e^{-\lambda }\nonumber \\&\quad -\frac{{\nu }^{\prime }}{r} e^{-\lambda } + \frac{(1 - e^{-\lambda })}{r^2} . \end{aligned}$$

(7)

Now let us consider the metric potentials [1] in the following forms:

$$\begin{aligned} e^{-\lambda }=\frac{7-10Cr^2-C^2r^4}{7+14Cr^2+7C^2r^4}, \end{aligned}$$

(8)

$$\begin{aligned} \nu =2\ln \psi , \end{aligned}$$

(9)

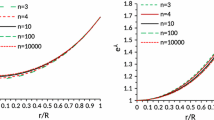
where $C$ is a positive constant and $\psi$ is a function which depends on the radial coordinate $r$. The plots for these quantities are shown in Fig. 1.

Fig. 1

Variations of the metric potentials with radial coordinate $r/R$. (i) $e^{\nu }$ is plotted with dotted line for Her X-1 and short-dashed line for white dwarf, (ii) $e^{\lambda }$ is plotted with a continuous line for Her X-1 and a long-dashed line for a white dwarf

Equation (7) together with Eqs. (8) and (9) becomes

$$\begin{aligned} \Delta= & {} \left[ \frac{7-10Cr^2-C^2r^4}{7(1+Cr^2)^2}\right] \frac{{\psi }^{\prime \prime }}{\psi }\nonumber \\&+\left[ \frac{C^3r^6+19C^2r^4-21Cr^2-7}{7r(1+Cr^2)^3}\right] \frac{{\psi }^{\prime }}{\psi }\nonumber \\&+\left[ \frac{8C^2r^2(Cr^2+5)}{7(1+C{r}^2)^3}\right] . \end{aligned}$$

(10)

3 The solutions for the model

Here our initial aim is to find the pressure anisotropic function $\Delta$, which is zero at the center and monotonic increasing for suitable choices of $\psi$. However, Lake [2] imposes the condition that $\psi$ should be a regular and monotonic increasing function of the radial coordinate $r$.

Let us therefore take the form of $\psi$ as follows:

$$\begin{aligned} \psi =(1-\alpha +Cr^2)^2, \end{aligned}$$

(11)

where $\alpha > 0$.

Substituting the value of $\psi$ from Eq. (11) in Eq. (10), we get

$$\begin{aligned} \Delta =-{\frac{8}{7}}\,{\frac{\alpha \,{C}^{2}{r}^{2}[2\,{C}^{2}{r}^{ 4}+ ( 16-\alpha ) C{r}^{2}-5\,\alpha -2]}{ ( 1+C{r}^{2} ) ^{3} (1-\alpha +C{r}^{2}) ^{2}}}.\nonumber \\ \end{aligned}$$

(12)

For $\alpha > 0$ and $0 < Cr^2 < \frac{\sqrt{{\alpha }^{2}+8\alpha +272}-(16-K)}{4}$, the pressure anisotropy is finite as well as positive everywhere, as can be seen in Fig. 2.

Fig. 2

Variation of the anisotropy factor with radial coordinate $r/R$. (i) $\Delta$ is plotted with a short-dashed line for Her X-1, (ii) $\Delta$ is plotted with a continuous line for a white dwarf

By inserting the above value of $\Delta$ in Eq. (12), we get

$$\begin{aligned}&\psi ^{\prime \prime }+\left[ \frac{C^3r^6+19C^2r^4-21Cr^2-7}{r(1+Cr^2)(7-10Cr^2-C^2r^4)}\right] \psi ^{\prime } \nonumber \\&\quad +\frac{1}{7-10Cr^2-C^2r^4}\left[ \frac{8C^2r^2(Cr^2+5)}{(1+Cr^2)}\right. \nonumber \\&\quad \left. + \frac{8\alpha C^2r^2[2C^2r^4+(16-\alpha )Cr^2-(5\alpha +2)]}{(1+Cr^2)(1-\alpha +Cr^2)^2}\right] \psi =0.\nonumber \\ \end{aligned}$$

(13)

Now our next task is to obtain the most general solution of the differential equation (13). Here we shall use the change of dependent variable method. We consider the differential equation of the form

$$\begin{aligned} y^{\prime \prime }+p(r)y^{\prime }+q(r)y=0. \end{aligned}$$

(14)

Let $y=y_{1}$ be the particular solution of the differential equation (14). Then $y=y_{1}U$ will be complete solution of the differential equation (14), where

$$\begin{aligned} U=a_{1}+b_{1}\int \exp \left[ -\int (p(r)+\frac{2y^{\prime }}{y_{1}})\mathrm{d}r\right] \mathrm{d}r, \end{aligned}$$

where $a_{1}$ and $b_{1}$ are arbitrary constants.

Again let us assume here that $\psi =(1-\alpha +Cr^2)^2=\psi _{\alpha r}$ is a particular solution of Eq. (13). So, the most general solution of the differential equation (13) can be given by

$$\begin{aligned} \psi= & {} (1-\alpha +Cr^2)^2\nonumber \\&\times \left[ \tilde{B}\!+\!\tilde{A}\int \exp \left\{ -\int \left( \frac{C^{3}r^{6} \!+\!19C^{2}r^{4}\!-\!21Cr^{2}-7}{r(1\!+\!Cr^{2})(7\!-\!10Cr^{2}\!-\!C^{2}r^{4})}\right. \right. \right. \nonumber \\&+\, \left. \left. \left. \frac{8Cr^{2}}{r(1-\alpha +Cr^2)}\right) \mathrm{d}r\right\} \mathrm{d}r\right] , \end{aligned}$$

(15)

where $\tilde{A}$ and $\tilde{B}$ are arbitrary constants.

After integrating it, we get

$$\begin{aligned} \psi =\psi _{\alpha r}\left[ B-A\left\{ \frac{\{\psi _{\alpha 1}+\psi _{\alpha 2}(1-\alpha +Cr^2)+\psi _{\alpha 3}\psi _{\alpha r}\}\sqrt{(\psi _{\alpha 5}-2(4+\alpha )(1-\alpha +Cr^2) -\psi _{\alpha r})}}{(1-\alpha +Cr^2)^3} +W(r)\right\} \right] , \end{aligned}$$

(16)

where

$$\begin{aligned} \psi _{\alpha r}=(1-\alpha +Cr^2)^2, \end{aligned}$$

(17)

$$\begin{aligned} W(r)=\frac{\psi _{\alpha 4}}{\sqrt{\psi _{\alpha 5}}} \log \left[ \frac{\psi _{\alpha 5}-(4+\alpha )(1-\alpha +Cr^{2})+ \sqrt{\psi _{\alpha 5}}\sqrt{(\psi _{\alpha 5}-2(4+\alpha )(1-\alpha +Cr^2)-\psi _{\alpha r})}}{(1-\alpha +Cr^2)\psi _{\alpha 5}}\right] , \end{aligned}$$

(18)

and $A$ and $B$ are arbitrary constants with

$\psi _{\alpha 1}=\frac{\alpha }{3(16-8\alpha -\alpha ^{2})}$,

$\psi _{\alpha 2}=\frac{24-2\alpha +\alpha ^{2}}{3(16-8\alpha -\alpha ^{2})^{2}}$,

$\psi _{\alpha 3}=\frac{288+80\alpha -10\alpha ^{2}+\alpha ^{3}}{3(16-8\alpha -\alpha ^{2})^{3}}$,

$\psi _{\alpha 4}=\frac{1536-384\alpha +48\alpha ^{2}-2\alpha ^{3}}{3(16-8\alpha -\alpha ^{2})^{3}}$,

$\psi _{\alpha 5}=(16-8\alpha -\alpha ^{2})$.

Using Eqs. (8), (12), and (16) the expressions for the energy-density and pressure read

$$\begin{aligned} \frac{\kappa \rho }{C}=\frac{8(9+2Cr^{2}+C^{2}r^{4})}{7(1+Cr^{2})^{3}} \end{aligned}$$

(19)

and

$$\begin{aligned} \frac{\kappa p_\mathrm{r}}{C}= & {} \frac{4(7-10Cr^2 \!-\! C^{2}r^{4})}{7(1+Cr^{2})^2}\left[ \frac{\psi _{pr}(1\!-\!\alpha +Cr^2)^{3}+2\psi }{\psi (1-\alpha +Cr^2)}\right] \nonumber \\&- \frac{8(Cr^{2}+3)}{7(1+Cr^{2})^{2}}, \end{aligned}$$

(20)

where

$$\begin{aligned} \psi _{pr}=\frac{A(1+Cr^{2})}{(1-\alpha +Cr^2)^{4}\sqrt{(7-10Cr^{2}-Cr^{2})}}. \end{aligned}$$

(21)

In Figs. 3, 4, and 5 we have plotted the nature of the above physical quantities, which show the viability of the features of the present model.

Fig. 3

Variation of the density with radial coordinate $r/R$. (i) $\rho$ is plotted with a continuous line for Her X-1, (ii) $\rho$ is plotted with a dashed line for a white dwarf

Fig. 4

Variation of the density with radial coordinate. (i) $p_\mathrm{r}$ is plotted with a continuous line for Her X-1 and a short-dashed line for a white dwarf in the left graph (left panel), (ii) $p_\mathrm{t}$ is plotted with a continuous line for Her X-1 and a short-dashed line for a white dwarf in the right graph (right panel)

Fig. 5

Variation of the density with radial coordinate $r/R$. (i) $p_\mathrm{r}/\rho$ is plotted with a short-dashed line for Her X-1 and a continuous line for a white dwarf (left panel), (ii) $p_\mathrm{t}/\rho$ is plotted with a short-dashed line for Her X-1 and a continuous line for a white dwarf (right panel)

3.1 Matching condition

The above system of equations is to be solved subject to the boundary condition that radial pressure $p_\mathrm{r}=0$ at $r=R$ (where $r=R$ is the outer boundary of the fluid sphere). It is clear that $m (r=R)=M$ is a constant and, in fact, the interior metric (2.1) can be joined smoothly at the surface of spheres ($r=R$) to an exterior Schwarzschild metric whose mass is the same as above, i.e. $m (r=R)=M$ [28].

The exterior spacetime of the star will be described by the Schwarzschild metric given by

$$\begin{aligned} \mathrm{d}s^2= & {} - \left( 1-\frac{2M}{r}\right) ^{-1}\mathrm{d}r^2 - r^2(\mathrm{d}\theta ^2 + \mathrm{sin}^2\theta \mathrm{d}\phi ^2)\nonumber \\&+ \left( 1-\frac{2M}{r}\right) \mathrm{d}t^2. \end{aligned}$$

(22)

The continuity of the metric coefficients $g_{tt}$, $g_{rr}$ across the boundary surface $r=R$ between the interior and the exterior regions of the star yields the following conditions:

$$\begin{aligned} \left( 1-\frac{2M}{r}\right) ^{-1} = e^{\lambda (R)}, \end{aligned}$$

(23)

$$\begin{aligned} \left( 1-\frac{2M}{r}\right) = \psi ^{2}_R, \end{aligned}$$

(24)

where $\psi (r=R)=\psi _{R}$.

Equations (23) and (24), respectively, give

$$\begin{aligned} M=\frac{R}{2}\left[ \frac{8CR^{2}(3+CR^{2})}{7(1+CR^2)^2}\right] , \end{aligned}$$

(25)

$$\begin{aligned} A=\frac{\sqrt{7-10CR^{2}-C^{2}R^{4}}}{\sqrt{7}(1+CR^{2})\psi _{\alpha R}(\frac{B}{A}- \Omega (R))}. \end{aligned}$$

(26)

That the radial pressure $p_\mathrm{r}$ is zero at the boundary ($r=R$) leads to

$$\begin{aligned} \frac{B}{A}\!=\!\frac{(1\!+\!CR^{2})\sqrt{7-10CR^{2}\!-\!C^{2}R^{2}}}{2(1\!-\!\alpha \!+\!CR^{2})^{3}[(1\!-\!\alpha \!+\!CR^{2})(3\!+\!CR^{2})\!-\!(7\!-\!10CR^{2}\!-\!C^{2}R^{4})]} \Omega (R),\nonumber \\ \end{aligned}$$

(27)

where

$$\begin{aligned} \psi _{\alpha R}=(1-\alpha +CR^{2})^{2}, \end{aligned}$$

(28)

$$\begin{aligned}&\Omega (R)=\frac{\{\psi _{\alpha 1}+\psi _{\alpha 2}(1-\alpha +CR^2)+\psi _{\alpha 3}\psi _{\alpha R}\} \sqrt{\psi _{\alpha 5}-2(4+\alpha )(1-\alpha +CR^2)-\psi _{\alpha R}}}{(1-\alpha +CR^{2})^3} + W(R),\end{aligned}$$

(29)

$$\begin{aligned}&W(R)=\frac{\psi _{\alpha 4}}{\sqrt{\psi _{\alpha 5}}}\log \left[ \frac{\psi _{\alpha 5}-(4+\alpha )(1-\alpha +CR^{2})+ \sqrt{\psi _{\alpha 5}}\sqrt{\psi _{\alpha 5}-2(4+\alpha )(1-\alpha +CR^{2})-\psi _{\alpha R}}}{(1-\alpha +CR^{2})\psi _{\alpha 5}}\right] . \end{aligned}$$

(30)

4 Some physical features of the model

4.1 Regularity at center

The density $\rho$, and the radial pressure $p_\mathrm{r}$ and the tangential pressure $p_\mathrm{t}$ should be positive inside the star. The central density at the center for the present model is

$$\begin{aligned} \rho _{0}=\rho (r=0)=\frac{72C}{7}. \end{aligned}$$

(31)

The metric Eq. (22) implies that $C=\frac{7\rho _{0}}{72}$ is positive finite.

Again, from Eq. (20), we obtain

$$\begin{aligned} \frac{p_\mathrm{r}(r=0)}{C}=\frac{4A}{\sqrt{7} (1-\alpha )^{2}\psi _{r=0}} - \frac{24}{7}, \end{aligned}$$

(32)

where $p_\mathrm{r}(r=0)>0$.

This immediately implies that

$$\begin{aligned}&\frac{B}{A}<\frac{\sqrt{7}}{6(1-\alpha )^4} \nonumber \\&\quad + \frac{\{\psi _{\alpha 1} +\psi _{\alpha 2}(1-\alpha )+\psi _{\alpha 3}(1-\alpha )^2\}\sqrt{\psi _{\alpha 5}-2(4+\alpha )(1-\alpha )-(1-\alpha )^2}}{(1-\alpha )^3} \nonumber \\&\quad + \frac{\psi _{\alpha 4}}{\sqrt{\psi _{\alpha 5}}}\nonumber \\&\quad \times \log \left[ \frac{\psi _{\alpha 5}-(4+\alpha )(1-\alpha )\!+\!\sqrt{\psi _{\alpha 5}}\sqrt{\psi _{\alpha 5}\!-\!2(4+\alpha )(1-\alpha )\!-\!(1\!-\!\alpha )^2}}{(1-\alpha )\psi _{\alpha 5}}\right] .\nonumber \\ \end{aligned}$$

(33)

4.2 Causality conditions

Inside the fluid sphere the speed of sound should be less than the speed of light i.e. $0 \le V_\mathrm{sr}=\sqrt{\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }}<1$ and $0 \le V_\mathrm{st}=\sqrt{\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho }}<1$. Therefore

$$\begin{aligned}&{V^{2}}_\mathrm{sr}=(1+Cr^{2})\left[ \frac{4(C^{2}r^{4}+10Cr^{2}-7)(1+Cr^{2})(\psi _{r1} -\psi _{r2}-\psi _{r3})-8(Cr^{2}+5)}{8(C^{2}r^{4}+2Cr^{2}+25)}\right] ,\end{aligned}$$

(34)

$$\begin{aligned}&{V^{2}}_\mathrm{st}=(1+Cr^{2})\left[ \frac{4(C^{2}r^{4}+10Cr^{2}-7)(1+Cr^{2})(\psi _{r1} -\psi _{r2}-\psi _{r3})-8(Cr^{2}+5)-\psi _{r4}}{8(C^{2}r^{4}+2Cr^{2}+25)}\right] , \end{aligned}$$

(35)

where

$$\begin{aligned} \psi _{pr}=\frac{A(1+Cr^{2})}{(1-\alpha +Cr^{2})^{4}\sqrt{(7-10Cr^{2}-Cr^{2})}}, \end{aligned}$$

(36)

$$\begin{aligned} \psi _{r1}=\left[ \frac{2}{(1-\alpha +Cr^{2})^{2}} + \frac{4(3-Cr^{2})(1-\alpha +Cr^{2})^{2}\psi _{pr}}{\psi (1+Cr^{2})(7-10Cr^{2}-C^{2}r^{4})}\right] ,\nonumber \\ \end{aligned}$$

(37)

$$\begin{aligned} \psi _{r2}=\left[ \frac{2K}{(1-\alpha +Cr^{2})} + \frac{(1-\alpha +Cr^{2})^{2}\psi _{pr}}{\psi }\right] ^{2}, \end{aligned}$$

(38)

$$\begin{aligned} \psi _{r3}&=\frac{8(3-Cr^{2})}{(7-10Cr^{2}-C^{2}r^{4})(1+Cr^{2})}\left[ \frac{2}{(1-\alpha +Cr^{2})}\right. \nonumber \\&\left. \quad + \frac{(1-\alpha +Cr^{2})^{2}\psi _{pr}}{\psi }\right] , \end{aligned}$$

(39)

$$\begin{aligned}&\psi _{r4}\nonumber \\&\quad =\left[ 4\alpha \frac{(1+Cr^{2})(1-\alpha +Cr^{2})\psi _{r5} - Cr^{2}\psi _{r6}(5-3\alpha +5Cr^{2})}{(1+Cr^{2})(1-\alpha +Cr^{2})^{3}}\right] ,\nonumber \\ \end{aligned}$$

(40)

$$\begin{aligned} \psi _{r5}=[12C^{2}r^{4}+4(16-\alpha )Cr^{2}-(10\alpha +4)], \end{aligned}$$

(41)

$$\begin{aligned} \psi _{r6}=[4C^{2}r^{4}+2(16-\alpha )Cr^{2}-(10\alpha +4)]. \end{aligned}$$

(42)

The physical quantities related to the above equations are plotted in Figs. 6 and 7.

Fig. 6

Variation of the sound velocity with radial coordinate $r/R$. (i) $V_\mathrm{r}$ is plotted with a dashed line for Her X-1, (ii) $V_\mathrm{r}$ is plotted with a marker continuous line for a white dwarf, (iii) $V_\mathrm{t}$ is plotted with a continuous line for Her X-1, (iv) $V_\mathrm{t}$ is plotted with a dotted line for a white dwarf

Fig. 7

Variation of the sound velocity with radial coordinate $r/R$. (i) $V^2_\mathrm{sr}$ is plotted with a dotted line for Her X-1, (ii) $V^2_\mathrm{sr}$ is plotted with a dashed line for a white dwarf, (iii) $V^2_\mathrm{st}$ is plotted with a marker continuous line for Her X-1, (iv) $V^2_\mathrm{st}$ is plotted with a continuous line for a white dwarf

4.3 Well behaved condition

The velocity of sound is monotonically decreasing away from the center and it is increasing with the increase of density, i.e. $\frac{\mathrm{d}}{\mathrm{d}r}(\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho })<0$ or $(\frac{\mathrm{d}^{2}p_\mathrm{r}}{\mathrm{d}\rho ^{2}})>0$ and $\frac{\mathrm{d}}{\mathrm{d}r}(\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho })<0$ or $(\frac{\mathrm{d}^{2}p_\mathrm{t}}{\mathrm{d}\rho ^{2}})>0$ for $0 \le r \le R$. In this context it is worth mentioning that the equation of state at an ultra-high distribution has the property that the sound speed is decreasing outward [29] as can be observed from Fig. 6.

4.4 Energy conditions

The anisotropic fluid sphere composed of strange matter will satisfy the null energy condition (NEC), the weak energy condition (WEC), and the strong energy condition (SEC), if the following inequalities hold simultaneously at all points in the star:

NEC: $\rho \ge 0$,

WEC: $\rho + p_\mathrm{r} \ge 0$,

WEC: $\rho + p_\mathrm{t} \ge 0$,

SEC: $\rho + p_\mathrm{r} +2p_\mathrm{t} \ge 0$.

We have shown the energy conditions in Fig. 8 for Her X-1 in (i) and for a white dwarf in (ii).

Fig. 8

Variation of the energy conditions with radial coordinate $r/R$. (i) $NEC$ is plotted with a marker long-dashed line, $WEC_\mathrm{r}$ with a marker short-dashed line, and $SEC$ with a continuous line (for Her X-1), (ii) $NEC$ is plotted with a marker continuous line, $WEC_\mathrm{r}$ with a long-dashed line, and $SEC$ with a short-dashed line (for a white dwarf)

4.5 Stability conditions

4.5.1 Case 1

In order to have an equilibrium configuration the matter must be stable against the collapse of local regions. This requires Le Chatelier’s principle, also known as the local or microscopic stability condition: that the radial pressure $p_\mathrm{r}$ must be a monotonically non-decreasing function of $r$ such that $\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho } \ge 0$ [30]. Heintzmann and Hillebrandt [31] also proposed that a neutron star with an anisotropic equation of state is stable for $\gamma > 4/3$ as is observed from Fig. 9 and also shown in Tables 1 and 2 for our model related to compact stars.

Fig. 9

Variation of the adiabatic index with radial coordinate $r/R$. (i) $\gamma$ is plotted with a continuous line for Her X-1, (ii) $\gamma$ is plotted with a dashed line for a white dwarf

Table 1 Values of different physical parameters of a white dwarf star for $\alpha =0.10$, $CR^2=0.068$, $M=0.8882$ $M_{\odot }$, $R=12.5202$ Km

Table 2 Values of different physical parameters of the strange star Her X-1 for $\alpha =0.11$, $CR^2=0.1178$, $M=0.8804$ $M_{\odot }$, $R=7.7214$ Km

4.5.2 Case 2

For a physically acceptable model, one expects that the velocity of sound should be within the range $0=V_\mathrm{si}^2=(\mathrm{d}p_{i}/\mathrm{d}\rho ) \le 1$ [32, 33]. We plot the radial and transverse velocity of sound in Fig. 7 and conclude that all parameters satisfy the inequalities $0=V_\mathrm{sr}^2=(\mathrm{d}p_{i}/\mathrm{d}\rho ) \le 1$ and $0=V_\mathrm{st}^2=(\mathrm{d}p_{i}/\mathrm{d}\rho ) \le 1$ everywhere inside the star models. Also $0=V_\mathrm{st}^2 \le 1$ and $0=V_\mathrm{sr}^2 \le 1$; therefore $|V_\mathrm{st}^2-V_\mathrm{sr}^2| \le 1$. In order to examine the stability of local anisotropic fluid distribution, we follow the cracking concept of Herrera [32] which states that the region for which the radial speed of sound is greater than the transverse speed of sound is a potentially stable region.

To this aim, we calculate the difference of the velocities as follows:

$$\begin{aligned}&V_\mathrm{st}^2-V_\mathrm{sr}^2\nonumber \\&\quad =\alpha \left[ \frac{(1+Cr^2)(1-\alpha +Cr^2)\psi _{r5}-Cr^2\psi _{r6}(5-3\alpha +5Cr^2)}{2(1+Cr^2)^3(1-\alpha +Cr^2)^3(C^2r^4+2Cr^2+25)}\right] ,\nonumber \\ \end{aligned}$$

(43)

where

$$\begin{aligned} \psi _{r5}=[12C^{2}r^{4}+4(16-\alpha )Cr^{2}-(10\alpha +4)], \end{aligned}$$

(44)

$$\begin{aligned} \psi _{r6}=[4C^{2}r^{4}+2(16-\alpha )Cr^{2}-(10\alpha +4)]. \end{aligned}$$

(45)

It can be seen that $|V_\mathrm{st}^2-V_\mathrm{sr}^2|$ at the center lies between 0 and 1 (see Fig. 10). This implies that we must have $0 \le \frac{\alpha (10\alpha +4)}{50(1-\alpha )^2} \le 1$. Then $\alpha$ should satisfy the following condition: $0 \le \alpha \le \frac{52-\sqrt{704}}{40}$.

Fig. 10

Variation of the absolute value of square of sound velocity with radial coordinate $r/R$. (i) $|V^2_\mathrm{st} - V^2_\mathrm{sr}|$ is plotted with a short-dashed line for Her X-1, (ii) $|V^2_\mathrm{st} - V^2_\mathrm{sr}|$ is plotted with a continuous line for a white dwarf

4.6 Generalized TOV equation

The generalized Tolman–Oppenheimer–Volkoff (TOV) equation is

$$\begin{aligned} -\frac{M_\mathrm{G}\left( \rho +p_\mathrm{r}\right) }{r^2}e^{\frac{\lambda -\nu }{2}}-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r} +\frac{2}{r}\left( p_\mathrm{t}-p_\mathrm{r}\right) =0, \end{aligned}$$

(46)

where $M_\mathrm{G}=M_\mathrm{G}(r)$ is the effective gravitational mass, which is given by

$$\begin{aligned} M_\mathrm{G}(r)=\frac{1}{2}r^2e^{\frac{\nu -\lambda }{2}}\nu ^{\prime }. \end{aligned}$$

(47)

Substituting the value of $M_\mathrm{G}(r)$ in Eq. (46), we get

$$\begin{aligned} -\frac{1}{2}\nu ^{\prime }(\rho +p_\mathrm{r})-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r} +\frac{2}{r}\left( p_\mathrm{t}-p_\mathrm{r}\right) =0. \end{aligned}$$

(48)

Equation (48) basically describes the equilibrium condition for an anisotropic fluid subject to gravitational ($F_\mathrm{g}$), hydrostatic ($F_\mathrm{h}$), and anisotropic stress ($F_\mathrm{a}$), which can, in a compact form, be expressed as

$$\begin{aligned} F_\mathrm{g}+ F_\mathrm{h}+ F_\mathrm{a}=0, \end{aligned}$$

(49)

where

$$\begin{aligned} F_\mathrm{g}=-\frac{1}{2}\nu ^{\prime }(\rho +p_\mathrm{r}), \end{aligned}$$

(50)

$$\begin{aligned} F_\mathrm{h}=-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}, \end{aligned}$$

(51)

$$\begin{aligned} F_\mathrm{a}=\frac{2}{r}\left( p_\mathrm{t}-p_\mathrm{r}\right) . \end{aligned}$$

(52)

The above forces can be expressed in the following explicit forms:

$$\begin{aligned} F_\mathrm{g}= & {} -\frac{1}{2}\nu ^{\prime }(\rho +p_\mathrm{r})\nonumber \\= & {} \frac{C^{2}r}{8\pi }\left[ \frac{8(6-2Cr^2)}{7(1+Cr^2)^3}\frac{[\psi _{pr}(1-\alpha +Cr^2)^3+2\psi ]}{\psi (1-\alpha +Cr^2)} \right. \nonumber \\&+ \left. \frac{4(7-C^2r^4-10Cr^2)}{7(1+Cr^2)^2}\left( \frac{\psi _{pr}(1-\alpha +Cr^2)^3+2\psi }{\psi (1-\alpha +Cr^2)}\right) ^2\right] ,\nonumber \\ \end{aligned}$$

(53)

$$\begin{aligned} F_\mathrm{h}= & {} -\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}=\frac{C^{2}r}{4\pi }\left[ \frac{4(C^2r^4+10Cr^2-7)}{7(1+Cr^2)^2}(\psi _{r1}-\psi _{r2}-\psi _{r3})\right. \nonumber \\&\left. -\frac{8(Cr^2+5)}{7(1+Cr^2)^3}\right] , \end{aligned}$$

(54)

$$\begin{aligned} F_\mathrm{a}= & {} \frac{2}{r}\left( p_\mathrm{t}-p_\mathrm{r}\right) \nonumber \\= & {} \frac{C^2r}{\pi }\left[ \frac{2\alpha [(5\alpha +2)-(16-\alpha )Cr^2-2C^2r^4]}{7(1+Cr^2)^3(1-\alpha +Cr^2)^2}\right] .\nonumber \\ \end{aligned}$$

(55)

The variation of different forces and the attainment of equilibrium has been drawn in Fig. 11. At this point, however, it is justified to note that the stability issues in Sects. 4.5 and 4.6 have also been analyzed in general and in full detail in the case of anisotropic fluids by Chan et al. [34].

Fig. 11

Variation of the forces with radial coordinate $r/R$. $F_\mathrm{g}$ is plotted with a long-dashed line, $F_\mathrm{h}$ with a continuous line, and $F_\mathrm{a}$ with a short-dashed line

4.7 Effective mass–radius relation and surface redshift

Let us now turn our attention towards the effective mass-to-radius relationship. For a static spherically symmetric perfect fluid star, Buchdahl [35] has proposed an absolute constraint on the maximally allowable mass-to-radius ratio ($M/R$) for isotropic fluid spheres as $2M/R \le 8/9$ (in the units $c = G = 1$). This basically states that for a given radius a static isotropic fluid sphere cannot be arbitrarily massive. However, for a more generalized expression for the mass-to-radius ratio one may refer to the paper by Mak and Harko [11].

For the present compact star model, the effective mass is written as

$$\begin{aligned} M_\mathrm{eff}= & {} 4\pi \int _0^R \rho r^2\mathrm{d}r\nonumber \\= & {} \frac{1}{2}R[1-e^{-\lambda (R)}]=\frac{1}{2}R\left[ \frac{8CR^2(3+CR^2)}{7(1+2CR^2+C^2R^4)}\right] .\nonumber \\ \end{aligned}$$

(56)

The compactness of the star is therefore given by

$$\begin{aligned} u=\frac{M_\mathrm{eff}}{R}=\frac{1}{2}\left[ \frac{8CR^2(3+CR^2)}{7(1+2CR^2+C^2R^4)}\right] . \end{aligned}$$

(57)

Therefore, the surface redshift ($Z$) corresponding to the above compactness factor ($u$) is obtained as

$$\begin{aligned} Z= & {} [1-2u]^{-1/2} - 1\nonumber \\= & {} \left[ 1-\frac{8CR^2(3+CR^2)}{7(1+2CR^2+C^2R^4)}\right] ^{-1/2} - 1. \end{aligned}$$

(58)

We have shown the variation of the physical quantities related to Buchdahl’s mass-to-radius ratio ($2M/R$) for isotropic fluid spheres, and also surface redshift are plotted in Figs. 12 and 13.

Fig. 12

Variation of the mass with radial coordinate $r/R$. (i) $2M/R$ is plotted with a short-dashed line for Her X-1 and a long-dashed line for its upper bound (left panel), (ii) $2M/R$ is plotted with a short-dashed line for a white dwarf and a long-dashed line for its upper bound (right panel)

Fig. 13

Variation of the redshift index radial coordinate $r/R$. $Z$ is plotted with a continuous line for Her X-1 and a long-dashed line for a white dwarf

5 Model parameters and comparison with some of the compact stars

In this section we prepare several data sheets for the model parameters in Tables 1, 2, and 3 and compare those with some of the compact stars, e.g. the strange star Her X-1 and a white dwarf in Table 4. In our present investigation we propose a stable compact star model with the parameters $R=12.5202$ Km and $M=0.8882~M_{\odot }$ (for a white dwarf) and $R=7.7214$ Km and $M=0.8804$ $M_{\odot }$ (for Her X-1). The values of these data points have already been used for plotting the graphs in all figures in Sects. 3 and 4.

Table 3 Values of the model parameters $A$, $B$, $C$, and $\alpha$ for different compact stars

Table 4 Energy densities, central pressure, and Buchdahl condition for different compact star candidates for the above parameter values of Tables 1, 2, and 3

What we have done in the tables is as follows: in Tables 1, 2, and 3 the values of different physical parameters of the strange star Her X-1 and a white dwarf have been provided. Under this data set, we calculate some physical parameters of the compact star, say the central density, the surface density, the central pressure etc. in Table 4. It can be observed that these data are quite satisfactory for the compact stars—whether it is strange star with central density $1.0913 \times 10^{15}$ $\mathrm{gm}/\mathrm{cm}^{-3}$ or a white dwarf with central density $2.3961 \times 10^{14}$ $\mathrm{gm}/\mathrm{cm}^{-3}$. Likewise this feature of compact stars can be explored for some other physical parameters also.

6 Discussion and conclusion

In the present work we have investigated an anisotropic analog of the model due to Durgapal and Fuloria [1] and the possibilities for there being interesting physical properties of the proposed model. As a necessary step we have contracted the anisotropic factor $\Delta$ with the help of both metric potentials $e^{\nu }$ and $e^{\lambda }$. However, $e^{\lambda }$ is considered as in Durgapal and Fuloria [1], whereas $e^{\nu }$ is given by Lake [2].

The field equations are solved by the change of dependent variable method, and under suitable boundary condition the interior metric (2.1) has been joined smoothly at the surface of spheres ($r=R$), to an exterior Schwarzschild metric whose mass is the same as m$(r=R)=M$ [28]. The solution set thus obtained is correlated with the physical properties of some of the compact stars, which include strange stars as well as white dwarfs. It is observed that the model is viable in connection to several physical features, which are quite interesting and acceptable as proposed by other researchers within the framework of General Theory of Relativity.

As a detailed discussion we would like to put forward here that several verification schemes of the model have been performed and we extract expected results some of which are as follows:

• (1) Regularity at the center: the density $\rho$ and radial pressure $p_\mathrm{r}$ and tangential pressure $p_\mathrm{t}$ should be positive inside the star. It is shown that the central density at the center is $\rho _{0}=\rho (r=0)=\frac{72C}{7}$ and $p_\mathrm{r}(r=0)>0$. This means that the density $\rho$ as well as radial pressure $p_\mathrm{r}$ and tangential pressure $p_\mathrm{t}$ all are positive inside the star.

• (2) Causality conditions: it is shown that inside the fluid sphere the speed of sound is less than the speed of light i.e. $0 \le V_\mathrm{sr}=\sqrt{\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }}<1$,    $0 \le V_\mathrm{st}=\sqrt{\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho }}<1$.

• (3) Well behaved condition: the velocity of sound is monotonically decreasing away from the center and it is increasing with the increase of density as can be observed from Fig. 6.

• (4) Energy conditions: from Fig. 9 we observe that the anisotropic fluid sphere composed of strange matter satisfy the null energy condition, the weak energy condition, and the strong energy condition simultaneously at all points in the star.

• (5) Stability conditions: Following Heintzmann and Hillebrandt [31] we note that a neutron star with an anisotropic equation of state is stable for $\gamma > 4/3$ as is observed in Tables 1 and 2 for our model. Also, it is expected that the velocity of sound should be within the range $0=V_\mathrm{si}^2=(\mathrm{d}p_{i}/\mathrm{d}\rho ) \le 1$ [32, 33]. The plots for the radial and transverse velocity of sound in Fig. 7 is everywhere inside the star models.

• (6) Generalized TOV equation: the generalized Tolman–Oppenheimer–Volkoff equation describes the equilibrium condition for the anisotropic fluid subject to gravitational ($F_\mathrm{g}$), hydrostatic ($F_\mathrm{h}$), and anisotropic stress ($F_\mathrm{a}$). Figure 8 shows that the gravitational force is balanced by the joint action of hydrostatic and anisotropic forces to attain the required stability of the model. However, the effect of an anisotropic force is very much less than the hydrostatic force.

• (7) Effective mass–radius relation and surface redshift: for a static spherically symmetric perfect fluid star, the Buchdahl [35] absolute constraint on the maximally allowable mass-to-radius ratio ($M/R$) for isotropic fluid spheres as $2M/R \le 8/9 = 0.8888$ is seen to be maintained in the present model as can be observed from Table 4.

In Sect. 5 we have made a comparative study by using the model parameters and data of two of the compact stars which are, in general, very satisfactory as compared to the observational results. However, at this point we would like to comment that the sample data used for verifying the present model are to be increased to obtain more satisfactory and exhaustive physical features.