1 Introduction

In modern cosmology, our notions concerning the physics of the very early Universe have introduced a new element, the inflationary period [1–6], which provides an attractive approach for solving some problems of the standard Big-Bang model, like the flatness, horizon, and monopoles, among others. However, the essential feature of inflation is that it can generate a novel mechanism to explain the large-scale structure (LSS) of the Universe [7–11] and provide a causal interpretation of the anisotropies observed in the cosmic microwave background (CMB) radiation [12–18].

On the other hand, with respect to the dynamical mechanisms of inflation, the warm inflation scenario, as opposed to the standard cold inflation, has the attractive feature that it avoids the reheating period at the end of the accelerated expansion, because of the decay of the inflaton field into radiation and particles during the slow-roll phase [19, 20]. In the warm inflation scenario the dissipative effects are important, since radiation production occurs concurrently with the inflationary expansion. The dissipating effects arise from a friction term which describes the process of the scalar field decaying into a thermal bath. Also, for the scenario of warm inflation the thermal fluctuations arising from the inflationary epoch may play a fundamental role in producing the initial fluctuations indispensable for the LSS formation [21, 22]. An indispensable condition for the warm inflation scenario to occur is the presence of a radiation field with temperature \(T>H\) during the inflationary expansion of the Universe. Since the thermal and quantum fluctuations are proportional to \(T\) and \(H\), respectively, [19–22], when \(T>H\), the thermal fluctuations of the inflaton field predominates over the quantum fluctuations. Also, inflation ends when the Universe heats up to become radiation dominated, and then the Universe smoothly enters the radiation dominated era, without the need of a reheating scenario [19, 20]. For a review of warm inflation, see e.g. Refs. [23, 24].

On the other hand, cosmological implications of string/M-theory have currently attracted a great deal of attention; specifically, some were concerned with brane–antibrane configurations such as space-like branes [25]. In this configuration, the standard model of particles is confined to the brane, while gravitation propagates into the bulk spacetime. Here, extra dimensions induce extra terms in the Friedmann equation [26–34]. In particular, the cosmological Randall–Sundrum II model (RS II) has received a great deal of attention in the last years [35]. Randall and Sundrum suggested two similar but phenomenologically different brane-world scenarios. In this form, there are two versions of the Randall–Sundrum model, generally called Randall–Sundrum I (RS1) [36] and Randall–Sundrum II (RS2) [35]. Somewhat confusingly, the RS1 model includes two branes, while the RS2 model only contains a single brane.

In the RS1 model, we have two 3-branes separated by a region of five-dimensional anti-de Sitter spacetime. Here, the fifth coordinate is compactified on \(S^1/Z_2\), and the branes have equal magnitude of the brane tension, but with opposite sign; positive and negative tension branes are on the two specified points. In this model of the brane the matter fields are confined on the two branes and the gravity propagates in the five-dimensional bulk. However, one important point of discussion in this brane model is the mechanism that works to select the necessary separation distance between the two branes, called the radius stabilization [37, 38] (see also Refs. [39–47]). Similarly, the stabilization mechanism plays a crucial role in the recuperation of four-dimensional Einstein gravity [48, 49].

In contrast, the RS2 model [35] contains a single, positive tension brane and a non-compact extra dimension is infinite in extent and the radius stabilization is not present in this brane model. On the other hand, in the RS2 model, the observable universe is a four-dimensional time-like hypersurface. The five-dimensional energy-momentum tensor can be split into a regular and a distributional part. The regular part describes the non-standard matter fields in five dimensions and the distributional term containing the brane tension and the standard matter fields on the brane. Except gravitation, all standard model interactions and matter fields are confined to the brane.

These alternatives to Einstein’s general relativity cosmology belong to the so-called brane-world cosmological models. For a comprehensible review of brane-world cosmology, see e.g. Refs. [50, 54–61]. In the observational aspect, nowadays there is strong evidence that the very early Universe could have experienced an inflationary expansion period, as was pointed out in the introduction. An important feature of the inflationary period is that it belongs to a period of cosmological evolution where the effects predicted by string/M-theory are relevant. For this reason, over the last decade, there has been great interest in the construction of inflationary models inspired by these theories. In the following we will concentrate only on the RS2 model, which forms the basis for the rest of this work.

As regards exact solutions, one of the most interesting in the inflationary Universe can be found by using an exponential potential, which is often called power-law inflation, since the scale factor has a power-law-type evolution. Here the scale factor is given by \(a(t)\sim t^{p}\), in which \(p>1\) [62]. Also, an exact solution can be obtained in the de Sitter inflationary Universe, where a constant effective potential is considered; see Ref. [1]. Moreover, exact solutions can also be found for the scenario of intermediate inflation, for which the scale factor \(a(t)\) evolves as

$$\begin{aligned} a(t)=\exp [\,A\,t^{f}], \end{aligned}$$
(1)

where \(A\) and \(f\) are two constants; \(A>0\) and \(0<f<1\) [63–66]. It is well known that the expansion rate in this model is slower than de Sitter inflation, but faster than power-law inflation; this is why it is known as “intermediate”. This inflationary model was originally developed as an exact solution, however, intermediate inflation may be described by a slow-roll analysis. Under the slow-roll approximation the scalar spectral index \(n_s\sim 1\), and for the specific value of \(f\) given by \(f=2/3\) the spectral index is \(n_s=1\) (Harrizon–Zel’dovich spectrum) [67–72]. Also, an important observational quantity in this model is the tensor-to-scalar ratio \(r\), which is significant, \(r\ne 0\) [73–76]. Another motivation to consider this type of expansion for the scale factor comes from string/M-theory, which appears to be relevant in the low-energy string effective action [77–79] (see also Refs. [80–87]). These theories can be utilized to resolve the initial singularity and describe the present acceleration in the universe, among others [88–90]. Also, the approach of considering the warm intermediate inflation has already been studied in the literature [74, 91–94] in the context of other frameworks.

In this way, the goal of this paper is to analyze the possibility that a higher dimensional scenario, in particular the RS II brane-world model, can describe the dynamics of the Universe in its very early epochs. We propose this possibility in the context of a warm inflation scenario for a Universe evolving according to the intermediate scale factor, and we describe how a generalized form of the dissipative coefficient \(\Gamma (T,\phi )\propto T^{m}/\phi ^{m-1}\) influences the dynamics of our model. In order to study our brane-warm-intermediate model we will consider the full effective Friedmann equation, and not the lower energy limit or the high energy limit for the effective Friedmann equation. Also, we will study the cosmological perturbations, which are written in terms of several parameters. Here, the parameters are constrained by the BICEP2 data [95, 96] together with the Planck satellite [17] and Planck 2015 [18] results. On the other hand, it is well known that the BICEP2 experiment data has important theoretical significance for the amplitude of primordial gravitational waves produced during inflation. In this form, the tensor-to-scalar ratio \(r\) from the BICEP2 data has been found at more than 5\(\sigma \) confidence level (CL), in which the ratio \(r=0.2_{-0.05}^{+0.07}\) at 68 \(\%\) CL and with foreground subtracted \(r=0.16_{-0.05}^{+0.06}\) [95, 96]. Nevertheless, this value of the tensor-to-scalar ratio has become less transparent; see e.g. Ref. [97]. In this way, a detailed analysis of the Planck and BICEP2 data would be necessary for a definitive answer to the question of diffuse Galactic dust contamination. Recently, the Planck collaboration published new data of enhanced precision of the CMB anisotropies [18]. Here, the Planck full mission data improved the upper bound on the tensor-to-scalar ratio \(r_{0.002}<0.11 (95\,\% \,\mathrm{CL})\), and this upper bound for the ratio \(r\) is similar to that obtained from Refs. [17, 95, 96], in which \(r<0.12 (95\,\% \,\mathrm{CL})\).

The outline of the paper is as follows: The next section presents a short review of the effective Friedmann equation for the Randall–Sundrum type II scenario. In Sect. 2 we study the dynamics of warm inflation in this brane-world model, in the weak and strong dissipative regimes; specifically, we obtain explicit expressions for the inflaton scalar field, the dissipative coefficient, and the effective scalar potential. Immediately, we compute the cosmological perturbations in both dissipative regimes, obtaining expressions for observational quantities such as the scalar power spectrum, the scalar spectral index, and the tensor-to-scalar ratio. Finally, Sect. 3 summarizes our results and exhibits our conclusions. We choose units so that \(c=\hbar =1\).

2 The brane-intermediate warm inflation scenario

Following Refs. [32–34] we consider a five-dimensional scenario, for which the modified Friedmann equation for a spatially flat Friedmann–Robertson–Walker (FRW) metric has the form

$$\begin{aligned} H^2=\kappa \,\rho \left[ 1+\frac{\rho }{2\tau }\right] +\frac{\Lambda _4}{3}+\frac{\xi }{a^4}, \end{aligned}$$
(2)

where \(H=\dot{a}/a\) represents the Hubble parameter, \(a\) denotes the scale factor, the constant \(\kappa =8\pi G/3=8\pi /3m_p^2\), and the energy density \(\rho \) corresponds to the energy density of the matter content confined to the brane, \(\Lambda _{4}\) is the effective four-dimensional cosmological constant on the brane, and \(\xi /a^4\) denotes the influence of the bulk gravitons on the brane, where \(\xi \) is an integration constant. The term \(\tau \) represents the brane tension and, considering the nucleosynthesis epoch, the value of the brane tension is constrained to be \(\tau >\) (1 MeV)\(^4\) [51]. However, a stronger limit for the value of the brane tension results from the usual tests of a deviation from Newton’s law, for which \(\tau \ge \) (10 TeV)\(^4\); see Refs. [52, 53].

In the following, we will consider that the cosmological constant \(\Lambda _{4}=0\), and once inflation begins, the term \(\xi /a^4\) rapidly becomes unimportant. In this form, the effective Friedmann equation given by Eq. (2) becomes

$$\begin{aligned} H^{2}=\kappa \,\rho \,\left[ 1+{\rho \over 2\,\tau }\right] . \end{aligned}$$
(3)

On the other hand, during warm inflation the Universe is filled with a self-interacting scalar field with energy density \(\rho _{\phi }\) together with a radiation field with energy density \(\rho _{\gamma }\). In this form, the total energy density \(\rho \) of the Universe can be written as \(\rho =\rho _{\phi }+\rho _{\gamma }\). Here, the energy density \(\rho _{\phi }\) and the pressure \(P_{\phi }\) of the scalar field are given by \(\rho _{\phi }=\dot{\phi }^{2}/2+V(\phi )\) and \(P_{\phi }=\dot{\phi }^{2}/2-V(\phi )\), respectively. The term \(V(\phi )\) represents the effective scalar potential. In the following, the dots mean derivatives with respect to cosmic time.

We will assume that the total energy density \(\rho \) is confined in the brane, and then the continuity equation for the total energy density becomes \(\dot{\rho }+3\,H\,(\rho +P)=0\). In this way, following Refs. [19, 20], the dynamical equations for \(\rho _{\phi }\) and \(\rho _{\gamma }\) during warm inflation can be written as

$$\begin{aligned} \dot{\rho _{\phi }}+3\,H\,(\rho _{\phi }+P_{\phi })=-\Gamma \dot{\phi }^{2} \end{aligned}$$
(4)

and

$$\begin{aligned} \dot{\rho }_{\gamma }+4H\rho _{\gamma }=\Gamma \dot{\phi }^{2}. \end{aligned}$$
(5)

Here, \(\Gamma >0\) represents the dissipative coefficient and describes the process of scalar field decaying into radiation during the inflationary expansion [19, 20]. In the context of the brane-warm inflationary model, in Ref. [98] a high energy scenario was studied in the case of the strong dissipative regime.

From quantum field theory, the dissipative coefficient \(\Gamma \) was computed in a supersymmetric model for a low-temperature scenario [99]. In particular, for a scalar field with multiplets of heavy and light fields, it is possible to obtain several expressions for the dissipative coefficient \(\Gamma \); see e.g., [99–105].

Following Refs. [102, 103], we consider a general form for the dissipative coefficient \(\Gamma (T,\phi )\), given by

$$\begin{aligned} \Gamma (T,\phi )=C_{\phi }\,\frac{T^{m}}{\phi ^{m-1}}, \end{aligned}$$
(6)

where the constant \(C_\phi \) is related with the dissipative microscopic dynamics and the exponent \(m\) is an integer. This expression for the dissipative coefficient includes different cases, depending of the values of \(m\); see Refs. [102, 103]. Concretely, for the special value of \(m=3\), for which \(\Gamma = C_{\phi } T^{3}\phi ^{-2}\), the parameter \(C_{\phi }\) agrees with \(C_{\phi }=0.02\,h^{2}\, \mathcal {N}_{Y}\), where a generic supersymmetric model with chiral superfields \(\Phi \), \(X\), and \(Y_i\), \(i=1,\ldots ,\mathcal {N}_Y\), is studied [104–106]. For the special case \(m=1\), the dissipative coefficient is related with the high temperature supersymmetry (SUSY) case. Finally, for the cases \(m=0\) and \(m=-1\), the term \( \Gamma (T,\phi )\) represents an exponentially decaying propagator in the high temperature SUSY model and the non-SUSY case, respectively [100, 107, 108].

Considering that in the scenario of warm inflation the energy density \(\rho _{\phi }\) predominates over the density \(\rho _{\gamma }\) [19–21], Eq. (3) becomes

$$\begin{aligned} H^{2}\approx & {} \kappa \,\rho _{\phi }\,\left( 1+{\rho _{\phi } \over 2\,\tau }\right) \nonumber \\= & {} \kappa \,\left( \frac{\dot{\phi }^2}{2}+V(\phi )\right) \left[ 1+{\dot{\phi }^2+2V(\phi )\over 4\,\tau }\right] . \end{aligned}$$
(7)

In the following, we will not study the effective Friedmann equation, given by Eq. (7), in the lower energy limit i.e., \(\rho _\phi \ll \tau \) or in the high energy limit i.e., \(\rho _\phi \gg \tau \) as our starting point; instead we will consider the full effective Friedmann equation (7). Here, we note that there are two ways of deriving the Friedmann equation from the five-dimensional Einstein equations. The first method is rather simple and considers only the bulk equations. The second approach utilizes the geometrical relationship between four-dimensional and five-dimensional quantities. However, the Einstein equations and, in particular, the Friedmann equation in the bulk include different functions (from the FRW metric in the five-dimensional case). In particular, these functions are subject to conditions (junction conditions) on the brane localized at \(y=0\) and symmetry (\(Z_2\)-symmetry) when integrating over \(y\). In this form, we could not obtain analytical solutions considering the full five-dimensional equations of motion from four-dimensional analytical solutions. In the following, we will obtain analytical solutions in the four-dimensional case of the full effective Friedmann equation only.

In this form, solving the quadratic equation (7) for \(\rho _{\phi }\) (where we take the solution for which \(\dot{\rho }_{\phi }<0\)), and combining with Eq. (4),

$$\begin{aligned} \dot{\phi }^{2}= {\frac{2 }{3\kappa }}\frac{(-\dot{H})}{(1+R)} \,\left[ 1+{2\,H^2 \over \kappa \,\tau }\right] ^{-1/2}, \end{aligned}$$
(8)

results, where the quantity \(R\) denotes the ratio between \(\Gamma \) and the Hubble parameter, defined as

$$\begin{aligned} R=\frac{\Gamma }{3H}. \end{aligned}$$
(9)

In the following, we will assume that for the case of the weak or strong dissipation regime, the ratio \(R\) satisfies \(R<1\) or \(R>1\), respectively.

Also, following Refs. [19–21], we consider that during warm inflation the radiation production is quasi-stable, i.e., \(\dot{\rho }_{\gamma }\ll 4H\rho _{\gamma }\) and \(\dot{\rho }_{\gamma }\ll \Gamma \dot{\phi }^{2} \). In this form, combining Eqs. (5) and (8), the energy density of the radiation field results:

$$\begin{aligned} \rho _{\gamma }=\frac{\Gamma \dot{\phi }^{2}}{4H}=\frac{\Gamma (-\dot{H})}{6\kappa H(1+R)} \,\left[ 1+{2\,H^2 \over \kappa \,\tau }\right] ^{-1/2}. \end{aligned}$$
(10)

On the other hand, we assume that the energy density of the radiation field is given by \(\rho _{\gamma }=C_{\gamma }\,T^{4}\), where the constant \(C_{\gamma } =\pi ^{2}\,g_{*}/30\) and the term \(g_{*}\) represents the number of relativistic degrees of freedom. Combining the above expression for the energy density \(\rho _{\gamma }\) and Eq. (10), we find that the temperature of the thermal bath \(T\) yields

$$\begin{aligned} T=\left[ \frac{\Gamma \,(-\dot{H})}{6\,\kappa \,\,C_{\gamma }H\,(1+R)}\right] ^{1/4} \,\left[ 1+{2\,H^2 \over \kappa \,\tau }\right] ^{-1/8}. \end{aligned}$$
(11)

From Eqs. (3) and (8), the effective scalar potential results:

$$\begin{aligned} V= & {} \tau \,\left( -1+\sqrt{1+{2\,H^2 \over \kappa \,\tau }}\right) \nonumber \\&+\,\frac{\dot{H}}{3\kappa (1+R)} \,\left( 1+{2\,H^2 \over \kappa \,\tau }\right) ^{-1/2}. \end{aligned}$$
(12)

Here, we note that the effective potential could be determined explicitly in terms of the scalar field \(\phi \), in the weak (or strong) dissipative regime.

Now, combining Eqs. (11) and (6) we get

$$\begin{aligned} \Gamma ^{{\frac{4-m }{4}}}\!=\!C_{\phi }\phi ^{1-m} \left[ \frac{-\dot{H}}{6\kappa \, C_{\gamma }H(1+R)}\right] ^{m/4}\, \left( 1\!+\!{2\,H^2 \over \kappa \,\tau }\right) ^{-m/8}. \end{aligned}$$
(13)

We note that the above expression determines the dissipation coefficient in the weak (or strong) dissipative regime in terms of the scalar field \(\phi \).

In the following, we will study our brane model for the general form of the dissipative coefficient, given by Eq. (6), during intermediate inflation, where the scale factor evolves according to Eq. (1). We will restrict ourselves to the cases \(R<1\) (weak regime) and \(R>1\) (strong regime). Also, in the following, we will study the cases \(m=3\), \(m=1\), \(m=0\), and \(m=-1\), corresponding to the dissipative coefficient \(\Gamma =\Gamma (T,\phi )\).

2.1 The weak dissipative regime

Firstly, we assume that our brane model evolves in agreement with the weak dissipative regime, i.e., \(R<1\) (or analogously \(\Gamma <3H\)). In this form, combining Eqs. (1) and (8), the solution for the standard scalar field \(\phi \) results:

$$\begin{aligned} \phi (t)-\phi _{0}=\frac{B[t]}{K}, \end{aligned}$$
(14)

here the quantity \(\phi (t=0)=\phi _0\) is an integration constant that can be assumed to obey \(\phi (t=0)=\phi _0=0\) (without loss of generality), and the constant \(K\) is specified by \( K= \sqrt{\frac{6\,\kappa \,(1-f)}{A\,f}}\left( { \kappa \,\tau \over 2A^2f^2}\right) ^{\frac{1}{2(1-f)}}. \) The function \(\mathcal {B}[t]\), represents the incomplete Beta function [109–112], given by

$$\begin{aligned} B[t]= B\left[ -\frac{\kappa \tau \,t^{2(1-f)} }{2(Af)^{2}};\frac{1}{4(1-f)},\frac{3}{4}\right] . \end{aligned}$$

From Eqs. (1) and (14), we find that the Hubble parameter \(H\) as a function of the scalar field results; \( H(\phi )=A\,f\,\left( B^{-1}[K\,\phi ]\right) ^{-(1-f)}\). Here, the function \(B^{-1}[K\,\phi ]\) corresponds to the inverse of the incomplete Beta function \(B[t]\) [109–112].

The effective potential as a function of the scalar field \(\phi \), from Eq. (12) and considering that \(V>\dot{\phi }^2/2\), results:

$$\begin{aligned} V(\phi )\simeq \tau \,\left( -1+ \sqrt{1+{2\,A^2f^2\left( B^{-1}[K\,\phi ]\right) ^{-2(1-f)} \over \kappa \,\tau }}\right) . \end{aligned}$$
(15)

Taking \(R<1\), from Eq. (13), the dissipative coefficient \(\Gamma \) in terms of the scalar field becomes

$$\begin{aligned}&\Gamma (\phi )=\,C_{\phi }^{{\frac{4}{4-m}}}\left[ \frac{1-f}{6\kappa \,C_{\gamma }\,B^{-1}[K\,\phi ]}\right] ^{\frac{m}{4-m}}\nonumber \\&\quad \times \,\phi ^{{\frac{4(1-m) }{4-m}}} \,\left( 1+{2\,A^2f^2\left( B^{-1}[K\,\phi ]\right) ^{-2(1-f)}\over \kappa \,\tau }\right) ^{-\frac{m}{2(4-m)}},\nonumber \\ \end{aligned}$$
(16)

for the case \(m \ne 4\).

From the definition of the dimensionless slow-roll parameter \(\varepsilon =-\frac{\dot{H}}{H^{2}}\), we find that \( \varepsilon =\left( {\frac{1-f}{Af}}\right) {1\over (B^{-1}[K\,\phi ])^{f}}. \) In this form, and considering that the condition for inflation to occur is determined by \(\varepsilon <\)1 (or equivalently \(\ddot{a}>0\)), the scalar field during warm inflation satisfies the condition \(\phi >{1\over K}B\left[ \left( {\frac{1-f}{Af}}\right) ^{1/f}\right] \).

On the other hand, from Eqs. (1) and (14), the number of e-folds \(N\) between two different values of the scalar field, denoted \(\phi _{1}\) and \(\phi _{2}\), is

$$\begin{aligned} N= & {} \int _{t_{1}}^{t_{2}}\,H\,\mathrm{d}t=A\,\left( t_{2}^{f}-t_{1}^{f}\right) \nonumber \\= & {} A\left[ (B^{-1}[K\,\phi _{2}])^{f}-(B^{-1}[K\,\phi _{1}])^{f} \right] . \end{aligned}$$
(17)

Following Refs. [75, 76], the inflationary phase begins at the earliest possible scenario. In this way, the scalar field \(\phi _{1}\) takes the value

$$\begin{aligned} \phi _{1}={1\over K}B\left[ \left( {\frac{1-f}{Af}}\right) ^{1/f}\right] \;. \end{aligned}$$
(18)

In the following, we will study the scalar and tensor perturbations for our brane-warm model during the weak dissipative regime. For the case of the scalar perturbation, it could be stated as \({\mathcal {P} _{\mathcal {R}}}^{1/2}=\frac{H}{\dot{\phi }}\,\delta \phi \) [19, 20]. It is well known that in the warm inflation scenario the scalar field fluctuations are predominantly thermal rather than quantum [19–21]. In particular, for the weak dissipation regime, the amplitude of the scalar field fluctuation \(\delta \phi ^{2}\) is given by \(\delta \phi ^{2}\simeq H\,T\) [21]. In this way, from Eqs. (8), (11), and (13), the power spectrum, \({\mathcal {P}_{\mathcal {R}}}\), results:

$$\begin{aligned} {\mathcal {P}_{\mathcal {R}}}= & {} {3\sqrt{3\pi }\,\kappa \over 4}\, \left( \frac{C_{\phi }}{6\kappa C_{\gamma }}\right) ^{{\frac{1}{4-m}}}\phi ^{{\frac{1-m}{4-m}}}H^{{\frac{11-3m}{4-m}}}(-\dot{H})^{-{\frac{(3-m)}{4-m}}}\nonumber \\&\times \left( 1+{2 H^{2}\over \kappa \tau } \right) ^{{\frac{3-m}{2(4-m)}}}. \end{aligned}$$
(19)

Now, combining Eqs. (1) and (14), we find that the power spectrum as a function of the field \(\phi \) can be written as

$$\begin{aligned} {\mathcal {P}_{\mathcal {R}}}(\phi )= & {} k_{1}\,\,\phi ^{\,\frac{1-m}{4-m}} \left( B^{-1}[K\,\phi ] \right) ^{\frac{2f(4-m)+m-5}{4-m}} \nonumber \\&\times \left[ 1+\frac{2A^{2}f^{2}}{\kappa \tau (B^{-1}[K\,\phi ])^{2(1-f)}} \right] ^{\frac{3-m}{2(4-m)}}, \end{aligned}$$
(20)

where the constant \(k_{1}\) is defined as \(k_{1}={3\sqrt{3\pi }\,\kappa \over 4}\left( \frac{C_{\phi }}{6\kappa C_{\gamma }}\right) ^{{\frac{1}{4-m}}}(A\,f)^{{8-2m\over 4-m}} \,(1-f)^{{\frac{m-3}{4-m}}}\).

On the other hand, the scalar power spectrum can be expressed in terms of the number of \(e\)-folds \(N\) as

$$\begin{aligned} {\mathcal {P}_{\mathcal {R}}}(N)= & {} k_{2}\,\,(B[J(N)])^{\,\frac{1-m}{4-m}} \left( J[N] \right) ^{\frac{2f(4-m)+m-5}{4-m}} \nonumber \\&\times \left[ 1+\frac{12A^{2}f^{2}}{\kappa \tau (J[N])^{2(1-f)}} \right] ^{\frac{3-m}{2(4-m)}}, \end{aligned}$$
(21)

where the quantities \(J(N)\) and \(k_{2}\) are given by \( J(N)=\left[ {1+f(N-1)\over Af} \right] ^{\frac{1}{f}}, \) and \( k_{2}=k_{1}K^{-\frac{1-m}{4-m}} \), respectively.

From the definition of the scalar spectral index \(n_{s}\), given by the relation \(n_{s}-1=\frac{\mathrm{d}\ln \,{\mathcal {P}_{R}}}{\mathrm{d}\ln k}\), and combining Eqs. (14) and (20), the scalar spectral index can be written as

$$\begin{aligned} n_{s}=1-{5-m-2f(4-m)\over Af(4-m)(B^{-1}[K\,\phi ])^f} +n_2 +n_3, \end{aligned}$$
(22)

where \(n_2\) and \(n_3\) are defined as

$$\begin{aligned} n_{2}= & {} {1-m \over 4-m}\sqrt{{2(1-f)\over 3 \kappa Af}} {(B^{-1}[K\,\phi ])^{-f/2}\over \phi }\nonumber \\&\times \left[ 1+\frac{2A^{2}f^{2}}{\kappa \tau (B^{-1}[K\,\phi ])^{2(1-f)}} \right] ^{-1/4} \end{aligned}$$

and

$$\begin{aligned} n_{3}= & {} -{2Af(1-f)(3-m) \over \kappa \tau (4-m)}(B^{-1}[K\,\phi ])^{-(2-f)} \nonumber \\&\times \left[ 1+\frac{2A^{2}f^{2}}{\kappa \tau (B^{-1}[K\,\phi ])^{2(1-f)}} \right] ^{-1}. \end{aligned}$$

Analogously to the scalar power spectrum, the scalar spectral index can be expressed in terms of the number of \(e\)-folds. Considering Eqs. (17) and (18) yields

$$\begin{aligned} n_{s}=1-\frac{5-m-2f(4-m)}{(4-m)[1+f(N-1)]}+n_2 +n_3, \end{aligned}$$
(23)

where now

$$\begin{aligned} n_{2}= & {} K{1-m \over 4-m}\sqrt{{2(1-f)\over \kappa Af}} {(J[N])^{-f/2}\over B[J(N)]}\\&\times \left[ 1+\frac{12A^{2}f^{2}}{\kappa \tau (J[N])^{2(1-f)}}\right] ^{-1/4} \end{aligned}$$

and

$$\begin{aligned} n_{3}= & {} -{2Af(1-f)(3-m) \over \kappa \tau (4-m)}(J[N])^{-(2-f)}\\&\times \left[ 1+\frac{12A^{2}f^{2}}{\kappa \tau (J[N])^{2(1-f)}}\right] ^{-1}. \end{aligned}$$

It is well known that the generation of tensor perturbations during the inflationary scenario would produce gravitational waves. The power spectrum of the tensor perturbations is more complicated in our model because in the brane-world gravitons propagate into the bulk. In this form, following Ref. [113], the power spectrum of the tensor perturbations \({\mathcal {P}}_{g}\) is given by \({\mathcal {P}}_{g}=24\kappa (H/2\pi )^{2}F^{2}(x)\). Here, \(x\) is defined as \( x=Hm_p\,\sqrt{3/(4\pi \tau )}, \) and the function \(F(x)\) is given by

$$\begin{aligned} F(x)=[\sqrt{1+x^2}-x^2\,\sinh ^{-1}(1/x)]^{-1/2}. \end{aligned}$$

The function \(F(x)\) is a correction to the standard general relativity and arises from the normalization of a graviton zero-mode [113].

In this way, we may compute an important observational quantity, the tensor-to-scalar ratio \(r\), defined as \(r={\mathcal {P}}_{g}/{\mathcal {P}_{\mathcal {R}}}\). Then considering Eq. (20) and \({\mathcal {P}}_{g}\) in terms of the scalar field, the tensor-to-scalar ratio can be written as

$$\begin{aligned} r(\phi )= & {} {6\,\kappa \,A^2 f^2 \over \pi ^2\,k_{1}} \,\phi ^{\,-\frac{1-m}{4-m}} \left( B^{-1}[K\,\phi ] \right) ^{-\frac{3-m}{4-m}} \nonumber \\&\times \left[ 1+\frac{2A^{2}f^{2}}{\kappa \tau (B^{-1}[K\,\phi ])^{2(1-f)}}\right] ^{-\frac{3-m}{2(4-m)}}F^{2}(\phi ). \end{aligned}$$
(24)

Similarly to before, the tensor-to-scalar ratio can be expressed in terms of the number of \(e\)-folds, yielding

$$\begin{aligned} r(N)= & {} {6\,\kappa \,A^2 f^2 \over \pi ^2\,k_{2}} (B[J(N)])^{-\frac{1-m}{4-m}} \left( J[N] \right) ^{-\frac{3-m}{4-m}}\nonumber \\&\times \left[ 1+\frac{12A^{2}f^{2}}{\kappa \tau (J[N])^{2(1-f)}} \right] ^{-\frac{3-m}{2(4-m)}}F^{2}(N). \end{aligned}$$
(25)
Fig. 1
figure 1

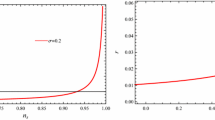
The evolution of the ratio \(\Gamma \!/\!3H\) versus the scalar spectrum index \(n_s\) (upper panel) and the evolution of the ratio \(T\!/\!H\) versus the scalar spectral index \(n_s\) (lower panel) in the weak dissipative regime for the special case \(m=1\) (\(\Gamma \propto T\)), for different values of the parameter \(C_\phi \). In both panels, the solid, dotted, and dashed lines correspond to the pairs (\(A=0.19\), \(f=0.31\)), (\(A=0.28\), \(f=0.32\)), and (\(A=0.32\), \(f=0.30\)), respectively. Also, in these plots we have used the values \(C_\gamma =70\), \(m_p=1\), and \(\tau =10^{-14}\)

Full size image
Fig. 2
figure 2

The upper and lower panels show the evolution of the tensor-to-scalar ratio \(r\) versus the scalar spectral index \(n_s\) in the weak dissipative regime for the special case \(m=0\) (\(\Gamma \propto \phi \)), for different values of the parameter \(C_\phi \). In both panels, the solid, dotted, and dashed lines correspond to the pairs (\(A=0.47\), \(f=0.29\)), (\(A=0.43\), \(f=0.28\)), and (\(A=0.39\), \(f=0.29\)), respectively. Also, in both panels we have used the values \(C_\gamma =70\), \(m_p=1\), \(\tau =10^{-14}\), and the two-dimensional marginalized constraints from Refs. [95, 96] (upper panel) and the new data from Planck 2015 [18] (lower panel)

Full size image

In Fig. 1 we show the evolution of the ratio \(\Gamma /3H\) versus the scalar spectral index (upper panel) and the evolution of the ratio \(T\!/\!H\) versus the scalar spectral index (lower panel), in the weak dissipative regime for the specific case in which the dissipative coefficient is given by \(\Gamma (\phi ,T)=C_\phi \,T\), i.e., \(m=1\). In both panels, we have used three different values of the parameter \(C_\phi \). The upper panel shows the condition for the weak dissipative regime in which \(\Gamma <3H\). In the lower panel we show the necessary condition for warm inflation scenario, in which the temperature \(T>H\). Combining Eqs. (1), (13), and (14), we numerically find the ratio \(\Gamma /3H\) as a function of the scalar spectral index \(n_s\). Analogously, from Eqs. (1) and (11), we numerically obtain the ratio between the temperature of the thermal bath \(T\) and the Hubble parameter \(H\), i.e., \(T\!/\!H\) in terms of the spectral index \(n_s\). In both plots, we consider the values \(C_\gamma =70\), \(m_p=1\), and \(\tau =10^{-7}\). Also, numerically from Eqs. (21) and (23) we obtain the values \(A=0.19\) and \(f=0.31\) corresponding to the value of the parameter \(C_\phi =10^{-2}\), for the values \({\mathcal {P}_{\mathcal {R}}}=2.43\times 10^{-9}\), \(n_s=0.96\), and the number of \(e\)-folds \(N=60\). Analogously, for the value \(C_\phi =10^{-4}\), the values obtained for the parameters \(A\) and \(f\) are given by \(A=0.28\) and \(f=0.32\), respectively. Finally, for the value \(C_\phi =10^{-6}\), we obtain the values \(A=0.32\) and \(f=0.30\). From the upper plot, we find an upper bound for the parameter \(C_\phi \), from the condition of the weak dissipative regime, i.e., \(\Gamma <3H\), for which \(C_\phi \le 10^{-2}\). From the lower panel we obtain a lower bound for \(C_\phi \), considering the essential condition for warm inflation \(T>H\), where \(C_\phi \ge 10^{-6}\). In relation to the consistency relation \(r=r(n_s)\), we find the ratio \(r\sim 0\) for this range of \(C_\phi \); then the case \(m=1\) (or equivalently \(\Gamma \propto T\)) during the weak dissipative regime is disproved by the BICEP2 experiment, because \(r=0.2_{-0.05}^{+0.07}\) and further the ratio \(r=0\) is discarded at 7.0\(\sigma \). However, the Planck data analysis obtained only an upper limit for the tensor-to-scalar ratio \(r\) given by \(r<0.11\); then the range of \(C_\phi \) is well corroborated by the Planck satellite results. In this form, for the specific case of \(m=1\), the range of the parameter \(C_\phi \) is given by \(10^{-6}\le C_\phi \le 10^{-2}\). Also, we note that when we decrease the value of the parameter \(C_\phi < 10^{-6}\), the value of the tensor-to-scalar ratio \(r\simeq 0\). In particular, for the value \(C_\phi =10^{-6}\), we get \(r\mid _{n_s=0.96}\) \(\simeq \) \(7\times 10^{-4}\). It is interesting to note that the range for the parameter \(C_\phi \) for the case \(\Gamma \propto T\) results from the conditions \(\Gamma <3H\) and \(T>H\).

In Fig. 2 we show the tensor-to-scalar ratio \(r\) versus the scalar spectral index \(n_s\), for the special case of \(m=0\), i.e., \(\Gamma \propto \phi \) in the weak dissipative regime (\(\Gamma <3H\)). In the upper panel we show the two-dimensional marginalized constraints for the tensor-to-scalar ratio \(r=r(n_s)\) (at 68 and 95 \(\%\) levels of confidence), from the BICEP2 experiment data in connection with Planck satellite\(+\) WP\(+\) highL [95, 96]. In the lower panel are the new results from Planck 2015 [18]. Here, the marginalized joint 68 and 95 \(\%\) CL regions for the spectral index \(n_s\) and \(r_{0.002}\). From Eqs. (23) and (25), we numerically obtain the consistency relation \(r=r(n_s)\) and, as before, we consider three values of the parameter \(C_\phi \). Again, we take the values \(C_\gamma =70\), \(m_p=1\), and \(\tau =10^{-14}\). From these plots we observe the tensor-to-scalar ratio \(r\sim 0\) for the specific case of \(m=0\), and then this case is disproved by the BICEP2 experiment (upper panel); however, it is well corroborated by the Planck data and in particular by the new data (lower panel). We observe that the new results from Planck 2015 place more substantial limits on the consistency relation \(r=r(n_s)\) compared with the BICEP2 experiment.

In particular for the value of \(C_\phi =10^{-21}\) (solid line in the figure), we get \(r\mid _{n_s=0.96}\) \(\simeq \) \(2\times 10^{-3}\). From the essential condition for warm inflation \(T>H\), we find a lower limit for the parameter \(C_\phi \) given by \(C_\phi \ge 10^{-21}\) and, considering the condition of the weak dissipative regime, where \(\Gamma <3H\), we obtain an upper bound for \(C_\phi \), and it corresponds to \(C_\phi \le 10^{-15}\) (figure not shown). In this form, for the special case of \(m=0\) (or equivalently \(\Gamma \propto \phi \)), the range for the parameter \(C_\phi \) is given by \(10^{-21}\le C_\phi \le 10^{-15}\).

For the cases \(m=3\) and \(m=-1\), we find the tensor-to-scalar ratio \(r\sim 0\); then these cases are disproved by the BICEP2 data. Nevertheless, they are well corroborated by the Planck satellite and Planck 2015 data. Considering the essential condition for warm inflation \(T>H\), we obtain a lower bound for the parameter \(C_\phi \); for the case \(m=3\) the bound is \(10^{22}\le C_\phi \) and for the case \(m=-1\) it corresponds to \(10^{-34}\le C_\phi \). In particular, for the value \(C_\phi =10^{22}\) it corresponds to \(\left( \frac{T}{H}\right) \mid _{n_s=0.96}\) \(\simeq \) \(1.86\) when \(m=3\), and for \(C_\phi =10^{-34}\) it corresponds to \(\left( \frac{T}{H}\right) \mid _{n_s=0.96}\) \(\simeq \) \(1.57\) for the case \(m=-1\). From the condition of a weak dissipative regime, \(\Gamma <3H\), we find an upper bound for \(C_\phi \); for the case \(m=3\) the upper bound is \(C_\phi \le 10^{23}\), and for the specific case \(m=-1\), \(C_\phi \le 10^{-28}\) results. In particular, for the value \(C_\phi =10^{23}\) it corresponds to \(\left( \frac{\Gamma }{3H}\right) \mid _{n_s=0.96}\) \(\simeq \) \(0.44\) when \(m=3\), and for \(C_\phi =10^{-28}\) it corresponds to \(\left( \frac{\Gamma }{3H}\right) \mid _{n_s=0.96}\) \(\simeq \) \(0.18\) for the case \(m=-1\). In this form, from the conditions \(T>H\) and \(\Gamma <3H\), the ranges for the parameter \(C_\phi \) are given by \(10^{22}\le C_\phi \le 10^{23}\) for the case \(m=3\) and \(10^{-34}\le C_\phi \le 10^{-28}\) for the case \(m=-1\).

2.2 The strong dissipative regime

Now we consider the case of a strong dissipative regime \(R>1\) (or equivalently \(\Gamma >3H\)), together with the scalar factor \(a(t)\) of intermediate inflation; see Eq. (1). Considering Eqs. (8) and (13), we find the solution for the scalar field \(\phi (t)\). In particular, we must analyze our solution for two separate cases, namely \(m=3\) and \(m\ne 3\). For the special case of \(m=3\), the solution for the scalar field results:

$$\begin{aligned} \phi (t)-\phi _0=\frac{\tilde{B}[t]}{\tilde{K}}, \end{aligned}$$
(26)

as before, the value of \(\phi (t=0)=\phi _{0}\) is an integration constant and \(\tilde{K}\) is a constant given by

$$\begin{aligned} \tilde{K}\equiv & {} \left( \frac{4C_{\phi }}{\tau }\right) ^{1/2}\left( \frac{1}{2\kappa C_{\gamma }}\right) ^{3/8}\\&\times \left[ \left( \frac{\kappa \tau }{2}\right) ^{\frac{4-3(f-2)}{2(1-f)}}\left( \frac{(1-f)^{1-f}}{Af}\right) ^{7}\right] ^{1/8(1-f)}, \end{aligned}$$

and \(\tilde{B}[t]\) is a new function that is defined by

$$\begin{aligned} \tilde{B}[t]\equiv B\left[ -\frac{\kappa \tau }{2(Af)^2}t^{2(1-f)};\,\frac{4f+3}{16(1-f)},\, \frac{15}{16}\right] , \end{aligned}$$
(27)

and it corresponds to the incomplete beta function [109–112].

On the other hand, the solution of the scalar field for the special case \(m\ne 3\) yields

$$\begin{aligned} \varphi (t)-\varphi _0=\frac{\tilde{B}_{m}[t]}{\tilde{K}_{m}}, \end{aligned}$$
(28)

where the scalar field \(\phi (t)\) is redefined as \(\varphi (t)=\frac{2}{3-m}\phi (t)^{\frac{2}{3-m}}\) and as before \(\varphi _0\) is an integration constant that can be assumed \(\varphi _0=0\). The quantity \(\tilde{K}_m\) is a new constant given by \(\tilde{K}_m\equiv \left( \frac{4C_{\phi }}{\tau }\right) ^{1/2}\left( \frac{1}{2\kappa C_{\gamma }}\right) ^{m/8}\left[ \left( \frac{\kappa \tau }{2}\right) ^ {\frac{4-m(f-2)}{2(1-f)}}\right. \times \left. \left( \frac{(1-f)^{1-f}}{Af}\right) ^{4+m}\right] ^{1/8(1-f)}\), and the new function \(\tilde{B}_m[t]\) for the special case in which \(m\ne 3\) is defined as

$$\begin{aligned} \tilde{B}_m[t]\equiv B\left[ -\frac{\kappa \tau }{2(Af)^2}t^{2(1-f)}; \,\frac{4f+m}{16(1-f)},\,\frac{12+m}{16}\right] . \end{aligned}$$
(29)

From Eqs. (1), (26), and (28), we find that the Hubble parameter \(H=H(\phi )\) yields

$$\begin{aligned} H(\phi )=\frac{Af}{(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{1-f}},\quad \text {for}\,m=3, \end{aligned}$$
(30)

and for the special case of \(m\ne 3\) we have

$$\begin{aligned} H(\phi )=\frac{Af}{(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{1-f}}. \end{aligned}$$
(31)

By considering Eq. (12), the scalar potential under the slow-roll approximation for both values of \(m\) is given by

$$\begin{aligned} V(\phi )= \tau \left( -1+\left[ 1+\frac{2A^2f^2}{\kappa \tau (\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{2(1-f)}}\right] ^{1/2}\right) , \end{aligned}$$
(32)

for the special case \(m=3\), and

$$\begin{aligned} V(\phi )=\tau \left( -1+\left[ 1+\frac{2A^2f^2}{\kappa \tau (\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{2(1-f)}}\right] ^{1/2}\right) , \end{aligned}$$
(33)

for the value of \(m\ne 3\).

The dissipative coefficient \(\Gamma \) in terms of the scalar field, can be obtained combining Eqs. (13), (26), and (28) to give

$$\begin{aligned} \Gamma (\phi )=\delta \phi ^{-2}(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{-\frac{3(2-f)}{4}}\left[ 1+\frac{2H^2}{\kappa \tau }\right] ^{-3/8}, \end{aligned}$$
(34)

for the case \(m=3\), in which the constant \(\delta \) is defined as \(\delta =C_{\phi }\left[ \frac{Af(1-f)}{2\kappa C_{\gamma }}\right] ^{3/4}\). For the value of \(m\ne 3\) we find

$$\begin{aligned} \Gamma (\phi )=\delta _m \phi ^{1-m}(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-\frac{m(2-f)}{4}}\left[ 1+\frac{2H^2}{\kappa \tau }\right] ^{-m/8}, \end{aligned}$$
(35)

where \(\delta _m\) is a constant and is given by \(\delta _m\!=\!C_{\phi }\left[ \frac{Af(1-f)}{2\kappa C_{\gamma }}\right] ^{m/4}\).

Analogous to the case of the weak dissipative regime, the dimensionless slow-roll parameter \(\varepsilon \) is given by \( \varepsilon =-\frac{\dot{H}}{H^{2}}=\frac{1-f}{Af(\tilde{B}^{-1}[\tilde{K}\ln \phi ]) ^f}\) for \(m=3\), and for the value of \(m\ne 3\) we find \(\varepsilon =\frac{1-f}{Af(\tilde{B}_m^{-1}[\tilde{K}_ m\varphi ])^f}\). Again, if \(\ddot{a}>0\), then the scalar field \(\phi >\exp \left[ \frac{1}{\tilde{K}}\tilde{B}\left[ (\frac{1-f}{Af})^{1/f}\right] \right] \), for the special case \(m=3\), and for the case \(m\ne 3\) the new scalar field satisfies \(\varphi >\frac{1}{\tilde{K}_m}\tilde{B}_m\left[ (\frac{1-f}{Af})^{1/f}\right] \). Analogously to before, the inflationary scenario begins (\(\varepsilon =1\)) when the scalar field takes the value \(\phi _1=\exp \left[ \frac{1}{\tilde{K}}\tilde{B}\left[ (\frac{1-f}{Af})^{1/f}\right] \right] \), for \(m=3\), and \(\varphi _1=\frac{1}{\tilde{K}_m}\tilde{B}_m\left[ (\frac{1-f}{Af})^{1/f}\right] \) for the special case of \(m\ne 3\).

The number of e-folds \(N\) in this regime can be written using Eqs. (1), (26), and (28), to give

$$\begin{aligned} N=\int _{t_{1}}^{t_{2}}\,H\,\mathrm{d}t=A[(\tilde{B}^{-1}[\tilde{K}\ln \phi _2])^f-(\tilde{B}^{-1}[\tilde{K}\ln \phi _1])^f], \end{aligned}$$
(36)

for the case of \(m=3\), and for the special case of \(m\ne 3\) we have

$$\begin{aligned} N=A[(\tilde{B}_m^{-1}[\tilde{K}_m\varphi _2])^f-(\tilde{B}_ m^{-1}[\tilde{K}_m\varphi _1])^f]. \end{aligned}$$
(37)

Analogous to the case of the weak dissipative regime, now we will analyze the cosmological perturbations in which \(R=\Gamma /3H>1\) (strong dissipative regime). For the strong dissipative regime, the fluctuation \(\delta \phi ^2\) is given by \(\delta \phi ^{2}\simeq \frac{k_{F}T}{2\pi ^{2}}\), see Refs. [19, 20], where \(k_{F}\) corresponds to the wave-number; it is determined as \(k_{F}=\sqrt{\Gamma H}=H\sqrt{3R}>H\). In this way, the power spectrum of the scalar perturbation in this regime, from Eqs. (1), (11), and (13), can be written as

$$\begin{aligned} P_{\mathcal {R}}\simeq \frac{H^{\frac{5}{2}}\Gamma ^{\frac{1}{2}}T}{2\pi ^{2} \dot{\phi }^{2}}= & {} \frac{\kappa }{4\pi ^2}C_{\phi }^{3/2}\phi ^{\frac{3(1-m)}{2})}H^{3/2}(-\dot{H})^{\frac{3m-6}{8}}\nonumber \\&\times \left[ 1+\frac{2H^2}{\kappa \tau }\right] ^{-\frac{(3m-6)}{16}}. \end{aligned}$$
(38)

Analogously to before, we can find the power spectrum \(\mathcal {P}_{\mathcal {R}}\) in terms of the scalar field \(\phi \) for both values of the parameter \(m\). In this form, considering Eqs. (1), (26), (28), and (38) yields

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}= & {} k(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^ {\frac{3(5f-6)}{8}}\phi ^{-3}\nonumber \\&\times \left[ 1+\frac{2(Af)^2(\tilde{B}^{-1} [\tilde{K}\ln \phi ])^{-2(1-f)}}{\kappa \tau }\right] ^{-3/16}, \end{aligned}$$
(39)

for the case of \(m=3\). Here the constant \(k\) is given by \(k=\frac{k}{4\pi ^2}C_{\phi }^{3/2} \left( \frac{1}{2\kappa C_{\gamma }}\right) ^{11/8}(Af)^{15/8}(1-f)^{3/8}\).

Now, the spectrum of the scalar perturbation for the special case of \(m\ne 3\) results:

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}= & {} k_m(\tilde{B}_m^{-1}[\tilde{K}_\varphi ])^{\frac{3[f(2+m)-2m]}{8}}\phi ^{\frac{3(1-m)}{2}}\nonumber \\&\times \left[ 1+\frac{2(Af)^2(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-2(1-f)}}{\kappa \tau }\right] ^{-\frac{(3m-6)}{16}}, \end{aligned}$$
(40)

where \(k_m\) is a constant given by \(k_m=\frac{k}{4\pi ^2}C_{\phi }^{3/2}\left( \frac{1}{2\kappa C_{\gamma }}\right) ^{\frac{3m+2}{8}}(Af)^{\frac{3m+6}{8}}(1-f)^{\frac{3m-6}{8}}\).

Also, the scalar power spectrum can be rewritten in terms of the number of \(e\)-folds \(N\). From Eqs. (36) and (37), the power spectrum \(\mathcal {P}_{\mathcal {R}}\) becomes

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}= & {} k(J[N])^{\frac{3(5f-6)}{8}}\exp \left( -\frac{\tilde{B}[J[N]]}{\tilde{K}}\right) \nonumber \\&\times \left[ 1+\frac{2(Af)^2(J[N])^{-2(1-f)}}{\kappa \tau }\right] ^{-3/16}, \end{aligned}$$
(41)

for the specific case of \(m=3\), and for the case \(m\ne 3\) we have

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}= & {} \tilde{\gamma }_m(J[N])^{\frac{3[f(2+m)-2m]}{8}}(\tilde{B}_m[J[N]])^{\frac{3(1-m)}{3-m}}\nonumber \\&\times \left[ 1+\frac{2(Af)^2(J[N)^{-2(1-f)}}{\kappa \tau }\right] ^{-\frac{(3m-6)}{16}}, \end{aligned}$$
(42)

where the constant \(\tilde{\gamma }_m\) in the above equation is given by \(\tilde{\gamma }_m=k_m\left( \frac{2\tilde{K}_m}{3-m}\right) ^{-\frac{3(1-m)}{3-m}}\).

For this regime the scalar spectral index \(n_s\) for the specific case of \(m=3\) from Eqs. (39) and (40) results

$$\begin{aligned} n_s=1+\frac{3(5f-6)}{8Af}(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{-f}+ n_1+n_2. \end{aligned}$$
(43)

Here the new functions \(n_1\) and \(n_2\) are given by \(n_1=-3\left( \frac{2}{\kappa }\right) ^{1/2}\frac{1}{C_{\phi }^{1/2}}\left( \frac{1}{2\kappa C_{\gamma }}\right) ^{-3/8}(Af)^{-3/8}\times (1-f)^{1/8}\left[ 1+\frac{2(Af)^2(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{-2(1-f)}}{\kappa \tau }\right] ^{-1/16}\) and \(n_2=\frac{3Af(1-f)}{4\kappa \tau }(\tilde{B}^{-1}[\tilde{K}\ln \phi ]) ^{f-2}\times \left[ 1\!+\!\frac{2(Af)^2(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{-2(1-f)} }{\kappa \tau }\right] ^{-1}\), respectively. On the other hand, the scalar spectral index for the case \(m\ne 3\) becomes

$$\begin{aligned} n_s=1+\frac{3[f(m+2)-2m]}{8Af}(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-f}+n_{1_{m}}+n_{2_{m}}, \end{aligned}$$
(44)

where now the new functions \(n_{1_{m}}\) and \(n_{2_{m}}\) are defined by \(n_{1_{m}}=\frac{3(1-m)}{2Af}\left( \frac{2}{\kappa }\right) ^{1/2}\left( \frac{1}{2\kappa C_{\gamma }}\right) ^{-m/8}\times \frac{1}{C_{\phi }^{1/2}}(Af)^{\frac{8-m}{8}}(1-f)^{\frac{4-m}{8}}(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-\frac{[4+m(f-2)]}{8}}\phi ^{\frac{m-3}{2}} \left[ 1+\right. \left. \frac{2(Af)^2(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-2(1-f)}}{\kappa \tau }\right] ^{\frac{m-4}{16}}\) and \(n_{2_{m}}=\frac{(3m-6)}{4\kappa \tau }(Af)(1-f)(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{f-2}\left[ 1+\frac{2(Af)^2(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-2(1-f)}}{\kappa \tau }\right] ^{-1}\).

Analogously to before, from Eqs. (36) and (37), the scalar spectral index \(n_s\) can be rewritten in terms of the number of \(e\)-folds as

$$\begin{aligned} n_s=1+\frac{3(5f-6)}{8Af}(J[N])^{-f}+n_1+n_2, \end{aligned}$$
(45)

for the specific case of \(m=3\). Here the quantities \(n_1(J[N])\) and \(n_2(J[N])\) are defined as \(n_1(J[N])=-3\left( \frac{2}{\kappa }\right) ^{1/2}\frac{1}{C_{\phi }^{1/2}}\left( \frac{1}{2\kappa C_{\gamma }}\right) ^{-3/8}(Af)^{-3/8} (1\!-\!f)^{1/8}\left[ \!1\!+\!\frac{2(Af)^2(J[N])^{-2(1-f)}}{\kappa \tau }\right] ^{-1/16}\) and \(n_2(J[N])\!=\!\frac{3Af(1-f)}{4\kappa \tau }(J[N])^{f-2}\times \left[ 1+ \frac{2(Af)^2(J[N])^{-2(1-f)}}{\kappa \tau }\right] ^{-1}\), respectively. Analogously, the scalar spectral index for the value of \(m\ne 3\) becomes

$$\begin{aligned} n_s=1+\frac{3[f(m+2)-2m]}{8Af}(J[N])^{-f}+n_{1_{m}}+n_{2_{m}}, \end{aligned}$$
(46)

where \(n_{1_{m}}(J[N])\!=\!\frac{6(1-m)}{3-m}\left( \frac{\kappa }{2}\right) ^{\frac{[f(16-m)+2(m-6)]}{16(1-f)}}({ Af})^{-\frac{[4+m(2-f)]}{8(1-f)}}\left[ 1+\frac{2(Af)^2(J[N])^{-2(1-f)}}{\kappa \tau }\right] ^{\frac{m-4}{16}}\times (J[N])^{-\frac{[4+m(f-2)]}{8(1-f)}}(\tilde{B}_m\times [J[N]])^{-1}\) and \(n_{2_{m}}(J[N])=\frac{(3m-6)}{4\kappa \tau }(Af)(1-f)(J[N])^{f-2}\times \left[ 1+\frac{2(Af)^2(J[N])^{-2(1-f)}}{\kappa \tau }\right] ^{-1}\).

Analogous to the case of the weak dissipative regime, the tensor-to-scalar ratio \(r\) for the specific case \(m=3\) can be expressed in terms of the scalar field to give

$$\begin{aligned} r= & {} \frac{6\kappa }{\pi ^2 k}(Af)^2(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{\frac{(f+2)}{8}}\phi ^3\nonumber \\&\times \left[ 1\!+\!\frac{2(Af)^2(\tilde{B}^{-1}[\tilde{K}\ln \phi ])^{-2(1-f)}}{\kappa \tau }\right] ^{\frac{3}{16}}F^2(\phi ), \end{aligned}$$
(47)

and the tensor-to-scalar ratio for the case \(m\ne 3\) yields

$$\begin{aligned} r= & {} \frac{6\kappa }{\pi ^2 k_m}(Af)^2(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{ \frac{1}{8}[6m+f(10-3m)-16]}\phi ^{\frac{3}{2}(m-1)}\nonumber \\&\times \left[ 1+\frac{2(Af)^2(\tilde{B}_m^{-1}[\tilde{K}_m\varphi ])^{-2(1-f)}}{\kappa \tau }\right] ^{\frac{(3m-6)}{16}}F^2(\phi ).\nonumber \\ \end{aligned}$$
(48)

Also, we obtain the tensor-to-scalar ratio in terms of the number of \(e\)-folds. In this form, combining Eqs. (36) and (47) we get

$$\begin{aligned} r= & {} \frac{6\kappa }{\pi ^2 k}(Af)^2(J[N])^{\frac{(f+2)}{8}}\exp \left[ 3\frac{\tilde{B}[J[N]]}{\tilde{K}}\right] \nonumber \\&\times \left[ 1+\frac{2(Af) ^2(J[N])^{-2(1-f)}}{\kappa \tau }\right] ^{\frac{3}{16}}F^2(N), \end{aligned}$$
(49)

for the specific case of \(m=3\). From Eqs. (37) and (48), the tensor-to-scalar ratio becomes

$$\begin{aligned} r= & {} \frac{6\kappa }{\pi ^2 k_m}(Af)^2(J[N])^{\frac{1}{8}[6m+f(10-3m)-16]}\nonumber \\&\times \left( \frac{3-m}{2}\frac{\tilde{B}_m[J[N]]}{\tilde{K}_m}\right) ^{\frac{3(m-1)}{3-m}}\nonumber \\&\times \left[ 1+\frac{2(Af)^2(J[N])^{-2(1-f)}}{\kappa \tau }\right] ^ {\frac{(3m-6)}{16}}F^2(N), \end{aligned}$$
(50)

for the case of \(m\ne 3\).

Fig. 3
figure 3

The evolution of the tensor-to-scalar ratio \(r\) (upper panel) and the evolution of the ratio \(\Gamma /3H\) versus the scalar spectral index \(n_s\) (lower panel) in the strong dissipative regime, for the special case \(m=3\) (\(\Gamma \propto T^3/\phi ^2\)) for three different values of the parameter \(C_\phi \). In both panels, the solid, dotted, and dashed lines correspond to the pairs (\(A=1.32\times 10^{-5}\), \(f=0.75\)), (\(A=7.68\times 10^{-6}\), \(f=0.87\)), and (\(A=5.40\times 10^{-6}\), \(f=0.97\)). In both panels we have used the values \(C_\gamma =70\), \(m_p=1\), \(\tau =10^{-14}\), and the two-dimensional marginalized constraints from Refs. [95, 96]

Full size image

In Fig. 3 we show the evolution of the tensor-to-scalar ratio \(r\) and the ratio \(\Gamma /3H\) on the spectral index \(n_s\) in the strong dissipative regime, for the special case in which \(\Gamma =C_\phi \,T^3/\phi ^2\), i.e., \(m=3\). In both panels we have used three different values of the parameter \(C_\phi \). In the upper panel, as before, we show the two-dimensional constraints in the \(n_s\)–\(r\) plane from the BICEP2 and Planck data (\(68\) and \(95\,\%\) levels of confidence) [95, 96]. In the lower panel we show the evolution of the ratio \(\Gamma /3H\) during the warm inflation scenario, and we find corroboration that our model satisfies the strong dissipative regime, i.e., \(\Gamma >3H\). In order to write down the consistency relation \(r=r(n_s)\), we numerically find from Eqs. (45) and (49) the relation \(r=r(n_s)\) (upper panel). Similarly, from Eqs. (34), (37), and (45) we obtain the ratio \(\Gamma /3H\) as a function of the spectral index \(n_s\) (lower panel). In these plots we consider the values of \(C_\gamma =70\), \(m_p=1\), and \(\tau =10^{-14}\). Also, numerically from Eqs. (41) and (45) for the special case of \(m=3\), we obtain the values \(A=1.32\times 10^{-5}\) and \(f=0.75\), corresponding to the value \(C_\phi =10^9\), for \(P_{\mathcal {R}}=2.43\times 10^{-9}\), \(n_s=0.96\), and \(N=60\). Analogously, for the parameter \(C_\phi =10^8\), we numerically find the values \(A=7.68\times 10^{-6}\) and \(f=0.87\). Finally, for the value \(C_\phi =10^7\) we obtain \(A=5.40\times 10^{-6}\) and \(f=0.97\). From the upper panel we see that the range for the parameter \(C_{\phi }\) is \(10^7\le C_\phi \le 10^9\), which is well supported by the observational data. However, from the lower panel we observe that for values of \(C_\phi \le 10^8\) the model is disfavored by the condition of the strong dissipative regime, since the ratio \(\Gamma /3H<1\). Here, we note that from the condition of the strong dissipative regime, i.e., \(\Gamma >3H\), we have obtained a lower bound for the parameter \(C_\phi \). In this form, for the value \(m=3\) (in which \(\Gamma \propto T^3/\phi ^2\)) the range for the parameter \(C_\phi \) is given by \(10^8\le C_\phi \le 10^9\), which is well supported by observational data together with the conditions of the strong dissipative regime \(\Gamma >3H\) and \(T>H\).

During the strong dissipative regime for the specific case of \(m=1\) (\(\Gamma \propto T\)), we see that for the value of the parameter \(C_\phi \ge 10^{-1}\) the model is well corroborated by the condition \(\Gamma >3H\) and the necessary condition for warm inflation \(T>H\) (figure not shown). For the tensor-to-scalar ratio, we find that the ratio \(r\sim 0\) for this lower bound; then the case \(m=1\) is disproved by BICEP2 experiment, since the ratio \(r=0\) is discarded at 7.0\(\sigma \). However, by the Planck data, the value \(C_\phi \ge 10^{-1}\) is well supported. Also, we note that when we increase the value of the parameter \(C_\phi > 10^{-1}\), the value of the tensor-to-scalar ratio \(r\simeq 0\).

For the cases \(m=0\) (\(\Gamma \propto \phi \)) and \(m=-1\) (\(\Gamma \propto \phi ^2/T\)), we find that these models in the strong dissipative models are disproved by the BICEP2 and Planck data, because the scalar spectral index \(n_s>1\), and then these models do not work.

3 Conclusions

In this paper we have studied warm-intermediate inflation in the context of the Randall–Sundrum II brane-world cosmological model. Considering the slow-roll approximation during the weak and strong regime, we have obtained analytical solutions of the full effective Friedmann equation for a flat Universe in this brane-world model. Here we have considered a standard scalar field \(\phi \) together with a general form of the dissipative coefficient, \(\Gamma \propto \,T^m/\phi ^{m-1}\). In particular, we analyzed the values \(m=3\), \(m=1\), \(m=0\), and \(m=-1\), which can be found in the literature for this dissipation coefficient. Studying the weak and strong dissipative regimes, we have obtained analytical expressions for the appropriate Hubble parameter, the effective potential, the scalar power spectrum, the scalar spectral index, and the tensor-to-scalar ratio. During both regimes we have studied the slow-roll analysis and we compared with the two-dimensional marginalized constraints (68 and 95 \(\%\) CL) \(r=r(n_s)\) plane from observational data. Also, we have obtained a constraint for the parameter \(C_\phi \) [see Eq. (6)] from the BICEP2 and Planck 2015 data together with the essential condition for warm inflation \(T>H\) and the condition of the weak, \(\Gamma <3H\) (or strong, \(\Gamma >3H\)) regime.

For all the models (different values of the parameter \(m\)) in the weak dissipative regime, we have found a lower bound for the parameter \(C_\phi \), from the essential condition for warm inflation, in which the temperature of the thermal bath \(T>H\). Also, we have obtained an upper bound for \(C_\phi \), from the condition \(\Gamma <3H\), i.e., the weak dissipative regime. Additionally, we have observed the consistency relation \(r=r(n_s)\sim 0\), in the weak dissipative scenario, and the models are disproved by the BICEP2, but are well corroborated by the Planck satellite results, since \(r<0.11\).

For the strong dissipative scenario, we have found that the range for the parameter \(C_\phi \) is given by \(10^8\le C_\phi \le 10^9\) in the specific case of \(m=3\), i.e., \(\Gamma \propto T^3/\phi ^2\). Here, we have found an upper bound from the BICEP2 to the Planck \(r\)–\(n_s\) plane and a lower bound from the condition of the dissipative regime in which \(\Gamma >3H\); also in this range of \(C_\phi \) the necessary condition for warm inflation \(T>H\) is satisfied. For the case \(m=1\) (\(\Gamma \propto T\)), we have found that the tensor-to-scalar ratio \(r\sim 0\), and also we have found a lower limit for the parameter \(C_\phi \) from the condition \(\Gamma >3H\). Finally, we have found that for the cases \(m=0\) and \(m=-1\), these warm-intermediate inflationary models are disproved by the observational data, since the scalar spectral index \(n_s>1\); then the models \(\Gamma \propto \phi \) and \(\Gamma \propto \phi ^2/T\) do not work.