1 Introduction

The expansion of the universe with acceleration occurs in two eras: inflation and late-time (or recent) accelerating expansion. The discovery of the accelerated expansion of the universe and other evidence related to the existence of an early-time acceleration after the Big Bang called the inflation [1, 2] suggest the presence of ‘dark’ fluids different from standard matter and radiation at the cosmological level. After the big bang, an unimaginable hot and dense point, there occurred an incredible burst of expansion with acceleration which is called inflation. However, after the inflationary era, the universe began to decelerate with expansion through the radiation and matter dominated phases. The recent accelerated expansion of the universe is one of the biggest achievements in the subject of cosmology [3–7]. This expansion phenomenon follows through a mysterious form of force called dark energy (DE). However, the nature of DE is still unknown. Different researchers have tried to explore its nature as regards various aspects theoretically and observationally.

General relativity laid down the foundation of modern cosmology; it proposed the cosmological constant (homogeneous energy density) as a pioneer candidate of DE. The cosmological constant represents the vacuum energy having a positive (constant) energy density and a negative pressure, which accelerates the expansion of the universe. However, it has two severe issues [8]: one is the fine tuning problem, which is related to its inconsistent values (obtained by using observational and theoretical approaches). Its observational and theoretical values are approximately equal to \(10^{-47}\) and \(10^{74}\), respectively, indicating a difference of the order of \(10^{121}\) between these two values. Hence, in order to explain the current cosmic acceleration through the cosmological constant, we must find a tiny value of cosmological constant compatible with observations.

The second problem is that the fractional energy densities of DE and DM are comparable at the present time when the universe undergoes accelerated expansion. Thus, two alternatives, i.e., dynamical DE models and modified (or extra dimensional) theories of gravity, have been used extensively for describing the present status of the universe. In the first approach, the modification of the matter part of the Einstein field equations takes place by specifying different forms of the energy-momentum tensor, including quintessence, k-essence, and perfect fluid models [9]. The perfect fluid models with a specific form of equation of state (EoS) include the Chaplygin gas family [10–12], holographic [13, 14], new agegraphic [15], polytropic gas [16], and pilgrim [17–19] DE models.

The gravitational modification results in modified theories of gravity which involve some invariants depending upon particular features such as curvature, torsion, scalars, etc. These theories involve \(f(R)\) theory [20–22] where \(f\) is a general differentiable function of the curvature scalar \(R\). Another one is generalized teleparallel gravity, \(f(T)\) theory [23–25], contributing in the gravitational interaction through the torsion scalar \(T\). Others are Brans–Dicke theory, using a scalar field [26], Gauss–Bonnet theory and its modified version involving the Gauss–Bonnet invariant \(G\) [27, 28], \(f(R,\mathcal {T})\) theory where \(\mathcal {T}\) is the trace of the energy-momentum tensor [29], etc. The dynamical DE models are the outcome of a geometrical modification.

The holographic DE (HDE) has become an attractive DE model nowadays, which is developed in the context of quantum gravity and widely used in solving the cosmological problems. The main idea of this model has come from the holographic principle which is stated thus: the number of degrees of freedom of a physical system should scale with its bounding area rather than its volume [30]. With the help of this principle, a relationship between ultraviolet and infrared (IR) cutoffs has been proposed by suggesting that the size of a system should not exceed the size associated with the mass of a black hole (BH) [31]. By using this relationship, Li [14] developed the HDE density as follows:

$$\begin{aligned} \rho _{\Lambda }=3n^{2}m^2_{\mathrm{pl}}L^{-2}, \end{aligned}$$

here, \(n, m_{\mathrm{pl}}, L\) indicate the HDE constant, the reduced Planck constant, and the IR cutoff, respectively. On the basis of the compatibility of HDE with the present day observations, different IR cutoffs have been proposed, including Hubble, particle, event horizons, conformal age of the universe, Ricci scalar, Granda–Oliveros and higher derivative of the Hubble parameter [14, 32–35], etc.

As Cohen et al. [31] suggested, the bound of the energy density contradicts the idea of formation of BHs in quantum gravity. It is suggested that the formation of a BH can be avoided through an appropriate repulsive force which resists the phenomenon of matter collapse. This force can only provide phantom DE in spite of other phases of DE like vacuum and quintessence DE. By keeping in mind this phenomenon, Wei [17] has suggested the DE model called pilgrim DE (PDE) by the speculation that phantom DE possesses a large negative pressure as compared to the quintessence DE which helps in violating the null energy condition and possibly prevents the formation of BHs. In the past, many applications of phantom DE existed in the literature. For instance, phantom DE also plays an important role in wormhole physics where the event horizon can be avoided due to its presence [36–39].

Also, it plays a role in the reduction of mass due to its accretion process onto a BH. Much work has been done to support this through a Chaplygin gas family [40–46]. It was also argued in the context of the scalar field that the BH area reduces up to 50 % through phantom scalar field accretion onto it [47]. According to Sun [48], the mass of a BH tends to zero when the universe approaches a big rip singularity. It was also suggested that BHs might not exist in the universe in the presence of quintessence-like DE which violates only the strong energy condition [49, 50]. However, all this does not correspond to reality because quintessence DE does not contain enough resistive force to avoid the formation of BHs.

The above discussion has motivated Wei [17] in developing the PDE model. He analyzed this model with a Hubble horizon as regards different theoretical as well as observational aspects. Also, Saridakis et al. [51–59] have discussed the widely known crossing of phantom divide line, and the quintom as well as phantom-like nature of the universe in different frameworks. They found interesting results in this respect. Recently, we have investigated this model by taking different IR cutoffs in flat as well as non-flat FRW universe with different cosmological parameters as well as cosmological planes [18, 19]. This model has also been investigated in different modified gravities [60–62]. In the present paper, we check the role of PDE in loop quantum cosmology (LQC). We develop different cosmological parameters and planes. The format of the paper is as follows. In the next section, we provide the basic equations corresponding to PDE models. Also, we discuss the Hubble parameter, the EoS parameter, and the squared speed of sound in Sect. 3. Section 4 explores \(\omega _{\vartheta }\)–\(\omega _{\vartheta }'\) as well as statefinders planes. In the last section, we summarize our results.

2 Loop quantum cosmology and pilgrim dark energy

Nowadays, the DE phenomenon has widely been discussed in the context of LQC to describe the quantum effects on our universe. The LQC is an interesting and attractive application of the loop quantum gravity in the cosmological framework and it possesses the properties of a non-perturbative and background independent quantization of gravity [63–68]. In recent years, many DE models have been studied in the scenario of LQC [69, 70]. Jamil et al. [71] have explored the cosmic coincidence problem phenomenon of modern cosmology by taking a modified Chaplygin gas coupled to dark matter. Also, some authors found that the future singularity appearing in the standard FRW cosmology can be avoided by loop quantum effects [72]. Chakraborty et al. [73] have made an observational study of the modified Chaplygin gas in LQC. Here, we develop the basic scenario of interacting PDE (with Hubble horzion) with cold dark matter (CDM) in LQC. The equation of motion in LQC has the form

$$\begin{aligned} H^2=\frac{1}{3m^2_{\mathrm{pl}}}\rho \left( 1-\frac{\rho }{\rho _\mathrm{c}}\right) , \end{aligned}$$
(1)

where \(\rho \) indicates the sum of CDM and PDE densities, i.e., \(\rho =\rho _m+\rho _\vartheta \). Also, \(\rho _{\mathrm{c}}=\frac{\sqrt{3}}{16\pi ^2\gamma ^3G^2\hbar }\) represents the critical loop quantum density, \(\gamma \) stands for the dimensionless Barbero–Immirzi parameter. It is predicted that the big bang, big rip, and other future singularities at the semi classical regime can be avoided in LQC. Moreover, the modification in standard FRW cosmology due to LQC becomes more dominant and the universe begins to bounce and then oscillate forever.

It is argued that phantom DE with a strong negative pressure can push the universe toward the big rip singularity where all the physical objects lose the gravitational bounds and finally get dispersed. The PDE model is also developed in favor of this scenario; it is defined as

$$\begin{aligned} \rho _{\vartheta }=3n^2 m_{\mathrm{pl}}^{4-u}L^{-u}, \end{aligned}$$
(2)

here \(u\) represents the PDE parameter. Wei explored the PDE model in different possible theoretical and observational ways to find the BH free phantom universe with a Hubble horizon (\(L=H^{-1}\)) through the PDE parameter. The above equation becomes

$$\begin{aligned} \rho _{\vartheta }=3n^2 m_{\mathrm{pl}}^{4-u}H^u. \end{aligned}$$
(3)

In the present work, we also choose PDE with a Hubble horizon, which is the pioneer IR cutoff. Initially, it is plagued by the problem that its EoS parameter provides a behavior inconsistent with the present status of the universe [14]. This deficiency has been settled on with the passage of time by pointing out that HDE with this IR cutoff can explain the present scenario of the universe in the presence of the interaction with DM [74, 75]. Also, the results of different cosmological parameters have been established through different observational schemes by choosing a HDE model with a Hubble scale [76, 77]. Sheykhi [78] has discussed this model by taking the interaction with CDM and pointed out that such a model possesses the ability to explain the present scenario of the universe.

Moreover, we take an interaction between PDE with CDM which has the following form:

$$\begin{aligned} \dot{\rho }_{m}+3H\rho _{m}=\Theta ,\quad \dot{\rho }_{\vartheta }+3H\rho _{\vartheta }(1+\omega _{\vartheta })=-\Theta , \end{aligned}$$
(4)

where \(\Theta \) is of a dynamical nature and appears as an interaction term between CDM and PDE. Different forms of this interaction term have been proposed, out of which we use the following form:

$$\begin{aligned} \Theta =3d^2H\rho _{m}, \end{aligned}$$
(5)

where \(d^2\) is an interacting constant which stands for the interaction parameter and exchanges the energy between CDM and DE components. This form of the interaction term has been explored for energy transfer through different cosmological constraints. The sign of the coupling constant decides the decay of energies; either DE decays into CDM (when the interacting parameter is positive) or CDM decays into DE (when the interacting parameter is negative). The present analysis of different aspects implies that the phenomenon of DE decays into CDM is more acceptable and favors the observational data. Hence, Eqs. (4) and (5) give

$$\begin{aligned} \rho _{m}=\rho _{m0}a^{3(d^2-1)}. \end{aligned}$$
(6)

Also, by taking the derivative of \(\rho _{\vartheta }\) (with Hubble horizon) with respect to \(x=\ln a\), we get

$$\begin{aligned} \rho '_{\vartheta }=u\rho _{\vartheta }\frac{\dot{H}}{H^2}. \end{aligned}$$
(7)

3 Cosmological parameters in LQC

In this section, we will discuss the physical significance of cosmological parameters corresponding to PDE with a Hubble horizon in the LQC scenario.

3.1 Hubble parameter

In order to check the behavior of the Hubble parameter in this framework, we differentiate Eq. (1) with respect to \(t\), and on inserting (6) and (7), it yields

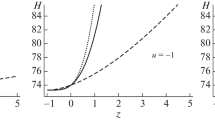
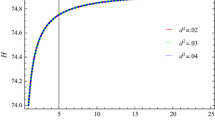
$$\begin{aligned} \frac{\dot{H}(a)}{H(a)^2}= & {} -\frac{3\Omega _{m0}H^2_0a^{3(d^2-1)}}{H^2(a)}\nonumber \\&\times \Bigg [\frac{2}{1-6\rho ^{-1}_c(n^2H^{u}(a)+\Omega _{m0}H^2_0a^{3(d^2-1)})}\nonumber \\&-un^2H(a)^{u-2}\Bigg ]. \end{aligned}$$
(8)

In the above expression, we use the dimensionless density parameter \(\Omega _{m0}=\frac{\rho _{m0}}{3m^2_{p}H_0^2}\) (we use this parameter in all the following expressions as well as in our plots). We solve the above differential equation (8) numerically by using Eqs. (1)–(7) in terms of \(H\) and plot it against the scale factor \(a\) for four different values of \(u=2, 1,-1,-2\), as shown in Fig. 1. The initial condition of \(H\) is taken as \(H_0=H[a_0]=H[1]\simeq 74,~\Omega _{m0}=0.27\) as mentioned in the Planck observations [79]. It can be observed that the trajectories of the Hubble parameter \(H(a)\) attain the values approximately corresponding to \(74^{+0.005}_{-0.005}\).

Fig. 1
figure 1

Plot of \(H\) versus \(a\) for PDE in LQC with \(u=2, 1,-1,-2\)

Full size image

3.2 Equation of state parameter

In order to obtain the EoS parameter, we substitute Eqs. (5), (6), (7), and (8) in the continuity equation (4). It follows that

$$\begin{aligned} \omega _{\vartheta }= & {} -1-\frac{d^2\Omega _{m0}H^2_0a^{3(d^2-1)}}{n^2H^u(a)}\nonumber \\&+\Bigg [\frac{2}{1-6\rho ^{-1}_c(n^2H^{u}(a)+\Omega _{m0}H^2_0a^{3(d^2-1)})}\nonumber \\&\qquad -un^2H(a)^{u-2}\Bigg ]\frac{u\Omega _{m0}H^2_0a^{3(d^2-1)}}{H^2(a)}. \end{aligned}$$
(9)

To plot this parameter, \(H(a)\) is taken numerically. The plots of the EoS parameter versus \(a\) are shown in Fig. 2 for four different values of \(u\). In the first plot (\(u=2\)), the trajectory of \(\omega _{\vartheta }\) starts from the phantom region, and with the passage of time it approaches the \(\Lambda \)CDM limit for the interacting cases \(d^2=0.2,0.3\). However, it remains in the phantom region for the interacting case \(d^2=0.4\). In the case of \(u=1\) (second plot), the trajectories of the EoS parameter remain in the quintessence region for \(d^2=0.4\), while they approach (from the quintessence region) the \(\Lambda \)CDM limit for the other two cases of \(d^2\). For \(u=-1,-2\) (lower left and right plots), the EoS starts from the phantom case with a comparatively high value and goes toward the \(\Lambda \)CDM limit for \(d^2=0.2,0.3\) and always remains in the phantom range for the other \(d^2\).

Fig. 2
figure 2

Plot of \(\omega _{\vartheta }\) versus \(a\) for PDE in LQC with \(u=2,1,-1,-2\)

Full size image

3.3 The square speed of sound

In order to analyze the stability of the PDE model in this scenario, we extract the squared speed of sound, which is given by

$$\begin{aligned} \upsilon _{s}^2=\frac{\dot{p_\vartheta }}{\dot{\rho _\vartheta }}=\frac{p'_\vartheta }{\rho '_\vartheta }, \end{aligned}$$
(10)

where the pressure corresponds to PDE only. Differentiating the relation \(p_\vartheta =\rho _\vartheta \omega _\vartheta \) with respect to \(\ln a\) and dividing by \(\rho '_\vartheta \), we get

$$\begin{aligned} \frac{p'_\vartheta }{\rho '_\vartheta }=\omega _\vartheta +\frac{\rho _\vartheta }{\rho '_\vartheta }\omega '_\vartheta . \end{aligned}$$
(11)

In order to get the expression of \(\upsilon _{s}^2\), we evaluate the derivative of \(\omega _\vartheta \) with respect to \(x=\ln a\) by using Eqs. (7), (8), and (9) as follows:

$$\begin{aligned} \omega '_{\vartheta }= & {} (3H(a)^4)^{-1}a^{-4+3d^2}\rho _{m0}(a^{-3+3d^2}d^4\rho _{m0} u^2 \nonumber \\&- (3(-1+d^2)d^4H(a)^{4-u}) \times n^{-2}\nonumber \\&-3(-1+d^2)u^2 n^2H(a)^{1+u}\nonumber \\&- a^{-3+3d^2}\rho _{m0}(-3+u)u^3n^4H(a)^{-3+2u} \nonumber \\&+ (6a^6(\!-\!1\!+\!d^2)u\rho _c H(a)^3(\rho _c\!-\!6n^2H(a)^u))(2a^{3d^2}\rho _{m0}\nonumber \\&- a^3 \rho _c+6a^3 \times n^2H(a)^u)^{-2}\nonumber \\&+(2a^{3d^2}d^4\rho _{m0}u\rho _c H(a)^{2-u}) \nonumber \\&\times (n^2(2a^{3d^2}\rho _{m0}-a^3\rho _c +6a^3n^2H(a)^u))^{-2} \nonumber \\&+ (2a^{3d^2}\rho _{m0}u^2\rho _c n^2H(a)^{-1+u}(-(-4+u)(2a^{3d^2}\rho _{m0} \nonumber \\&- a^3 \rho _c)+ 24a^3 n^2H(a)^u))(2a^{3d^2}\rho _{m0}-a^3\rho _c\nonumber \\&+ 6a^3n^2H(a)^u)^{-2}+(4a^{3+ 3d^2} \times \rho _{m0} u\rho _c^2H(a)\nonumber \\&\times (2a^{3 d^2}\rho _{m0} \!-\! a^3\rho _c \!+\!6a^3(1\!+\!u)n^2H(a)^u))(2a^{3 d^2}\rho _{m0}\nonumber \\&- a^3\rho _c+6a^3n^2H(a)^u)^{-3}). \end{aligned}$$
(12)

Finally, we obtain squared speed of sound as follows:

$$\begin{aligned} \upsilon ^2_{s}= & {} \frac{1}{3}(-3-(a^{-3+3d^2}d^2\rho _{m0}H(a)^{-u})n^{-2}\\&+(a^{-3+3d^2}\rho _{m0}u(-un^2 \times H(a)^{-2 + u}\\&+2\rho _{c}(-2a^{-3\!+\!3d^2}d\!+\!\rho _{c}-6n^2H(a)^u)^{-1}))\times H^{-2}(a)\\&-(a^{-3+3d^2}d^2\rho _{m0}u^2-(3(-1+d^2)d^2H(a)^{4-u})n^{-2}\\&- 3(-1+d^2)u^2 n^2H(a)^{1 + u}-a^{-3+3d^2}\rho _{m0}\\&\times (-3+u)u^3n^4H(a)^{-3+2u}\\&+ (6a^6(-1+d^2)u \rho _{c} H(a)^3(\rho _{c}-6n^2H(a)^u))\\&\times (2a^{3d^2}\rho _{m0}-a^3\alpha + 6a^3 n^2 H(a)^u)^{-2}\\&+(2a^{3d^2}d^2\rho _{m0}u\rho _{c} H(a)^{2-u})(n^2(2a^{3d^2}\rho _{m0}-a^3\rho _{c}\\&+ 6a^3n^2H(a)^u))^{-1}\\&+(2a^{3 d^2}\rho _{m0}u^2\rho _{c} n^2H(a)^{-1+u}(-(-4+u)(2a^{3 d^2}\rho _{m0}\\&- a^3 \rho _{c})+24a^3n^2H(a)^u))(2 a^{3d^2}\rho _{m0}-a^3\rho _{c}\\&+6a^3n^2H(a)^u)^{-2}+ (4a^{3+3d^2}\rho _{m0}u \rho _{c}^2H(a)\\&\times (2a^{3d^2}\rho _{m0}-a^3\rho _{c}+6a^3(1+u)n^2H(a)^u))(2a^{3d^2}\\&\times \rho _{m0}-a^3\rho _{c}+6a^3n^2H(a)^u)^{-3})\\&\times (au H(a)^3(-un^2H(a)^{-2+u} \\&+ (2\rho _{c})(-2a^{-3+3d^2}\rho _{m0}+\rho _{c}-6n^2H(a)^u)^{-1}))^{-1}). \end{aligned}$$

The plots of squared speed of sound versus \(a\) for three different values of \(d^2\) and four values of \(u=2,1,-1,-2\) are shown in Fig. 3. It can be observed from the plots that the squared speed of sound remains positive for all cases of \(u\) and \(d^2\), which exhibits the stability of the PDE in LQC scenario.

Fig. 3
figure 3

Plot of \(\upsilon ^2_s\) versus \(a\) for PDE in LQC with \(u=2, 1,-1,-2\)

Full size image

4 Cosmological planes in LQC

Here, we will discuss the physical significance of the cosmological planes corresponding to PDE with a Hubble horizon in the LQC scenario.

4.1 \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) analysis

Here, we find the regions on the \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) plane; (\(\omega '_{\vartheta }\) represents the evolution of \(\omega _{\vartheta }\)) as defined by Caldwell and Linder [80] for the models under consideration. The models can be categorized in two different classes: the thawing and freezing regions on the \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) plane. The thawing models describe the region \(\omega '_{\vartheta }>0\) when \(\omega _{\vartheta }<0\) and the freezing models represent the region \(\omega '_{\vartheta }<0\) when \(\omega _{\vartheta }<0\). Initially, this phenomenon was applied for analyzing the behavior of the quintessence model and one found that the corresponding area occupied on the \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) plane describes the thawing and freezing regions. In order to plot \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\), we use Eqs. (9) and (12).

We also construct the \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) plane for the PDE model with different values of \(u\) in LQC as shown in Fig. 4. In all cases of \(u\) and \(d^2\), the \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) plane corresponds to the \(\Lambda \)CDM limit, i.e., \((\omega _{\vartheta },\omega '_{\vartheta })=(-1,0)\). Also, the \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) plane shows the thawing regions for the cases \(u=2,-1,-2\) and corresponds to the freezing region for the case \(u=1\).

Fig. 4
figure 4

Plot of \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) for PDE in LQC with \(u=2, 1,-1,-2\)

Full size image

4.2 Statefinder parameters

The statefinder parameters are defined as follows [81]:

$$\begin{aligned} r=\frac{\dddot{a}}{aH^3},\quad s=\frac{r-1}{3\left( q-\frac{1}{2}\right) }, \end{aligned}$$
(13)

where \(q\) is the deceleration parameter, defined as

$$\begin{aligned} q=-\frac{\ddot{a}}{aH^2}=-\left( 1+\frac{\dot{H}}{H^2}\right) . \end{aligned}$$
(14)

Combining the Hubble and deceleration parameters, the statefinders are expressed as

$$\begin{aligned} r=2q^{2}+q-\frac{\dot{q}}{H},\quad s=\frac{r-1}{3(q-\frac{1}{2})}. \end{aligned}$$
(15)

These parameters are dimensionless and possess the ability to explain the current accelerated scenario. These parameters have geometrical diagnostic due to their total dependence on the expansion factor. The statefinders are useful in the sense that we can find the distance of a given DE model from the \(\Lambda \)CDM limit. The well-known regions described by these cosmological parameters are as follows: \((r,s)=(1,0)\) indicates the \(\Lambda \)CDM limit, \((r,s)=(1,1)\) shows the CDM limit, while \(s>0\) and \(r<1\) represent the region of the phantom and quintessence DE eras. Following Refs. [18, 19], we insert Eq. (8) to find \(q\) which is used in Eq. 15 and obtain the following form of the statefinders:

$$\begin{aligned} r= & {} 1+\frac{1}{2}a^{-3+3d^2}\rho _{m0}(-u^2n^2H a^{-3+u}-(d^4 H(a)^{-u})n^{-2}\nonumber \\&+(2u\rho _{c})(H(a) (-2a^{-3+3d^2}\rho _{m0}+\rho _{c}-6n^2 H(a)^u))^{-1})\nonumber \\&\times (-3-(a^{-3+3d^2}d^4\rho _{m0} H(a)^{-u})n^{-2} \nonumber \\&+(a^{-3+3d^2}\rho _{m0}u(-un^2H(a)^{-2 +u}+(2\rho _{c}) \nonumber \\&\times (-2a^{-3+3d^2}\rho _{m0}+\rho _{c} - 6n^2H(a)^u)^{-1}))H(a)^{-1}\nonumber \\&-(3a^{3-3d^2}H(a) \omega '_{\vartheta })(\rho _{m0}u(-un^2H(a)^{-2+u} \nonumber \\&+ (2\rho _{c})(-2a^{-3+3d^2}\rho _{m0}+\rho _{c}- 6n^2H(a)^u)^{-1}))^{-1})\nonumber \\ \end{aligned}$$
(16)

and

$$\begin{aligned} s= & {} \frac{1}{9}a^{-3+3d^2}\rho _{m0}(-u^2n^2H(a)^{-3 + u}-(d^4 H(a)^{-u})n^{-2}\nonumber \\&+(2u\rho _{c})(H(a) (-2a^{-3 + 3d^2}\rho _{m0}+\rho _{c}\nonumber \\&-6n^2 H(a)^u))^{-1})(-3-(a^{-3+3d^2}d^4\rho _{m0}H(a)^{-u}) \nonumber \\&\times n^{-2}+(a^{-3 + 3 d^2}\rho _{m0} u(-un^2H(a)^{-2 + u}\nonumber \\&+(2\rho _{c})(-2a(-3+3d^2)\rho _{m0} + \rho _{c}- 6n^2H(a)^u)^{-1}))H(a)^{-1}\nonumber \\&-(3a^{3-3d^2}H(a)\omega '_{\vartheta })(\rho _{m0} u(-un^2H(a)^{-2+u} \nonumber \\&+ (2\rho _{c})(-2a^{-3+3d^2}\rho _{m0}+\rho _{c}- 6n^2H(a)^u)^{-1}))^{-1}).\nonumber \\ \end{aligned}$$
(17)

We also develop the \(r\)–\(s\) planes corresponding to the present cosmological scenario for different values of \(u\) as shown in Fig. 5. The \(r\)–\(s\) region corresponds to the \(\Lambda \)CDM limit for all cases of \(u\).

Fig. 5
figure 5

Plot of \(r\)–\(s\) for PDE in LQC with \(u=2, 1,-1,-2\)

Full size image

5 Concluding remarks

In the LQC framework, cosmological implications have been discussed with the help of various interaction terms between different DE models and DM. Up to now, most of the work has been done in the direction of an analysis of the dynamics of interacting DE models and evolution of the universe through the EoS parameter [82–87]. In this work, we analyze the versatile cosmological scenario and construct the possible constraints of the PDE parameter \(u\) where it agrees with the PDE phenomenon. We have considered the scenario of an interacting PDE with a Hubble horizon in LQC framework. For this purpose, we have constructed the Hubble parameter, the EoS parameter, the squared speed of sound, \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\), and the \(r\)–\(s\) planes numerically. We have discussed these parameters corresponding to the four values of \(u=2, 1,-1,-2\) and the three values of \(d^2=0.2, 0.3, 0.4\). We have observed that the trajectories of the Hubble parameter \(H(a)\) for all cases of \(u\) approximately attain the values \(74^{+0.005}_{-0.005}\) (Fig. 1). The obtained range of \(H(a)\) shows consistency with the observational data [79, 88, 89] as shown in Table 1.

Table 1 Summary of the observational data on \(H_0\)
Full size table

Moreover, the EoS parameter also shows consistency with the present day observations. For instance, the trajectory of \(\omega _{\vartheta }\) exhibits the ranges \(-1-0.0050\) and \(-1+0.00005\) for the cases \(u=2, 1\), as shown in the upper plots of Fig. 2. For \(u=-1,-2\) (lower plots), the EoS parameter lies in the ranges \((-1.12,-1)\) and \((-5,-1)\), respectively. These constraints on the EoS parameter are compatible with the constraints as obtained by Ade et al. [79] (Planck data) and nine-year WMAP observational data as shown in Table 2. It can also be observed from Fig. 3 that the squared speed of sound remains positive for all cases of \(u\) and \(d^2\), which exhibits the stability of the PDE in the LQC scenario.

Table 2 Summary of the observational data on \(\omega _{\vartheta 0}\)
Full size table

We have also observed that the \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) plane corresponds to the \(\Lambda \)CDM limit, i.e., \((\omega _{\vartheta },\omega '_{\vartheta })=(-1,0)\) in all cases of \(u\) and \(d^2\). Also, the \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) plane shows thawing regions for the cases \(u=2,-1,-2\) (Fig. 4) and a freezing region for the case \(u=1\). In the present case, the trajectories of \(\omega '_{\vartheta }\) against \(\omega _{\vartheta }\) also meet the observational constraints (Table 3) for all cases of the interacting parameter as shown in Fig. 4. Hence, the \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\) plane provides a behavior consistent with the present day observations in all cases of \(u\). Also, \(r\)–\(s\) corresponds to the \(\Lambda \)CDM limit for all cases of \(u\).

Table 3 Summary of the observational data on \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\)
Full size table

Moreover, on the basis of a discussion as regards the behavior of EoS parameter, we can suggest that the formation of BHs can be avoided through this framework of PDE with \(u=2,-1,-2\) and it gives support to the idea of Wei [17]. Also, the \(\Lambda \)CDM limit has been obtained in all mentioned cases of \(u\) and \(d^2\) through viable cosmological parameters such as \(\omega _{\vartheta }\), \(\omega _{\vartheta }\)–\(\omega '_{\vartheta }\), and \(r\)–\(s\), which exhibits the credibility of the chosen constraints. Finally, it is remarked that all the cosmological parameters corresponding to PDE with the constraints \(u=\pm 2, \pm 1\) and \(d^2=0.2^{+1}_{-1}\) in the scenario of LQC shows compatibility with the current well-known observational data [79, 88–90].