Abstract
The measurement of primary \(\pi ^{\pm }\), \(K^{\pm }\), \(p\) and \({\overline{{p}}}\) production at mid-rapidity (\(|y| <\) 0.5) in proton–proton collisions at \(\sqrt{s}\) \(=\) 7 TeV performed with a large ion collider experiment at the large hadron collider (LHC) is reported. Particle identification is performed using the specific ionisation energy-loss and time-of-flight information, the ring-imaging Cherenkov technique and the kink-topology identification of weak decays of charged kaons. Transverse momentum spectra are measured from 0.1 up to 3 GeV/\(c\) for pions, from 0.2 up to 6 GeV/\(c\) for kaons and from 0.3 up to 6 GeV/\(c\) for protons. The measured spectra and particle ratios are compared with quantum chromodynamics-inspired models, tuned to reproduce also the earlier measurements performed at the LHC. Furthermore, the integrated particle yields and ratios as well as the average transverse momenta are compared with results at lower collision energies.
1 Introduction
The majority of the particles produced at mid-rapidity in proton–proton collisions are low-momentum hadrons not originating from the fragmentation of partons produced in scattering processes with large momentum transfer. Their production, therefore, cannot be computed from first principles via perturbative quantum chromodynamics (pQCD). Currently available models describing hadron-hadron collisions at high energy, such as the event generators PYTHIA6 [1], PYTHIA8 [2, 3], EPOS [4, 5] and PHOJET [6], combine pQCD calculations for the description of hard processes with phenomenological models for the description of the soft component. The measurement of low-momentum particle production and species composition is therefore important as it provides crucial input for the modelling of the soft component and of the hadronisation processes. Furthermore, it serves as a reference for the same measurement in Pb–Pb collisions to study the properties of the hot and dense strongly interacting medium with partonic degrees of freedom, the quark–gluon plasma, which is created in these collisions. In this paper, the measurement of primary \(\pi ^{\pm }\), \(K^{\pm }\), \(p\) and \({\overline{{p}}}\) production at mid-rapidity in proton–proton collisions at \(\sqrt{s}\) \(=\) 7 TeV using the ALICE detector [7–10] is presented. Primary particles are defined as prompt particles produced in the collision including decay products, except those from weak decays of light flavour hadrons and muons. Pions, kaons and protons are identified over a wide momentum range by combining the information extracted from the specific ionisation energy loss (d\(E\)/d\(x\)) measured in the inner tracking system (ITS) [11] and in the time projection chamber (TPC) [12], the time of flight measured in the time-of-flight (TOF) detector [13], the Cherenkov radiation measured in the high-momentum particle identification detector (HMPID) [14] and the kink-topology identification of the weak decays of charged kaons. Similar measurements in proton–proton collisions at \(\sqrt{s}\) \(=\) 900 GeV and 2.76 TeV are reported in [15–17] and are included, together with lower energy data [18–24], in the discussion of the evolution of particle production with collision energy. Similar measurement at the LHC have also been performed in the forward region [25].
The paper is organised as follows. In Sect. 2 the ALICE experimental setup is described, focusing on the detectors and the corresponding particle identification (PID) techniques relevant for the present measurement. Details of the event and track selection criteria and the corrections applied to the measured raw yields are also presented. In Sect. 3 the results on the production of primary \(\pi ^{\pm }\), \(K^{\pm }\), \(p\) and \({\overline{{p}}}\) are shown. These include the transverse momentum (\(p_\mathrm{{T}}\)) distributions and the \(p_\mathrm{{T}}\)-integrated production yields of each particle species and the K/\(\pi \) and p/\(\pi \) ratios. The evolution with collision energy of the \(p_\mathrm{{T}}\)-integrated particle yields, of their ratios and of their average transverse momenta \(\langle p_\mathrm{T} \rangle \) is also presented. In Sect. 4 particle spectra and their ratios (K/\(\pi \) and p/\(\pi \)) are compared with models, in particular with different PYTHIA tunes [1–3, 25, 26], EPOS [4, 5] and PHOJET [6]. Section 5 concludes the paper summarizing the results.
2 Experimental setup and data analysis
2.1 The ALICE detector
The ALICE detector was specifically optimised to reconstruct and identify particles over a wide momentum range thanks to the low material budget, the moderate magnetic field and the presence of detectors exploiting all the known PID techniques. A comprehensive description of the ALICE experimental setup and performance can be found in [7–10]. In the following, the PID detectors relevant for the analysis presented in this paper are briefly described, namely ITS, TPC, TOF and HMPID. They are located in the ALICE central barrel in a \(B= 0.5\) T solenoidal magnetic field directed along the beam axis. The ITS, TPC and TOF detectors cover the full azimuth (\(\varphi \)) and have a pseudorapidity coverage of \(|\eta | < 0.9\), while the HMPID covers the pseudorapidity interval \(|\eta | < 0.55\) and the azimuthal angle range \(1.2^{\circ } < \varphi < 58.5^{\circ }\).
The ITS [11] is the innermost central barrel detector. It is composed of six cylindrical layers of silicon detectors, located at radial distances between 3.9 and 43 cm from the beam axis. The two innermost layers are equipped with silicon pixel detectors (SPD), the two intermediate ones are silicon drift detectors (SDD), while the two outermost ones are silicon strip detectors (SSD). The ITS provides high resolution tracking points close to the beam line, which allows us to reconstruct primary and secondary vertices with high precision, to measure with excellent resolution the distance of closest approach (DCA) of a track to the primary vertex, and to improve the track \(p_\mathrm{{T}}\) resolution. It is also used as a stand-alone tracker to reconstruct particles that do not reach the TPC or do not cross its sensitive areas. The SDD and SSD are equipped with analogue readout enabling PID via d\(E\)/d\(x\) measurements with a relative resolution of about 10 %.
The TPC [12] is the main tracking detector of the ALICE central barrel. It is a large volume cylindrical chamber with high-granularity readout that surrounds the ITS covering the region 85 \(< r <\) 247 and \(-250 < z <\) +250 cm in the radial \(r\) and longitudinal \(z\) directions, respectively. It provides three-dimensional space points and specific ionisation energy loss d\(E\)/d\(x\) with up to 159 samples per track. The relative d\(E\)/d\(x\) resolution is measured to be about 5.5 % for tracks that cross from the centre of the outer edge of the detector.
The TOF detector [13] is a large-area array of multigap resistive plate chambers with an intrinsic time resolution of 50 ps, including the electronic readout contribution. It is a cylindrical detector located at a radial distance 370 \(< r <\) 399 cm from the beam axis. Particles are identified using simultaneously the TOF information with the momentum and track length measured with the ITS and the TPC.
The HMPID [14] is a single-arm proximity-focusing ring imaging Cherenkov (RICH) detector located at 475 cm from the beam axis. The Cherenkov radiator is a 15-mm-thick layer of liquid C\(_6\)F\(_{14}\) (perfluorohexane) with a refractive index of \(n = 1.2989\) at a photon wave length \(\lambda = 175\) nm, corresponding to a minimum particle velocity \(\beta _\mathrm{{min}} = 0.77\).
In addition to the detectors described above that provide PID information, the VZERO system [27] is used for trigger and event selection. It is composed of two scintillator arrays, which cover the pseudorapidity ranges \(2.8<\eta <5.1\) and \(-3.7<\eta <-1.7\).
2.2 Data sample, event and track selection
The results presented in this paper are obtained combining five independent analyses, namely ITS stand-alone, TPC–TOF, TOF, HMPID, kink, using different PID methods. The analysed data are proton–proton collisions at \(\sqrt{s}\) \(=\) 7 TeV collected in 2010. During that period, the instantaneous luminosity at the ALICE interaction point was kept within the range 0.6–\(1.2\times 10^{29}\,\mathrm cm^{-2}\, s^{-1}\) to limit the collision pile-up probability. Only runs with a collision pile-up probability smaller than 4 % are used in this analysis, leading to an average pile-up rate of 2.5 %. The number of events used in the five independent analyses is reported in Table 1. The data were collected using a minimum-bias trigger, which required a hit in the SPD or in at least one of the VZERO scintillator arrays in coincidence with the arrival of proton bunches from both directions. This trigger selection essentially corresponds to the requirement of having at least one charged particle in 8 units of pseudorapidity.
The contamination due to beam-induced background is removed off-line by using the timing information from the VZERO detector, which measures the event time with a resolution of about 1 ns, and the correlation between the number of clusters and track segments (tracklets) in the SPD [15]. Selected events are further required to have a reconstructed primary vertex. For 87 % of the triggered events, the interaction vertex position is determined from the tracks reconstructed in TPC and ITS. For events that do not have a vertex reconstructed from tracks, which are essentially collisions with low multiplicity of charged particles, the primary vertex is reconstructed from the SPD tracklets, which are track segments built from pairs of hits in the two innermost layers of the ITS. Overall, the fraction of events with reconstructed primary vertex, either from tracks or from SPD tracklets, is of 91 %. Accepted events are required to have the reconstructed vertex position along the beam direction, \(z\), within \(\pm \)10 cm from the centre of the ALICE central barrel. This ensures good rapidity coverage, uniformity of the particle reconstruction efficiency in ITS and TPC and reduction of the remaining beam-gas contamination. In the following analyses two different sets of tracks are used: the global tracks, reconstructed using information from both ITS and TPC, and the ITS-sa tracks, reconstructed by using only the hits in the ITS. To limit the contamination due to secondary particles and tracks with wrongly associated hits and to ensure high tracking efficiency, tracks are selected according to the following criteria. The global tracks are required to cross over at least 70 TPC readout rows with a value of \(\chi ^{2} / N_\mathrm{{clusters}}\) of the momentum fit in the TPC lower than 4, to have at least two clusters reconstructed in the ITS out of which at least one is in the SPD layers and to have a DCA to the interaction vertex in the longitudinal plane, DCA\(_z\) \(<\) 2 cm. Furthermore, the daughter tracks of reconstructed kinks are rejected. This last cut is not applied in the kink analysis where a further \(p_\mathrm{{T}}\)-dependent selection on the DCA of the selected tracks to the primary vertex in the transverse plane (DCA\(_{xy}\)) is requested. The global tracks that satisfy these selection criteria have a \(p_\mathrm{{T}}\) resolution of 1 % at \(p_\mathrm{{T}}\) \(=\) 1 GeV/\(c\) and 2 % at \(p_\mathrm{{T}}\) \(=\) 10 GeV/\(c\). The ITS-sa tracks are required to have at least four ITS clusters out of which at least one in the SPD layers and three in the SSD and SDD, \(\chi ^{2} / N_\mathrm{{clusters}} < 2.5\) and a DCA\(_{xy}\) satisfying a \(p_\mathrm{{T}}\)-dependent upper cut corresponding to 7 times the DCA resolution. The selected ITS-sa tracks have a maximum \(p_\mathrm{{T}}\) resolution of 6 % for pions, 8 % for kaons and 10 % for protons in the \(p_\mathrm{{T}}\) range used in the analysis. Global and ITS-sa tracks have a similar resolution in the DCA\(_{xy}\) parameter, that is, 75 \(\upmu \)m at \(p_\mathrm{{T}}\) \(=\) 1 GeV/\(c\) and 20 \(\upmu \)m at \(p_\mathrm{{T}}\) \(=\) 15 GeV/\(c\) [28], which is well reproduced in the simulation of the detector performance. The final spectra are calculated for \(|y|<0.5\).
2.3 Particle identification strategy
To measure the production of \(\pi ^{\pm }\), \(K^{\pm }\), \(p\) and \({\overline{{p}}}\) over a wide \(p_\mathrm{{T}}\) range, results from five independent analyses, namely ITS-sa, TPC–TOF, TOF, HMPID and kink, are combined. Each analysis uses different PID signals in order to identify particles in the complementary \(p_\mathrm{{T}}\) ranges reported in Table 1. In the following, the PID strategies used by ITS-sa, TPC–TOF and TOF analyses are briefly summarised since they are already discussed in detail in [15, 29], while the HMPID analysis, presented here for the first time, and the kink analysis, modified with respect to that described in [15], are presented in more detail.
2.3.1 ITS stand-alone analysis
In this analysis ITS-sa tracks are used and particles are identified by comparing the d\(E\)/d\(x\) measurement provided by the ITS detector with the expected values at a given momentum \(p\) under the corresponding mass hypotheses.
Distribution of d\(E\)/d\(x\) as a function of momentum (\(p\)) measured in the ITS using ITS-sa tracks in \(|\eta |<0.9\). The continuous curves represent the parametrisation of d\(E\)/d\(x\) for e, \(\pi \), \(K\) and \(p\) while the dashed curves are the bands used in the PID procedure
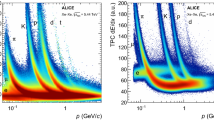
In Fig. 1, the measured d\(E\)/d\(x\) values are shown as a function of track momentum together with the curves of the energy loss for the different particle species, which are calculated using the PHOBOS parametrisation [30] of the Bethe–Bloch curves at large \(\beta \gamma \) and with a polynomial to correct for instrumental effects. A single identity is assigned to each track according to the mass hypothesis for which the expected specific energy-loss value is the closest to the measured d\(E\)/d\(x\) for a track with momentum \(p\). No explicit selection on the difference between the measured and expected values is applied except for a lower limit on pions set to two times the d\(E\)/d\(x\) resolution (\(\sigma \)) and an upper limit on protons given by the mid-point between the proton and the deuteron expected d\(E\)/d\(x\). The ITS d\(E\)/d\(x\) is calculated as a truncated mean of three or four d\(E\)/d\(x\) values provided by the SDD and SSD layers. The truncated mean is the average of the lowest two d\(E\)/d\(x\) values in case signals in all the four layers are available, or as a weighted average of the lowest (weight 1) and the second lowest (weight 1/2) values in the case where only three d\(E\)/d\(x\) samples are measured. Even with this truncated mean approach, used to reduce the effect of the tail of the Landau distribution at large d\(E\)/d\(x\), the small number of samples results in residual non-Gaussian tails in the d\(E\)/d\(x\) distribution, which are partially reproduced in simulation. These non-Gaussian tails increase the misidentification rate, e.g. pions falling in the kaon identification bands. The misidentification probability is estimated using a Monte-Carlo simulations where the particle abundances were adjusted to those observed in data. This correction is at most 10 % in the \(p_\mathrm{{T}}\) range of this analysis. In order to check possible systematic effects due to these non-Gaussian tails and their imperfect description in Monte-Carlo simulations, the analysis was repeated with different strategies for the particle identification, namely using a 3\(\sigma \) compatibility band around the expected d\(E\)/d\(x\) curves and extracting the yields of pions, kaons and protons using the unfolding method described in [15], which is based on fits to the d\(E\)/d\(x\) distributions in each \(p_\mathrm{{T}}\) interval. The difference among the results from these different analysis strategies is assigned as a systematic uncertainty due to the PID.
2.3.2 TPC–TOF analysis
In this analysis global tracks are used and particle identification is performed by comparing the measured PID signals in the TPC and TOF detectors (d\(E\)/d\(x\), time of flight) with the expected values for different mass hypotheses. An identity is assigned to a track if the measured signal differs from the expected value by less than three times its resolution \(\sigma \). For pions and protons with \(p_\mathrm{{T}}\) \(<\) 0.6 GeV/\(c\) and kaons with \(p_\mathrm{{T}}\) \(<\) 0.5 GeV/\(c\), a compatibility within 3\(\sigma \) is required on the d\(E\)/d\(x\) measurement provided by the TPC computed as a truncated mean of the lowest 60 % of the available d\(E\)/d\(x\) samples. The d\(E\)/d\(x\) resulting from this truncated mean approach is Gaussian and it is shown in Fig. 2 as a function of the track momentum together with the expected energy-loss curves (see [31] for a discussion of the d\(E\)/d\(x\) parametrisation).
Distribution of d\(E\)/d\(x\) as a function of momentum (\(p\)) measured in the TPC using global tracks for \(|\eta | < 0.9\). The continuous curves represent the Bethe–Bloch parametrisation
Above these \(p_\mathrm{{T}}\) thresholds, i.e. \(p_\mathrm{{T}}\) \(\ge \) 0.6 GeV/\(c\) for pions and protons and \(p_\mathrm{{T}}\) \(\ge \) 0.5 GeV/\(c\) for kaons, a three \(\sigma \) requirement is applied to both the d\(E\)/d\(x\) measurement provided by the TPC and the time of flight \(t_\mathrm{{tof}}\) provided by the TOF detector. The time of flight \(t_\mathrm{{tof}}\), as will be described in more detail in the next section, is the difference between the arrival time \(\tau _\mathrm{TOF}\) measured with the TOF detector and the event start time \(t_0\), namely \(t_\mathrm{{tof}}=\tau _\mathrm{{TOF}}-t_{0}\). The additional condition on the TOF signal helps in extending the particle identification on a track-by-track basis to higher \(p_\mathrm{{T}}\) where the TPC separation power decreases. The particles for which the TOF signal is available are a sub-sample of the global tracks reconstructed using ITS and TPC information. The TOF information is not available for tracks that cross inactive regions of the TOF detector, for particles that decay or interact with the material before the TOF and for tracks whose trajectory, after prolongation from the TPC outer radius, is not matched with a hit in the TOF detector. The fraction of global tracks with associated TOF information (TOF matching efficiency) depends on the particle species and \(p_\mathrm{{T}}\) as well as on the fraction of the TOF active readout channels. For the data analysis presented in this paper the matching efficiency increases with increasing \(p_\mathrm{{T}}\) until it saturates, e.g. at about 65 % for pions with \(p_\mathrm{{T}}\) \(>\) 1 GeV/\(c\). In Fig. 3 the velocity \(\beta \) of the tracks, computed from the trajectory length measured with the ITS and TPC and the time of flight measured with the TOF, is reported as a function of the rigidity \(p/z\), where \(z\) is the charge assigned based on the measured direction of the track curvature.
Particle velocity \(\beta \) measured by the TOF detector as a function of the rigidity \(p/z\), where \(z\) is the particle charge, for \(|\eta | < 0.9\)
More than one identity can be assigned to a track if it fulfils PID and rapidity selection criteria for different particle species. The frequency of such cases is at most 0.5 % in the momentum range used in this analysis. The misidentification of primary particles is computed and corrected for using Monte-Carlo simulations. It is at most 2 % for pions and protons and 8 % for kaons in the considered \(p_\mathrm{{T}}\) ranges. The correction of the raw spectra for the misidentified particles provides also a way to remove the overestimation of the total number of particles introduced by the possibility, described above, to assign more than one identity to a track.
2.3.3 TOF analysis
This analysis uses the sub-sample of global tracks for which a TOF measurement is available. The PID procedure utilises a statistical unfolding approach that provides a \(p_\mathrm{{T}}\) reach higher than the three \(\sigma \) approach described in the previous section. The procedure is based on the comparison between the measured time of flight from the primary vertex to the TOF detector, \(t_\mathrm{{tof}}\), and the time expected under a given mass hypothesis, \(t^\mathrm{{exp}}_{i}\) (\(i\) \(=\) \(\pi \), \(K\), \(p\)), namely on the variable \(\Delta t_{i} = t_\mathrm{{tof}} - t^\mathrm{{exp}}_{i}\). As mentioned in the previous section, the time of flight \(t_\mathrm{{tof}}\) is defined as the difference between the time measured with the TOF detector \(\tau _\mathrm{TOF}\) and the event start time \(t_0\). The \(t_{0}\) value is computed from the analysed tracks themselves on an event-by-event basis, using a combinatorial algorithm which compares the measured \(\tau _\mathrm{{TOF}}\) with the expected ones for different mass hypotheses. The track under study is excluded to avoid any bias in the PID procedure [13, 15]. In case the TOF \(t_{0}\) algorithm fails, the average beam-beam interaction time is used. The former approach provides a better \(t_{0}\) resolution, but it requires at least three reconstructed tracks with an associated TOF timing measurement. The yield of particles of species \(i\) in a given \(p_\mathrm{{T}}\) interval is obtained by fitting the distribution of the variable \(\Delta t_{i}\) obtained from all the tracks regardless of the method used to compute the \(t_{0}\). This distribution is composed of the signal from particles of species \(i\), which is centred at \(\Delta t_{i}=0\), and two distinct populations corresponding to the other two hadron species, \(j,k \ne i\). The \(\Delta t_{i}\) distribution is therefore fitted with the sum of three functions \(f(\Delta t_i)\), one for the signal and two for the other hadron species, as shown in Fig. 4. The \(f(\Delta t_i)\) functional forms are defined using the data in the region of clear species separation. The TOF signal is not purely Gaussian and it is described by a function \(f(\Delta t_i)\) that is composed of a Gaussian term and an exponential tail at high \(\Delta t_{i}\) mainly due to tracks inducing signals in more than one elementary detector readout element [13]. The raw yield of the species \(i\) is given by the integral of the signal fit function.
Distribution of \(\Delta t_{i}\) assuming the pion mass hypothesis in the transverse momentum interval 1.9 \(<\) \(p_\mathrm{{T}}\) \(<\) 2.0 GeV/\(c\). The data (black points) are fitted with a function (light blue line) that is the sum of the signal due to pions (green dotted line) and the two populations corresponding to kaons (red dotted line) and protons (purple dashed line)
The reach in \(p_\mathrm{{T}}\) of this PID method depends on the resolution of \(\Delta t_{i}\), that is, the combination of the TOF detector intrinsic resolution, the uncertainty on the start time and the tracking and momentum resolution. Its value, for the data used in this analysis, is about 120 ps leading to 2\(\sigma \) pion–kaon and kaon–proton separation at \(p_\mathrm{{T}}\) \(=\) 2.5 GeV/\(c\) and \(p_\mathrm{{T}}\) \(=\) 4.0 GeV/\(c\), respectively. This PID procedure has the advantage of not requiring a Monte-Carlo-based correction for misidentification because the contamination under the signal of particles of species \(i\) due to other particle species is accounted for by the background fit functions.
2.3.4 HMPID analysis
The HMPID is a RICH detector in a proximity focusing layout in which the primary ionizing charged particle generates Cherenkov light inside a liquid C\(_6\)F\(_{14}\) radiator [14]. The UV photons are converted into photoelectrons in a thin CsI film of the PhotoCathodes (PCs) and the photoelectrons are amplified in an avalanche process inside a multi-wire proportional chamber operated with CH\(_4\). To obtain the position sensitivity for the reconstruction of the Cherenkov rings, the PCs are segmented into pads. The final image of a Cherenkov ring is then formed by a cluster of pads (called a “MIP” cluster) associated to the primary ionisation of the particle and the photoelectron clusters associated to Cherenkov photons. In Fig. 5 a typical Cherenkov ring is shown.
Display of a Cherenkov ring detected in a module of HMPID for an inclined track crossing the detector. The colours are proportional to the pad charge signal
In this analysis, the sub-sample of global tracks that reach the HMPID detector and produce the Cherenkov rings is used. Starting from the photoelectron cluster coordinates on the photocathode, a back-tracking algorithm calculates the corresponding single photon Cherenkov angle by using the impact angle of a track extrapolated from the central tracking detectors up to the radiator volume. A selection on the distance (\(d_\mathrm{{MIP-trk}}\)) computed on the cathode plane between the centroid of the MIP cluster and the track extrapolation, set to \(d_\mathrm{{MIP-trk}}\) \(<\) 5 cm, rejects fake associations in the detector. Background discrimination is performed using the Hough transform method (HTM) [32]. The mean Cherenkov angle \(\langle \theta _\mathrm{{ckov}}\rangle \) is obtained if at least three photoelectron clusters are detected.
For a given track, \(\langle \theta _\mathrm{{ckov}}\rangle \) is computed as the weighted average of the single photon angles (if any) selected by HTM. Pions, kaons and protons become indistinguishable at high momentum when the resolution on \(\langle \theta _\mathrm{{ckov}}\rangle \) reaches 3.5 mrad. The angle \(\langle \theta _\mathrm{{ckov}}\rangle \) as a function of the track momentum is shown in Fig. 6, where the solid lines represent the \(\theta _\mathrm{{ckov}}\) dependence on the particle momentum
where \(n\) is the refractive index of the liquid radiator, \(m\) the mass of the particle and \(p\) its momentum.
Mean Cherenkov angle \(\langle \theta _\mathrm{{ckov}}\rangle \) measured with HMPID in its full geometrical acceptance as a function of the particle momentum \(p\) for positively and negatively charged tracks. The solid lines represent the theoretical curves for each particle species
This analysis is performed for \(p\) \(>\)1.5 GeV/c, where pions, kaons and protons produce a ring with enough photoelectron clusters to be reconstructed. If the track momentum is below the threshold to produce Cherenkov photons, background clusters could be wrongly associated to the track. As an example the few entries visible in Fig. 6 between the pion and kaon bands at low \(\langle \theta _\mathrm{{ckov}}\rangle \) correspond to wrong associations of clusters with a kaon or a proton below the threshold to produce Cherenkov photons.
The particle yields are extracted from a fit to the Cherenkov angle distribution in narrow transverse momentum intervals. In Fig. 7, examples of the reconstructed Cherenkov angle distributions in two narrow \(p_\mathrm{{T}}\) intervals (3.4 \(<\) \(p_\mathrm{{T}}\) \(<\) 3.6 GeV/\(c\) and 5 \(<\) \(p_\mathrm{{T}}\) \(<\) 5.5 GeV/\(c\)) for negatively charged tracks are shown.
The background, mainly due to noisy pads and photoelectron clusters from other rings overlapping to the reconstructed one, is negligible in the momentum range considered in this analysis. The fit function (shown as a solid line in Fig. 7) is a sum of three Gaussian functions, one for each particle species (dashed lines), whose mean and sigma are fixed to the Monte-Carlo values.
Distributions of \(\langle \theta _\mathrm{{ckov}}\rangle \) measured with the HMPID in the two narrow \(p_\mathrm{{T}}\) intervals 3.4 \(<\) \(p_\mathrm{{T}}\) \(<\) 3.6 GeV/\(c\) (top) and 5 \(<\) \(p_\mathrm{{T}}\) \(<\) 5.5 GeV/\(c\) (bottom) for tracks from negatively charged particles. Solid lines represent the total fit (sum of three Gaussian functions). Dotted lines correspond to pion, kaon and proton signals. The background is negligible
The extracted separation power of hadron identification in the HMPID as a function of \(p_\mathrm{{T}}\) is shown in Fig. 8. The separation between pions and kaons (kaons and protons) is expressed as the difference between the means of the \(\langle \theta _\mathrm{{ckov}}\rangle \) angle Gaussian distributions for the two given particle species (\(\Delta _\mathrm{{\pi ,K}}\) or \(\Delta _{{K,p}}\)) divided by the average of the Gaussian widths of the two distributions, i.e. (\(\sigma _\mathrm{\pi }+\sigma _{K}\))/2 or (\(\sigma _{K}+\sigma _{p}\))/2. A separation at 3\(\sigma \) level in \(\langle \theta _\mathrm{{ckov}}\rangle \) is achieved up to \(p_\mathrm{{T}}\) \(=\) 3 GeV/\(c\) for \(K\)–\(\pi \) and up to \(p_\mathrm{{T}}\) \(=\) 5 GeV/\(c\) for \(K\)–\(p\). The separation at 6 GeV/\(c\) for \(K\)–\(p\) can be extrapolated from the curve and it is about 2.5\(\sigma \).
Separation power (\(n_{\sigma }\)) of hadron identification in the HMPID as a function of \(p_\mathrm{{T}}\). The separation n\(_{\sigma }\) of pions and kaons (kaons and protons) is defined as the difference between the average of the Gaussian distributions of \(\langle \theta _\mathrm{{ckov}}\rangle \) for the two hadron species divided by the average of the Gaussian widths of the two distributions
The HMPID geometrical acceptance is about 5 % for tracks with high momentum. Therefore the analysis of HMPID required one to analyse a larger data sample with respect to the other PID methods, as reported in Table 1. The total efficiency is the convolution of the tracking, matching and PID efficiencies. The PID efficiency of this method is determined by the Cherenkov angle reconstruction efficiency. It has been computed by means of Monte-Carlo simulations and it reaches 90 % for particles with velocity \(\beta \sim \) 1. As a cross check, the PID efficiency has been determined using clean samples of protons and pions from \(\Lambda \) and \(K^0_\mathrm{s}\) decays. The measured efficiency agrees within the statistical uncertainties with the Monte-Carlo estimates, in the momentum range 1.5 \(<\) \(p_\mathrm{{T}}\) \(<\) 6 GeV/\(c\). Moreover, the correction due to the \(d_\mathrm{{MIP-trk}}\) cut is computed from the same sample of identified protons and pions from \(\Lambda \) and \(K^{0}_\mathrm{s}\) decays.
2.3.5 Kink analysis
Charged kaons can also be identified in the TPC by reconstructing their weak-decay vertices, which exhibit a characteristic kink topology defined by a decay vertex with two tracks (mother and daughter) having the same charge. This procedure extends the measurement of charged kaons on a track-by-track basis to \(p_\mathrm{{T}}\) \(=\) 6 GeV/\(c\). The algorithm for the kink reconstruction is applied inside a fiducial volume of the TPC, namely 130 \( < R < \) 200 cm, needed to reconstruct both the mother and the daughter tracks. The mother track is selected with similar criteria to the global tracks (Sect. 2.2), but with a looser selection on the minimum number of TPC clusters, which is set to 20, and a wider rapidity range set to \(|y|< 0.7\) to increase the statistics of kink candidates. No selections are applied on the charged daughter track. The reconstructed invariant mass \(M_{\mu \nu }\) is calculated assuming the charged daughter track to be a muon and the undetected neutral daughter track to be a neutrino. The neutrino momentum is the difference between the measured momenta of the mother particle and of the charged daughter.
Kink invariant mass \(M_{\mu \nu }\) in data (red circles) and Monte-Carlo (black line) for summed particles and antiparticles, integrated over the mother transverse momentum range 0.2 \(<\) \(p_\mathrm{{T}}\) \(< 6.0 \) GeV/\(c\) and \(|y| < 0.7\) before (top panel) and after (bottom panel) the topological selections, based mainly on the \(q_\mathrm {T}\) and the maximum decay opening angle