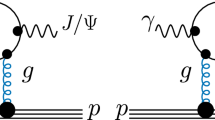On relevance of triple-gluon fusion in $J/\psi$ hadroproduction

Abstract

A contribution to $J/\psi$ hadroproduction is analyzed in which the meson production is mediated by three-gluon partonic state, with two gluons coming from the target and one gluon from the projectile. This mechanism involves double gluon density in one of the protons, hence this contribution enters at a non-leading twist. It is, however, relevant due to an enhancement factor coming from large double gluon density at small $x$. We calculate the three-gluon contribution to $J/\psi$ hadroproduction within perturbative QCD in the $k_T$-factorization framework. Results are obtained for differential $p_T$-dependent cross sections for all $J/\psi$ polarizations and for the sum over the polarization components. The rescattering contribution is found to provide a significant correction to the standard leading twist cross section at the energies of the Tevatron or the LHC at moderate $p_T$. We suggest $J/\psi$ production in proton–nucleus collision as a possible probe of the triple-gluon mechanism.

1 Introduction

Production of heavy vector quarkonia in proton collisions has been a subject of intense experimental and theoretical investigations since CDF found huge excess of the measured cross sections of prompt $J/\psi$ [1, 2] with respect to the standard theoretical predictions in QCD. Initially the theory predictions were based on a leading order collinear QCD approximation, in which the hard matrix element of a partonic color singlet subprocess $gg \rightarrow J/\psi g$ gives the dominant contribution. This approximation, however, badly underestimates the measured cross section and yields an incorrect $p_T$ distribution of the produced mesons, so it was necessary to consider alternative mechanisms of quarkonia hadroproduction. In particular, two theoretical concepts received a lot of attention: the so-called color octet model (COM) [3–12] and the other approach based on the $k_T$-factorization (KTF) scheme [13–19]. For a comprehensive theory review of various approaches to quarkonium hadroproduction see [20].

The COM is based on the fact that the hadron wave functions contain higher Fock components. For heavy quarkonia it implies that the heavy quark–antiquark ($Q\bar{Q}$) pair in a heavy meson may be accompanied e.g. by one or more gluons. So the $Q\bar{Q}$-pair may appear in the meson in a color octet state [3]. The amplitudes of such octet components are subleading (w.r.t. the standard, color singlet component) in heavy quark velocity expansion within the Heavy Quark Effective Theory [3], but in the vector meson hadroproduction the color octet states contributions are enhanced by the corresponding hard partonic cross section for the production of such states [4, 5]. With only a few free parameters the color octet model is quite successful in describing the magnitude and $p_T$-dependence of the prompt $J/\psi$ hadroproduction [9–12], however, it faces some problems with an accurate description of the produced mesons polarization. In particular, predictions for the meson polarization change a lot when going from LO to NLO accuracy [10, 12]. Besides, neither LO nor NLO COM estimates of prompt $J/\psi$ polarization are fully consistent with the data. It is fair to add that in the COM the amplitudes of color octet $Q\bar{Q}$ transitions into mesons are not known from first principles, and the theoretical estimates of the cross section magnitudes rely upon fitted parameters. On the other hand, the kinematical dependence of the cross sections, e.g. the $p_T$-dependence, is already a genuine QCD prediction (for each partonic subprocess separately) and the good description of the meson $p_T$-dependence within the COM supports the strong validity of this approach. The COM may also be understood within the hard factorization theorem in QCD, where universal (independent on the environment) fragmentation functions exist of $Q\bar{Q}$ partonic states with various quantum numbers (including color octet) into final state quarkonia [21, 22].

Another theoretical approach to quarkonia hadroproduction relies on the $k_T$-factorization scheme. In this framework, one allows for non-zero transverse momentum of colliding partons. Because of multiple emissions in the course of QCD evolution the parton momentum may become sizable if the evolution length is sufficiently large. This effect is especially pronounced if gluons are probed at small $x$, which is the case for prompt quarkonia production at the Tevatron or at the LHC. Then the kinematical distributions of produced quarkonia may be strongly affected by $k_T$ of the incoming gluons. Indeed, inclusion of gluon $k_T$ in the analysis brings theoretical estimates much closer to the experimental data, both for the magnitude and for the shape of the distributions, already at the lowest order in QCD. This works rather well for the $C$-even charmonia, like $\chi _\mathrm{c}$, but for an accurate description of Tevatron data on prompt $J/\psi$ and $\psi '$ production a color octet component was necessary also in the KTF approach [16], although smaller than in the collinear approximation. For the recent LHC data on prompt charmonia production, however, a good theoretical description of magnitude, kinematics, and polarization was found within KTF without including the color octet mechanism [18]. This good description in KTF CSM was achieved by using a more advanced unintegrated parton density, CCFMA0 [23, 24]. Still, it is fair to say that a global, consistent description of quarkonia production in KTF has not been formulated yet.

It follows from this discussion that the theoretical understanding of heavy quarkonia hadroproduction is not yet fully satisfactory. A polarization description and the need of fitting key parameters are somewhat weak points of the color octet model, and a global description of $J/\psi$, $\psi '$, and $\chi _\mathrm{c}$ hardroproduction has not been formulated yet in the KTF approach. Therefore it is possible that both proposed approaches are not complete and need to be supplemented by another mechanism.

The COM and CSM approaches both in the collinear and KTF framework share an important common feature – it is assumed that at the parton level the quarkonia production is initiated by two gluons. At very large energies, however, when the gluon density becomes large, it is expected that sizable corrections to this picture may come from subprocess with more than two initial state partons, which would be classified as rescattering or shadowing/anti-shadowing contributions. Such effects are expected to be particularly important in collisions with heavier nuclei. First estimates of such multiple-gluon contributions to heavy quarkonia production in $pp$ and $p\bar{p}$ collisions were performed by Khoze et al. [25], who considered a three-gluon initial partonic state. Recently, Ma and Venugopolan [26] proposed a resummation of rescattering contributions within the color glass condensate (CGC) formalism [27–29]. A good description of unpolarized data for $J/\psi$ and $\psi '$ was achieved down to very low $p_T$ by matching the resummed CGC cross section with predictions of the collinear NRQCD COM approach [26, 30].

In this paper, following the idea of Khoze et al. [25], we shall investigate the three-gluon mechanism of quarkonia hadroproduction in which hard rescattering plays the key rôle in color neutralization of the $Q\bar{Q}$ pair. Thus, we shall consider the three-gluon fusion process at the parton level: $3g \rightarrow J/ \psi$ in the color singlet channel instead of the standard color singlet process $gg \rightarrow J/\psi g$. This three-gluon fusion partonic process is, of course, a higher twist correction to the cross section, as it couples to a double gluon density in one of the protons. Therefore, one expects it to be suppressed w.r.t. the standard, leading twist contribution by powers of the hard scale. In high energy collisions, however, this rescattering term receives a significant enhancement due to the large gluon density, reflected by a large ratio of double and single gluon density at small $x$. Moreover, the matrix elements of the rescattering term $3g \rightarrow J/\psi$ and the standard one $gg \rightarrow J/\psi g$ come at the same order of perturbation theory, so no additional $\alpha _s$ suppression of the rescattering piece occurs in the matrix element. Hence, despite the higher twist nature, it may still be important. As already stated, such processes were already proposed in Ref. [25] where estimates were given showing that rescattering might explain the discrepancy between the data and the predictions based on the color singlet mechanism. We address and develop this idea in more detail by performing a complete calculation of the rescattering contribution in the KTF framework, including an explicit calculation of the $p_T$ distribution of the produced quarkonia and the polarization composition. We find that the rescattering correction is a significant contribution to the prompt $J/\psi$ cross section especially at moderate $p_T$ and should be included in a precise description of the data. It should be stressed that the rescattering correction complements in a natural way both the COM and the standard KTF approach, providing a kinematics- and process-dependent mechanism of color neutralization. Also, we expect that the rescattering mechanism should be strongly enhanced and thus even more important for heavy quarkonia production in collisions with nuclei.

It is important to note that the triple-gluon mechanism of the $J/\psi$ hadroproduction employs the double gluon density (DGD). In this paper we use the simplest, uncorrelated model of the DGD. A more advanced treatment of the DGD including the QCD evolution [31] leads to nontrivial correlations that grow with the increasing evolution length. Recently this issue was vividly studied; see e.g. Refs. [32–37]. The predicted correlations lead to an enhancement of the DGD at small $x$ and hence they affect the magnitude of the predicted cross sections. Within current theoretical understanding these effects are moderate at the scales relevant for the $J/\psi$ hadroproduction at low and mid $p_T$. Based on these estimates one finds that our predictions are somewhat underestimated, however, the numerical results described in Sect. 4. A show that the key theoretical uncertainties to the estimates come from the uncertainty of the factorization scale and of the shape of the unintegrated parton density.

The paper is organized as follows: in Sect. 2 we introduce the kinematics of the process and the notation, in Sect. 3 we derive analytic formulas for the amplitudes and cross sections of the direct quarkonium production by rescattering, in Sect. 4 we give numerical estimates for the cross sections, and conclusions are given in Sect. 5. Technical pieces of the derivations are given in the Appendix A.

2 Kinematics

We consider direct inclusive production of heavy quarkonia in high energy proton–(anti-) proton collisions and focus on a process mediated by partonic subprocess with tree incoming gluons: $3g \rightarrow V$. In general, $V$ can be any heavy vector quarkonium, $J/\psi$, $\psi '$, $\Upsilon$, and so on, but we choose the best measured $J/\psi$ production as the reference process. The three-gluon fusion contribution enters as a higher twist correction to the direct vector quarkonium production. The notation for the four-momenta of incoming protons ($p_A$, $p_B$), the outgoing meson, $p$, outgoing hadronic final states ($p'_A$ for $A'$ and $p'_B$ for $B'$) is explained in the left panel of Fig. 1.

Fig. 1

a The amplitude $\mathcal {M}$ of the $J/\psi$ hadroproduction in the triple-gluon fusion mechanism; b the dominant diagram in the square of the amplitude, $|\mathcal {M}|^2$

We analyze the process within perturbative QCD in the high energy approximation, using the framework of $k_T$-factorization. In the high energy limit, only the leading power of $s= (p_A + p_B)^2$ is retained. In this approximation the proton masses may be neglected, $p_A^2=p_B^2=0$, and $s \simeq 2 p_A \cdot p_B$. The masses of outgoing states are denoted by $p^2 = M^2_{J/\psi }$, $p_{A^\prime }^2=M_{A^\prime }^2$, $p_{B^\prime }^2=M_{B^\prime }^2$ for the $J/\psi$ and hadronic final states $A'$ and $B'$ emerging from the target and the projectile, respectively.

The diagram in Fig. 1a illustrates the partonic topology of the amplitude for direct vector quarkonium production with three intermediate gluons. The four-momenta of intermediate gluon couplings to $p_A \rightarrow A'$ and $p_B \rightarrow B'$ transitions are denoted by $k_1$, $k_2$, and $l$, respectively. The four-momentum conservation imposes constraints on the four-momenta,

$$\begin{aligned} p_A = p_{A^\prime }+k_1+k_2,\quad p_B=p_{B^\prime }+l,\quad p = k_1+k_2+l.\nonumber \\ \end{aligned}$$

(1)

We employ the Sudakov parameterization of the four-momenta,

$$\begin{aligned} p_{A^\prime (B^\prime )}= & {} \alpha _{A(B)}p_A + \beta _{A(B)}p_B + p_{A^\prime (B^\prime )\perp },\nonumber \\ p= & {} \alpha p_A+\beta p_B+p_\perp , \end{aligned}$$

(2)

where the transverse directions are in the plane orthogonal to the direction of the collision axis in the CMS frame. Then the kinematic constraints lead to

$$\begin{aligned} \beta _A = \frac{{\varvec{p}}^{\,2}+M_{A^\prime }^2}{\alpha _A s},\quad \alpha _B = \frac{{\varvec{p}}^{\,2}+M_{A^\prime }^2}{\beta _B s},\quad \beta = \frac{{\varvec{p}}^{\,2}+M_{J/\psi }^2}{\alpha s}.\nonumber \\ \end{aligned}$$

(3)

The process of $J/\psi$ production is analyzed in the kinematical domain where $\alpha _A=O(1), \beta _B=O(1)$, and consequently $\beta _A\ \sim \alpha _B \sim O(1/s)$. Thus, the gluon momenta satisfy

$$\begin{aligned}&k \equiv k_1+k_2 \approx (1-\alpha _A)p_A-p_{A^\prime \perp },\nonumber \\&l\approx (1-\beta _B)p_B-p_{B^\prime \perp } \end{aligned}$$

(4)

and from the last term of (1) one gets

$$\begin{aligned} \alpha \approx 1-\alpha _A,\quad \beta \approx 1-\beta _B,\quad p_{\perp } = -p_{A^\prime \perp }-p_{B^\prime \perp }. \end{aligned}$$

(5)

In the Sudakov parameterization of the gluon momenta $k_i=\alpha ^k_i p_A+\beta ^k_i p_B+k_{i\perp }$, $l=\alpha ^l p_A+\beta ^l p_B+l_{\perp }$ (see Fig. 1a) one has the relations:

$$\begin{aligned}&\alpha ^k_1+\alpha ^k_2 = \alpha , \quad \beta ^k_1+\beta ^k_2 = O(1/s),\nonumber \\&\alpha ^l = O(1/s), \quad \beta _1=\beta . \end{aligned}$$

(6)

3 The triple-gluon contribution: analytic formulas

3.1 The triple-gluon amplitude

The amplitude in Fig. 1a reads

$$\begin{aligned} -i\mathcal {M}= & {} \frac{1}{2!} S^{\,b_1}_{B\,\mu _1}(p_B,r_B,B^\prime ,l)\frac{\mathrm{d}^{\mu _1\sigma _1}}{l^2}\nonumber \\&\times \int \frac{\mathrm{d}^4k_1}{(2\pi )^4}S^{\,b_1a_1a_2}_{\sigma _1\rho _1\rho _2}(p,\epsilon ;l,k_1,k_2,p)\nonumber \\&\times \frac{\mathrm{d}^{\rho _1\nu _1}\mathrm{d}^{\rho _2\nu _2}}{k_1^2k_2^2} S^{a_1a_2}_{A\,\nu _1\nu _2}(p_A,r_A,A^\prime ,k_1,k_2) \end{aligned}$$

(7)

where $S^{\,b_1}_{B\,\mu _1} = \langle p_{B^\prime },l|J_{\mu _1}^{b_1}(0)|p_b,r_B\rangle$ and $S^{a_1a_2}_{A\,\nu _1\nu _2}(p_A,r_A, A^\prime ,k_1,k_2)$ give the amplitudes of finding a gluon with color $b_1$ and four-momentum $l$, and two gluons of colors $a_1,a_2$ and momenta $k_1, k_2=k-k_1$, respectively, in the decay products of a struck proton. The incoming proton polarizations are denoted by $r_{A,B}$. The vertex $S^{\,b_1a_1a_2}_{\sigma _1\rho _1\rho _2}(l,k_1,k_2; p,\epsilon )$ describes the amplitude of $J/\psi$ production with momentum $p$ and polarization $\epsilon$. In the standard Regge kinematics of high energy scattering at a small momentum transfer one can approximate the polarization tensors of the gluons (in the Feynman gauge) as $\mathrm{d}^{\mu _1\sigma _1} \approx -2p_A^{\mu _1}p_B^{\sigma _1}/s$ and $\mathrm{d}^{\rho _i\nu _i} \approx -2p_A^{\rho _i}p_B^{\nu _i}/s$ for $i=1,2$. Then one can write the amplitude (7) in the following form:

$$\begin{aligned} -i\mathcal {M}= & {} \frac{2s}{(2\pi )^4} \Phi ^{b_1} _{B}(p_B,r_B,B';\alpha _l, \beta _l, {\varvec{l}})\, \frac{1}{l^2} \int \frac{\mathrm{d}^2{\varvec{k}}_{1}}{{\varvec{k}}_{1 }^{\,2}({\varvec{k}} -{\varvec{k}}_{1 })^2}\nonumber \\&\times \Phi ^{a_1a_2}_A(p_A,r_A,A^\prime ;\alpha _k,\beta _k;{\varvec{k}}_{1 },{\varvec{k}} -{\varvec{k}}_{1 }) \nonumber \\&\times \Phi ^{b_1a_1a_2}_{J/\psi }(\alpha _k,\beta _l;{\varvec{l}} ,{\varvec{k}}_{1 },{\varvec{k}} -{\varvec{k}}_{1 };p,\epsilon ), \end{aligned}$$

(8)

where the impact factors (at the amplitude level) for a $p_B \rightarrow B' + g$, $p_A \rightarrow A' + 2g$, and $2g + g \rightarrow J/\psi$ transitions read, respectively,

$$\begin{aligned}&\Phi ^{b_1} _{B}(p_B,r_B,B';\alpha _l, \beta _l, {\varvec{l}}) = S^{\,b_1}_{B\,\mu _1}(p_B,r_B,B';l)\,\frac{p_A^{\mu _1}}{s},\end{aligned}$$

(9)

$$\begin{aligned}&\Phi ^{a_1a_2}_A(p_A,r_A,A^\prime ;\alpha _k,\beta _k;{\varvec{k}}_{1 },{\varvec{k}} -{\varvec{k}}_{1 })\nonumber \\&\quad = \int \mathrm{d}\beta _1^k S^{a_1a_2}_{A\,\nu _1\nu _2}(p_A,r_A,A^\prime ,k_1,k-k_1)\frac{p_B^{\nu _1}p_B^{\nu 2}}{s} ,\end{aligned}$$

(10)

$$\begin{aligned}&\Phi ^{b_1a_1a_2}_{J/\psi }(\alpha _k,\beta _l;{\varvec{l}} ,{\varvec{k}}_{1 },{\varvec{k}} -{\varvec{k}}_{1 };p\,\epsilon )\nonumber \\&\quad =\int \mathrm{d}\alpha _1^k S^{\,b_1a_1a_2}_{\sigma _1\rho _1\rho _2}(l,k_1,k-k_1;p,\epsilon )\frac{p_B^{\sigma _1}p_A^{\rho _1}p_A^{\rho _2}}{s} . \end{aligned}$$

(11)

The total contribution of three gluons to the $J/\psi$ production amplitude comes from a diagram depicted in Fig. 1a and an ‘upside-down’ diagram with the same topology, but with two gluons coupling to the lower vertex $p_B \rightarrow B'$. The contribution of the other diagram, $\mathcal {M}'$, may be obtained from $\mathcal {M}$, corresponding to the diagram in Fig. 1a by exchange of kinematical variables: $\alpha \leftrightarrow \beta$. It is important to note that the interference of these two amplitudes, $\mathcal {M}$ and $\mathcal {M}'$, is a subleading effect. This is because terms $\mathcal {M}^*\mathcal {M}$ and $\mathcal {M}'^*\mathcal {M}'$ are driven by the QCD evolution of a four-gluon $t$-channel state (two ladders in the large $N_\mathrm{c}$ limit) emerging from one proton and a two-gluon $t$-channel state from the other proton (see Fig. 2a), whereas the interference terms $\mathcal {M}^*\mathcal {M}'$ and $\mathcal {M}'^*\mathcal {M}$ are driven by subleading three-gluon $t$-channel states from both sides; see Fig. 2b. Hence, at large energies and for large scales, the interference terms, shown in Fig. 2b, may be neglected and the contribution to the $J/\psi$ production cross section from three intermediate gluons is $\mathrm{d}\sigma \propto |\mathcal {M}|^2 + |\mathcal {M'}|^2$.

Fig. 2

Topologies contributing to the rescattering correction in the $J/\psi$ cross section: a the topology with three two-gluon ladders (leading), b the topology of two three-gluon BKP states (suppressed)

3.2 The uncorrelated triple-gluon cross section

The simplest model of the two-gluon distribution in the proton assumes lack of correlations of the gluons in the transverse plane. This means that the double gluon density is proportional to a product of independent single gluon distributions. Below we estimate the triple-gluon contribution to $J/\psi$ hadroproduction in this scenario.

The contribution to $J/\psi$ cross section, corresponding to the diagram shown in Fig. 1b takes the following form:

$$\begin{aligned} \mathrm{d}\sigma _{pp\rightarrow J/\psi X}= & {} \frac{2}{(2\pi )^8} \int \frac{\mathrm{d}^4l}{(2\pi )^4}\frac{1}{(l^2)^2} \Phi ^{b_1b_2}_{2,p} (\alpha _l,\beta _l,{\varvec{l}}_{ }) \nonumber \\&\times \int \frac{\mathrm{d}^4k}{(2\pi )^4}\int \frac{\mathrm{d}^2{\varvec{k}}_1}{{\varvec{k}}_{1 }^{\,2}({\varvec{k}}-{\varvec{k}}_{1 })^2} \int \frac{\mathrm{d}^2{\varvec{k}}_3}{{\varvec{k}}_{3 }^{\,2}({\varvec{k}}-{\varvec{k}}_{3 })^2}\nonumber \\&\times \Phi ^{a_1a_2a_3a_4}_{4,p}(\alpha _k,\beta _k,{\varvec{k}}_{1 },{\varvec{k}}_{ }-{\varvec{k}}_{1 };{\varvec{k}}_{3 },{\varvec{k}}_{ }-{\varvec{k}}_{3 }) \nonumber \\&\times \Phi ^{b_1a_1a_2}_{J/\psi }(\alpha _k,\beta _l;{\varvec{l}} ,{\varvec{k}}_{1 };,{\varvec{k}} -{\varvec{k}}_{1 },p;\epsilon )\nonumber \\&\times \Phi ^{b_2a_3a_4\,*}_{J/\psi }(\alpha _k,\beta _l;{\varvec{l}} ,{\varvec{k}}_{3 },{\varvec{k}} -{\varvec{k}}_{3 },p\,;\epsilon ) \nonumber \\&\times (2\pi )^4\delta (l+k-p)\frac{\mathrm{d}^4p}{(2\pi )^4}\theta (p_0) \nonumber \\&\times 2\pi \delta (p^2-M_{J/\psi }^2)+ ( U \leftrightarrow L), \end{aligned}$$

(12)

where the last term describes the contribution from the graph where upper and lower vertices from Fig. 1b are interchanged. The pomeron–proton impact factor is defined by the formula

$$\begin{aligned} \Phi ^{b_1b_2}_{2,p} (\alpha _l,\beta _l,{\varvec{l}})= & {} \frac{1}{2}\, \sum _{r_B}\sum _{B^\prime } \int \mathrm{d}\Phi _{B^\prime } (2\pi )^4\nonumber \\&\times \delta (l-p_B+p_{B^\prime })\, S^{\,b_1}_{B\,\mu _1}S^{\,b_2\,*}_{B\,\mu _2}\, \frac{p_A^{\mu _1}p_A^{\mu _2}}{s}, \end{aligned}$$

(13)

whereas

$$\begin{aligned}&\Phi ^{a_1a_2a_3a_4}_{4,p}(\alpha _k,\beta _k,{\varvec{k}}_{1 },{\varvec{k}}_{ }-{\varvec{k}}_{1 };{\varvec{k}}_{3 },{\varvec{k}}_{ }-{\varvec{k}}_{3 })\nonumber \\&\quad = \frac{1}{2}\sum _{r_A}\sum _{A^\prime } \int \mathrm{d}\Phi _{A^\prime } (2\pi )^4\delta (k-p_A+p_{A^\prime }) \nonumber \\&\qquad \times \Phi ^{a_1a_2}_A(p_A,r_A,A^\prime ;\alpha _k,\beta _k;{\varvec{k}}_{1 },{\varvec{k}} -{\varvec{k}}_{1 })\nonumber \\&\qquad \times \Phi ^{a_3a_4\,*}_A(p_A,r_A,A^\prime ;\alpha _k,\beta _k,{\varvec{k}}_{3 },{\varvec{k}} -{\varvec{k}}_{3 }) \end{aligned}$$

(14)

gives the two-pomeron–proton impact factor ($2\mathbb {P}p$). In the last line the energy–momentum conservation delta function in the $J/\psi$ vertex gives $\alpha _k\approx \alpha , \beta _l\approx \beta$.

Several remarks are in order here:

• 1. The pomeron–proton impact factor $\Phi _{2,p}$ (see Fig. 3) integrated over longitudinal variables gives

  $$\begin{aligned} \int \mathrm{d}\alpha _l \mathrm{d}\beta _l\Phi ^{b_1b_2}_{2,p} (\alpha _l,\beta _l,{\varvec{l}}) = \frac{(2\pi )^3}{N_\mathrm{c}^2-1} f(\beta ,l^2)\delta ^{b_1b_2},\nonumber \\ \end{aligned}$$

  (15)

  where $\beta _l\approx \beta$ follows from the energy–momentum conservation in $J/\psi$ vertex and $f(\beta ,l^2)$ is an unintegrated gluon distribution.

• 2. The $2\mathbb {P}p$ impact factor integrated over longitudinal variable $\beta _k$ can be decompose in the following way (see the Appendix A for the derivation):

  $$\begin{aligned}&\int \mathrm{d}\alpha _k \mathrm{d}\beta _k \Phi ^{a_1a_2a_3a_4}_{4,p}(\alpha _k,\beta _k,{\varvec{k}}_{1},{\varvec{k}}-{\varvec{k}}_{1 };{\varvec{k}}_{3},{\varvec{k}}-{\varvec{k}}_{3 }) \nonumber \\&\quad = \frac{R_{\text{ sh }}^2(2\pi )^7}{(N_c^2-1)^2s} \left[ \delta ^{a_1a_3}\delta ^{a_2a_4} f(\alpha ,k_1 ^2)f(\alpha ,({\varvec{k}}-{\varvec{k}}_{1 })^2)\right. \nonumber \\&\qquad \times S^2({\varvec{k}}_{1 }-{\varvec{k}}_{3 }) + \delta ^{a_1a_4}\delta ^{a_2a_3} f(\alpha ,k_1^2)f(\alpha ,({\varvec{k}}_{ }-{\varvec{k}}_{1 })^2)\nonumber \\&\qquad \times \left. S^2({\varvec{k}}_{1 }+{\varvec{k}}_{3 }-{\varvec{k}} ) + \delta ^{a_1a_2}\delta ^{a_3a_4}...\right] , \end{aligned}$$

  (16)

  where $\alpha _k\approx \alpha$ follows from the energy–momentum conservation in the $J/\psi$ vertex. The last term in parentheses does not contribute to the cross section due to the color factor contraction with the $J/\psi$ vertex. $S({\varvec{k}})$ is a symmetric function peaked around ${\varvec{k}}=0$ and $R_{\mathrm {sh}}$ is the Shuvaev factor [38] introduced to account for the fact that longitudinal variables of the gluons are not equal and the off-diagonal gluon distributions enter the cross section.

• 3. The $J/\psi$ triple-gluon vertex reads [39]

  $$\begin{aligned}&\Phi ^{b_1a_1a_2}_{J/\psi }(\alpha ,\beta ;{\varvec{l}} ,{\varvec{k}}_{1 };,{\varvec{k}} -{\varvec{k}}_{1 },p;\epsilon ) \nonumber \\&\quad = g^3\frac{\mathrm{d}^{a_1a_2b_1}}{N_c} V_{J/\psi }(\alpha ,\beta ;{\varvec{l}}_{ },{\varvec{k}}_{1 },{\varvec{k}}_{2 };\epsilon ), \nonumber \\&V_{J/\psi }(\alpha ,\beta ;{\varvec{l}}_{ },{\varvec{k}}_{1 },{\varvec{k}}_{2 };\epsilon )\nonumber \\&\quad = 4\pi m_c g_{J/\psi } \left[ -\frac{\epsilon ^*\cdot (x p_A + l_{\perp })}{{\varvec{l}}_{ }^{\,2}+({\varvec{k}}_{1 }+{\varvec{k}}_{2 })^2+4m_c^2} \right. \nonumber \\&\qquad + \left. \frac{\epsilon ^*\cdot p_A (x-\frac{4{\varvec{k}}_{1 }\cdot {\varvec{k}}_{2 }}{y s})+\epsilon ^*\cdot l_{\perp }}{{\varvec{l}}_{ }^{\,2}+({\varvec{k}}_{1 }-{\varvec{k}}_{2 })^2+4m_c^2}\right] , \end{aligned}$$

  (17)

  where ${\varvec{k}}_2={\varvec{k}}-{\varvec{k}}_1$.

Substituting Eqs. (13) through (17) into (12), and performing delta function integrations and color factor contractions one arrives at the final formula for the rescattering correction to polarization dependent differential $J/\psi$ hadroproduction cross section,

$$\begin{aligned}&\frac{\mathrm{d}^3\sigma _{pp\rightarrow J/\psi X}}{\mathrm{d}\ln \beta dp^2_\perp } = \frac{2}{\pi }\frac{N_c^2-4}{N_c^3(N_c-1)^2}\frac{R_{\text{ sh }}^2}{\sigma _{\mathrm {eff}}}\nonumber \\&\quad \times \int \mathrm{d}^2{\varvec{k}}\mathrm{d}^2{\varvec{k}}_{1} \frac{\alpha _s^3 f(\beta ,({\varvec{p}}_{ }-{\varvec{k}}_{ })^2) f(\alpha ,k_1 ^2) f(\alpha ,({\varvec{k}}_{ }-{\varvec{k}}_{1 })^2)}{\left( ({\varvec{p}} -{\varvec{k}}_{ })^2{\varvec{k}}_{1 }^{\,2}({\varvec{k}}-{\varvec{k}}_{1 })^2\right) ^2} \nonumber \\&\quad \times |V_{J/\psi }(\alpha ,\beta ;{\varvec{k}}_{1 },{\varvec{k}}-{\varvec{k}}_{1 },{\varvec{p}}_{ }-{\varvec{k}}_{ };\epsilon )|^2 + (\alpha \leftrightarrow \beta ,p_A\leftrightarrow p_B),\nonumber \\ \end{aligned}$$

(18)

where the last term describes the contribution from the graph as in Fig. 1b where four gluons are attached to the $p_B$ instead of $p_A$ vertex. In the derivation one needs to evaluate the integral $\int \mathrm{d}^2{\varvec{k}}_\perp S^2({\varvec{k}}_\perp )$, which, assuming the Gaussian form of $\tilde{S}({\varvec{b}})$, may be related to the inverse of the multiple scattering parameter, $\int \mathrm{d}^2{\varvec{k}}_\perp S^2({\varvec{k}}_\perp ) = 8\pi ^2 \sigma ^{-1}_{\mathrm {eff}}$.

Fig. 3

The unintegrated gluon distribution

3.3 Triple-gluon cross section with gluon correlations

Equation (18) describes the distributions of transverse positions of two gluons coming from one of the protons as being independent, i.e. uncorrelated, in the transverse plane. At large $p_T$ of the meson one should, however, expect some correlations of these distribution to emerge in the course of the QCD evolution of double gluon density. In this evolution [31], a single parton ladder may split into two ladders, emerging at the same impact parameter, which introduces correlations of the parton positions.

A diagram that describes the gluon parton splitting into two gluons is shown in Fig. 4. This contribution to $J/\psi$ hadroproduction was discussed in [25] in the collinear limit and using only an approximate estimate of QCD evolution of the double gluon state. This correlated rescattering correction is potentially important, as it is expected to lead to a less steep $p_T$ dependence of the resulting differential cross section component than the one obtained with the uncorrelated gluon distributions. We calculated this amplitude with full $k_T$-dependence of the three gluons that enter the $J/\psi$ vertex, and assuming that the initial gluon in an upper vertex, which acts as a source of the double gluon, is collinear with the parent proton. After the standard steps we obtained the following cross section:

$$\begin{aligned}&\frac{\mathrm{d}^3\sigma _{pp\rightarrow J/\psi X}}{\mathrm{d}\ln \beta dp^2_\perp } = \frac{\alpha _s^3\alpha _s^2}{\pi ^4}\frac{9}{4}\frac{N_c^2-4}{N_c^3(N_c-1)}\nonumber \\&\quad \times \int g(\xi ,\mu )\mathrm{d}\xi \int \frac{\mathrm{d}^2{\varvec{k}}\mathrm{d}^2{\varvec{k}}_{1}\mathrm{d}^2{\varvec{k}}_{2} f(\beta ,({\varvec{p}}-{\varvec{k}})^2)}{({\varvec{p}} -{\varvec{k}}_{ })^4{\varvec{k}}_{1 }^{\,2}({\varvec{k}}-{\varvec{k}}_{1 })^2{\varvec{k}}_{2 }^{\,2}({\varvec{k}}-{\varvec{k}}_{2 })^{\,2}} \nonumber \\&\quad \times V_{J/\psi }(\alpha ,\beta ;{\varvec{k}}_{1 },{\varvec{k}}-{\varvec{k}}_{1 },{\varvec{p}}_{ }-{\varvec{k}}_{ };\epsilon )\nonumber \\&\quad \times V^*_{J/\psi }(\alpha ,\beta ;{\varvec{k}}_{2 },{\varvec{k}}-{\varvec{k}}_{2 },{\varvec{p}}_{ }-{\varvec{k}}_{ };\epsilon ). \end{aligned}$$

(19)

An analogous formula is valid for a quark from the target, replacing the gluon as a source of the two correlated $t$-channel gluons after the suitable replacement of the pdfs and the color factor. This formula provides the lowest order approximation to the correlated rescattering amplitude, which is only an input amplitude for the evolution of the two-gluon state from the parent gluon to the $J/\psi$ vertex. Since the typical evolution length in rapidity is sizable for this evolution one expects potentially large effects of the QCD evolution to occur. The treatment of this evolution in the framework of the small $x$ resummation is possible, but it is a highly nontrivial task and it is beyond the scope of the present analysis. However, we estimated numerically the lowest order contribution of (19) and found it to be significantly smaller than the uncorrelated rescattering contribution of (18). Thus in the present analysis this contribution will be disregarded.

Fig. 4

The correlated triple-gluon contribution

4 Numerical results

4.1 Triple-gluon corrections in $p\bar{p}$ and $pp$ collisions

In the numerical evaluations the unintegrated gluon densities were used derived from the CT10 collinear gluon density [42] using Kimber–Martin–Ryskin (KMR) scheme [43] with the factorization scale given by the transverse meson mass, $\mu ^2 = M_{J/\psi } ^2 + p_T^2$. The running strong coupling constant of a gluon with virtuality $k^2$ was evaluated at the scale $\mu _0 ^2 = M_c^2 + k^2$, with $M_c = M_{J/\psi } /2$. This choice of scale is consistent with the KMR prescription. We set the multiple scattering parameter value $\sigma _{\mathrm {eff}} = 15$ mb, in accordance with the experimental results from the Tevatron [44, 45]. For the effective gluon distribution $\lambda$ in the Shuvaev factor $R_{\mathrm {Sh}}$ we set $\lambda = 0.3$, which leads to $R_{\mathrm {Sh}} = 1.3$.

In order to visualize the relevance of the triple-gluon correction we compare the obtained results to a limited choice of experimental results from the Tevatron and the LHC, and to the standard collinear QCD fits within the color singlet and octet models. In this paper we do not aim to fit the data, nor provide the global description, so, for clarity, only $p_T$ dependencies near the central rapidity $Y=0$ are shown.

In Fig. 5a the results of numerical evaluation of the triple-gluon correction to the differential meson production cross section $\left. \frac{\mathrm{d}\sigma _{pp\rightarrow J/\psi X}}{\mathrm{d}p_T}\right| _{|Y|<0.6} \times \mathrm {Br}(J/\psi \rightarrow \mu ^+ \mu ^-)$ (including the branching ratio of the meson decay to muons) are shown for the Tevatron energy ($\sqrt{s} = 1.96$ GeV) – the bold continuous line. For reference we display also the CDF data [40] and the results of collinear calculations of the color singlet and CS $+$ CO predictions at LO and NLO [9]. Clearly, the triple-gluon contribution enters as a subleading correction to the prompt $J/\psi$ cross section, which may reach 20–25 % of the total cross section at moderate $p_T$ and becomes negligible at larger $p_T$. On the other hand, the triple-gluon contribution exceeds the standard (collinear) color singlet contribution in the relevant $p_T$ range.

Fig. 5

Differential cross sections for $J/\psi$ hadroproduction: a $\left. \frac{\mathrm{d}\sigma _{pp\rightarrow J/\psi X}}{\mathrm{d}p_T}\right| _{|Y|<0.6} \times \mathrm {Br}(J/\psi \rightarrow \mu ^+ \mu ^-)$ at the Tevatron, $\sqrt{s} = 1.96$ TeV and b $\left. \frac{\mathrm{d}\sigma _{pp\rightarrow J/\psi X}}{\mathrm{d}Y\, \mathrm{d}p_T}\right| _{|Y|<0.75} \times \mathrm {Br}(J/\psi \rightarrow \mu ^+ \mu ^-)$ at the LHC, $\sqrt{s} = 7$ TeV. The data-points shown: a CDF [40] and b ATLAS [41]. The curves shown: bold continuous is for the triple gluon contribution computed in this paper, the dashed and dotted thin curves represent results of Ref. [9] in the collinear approach: color singlet (LO and NLO) and combined color octet and color singlet results (see the legend in the plots)

In Fig. 5b we also show a similar comparison for the ATLAS data in the central rapidity region. Note that the data-points here describe the double-differential cross section, $\left. \frac{\mathrm{d}\sigma _{pp\rightarrow J/\psi X}}{\mathrm{d}Y\mathrm{d}p_T}\right| _{|Y|<0.75} \times \mathrm {Br}(J/\psi \rightarrow \mu ^+ \mu ^-)$. The overall pattern of different contributions and the data-points is similar to the pattern described above for the Tevatron energies. Again, the triple gluon contribution exceeds the CSM contributions, but it makes up not more than 20–25 % of the total prompt $J/\psi$ cross section, and the triple-gluon correction becomes negligible at larger $p_T$.

In Fig. 6a polarized components are shown of the triple gluon correction in the helicity frame for the Tevatron (at $\sqrt{s} = 1.96$ TeV) and in Fig. 6b for the LHC (at $\sqrt{s} = 7$ TeV) and for the central rapidity, $Y=0$. The transverse polarization 1 in the plot is referred to the transverse polarization contained in the plane spanned by the beam axis and the meson three-momentum in the laboratory frame, and the transverse polarization 2 is perpendicular to this plane. Clearly, at low transverse momentum the longitudinal and the total transverse cross sections are close to each other, and with increasing $p_T$ the longitudinal component becomes dominant, almost saturating the total triple-gluon correction at $p_T = 20$  GeV. As seen from Fig. 6c the pattern of polarized cross section for the Tevatron and the LHC is very similar.

Fig. 6

Polarization components of the triple-gluon correction: a $\left. \mathrm{d}^2 \sigma _{p\bar{p}\rightarrow J/\psi (\sigma ) X}/\mathrm{d}Y \mathrm{d}p_T\right| _{Y=0}$ for the Tevatron at $\sqrt{s} = 1.96$ TeV, b $\left. \mathrm{d}^2 \sigma _{pp\rightarrow J/\psi (\sigma ) X} / \mathrm{d}Y \mathrm{d}p_T\right| _{Y=0}$ for the LHC at $\sqrt{s} = 7$ TeV, c ratio of the cross section for longitudinal and transverse polarizations. In a and b the polarizations $\sigma$ are chosen in the helicity frame

The presented results for the triple-gluon correction in $J/\psi$ hadroproduction are our central theoretical predictions. There is, however, theoretical uncertainty of these results coming from the choices of the scale in the running coupling constant, the details of the unintegrated gluon densities, and from the unknown higher order corrections. The full analysis of these uncertainties is beyond the scope of this paper; however, we performed some first estimates and tested the sensitivity of the results to the $\mu _0$ scale variation in $\alpha _s (\mu _0)$ and collinear parton choice in the KMR scheme. The results depend weakly on the collinear parton set; however, the increase of $\mu _0$ to $2\mu _0$ leads to a reduction of the cross sections by about 50 % in the moderate $p_T$ range. For increasing $p_T$ this effect is weaker. On the other hand, applications of the unintegrated gluon densities (and related schemes) CCFMA0 [23, 24] and JH2013 [46] instead of the KMR scheme gave results larger by a factor of 2–3 in moderate $p_T$ (say for $p_T < 5$ GeV), and at larger $p_T$ (say for $p_T>7$ GeV) the CCFMA0 and JH2013 results are close to our central predictions. Summarizing these theoretical uncertainty checks, the normalization of our predictions in uncertainty are by a factor 2 up or down for moderate $p_T$, and the normalization and shape of the distributions at large $p_T$ is much less uncertain.

4.2 Probing the triple-gluon contribution with nuclear beams

In $pp$ and $p\bar{p}$ the contributions of triple (or multiple) gluon exchange mechanisms of heavy vector meson hadroproduction may not be easy to disentangle from the standard mechanism of production within the CSM and COM. In particular, the triple-gluon contribution may be to some extent absorbed into the fit parameters of the COM. A more sensitive probe of the triple- and multiple-gluon exchange effects in vector quarkonia hadroproduction should be provided in experiments with nuclear beams, in particular, in proton–nucleus collisions, $pA$, where $A$ is the number of nucleons in the nucleus. In such collisions the triple-gluon contribution scales with $A$ in a different way from the standard (two-gluon) contributions.

Let us write the $pA$ cross section $\sigma ^{pA}_V$ as a sum of the standard gluon–gluon contribution $\sigma ^{pA}_{gg}$, a contribution with two gluons coming from the proton $\sigma ^{pA} _{(gg)g}$, and a contribution with two gluon coming from a nucleus $\sigma ^{pA} _{g(gg)}$,

$$\begin{aligned} \sigma ^{pA} _V = \sigma ^{pA}_{gg} + \sigma ^{pA} _{(gg)g} + \sigma ^{pA} _{g(gg)}. \end{aligned}$$

(20)

In particular, for the $pp$ scattering it reduces to $\sigma ^{pp} _V = \sigma ^{pp}_{gg} + \sigma ^{pp} _{(gg)g} + \sigma ^{pp} _{g(gg)}$. Since in $\sigma ^{pA}_{gg}$ and in $\sigma ^{pA} _{(gg)g}$ one probes a single density of gluons in the nucleus, these cross sections are enhanced by a factor of $A$ w.r.t. the proton–proton cross sections, $\sigma ^{pA} _{gg} = A\sigma ^{pp} _{gg}$ and $\sigma ^{pA} _{(gg)g} = A\sigma ^{pp} _{(gg)g}$.

The triple-gluon contribution to $J/\psi$ production with two gluons coming from the nucleus is enhanced by $A^2 R^2 _p/ R^2_A$, with $R_p$ and $R_A$ being the proton and the nucleus effective radius. This dependence on the radius $R_A$ comes from the integral of the nuclear impact parameter density $S_A({\varvec{b}})$ of the gluon distribution, $\int \mathrm{d}^2 {\varvec{b}} S_A^2({\varvec{b}}) \sim 1/ R_A^2$. Since $R_A \sim A^{1/3}R_p$, we have $\sigma ^{pA} _{g(gg)} = A^{4/3}\sigma ^{pp} _{g(gg)}$. Combining the $A$-dependencies of the chosen cross section components one finds for the nuclear modification factor,

$$\begin{aligned} \bar{R}_{pA} = \frac{\sigma ^{pA} _V}{A\sigma ^{pp} _V} = 1 + (A^{1/3} -1)\frac{\sigma ^{pp} _{g(gg)}}{\sigma ^{pp}_V}. \end{aligned}$$

(21)

Thus the deviation of $\bar{R}_{pA}$ from 1, $\delta _A = \bar{R}_{pA} - 1$, measures the nuclear effects of multiple gluons from the nucleus. In our approach we neglect the effects of more than two gluons coming from the nucleus, which is only motivated if the triple-gluon correction is not large, $\delta _A \ll 1$.

Based on the obtained results on the triple-gluon contribution we also performed an estimate of $\delta _A$ for ALICE experiment conditions, that is, for $J/\psi$ inclusive production in $p$Pb collisions at $\sqrt{s} = 5.02$ TeV, $-4.46 < Y < -2.96$ (the nucleus fragmentation region) and $2.03 < Y < 3.53$ (the forward region). We found $\delta _A \simeq 20\,\%$ in the backward region and $\delta _A \simeq 100\,\%$ in the forward region. The result for the backward region is slightly larger than the ALICE measurements, showing evidence for about 10 % nuclear enhancement of $R_{pA}$ with experimental errors of about 10 % [47]. Thus our estimates of the triple-gluon correction are at the upper limit of ALICE measurements and more precise measurements may be used to constrain the details of our calculation and of the unintegrated gluon densities. The available data prefer a conservative approach of our central theory prediction with the unintegrated gluon densities derived from the collinear gluon densities within the KMR scheme.

In the forward region the triple-gluon correction to $\bar{R}_{pA}$ is found to be large, over $100\,\%$. This implies that higher order rescattering corrections, with more than two gluons from the nucleus, are also important and the triple-gluon contribution $\sigma ^{pA} _{g(gg)}$ does not provide a reliable estimate of nuclear effects in the forward region for $p$Pb collisions at the LHC. Therefore, in this region one should perform a resummation of multiple scattering effects, as e.g. in the color glass condensate approach [26, 30]. We conclude that the triple-gluon contributions to $J/\psi$ hadroproduction may be experimentally constrained in $pA$ measurements with lighter nuclei and/or central to backward meson rapidities where the triple-gluon contribution is expected to bring a dominant correction to $\bar{R}_{pA}$. The key observable for such a measurement is the $A$-dependence of the nuclear modification factor $\bar{R}_{pA}$.

5 Conclusions

The performed calculations show that the uncorrelated triple-gluon contribution to $J/\psi$ hadroproduction introduces a sizable $\sim$20 % correction to the theoretical predictions of prompt $J/\psi$ hadroproduction. The relative correction is largest for moderate transverse momenta $p_T < 8$ GeV and it quickly becomes negligible with $p_T$ growing beyond this range. The result for a moderate $p_T$ is uncertain by about factor of $2$ (up or down), but the large $p_T$ shape and normalization are more stable against variations of the model details. It follows that the uncorrelated color singlet triple-gluon contribution is unable to explain the large excess of the $J/\psi$ hadroproduction cross section over the collinear color singlet predictions, especially at larger values of $p_T$. The triple-gluon contribution, however, is found to be larger than the NLO color singlet cross sections and therefore it should be relevant for theoretical analyses of heavy vector quarkonia hadroproduction. In particular, the estimated triple-gluon contribution exhibits a strong $p_T$ dependence of the meson polarization. At small $p_T$ this mechanism leads to equal rates of the longitudinally and transversally polarized mesons, whereas at larger $p_T$ the longitudinal polarization strongly dominates. So the rescattering correction may modify the polarization pattern following from the collinear COM or KTF descriptions, and it should be advantageous to complement with this contribution the fits to the quarkonia hadroproduction cross sections.

For proper theoretical understanding of the heavy vector meson hadroproduction it should be important to constrain experimentally the triple-gluon (or rescattering) corrections. This may not be easy in $pp$ and $p\bar{p}$ collisions where free parameters of the collinear COM or KTF fits may be used to absorb this correction. The multiple-gluon effects, however, are characterized by a distinct (nonlinear) dependence of the gluon densities of colliding beams. Such effects may be directly probed in proton–nucleus ($pA$) collisions, where the relative triple-gluon correction should be enhanced by a factor of $A^{1/3}$. Recent ALICE data on inclusive $J/\psi$ production in $p$Pb collisions at $\sqrt{s} = 5$ TeV in the nucleus fragmentation region show some evidence of such nonlinear nuclear enhancement; however, more extended and accurate measurements are needed to determine experimentally the magnitude of the triple-gluon correction with satisfactory precision.

Appendix A

The relation between the $2\mathbb {P}p$ impact factor and unintegrated gluon distributions is read off from the collinear limit of the semi-inclusive two particle production process $pp\rightarrow V_1V_2X$ described by the amplitude given in Fig. 7. The total cross section in the impact parameter space is given by the collinear formula (Fig. 8a)

Fig. 7

The amplitude for a semi-inclusive two particle production process $pp\rightarrow V_1V_2X$

Fig. 8

Colliding hadrons in the impact parameter space (left). The partonic amplitude for the production process $gg\rightarrow V_1$ (right)

$$\begin{aligned} \sigma= & {} \hat{\sigma }_1(\alpha _1,\beta _1)\hat{\sigma }_2(\alpha _2,\beta _2)g(\alpha _1,\mu )g(\alpha _2,\mu )g(\beta _1,\mu )g(\beta _2,\mu ) \nonumber \\&\times \int \mathrm{d}^2{\varvec{b}}\mathrm{d}^2{\varvec{b}}^A_1\mathrm{d}^2{\varvec{b}}^A_2 \tilde{S}({\varvec{b}}_1^A)\tilde{S}({\varvec{b}}-{\varvec{b}}_1^A)\tilde{S}({\varvec{b}}_2^A)\tilde{S}({\varvec{b}}-{\varvec{b}}_2^A),\nonumber \\ \end{aligned}$$

(A1)

where we assumed that the two-gluon density distribution factorizes into two single-gluon distributions $g(\alpha ,\mu )$, and $\hat{\sigma }_{1,2}$ are cross sections for the $gg\rightarrow V_{1,2}$ productions at the partonic level. A description of the double vector quarkonium is possible also in the $k_T$-factorization scheme as shown e.g. in Refs. [48, 49]. In this section, however, we refer to this process only to fix the overall normalization, and for this purpose the collinear approximation scheme is sufficient. The function $\tilde{S}({\varvec{b}})$, which is approximated by the Gaussian form, $S({\varvec{b}}) = \exp (-b^2 / R_p ^2) / \pi R_p^2$, is normalized

$$\begin{aligned} \int \mathrm{d}^2{\varvec{b}} \tilde{S}({\varvec{b}}) = 1, \end{aligned}$$

where $R_p$ is the effective proton radius. In the momentum space the total cross section reads

$$\begin{aligned} \sigma= & {} {\hat{\sigma }_1(\alpha _1,\beta _1)\hat{\sigma }_2(\alpha _2,\beta _2) \over \sigma _{\mathrm {eff}}}\nonumber \\&\times \, g(\alpha _1,\mu )g(\alpha _2,\mu )g(\beta _1,\mu )g(\beta _2,\mu ), \end{aligned}$$

(A2)

where

$$\begin{aligned} \sigma ^{-1}_{\mathrm {eff}} = \int \frac{\mathrm{d}^2{\varvec{k}}}{(2\pi )^2}S^4({\varvec{k}} ),\qquad \tilde{S}({\varvec{b}}) = \int \frac{\mathrm{d}^2{\varvec{k}}}{(2\pi )^2}S({\varvec{k}} )e^{i{\varvec{k}} {\varvec{b}}},\nonumber \\ \end{aligned}$$

(A3)

and the normalization condition translates into $S({\varvec{0}})=1$.

The partonic amplitude for the production $gg\rightarrow V_1$ has the form (see Fig. 8b)

$$\begin{aligned} \mathcal {M} = \epsilon _{(\lambda _k)}^{\rho _1}\epsilon _{(\lambda _l)}^{\sigma _1}S^{a_1b_1}_{1\,\rho _1\sigma _1}(k_1,l_1,p_1), \end{aligned}$$

where $S^{a_1b_1}_{1\,\rho _1\sigma _1}$ describes a production amplitude and $\epsilon _{(\lambda )}^{\rho }$ is a gluon polarization vector. The cross section, in leading $s$ approximation, reads

$$\begin{aligned} \hat{\sigma }_1 = \frac{\pi s}{N_c^2-1}\frac{\alpha _1\beta _1}{{\varvec{k}}^2_{1\perp }{\varvec{l}}^2_{1 }}|V_1(k_1,l_1,p_1)|^2\delta (\alpha _1\beta _1s-m^2_{1\perp }),\nonumber \\ \end{aligned}$$

(A4)

where $k_1\approx \alpha _1^kp_A+k_{1\perp }, l_1\approx \beta _1^lp_B+l_{1\perp }, p_1 = \alpha _1p_A+\beta _1p_B+p_{1\perp }$ and $\alpha _1\approx \alpha _1^k, \beta _1\approx \beta _1^l$. The effective vertex is related to the production amplitude via

$$\begin{aligned} V_1(k_1,l_1,p_1)\delta ^{a_1b_1} = S^{a_1b_1}_{1\,\rho _1\sigma _1}\frac{p_A^{\rho _1}p_B^{\sigma _1}}{s}. \end{aligned}$$

The amplitude for the process in Fig. 7 reads

$$\begin{aligned} -i\mathcal {M}= & {} \int \frac{\mathrm{d}^4k_1}{(2\pi )^4} S_{A\nu _1\nu _2}^{a_1a_2}(p_A,r_A,A^\prime ,k_1,k_2)\nonumber \\&\frac{\mathrm{d}^{\nu _1\rho _1}\mathrm{d}^{\nu _2\rho _2}}{k_1^2k_2^2} S_{1\,\rho _1\sigma _1}^{a_1b_1}(k_1,p_1-k_1,p_1) \nonumber \\&\times \; S_{2\,\rho _2\sigma _2}^{a_2b_2}(k_2,p_2-k_2,p_2)\frac{\mathrm{d}^{\sigma _1\mu _1}\mathrm{d}^{\sigma _2\mu _2}}{(p_1-k_1)^2(p_2-k_2)^2}\nonumber \\&\times S_{B\mu _1\mu _2}^{b_1b_2}(p_B,r_B,B^\prime ,p_1-k_1,p_2-k_2), \end{aligned}$$

(A5)

and $k_2=p_A-p_{A^\prime }-k_1$. The cross section is then expressed as

$$\begin{aligned}&\mathrm{d}\sigma _{pp\rightarrow V_1V_2X} = \frac{\bar{|\mathcal {M}|^2}}{4(p_A\cdot p_B)}\mathrm{d}\Phi _{pp\rightarrow V_1V_2X},\nonumber \\&\bar{|\mathcal {M}|^2} = \frac{1}{4}\sum _{r_A,r_B}\sum _{A^\prime , B^\prime } |\mathcal {M}|^2, \end{aligned}$$

(A6)

and the phase space integral takes the form

$$\begin{aligned} \mathrm{d}\Phi _{pp\rightarrow V_1V_2X}= & {} (2\pi )^4\delta (p_A+p_B-p_{A^\prime }\nonumber \\&-p_{B^\prime }-p_1-p_2)\mathrm{d}\Phi _{A^\prime }\mathrm{d}\Phi _{B^\prime }\mathrm{d}\Phi _{p_1}\mathrm{d}\Phi _{p_2}. \end{aligned}$$

(A7)

The integrals $\mathrm{d}\Phi _{A^\prime }, \mathrm{d}\Phi _{B^\prime }$ describe the phase space integrations of the $A^\prime$ and $B^\prime$ final states, whereas $\mathrm{d}\Phi _{p_1}, \mathrm{d}\Phi _{p_2}$ correspond to the single-particle phase spaces for the $V_1, V_2$ particles.

Using the appropriate eikonal approximation for the gluon polarization tensors and inserting unities in the form

$$\begin{aligned}&1=\int \frac{\mathrm{d}^4k}{(2\pi )^4} (2\pi )^4\delta (k-p_A+p_{A^\prime }),\nonumber \\&1=\int \frac{\mathrm{d}^4l}{(2\pi )^4} (2\pi )^4\delta (l-p_B+p_{B^\prime }), \nonumber \\&1=\int \frac{\mathrm{d}^4l_1}{(2\pi )^4} (2\pi )^4\delta (k_1+l_1-p_1),\nonumber \\&1=\int \frac{\mathrm{d}^4l_3}{(2\pi )^4} (2\pi )^4\delta (k_3+l_3-p_1), \end{aligned}$$

(A8)

one can write the cross section (A6) in a factorized form,

$$\begin{aligned} \mathrm{d}\sigma _{pp\rightarrow V_1V_2X}= & {} \frac{4s^4}{(2\pi )^{20}}\int \frac{\mathrm{d}^2{\varvec{k}}_{1}\mathrm{d}^2{\varvec{k}}_{2}\mathrm{d}^2{\varvec{k}}_{3}}{{\varvec{k}}^2_{1}{\varvec{k}}^2_{2}{\varvec{k}}^2_{3}({\varvec{k}}_{1 }+{\varvec{k}}_{2 }-{\varvec{k}}_{3 })^2}\nonumber \\&\times \frac{\mathrm{d}^2{\varvec{l}}_{1}\mathrm{d}^2{\varvec{l}}_{2}\mathrm{d}^2{\varvec{l}}_{3}}{{\varvec{l}}^2_{1}{\varvec{l}}^2_{2}{\varvec{l}}^2_{3}({\varvec{l}}_{1 }+{\varvec{l}}_{2 }-{\varvec{l}}_{3 })^2} \delta ({\varvec{k}}_{1 }+{\varvec{l}}_{1 }-{\varvec{k}}_{3 }-{\varvec{l}}_{3 })\nonumber \\&\times \int \mathrm{d}\beta _k\Phi _{4,\,p}^{a_1a_2a_3a_4}(\beta _k,{\varvec{k}}_{1 },{\varvec{k}}_{2 },{\varvec{k}}_{3 },{\varvec{k}}_{1 }+{\varvec{k}}_{2 }-{\varvec{k}}_{3 })\nonumber \\&\times \int \mathrm{d}\alpha _l\Phi _{4,\,p}^{a_1a_2a_3a_4}(\alpha _l,{\varvec{l}}_{1 },{\varvec{l}}_{2 },{\varvec{l}}_{3 },{\varvec{l}}_{1 }+{\varvec{l}}_{2 }-{\varvec{l}}_{3 }) \nonumber \\&\times \int \mathrm{d}\alpha _{1k}\mathrm{d}\beta _{1l}S_{1}^{a_1b_1}(\alpha _{1k},\beta _{1l},k_{1\perp },l_{1\perp },p_1)S_{1}^{a_3b_3\,*}\nonumber \\&\times (\alpha _{1k},\beta _{1l},k_{3\perp },l_{3\perp },p_1) \nonumber \\&\times \int \mathrm{d}\alpha _{2k}\mathrm{d}\beta _{2l}S_{2}^{a_2b_2}(\alpha _{2k},\beta _{2l},k_{2\perp },l_{2\perp },p_2)S_{2}^{a_4b_4\,*}\nonumber \\&\times (\alpha _{2k},\beta _{2l},{\varvec{k}}_{1 }+{\varvec{k}}_{2 }-{\varvec{k}}_{3 },{\varvec{l}}_{1 }+{\varvec{l}}_{2 }-{\varvec{l}}_{3 },p_2) \nonumber \\&\times (2\pi )^4\delta (k_1+l_1-p_1)\mathrm{d}\Phi _{p_1}\, (2\pi )^4\nonumber \\&\times \delta (k_2+l_2-p_2)\mathrm{d}\Phi _{p_2} \, , \end{aligned}$$

(A9)

and ${\varvec{k}}_{2 }={\varvec{k}}_{ }-{\varvec{k}}_{1 }, {\varvec{l}}_{2 }={\varvec{l}}_{ }-{\varvec{l}}_{1 }$. The $2\mathbb {P}p$ impact factors from the third line of Eq. (A9) can be decomposed into three color structures each (see Fig. 9),

$$\begin{aligned}&\int \mathrm{d}\beta _k\Phi _{4,\,p}^{a_1a_2a_3a_4}(\beta _k,{\varvec{k}}_{1},{\varvec{k}}_{2 },{\varvec{k}}_{3 },{\varvec{k}}_{4 }) \\&\quad =\mathcal {N}\left[ \delta ^{a_1a_2}\delta ^{a_3a_4}f({\varvec{k}}_{1 })S({\varvec{k}}_{1 }-{\varvec{k}}_{2 }) f({\varvec{k}}_{3 })S({\varvec{k}}_{3 }-{\varvec{k}}_{4 })\right. \\&\qquad + \; \delta ^{a_1a_3}\delta ^{a_2a_4}f({\varvec{k}}_{1 })S({\varvec{k}}_{1 }-{\varvec{k}}_{3 }) f({\varvec{k}}_{2 })S({\varvec{k}}_{2 }-{\varvec{k}}_{4 })\nonumber \\&\qquad \left. + \delta ^{a_1a_4}\delta ^{a_2a_3}f({\varvec{k}}_{1 })S({\varvec{k}}_{1 }-{\varvec{k}}_{4 }) f({\varvec{k}}_{2 })S({\varvec{k}}_{2 }-{\varvec{k}}_{3 }) \right] , \end{aligned}$$

and nine color terms are obtained after their multiplication. However, only one of these terms gives the leading contribution, the other ones being suppressed by the color factor ($1/N_c^2$) or the limiting phase space ($p_1\approx p_2$). The normalization constant $\mathcal {N}$ is determined comparing the collinear limit of Eq. (A9) to (A2). Indeed, using the decomposition (A10) and noting that the last three lines of (A9) convert into partonic cross sections (A4), the differential cross section (A9) can be written in the form

$$\begin{aligned}&\frac{\mathrm{d}^4\sigma _{pp\rightarrow V_1V_2X}}{\mathrm{d}\alpha _1\mathrm{d}\beta _1\mathrm{d}\alpha _2\mathrm{d}\beta _2} = \frac{s^2 16(N_c^2-1)^4}{(2\pi )^{20}}\frac{\mathcal {N}^2}{\alpha _1\beta _1\alpha _2\beta _2}\nonumber \\&\quad \times \int \frac{\mathrm{d}^2{\varvec{k}}_{1}}{{\varvec{k}}^2_{1 }}f(\alpha _1,k_1 ^2) \int \frac{\mathrm{d}^2{\varvec{k}}_{2}}{k^2_{2 }}f(\alpha _2,k_2 ^2) \int \frac{\mathrm{d}^2{\varvec{l}}_{1}}{{\varvec{l}}^2_{1 }}f(\beta _1,l_1 ^2)\nonumber \\&\quad \times \int \frac{\mathrm{d}^2{\varvec{l}}_{2}}{{\varvec{l}}^2_{2 }} f(\beta _2,l_2 ^2) \hat{\sigma }_1(\alpha _1,\beta _1)\hat{\sigma }_2(\alpha _2,\beta _2) \int \frac{\mathrm{d}^2{\varvec{k}}}{(2\pi )^2}S^4({\varvec{k}} ).\nonumber \\ \end{aligned}$$

(A10)

Then it follows that

$$\begin{aligned} \mathcal {N}=\frac{(2\pi )^7}{s(N_c^2-1)^2}, \end{aligned}$$

where the general correspondence between the unintegrated $f(\alpha ,{\varvec{k}}^2)$ and collinear $g(\alpha ,\mu )$ gluon distributions

$$\begin{aligned} \int ^{\mu ^2} \frac{\mathrm{d}^2{\varvec{k}}}{{\varvec{k}}^2_{ }}f(\alpha ,k^2) = \pi \alpha g(\alpha ,\mu ) \end{aligned}$$

was used.

Fig. 9

The double gluon distribution