Semileptonic $B_{s} \rightarrow D_{s2}^{*}(2573)\ell \bar{\nu }_{\ell }$ transition in QCD

Abstract

We analyze the semileptonic $B_{s} \rightarrow D_{s2}^{*}(2573)\ell \bar{\nu }_{\ell }$ transition, where $\ell =\tau ,~\mu$ or $e$, within the standard model. We apply the QCD sum rule approach to calculate the transition form factors entering the low energy Hamiltonian defining this channel. The fit functions of the form factors are used to estimate the total decay widths and branching fractions in all lepton channels. The orders of the branching ratios indicate that this transition is accessible at LHCb in the near future.

1 Introduction

The semileptonic $B$ meson decay channels are known as useful tools to accurately calculate the Standard Model (SM) parameters like determination of the Cabibbo–Kobayashi–Maskawa (CKM) quark mixing matrix, check the validity of the SM, describe the origin of the CP violation and search for new physics effects. By recent experimental progress, precise measurements have become available, and it is possible to perform precision calculations. Although the $B$ meson decays are studied efficiently both theoretically and experimentally (see for instance [1–11]), most of $B_{s}$ properties are not very clear yet (for some related theoretical and experimental studies on this meson see [12–21] and references therein). Since the detection and identification of this heavy meson is relatively difficult in the experiment, the theoretical and phenomenological studies on the spectroscopy and decay properties of this mesons can play an essential role in our understanding of its non-perturbative dynamics, calculating the related parameters of the SM and providing opportunities to search for possible new physics contributions.

In the literature, there are a lot of theoretical studies devoted to the semileptonic transition of $B_{s}$ into the pseudoscalar $D_{s}$ and vector $D^*_{s}$ charmed-strange mesons. But there is no study on the semileptonic transitions of this meson into the tensor charmed-strange meson in the final state, although it is expected to have a considerable contribution to the total decay width of the $B_{s}$ meson. In accordance with this, in the present study, we investigate the semileptonic $B_{s} \rightarrow D_{s2}^{*}(2573)\ell \bar{\nu }_{\ell }$ transition in the framework of the three-point QCD sum rule [22] as one of the most attractive and powerful techniques in hadron phenomenology, where the $D_{s2}^{*}(2573)$ is the low lying charmed-strange tensor meson with $J^P=2^+$. In particular, we calculate the transition form factors entering the low energy matrix elements defining the transition under consideration. We find the working regions of the auxiliary parameters entering the calculations from different transformations, considering the criteria of the method used. This is followed by finding the behavior of the form factors in terms of the transferred momentum squared, which are then used to estimate the total width and branching fraction in all lepton channels. Note that the semileptonic $B\rightarrow D_{2}^{*}(2460)\ell \bar{\nu }_{\ell }$ decay channel is analyzed in [23] using the same method. The spectroscopic properties of the charmed-strange tensor meson $D_{s2}^{*}(2573)$ is also investigated in [24, 25] using a two-point correlation function.

The layout of the paper is as follows. In the next section, the QCD sum rules for the four form factors relevant to the semileptonic $B_{s} \rightarrow D_{s2}^{*}(2573)\ell \bar{\nu }_{\ell }$ transition are obtained. Section 3 contains a numerical analysis of the form factors, and a calculation of their behavior in terms of $q^2$ as well as the estimation of the total decay width and branching ratio for the transition under consideration.

2 Theoretical framework

In order to calculate the form factors, associated with the semileptonic $B_{s} \rightarrow D_{s2}^{*}(2573)\ell \bar{\nu }_{\ell }$ transition via QCD sum rule formalism, we consider the following three-point correlation function:

$$\begin{aligned} \Pi _{\mu \alpha \beta }= & {} i^2\int d^{4}x\int d^{4}y e^{-ip.x}e^{ip'.y}\nonumber \\&\times \left\langle 0\mid \mathcal{T}\Big [J_{\alpha \beta }^{D_{s2}^{*}(2573)}(y) J^{tr}_{\mu }(0) J^{B_{s}^{\dag }}(x)\Big ]\mid 0\right\rangle , \end{aligned}$$

(1)

where $\mathcal{T}$ is the time ordering operator and $J^{tr}_{\mu }(0)=\bar{c}(0)\gamma _{\mu }(1-\gamma _5)b(0)$ is the transition current. The interpolating currents of the $B_{s}$ and $D_{s2}^{*}(2573)$ mesons can be written in terms of the quark fields as

$$\begin{aligned} J^{B_{s}}=\bar{s}(x)\gamma _5b(x) \end{aligned}$$

(2)

and

(3)

Here is the covariant derivative that acts on the left and right, simultaneously. It is given as

(4)

with

$$\begin{aligned} \begin{aligned}&\overrightarrow{\mathcal{D}}_{\beta }(y)=\overrightarrow{\partial }_{\beta }(y)-i \frac{g}{2}\lambda ^aA^a_\beta (y),\\&\overleftarrow{\mathcal{D}}_{\beta }(y)=\overleftarrow{\partial }_{\beta }(y)+ i\frac{g}{2}\lambda ^aA^a_\beta (y), \end{aligned} \end{aligned}$$

(5)

where $\lambda ^a$ and $A^a_\beta (x)$ denote the Gell-Mann matrices and the external gluon fields, respectively.

According to the method used, in order to find the QCD sum rules for the transition form factors, we shall calculate the aforesaid correlation function, first in terms of hadronic parameters and second in terms of QCD parameters making use of the operator product expansion (OPE). By equating these two representations to each other through a dispersion relation, we obtain the sum rules for the form factors. To stamp down the contributions of the higher states and continuum, a double Borel transformation with respect to the $p^{2}$ and $p^{\prime ^{2}}$ is performed on both sides of the sum rules obtained and the quark–hadron duality assumption is used.

2.1 The hadronic representation

In order to calculate the hadronic side of the correlator in Eq. (1), we insert two complete sets of the initial $B_{s}$ and the final $D_{s2}^{*}(2573)$ states with the same quantum numbers as the interpolating currents into the correlator. After performing the four-integrals over $x$ and $y$, we obtain

$$\begin{aligned} \Pi _{\mu \alpha \beta }^{had}= & {} \frac{{\langle }0\mid J _{\alpha \beta }^{D_{s2}^{*}(2573)}\mid D_{s2}^{*}(2573)(p',\epsilon )\rangle {\langle }D_{s2}^{*}(2573)(p',\epsilon )\mid J _{\mu }^{tr}(0) \mid B_{s}(p)\rangle \langle B_{s}(p)\mid J_{B_{s}}^{\dag }\mid 0\rangle }{(p^2-m_{B_{s}}^2)(p'^2-m_{D_{s2}^{*}(2573)}^2)} + \cdots , \end{aligned}$$

(6)

where $\cdots$ represents contributions of the higher states and continuum, and $\epsilon$ is the polarization tensor of the $D_{s2}^{*}(2573)$ tensor meson. We can parameterize the matrix elements appearing in the above equation in terms of decay constants, masses, and form factors as

$$\begin{aligned}&{\langle }0\mid J_{\alpha \beta }^{D_{s2}^{*}(2573)}\mid D_{s2}^{*}(2573)(p',\epsilon )\rangle \nonumber \\&\quad =m_{D_{s2}^{*}(2573)}^3 f_{D_{s2}^{*}(2573)}\epsilon _{\alpha \beta },\nonumber \\&\langle B_{s}(p)\mid J_{B_{s}}^{\dag }\mid 0\rangle = -i\frac{f_{B_{s}} m_{B_{s}}^2}{m_s+m_b}, \nonumber \\&{\langle }D_{s2}^{*}(2573)(p',\epsilon )\mid J _{\mu }^{tr}(0) \mid B_{s}(p)\rangle \nonumber \\&\quad = h(q^2)\varepsilon _{\mu \nu \alpha \beta }\epsilon ^{*^{\nu \lambda }}P^{\lambda } P_{\alpha }q^{\beta }\!-\!iK(q^2)\epsilon ^{*_{\mu \nu }}P^{\nu }\nonumber \\&\qquad -\,i\epsilon ^{*_{\alpha \beta }}P^{\alpha }P^{\beta }\left[ P_{\mu }b_{+}(q^2)+q_{\mu }b_{-}(q^2) \right] , \end{aligned}$$

(7)

where $q=p-p'$, $P=p+p'$; note that $h(q^2)$, $K(q^2)$, $b_{+}(q^2)$, and $b_{-}(q^2)$ are transition form factors. Now, we combine Eqs. (6) and (7) and perform a summation over the polarization tensors via

$$\begin{aligned} \epsilon _{\alpha \beta }\epsilon _{\nu \theta }^*=\frac{1}{2}T_{\alpha \nu }T_{\beta \theta }+ \frac{1}{2}T_{\alpha \theta }T_{\beta \nu } -\frac{1}{3}T_{\alpha \beta }T_{\nu \theta }, \end{aligned}$$

(8)

where

$$\begin{aligned} T_{\alpha \nu }=-g_{\alpha \nu }+\frac{p'_\alpha p'_\nu }{m_{D_{s2}^{*}(2573)}^2}. \end{aligned}$$

(9)

This procedure takes us to the final representation of the hadronic side, viz.

$$\begin{aligned} \Pi _{\mu \alpha \beta }^{had}= & {} \frac{f_{D_{s2}^{*}}f_{B_{s}} m_{D_{s2}^{*}} m_{B_{s}}^2}{8(m_b+m_s)(p^2-m^2_{B_{s}})(p'^2-m_{D_{s2}^{*}}^2)}\nonumber \\&\times \Bigg \{\frac{2}{3}\Big [-\Delta K(q^2)+\Delta 'b_{-}(q^2) \Big ]q_{\mu }g_{\beta \alpha }\nonumber \\&+\frac{2}{3}\Big [(\Delta -4m_{D_{s2}^{*}}^2) K(q^2)+\Delta 'b_{+}(q^2) \Big ]P_{\mu }g_{\beta \alpha }\nonumber \\&+i(\Delta -4m_{D_{s2}^{*}}^2) h(q^2)\varepsilon _{\lambda \nu \beta \mu }P_{\lambda }P_{\alpha }q_{\nu } \nonumber \\&+\Delta K(q^2)q_{\alpha }g_{\beta \mu }+ \text{ other } \text{ structures }\Bigg \}+\cdots , \end{aligned}$$

(10)

where

$$\begin{aligned} \Delta= & {} m_{B_{s}}^2+3m_{D_{s2}^{*}}^2-q^2 \end{aligned}$$

(11)

and

$$\begin{aligned} \Delta '= & {} m_{B_{s}}^4-2m_{B_{s}}^2(m_{D_{s2}^{*}}^2+q^2)+(m_{D_{s2}^{*}}^2-q^2)^2. \end{aligned}$$

(12)

2.2 The OPE representation

The OPE side of the correlation function is calculated in the deep Euclidean region. For this aim, we insert the explicit forms of the interpolating currents into the correlation function in Eq. (1). After performing contractions via Wick’s theorem, we obtain the following result in terms of the heavy and light quark propagators:

(13)

The heavy and light quarks propagators appearing in the above equation and up to terms taken into account in the calculations are given by

$$\begin{aligned} S_{Q}^{i\ell }(x)= & {} \frac{i}{(2\pi )^4}\int d^4k e^{-ik \cdot x}\nonumber \\&\times \left\{ \frac{\delta _{i\ell }}{\!\not \!{k}-m_Q} -\frac{g_sG^{\alpha \beta }_{i\ell }}{4}\frac{\sigma _{\alpha \beta }(\!\not \!{k}+m_Q)+ (\!\not \!{k}+m_Q)\sigma _{\alpha \beta }}{(k^2-m_Q^2)^2}\right. \nonumber \\&\left. +\delta _{i\ell }\frac{\pi ^2}{3} \left\langle \frac{\alpha _sGG}{\pi }\right\rangle \frac{ m_Qk^2+m_Q^2\!\not \!{k}}{(k^2-m_Q^2)^4} +\cdots \right\} , \end{aligned}$$

(14)

where $Q=b$ or $c$, and

$$\begin{aligned} S_{s}^{ij}(x)= & {} i\frac{\!\not \!{x}}{ 2\pi ^2 x^4}\delta _{ij} -\frac{m_s}{4\pi ^2x^2}\delta _{ij}-\frac{\langle \bar{s}s\rangle }{12}\Big (1 -i\frac{m_s}{4} \!\not \!{x}\Big )\delta _{ij}\nonumber \\&-\frac{x^2}{192}m_0^2\langle \bar{s}s\rangle \Big (1-i\frac{m_s}{6} \!\not \!{x}\Big )\delta _{ij} \nonumber \\&-\frac{ig_s G_{\theta \eta }^{ij}}{32\pi ^2x^2}\big [\!\not \!{x}\sigma ^{\theta \eta }+\sigma ^{\theta \eta }\!\not \!{x}\big ] +\cdots . \end{aligned}$$

(15)

To proceed, we insert the expressions of the heavy and light propagators into Eq. (13) and perform the derivatives with respect to $x$ and $y$. Then we transform the calculations to the momentum space and make the $x_{\mu }\rightarrow i\frac{\partial }{\partial p_{\mu }}$ and $y_{\mu }\rightarrow -i\frac{\partial }{\partial p'_{\mu }}$ replacements. We perform the two four-integrals coming from the heavy quark propagators with the help of two Dirac delta functions appearing in the calculations. Finally, we perform the last four-integral using the Feynman parametrization, viz.

$$\begin{aligned} \int d^4t\frac{(t^2)^{\beta }}{(t^2+L)^{\alpha }}=\frac{i \pi ^2 (-1)^{\beta -\alpha }\Gamma (\beta +2)\Gamma (\alpha -\beta -2)}{\Gamma (2) \Gamma (\alpha )[-L]^{\alpha -\beta -2}}.\nonumber \\ \end{aligned}$$

(16)

Eventually, we get the OPE side of the three-point correlation function in terms of the selected structures and the perturbative and non-perturbative parts as

$$\begin{aligned} \Pi ^\mathrm{OPE}_{\mu \alpha \beta }= & {} \Big (\Pi ^{pert}_1(q^2)+\Pi ^{non-pert}_1(q^2)\Big )q_{\alpha }g_{\beta \mu }\nonumber \\&+ \Big (\Pi ^{pert}_2(q^2)+\Pi ^{non-pert}_2(q^2)\Big )q_{\mu }g_{\beta \alpha }\nonumber \\&+ \Big (\Pi ^{pert}_3(q^2)+\Pi ^{non-pert}_3(q^2)\Big )P_{\mu }g_{\beta \alpha }\nonumber \\&+ \Big (\Pi ^{pert}_4(q^2)+\Pi ^{non-pert}_4(q^2)\Big )\varepsilon _{\lambda \nu \beta \mu }P_{\lambda } P_{\alpha }q_{\nu } \nonumber \\&+\text{ other } \text{ structures }, \end{aligned}$$

(17)

where the perturbative parts $\Pi ^{pert}_i(q^2)$ can be written in terms of the double dispersion integrals as

$$\begin{aligned} \Pi ^{pert}_i(q^2)=\int ^{}_{}ds\int ^{}_{}ds' \frac{\rho _i(s,s',q^2)}{(s-p^2)(s'-p'^2)}. \end{aligned}$$

(18)

Fig. 1

Perturbative $\mathcal{O}(\alpha _s)$ diagrams contributing to the correlation function

The $O(1)$ spectral densities $\rho _i(s,s',q^2)$ are given by the imaginary parts of the $\Pi ^{pert}_{i}(q^2)$ functions, i.e., $\rho _i(s,s',q^2)=\frac{1}{\pi }Im[\Pi ^{pert}_{i}(q^2)]$. After lengthy calculations, the spectral densities corresponding to the selected structures are obtained as

$$\begin{aligned} \rho _1(s,s',q^2)= & {} \int _{0}^{1}dx\int ^{1-x}_{0} dy \Bigg \{{-}\frac{3 (m_c(4+6y-6x)+m_s(-2+y-x)+2 m_b (y-x))}{64\pi ^2}\Bigg \} \Theta [L(s,s',q^2)], \nonumber \\ \rho _2(s,s',q^2)= & {} \int _{0}^{1}dx\int ^{1-x}_{0} dy \Bigg \{\frac{3((y-x)(m_b x + m_c (-1+2y+x))}{32\pi ^2(-1+y+x)}\Bigg \}\Theta [L(s,s',q^2)], \nonumber \\ \rho _3(s,s',q^2)= & {} \int _{0}^{1}dx\int ^{1-x}_{0} dy \Bigg \{{-}\frac{3 (m_b x (-2+3y+x)+m_c(2y^2+y(-1+x)+(-1+x)x))}{32\pi ^2(-1+y+x)}\Bigg \}\Theta [L(s,s',q^2)], \nonumber \\ \rho _4(s,s',q^2)= & {} 0, \end{aligned}$$

(19)

where $\Theta [...]$ is the unit-step function and

$$\begin{aligned} L(s,s',q^2)= & {} -m_c^2y-s'y(x+y-1)\nonumber \\&-x\Big (m_b^2-q^2y+s(x+y-1)\Big ). \end{aligned}$$

(20)

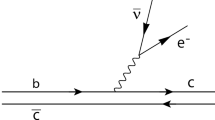
We also take into account the perturbative $\mathcal{O}(\alpha _s)$ corrections contributing to the correlation function. These corrections for massless quarks are calculated using the standard Cutkosky rules in [26, 27] for calculation of the pion form factor with both the pseudoscalar and the axial currents. These corrections are also calculated in the case of a transition between two infinitely heavy quarks with the spectator quark being massless in [28] using the universal Isgur–Wise function. We calculate the $\mathcal{O}(\alpha _s)$ corrections keeping also the spectator strange quark mass in the calculations. To this aim we consider the diagrams presented in Fig. 1. As an example we present the amplitude of diagram $(a)$ in Fig. 1, which is obtained as

$$\begin{aligned} \Pi _{\alpha _{s_{(a)}}}= & {} -16\pi \alpha _s\int \frac{d^4k}{(2\pi )^4}\int \frac{d^4k^{\prime }}{(2\pi )^4} \frac{Tr\Big [\Gamma _{\alpha \beta }(\!\not \!{p^{\prime }}+\!\not \!{k}+m_c)\gamma _{\mu }(1-\gamma _5) (\!\not \!{p}+\!\not \!{k}+m_b)\gamma _5(\!\not \!{k}+m_s)\gamma ^{\eta }(\!\not \!{k}-\!\not \!{k^{\prime }}+m_s) \gamma ^{\eta }(\!\not \!{k}+m_s)\Big ]}{[(p^{\prime ^2}+k)^2-m_c^2][(p+k)^2-m_b^2] [(k-k^{\prime })^2-m_s^2](k^2-m_s^2)^2k^{\prime ^2}} \nonumber \\ \end{aligned}$$

(21)

where

$$\begin{aligned} \Gamma _{\alpha \beta }= & {} \gamma _{\alpha }\left( 2k_{\beta }+p^{\prime }_{\beta }\right) +\gamma _{\beta }\left( 2k_{\alpha }+p^{\prime }_{\alpha }\right) \nonumber \\&-\frac{2}{3}\left( g_{\alpha \beta } -\frac{p^{\prime }_{\alpha }p^{\prime }_{\beta }}{p^{\prime ^2}}\right) (2 \!\not \!{k}+\!\not \!{p'}). \end{aligned}$$

(22)

After calculation of the four-integrals appearing in the amplitudes of all diagrams shown in Fig. 1 and taking the imaginary parts of the obtained results we select the above-mentioned structures to find the $\mathcal{O}(\alpha _s)$ spectral densities $\rho _{\alpha _{s_i}}(s,s',q^2)$. The details of the calculations for $\rho _{\alpha _{s_1}}(s,s',q^2)$ are given in Appendix A.

The $\Pi ^{non-pert}_i(q^2)$ functions are obtained up to five dimension operators. As they have also very lengthy expressions, we do not show their explicit form again.

Having calculated both the hadronic and the OPE sides of the correlation function, we match the coefficients of the selected structures from both sides and apply a double-Borel transformation. As a result, we get the following sum rules for the form factors:

$$\begin{aligned} K(q^2)= & {} \frac{8(m_b+m_s)}{\Delta }\frac{1}{f_{B_s} f_{D_{s2}^{*}} m_{D_{s2}^{*}} m_{B_s}^2}e^{\frac{m_{B_s}^2}{M^2}} e^{\frac{m_{D_{s2}^{*}}^2}{M'^2}}\nonumber \\&\times \left\{ \int ^{s_0}_{(m_b+m_s)^2}ds \int ^{s_{0}^{'}}_{(m_c+m_s)^2}ds'\left( \rho _{1}(s,s',q^2)\right. \right. \nonumber \\&\quad \left. \left. +\rho _{\alpha _{s_1}}(s,s',q^2)\right) e^{-\frac{s}{M^2}}e^{-\frac{s^{\prime }}{M^{\prime ^2}}} \!+\hat{B}\Pi _{1}^{non-pert}\!\right\} \!, \nonumber \\ b_{-}(q^2)= & {} \frac{12(m_b+m_s)}{f_{B_s} f_{D_{s2}^{*}} m_{D_{s2}^{*}} m_{B_s}^2\Delta '} e^{\frac{m_{B_s}^2}{M^2}} e^{\frac{m_{D_{s2}^{*}}^2}{M'^2}} \nonumber \\&\times \left\{ \int ^{s_0}_{(m_b+m_s)^2}ds \int ^{s_{0}^{'}}_{(m_c+m_s)^2}ds'\left( \rho _{2}(s,s',q^2)\right. \right. \nonumber \\&\quad \left. \left. +\rho _{\alpha _{s_2}}(s,s',q^2)\right) e^{-\frac{s}{M^2}}e^{-\frac{s^{\prime }}{M^{\prime ^2}}} +\hat{B}\Pi _{2}^{non-pert}\right\} \nonumber \\&\quad +\frac{\Delta }{\Delta '}K(q^2), \nonumber \\ b_{+}(q^2)= & {} \frac{12(m_b+m_s)}{f_{B_s} f_{D_{s2}^{*}} m_{D_{s2}^{*}} m_{B_s}^2 \Delta '}e^{\frac{m_{B_s}^2}{M^2}} e^{\frac{m_{D_{s2}^{*}}^2}{M'^2}} \nonumber \\&\times \left\{ \int ^{s_0}_{(m_b+m_s)^2}ds \int ^{s_{0}^{'}}_{(m_c+m_s)^2}ds'\left( \rho _{3}(s,s',q^2)\right. \right. \nonumber \\&\left. \left. +\rho _{\alpha _{s_3}}(s,s',q^2)\right) e^{-\frac{s}{M^2}}e^{-\frac{s^{\prime }}{M^{\prime ^2}}} +\hat{B}\Pi _{3}^{non-pert}\right\} \nonumber \\&-\frac{\Delta -4m^2_{D_{s2}^{*}}}{\Delta '}K(q^2), \nonumber \\ h(q^2)= & {} -i\frac{8(m_b+m_s)}{\Delta -4m^2_{D_{s2}^{*}}}\frac{1}{f_{B_s} f_{D_{s2}^{*}} m_{D_{s2}^{*}} m_{B_s}^2}e^{\frac{m_{B_s}^2}{M^2}} e^{\frac{m_{D_{s2}^{*}}^2}{M'^2}}\nonumber \\&\times \left\{ \int ^{s_0}_{(m_b+m_s)^2}ds \int ^{s_{0}^{'}}_{(m_c+m_s)^2}ds'\left( \rho _{4}(s,s',q^2)\right. \right. \nonumber \\&\left. \left. +\rho _{\alpha _{s_4}}(s,s',q^2)\right) e^{-\frac{s}{M^2}}e^{-\frac{s^{\prime }}{M^{\prime ^2}}} + B \Pi _{4}^{non-pert}\right\} \!, \nonumber \\ \end{aligned}$$

(23)

where $M^2$ and $M^{'2}$ are the Borel mass parameters; $s_0$ and $s'_0$ are continuum thresholds in the initial and final mesonic channels, respectively.

3 Numerical results

In this section we present our numerical results for the transition form factors derived from QCD sum rules and search for the behavior of the these quantities in terms of $q^2$. To obtain numerical values, we use some input parameters, presented in Table 1.

Table 1 Input parameters used in calculations

In our calculations, we also use the $\overline{MS}$ quark masses $m_{c}(m_c)=(1.275\pm 0.025)~\mathrm{GeV}$, $m_{b}(m_b)=(4.18\pm 0.03)~\mathrm{GeV}$, and $m_s(\mu =2~\mathrm{GeV})=(95\pm 5)~\mathrm{MeV}$ [29], and we take into account the energy-scale dependence of the $\overline{MS}$ masses from the renormalization group equation to bring the masses to the same scale (see also [32]),

$$\begin{aligned} \begin{aligned}&\displaystyle m_b(\mu )=m_b(m_b)\left[ \frac{\alpha _s(\mu )}{\alpha _s(m_b)}\right] ^{\frac{12}{23}}, \\&\displaystyle m_c(\mu )=m_c(m_c)\left[ \frac{\alpha _s(\mu )}{\alpha _s(m_c)}\right] ^{\frac{12}{25}}, \\&\displaystyle m_s(\mu )=m_s(2~GeV)\left[ \frac{\alpha _s(\mu )}{\alpha _s(2~GeV)}\right] ^{\frac{4}{9}}, \end{aligned} \end{aligned}$$

(24)

where

$$\begin{aligned} \alpha _s(\mu )= & {} \frac{1}{b_0~t}\left[ 1-\frac{b_1}{b_0^2~t}\log [t]\right. \nonumber \\&\left. +\frac{b_1^2 \left( \log ^2[t]-\log [t]-1\right) +b_0~b_2}{b_0^4~t^2}\right] , \end{aligned}$$

(25)

with

$$\begin{aligned} b_2= & {} \frac{1}{128~\pi ^3}\left[ 2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2\right] , \nonumber \\ b_1= & {} \frac{1}{24\pi ^2}\left( 153-19n_f\right) , \nonumber \\ b_0= & {} \frac{1}{12\pi }\left( 33-2n_f\right) , \nonumber \\ t= & {} \log \left[ \frac{\mu ^2}{\Lambda ^2}\right] . \end{aligned}$$

(26)

The parameter $\Lambda$ takes the values $\Lambda =213~\mathrm{MeV}$, 296 MeV and 339 MeV for the flavors $n_f=5$, $4$, and $3$, respectively [29, 32]. We take $n_f=4$ in the present study. In [32] the authors take $\mu =1$ GeV for the charmed and $\mu =3$ GeV for the bottom tensor mesons. As we have the bottom and charmed mesons, respectively, in the initial and final states in the transition under consideration, we take the interval $\mu =$(2–4) GeV for this parameter and discuss the rates of change in the form factors and other observables when going from $\mu =2$ GeV to $\mu =3$ GeV and when going from $\mu =3$ GeV to $\mu =4$ GeV.

To proceed, we shall find working regions of the four auxiliary parameters, namely the Borel mass parameters $M^2$ and $M'^2$ and continuum thresholds $s_0$ and $s'_0$, such that the transition form factors weakly depend on these parameters in those regions. The continuum thresholds $s_0$ and $s'_0$ are the energy squares which characterize the beginning of the continuum and depend on the energy of the first excited states in the initial and final channels, respectively. Our numerical calculations point out the following regions for the continuum thresholds $s_0$ and $s'_0$: $29~\mathrm{GeV^2}\le s_0\le 35~\mathrm{GeV^2}$ and $7~\mathrm{GeV^2}\le s'_0\le 11~\mathrm{GeV^2}$.

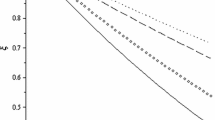
The working regions for the Borel mass parameters are calculated demanding that both the higher states and the continuum are sufficiently suppressed and the contributions of the operators with higher dimensions are small. As a result, we find the working regions $10~\mathrm{GeV^2}\le M^2\le 20~\mathrm{GeV^2}$ and $5~\mathrm{GeV^2}\le M'^2\le 10~\mathrm{GeV^2}$ for the Borel mass parameters. To see whether the contributions related to the mesons of interest in the initial and final states have been extracted by considering the above regions for the auxiliary parameters, we calculate the values of functions $-d/d(1/M^2) \ln [\Pi ^\mathrm{OPE}(s_0,s'_0,M^2,M^{'2},q^2)]$ and $-d/d(1/M^{'2}) \ln [ \Pi ^\mathrm{OPE}(s_0,s'_0,M^2,M^{'2},q^2)]$ in the Borel scheme. Taking into account all the input parameters we find the values $29.44~\mathrm{GeV^2}\sim m_{B_s}^2$ and $5.58~\mathrm{GeV^2}\sim m_{D_{s2}^{*}(2573)}^2$ for these functions, respectively, showing that the contributions of the related mesons in the initial and final states have been roughly extracted. We show, as an example, the dependence of the form factor $K(q^2)$ at $q^2=1$ on the Borel mass parameters $M^2$ and $M^{\prime ^2}$ in Fig. 2. With a quick look at this figure, we see that not only this form factor reveals a weak dependence on the Borel parameters on their working regions, but the perturbative contribution constitutes the main part of the total value.

Fig. 2

Left K($q^2=1$) as a function of the Borel mass $M^2$ at average values of the $s_0$, $s'_0$, and $M^{\prime ^2}$. Right K($q^2=1$) as a function of the Borel mass $M^{\prime ^2}$ at average values of the $s_0$, $s'_0$, and $M^2$

At this stage, we would like to find the behaviors of the considered form factors in terms of $q^2$ using the working regions for the continuum thresholds and Borel mass parameters. Our calculations depict that the form factors are truncated at $q^2\simeq 7~\mathrm{GeV^2}$. To extend the results to the whole physical region, we have to find a fit function such that it coincides with the QCD sum rules results at $q^2=(0-7)\,\mathrm{GeV^2}$ region. Here, we should also stress that at time-like momentum transfers the spectral representations mainly develop anomalous contributions, i.e., the double spectral densities receive contributions beyond those due to Landau-type singularities and deviate from the corresponding Feynman amplitudes. This problem is discussed in detail in [33]. Although these contributions do not affect the values of the form factors at $q^2=0$ and turn out to be small at higher values of $q^2$ by the above-mentioned ranges of the auxiliary parameters in the decay channel under consideration, we take also into account these small contributions in our numerical calculations. We find that the form factors are well fitted to the following function (see Fig. 3) [34]:

$$\begin{aligned} f(q^2)=\frac{f_0}{\Big (1-\frac{q^2}{m_{B_s}^2}\Big )\Big [1-\sigma _1\Big (\frac{q^2}{m_{B_s}^2}\Big ) +\sigma _2\Big (\frac{q^2}{m_{B_s}^2}\Big )^2\Big ]}, \end{aligned}$$

(27)

where the values of the parameters $f_0$, $\sigma _1$, and $\sigma _2$, as an example at $\mu =2~\mathrm{GeV}$, are presented in Table 2. The quoted errors in the results are due to the errors in the determinations of the working regions of the continuum thresholds, the Borel mass parameters as well as the uncertainties coming from other input parameters. Our numerical analysis shows that setting $\mu$ from 2 to $3~\mathrm{GeV}$ increases the values of the form factors roughly with an amount of 35 % at a fixed value of $q^2$. This rate of increase in the values of the form factors is roughly 25 % when going from $\mu =3$ GeV to $\mu =4~\mathrm{GeV}$. These rates of change reveal that the form factors considerably depend on the scale parameter $\mu$.

Table 2 Parameters appearing in the fit function of the form factors at $\mu =2~\mathrm{GeV}$

Fig. 3

K($q^2$) as a function of $q^2$ at $M^2=15\,\mathrm{GeV^2}$, $M^{\prime ^2}=7.5\,\mathrm{GeV^2}$, $s_0=35\,\mathrm{GeV^2}$, and $s_{0}^{\prime }=9\,\mathrm{GeV^2}$

In this part we would like to discuss the constraints that the HQET limit provides on the form factors under discussion as the considered decay channel is based on the heavy-to-heavy $b\rightarrow c$ transition at quark level. Taking into account all the definitions and the values of the related parameters discussed in [35] (and references therein) for a similar channel, namely $B_s\rightarrow D_{sJ}(2460)l \nu$, we find that the HQET limit affects the form factors $h(0)$ and $K(0)$ more than the form factors $b_+(0)$ and $b_-(0)$ such that the values of the form factors $h(0)$ and $K(0)$ decrease by 35 and 42 %, respectively. In contrast, the form factors $b_+(0)$ and $b_-(0)$ increase by 16 and 5 %, respectively.

Having found the fit function of the form factors in terms of $q^2$ over the full physical region, now we calculate the decay width of the process under consideration. The differential decay width for the $B_{s} \rightarrow D_{s2}^{*}(2573)\ell \bar{\nu }_{\ell }$ transition is obtained as (see also [36])

$$\begin{aligned} \frac{d\Gamma }{dq^2}= & {} \frac{\lambda (m_{B_{s}}^2,m_{D_{s2}^{*}}^2,q^2)}{4m_{D_{s2}^{*}}^2} \Big (\frac{q^2-m_{\ell }^2}{q^2}\Big )^2\nonumber \\&\times \frac{\sqrt{\lambda (m_{B_{s}}^2,m_{D_{s2}^{*}}^2,q^2)}G_F^2 V_{cb}^2}{384m_{B_{s}}^3\pi ^3}\nonumber \\&\times \Bigg \{\frac{1}{2q^2}\Bigg [3m_{\ell }^2\lambda (m_{B_{s}}^2,m_{D_{s2}^{*}}^2,q^2) [V_0(q^2)]^2 \nonumber \\&+(m_{\ell }^2+2q^2)\Big |\frac{1}{2m_{D_{s2}^{*}}}\Big [(m_{B_{s}}^2-m_{D_{s2}^{*}}^2-q^2)\nonumber \\&\times (m_{B_{s}}-m_{D_{s2}^{*}})V_1(q^2)\nonumber \\&-\frac{\lambda (m_{B_{s}}^2,m_{D_{s2}^{*}}^2,q^2)}{m_{B_{s}}-m_{D_{s2}^{*}}}V_2(q^2)\Big ]\Big |^2\Bigg ] \nonumber \\&+\frac{2}{3}(m_{\ell }^2+2q^2)\lambda (m_{B_{s}}^2,m_{D_{s2}^*}^2,q^2)\nonumber \\&\times \Bigg [\Big | \frac{A(q^2)}{m_{B_{s}}-m_{D_{s2}^{*}}}-\frac{(m_{B_{s}}-m_{D_{s2}^{*}})V_1(q^2)}{\sqrt{\lambda (m_{B_{s}}^2,m_{D_{s2}^{*}}^2,q^2)}} \Big |^2 \nonumber \\&+\Big | \frac{A(q^2)}{m_{B_{s}}-m_{D_{s2}^{*}}}+\frac{(m_{B_{s}}-m_{D_{s2}^{*}})V_1(q^2)}{\sqrt{\lambda (m_{B_{s}}^2,m_{D_{s2}^{*}}^2,q^2)}} \Big |^2\Bigg ]\Bigg \}, \end{aligned}$$

(28)

where

$$\begin{aligned} A(q^2)= & {} -(m_{B_{s}}-m_{D_{s2}^{*}})h(q^2), \nonumber \\ V_1(q^2)= & {} -\frac{K(q^2)}{m_{B_{s}}-m_{D_{s2}^{*}}}, \nonumber \\ V_2(q^2)= & {} (m_{B_{s}}-m_{D_{s2}^{*}})b_{+}(q^2), \nonumber \\ V_0(q^2)= & {} \frac{m_{B_{s}}-m_{D_{s2}^{*}}}{2m_{D_{s2}^{*}}}V_1(q^2)-\frac{m_{B_{s}}+m_{D_{s2}^{*}}}{2m_{D_{s2}^{*}}}V_2(q^2) \nonumber \\&-\frac{q^2}{2m_{D_{s2}^{*}}}b_{-}(q^2), \nonumber \\ \lambda (a,b,c)= & {} a^2+b^2+c^2-2ab-2ac-2bc. \end{aligned}$$

(29)

Table 3 Numerical results for the decay widths and branching ratios at different lepton channels for $\mu =2~\mathrm{GeV}$

Table 4 Numerical results for the decay widths and branching ratios at different lepton channels for $\mu =3~\mathrm{GeV}$

Table 5 Numerical results for the decay widths and branching ratios at different lepton channels for $\mu =4~\mathrm{GeV}$

Performing the integral over $q^2$ in the above equation over the whole physical region, finally, we obtain the values of the total decay widths and branching ratios for all lepton channels as presented in Tables 3, 4, and 5 for $\mu =2~\mathrm{GeV}$, $\mu =3~\mathrm{GeV}$, and $\mu =4~\mathrm{GeV}$, respectively. From these tables we see that when setting $\mu$ from $2~\mathrm{GeV}$ to $3~\mathrm{GeV}$, the decay rate and branching ratio increase by roughly 82 %, but when going from $\mu =3~\mathrm{GeV}$ to $\mu =4~\mathrm{GeV}$ the rate of increase in these quantities is roughly 40 % for all lepton channels. From these changes, we conclude that the results of these quantities also depend considerably on the scale parameter $\mu$. The orders of the branching fractions show that the semileptonic $B_{s} \rightarrow D_{s2}^{*}(2573)\ell \overline{\nu }_{\ell }$ is experimentally accessible at all lepton channels in near future.

In summary, taking into account the perturbative $\mathcal{O}(\alpha _s)$ corrections we have calculated the transition form factors governing the semileptonic $B_{s} \rightarrow D_{s2}^{*}(2573)\ell \bar{\nu }_{\ell }$ transition at all lepton channels using a suitable three-point correlation function. The fit functions of the form factors have been used to estimate the corresponding decay widths and branching ratios. The orders of the branching ratios indicate that such channels contribute considerably to the total width of the $B_s$ meson. We hope that it will be possible to study these channels at LHCb in the near future. Comparison of the future data with the theoretical results can help us understand the internal structure and nature of the $D_{s2}^{*}(2573)$ charmed-strange tensor meson.

Appendix

In this appendix, as an example, we briefly show how we calculate the perturbative $\mathcal{O}(\alpha _s)$ corrections for the structure $q_{\alpha }g_{\beta \mu }$, i.e., $\rho _{\alpha _{s_1}}(s,s',q^2)$. After performing the trace of Eq. (21) and taking into account also the contributions of all diagrams in Fig. 1, we use the Feynman parametrization to perform the four-$k$ and four-$k^{\prime }$ integrals. First we perform the four-integral over $k$. Using the Feynman parametrization, as an example for diagram (a) in Fig. 1, one can write

$$\begin{aligned}&\frac{1}{A_{1}^{a}A_{2}^{b}A_{3}^{c}A_{4}^{d}A_{5}^{e}}=\frac{\Gamma [a+b+c+d+e]}{\nonumber }\\&\quad \times {\Gamma [a]\Gamma [b]\Gamma [c]\Gamma [d]\Gamma [e]}\nonumber \\&\quad \times \int _{0}^{1}dx\int _{0}^{1}dy\int _{0}^{1}dz \int _{0}^{1}dt\int _{0}^{1}dt' \nonumber \\&\quad \times \frac{x^{a-1}y^{b-1}z^{c-1}t^{d-1}t'^{e-1}}{\{xA_1+yA_2+zA_3+tA_4+t'A_5\}^{a+b+c+d+e}}\nonumber \\&\quad \times \delta (x+y+z+t+t'-1), \end{aligned}$$

(30)

where $A_1=[(p'+k)^2-m_c^2]$, $A_2=[(p+k)^2-m_b^2]$, $A_3=[(k-k')^2-m_s^2]$, $A_4=[k^2-m_s^2]$, $A_5=k^{'2}$, and $a=b=c=d=e=1$ for diagram (a). The next step is to perform the integral over $t'$ using the Dirac delta in Eq. (30), rearrange the denominator of the integrand on the right-hand side of this equation, and use the shift

$$\begin{aligned} k\rightarrow k-\frac{p y+p' x-k' z}{x+y+z+t}, \end{aligned}$$

(31)

to make the denominator full-squared in terms of $k$, i.e., in the form of $k^2-\Delta$, where $\Delta$ is a function of $k'$, $p$, $p'$, $x$, $y$, $z$, $t$, and the quark masses.

The integral over $k$ is performed via the following $D$-dimensional integrals:

$$\begin{aligned}&\int \frac{d^Dk}{(2\pi )^D}\frac{1}{(k^2-\Delta )^n}\nonumber \\&\quad =\frac{i(-1)^n}{(4\pi )^{D/2}}\frac{\Gamma [n-D/2]}{\Gamma [n]}\left( \frac{1}{\Delta }\right) ^{n-D/2}, \nonumber \\&\int \frac{d^Dk}{(2\pi )^D}\frac{k^2}{(k^2-\Delta )^n}\nonumber \\&\quad =\frac{i(-1)^{n-1}}{(4\pi )^{D/2}}\frac{D}{2} \frac{\Gamma [n-D/2-1]}{\Gamma [n]}\left( \frac{1}{\Delta }\right) ^{n-D/2-1}, \nonumber \\&\int \frac{d^Dk}{(2\pi )^D}\frac{k^{\mu }k^{\nu }}{(k^2-\Delta )^n}\nonumber \\&\quad =\frac{i(-1)^{n-1}}{(4\pi )^{D/2}} \frac{g^{\mu \nu }}{2} \frac{\Gamma [n-D/2-1]}{\Gamma [n]}\left( \frac{1}{\Delta }\right) ^{n-D/2-1}, \nonumber \\&\int \frac{d^Dk}{(2\pi )^D}\frac{(k^2)^2}{(k^2-\Delta )^n}\nonumber \\&\quad =\frac{i(-1)^{n}}{(4\pi )^{D/2}}\frac{D(D+2)}{4} \frac{\Gamma [n-D/2-2]}{\Gamma [n]}\left( \frac{1}{\Delta }\right) ^{n-D/2-2}, \nonumber \\&\int \frac{d^Dk}{(2\pi )^D}\frac{k^{\mu }k^{\nu }k^{\rho }k^{\sigma }}{(k^2-\Delta )^n}\nonumber \\&\quad =\frac{i(-1)^{n}}{(4\pi )^{D/2}} \frac{\Gamma [n-D/2-2]}{\Gamma [n]}\left( \frac{1}{\Delta }\right) ^{n-D/2-2} \nonumber \\&\qquad \times \frac{1}{4}(g^{\mu \nu }g^{\rho \sigma }+g^{\mu \rho }g^{\nu \sigma }+g^{\mu \sigma }g^{\nu \rho }). \end{aligned}$$

(32)

Now, we proceed to perform the four-integral over $k^{\prime }$. Again we try to make the denominator of the integrand of the integration over $k'$ full-squared in terms of $k'$ viz. $k^{'2}-\Delta '$, with $\Delta '$ being a function of $p$, $p'$, $x$, $y$, $z$, $t$, and the quark masses, by using the shift

$$\begin{aligned}&k'\rightarrow k'\nonumber \\&\quad -\frac{(py+p'x)z}{x\!+\!y\!+\!z\!-\!t^2\!-\!z^2\!-\!(x\!+\!y)(x\!+\!y\!+\!z)\!-\!t(2x\!+\!2y\!+\!z\!-\!1)}.\nonumber \\ \end{aligned}$$

(33)

In this step, the integral over $k'$ is performed again using the above table of $D$-dimensional integrals. Now, we come back to the four dimensions. For the terms which converge we directly set $D=4$, but for those that diverge on setting $D=4$, the following relation is used:

$$\begin{aligned}&\frac{\Gamma [2-D/2]}{(4\pi )^{D/2}}\left( \frac{1}{\Delta '}\right) ^{2-D/2}\nonumber \\&\quad =\frac{1}{(4\pi )^2} \left( \frac{2}{\epsilon }-\log \Delta '-\gamma +\log (4\pi )+\mathcal{O}(\epsilon )\right) , \end{aligned}$$

(34)

with $\epsilon =4-D$ and $\Delta '$ negative. To obtain the imaginary part, we use the following relation:

$$\begin{aligned} \log [-|\Delta '|]=\log [e^{i\pi }|\Delta '|]=i\pi +\log [|\Delta '|]. \end{aligned}$$

(35)

We do similar calculations for all diagrams in Fig. 1. As a result, we obtain

$$\begin{aligned} \rho _{\alpha _{s_1}}= & {} \alpha _{s}\int _{0}^{1}dx\int _{0}^{1-x}dy\int _{0}^{1-x-y}dz\int _{0}^{1-x-y-z}\nonumber \\&\times dt \Bigg \{\frac{1}{4\pi ^3\Lambda ^5}\Bigg [-t(x+y+t-1)\Big ((x+y+t-1)^2\nonumber \\&\times (6m_c(t-3x+5y)+m_b(3t-5x+11y))\nonumber \\&+z(x+y+t-1) \Big (m_b(6t-2x+14y-3) \nonumber \\&+2m_s(5x-11y-3t)-6m_c(2x-6y-2t+1)\Big )\nonumber \\&+6z^2(x+y+t-1)(m_b-m_s+2m_c) \nonumber \\&+3z^3(m_b+2m_c-2m_s) \Big )\Theta \Big [L_{1}[s,s^{\prime },q^2,x,y,z,t]\Big ]\nonumber \\&+y(x+y+t-1)\Big ((x+y+t-1)^2(24m_c(x-y)\nonumber \\&+m_s(t-7x+9y)) +z(x+y+t-1)\nonumber \\&\times (24m_c(1-t-2y)-2m_b(t-7x+9y)\nonumber \\&+m_s(2x+18y+10t-2))-6z^2(x+y+t-1)\nonumber \\&\times (3m_b+8m_c-3m_s) -3z^3(6m_b+8m_c-3m_s)\Big )\nonumber \\&\times \Theta \Big [L_{2}[s,s^{\prime },q^2,x,y,z,t]\Big ]\nonumber \\&+x(x+y+t-1)\Big ((x+y+t-1)^2\nonumber \\&\times (m_s-m_b)(5t-3x+13y)-z(x+y+t-1)\nonumber \\&\times \Big (24m_c(t-x+3y)+(3+2t-6x+10y)\nonumber \\&\times (m_b-m_s)\Big )+6z^2(x+y+t-1) \nonumber \\&\times (m_b+4m_c-m_s)+3z^3(m_b+8m_c-m_s)\Big )\nonumber \\ \end{aligned}$$

$$\begin{aligned}&\times \Theta \Big [L_{3}[s,s^{\prime },q^2,x,y,z,t]\Big ]\Bigg ]\nonumber \\&+\int _{0}^{1-x-y-z-t}dw\Bigg [\frac{1}{4\pi ^3\Lambda ^{\prime ^5}}\Bigg (m_b(t^2+wr-3x\nonumber \\&+3x^2+w(3x+y-1)+y+2xy-y^2 +z \nonumber \\&+ 3xz-yz-z^2+t(4x+z+w-1))\nonumber \\&\times (12+11t^2+11w^2-23x-23y+23w(x+y-1)\nonumber \\&+ 11(x+y)^2-23z+22wz+23z(x+y)+11z^2\nonumber \\&+t(22x+22y+23z+23w-23)) +m_c\nonumber \\&\times (4t^4+w^4+2(x+y-1)^2(11x^2+y(9-7y)\nonumber \\&+x(4y-15))+z(x+y-1)(51x^2+y \nonumber \\&\times (57-37y)+x(14y-43)-18)\nonumber \\&+z^2(43+12x-44y) (x+y-1)\nonumber \\&-2z^3(13x+15y-16) \nonumber \\&- 7z^4+t^3(11w+34x-2y+7z-14)\nonumber \\&+w^2(13+40x^2-16y^2+3y-28yz+x(24y-6z\nonumber \\&- 53)+2z(8-9z))+w(73x -122x^2+55x^3\nonumber \\&-27y-56xy+77x^2y+66y^2-11xy^2-33y^3 \nonumber \\&+ 2z(x+y-1)(15+26x-30y)\nonumber \\&-2z^2(21x+27y-28)-20z^3-6)\nonumber \\&+2w^3 (5x+3y+2z- 4)\nonumber \\ \end{aligned}$$

$$\begin{aligned}&+t^2(16+12w^2+78x^2+6y(3-5y)\nonumber \\&-23yz-16z^2+x(48y+65z-102)+w(77x\nonumber \\&- 11y-4(7+z)))+t(8w^3+2(x+y-1)\nonumber \\&\times (3+35x^2+y(20-19y)+2x(8y-23))+w^2\nonumber \\&\times (52x-4y-12z-25)+z(109x^2+y(97-67y)\nonumber \\&+x(42y-94))+z^2(59-4x-60y) \nonumber \\&- 28z^3+w(23+121x^2 +38y-55y^2\nonumber \\&+34z-64yz-48z^2+6x(11y+8z-25))))-m_s\nonumber \\&\times (2t^4+11w^4+(x+y-1)^2(8x^2+y(5-4y)\nonumber \\&+x(4y-11))+z(x+y-1)(56x^2-55x \nonumber \\&+ 21y +40xy-16y^2-5)+z^2(x+y-1)\nonumber \\&\times (17+81x-23y)+z^3(19+25x-19y)-7z^4\nonumber \\&+ t^3(14x+2y+20z+16w-7)\nonumber \\&+w^3(47x+3y+26z-25)\nonumber \\&+w(60x-3-109x^2 +52x^3\nonumber \\&- 16y-70xy+84x^2y+39y^2+12xy^2-20y^3\nonumber \\&+16z(x+y-1)(10x-3y)+z^2(13+97x\nonumber \\ \end{aligned}$$

$$\begin{aligned}&- 35y)-10z^3)+t^2(8+27w^2+30xr-y(1+6y)\nonumber \\&-37z +24yz+29z^2+w(84x+12y\nonumber \\&+ 56z-35)+x(24y+96z-41))+w^2\nonumber \\&\times (17+79x^2+8y-31z-(y+z)(25y-12z)+x \nonumber \\&\times (54y+119z-96))+t(25w^3+26x^3-6y\nonumber \\&+y^2(19-10y)-3)+12z-12y^2z+6z^2 \nonumber \\&\times (y-2)+3z^3+w^2(106x+2y+53z-44)\nonumber \\&+x^2(42y+132z-61)+2x(19+3y(y-7) \nonumber \\&- 7z+60yz+55z^2)+w(22 +120x^2-24y^2+y\nonumber \\&\times (4+8z)+24x(4y+9z-6)+31z^2 \nonumber \\&- 56z))\Bigg )\Theta \Big [L_{4}[s,s^{\prime },q^2,x,y,z,t,w]\Big ]\nonumber \\&+\frac{1}{4\pi ^3\Lambda ^{\prime \prime ^5}}\Bigg (m_b (-6t^4+(x+y-1)^2 \nonumber \\&\times (33x^2+y(7-11y)+ x(22y-9))+z(x+y-1)\nonumber \\&\times (9+75x^2-y(13+29y)+x(46y-57))\nonumber \\&+z^2(24+81x^2+15x (6y-7)+y(9y-65))\nonumber \\&+ 3z^3(16x+12y-7)+6z^4\nonumber \\ \end{aligned}$$

$$\begin{aligned}&+w^3(18x+6y+6z-1)-t^3(12x \nonumber \\&+ 24y+12z+18w-19)+t^2(37x^2-18w^2\nonumber \\&+y(55-35y-12z)+17z-w(6x+42y+18z\nonumber \\&- 37)+x (15+2y+24z)-20)+w^2(2+59x^2\nonumber \\&-13y^2+z(18z-23)+y(48z-5)+x(46y\nonumber \\&+ 84z-45))+t(7-6w^3+75x^3+w^2(17+24x\nonumber \\&-12y)+y(60y-29y^2-38)) +4z-2yz\nonumber \\&\times (5+13y)+z^2(48y-23)+12z^3+x^2(121y\nonumber \\&+118z-88)+x(6-28y+17y^2-90z \nonumber \\&+ 92yz+84z^2)+2w(48x^2+25y-24y^2-3z\nonumber \\&+18yz+9z^2+3x(8y+18z-5))+w(75x^3 \nonumber \\&- 29y^3+y^2(38-4z)+2y(z-1)(4+39z)\nonumber \\&+x^2(121y+140z-110)+(z-1)(1-25z\nonumber \\&+ 18z^2)+x(17y^2+8y(17z-9)+6 (z-1)\nonumber \\ \end{aligned}$$

$$\begin{aligned}&\times (19z-6))))+m_s(17t^4-5w^4-(x+y-1)^2 \nonumber \\&\times (27x^2+10x(y-3)+18y-17y^2)+w^3(16\nonumber \\&-38x+6y-42z)-2z(x+y-1)(15+42x^2 \nonumber \\&+ 13y(1-2y) +x(16y-57))-z^2(x+y-1)\nonumber \\&\times (111x-25y-87)-4z^3(21x+10y-21)\nonumber \\&- 27z^4+t^3(8x+52y+24z+46w-52)+t^2\nonumber \\&\times (53+36w^3-67x^2-22w(4+x-5y) +69y^2 - 122y\nonumber \\&+2x(7+y-34z)-20z+6wz+64yz-30z^2)\nonumber \\&+2w(3-49x+88x^2-42x^3+21y \nonumber \\&+ 38xy-58x^2y-50y^2+10xy^2+26y^3\nonumber \\&-4z(x+y-1) (25x-9y-13)+y(30+28z)+2x \nonumber \\&\times (21y+80z-53))+2t(w^3-42x^3+(y-1)^2\nonumber \\&\times (26y-9)+x^2(77-58y-89z)+z(y-1) \nonumber \\ \end{aligned}$$

$$\begin{aligned}&\times (17+47y)+2z^2(29-7y)-32z^3\nonumber \\&-2w^2(5+17x-16y+15z)+2x(8y+5y^2+53z \nonumber \\&- 21yz-40z^2-13)+w(18-78x^2-76y+58y^2\nonumber \\&+48z+18yz-63z^2-2x(10y+57z \nonumber \\&- 30))))+m_c\{10w^4 -8t^4+(x+y-1)^2\nonumber \\&\times (x^2-3y(y-4)-2x(y+18))+z(x+y-1)\nonumber \\&\times (36+38x^2+31y-18y^2-101x+20xy)\nonumber \\&+2z^2(50+33x^2-y(23+11y)+x(22y-83)) \nonumber \\&+ z^3 (65x+29y-92)+28z^4+t^3(28-14w\nonumber \\&+13x-23y+4z)+w^3(39x+3y+58z-32)\nonumber \\&+ t^2(62x^2-26y^2+6w^2+58y-36z-17yz\nonumber \\&+60z^2+w(24+65x -43y+66z)+x(36y\nonumber \\&+ 91z-62)-32)+w^2(34+64x^2+6y-24y^2\nonumber \\&-156z+35yz+114z^2+x(40y+143z\nonumber \\&- 114))+w(38x^3-18y^3+y^2(51-46z)\nonumber \\ \end{aligned}$$

$$\begin{aligned}&+y(z-1)(21+61z)+x^2(58y+130z-137)\nonumber \\&+ x(111+2y(y-43)-280z+84yz+169z^2)\nonumber \\&+2(z-1)(6-61z+47z^2))+t[12+22w^3\nonumber \\&+ 38x^3-47y+y^2 (53-18y)+68z\nonumber \\&+12yz(1-4y)+z^2(35y-156)+76z^3\nonumber \\&+w^2(91x-17y + 120z-36)\nonumber \\&+x^2(58y+128z-135)+x(85\nonumber \\&+2y(y-41)-228z+80yz+143z^2) +2w\nonumber \\&\times (1+63x^2+32y-25y^2-96z+9yz\nonumber \\&+87z^2+x(38y+117z-88))]\} \Bigg )\nonumber \\&\times \Theta \Big [L_{5}[s,s^{\prime },q^2,x,y,z,t,w]\Big ]\nonumber \\&-\frac{1}{4\pi ^3\Lambda ^{\prime \prime \prime ^5}}\Bigg (m_b(-11t^4-3(x^2+x(y-1)\nonumber \\&+y(y-1))(3+x(16+11x) -5y-16xy+2y^2) \nonumber \\ \end{aligned}$$

$$\begin{aligned}&+ z(15x^3+2x(y-1)(22+29y)+x^3(62y-92)\nonumber \\&+y^2(23-12y)-4y-7)+z^2(20+xz^2(61\nonumber \\&+ 53x-10y)-17y) +z^3(12y-26x-19)+6z^4\nonumber \\&+3t^3(w+y+z-22x-1)+w^3(1+8x\nonumber \\&- 6y+6z)+t^2(3w^2-132x^2+w(21x-16y\nonumber \\&+28z-16)+21x(y+z-1) -(13+19y\nonumber \\&- 25z)(y+z-1))+w^2(31x^2+y(23-18y)\nonumber \\&+x(58y-10z-7)+z(18z-17))+w(15x^3\nonumber \\&+ 2x(5+46y-22z)(y+z-1)+x^2 (40y\nonumber \\&+84z-70)-(y+z-1)(1+y(18y-25)\nonumber \\&+z(19- 18z)))+t(14w^3-110x^3\nonumber \\&+33x^2(y+z-1)-2x(y+z-1)\nonumber \\&\times (26+5y-39z) +(y+z-1)^2 (1+48y-20z)\nonumber \\&+w^2(34x+76y+8z-27)\nonumber \\ \end{aligned}$$

$$\begin{aligned}&+w(33x^2+2(y+z-1)(55y-13z-6)+2x \nonumber \\&\times (12y+56z-43))))+m_s(5t^4+5w^4+3(x^2\nonumber \\&+x(y-1)+y(y-1))(9x^2+(y-1)(9y-21x\nonumber \\&- 1))+2w^3(7x+21y-z-8)-2z(x^2(18x-43)\nonumber \\&-62x-9-17y+xy (31x+58)+2y^2(29 \nonumber \\&+ 2x)-32y^3)+z^2(10y(2+3y)-53x^2-53\nonumber \\&+2x(56y-79))+4z^3(13+16x-6y)-17z^4\nonumber \\&+ t^3(42x-8w -8(y+z-1))-t^2(3w^3-96x^2\nonumber \\&-(7+19y-25z-52x)(y+z-1)+52wx\nonumber \\&+2w(14z-8y-5))+w^2(17-31x^2-116y+20z\nonumber \\&+12 (8y-3z)(y+z)+x(92z-8y-58))\nonumber \\ \end{aligned}$$

$$\begin{aligned}&+ 2w(x^2(32-20y-42z)-18x^3-x(y+z-1)\nonumber \\&\times (37+29y-71z)+(y+z-1)(3+43y^2+z\nonumber \\&\times (21-23z) +y(20z-49)))+2t(43x^3-4w^3\nonumber \\&+x(y+z-1)(20+5y-39z-40x)-(29y \nonumber \\&- 21z+3)(y+z-1)^2+w^2(5-17x-37y+13z)\nonumber \\&- w(40x^2+2(y+z-1)(1+31y-19z)\nonumber \\&+ x(12y+56z-37))) )+m_c\{t^4-10w^4+36x\nonumber \\&+17x^2-52x^3-x^4+36y-47xy-41x^2y \nonumber \\&+ 52x^3y-100y^2-14xy^2+24x^2y^2+92y^3\nonumber \\&+25xy^3-28y^4 +z(52x^3-x(y-1)(y-123) \nonumber \\&+ x^2(52y-45)-4(y-1)(19y^2-20y-3))\nonumber \\&+z^2(32+28x^2+x(138-77y)+12y(3-5y)) \nonumber \\&- z^3(51x+4 (7+y))+8z^4+t^2(y+z+w-1)\nonumber \\&\times (6w+84x+4y+8z-3)-w^3(13x+58y \nonumber \\&+ 22z-32)+2t^3(8w+x+8(y+z-1))\nonumber \\&+w^2(26x^2+156y+36z- 6(y+z)(19y+z)-x\nonumber \\ \end{aligned}$$

$$\begin{aligned}&\times (y+77z-62))+w(52x^3+x(y+z-1)\nonumber \\&\times (85+37y-115z)+x^2(50y+54z-43)\nonumber \\&-2(y+z - 1)(6+47y^2+z(5-7z)\nonumber \\&+y(40z-61)))+t[5w^3-2x^3+w^2(2+32x\nonumber \\&+53y-23z)+120x^2 (y+z-1)\nonumber \\&+(y+z-1)^2(12+43y-33z)\nonumber \\&+4x(y+z-1)(7y+9z-5)+ w(120x^2+(y\nonumber \\&+z-1)(19+91y-61z)+x(60y+68z-52))]\}\Bigg )\nonumber \\&\Theta \Big [L_{6}[s,s^{\prime },q^2,x,y,z,t,w]\Big ] \Bigg ] \Bigg \}, \end{aligned}$$

(36)

where

$$\begin{aligned}&L_{1}[s,s^{\prime },q^2,x,y,z,t]\nonumber \\&\quad =\frac{(x+y+z+t)}{\Lambda ^2}\Big [(x+y+t-1)\nonumber \\&\quad \quad \times \Big (-s^{\prime }xt -sty-q^2xy+m_b^2y(x+t) \nonumber \\&\quad \quad +m_b^2y^2+m_c^2x(x+y+t)\Big )+z(x+y+t-1)\nonumber \\&\quad \quad \times (m_c^2x-s^{\prime }x+m_b^2y-sy) \nonumber \\&\quad \quad +z^2(m_c^2x-s^{\prime }x+m_b^2y-sy) +m_s^2(t+z)\Lambda \Big ], \nonumber \\ \end{aligned}$$

$$\begin{aligned}&L_{2}[s,s^{\prime },q^2,x,y,z,t]\nonumber \\&\quad =\frac{(x+y+z+t)}{\Lambda ^2}\Big [(x+y+t-1)\Big (-s^{\prime }xt-sty\nonumber \\&\quad \quad -q^2xy+m_b^2y(x+t)+m_b^2y^2+m_c^2x(x+y+t)\Big )\nonumber \\&\quad \quad +z(x+y+t-1)(m_c^2x+m_b^2(x+2y+t)-st\nonumber \\&\quad \quad -q^2x)+z^2(m_c^2x-st-q^2x+m_b^2(x+2y+t-1))\nonumber \\&\quad \quad +m_b^2z^3+m_s^2t\Lambda \Big ], \nonumber \\ \end{aligned}$$

$$\begin{aligned}&L_{3}[s,s^{\prime },q^2,x,y,z,t]\nonumber \\&\quad =\frac{(x+y+z+t)}{\Lambda ^2}\Big [(x+y+t-1)\Big (-s^{\prime }xt -sty\nonumber \\&\quad \quad -q^2xy+m_b^2(x+y+t)\Big )-z(x+y+t-1)\nonumber \\&\quad \quad \times (s^{\prime }t-ym_b^2+yq^2)-z^2(s^{\prime }t-ym_b^2+yq^2) \nonumber \\&\quad \quad +m_s^2t\Lambda +m_c^2(x+z)\Lambda \Big ], \nonumber \\ \end{aligned}$$

$$\begin{aligned}&L_{4}[s,s^{\prime },q^2,x,y,z,t,w]\nonumber \\&\quad =\frac{(x+y+z+t+w)}{\Lambda ^{\prime ^2}}\Big [stx-st^2x+swx-stwx\nonumber \\&\quad \quad -sw^2x-stx^2 -swx^2 -m_c^2ty+s^{\prime }ty+m_c^2t^2y\nonumber \\&\quad \quad -s^{\prime }t^2y-m_c^2wy+s^{\prime }wy+twy(m_c^2-s^{\prime })+m_c^2w^2y\nonumber \\&\quad \quad -s^{\prime }w^2y-m_c^2xy+q^2xy+2m_c^2txy-q^2txy-stxy\nonumber \\&\quad \quad -s^{\prime }txy+m_c^2wxy -swxy-s^{\prime }wxy+m_c^2x^2y\nonumber \\&\quad \quad -q^2x^2y -m_c^2y^2+2m_c^2ty^2 -s^{\prime }ty^2+m_c^2wy^2-s^{\prime }wy^2\nonumber \\&\quad \quad +2m_c^2xy^2-q^2xy^2+m_c^2y^3 +z(-s^{\prime }\nonumber \\&\quad \quad \times (t^2+w(w+y-1)+t(x+y+w-1))\nonumber \\&\quad \quad -x(sw+q^2(x+y+t+w-1))\nonumber \\&\quad \quad +m_c^2(t^2+w^2+(x+2y)(x+y-1)+w(x+3y-1) \nonumber \\&\quad \quad +t(2x+3y+w-1))) +z^2(-s^{\prime }(t+w) \nonumber \\&\quad \quad - q^2x+m_c^2(x+2y+2w+t-1))+m_c^2z^3\nonumber \\&\quad \quad +m_s^2(t+w)\Lambda ^{\prime } +m_b^2x\Lambda ^{\prime }\Big ], \nonumber \\ \end{aligned}$$

$$\begin{aligned}&L_{5}[s,s^{\prime },q^2,x,y,z,t,w]\nonumber \\&\quad =\frac{(x+y+z+t+w)}{\Lambda ^{\prime \prime ^2}}\Big [s^{\prime }tw(1-t-w) -m_b^2tx\nonumber \\&\quad \quad +q^2tx+m_b^2t^2x-q^2t^2x- m_b^2wx+swx+2m_b^2twx\nonumber \\&\quad \quad -q^2twx-stwx+m_b^2w^2x-sw^2x-m_b^2x^2+ m_b^2tx^2 \nonumber \\&\quad \quad -q^2txr+m_b^2wx^2-swx^2+m_b^2x^3+s^{\prime }wy-s^{\prime }twy\nonumber \\&\quad \quad -s^{\prime }w^2y- m_b^2xy+q^2xy+m_b^2txy-q^2txy+m_b^2wxy\nonumber \\&\quad \quad -swxy-s^{\prime }wxy+2m_b^2x^2y-q^2x^2y-s^{\prime }wy^2\nonumber \\&\quad \quad +m_b^2xy^2-q^2xy^2+\Big (q^2 (y(1-y)-t(x+w+t-1)\nonumber \\&\quad \quad - y(x+w+t))-w(s(x+w+t-1)+s^{\prime }(y+t))\nonumber \\&\quad \quad +m_b^2z(t^2+w^2+(x+ y-1)(2x+y)\nonumber \\&\quad \quad +w(3x+y-1)+ t(3x+y+2w-1))\nonumber \\&\quad \quad +z^2(m_b^2(2x+y+2w+2t-1)-q^2(t+y)-sw)\nonumber \\&\quad \quad +m_b^2z^3+m_s^2w\Lambda ^{\prime \prime }+m_c^2(y+t)\Lambda ^{\prime \prime }\Big )\Big ],\nonumber \\ \end{aligned}$$

$$\begin{aligned}&L_{6}[s,s^{\prime },q^2,x,y,z,t,w]\nonumber \\&\quad =\frac{(x+y+z+t+w)}{\Lambda ^{\prime \prime \prime ^2}}\Big [s(-t^2(x+y)\nonumber \\&\quad \quad -t(x^2+x(w+y-1)+y(w+y- 1))\nonumber \\&\quad \quad -w(x^2+x(w+y-1)+y(w+y-1)))\nonumber \\&\quad \quad +z(-x(sw+q^2(x+w+ t-1))\nonumber \\&\quad \quad -y(s(t+w)+qr(x+w-1))\nonumber \\&\quad \quad -q^2y^2 -s^{\prime }(t^2+w(w+y-1)+t(x+y+w-1))\nonumber \\&\quad \quad +m_c^2(t^2+w^2+x(x-1)+y(x-1)+y^2\nonumber \\&\quad \quad +t(2x+y+w-1)+ w(x+2y-1)))\nonumber \\&\quad \quad +z^2 (m_c^2(x+2y+2w+t-1)-q^2(x+y)\nonumber \\&\quad \quad -s^{\prime }(t+w))m_c^2z^3+m_s^2(t+w)\Lambda ^{\prime \prime \prime }+m_b^2(x+y)\Lambda ^{\prime \prime \prime }\Big ],\nonumber \\ \end{aligned}$$

(37)

and

$$\begin{aligned}&\Lambda =t^2-x-y-z(1-z)+(x+y)\nonumber \\&\qquad \quad \times (x+y+z)+t(2x+2y+z-1),\nonumber \\&\Lambda ^{\prime }=t^2+w^2+z^2+(x+y)(x+y+z)\nonumber \\&\qquad \quad +t(2x+2y+z+w-1)+w(x+y+2z-1)\nonumber \\&\qquad \quad - x-y-z,\nonumber \\&\Lambda ^{\prime \prime }=t^2+w^2+z^2+(x+y)\nonumber \\&\qquad \quad \times (x+y+z)+t(x+y+2z+2w-1)\nonumber \\&\qquad \quad +w(x+y+2z-1)- x-y-z,\nonumber \\&\Lambda ^{\prime \prime \prime }=t^2+w^2+z^2+x^2+y^2\nonumber \\&\qquad \quad +xy+z(x+2y-1)+t(2x+y+z+w-1)\nonumber \\&\qquad \quad +w(x+2y+2z-1)- x-y. \end{aligned}$$

(38)