Analysis of the semileptonic $B_c\rightarrow D_1^0$ transition in QCD sum rules and HQET

Abstract

We investigate the structure of the $D_{1}^0(2420[2430])(J^P=1^+)$ mesons via analyzing the semileptonic $B_{c}\rightarrow D_{1}^0 l\nu$ transition in the frame work of the three-point QCD sum rules and the heavy-quark effective theory. We consider the $D_{1}^0$ meson in three ways: as a pure $|c\bar{u}\rangle$ state, as a mixture of the two $|^3P_1\rangle$ and $|^1P_1\rangle$ states with a mixing angle $\theta$, and as a combination of the two mentioned states with mixing angle $\theta =35.3^\circ$ in the heavy-quark limit. Taking into account the gluon condensate contributions, the relevant form factors are obtained for the three above conditions. These form factors are numerically calculated for $|c\bar{u}\rangle$ and the heavy-quark limit cases. The obtained results for the form factors are used to evaluate the decay rates and the branching ratios. Also for mixed states, all of the mentioned physical quantities are plotted with respect to the unknown mixing angle $\theta$.

1 Introduction

There is some difference between the measured and predicted masses of the even-parity charmed mesons $(J^P=1^+)$, observed in the laboratories [1–5] and considered in many phenomenological models [6–11]. So many efforts have been made to realize this unexpected disparity between theory and experiment [12–18]. Therefore the study of the processes involving these mesons is important for understanding of the structure and quark content of them. Some physicists presumed that these discovered states are conventional $c\bar{u}$ and $c\bar{s}$ mesons [19–27]. Among these mesons, we focus on the non-strange $D_1^0$ meson. So far the two confirmed $D^0_1$ states, with mass of $2423.4\pm 3.2$ and $2427\pm 26\pm 25$ MeV, have been observed [5]. The narrow-width state with lower mass is known as $D_1^0(2420)$ and the wide-width state with higher mass is identified as $D_1^0(2430)$ [28]. Theoretically, the discovered states do not fit easily into the $c\bar{u}$ spectroscopy [22]. One of the proposals is the introduction of the $D_1^0$ meson as a mixture of two $|^1P_1\rangle$ and $|^3P_1\rangle$ states with the $c\bar{u}$ quark content [19–22, 29, 30]. In this work, we plan to analyze the $D_1^0$ meson as a conventional meson with pure $|c\bar{u}\rangle$ state and also as a combination of $|^1P_1\rangle$ and $|^3P_1\rangle$ states.

Heavy–light mesons are not charge conjugation eigenstates and so mixing can occur among states with the same $J^P$ and different mass that are forbidden for neutral states [22]. So the mixing of the physical $D_{1}$ and $D'_{1}$ states can be parameterized in terms of a mixing angle $\theta$, as follows:

$$\begin{aligned} \left[ \begin{array}{c} |D_1\rangle \\ |D'_1\rangle \end{array} \right] = \left[ \begin{array}{cc} \cos \theta &{} \sin \theta \\ -\sin \theta &{} \cos \theta \end{array} \right] \times \left[ \begin{array}{c} |^1P_1\rangle \\ |^3P_1\rangle \end{array} \right] , \end{aligned}$$

(1)

where we used the spectroscopic notation $^{2S+1}L_{J}$ for introduction of the mixing states. Considering $|^3P_1\rangle \equiv |D_{1}1\rangle$ and $|^1P_1\rangle \equiv |D_{1}2\rangle$ with different masses and decay constants [22, 29], we can apply these relations, beyond the heavy-quark model, for axial vectors $D_{1}(2420)$ and $D_{1}(2430)$ mesons with two different masses, i.e.,

$$\begin{aligned} \begin{aligned}&\displaystyle |D_{1}(2420)\rangle = \sin \theta ~|D_{1}1\rangle ~+\cos \theta ~|D_{1}2\rangle , \\&\displaystyle |D_{1}(2430)\rangle = \cos \theta ~|D_{1}1\rangle ~-\sin \theta ~|D_{1}2\rangle . \end{aligned} \end{aligned}$$

(2)

The masses and decay constants of the $D_{1}1$ and $D_{1}2$ states are presented in Tables 1 and 2.

Table 1 Masses of $D_11(^3P_1)$ and $D_12(^1P_1)$ states in GeV

Table 2 Decay constants of $D_11(^3P_1)$ and $D_12(^1P_1)$ states in MeV

In the heavy-quark limit where the quark mass $m_{c}\rightarrow \infty$, both axial vector $D_1^0(2420)$ and $D_{1}^0(2430)$ mesons can be produced and identified with $|P_1^{3/2}\rangle$ and $|P_1^{1/2}\rangle$, respectively. It is useful to change from the $L$–$S$ basis $^{2S+1}L_J$ to the $j$–$j$ coupling basis $L^j_J$, where $j$ is the total angular momentum of the light quark. The relationship between these states is given as [22, 29, 30]

$$\begin{aligned} \left[ \begin{array}{c} D_{1}^0(2420)\equiv |P_1^{3/2}\rangle \\ D_{1}^0(2430)\equiv |P_1^{1/2}\rangle \end{array} \right] =\left[ \begin{array}{cc} \sqrt{\frac{2}{3}} &{} \sqrt{\frac{1}{3}}\\ -\sqrt{\frac{1}{3}}&{} \sqrt{\frac{2}{3}} \end{array} \right] \times \left[ \begin{array}{c} |D_12\rangle \equiv |^1P_1\rangle \\ |D_11\rangle \equiv |^3P_1\rangle \end{array} \right] . \end{aligned}$$

(3)

These relations occur for the mixing angle $\theta =35.3^\circ$ in Eq. (1). But note that the value of the mixing angle can be positive equal to $\theta =35.3^\circ$ or negative corresponding $\theta =-54.7^\circ$ if the expectation of the heavy-quark spin–orbit interaction is positive or negative, respectively [22].

The $B_c \rightarrow D^{*0} l \nu$ [32] and $B_c \rightarrow D ll/ \nu \bar{\nu }$ [33] have been studied via three-point QCD sum rules (3PSR). In this work, we analyze the semileptonic $B_c \rightarrow D_1^0(2420[2430]) l \nu$ decays in 3PSR and heavy-quark effective theory (HQET). To this aim, we consider the structure of the $D_1^0$ meson in three conditions:

• 1. The $D_1^0$ meson as a pure state $(|c\bar{u}\rangle )$.

• 2. The $D_1^0$ meson as a mixture of two states of the $|^1P_1\rangle$ and $|^3P_1\rangle$ with a mixing angle $\theta$ [see Eq. (2)].

• 3. The $D_1^0$ meson as a combination of two $|^1P_1\rangle$ and $|^3P_1\rangle$ states with the mixing angle $\theta =35.3^\circ$ in the heavy-quark limit [see Eq. (3)].

Taking into account the gluon condensate corrections, as the important term of the non-perturbative part of the correlation function, the form factors of the $B_c \rightarrow D_1^0$ transition are obtained within 3PSR for the conditions 1, 2 and within the HQET approach for the condition 3. For the conditions 1 and 3, the form factors of the $B_c\rightarrow D_1^0(2420[2430])$ transitions are a function of the transferred momentum square $q^2$. So, we plot these form factors and decay widths of these decays with respect to $q^2$. Also the branching ratios for these cases are evaluated. But it should be remarked, when we consider the $D_1^0$ as a mixture of two states with mixing angle $\theta$ in the region $-180\le \theta \le 180$, that the transition form factors of the $B_c\rightarrow D_1^0(2420[2430])$ decays are functions of two variables, $\theta$ and $q^2$. Since the decay width of the $B_c\rightarrow D_1^0$ transition is related to the form factors, it is a function of the mixing angle $\theta$ and $q^2$, too. For a better analysis, we plot the form factors and the decay widths of the $B_c\rightarrow D_1^0(2420[2430])$ in three dimensions. In this case, the branching ratios are shown with respect to the mixing angle $\theta$. Detection of these channels and their comparison with the phenomenological models like QCD sum rules could give useful information as regards the structure of the $D_{1}^0$ meson and the unknown mixing angle $\theta$.

This paper is organized as follows. In Sect. 2, we calculate the form factors for the $B_c\rightarrow D_{1}^0$ transition in 3PSR for above conditions 1 and 2. In Sect. 3, the transition form factors are evaluated via HQET approach for condition 3. Finally, Sect. 4 is devoted to the numeric results and discussions.

2 Sum rules method

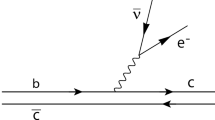
In this section, we study the transition form factors of the semileptonic $B_c\rightarrow D_1^0 l \nu$ decay by QCD sum rules mechanism. To this aim, first, we consider the $D_1^0$ meson as a pure state. The $B_c\rightarrow D_1^0 l \nu$ process is governed by the tree level $b\rightarrow u l \nu$ transition and $c$ quark is the spectator, at quark level (see Fig. 1).

Fig. 1

The bare-loop diagram for $B_c \rightarrow D_1^0 l \nu$ transition

The three-point correlation function is considered for the evaluation of the transition form factors in the framework of the 3PSR. The three-point correlation function is constructed from the vacuum expectation value of time ordered product of three currents as follows:

$$\begin{aligned}&\Pi _{\mu \nu } (p^2,p'^2,q^2) \nonumber \\&\quad = i^2 \int \mathrm{d}^4 x \mathrm{d}^4 y ~e^{+i p^\prime x - i p y}\left\langle 0 \left| \text{ T } \left\{ J^{D_1^0}_\nu (x) J^{W}_\mu (0) {J^{B_c}}^{\dagger }(y)\right\} \right| 0\right\rangle ,\nonumber \\ \end{aligned}$$

(4)

where $J^{D_1^0}_\nu (x)=\overline{c}\gamma _{\nu }\gamma _{5}u$ and $J^{B_{c}}(y)=\overline{c}\gamma _{5}b$ are the interpolating currents of the $D_1^0$ and $B_{c}$ mesons. $J_{\mu }^{W}=\overline{u}\gamma _{\mu }(1-\gamma _{5})b$ is the current of the weak transition.

We can obtain the correlation function of Eq. (4) in two respects. The phenomenological or physical part is calculated saturating the correlation by a tower of hadrons with the same quantum numbers as interpolating currents. The QCD or theoretical part, on the other side is obtained in terms of the quarks and gluons interacting in the QCD vacuum. To derive the phenomenological part of the correlation given in Eq. (4), two complete sets of intermediate states with the same quantum numbers as the currents $J_{D^0_1}$ and $J_{B_{c}}$ are inserted. This procedure leads to the following representations of the above-mentioned correlation:

$$\begin{aligned}&\Pi _{\mu \nu }(p^2,p'^2,q^2)\nonumber \\&\quad =\frac{\left\langle 0 {\mid } J_{\nu }^{ D_1^0}{\mid } D_1^0(p',{\varepsilon })\rangle \langle D_1^0(p',{\varepsilon }){\mid } J^{W}_{\mu }{\mid } B_{c}(p)\rangle \langle B_{c}(p){\mid } {J^{B_c}}^{\dag }{\mid } 0\right\rangle }{\left( p'^2-m_{D_1^0}^2\right) \left( p^2-m_{B_c}^2\right) }\nonumber \\&\quad \quad +\text{ higher } \text{ resonances } \text{ and } \text{ continuum } \text{ states }. \end{aligned}$$

(5)

The general expression for the hadronic matrix element of the weak current with the definition of the transition form factors is given by the formula:

$$\begin{aligned}&\langle D_1^0(p^{\prime },\varepsilon ){{\mid }}\overline{u}\gamma _{\mu }(1-\gamma _5) b{\mid } B_c(p)\rangle \nonumber \\&\quad =f^{'}_{V}(q^2)\varepsilon _{\mu \nu \alpha \beta } \varepsilon ^{*\nu }p^\alpha {p^{\prime }}^\beta \nonumber \\&\quad \quad -i[f^{'}_{0}(q^2)\varepsilon _{\mu }^{*} + f^{'}_{1}(q^2)(\varepsilon ^{*}p)P_{\mu } + f^{'}_{2}(q^2)(\varepsilon ^{*}p)q_{\mu }],\nonumber \\ \end{aligned}$$

(6)

where

$$\begin{aligned} f_{V}^{\prime }(q^2)= & {} \frac{2f_{V}(q^2)}{\left( m_{B_c}+m_{D_1^0}\right) }, \quad f_{0}^{\prime }(q^2)=f_{0}(q^2)\left( m_{B_c} +m_{D_1^0}\right) ,\nonumber \\ f_{1}^{\prime }(q^2)= & {} -\frac{f_{1}(q^2)}{\left( m_{B_c}+m_{D_1^0}\right) },\quad f_{2}^{\prime }(q^2)=-\frac{f_{2}(q^2)}{\left( m_{B_c}+m_{D_1^0}\right) }, \end{aligned}$$

(7)

and the $f_{V}(q^2)$, $f_{0}(q^2)$, $f_{1}(q^2)$, and $f_{2}(q^2)$ are the transition form factors, $P_{\mu }=(p+p^{\prime })_{\mu }$, $q_{\mu }=(p-p^{\prime })_{\mu }$, and $\varepsilon$ is the four-polarization vector of the $D_1^0$ meson. Also the following matrix elements are defined in the standard way in terms of the leptonic decay constants of the $D_1^0$ and $B_c$ mesons:

$$\begin{aligned} \left\langle 0 {\mid } J^{\nu }_{D_1^0} {\mid } D_1^0(p',{\varepsilon })\right\rangle= & {} f_{D_1^0}m_{D_1^0}\varepsilon ^{\nu },~~\langle 0 {\mid } J_{B_c}{\mid } B_{c}(p)\rangle \nonumber \\= & {} i\frac{f_{B_{c}}m_{B_{c}}^2}{m_{b}+m_{c}}, \end{aligned}$$

(8)

where $f_{D_1^0}$ and $f_{B_c}$ are the leptonic decay constants of $D_1^0$ and $B_c$ mesons, respectively. Using Eqs. (6) and (8) in Eq. (5) and performing summation over the polarization of the $D_1^0$ meson, we get the following result for the physical part:

$$\begin{aligned} \Pi _{\mu \nu }(p^2,p'^2,q^2)= & {} -\frac{f_{B_c}m_{B_c}^2}{(m_{b}+m_{c})}\frac{f_{D_1^0}m_{D_1^0}}{\left( p'^2-m_{D_1^0}^2\right) \left( p^2-m_{B_c}^2\right) }\nonumber \\&\times [if'_V(q^2)\varepsilon _{\mu \nu \alpha \beta }p^{\alpha }p'^{\beta }+f'_{0}(q^2)g_{\mu \nu } \nonumber \\&+ f'_{1}(q^2)P_{\mu }p_{\nu } +f'_{2}(q^2)q_{\mu }p_{\nu }]\nonumber \\&+\text{ excited } \text{ states. } \end{aligned}$$

(9)

The coefficients of the Lorentz structures $i\epsilon _{\mu \nu \alpha \beta }p^{\alpha }p^{'\beta }$, $g_{\mu \nu }$, $P_{\mu }p_{\nu }$, and $q_{\mu }p_{\nu }$ in the correlation function $\Pi _{\mu \nu }$ will be chosen in determination of the form factors $f_{V}(q^2)$, $f_{0}(q^2)$, $f_{1}(q^2)$, and $f_{2}(q^2)$, respectively. So the Lorentz structures in the correlation function can be written down as

$$\begin{aligned} \Pi _{\mu \nu }(p^2,p'^2,q^2)= & {} i~\Pi _{V}\varepsilon _{\mu \nu \alpha \beta }p^{\alpha }p'^{\beta }+\Pi _{0}g_{\mu \nu }\nonumber \\&+\,\Pi _{1}P_{\mu }p_{\nu }+\Pi _{2}q_{\mu }p_{\nu }, \end{aligned}$$

(10)

where each $\Pi _{i}$ function is defined in terms of the perturbative and non-perturbative parts as

$$\begin{aligned} \Pi _{i}(p^2,p'^2,q^2)= & {} \Pi _{i}^{\mathrm{per}}(p^2,p'^2,q^2)\nonumber \\&+\,\Pi _{i}^{\mathrm{nonper}}(p^2,p'^2,q^2). \end{aligned}$$

(11)

With the help of the operator product expansion, in the deep Euclidean region where $p^2\ll (m_b+m_c)^2$ and $p'^2\ll m_c^2$, the vacuum expectation value of the expansion of the correlation function in terms of the local operators is written as follows [32, 34]:

$$\begin{aligned} \Pi _{\mu \nu } (p^2,p'^2,q^2)= & {} (C_0)_{\mu \nu } + (C_3)_{\mu \nu }\langle \bar{q} q \rangle + (C_4)_{\mu \nu } \langle G^2 \rangle \nonumber \\&+\,(C_5)_{\mu \nu } \langle \bar{q}\sigma _{\alpha \beta } G^{\alpha \beta } q \rangle \nonumber \\&+\, (C_6)_{\mu \nu } \langle \bar{q} \Gamma q \bar{q} \Gamma ^\prime q \rangle , \end{aligned}$$

(12)

where $(C_i)_{\mu \nu }$ are the Wilson coefficients, $G_{\alpha \beta }$ is the gluon field strength tensor, $\Gamma$ and $\Gamma ^{'}$ are the matrices appearing in the calculations. The non-perturbative part contains the quark and gluon condensate diagrams. We consider the condensate terms of dimension $3, 4$, and $5$. It is found that the heavy-quark condensate contributions are suppressed by inverse of the heavy-quark mass and can be safely omitted. The light $u$ quark condensate contribution is zero after applying the double Borel transformation with respect to the both variables $p^2$ and $p'^2$, because only one variable appears in the denominator. Therefore in this case, we consider the two gluon condensate diagrams with mass dimension $4$ as an important term of the non-perturbative corrections, only, i.e.,

$$\begin{aligned} \Pi _i(p^2,p'^2,q^2)= & {} \Pi _i^{\mathrm{per}}(p^2,p'^2,q^2)\nonumber \\&+\, \Pi _i^{\langle G^2 \rangle } (p^2,p'^2,q^2) \left\langle \frac{\alpha _s}{\pi } G^2\right\rangle . \end{aligned}$$

(13)

The diagrams for contribution of the gluon condensates are depicted in Fig. 2. To obtain the contributions of these diagrams, the Fock–Schwinger fixed-point gauge, $x^\mu A_\mu ^a=0$, are used; here $A_\mu ^a$ is the gluon field. The procedure of the evaluation of such as diagrams in Fig. 2 has been discussed in Ref. [32] completely.

Fig. 2

Contribution of two gluon condensates for $B_c \rightarrow D^0_1$ transition

Using the double dispersion representation, the bare-loop contribution is determined:

$$\begin{aligned} \Pi _i^{\mathrm{per}}= & {} - \frac{1}{(2 \pi )^2} \int \int \frac{\rho _i^{\mathrm{per}}(s,s^\prime , q^2)}{(s-p^2) (s^\prime - p^{\prime 2})} \mathrm{d}s \mathrm{d}s^\prime \nonumber \\&+\, \text{ subtraction } \text{ terms }. \end{aligned}$$

(14)

By replacing the propagators with the Dirac-delta functions (Cutkosky rules) we have

$$\begin{aligned} \frac{1}{k^2-m^2} \rightarrow -2i\pi \delta (k^2-m^2), \end{aligned}$$

(15)

and the spectral densities $\rho _i^{\mathrm{per}}(s,s^{'},q^2)$ are found as

$$\begin{aligned} \rho _V^{\mathrm{per}}= & {} \frac{N_c}{\lambda ^{1/2}(s,s',q^2)}~\left\{ \frac{(2s'\Delta -\Delta 'u)(m_b-m_c)}{\lambda (s,s',q^2)}-\frac{(2s'\Delta -\Delta 'u)(m_{u}+m_c)}{\lambda (s,s',q^2)}-m_c\right\} ,\nonumber \\ \rho _0^{\mathrm{per}}= & {} \frac{-N_c}{2\lambda ^{1/2}(s,s',q^2)}~\left\{ \Delta (m_c+m_{u})-\Delta ^{\prime }(m_b-m_c)+2 m_c^2(m_b-m_c-m_{u})\right. \nonumber \\&\left. +\frac{2(4ss'm_c^2-s\Delta '^2-s'\Delta ^2-u^2m_c^2+u\Delta \Delta ')(m_b-m_c)}{\lambda (s,s',q^2)}+m_c(2m_b m_{u}-u)\right\} ,\nonumber \\ \rho _1^{\mathrm{per}}= & {} \frac{N_c}{2\lambda ^{1/2}(s,s',q^2)}\left\{ \frac{(2s'\Delta -\Delta 'u)(m_b-3m_c)}{\lambda (s,s',q^2)} -\frac{(2s\Delta '-\Delta u)(m_c+m_{u})}{\lambda (s,s',q^2)}\right. \nonumber \\&-\frac{2(8ss'^2m_c^2-2ss'\Delta '^2-6s'^2\Delta ^2-2u^2s'm_c^2+6s'u\Delta \Delta '-u^2\Delta '^2)(m_b-m_c)}{\lambda ^2(s,s',q^2)}\nonumber \\&\left. +\frac{2(4ss'um_c^2+4ss'\Delta \Delta '-3su\Delta '^2-3u\Delta ^2s'-u^3m_c^2+2u^2\Delta \Delta ')(m_b-m_c)}{\lambda ^{2}(s,s',q^2)}-m_c\right\} ,\nonumber \\ \rho _2^{\mathrm{per}}= & {} \frac{N_c}{2\lambda ^{1/2}(s,s',q^2)}\left\{ \frac{(2s\Delta '-\Delta u)(m_c+m_{u})}{\lambda (s,s',q^2)}-\frac{(2s'\Delta -\Delta 'u)(m_b+m_c)}{\lambda (s,s',q^2)}\right. \nonumber \\&-\left. \frac{2(8ss'^2m_c^2-2ss'\Delta '^2-6s'^2\Delta ^2-2u^2s'm_c^2+6s'u\Delta \Delta '-u^2\Delta '^2)(m_b-m_c)}{\lambda ^2(s,s',q^2)}\right. \nonumber \\&-\left. \frac{2[4ss'um_c^2+4ss'\Delta \Delta '-3su\Delta '^2-3u\Delta ^2s'-u^3m_c^2+2u^2\Delta \Delta '](m_b-m_c)}{\lambda ^{2}(s,s',q^2)}+m_c\right\} , \end{aligned}$$

(16)

where $\lambda (a,b,c)=a^2+b^2+c^2-2ac-2bc-2ab$. The $N_c=3$ is the color factor, $u=s+s^\prime -q^2$, $\Delta =s+m_c^2-m_b^2$, and $\Delta '=s^\prime +m_c^2-m^2_{u}$.

For the heavy quarkonium $b\bar{c}$, where the relative velocity of quark movement is small, an essential role is taken by the Coulomb-like $\alpha _s/v$-corrections [35]. It leads to the finite renormalization for $\rho _i^{\mathrm{per}}$, so that

$$\begin{aligned} \rho ^{c}_i=\mathcal{C} \rho _i^{\mathrm{per}}, \end{aligned}$$

(17)

with

$$\begin{aligned} \mathcal{C}^2=\frac{4\pi \alpha _s^\mathcal{C}}{3v}\,\frac{1}{\displaystyle 1-\exp \left( -\frac{4\pi \alpha _s^\mathcal{C}}{3v}\right) }, \end{aligned}$$

(18)

where $\alpha _s^\mathcal{C}$ is the coupling constant of effective coulomb interactions. Also $v$ is the relative velocity of quarks in the $b\bar{c}$-system,

$$\begin{aligned} v=\sqrt{1-\frac{4 m_b m_c}{p^2-(m_b-m_c)^2}}. \end{aligned}$$

(19)

The value of $\alpha _s^\mathcal{C}$ for $B_c$ meson is [35]

$$\begin{aligned} \alpha _s^\mathcal{C}[b\bar{c}]=0.45. \end{aligned}$$

(20)

By performing the double Borel transformations over the variables $p^2$ and $p'^2$ on the physical parts of the correlation functions and bare-loop diagrams and also equating two representations of the correlation functions, the sum rules for the $f'_i(q^2)$ are obtained:

$$\begin{aligned}&f'_{i}(q^2) = \frac{(m_b+m_c)}{f_{B_c} m_{B_c}^2 f_{D_1^0}m_{D_1^0}}~ e^{\frac{m_{B_c}^2}{M_1^2}}e^{\frac{m_{D_1}^2}{M_2^2}} \nonumber \\&\quad \times \left\{ -\frac{1}{4 \pi ^2} \int _{m_b^2}^{s_0^\prime }\mathrm{d}s^\prime \int _{s_L}^{s_0} \rho _{i}^{c} (s,s^\prime ,q^2)e^\frac{-s}{M_1^2} e^\frac{-s^{'}}{M_2^2}\right. \nonumber \\&\quad - \left. iM^{2}_{1}M^{2}_{2}\left\langle \frac{\alpha _s}{\pi } G^2 \right\rangle \frac{C_i^4}{6} \right\} , \end{aligned}$$

(21)

where $i=V,0,1$ and $2$, $s_0$, and $s_0^{'}$ are the continuum thresholds in the pseudoscalar $B_c$ and axial vector $D_1^0$ channels, respectively, and the lower bound integration limit of $s_{L}$ is as follows:

$$\begin{aligned} s_L= & {} \frac{(m_c^2+q^2-m_b^2-s^\prime ) (m_b^2 s^\prime -m_c^2 q^2)}{(m_b^2-q^2) (m_c^2-s^\prime )}. \end{aligned}$$

The explicit expressions for $C_i^{4}$ are presented in Appendix A.

Now, we would like to consider the form factors related to the $B_c\rightarrow D_1^0$ transition when the $D_1^0$ meson is a mixture of the two $|^1P_1\rangle$ and $|^3P_1\rangle$ states. To this aim, first the $f_i^{'B_c\rightarrow D_11(2)}(q^2)$ are obtained from the above equations, replacing the $f_{D^0_1}$ by decay constant $f_{{D_1}1(2)}$, and $m_{D^0_1}$ with $m_{{D_1}1(2)}$, i.e.,

$$\begin{aligned} f_{i}^{'B_c\rightarrow D_11(2)}(q^2)= & {} -\frac{(m_b+m_c)}{f_{B_c} m_{B_c}^2f_{D_11(2)} m_{D_11(2)}} e^\frac{m_{B_c}^2}{M_1^2}e^\frac{m_{D_11(2)}^2}{M_2^2}\nonumber \\&\times \left\{ -\frac{1}{4 \pi ^2}\int _{m_c^2}^{s_0^\prime } \mathrm{d}s^\prime \int _{s_L}^{s_0} \rho _{i}^{c}(s,s^\prime ,q^2) e^\frac{-s}{M_1^2}e^\frac{-s^{'}}{M_2^2}\right. \nonumber \\&-\left. iM^{2}_{1}M^{2}_{2} \left\langle \frac{\alpha _s}{\pi } G^2\right\rangle \frac{C_{i}^{4}}{6} \right\} , \end{aligned}$$

(22)

where $f_{D_11} = (183\pm 25)$ MeV, and $f_{D_12} = (89\pm 7)$ MeV [29]. Then by straightforward calculations, the $f_{i}^{(2420)}(q^2)$ form factors of $B_{c}\rightarrow D^0_1(2420)$ transition are found as follows:

$$\begin{aligned} f_0^{(2420)}(q^2)= & {} \left( \frac{m_{B_c}+m_{D_11}}{m_{B_c}+m_{D^0_1}}\right) f_0^{B_{c}\rightarrow D_11}(q^2)~\sin \theta \nonumber \\&+\left( \frac{m_{B_c}+m_{D_12}}{m_{B_c}+m_{D^0_1}}\right) f_0^{B_{c}\rightarrow D_12}(q^2)~\cos \theta ,\nonumber \\ f_{i'}^{(2430)}(q^2)= & {} \left( \frac{m_{B_c}+m_{D^0_1}}{m_{B_c}+m_{D_11}}\right) ~f_{i'}^{B_{c}\rightarrow D_11}(q^2)~\sin \theta \nonumber \\&+\left( \frac{m_{B_c}+m_{D^0_1}}{m_{B_c}+m_{D_12}}\right) ~f_{i'}^{B_{c}\rightarrow D_12}(q^2)~\cos \theta ,\nonumber \\ \end{aligned}$$

(23)

where $i'=V, 1, 2$. Note that the $f_{i}^{(2430)}(q^2)$ form factors of the $B_{c}\rightarrow D^0_1(2430)$ decay are obtained from the above equations by replacing the $\sin {\theta }\rightarrow \cos {\theta }$ and $\cos {\theta }\rightarrow -\sin {\theta }$.

3 Heavy-Quark Effective Theory

In this section, we apply the HQET to analyze the form factors of $B_c\rightarrow D_1^0 l \nu$ calculated by 3PSR. As mentioned in the introduction, in the heavy-quark mass limit, when $m_c\rightarrow \infty$, the $D_1^0$ meson can be considered as Eq. (3). Therefore, to estimate the $f_i^{\mathrm{HQ}}$ form factors in this approach, first, we present the dependence of the $f_i^{\mathrm{HQ}(B_c\rightarrow D_1k)}$ $(k=1, 2)$ on $y$ where

$$\begin{aligned} y=\nu \nu '=\frac{m_{B_{c}}^2+m_{D_1k}^2-q^2}{2m_{B_{c}}m_{D_1k}}. \end{aligned}$$

(24)

Here, $\nu$ and $\nu '$ are the four velocities of $B_c$ and $D_1k$ mesons, respectively (for some details see Refs. [36, 37]). After some complicated calculations, the y-dependent expressions of the $f_i^{\mathrm{HQ}(B_c\rightarrow D_1k)}(y)$ are obtained as follows:

$$\begin{aligned} f_{V}^{\mathrm{HQ}(B_c\rightarrow D_1k)}(y)= & {} \frac{1}{\hat{f}_{B_{c}}\hat{f}_{D_1k}}e^{\frac{\Lambda }{T_{1}}}e^{\frac{\overline{{\Lambda }}}{T_{2}}}\left\{ \frac{1}{{( 1+\sqrt{Z} ){Z}^{\frac{7}{4}}\sqrt{{\frac{-1+{y}^{2}}{Z}}}}}\right. \nonumber \\&\times [-3+ 3( 3y+1 ) \sqrt{Z}-6\,(y^2+y ) Z] \nonumber \\&\times \frac{-1}{(2\pi )^2}\int _{0}^{\nu _{0}}\mathrm{d}\nu \int _{0}^{\nu _{0}^{^{\prime }}}\mathrm{d}{\nu }^{^{\prime }}e^{-\frac{\nu }{2T_{1}}}e^{-\frac{{\nu }^{_{^{\prime }}}}{2T_{2}}}\theta \nonumber \\&\times (2y\nu \nu ^{^{\prime }}-\nu ^{2}-{{\nu }^{_{^{\prime }}}}^{2})\nonumber \\&+\left( i~\frac{2Z^{\frac{1}{4}}}{3(1+\sqrt{Z})}T_1T_2~\left\langle \frac{\alpha _{s}}{\pi }G^{2}\right\rangle \right) \nonumber \\&\times \left. \lim _{m_{b}\rightarrow \infty }C_{V}^{\mathrm{HQET}}\right\} , \end{aligned}$$

(25)

$$\begin{aligned} f_{0}^{\mathrm{HQ}(B_c\rightarrow D_1k)}(y)= & {} \frac{1}{\hat{f}_{B_{c}}\hat{f}_{D_1k}}e^{\frac{\Lambda }{T_{1}}}e^{\frac{\overline{{\Lambda }}}{T_{2}}}\left\{ \frac{1}{{2( 1+\sqrt{Z} )^{3}{Z}^{\frac{7}{4}}\sqrt{{ \frac{-1+{y}^{2}}{Z}}}}}\right. \nonumber \\&\times [ -3-3(4y-1)\sqrt{Z} -6(3y^2-2y-1)Z\nonumber \\&+12(y^3+y^2-y)Z^{\frac{3}{2}}] \nonumber \\&\times \frac{-1}{(2\pi )^2}\int _{0}^{\nu _{0}}\mathrm{d}\nu \int _{0}^{\nu _{0}^{^{\prime }}}\mathrm{d}{\nu }^{^{\prime }}e^{-\frac{\nu }{2T_{1}}}e^{-\frac{{\nu }^{_{^{\prime }}}}{2T_{2}}}\theta \nonumber \\&\times (2y\nu \nu ^{^{\prime }}-\nu ^{2}-{{\nu }^{_{^{\prime }}}}^{2})\nonumber \\&+\left( i~\frac{2Z^{\frac{5}{4}}}{3{(1+\sqrt{Z})^{3}}}T_1T_2~\left\langle \frac{\alpha _{s}}{\pi }G^{2}\right\rangle \right) \nonumber \\&\times \left. \lim _{m_{b}\rightarrow \infty }C_{0}^{\mathrm{HQET}}\right\} , \end{aligned}$$

(26)

$$\begin{aligned} f_{1}^{\mathrm{HQ}(B_c\rightarrow D_1k)}(y)= & {} \frac{1}{\hat{f}_{B_{c}}\hat{f}_{D_1k}}e^{\frac{\Lambda }{T_{1}}}e^{\frac{\overline{{\Lambda }}}{T_{2}}}\left\{ \frac{1}{4(1+\sqrt{Z})({\frac{-1+{y}^{2}}{Z}})^{\frac{3}{2}}{Z}^{{\frac{15}{4}}}}\right. \nonumber \\&\times [-9+9(5y+1)\sqrt{Z}-3(26y^2+15y-2)Z \nonumber \\&+6(9y^3+11y^2-3y+1){Z}^{\frac{3}{2}}\nonumber \\&-12(y^4+2y^3-y^2+y){Z}^{2}] \nonumber \\&\times \frac{-1}{(2\pi )^2}\int _{0}^{\nu _{0}}\mathrm{d}\nu \int _{0}^{\nu _{0}^{^{\prime }}}\mathrm{d}{\nu }^{^{\prime }}e^{-\frac{\nu }{2T_{1}}}e^{-\frac{{\nu }^{_{^{\prime }}}}{2T_{2}}}\theta \nonumber \\&\times (2y\nu \nu ^{^{\prime }}-\nu ^{2}-{{\nu }^{_{^{\prime }}}}^{2})\nonumber \\&+\left( i~\frac{2Z^{\frac{1}{4}}}{3{(1+\sqrt{Z})}}T_1T_2~\left\langle \frac{\alpha _{s}}{\pi }G^{2}\right\rangle \right) \nonumber \\&\times \left. \lim _{m_{b}\rightarrow \infty }C_{1}^{\mathrm{HQET}}\right\} , \end{aligned}$$

(27)

$$\begin{aligned} f_{2}^{\mathrm{HQ}(B_c\rightarrow D_1k)}(y)= & {} \frac{1}{\hat{f}_{B_{c}}\hat{f}_{D_1k}}e^{\frac{\Lambda }{T_{1}}}e^{\frac{\overline{{\Lambda }}}{T_{2}}}\left\{ \frac{1}{4(1+\sqrt{Z})({\frac{-1+{y}^{2}}{Z}})^{\frac{3}{2}}{Z}^{{\frac{15}{4}}}}\right. \nonumber \\&\times [-9+9(3y+1)\sqrt{Z}-9(2y^2+3y-2)Z \nonumber \\&-6(y^3-y^2+5y+1){Z}^{\frac{3}{2}}\nonumber \\&+12(y^4+2y^3-y^2+y){Z}^{2} ] \nonumber \\&\times \frac{-1}{(2\pi )^2}\int _{0}^{\nu _{0}}\mathrm{d}\nu \int _{0}^{\nu _{0}^{^{\prime }}}\mathrm{d}{\nu }^{^{\prime }}e^{-\frac{\nu }{2T_{1}}}e^{-\frac{{\nu }^{_{^{\prime }}}}{2T_{2}}}\theta \nonumber \\&\times (2y\nu \nu ^{^{\prime }}-\nu ^{2}-{{\nu }^{_{^{\prime }}}}^{2})\nonumber \\&+\left( i~\frac{2Z^{\frac{1}{4}}}{3{(1+\sqrt{Z})}}T_1T_2~\left\langle \frac{\alpha _{s}}{\pi }G^{2}\right\rangle \right) \nonumber \\&\times \left. \lim _{m_{b}\rightarrow \infty }C_{2}^{\mathrm{HQET}}\right\} . \end{aligned}$$

(28)

In these heavy-quark limit expressions $\Lambda =m_{B_c}-m_{b}$, $\bar{\Lambda }=m_{D_1k}-m_c$, $\sqrt{Z}=y+\sqrt{y^2-1}$, $\hat{f}_{B_c}=\sqrt{m_b}f_{B_c}$, $\hat{f}_{D_1k}=\sqrt{m_c}f_{D_1k}$. The continuum thresholds $\nu _{0}$, $\nu _{0}^{'}$, and integration variables $\nu$, $\nu ^{'}$ are defined as

$$\begin{aligned} \nu _{0}=\frac{s_{0}-m_{b}^2}{m_{b}},\quad \nu '_{0}=\frac{s'_{0}-m_{c}^2}{m_{c}}, \end{aligned}$$

(29)

$$\begin{aligned} \nu =\frac{s-m_{b}^2}{m_{b}},\quad \nu '=\frac{s'-m_{c}^2}{m_{c}}. \end{aligned}$$

(30)

Also we apply $T_1=M_1^2/2m_b$, $T_2=M_2^2/2m_c$, and $m_c=m_b/\sqrt{Z}$.

The explicit expressions of the coefficients $C_{i}^{\mathrm{HQET}}$ are given in Appendix B. In the expressions of the $C_{i}^{\mathrm{HQET}}$, $\bar{I}_0(a,b,c)$, $\bar{I}_{1(2)}(a,b,c)$, $\bar{I}_j(a,b,c)$; $j=3,4,5$, and $\bar{I}_6(a,b,c)$ are defined as

$$\begin{aligned}&\bar{I}_0(a,b,c) = \frac{(-1)^{a+b+c}}{16\pi ^2\,\Gamma (a)\Gamma (b) \Gamma (c)} \left( \frac{1}{\sqrt{Z}}\right) ^{2-a-c}\nonumber \\&\qquad \qquad \quad \qquad \times \,(2m_b)^{4-2a-b-c}~T_1^{2-a-b} ~T_2^{2-a-c}\nonumber \\&\qquad \qquad \quad \qquad \times \,\mathcal {U}_0^{\mathrm{HQET}}(a+b+c-4,1-c-b), \nonumber \\&\bar{I}_{1(2)}(a,b,c) = i \frac{(-1)^{a+b+c+1}}{16\pi ^2\,\Gamma (a) \Gamma (b)\Gamma (c)}\left( \frac{1}{\sqrt{Z}}\right) ^{4-a-c-1(2)}\nonumber \\&\quad \qquad \qquad \quad \qquad \times \,(2m_b)^{5-2a-b-c}~T_1^{1-a-b+1(2)}~T_2^{4-a-c-1(2)} \,\nonumber \\&\quad \qquad \quad \qquad \qquad \times \,\mathcal {U}_0^{\mathrm{HQET}}(a+b+c-5,1-c-b), \nonumber \\&\bar{I}_j(a,b,c) = i \frac{(-1)^{a+b+c}}{16\pi ^2\,\Gamma (a) \Gamma (b) \Gamma (c)}\left( \frac{1}{\sqrt{Z}}\right) ^{7-a-c-j}\nonumber \\&\qquad \quad \qquad \qquad \times \,(2m_b)^{6-2a-b-c}~T_1^{-a-b-1+j}~T_2^{7-a-c-j} \,\nonumber \\&\qquad \quad \qquad \qquad \times \,\mathcal {U}_0^{\mathrm{HQET}}(a+b+c-6,1-c-b), \nonumber \\&\bar{I}_6(a,b,c) = i \frac{(-1)^{a+b+c+1}}{32\pi ^2\,\Gamma (a) \Gamma (b) \Gamma (c)}\left( \frac{1}{\sqrt{Z}}\right) ^{3-a-c}\nonumber \\&\qquad \quad \qquad \qquad \times \,(2m_b)^{6-2a-b-c}~T_1^{3-a-b}~T_2^{3-a-c} \,\nonumber \\&\qquad \quad \qquad \qquad \times \,\mathcal {U}_0^{\mathrm{HQET}}(a+b+c-6,2-c-b). \end{aligned}$$

(31)

The function $\mathcal {U}_0^{\mathrm{HQET}}(m,n)$ takes the following form:

$$\begin{aligned} \mathcal {U}_0^{\mathrm{HQET}}(m,n)= & {} \int _{0}^{\infty }\!(2m_b)^{m}~\left( \frac{x}{2m_b}+T_1+\frac{T_2}{\sqrt{Z}}\right) ^{m}~x^{n}\nonumber \\&\times \left[ -\frac{\overline{B}_{-1}}{x}-\overline{B}_{0}-\overline{B}_{1}x\right] {\mathrm{d}x}, \end{aligned}$$

(32)

with

$$\begin{aligned}&\displaystyle \overline{B}_{-1}=\frac{\sqrt{Z}}{T_1T_2}~\left[ \frac{mb^2}{Z}~T_2^2+\frac{1}{\sqrt{Z}}T_1T_2(m_b^2-q^2)\right] ,\\&\displaystyle \overline{B}_{0}=\frac{\sqrt{Z}}{2m_bT_1T_2}~\left[ m_c^2T_1+\frac{T_2}{\sqrt{Z}}(m_b^2+m_c^2)\right] ,\\&\displaystyle \overline{B}_{1}=\frac{1}{4\sqrt{Z}T_1T_2}. \end{aligned}$$

(33)

Then by considering $D_1^0$ meson as a combination of the two states $|D_1k\rangle$ $(k=1, 2)$ the $f_i^{\mathrm{HQ}(2420)}(y)$ and $f_i^{\mathrm{HQ}(2430)}(y)$ form factors for the $B_c\rightarrow D_1^0(2420) l \nu$ and $B_c\rightarrow D_1^0(2430) l \nu$ decays are obtained as

$$\begin{aligned} f_i^{\mathrm{HQ}(2420)}(y)= & {} \sqrt{\frac{1}{3}}f_0^{\mathrm{HQ}(B_{c}\rightarrow D_11)}(y)+\sqrt{\frac{2}{3}}f_0^{\mathrm{HQ}(B_{c}\rightarrow D_12)}(y),\nonumber \\ f_{i}^{\mathrm{HQ}(2430)}(y)= & {} \sqrt{\frac{2}{3}}~f_{i'}^{\mathrm{HQ}(B_{c}\rightarrow D_11)}(y)-\sqrt{\frac{1}{3}}~f_{i'}^{\mathrm{HQ}(B_{c}\rightarrow D_12)}(y),\nonumber \\ \end{aligned}$$

(34)

where $i=V, 0, 1, 2$.

4 Numerical Analysis

Now, we present our numerical analysis of the form factors $f_{i}(q^2)$ $(i=V, 0, 1, 2)$ via 3PSR and HQET. From the sum rules expressions of the form factors, it is clear that the main input parameters entering the expressions are gluon condensates, element of the CKM matrix $V_{ub}$, leptonic decay constants $f_{B_c}$, $f_{D_{1}^0}$ (see Table 3), $f_{D_{1}1}$, and $f_{D_{1}2}$, Borel parameters $M_{1}^2$ and $M_{2}^2$ as well as the continuum thresholds $s_{0}$ and $s'_{0}$.

Table 3 Input values in numerical calculations

The sum rules for the form factors contain also four auxiliary parameters: Borel mass squares $M_{1}^2$ and $M_{2}^2$ and continuum thresholds $s_{0}$ and $s'_{0}$. These are not physical quantities, so the form factors as physical quantities should be independent of them. The parameters $s_0$ and $s_0^\prime$, which are the continuum thresholds of $B_c$ and $D_{1}^0$ mesons, respectively, are determined from the condition that guarantees the sum rules to practically be stable in the allowed regions for $M_1^2$ and $M_2^2$. The values of the continuum thresholds calculated from the two-point QCD sum rules are taken to be $s_0=$ (45–50) $\mathrm{GeV}^2$ [41] and $s_0^\prime =$ (6–8) $\mathrm{GeV}^2$ [42]. We search for the intervals of the Borel mass parameters so that our results are almost insensitive to their variations. One more condition for the intervals of these parameters is the fact that the aforementioned intervals must suppress the higher states, continuum, and contributions of the highest-order operators. In other words, the sum rules for the form factors must converge (for more details, see [43]). As a result, we get $10~{\mathrm{GeV}}^{2}\le M_{1}^{2} \le 25\,{\mathrm{GeV}}^2$ and $7\,{\mathrm{GeV}}^2\le M_{2}^{2}\le 13\,{\mathrm{GeV}}^2$. To show how the form factors depend on the Borel mass parameters, for example, we depict the variations of the form factors for $B_{c}\rightarrow D_{1}^0(2420)$ at $q^{2} = 0$ with respect to the variations of the $M_1^2$ and $M_2^2$ parameters in their working regions in Fig. 3. From these figures, it is revealed that the form factors weakly depend on these parameters in their working regions.

Fig. 3

The dependence of the transition form factors on the Borel parameters for the $B_c\rightarrow D_{1}^0(2420)$ transition

For an analysis of the form factors of the semileptonic $B_c\rightarrow D_1^0(2420[2430]) l \nu$ decays, first, we consider the $D_1^0$ meson as a pure state, i.e., $|c\bar{u}\rangle$ and analyze the form factors and the value of the branching ratios of the $B_c\rightarrow D_1^0(2420[2430])$ transitions in 3PSR. Then the form factors, decay widths, and branching ratios of these decays are plotted when the $D_1^0$ meson is a combination of two states with mixing angle $\theta$. Finally, considering the $D_1^0$ meson as Eq. (3), we investigate and estimate this mentioned physical quantities via the HQET approach in $m_b(m_c)\rightarrow \infty$ limit. Therefore, there are three conditions for the study of the form factors of the $B_c\rightarrow D_1^0(2420[2430]) l \nu$ decays, related to the structure of the $D_1^0$ meson as follows.

4.1 $\bullet$ Pure state or $|c\bar{u}\rangle$ state

If the $D_{1}^0$ meson is the pure $|c\bar{u}\rangle$ state, using Eqs. (7) and (21), the values of the form factors at $q^2=0$ are presented in Table 4. In this case, the values of the transition form factors at $q^2=0$ for $B_c\rightarrow D_1^0(2420) l \nu$ decay are the same as those for $B_c\rightarrow D_1^0(2430) l \nu$. Our calculations show that the other physical quantities of these decays are nearly the same.

Table 4 The value of the form factors of the conventional $B_{c}\rightarrow D_{1}^0(2420,2430)$ transitions at $q^2=0$, $M_1^2=15\,\mathrm{GeV}^2$, and $M_2^2=8\,\mathrm{GeV}^2$

The sum rules for the form factors are truncated at about $9\,\mathrm{GeV}^2$, so to extend our results to the full physical region, we look for a parametrization of the form factors in such a way that in the region $0 \le q^2 \le (m_{B_c}-m_{D_{1}^0})^2\,\mathrm{GeV}^2$, this parametrization coincides with the sum rules predictions. Our numerical calculations show that the sufficient parametrization of the form factors with respect to $q^2$ is as follows [44]:

$$\begin{aligned} f_{i}(q^2)=\frac{a}{\left( 1- \frac{q^2}{m^{2}_{\mathrm{fit}}}\right) }+ \frac{b}{\left( 1-\frac{q^2}{m^{2}_{\mathrm{fit}}}\right) ^2}. \end{aligned}$$

(35)

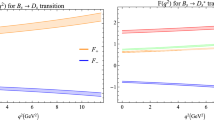
The values of the parameters $a, b$, and $m_{\mathrm{fit}}$ are given in Table 5. Figure 4 depicts the fit function of the form factors $f_i^{(2420,2430)}(q^2)$ $(i=V, 0, 1, 2)$ of the $B_c\rightarrow D^0_1(2420,2430) l\nu$ decays with respect to the transferred momentum square $q^2$. This figure also contains the form factors obtained via 3PSR [see Eq. (21)]. The form factors and their fit functions coincide well in the interval $0 \le q^2 \le 9\, \mathrm{GeV}^2$.

Fig. 4

The dependence of the form factors as well as the fit parametrization of the form factors on $q^2$. The small boxes correspond to the form factors, the solid lines belong to the fit parametrization of the form factors

Table 5 Parameters appearing in the fit function for the form factors of the $B_{c}\rightarrow D_{1}(2420,2430)$ at $M_1^2=15\,\mathrm{GeV}^2$ and $M_2^2=8\,\mathrm{GeV}^2$

By using the expressions for the form factors, the differential decay width ${\mathrm{d}\Gamma }/{\mathrm{d}q^2}$ for the process $B_c\rightarrow D_1^0 l \nu$ in terms of $H_{i}$ can be presented as follows:

$$\begin{aligned}&\frac{\mathrm{d}\Gamma _{\pm }(B_{c}\rightarrow D_1^0 l \nu )}{\mathrm{d}q^2}\nonumber \\&\quad =\frac{G^{2}\left| V_{ub}\right| ^{2}}{192\pi ^{3}m^3_{B_c}}~q^{2}\lambda ^{1/2}\left( m^2_{B_c},m^2_{D_1^0},q^{2}\right) \left| H_{\pm }\right| ^{2}, \nonumber \\&\frac{\mathrm{d}\Gamma _{0}(B_{c}\rightarrow D_1^0 l \nu )}{\mathrm{d}q^2}\nonumber \\&\quad =\frac{G^{2}\left| V_{ub}\right| ^{2}}{192\pi ^{3}m^3_{B_c}}~q^{2}\lambda ^{1/2}\left( m^2_{B_c},m^2_{D_1^0},q^{2}\right) \left| H_{0}\right| ^{2},\nonumber \\&\frac{\mathrm{d}\Gamma _{\mathrm{tot}}(B_{c}\rightarrow D_1^0 l \nu )}{\mathrm{d}q^2}\nonumber \\&\quad =\frac{\mathrm{d}\Gamma _{\pm }(B_{c}\rightarrow D_1^0 l\nu )}{\mathrm{d}q^2}+\frac{\mathrm{d}\Gamma _{0}(B_{c}\rightarrow D_1^0 l\nu )}{\mathrm{d}q^2}; \end{aligned}$$

(36)

$H_{\pm }$ and $H_{0}$ are defined as

$$\begin{aligned} H_{\pm }(q^{2})= & {} \left( m_{B_c}+m_{D_1^0}\right) f_{0}(q^{2})\mp \frac{\lambda ^{1/2}\left( m^2_{B_c},m^2_{D_1^0},q^{2}\right) }{m_{B_c}+m_{D_1^0}}f_{V}(q^{2}), \\ H_{0}(q^{2})= & {} \frac{1}{2m_{D_1^0}\sqrt{q^2}}\left[ \left( m^2_{B_c}-m^2_{D_1^0}-q^{2}\right) \left( m_{B_c}+m_{D_1^0}\right) f_{0}(q^{2})\right. \\&-\left. \frac{\lambda \left( m^2_{B_c},m^2_{D_1^0},q^{2}\right) }{m_{B_c}+m_{D_1^0}}f_{1}(q^{2})\right] , \end{aligned}$$

where $\pm , 0$ refer to the $D_1^0$ helicities. Note that in the limit of vanishing lepton mass (in our case the electron and muon) the $f_2(q^2)$ form factor does not contribute to the decay width formula.

To calculate the branching ratios of the $B_c\rightarrow D_{1}(2420,2430)l \nu$ decays, we integrate Eq. (36) over $q^2$ in the whole physical region and use the total mean life time $\tau _{B_c}=(0.46\pm 0.07)$ ps. Our numerical analysis shows that the contribution of the non-perturbative part (the gluon condensate diagrams) is about $13\,\%$ of the total and the main contribution comes from the perturbative part of the form factors. The value for the branching ratio of these decays is obtained as presented in Table 6. The function of decay width of $B_c\rightarrow D_1^0(2420,2430) l \nu$ decays with respect to $q^2$ is shown in Fig. 5.

Fig. 5

The dependence of the decay width of the $B_c\rightarrow D_1^0(2420,2430)$ decays on $q^2$

Table 6 The branching ratio value of the semileptonic $B_c\rightarrow D_{1}^0(2420,2430)l \nu$ decays

4.2 $\bullet$ Mixture of $|^3P_1\rangle$ and $|^1P_1\rangle$ states

Now, we would like to analyze the form factors of the $B_c\rightarrow D_1^0$ transition when we consider the $D_{1}^0$ meson as a mixture of two $|^3P_1\rangle$ and $|^1P_1\rangle$ states with mixing angle $\theta$ [see Eq. (23)]. The transition form factors of the $B_c\rightarrow D_{1}^0(2420[2430]) l \nu$ at $q^2=0$ in the interval $-180^\circ \le \theta \le 180^\circ$ are shown in Figs. 6 and 7. The dependence of the form factors of the $B_c\rightarrow D_{1}^0(2420)$ and $B_c\rightarrow D_{1}^0(2430)$ decays on the mixing angle $\theta$ and the transferred momentum square $q^2$ are plotted in Figs. 8 and 9 in the regions $0 \le q^2 \le (m_{B_c}-m_{D_{1}^0})^2\,\mathrm{GeV}^2$ and $\theta =\pm N\pi /6,~ N= 1, 2, 3$. Using Eq. (36), we denote the variation of the decay widths with respect to $q^2$ and $\theta$ in the same regions for each decay in Fig. 10. Also the branching ratios only in terms of the mixing angle $\theta$ are shown in Fig. 11.

Fig. 6

The dependence of the form factors on $\theta$ at $q^2=0$ for the $B_c\rightarrow D_{1}^0(2420)$ transition

Fig. 7

The dependence of the form factors on $\theta$ at $q^2=0$ for the $B_c\rightarrow D_{1}^0(2430)$ transition

Fig. 8

The dependence of the transition form factors on $q^2$ and $\theta =\pm N\pi /6,~ N= 1, 2, 3$ for the $B_c\rightarrow D_{1}^0(2420)$ transition

Fig. 9

The dependence of the transition form factors on $q^2$ and $\theta =\pm N\pi /6,~ N= 1, 2, 3$ for the $B_c\rightarrow D_{1}^0(2430)$ transition

Fig. 10

The decay width for $B_c\rightarrow D_{1}^0 l\nu$ with respect to $q^2$ and $\theta =\pm N\pi /6,~ N= 1, 2, 3$

Fig. 11

The branching ratio functions of the $B_c\rightarrow D_{1}^0(2420[2430])$ with respect to $\theta$

4.3 $\bullet$ Compound state in the heavy-quark limit

Eventually, we study the structure of the $D_1^0$ meson as a mixture of two $|^3P_1\rangle$ and $|^1P_1\rangle$ states with the mixing angle $\theta =35.3^\circ$ in the heavy-quark limit. The HQET form factors of the $B_c\rightarrow D_1^0$ transition were evaluated in Eq. (34). Figures 12 and 13 depict the $f_i^{\mathrm{HQ}(2420)}$ and $f_i^{\mathrm{HQ}(2430)}$ with respect to the $q^2$ for $B_c\rightarrow D_1^0(2420) l \nu$ and $B_c\rightarrow D_1^0(2430) l \nu$, respectively. It is noted, at $y=1$ in Eq. (24) called the zero recoil limit [corresponding to $q^2=(m_{B_c}-m_{D^0_1})^2$], that the HQET limits of the form factors are not finite. For other values of y and the corresponding $q^2$, the behavior of the $f_i^{(2420,2430)}$ form factors shown in Fig. 4 and their HQET form factors $f_i^{\mathrm{HQ}(2420)}$ and $f_i^{\mathrm{HQ}(2430)}$ in Figs. 12 and 13 are the same, i.e., when $q^2$ increases ($y$ decreases), both the form factors and their HQET values increases.

Fig. 12

The dependence of the HQET form factors on $q^2$ for the $B_c\rightarrow D_{1}^0(2420)$ transition

Fig. 13

The dependence of the HQET form factors on $q^2$ for the $B_c\rightarrow D_{1}^0(2430)$ transition

The values of the HQET form factors at $q^2=0$ are presented in Table 7.

Table 7 The value of the form factors of the $B_{c}\rightarrow D_{1}^0(2420)$ and $B_{c}\rightarrow D_{1}^0(2430)$ transitions via HQET at $q^2=0$

Also using Eq. (36) and the HEQT form factors, we evaluated the branching ratios of the $B_c\rightarrow D_1^0(2420[2430]) l \nu$ decays as given in Table 8. Figure 14 depicts the dependence of the decay widths of these decays on the $q^2$ in HQET approach.

Fig. 14

The decay widths of the $B_c\rightarrow D_1^0(2420[2430])$ decays in HQET approach with respect to $q^2$

Table 8 The branching ratio values of the semileptonic $B_c\rightarrow D_{1}^0(2420)l \nu$ and $B_c\rightarrow D_{1}^0(2430)l \nu$ decays via HQET

5 Conclusion

In summary, we analyzed the semileptonic $B_{c}\rightarrow D_{1}^0 (2420[2430])l\nu$ decays in the framework of the 3PSR and HQET approach. First, we assumed the $D_{1}^0(2420)$ and $D_{1}^0(2430)$ axial vector mesons as the pure $|c\bar{u}\rangle$ state. In this case, the related form factors were computed. The branching ratios of these decays were also estimated. Second, the $D_{1}^0(2420[2430])$ mesons were considered as a combination of two states $|^3P_1\rangle \equiv |D_{1}1\rangle$ and $|^1P_1\rangle \equiv |D_{1}2\rangle$ with different masses and decay constants. We evaluated the transition form factors and the decay widths of these decays with respect to the mixing angle $\theta$ and the transferred momentum square $q^2$. The dependence of the branching ratios on $\theta$ was also presented. Finally, we obtained all of the mentioned physical quantities in the HQET approach. Any future experimental measurement on these form factors as well as decay rates and branching fractions and their comparison with the obtained results in the present work can give considerable information as regards the structure of these mesons and the unknown mixing angle $\theta$.

Appendices

Appendix A

In this appendix, the explicit expressions of the coefficients of the gluon condensate entering the sum rules of the form factors $f_i(q^2)$ $(i=V, 0, 1, 2)$ are given:

$$\begin{aligned} C_{V}^{4}= & {} -10\,\hat{I}_{{1}}(3,2,2){m_{{b}}}^{3}{m_{{c}}}^{2}+10\,\hat{I}_{{1}}(3,2,2){m_{{b}}}^{2}{m_{{c}}}^{3}\\&+10\,\hat{I}_{{2}}(3,2,2){m_{{b}}}^{2}{m_{{c}}}^{3}+10\,\hat{I}_{{0}}(3,2,2){m_{{b}}}^{2}{m_{{c}}}^{3}\\&+60\,\hat{I}_{{2}}(1,4,1){m_{{b}}}^{2}m_{{c}}-20\,\hat{I}_{{2}}(3,2,1){m_{{b}}}^{2}m_{{c}}\\&+10\,\hat{I}_{2}^{[0,1]}(3,2,2){m_{{b}}}^{2}m_{{c}}-20\,\hat{I}_{{0}}(3,2,1){m_{{b}}}^{2}m_{{c}}\\&+10\,\hat{I}_{{1}}(3,2,1)m_{{b}}{m_{{c}}}^{2}+40\,\hat{I}_{{2}}(2,3,1)m_{{b}}{m_{{c}}}^{2}\\&-10\,\hat{I}_{{0}}(3,2,1)m_{{b}}{m_{{c}}}^{2}+20\,\hat{I}_{{1}}(2,3,1)m_{{b}}{m_{{c}}}^{2}\\&-10\,\hat{I}_{{0}}(3,2,2){m_{{c}}}^{5}+20\,\hat{I}_{{1}}(3,2,1){m_{{b}}}^{3}\\&+10\,\hat{I}_{{1}}(2,2,2){m_{{b}}}^{3}-20\,\hat{I}_{{1}}(2,3,1){m_{{b}}}^{3}\\&+10\,\hat{I}_{{0}}(3,2,1){m_{{c}}}^{3}-10\,\hat{I}_{{2}}(3,1,2){m_{{c}}}^{3}\\&-20\,\hat{I}_{{0}}(2,2,2){m_{{c}}}^{3}-20\,\hat{I}_{{2}}(2,2,2){m_{{c}}}^{3}\\&-10\,\hat{I}_{{0}}(3,1,2){m_{{c}}}^{3}+20\,\hat{I}_{0}^{[0,1]}(3,2,2){m_{{c}}}^{3}\\&-50\,\hat{I}_{{1}}(2,2,1)m_{{b}}+20\,\hat{I}_{1}^{[0,1]}(2,3,1)m_{{b}} \\&-20\,\hat{I}_{1}^{[0,1]}(3,1,2)m_{{b}}-20\,\hat{I}_{{0}}(2,2,1)m_{{b}}\\&+30\,\hat{I}_{{1}}(2,1,2)m_{{b}}+100\,\hat{I}_{{2}}(1,3,1)m_{{b}} \\&+30\,\hat{I}_{{0}}(2,2,1)m_{{c}}+30\,\hat{I}_{2}^{[0,1]}(3,1,2)m_{{c}}\\&+20\,\hat{I}_{2}^{[0,1]}(3,2,1)m_{{c}}+10\,\hat{I}_{0}^{[0,1]}(3,2,1)m_{{c}} \\&+20\,\hat{I}_{{2}}(2,2,1)m_{{c}}-30\,\hat{I}_{{2}}(2,1,2)m_{{c}}\\&+10\,\hat{I}_{{0}}(3,1,1)m_{{c}}+20\,\hat{I}_{0}^{[0,1]}(2,2,2)m_{{c}}\\&+20\,\hat{I}_{2}^{[0,1]}(2,2,2)m_{{c}}-10\,\hat{I}_{{2}}(3,1,1)m_{{c}}\\&-20\,\hat{I}_{{1}}(2,1,2)m_{{c}}-30\,\hat{I}_{{0}}(2,1,2)m_{{c}}, \\ \end{aligned}$$

$$\begin{aligned} C_{0}^{4}= & {} -20\,\hat{I}_{{6}}(3,2,2){m_{{c}}}^{5}-40\,\hat{I}_{{6}}(3,2,1){m_{{c}}}^{3}\\&-20\,\hat{I}_{{6}}(3,1,2){m_{{c}}}^{3}+40\,\hat{I}_{6}^{[0,6]}(3,2,2){m_{{c}}}^{3} \\&+20\,\hat{I}_{{6}}(2,2,2){m_{{b}}}^{3}+5\,\hat{I}_{{0}}(2,2,1){m_{{b}}}^{3}\\&-120\,\hat{I}_{{6}}(1,4,1){m_{{b}}}^{3}+40\,\hat{I}_{{6}}(2,3,1){m_{{b}}}^{3} \\&+10\,\hat{I}_{0}^{[0,1]}(2,2,2){m_{{b}}}^{3}-5\,\hat{I}_{{0}}(1,2,2){m_{{b}}}^{3}\\&-20\,\hat{I}_{6}^{[0,1]}(3,2,2){m_{{b}}}^{3}+20\,\hat{I}_{6}^{[0,1]}(3,1,2)m_{{c}} \\&+5\,\hat{I}_{0}^{[0,1]}(3,1,1)m_{{c}}+5\,\hat{I}_{{0}}(1,1,2)m_{{c}}\\&+20\,\hat{I}_{{6}}(2,1,2)m_{{c}}+40\,\hat{I}_{{6}}(3,1,1)m_{{c}} \\&-10\,\hat{I}_{0}^{[0,1]}(1,3,1)m_{{b}}-15\,\hat{I}_{{0}}(1,2,1)m_{{b}}\\&-40\,\hat{I}_{{6}}(2,2,1)m_{{b}}+15\,\hat{I}_{0}^{[0,1]}(2,2,1)m_{{b}}\\&-20\,\hat{I}_{6}^{[0,1]}(2,2,2)m_{{b}}+20\,\hat{I}_{6}^{[0,2]}(3,2,2)m_{{b}}\\&-40\,\hat{I}_{6}^{[0,1]}(3,1,2)m_{{b}}-15\,\hat{I}_{{0}}(1,1,2)m_{{b}} \\&+10\,\hat{I}_{0}^{[0,1]}(3,1,1)m_{{b}}-15\,\hat{I}_{0}^{[0,2]}(3,2,1)m_{{b}}\\&-20\,\hat{I}_{{6}}(1,2,2)m_{{b}}-40\,\hat{I}_{6}^{[0,1]}(2,3,1)m_{{b}} \\&-10\,\hat{I}_{{0}}(2,3,1){m_{{c}}}^{4}m_{{b}}+15\,\hat{I}_{0}^{[0,1]}(3,2,2){m_{{c}}}^{4}m_{{b}}\\&+20\,\hat{I}_{{6}}(3,2,2){m_{{c}}}^{4}m_{{b}}-15\,\hat{I}_{{0}}(2,2,2){m_{{c}}}^{4}m_{{b}} \\&+5\,\hat{I}_{{0}}(3,2,2){m_{{c}}}^{5}{m_{{b}}}^{2}-30\,\hat{I}_{{0}}(1,4,1)m_{{c}}{m_{{b}}}^{4}\\&-5\,\hat{I}_{0}^{[0,1]}(3,2,2)m_{{c}}{m_{{b}}}^{4}+10\,\hat{I}_{{0}}(3,2,1)m_{{c}}{m_{{b}}}^{4} \\&-10\,\hat{I}_{0}^{[0,1]}(3,2,2){m_{{c}}}^{3}{m_{{b}}}^{2}+5\,\hat{I}_{{0}}(3,2,1){m_{{c}}}^{3}{m_{{b}}}^{2}\\&+15\,\hat{I}_{{0}}(4,1,1){m_{{c}}}^{3}{m_{{b}}}^{2}+20\,\hat{I}_{{6}}(2,2,2){m_{{c}}}^{2}m_{{b}} \\&+10\,\hat{I}_{{0}}(1,3,1){m_{{c}}}^{2}m_{{b}}+20\,\hat{I}_{0}^{[0,1]}(3,2,1){m_{{c}}}^{2}m_{{b}}\\&-20\,\hat{I}_{{0}}(1,2,2){m_{{c}}}^{2}m_{{b}}-15\,\hat{I}_{{0}}(2,1,2){m_{{c}}}^{2}m_{{b}} \\&-10\,\hat{I}_{{0}}(3,1,1){m_{{c}}}^{2}m_{{b}}+20\,\hat{I}_{{6}}(3,1,2){m_{{c}}}^{2}m_{{b}}\\&+15\,\hat{I}_{{0}}(2,2,1){m_{{c}}}^{2}m_{{b}}+20\,\hat{I}_{0}^{[0,1]}(2,3,1){m_{{c}}}^{2}m_{{b}} \\&+15\,\hat{I}_{{0}}(2,1,2)m_{{c}}{m_{{b}}}^{2}+5\,\hat{I}_{{0}}(3,1,1)m_{{c}}{m_{{b}}}^{2}\\&-20\,\hat{I}_{0}^{[0,1]}(3,1,2)m_{{c}}{m_{{b}}}^{2}-20\,\hat{I}_{{6}}(2,2,2)m_{{c}}{m_{{b}}}^{2} \\&-10\,\hat{I}_{{0}}(2,2,1)m_{{c}}{m_{{b}}}^{2}+5\,\hat{I}_{0}^{[0,2]}(3,2,2)m_{{c}}{m_{{b}}}^{2}, \end{aligned}$$

$$\begin{aligned} C_{1}^{4}= & {} -40\,\hat{I}_{4}^{[0,1]}(2,3,1)m_{{b}}+20\,\,\hat{I}_{4}^{[0,2]}(3,2,2)m_{{b}}\\&-40\,\hat{I}_{{3}}(2,2,1)m_{{b}}-20\,\hat{I}_{{1}}(1,2,2)m_{{b}} -20\,\hat{I}_{3}^{[0,1]}(2,2,2)m_{{b}}\\&-20\,\hat{I}_{{3}}(1,2,2)m_{{b}}-20\,\hat{I}_{{4}}(1,2,2)m_{{b}}-10\,\hat{I}_{1}^{[0,1]}(2,3,1)m_{{b}} \\&-15\,\hat{I}_{{1}}(3,2,2){m_{{c}}}^{5}-45\,\hat{I}_{{1}}(3,2,1){m_{{c}}}^{3}-20\,\hat{I}_{{4}}(3,1,2){m_{{c}}}^{3}\\&-20\,\hat{I}_{{2}}(3,2,1){m_{{c}}}^{3} -45\,\hat{I}_{{1}}(4,1,1){m_{{c}}}^{3}-20\,\hat{I}_{{4}}(3,2,2){m_{{c}}}^{5}\\&-5\,\hat{I}_{{0}}(3,1,2){m_{{c}}}^{3}-40\,\hat{I}_{{3}}(2,2,2){m_{{c}}}^{3} -15\,\hat{I}_{{0}}(4,1,1){m_{{c}}}^{3}\\&-5\,\hat{I}_{{2}}(3,1,2){m_{{c}}}^{3}-10\,\hat{I}_{{0}}(2,2,2){m_{{c}}}^{3}-20\,\hat{I}_{{1}}(3,1,2){m_{{c}}}^{3}\\&-20\,\hat{I}_{{3}}(3,2,2){m_{{c}}}^{2}{m_{{b}}}^{3}+20\,\hat{I}_{{4}}(2,2,2){m_{{c}}}^{2}m_{{b}}\\&-20\,\hat{I}_{{0}}(2,3,1){m_{{c}}}^{2}m_{{b}}+40\,\hat{I}_{{4}}(3,2,1){m_{{c}}}^{2}m_{{b}}\\&+20\,\hat{I}_{{3}}(3,1,2){m_{{c}}}^{2}m_{{b}}+20\,\hat{I}_{{3}}(2,2,2){m_{{c}}}^{2}m_{{b}}\\&+5\,\hat{I}_{{1}}(3,2,2){m_{{c}}}^{4}m_{{b}}+20\,\hat{I}_{{3}}(3,2,2){m_{{c}}}^{4}m_{{b}}\\&+15\,\hat{I}_{{1}}(3,2,2){m_{{c}}}^{3}{m_{{b}}}^{2}+20\,\hat{I}_{{3}}(3,2,2){m_{{c}}}^{3}{m_{{b}}}^{2}\\&-20\,\hat{I}_{{4}}(3,2,2){m_{{c}}}^{2}{m_{{b}}}^{3}-5\,\hat{I}_{{1}}(3,2,2){m_{{c}}}^{2}{m_{{b}}}^{3}\\&-50\,\hat{I}_{{1}}(2,3,1){m_{{c}}}^{2}m_{{b}}-10\,\hat{I}_{1}^{[0,1]}(3,2,2){m_{{c}}}^{2}m_{{b}}\\&+35\,\hat{I}_{{1}}(3,2,1){m_{{c}}}^{2}m_{{b}}+20\,\hat{I}_{{4}}(3,1,2){m_{{c}}}^{2}m_{{b}}\\&+40\,\hat{I}_{{3}}(2,3,1){m_{{b}}}^{3}+20\,\hat{I}_{{3}}(2,2,2){m_{{b}}}^{3}-5\,\hat{I}_{1}^{[0,1]}(3,2,2){m_{{b}}}^{3}\\&+40\,\hat{I}_{{4}}(2,3,1){m_{{b}}}^{3} +20\,\hat{I}_{{4}}(3,2,1){m_{{b}}}^{3}+10\,\hat{I}_{{1}}(2,3,1){m_{{b}}}^{3}\\&-30\,\hat{I}_{{1}}(1,4,1){m_{{b}}}^{3}-40\,\hat{I}_{{4}}(2,2,2){m_{{c}}}^{3} -20\,\hat{I}_{{4}}(2,2,2)m_{{c}}{m_{{b}}}^{2}\\&-30\,\hat{I}_{{1}}(3,2,1)m_{{c}}{m_{{b}}}^{2}+90\,\hat{I}_{{1}}(1,4,1)m_{{c}}{m_{{b}}}^{2}\\&+120\,\hat{I}_{{3}}(1,4,1)m_{{3}}{m_{{b}}}^{2} +40\,\hat{I}_{{3}}(3,1,1)m_{{c}}\\&-5\,\hat{I}_{{0}}(2,2,1)m_{{c}}+10\,\hat{I}_{0}^{[0,1]}(2,2,2)m_{{c}}\\&+20\,\hat{I}_{{4}}(2,1,2)m_{{c}}+40\,\hat{I}_{3}^{[0,1]}(3,2,1)m_{{c}}\\&+40\,\hat{I}_{4}^{[0,1]}(2,2,2)m_{{c}}+5\,\hat{I}_{{2}}(3,1,1)m_{{c}}\\&+20\,\hat{I}_{{4}}(2,2,2){m_{{b}}}^{3}+30\,\hat{I}_{{0}}(1,4,1)m_{{c}}{m_{{b}}}^{2}\\&+30\,\hat{I}_{{2}}(1,4,1)m_{{c}}{m_{{b}}}^{2}-20\,\hat{I}_{{4}}(3,2,1)m_{{c}}{m_{{b}}}^{2}\\&+15\,\hat{I}_{1}^{[0,1]}(3,2,2)m_{{c}}{m_{{b}}}^{2}-10\,\hat{I}_{{1}}(2,2,2)m_{{c}}{m_{{b}}}^{2} \\&-5\,\hat{I}_{2}^{[0,2]}(3,2,2)m_{{c}}+5\,\hat{I}_{{1}}(2,2,1)m_{{c}}\\&+40\,\hat{I}_{4}^{[0,1]}(3,2,1)m_{{c}}+10\,\hat{I}_{2}^{[0,1]}(3,2,1)m_{{c}} \\&-5\,\hat{I}_{0}^{[0,2]}(3,2,2)m_{{c}}+40\,\hat{I}_{3}^{[0,1]}(2,2,2)m_{{c}}\\&+20\,\hat{I}_{{3}}(2,1,2)m_{{c}}-15\,\hat{I}_{{0}}(2,1,2)m_{{c}} \\&+20\,\hat{I}_{3}^{[0,2]}(3,2,2)m_{{b}}-40\,\hat{I}_{{3}}(1,3,1)m_{{b}}\\&-40\,\hat{I}_{4}^{[0,1]}(3,1,2)m_{{b}}+10\,\hat{I}_{{1}}(1,3,1)m_{{b}} \\&+10\,\hat{I}_{{0}}(1,3,1)m_{{b}}-20\,\hat{I}_{4}^{[0,1]}(3,2,1)m_{{b}}\\&-20\,\hat{I}_{3}^{[0,2]}(3,2,2)m_{{c}}-10\,\hat{I}_{{0}}(3,1,1)m_{{c}}, \end{aligned}$$

$$\begin{aligned} C_{2}^{4}= & {} 15\,\hat{I}_{{2}}(4,1,1){m_{{c}}}^{2}m_{{b}}-40\,\hat{I}_{3}^{[0,1]}(3,2,2){m_{{c}}}^{2}m_{{b}}\\&-\,40\,\hat{I}_{{4}}(3,2,1){m_{{c}}}^{2}m_{{b}}-10\,\hat{I}_{{2}}(2,3,1){m_{{c}}}^{2}m_{{b}}\\&+\,40\,\hat{I}_{4}^{[0,1]}(3,2,2){m_{{c}}}^{2}m_{{b}}-60\,\hat{I}_{{4}}(4,1,1){m_{{c}}}^{2}m_{{b}}\\&+\,40\,\hat{I}_{{4}}(2,3,1){m_{{c}}}^{2}m_{{b}}+20\,\hat{I}_{{3}}(2,2,2){m_{{c}}}^{2}m_{{b}}\\&-\,20\,\hat{I}_{{4}}(3,1,2){m_{{c}}}^{2}m_{{b}}+10\,\hat{I}_{2}^{[0,1]}(3,2,2){m_{{c}}}^{3}\\&+\,60\,\hat{I}_{{4}}(4,1,1){m_{{c}}}^{3}-20\,\hat{I}_{{3}}(3,1,2){m_{{c}}}^{3}\\&-\,15\,\hat{I}_{{2}}(4,1,1){m_{{c}}}^{3}-5\,\hat{I}_{{2}}(3,2,1){m_{{c}}}^{3}\\&+\,10\,\hat{I}_{1}^{[0,1]}(3,2,2){m_{{c}}}^{3}+5\,\hat{I}_{{0}}(3,1,2){m_{{c}}}^{3}\\&-\,5\,\hat{I}_{{1}}(3,1,2){m_{{c}}}^{3}+15\,\hat{I}_{{0}}(4,1,1){m_{{c}}}^{3}\\&-\,20\,\hat{I}_{{1}}(3,2,1){m_{{c}}}^{3}+20\,\hat{I}_{4}^{[0,1]}(3,2,2){m_{{b}}}^{3}\\&-\,20\,\hat{I}_{4}^{[0,1]}(3,2,2)m_{{c}}{m_{{b}}}^{2}+5\,\hat{I}_{{2}}(3,1,2)m_{{c}}{m_{{b}}}^{2}\\&-\,20\,\hat{I}_{{3}}(3,2,1)m_{{c}}{m_{{b}}}^{2}+20\,\hat{I}_{{4}}(2,2,2)m_{{c}}{m_{{b}}}^{2} \\&-\,10\,\hat{I}_{{2}}(2,2,2)m_{{c}}{m_{{b}}}^{2}-30\,\hat{I}_{{0}}(1,4,1)m_{{c}}{m_{{b}}}^{2}\\&+\,120\,\hat{I}_{{3}}(1,4,1)m_{{c}}{m_{{b}}}^{2}+5\,\hat{I}_{1}^{[0,1]}(3,2,2)m_{{c}}{m_{{b}}}^{2} \\&+\,20\,\hat{I}_{{4}}(3,2,1)m_{{c}}{m_{{b}}}^{2}-10\,\hat{I}_{{1}}(3,2,1)m_{{c}}{m_{{b}}}^{2}\\&+\,30\,\hat{I}_{{2}}(1,4,1)m_{{c}}{m_{{b}}}^{2}+20\,\hat{I}_{{3}}(2,2,2){m_{{b}}}^{3}\\&-\,20\,\hat{I}_{{4}}(3,2,1){m_{{b}}}^{3}+10\,\hat{I}_{{2}}(2,3,1){m_{{b}}}^{3}\\&+\,10\,\hat{I}_{{2}}(3,2,1){m_{{b}}}^{3}-120\,\hat{I}_{{3}}(1,4,1){m_{{b}}}^{3} \\&+\,5\,\hat{I}_{{0}}(2,2,1)m_{{c}}+15\,\hat{I}_{1}^{[0,1]}(3,1,2)m_{{c}}\\&-\,5\,\hat{I}_{2}^{[0,2]}(3,2,2)m_{{c}}-15\,\hat{I}_{0}^{[0,1]}(3,2,1)m_{{c}} \\&+\,40\,\hat{I}_{{3}}(3,1,1)m_{{c}}+5\,\hat{I}_{{1}}(3,1,1)m_{{c}}\\&-\,20\,\hat{I}_{4}^{[0,1]}(3,1,2)m_{{c}}+10\,\hat{I}_{{0}}(3,1,1)m_{{c}} \\&+\,10\,\hat{I}_{1}^{[0,1]}(2,2,2)m_{{c}}+20\,\,\hat{I}_{3}^{[0,1]}(3,1,2)m_{{c}}\\&-\,20\,\hat{I}_{{4}}(2,1,2)m_{{c}}+20\,\hat{I}_{{3}}(2,1,2)m_{{c}} \\&+\,5\,\hat{I}_{{2}}(2,2,1)m_{{c}}+10\,\hat{I}_{2}^{[0,1]}(2,2,2)m_{{c}}\\&-\,15\,\hat{I}_{{1}}(2,1,2)m_{{c}}-15\,\hat{I}_{0}^{[0,1]}(3,1,2)m_{{c}} \\&-\,40\,\hat{I}_{3}^{[0,1]}(3,1,2)m_{{b}}+40\,\hat{I}_{4}^{[0,1]}(3,1,2)m_{{b}}\\&-\,20\,\hat{I}_{{2}}(2,1,2)m_{{b}}+20\,\hat{I}_{4}^{[0,1]}(3,2,1)m_{{b}} \\&+\,5\,\hat{I}_{2}^{[0,2]}(3,2,2)m_{{b}}+10\,\hat{I}_{{0}}(2,2,1)m_{{b}}\\&-\,20\,\hat{I}_{{3}}(2,1,2)m_{{b}}-10\,\hat{I}_{{1}}(2,2,1)m_{{b}} \\&-\,20\,\hat{I}_{{2}}(1,2,2)m_{{b}}+20\,\hat{I}_{{4}}(2,1,2)m_{{b}}\\&-\,40\,\hat{I}_{{3}}(3,1,1)m_{{b}}-10\,\hat{I}_{{2}}(1,3,1)m_{{b}} \\&+\,20\,\hat{I}_{3}^{[0,2]}(3,2,2)m_{{b}}-40\,\hat{I}_{{3}}(2,2,1)m_{{b}}\\&+\,20\,\hat{I}_{4}^{[0,1]}(2,2,2)m_{{b}}+40\,\hat{I}_{4}^{[0,1]}(2,3,1)m_{{b}} \\&+\,10\,\hat{I}_{{2}}(3,1,2){m_{{c}}}^{2}m_{{b}}+20\,\hat{I}_{{4}}(3,2,2){m_{{c}}}^{5}\\&+\,5\,\hat{I}_{{0}}(3,2,2){m_{{c}}}^{5}-5\,\hat{I}_{{2}}(3,2,2){m_{{c}}}^{5} \\&+\,40\,\hat{I}_{{4}}(3,2,1){m_{{c}}}^{3}+40\,\hat{I}_{3}^{[0,1]}(3,2,2){m_{{c}}}^{3}\\&+\,20\,\hat{I}_{{4}}(3,1,2){m_{{c}}}^{3}+5\,\hat{I}_{{2}}(3,2,2){m_{{c}}}^{4}m_{{b}} \\&+\,20\,\hat{I}_{{3}}(3,2,2){m_{{c}}}^{3}{m_{{b}}}^{2}-20\,\hat{I}_{{4}}(3,2,2){m_{{c}}}^{3}{m_{{b}}}^{2}\\&+\,5\,\hat{I}_{{2}}(3,2,2){m_{{c}}}^{3}{m_{{b}}}^{2}-5\,\hat{I}_{{2}}(3,2,2){m_{{c}}}^{2}{m_{{b}}}^{3}. \end{aligned}$$

where

$$\begin{aligned} \hat{I}_n^{[i,j]} (a,b,c)= & {} \left( M_1^2 \right) ^i \left( M_2^2 \right) ^j \frac{\mathrm{d}^i}{\mathrm{d}\left( M_1^2 \right) ^i} \frac{\mathrm{d}^j}{\mathrm{d}\left( M_2^2 \right) ^j}\\&\times \, \left[ \left( M_1^2 \right) ^i \left( M_2^2 \right) ^j \hat{I}_n(a,b,c) \right] . \end{aligned}$$

Appendix B

In this appendix, the explicit expressions of the coefficients of the gluon condensate entering the HQET limit of the form factors $f_{V}^{\mathrm{HQ}}, f_{0}^{\mathrm{HQ}}, f_{1}^{\mathrm{HQ}}$, and $f_{2}^{\mathrm{HQ}}$ are given:

$$\begin{aligned} C_{V}^{\mathrm{HQET}}= & {} 10\,{\frac{\bar{I}_{2}^{[0,1]}(3,2,1)}{\sqrt{Z}}}-10\,{\frac{\bar{I}_{2}^{[0,2]}(3,2,2)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{{0}}(2,2,1)}{\sqrt{Z}}}\\&-\,20\,{\frac{\bar{I}_{{2}}(1,2,2)}{\sqrt{Z}}} +20\,{\frac{\bar{I}_{0}^{[0,1]}(2,2,2)}{\sqrt{Z}}}-20\,{\frac{\bar{I}_{{1}}(2,1,2)}{\sqrt{Z}}}\\&+\,30\,{\frac{\bar{I}_{0}^{[0,1]}(3,1,2)}{\sqrt{Z}}}-30\,{\frac{\bar{I}_{{2}}(2,1,2)}{\sqrt{Z}}} +20\,{\frac{\bar{I}_{1}^{[0,2]}(3,2,1)}{\sqrt{Z}}}\\&-\,30\,{\frac{\bar{I}_{{0}}(2,1,2)}{\sqrt{Z}}}-10\,{\frac{\bar{I}_{1}^{[0,2]}(3,2,2)}{\sqrt{Z}}}-10\,{\frac{\bar{I}_{0}^{[0,2]}(3,2,2)}{\sqrt{Z}}} \\&+\,20\,{\frac{\bar{I}_{2}^{[0,1]}(2,2,2)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{1}^{[0,1]}(3,1,2)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{1}^{[0,1]}(2,2,2)}{\sqrt{Z}}}\\&+\,20\,{\frac{\bar{I}_{0}^{[0,1]}(3,2,1)}{\sqrt{Z}}} +30\,{\frac{\bar{I}_{{2}}(2,2,1)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{{1}}(2,2,1)}{\sqrt{Z}}}\\&-\,10\,{\frac{\bar{I}_{{1}}(3,1,1)}{\sqrt{Z}}}-20\,{\frac{\bar{I}_{{0}}(1,2,2)}{\sqrt{Z}}}+10\,{\frac{\bar{I}_{{2}}(3,1,1)}{\sqrt{Z}}}\\&-\,20\,{\frac{\bar{I}_{{1}}(1,2,2)}{\sqrt{Z}}}+30\,{\frac{\bar{I}_{2}^{[0,1]}(3,1,2)}{\sqrt{Z}}}-10\,{\frac{\bar{I}_{{0}}(3,1,1)}{\sqrt{Z}}} \\&+\,60\,\bar{I}_{{2}}(1,3,1)+20\,\bar{I}_{{1}}(1,3,1)-20\,\bar{I}_{1}^{[0,1]}(3,2,1)\\&+\,10\,\bar{I}_{1}^{[0,2]}(3,2,2) +20\,\bar{I}_{{1}}(1,2,2)+20\,\bar{I}_{1}^{[0,1]}(2,3,1)\\&-\,20\,\bar{I}_{1}^{[0,1]}(2,2,2)+100\,\bar{I}_{{0}}(1,3,1) -50\,\bar{I}_{{1}}(2,2,1)\\&-\,20\,\bar{I}_{{2}}(2,2,1)-20\,\bar{I}_{{0}}(2,2,1)-20\,\bar{I}_{1}^{[0,1]}(3,1,2)\\&+\,30\,\bar{I}_{{1}}(2,1,2)+40\,\bar{I}_{2}^{[0,1]}(2,3,1), \end{aligned}$$

$$\begin{aligned} C_{0}^{\mathrm{HQET}}= & {} -5\,{\frac{\bar{I}_{0}^{[0,1]}(3,2,1)}{\sqrt{Z}}}-20\,{\frac{\bar{I}_{0}^{[0,1]}(3,1,2)}{\sqrt{Z}}}+120\,{\frac{\bar{I}_{6}^{[0,1]}(1,4,1)}{\sqrt{Z}}}\\&+\,15\,{\frac{\bar{I}_{{0}}(2,1,2)}{\sqrt{Z}}} +10\,{\frac{\bar{I}_{{0}}(1,2,2)}{\sqrt{Z}}}-10\,{\frac{\bar{I}_{0}^{[0,1]}(2,2,2)}{\sqrt{Z}}}\\&+\,5\,{\frac{\bar{I}_{{0}}(3,1,1)}{\sqrt{Z}}}+5\,{\frac{\bar{I}_{0}^{[0,2]}(3,2,2)}{\sqrt{Z}}} -10\,{\frac{\bar{I}_{{0}}(2,2,1)}{\sqrt{Z}}}\\&-\,20\,{\frac{\bar{I}_{{6}}(3,2,1)}{\sqrt{Z}}}-30\,{\frac{\bar{I}_{{0}}(1,3,1)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{6}^{[0,1]}(3,2,2)}{\sqrt{Z}}}\\&-\,20\,{\frac{\bar{I}_{{6}}(2,2,2)}{\sqrt{Z}}}+15\,{\frac{\bar{I}_{{0}}(2,2,1)}{Z}}+30\,{\frac{\bar{I}_{0}^{[0,1]}(2,2,2)}{Z}}\\&+\,20\,{\frac{\bar{I}_{0}^{[0,1]}(2,3,1)}{Z}} -20\,{\frac{\bar{I}_{{0}}(1,2,2)}{Z}}-15\,{\frac{\bar{I}_{{0}}(2,1,2)}{Z}}\\&-\,40\,{\frac{\bar{I}_{{6}}(2,3,1)}{Z}}+20\,{\frac{\bar{I}_{0}^{[0,1]}(3,2,1)}{Z}} -15\,{\frac{\bar{I}_{0}^{[0,2]}(3,2,2)}{Z}}\\&+\,20\,{\frac{\bar{I}_{{6}}(3,1,2)}{Z}}+40\,{\frac{\bar{I}_{{6}}(3,2,1)}{Z}}+10\,{\frac{\bar{I}_{{0}}(1,3,1)}{Z}}\\&-\,10\,{\frac{\bar{I}_{{0}}(3,1,1)}{Z}}+60\,{\frac{\bar{I}_{{6}}(4,1,1)}{Z}}+15\,{\frac{\bar{I}_{0}^{[0,1]}(4,1,1)}{Z}}\\&+\,10\,{\frac{\bar{I}_{0}^{[0,1]}(3,1,2)}{Z}}-40\,{\frac{\bar{I}_{6}^{[0,1]}(3,2,2)}{Z}}+20\,{\frac{\bar{I}_{{6}}(2,2,2)}{Z}}\\&-\,40\,{\frac{\bar{I}_{{6}}(2,2,2)}{{Z}^{3/2}}}+40\,{\frac{\bar{I}_{6}^{[0,1]}(3,2,2)}{{Z}^{3/2}}}-40\,{\frac{\bar{I}_{{6}}(3,2,1)}{{Z}^{3/2}}}\\&-\,20\,{\frac{\bar{I}_{{6}}(3,1,2)}{{Z}^{3/2}}}+5\,{\frac{\bar{I}_{{0}}(3,1,1)}{{Z}^{3/2}}}-60\,{\frac{\bar{I}_{{6}}(4,1,1)}{{Z}^{3/2}}}\\&-\,5\,\bar{I}_{{0}}(1,2,2)+20\,\bar{I}_{{6}}(2,2,2)+20\,\bar{I}_{{6}}(3,2,1)\\&-\,30\,\bar{I}_{0}^{[0,1]}(1,4,1)-120\,\bar{I}_{{6}}(1,4,1)-5\,\bar{I}_{0}^{[0,2]}(3,2,2)\\&+\,5\,\bar{I}_{{0}}(2,2,1)-20\,\bar{I}_{6}^{[0,1]}(3,2,2)+10\,\bar{I}_{0}^{[0,1]}(2,3,1)\\&+\,40\,\bar{I}_{{6}}(2,3,1)-20\,\bar{I}_{{0}}(1,3,1)+10\,\bar{I}_{0}^{[0,1]}(2,2,2)\\&+\,15\,\bar{I}_{0}^{[0,1]}(3,2,1), \end{aligned}$$

$$\begin{aligned} C_{1}^{\mathrm{HQET}}= & {} 10\,{\frac{\bar{I}_{2}^{[0,1]}(2,2,2)}{\sqrt{Z}}}+10\,{\frac{\bar{I}_{0}^{[0,1]}(2,2,2)}{\sqrt{Z}}}+45\,{\frac{\bar{I}_{1}^{[0,1]}(3,2,1)}{\sqrt{Z}}}\\&+\,20\,{\frac{\bar{I}_{{4}}(2,2,1)}{\sqrt{Z}}} +40\,{\frac{\bar{I}_{{4}}(3,1,1)}{\sqrt{Z}}}-5\,{\frac{\bar{I}_{{0}}(2,2,1)}{\sqrt{Z}}}\\&+\,40\,{\frac{\bar{I}_{4}^{[0,1]}(2,2,2)}{\sqrt{Z}}}+40\,{\frac{\bar{I}_{3}^{[0,1]}(3,2,1)}{\sqrt{Z}}} -5\,{\frac{\bar{I}_{0}^{[0,2]}(3,2,2)}{\sqrt{Z}}}\\&+\,40\,{\frac{\bar{I}_{3}^{[0,1]}(2,2,2)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{{3}}(2,1,2)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{4}^{[0,1]}(3,1,2)}{\sqrt{Z}}}\\&+\,20\,{\frac{\bar{I}_{{3}}(2,2,1)}{\sqrt{Z}}}+40\,{\frac{\bar{I}_{4}^{[0,1]}(3,2,1)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{{4}}(2,1,2)}{\sqrt{Z}}}\\&+\,5\,{\frac{\bar{I}_{{2}}(3,1,1)}{\sqrt{Z}}} +5\,{\frac{\bar{I}_{{1}}(2,2,1)}{\sqrt{Z}}}-20\,{\frac{\bar{I}_{1}^{[0,2]}(3,2,2)}{\sqrt{Z}}}\\&-\,10\,{\frac{\bar{I}_{{0}}(3,1,1)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{{1}}(3,1,1)}{\sqrt{Z}}} -20\,{\frac{\bar{I}_{3}^{[0,2]}(3,2,2)}{\sqrt{Z}}}\\&-\,20\,{\frac{\bar{I}_{4}^{[0,2]}(3,2,2)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{3}^{[0,1]}(3,1,2)}{\sqrt{Z}}}+15\,{\frac{\bar{I}_{2}^{[0,1]}(3,1,2)}{\sqrt{Z}}} \\&+\,10\,{\frac{\bar{I}_{2}^{[0,1]}(3,2,1)}{\sqrt{Z}}}-15\,{\frac{\bar{I}_{{2}}(2,1,2)}{\sqrt{Z}}}+40\,{\frac{\bar{I}_{1}^{[0,1]}(2,2,2)}{\sqrt{Z}}}\\&-\,5\,{\frac{\bar{I}_{2}^{[0,2]}(3,2,2)}{\sqrt{Z}}} -25\,{\frac{\bar{I}_{{1}}(2,1,2)}{\sqrt{Z}}}+15\,{\frac{\bar{I}_{0}^{[0,1]}(3,1,2)}{\sqrt{Z}}}\\&+\,40\,{\frac{\bar{I}_{{3}}(3,1,1)}{\sqrt{Z}}}+15\,{\frac{\bar{I}_{0}^{[0,1]}(3,2,1)}{\sqrt{Z}}} +45\,{\frac{\bar{I}_{1}^{[0,1]}(3,1,2)}{\sqrt{Z}}}\\&-\,15\,{\frac{\bar{I}_{{0}}(2,1,2)}{\sqrt{Z}}}-40\,\bar{I}_{3}^{[0,1]}(2,3,1)-20\,\bar{I}_{4}^{[0,1]}(3,2,1)\\&+\,10\,\bar{I}_{{2}}(1,3,1)-40\,\bar{I}_{{4}}(2,2,1)-20\,\bar{I}_{{3}}(1,2,2)\\&-\,20\,\bar{I}_{{4}}(1,2,2)+10\,\bar{I}_{{0}}(1,3,1)-10\,\bar{I}_{{0}}(2,2,1)\\&-\,40\,\bar{I}_{{4}}(1,3,1)-20\,\bar{I}_{{1}}(1,2,2)-40\,\bar{I}_{{3}}(1,3,1)\\&-\,20\,\bar{I}_{3}^{[0,1]}(3,2,1)+20\,\bar{I}_{{1}}(1,3,1)-40\,\bar{I}_{4}^{[0,1]}(3,1,2)\\&-\,10\,\bar{I}_{{2}}(2,2,1)-40\,\bar{I}_{4}^{[0,1]}(2,3,1)-20\,\bar{I}_{4}^{[0,1]}(2,2,2)\\&-\,10\,\bar{I}_{1}^{[0,1]}(2,3,1)-40\,\bar{I}_{{1}}(2,2,1)-20\,\bar{I}_{3}^{[0,1]}(2,2,2)\\&+\,5\,\bar{I}_{1}^{[0,2]}(3,2,2)-40\,\bar{I}_{3}^{[0,1]}(3,1,2)-40\,\bar{I}_{{3}}(3,1,1)\\&-\,40\,\bar{I}_{{4}}(3,1,1)-20\,\bar{I}_{{1}}(2,1,2)-10\,\bar{I}_{1}^{[0,1]}(3,1,2)\\&-\,10\,\bar{I}_{1}^{[0,1]}(3,2,1)-20\,\bar{I}_{{4}}(2,1,2)+20\,\bar{I}_{3}^{[0,2]}(3,2,2)\\&+\,20\,\bar{I}_{4}^{[0,2]}(3,2,2)-20\,\bar{I}_{{3}}(2,1,2)-40\,\bar{I}_{{3}}(2,2,1), \end{aligned}$$

$$\begin{aligned} C_{2}^{\mathrm{HQET}}= & {} 20\,{\frac{\bar{I}_{{3}}(2,1,2)}{\sqrt{Z}}}+15\,{\frac{\bar{I}_{1}^{[0,1]}(3,1,2)}{\sqrt{Z}}}-20\,{\frac{\bar{I}_{{4}}(2,1,2)}{\sqrt{Z}}}\\&-\,5\,{\frac{\bar{I}_{{1}}(2,2,1)}{\sqrt{Z}}} +10\,{\frac{\bar{I}_{0}^{[0,1]}(2,2,2)}{\sqrt{Z}}}-15\,{\frac{\bar{I}_{{0}}(2,1,2)}{\sqrt{Z}}}\\&-\,5\,{\frac{\bar{I}_{0}^{[0,2]}(3,2,2)}{\sqrt{Z}}}+20\,{\frac{\bar{I}_{3}^{[0,1]}(3,1,2)}{\sqrt{Z}}} -10\,{\frac{\bar{I}_{{2}}(3,1,1)}{\sqrt{Z}}}\\&+\,40\,{\frac{\bar{I}_{3}^{[0,1]}(2,2,2)}{\sqrt{Z}}}-10\,{\frac{\bar{I}_{{0}}(3,1,1)}{\sqrt{Z}}}-40\,{\frac{\bar{I}_{4}^{[0,1]}(2,2,2)}{\sqrt{Z}}} \\&-\,5\,{\frac{\bar{I}_{{0}}(2,2,1)}{\sqrt{Z}}}-5\,{\frac{\bar{I}_{1}^{[0,1]}(3,2,1)}{\sqrt{Z}}}-40\,{\frac{\bar{I}_{4}^{[0,1]}(3,2,1)}{\sqrt{Z}}}\\&-\,20\,{\frac{\bar{I}_{3}^{[0,2]}(3,2,2)}{\sqrt{Z}}} -35\,{\frac{\bar{I}_{{1}}(2,1,2)}{\sqrt{Z}}}+15\,{\frac{\bar{I}_{0}^{[0,1]}(3,1,2)}{\sqrt{Z}}}\\&+\,30\,{\frac{\bar{I}_{{2}}(2,1,2)}{\sqrt{Z}}}-20\,{\frac{\bar{I}_{{4}}(2,2,1)}{\sqrt{Z}}} +20\,{\frac{\bar{I}_{{3}}(2,2,1)}{\sqrt{Z}}}\\&+\,40\,{\frac{\bar{I}_{3}^{[0,1]}(3,2,1)}{\sqrt{Z}}}-20\,{\frac{\bar{I}_{2}^{[0,1]}(2,2,2)}{\sqrt{Z}}}+40\,{\frac{\bar{I}_{{3}}(3,1,1)}{\sqrt{Z}}} \\&-\,20\,{\frac{\bar{I}_{2}^{[0,1]}(3,2,1)}{\sqrt{Z}}}-40\,{\frac{\bar{I}_{{4}}(3,1,1)}{\sqrt{Z}}}+15\,{\frac{\bar{I}_{0}^{[0,1]}(3,2,1)}{\sqrt{Z}}}\\&+\,20\,{\frac{\bar{I}_{4}^{[0,2]}(3,2,2)}{\sqrt{Z}}} -30\,{\frac{\bar{I}_{2}^{[0,1]}(3,1,2)}{\sqrt{Z}}}-20\,{\frac{\bar{I}_{4}^{[0,1]}(3,1,2)}{\sqrt{Z}}}\\&+\,10\,{\frac{\bar{I}_{2}^{[0,2]}(3,2,2)}{\sqrt{Z}}}+10\,\bar{I}_{1}^{[0,1]}(3,2,1)\\&+\,40\,\bar{I}_{{4}}(3,1,1)+40\,\bar{I}_{4}^{[0,1]}(2,3,1)\\&+\,40\,\bar{I}_{{4}}(1,3,1)+40\,\bar{I}_{4}^{[0,1]}(3,1,2)\\&-\,10\,\bar{I}_{{0}}(2,2,1)-40\,\bar{I}_{{3}}(3,1,1)\\&+\,20\,\bar{I}_{{1}}(1,2,2)-40\,\bar{I}_{{3}}(1,3,1)\\&+\,10\,\bar{I}_{1}^{[0,1]}(3,1,2)-40\,\bar{I}_{3}^{[0,1]}(3,1,2)\\&+\,20\,\bar{I}_{{2}}(2,2,1)+20\,\bar{I}_{{1}}(2,1,2)\\&-\,20\,\bar{I}_{{3}}(2,1,2)+20\,\bar{I}_{{4}}(2,1,2)\\&+\,10\,\bar{I}_{{0}}(1,3,1)-20\,\bar{I}_{{3}}(1,2,2)\\&-\,20\,\bar{I}_{3}^{[0,1]}(2,2,2)+20\,\bar{I}_{4}^{[0,1]}(2,2,2)\\&+\,40\,\bar{I}_{{4}}(2,2,1)-40\,\bar{I}_{{3}}(2,2,1)\\&+\,20\,\bar{I}_{{4}}(1,2,2)+10\,\bar{I}_{1}^{[0,1]}(2,3,1)\\&-\,20\,\bar{I}_{{2}}(1,3,1)+20\,\bar{I}_{3}^{[0,2]}(3,2,2)\\&-\,20\,\bar{I}_{4}^{[0,2]}(3,2,2)+20\,\bar{I}_{{1}}(1,3,1)\\&-\,5\,\bar{I}_{1}^{[0,2]}(3,2,2)-20\,\bar{I}_{3}^{[0,1]}(3,2,1)\\&+\,20\,\bar{I}_{4}^{[0,1]}(3,2,1)-40\,\bar{I}_{3}^{[0,1]}(2,3,1), \end{aligned}$$

where

$$\begin{aligned} \bar{I}_n^{[i,j]} (a,b,c)= & {} \frac{2^{i+j}}{(\sqrt{Z})^{j}} \left( T_1 \right) ^i \left( T_2 \right) ^j\frac{\mathrm{d}^i}{\mathrm{d}\left( T_1 \right) ^i} \frac{\mathrm{d}^j}{\mathrm{d}\left( T_2 \right) ^j}\\&\times \,\left[ \left( T_1 \right) ^i \left( T_2 \right) ^j \bar{I}_n(a,b,c) \right] . \end{aligned}$$