1 Introduction

In the last decade, the extra dimension models turned out to be a cornerstone of high energy physics [1, 2]. In particular, the Randall–Sundrum (RS) model brought the incredible idea of infinity extra dimensions through a warped geometry [2]. Some authors enhanced the RS model results to six dimensions. Since the two-dimensional transverse manifold has its own geometry, it leads to some nonexistent features in the RS models. Indeed, for an axisymmetric brane, the so-called string-like defect, the brane tension is related with the conical deficit angle of the transverse space [3–7]. Further, the Kaluza–Klein (KK) modes produce a smaller correction to the Newtonian potential [4]. The gauge bosons can be trapped to the brane by means of only the gravitational interaction [8]. Moreover, it is possible to localize the vector and spinor fields in the same geometry [9].

In spite of the aforementioned results, the string-like models exhibit some issues about their sources. In fact, these branes can be realized as a stable solution of a gauge and scalar fields [6, 7]. Nonetheless, the solution for the Einstein field equations for these models are still lacking. Amongst the string-like models, one which the width of the string vanishes and it is possible to concern with only the vacuum solution is the Gherghetta–Shaposhnikov (GS) model [4]. However, the thin-string-like models do not satisfy the dominant energy condition [10]. In order to overcome it, some authors solved numerically the equations for an Abelian vortex in six dimensions which exhibits a smooth geometry and satisfies all the energy conditions [11]. In the supersymmetric approach, a realistic and smooth cigar solution was also found by numerical means [12].

Another issue of the thin-string-like models, is that all the regularity conditions are not satisfied at the origin [10]. However, some authors added a conical behavior near the origin and studied its consequences [13–16], whereas others tried to smooth this conical behavior [16–24].

In this article we explore some features of a smooth extension of the GS model built analytically. Besides, using a smoothed warp function, the metric satisfies all the regularity conditions. We analyze the geometrical and physical properties of this model which yields an interior and exterior string-like solution, allowing near brane corrections to the GS model. The brane core is displaced from the origin. By studying the gravitational modes, we find a smoothed localized zero mode peaked around the shifted brane core. By means of a numerical analysis, we find a smooth near brane correction to the massive KK modes. Further, the quantum analog potential possesses an infinite well around the origin which barrier is strongly dependent on the bulk cosmological constant value.

This work is organized as follows: in Sect. 2, we review the main characteristics of the string-like branes and we present our extension. In Sect. 3, we study the properties of the source from the Einstein equations. Section 4 is devoted to the study of the massless and massive gravitational modes upon the geometry. Finally, in Sect. 5, some final remarks and perspectives are outlined.

2 Smoothed string-like geometry

In this section, we review the main properties of the string-like branes and propose another complete solution.

Let \(\mathcal {M}_{3}\) a \(3\)-brane and \(\mathcal {M}_{2}\) a two-dimensional Riemannian manifold. A string-like brane \(\mathcal {M}_{3}\) is a Lorentzian manifold with axial symmetry about \(\mathcal {M}_{2}\). Defining a gaussian radial coordinate \(\rho \in [0,\infty )\) and an angular coordinate \(\theta \in [0,2\pi ]\), a well-known ansatz for a warped six-dimensional string-like braneworld \(\mathcal {M}_{6}=\mathcal {M}_{p}\times \mathcal {M}_{2}\) is given by [3–8]

$$\begin{aligned} \mathrm{d}s^{2}= & {} G_{AB}(x^{\zeta },\rho ,\theta )\mathrm{d}x^{A}\mathrm{d}x^{B} \nonumber \\= & {} \sigma (\rho )\eta _{\mu \nu }\mathrm{d}x^{\mu }\mathrm{d}x^{\nu } + \mathrm{d}\rho ^{2} + \gamma (\rho )\mathrm{d}\theta ^{2}, \end{aligned}$$
(1)

where \(\sigma \) is the so-called warp function, the \(x^{\zeta }\) are on-brane coordinates, \((\rho ,\theta )\) are coordinates of the transverse manifold, and \(\gamma \) is an angular factor.

The action for the gravitational field is defined as

$$\begin{aligned} S_{g} =\int _{\mathcal {M}_{6}}{\left( \frac{1}{2\kappa _{6}}R-\Lambda +\mathcal {L}_{m}\right) \sqrt{-g}\, \mathrm{d}^{6}x}, \end{aligned}$$
(2)

where \(\kappa _{6}=8\pi /M_{6}^{4}\), \(M_{6}^{4}\) is the six-dimensional bulk Planck mass and \(\mathcal {L}_{m}\) is the matter Lagrangian for the source of the geometry. Note that in this convention, the bulk cosmological constant \(\Lambda \) has dimension \([\Lambda ]=L^{-6}=M^{6}\).

Consider an axisymmetric ansatz for the energy-momentum tensor [4, 8]:

$$\begin{aligned} T^{\mu }_{\nu }&= t_{0}(\rho )\delta ^{\mu }_{\nu },\end{aligned}$$
(3)
$$\begin{aligned} T^{\rho }_{\rho }&= t_{\rho }(\rho ),\end{aligned}$$
(4)
$$\begin{aligned} T^{\theta }_{\theta }&= t_{\theta }(\rho ), \end{aligned}$$
(5)

where

$$\begin{aligned} T_{AB}=\frac{2}{\sqrt{-g}}\frac{\partial (\sqrt{-g}\mathcal {L}_{m})}{\partial g^{AB}}. \end{aligned}$$
(6)

From the action (2), we obtain the Einstein equation

$$\begin{aligned} R_{AB}-\frac{R}{2}g_{AB} = -\kappa _{6}(\Lambda g_{AB} + T_{AB}). \end{aligned}$$
(7)

In order to guarantee a smooth \(3\)-brane at \(\rho =0\), we will adopt the usual regularity conditions [18, 19, 22, 23],

$$\begin{aligned} \sigma (0)= & {} 1 ,\quad \sigma '(0) = 0,\end{aligned}$$
(8)
$$\begin{aligned} \gamma (0)= & {} 0 ,\quad \left( \sqrt{\gamma (0)}\right) '=1, \end{aligned}$$
(9)

where the prime stands for the derivative \(\partial _{\rho }\).

A special analytical string-like braneworld is the GS model for which [4, 11]

$$\begin{aligned} \sigma (\rho ) = \text {e}^{-c \rho } \quad \text {and} \quad \gamma (\rho )=R_{0}^{2}\sigma (\rho ), \end{aligned}$$
(10)

where \(c\in \mathbb {R}\) is a constant of which the dimension is \([c]=L^{-1}\) and \(R_{0}\) is an arbitrary length scale. It is worthwhile to say that the ansatz (10) satisfies only the first regularity condition.

The GS model is constructed from the vacuum Einstein equation with cosmological constant [4]. Then

$$\begin{aligned} R=3\kappa _{6}\Lambda . \end{aligned}$$
(11)

The scalar curvature for the ansatz (8) is

$$\begin{aligned} R = - \frac{15}{2}c^{2}, \end{aligned}$$
(12)

which yields the well-known relationship [4, 8]

$$\begin{aligned} c^{2}=-\frac{2}{5}\kappa _{6}\Lambda . \end{aligned}$$
(13)

As a result, the GS model has a geometry of a \(AdS_{6}\) manifold. Indeed, performing the change of coordinates

$$\begin{aligned} z=z(\rho )=\frac{2}{c}\text {e}^{\frac{c}{2}\rho } \end{aligned}$$
(14)

and \(x_{4}=x_{4}(\theta )=R_{0}\theta \), the metric in Eq. (1) can be cast in the conformal form

$$\begin{aligned} \mathrm{d}s^{2}=\left( \frac{a}{z}\right) ^{2}\left( \mathrm{d}z^{2}+\mathrm{d}x_{1}^{2}+\mathrm{d}x_{2}^{2}+\mathrm{d}x_{3}^{2}+\mathrm{d}x_{4}^{2}-\mathrm{d}t^{2}\right) ,\nonumber \\ \end{aligned}$$
(15)

where \(a=\frac{2}{c}\) is the so-called \(AdS\) radius. Equation (15) is the \(Ads_{6}\) metric in the conformal coordinates [25, 26]. Since \(\rho \rightarrow \infty \Rightarrow z\rightarrow \infty \), then the conformal coordinates show that the warp factor shrinks the geometry to a point at infinity. Further, by means of the transformation

$$\begin{aligned} w=w(z)=\frac{a^{2}}{z}, \end{aligned}$$
(16)

the metric (15) can be written as

$$\begin{aligned} \mathrm{d}s^{2}\!=\!\left( \frac{w}{a}\right) ^{2}\left( \mathrm{d}x_{1}^{2}\!+\!\mathrm{d}x_{2}^{2}\!+\!\mathrm{d}x_{3}^{2}\!+\!\mathrm{d}x_{4}^{2}\!-\!\mathrm{d}t^{2}\right) \!+\! \left( \frac{a}{w}\right) ^{2}\mathrm{d}w^{2}.\nonumber \\ \end{aligned}$$
(17)

The metric in Eq. (17) is in the so-called Poincaré patch and it is used in the AdS–CFT correspondence [5, 27, 28].

In the Poincaré patch, the asymptotic point, also known as the \(AdS\) horizon, is located at \(w=0\). The decreasing behavior of the warp factor yields an asymptotic conical behavior. Ponton and Poppitz [5] proposed that it is possible to smooth out this horizon feature by embedding the GS model in the AdS–CFT correspondence. However, it is worthwhile to notice that, since the Ricci scalar is everywhere constant, the singularity at the horizon is not an essential singularity.

The existence of an apparent singularity at the horizon does not prevent the GS model to be a string-like geometry. Indeed, as shown by Israel, the general solution for a string-like geometry is given by the Kasner-like manifold

$$\begin{aligned} \mathrm{d}s^{2}_{4}\!=\!\mathrm{d}\rho ^{2}\!+\!\left( \frac{\rho }{\xi }\right) ^{2a_{1}}\mathrm{d}z^{2}\!+\! \chi ^{2}\left( \frac{\rho }{\xi }\right) ^{2a_{2}}\mathrm{d}\phi ^{2}\!-\!\left( \frac{\rho }{\xi }\right) ^{2a_{3}}\mathrm{d}t^{2},\nonumber \\ \end{aligned}$$
(18)

where \(a_{1}+a_{2}+a_{3}=a_{1}^{2}+a_{2}^{2}+a_{3}^{2}=1\) and \(\chi ,\xi \in \mathbb {R}\) [29]. The constant \(\chi \) measures the deficit angle whereas \(\xi \) provides the correct mass dimension for the metric. For \(a_{1}=a_{3}=0\) and \(a_{2}=1\) we obtain the Vilenkin string [30–32]. On the other hand, for \(a_{1}=a_{3}=\frac{2}{3}\) and \(a_{2}=-\frac{1}{3}\) we attain the so-called Melvin solution [33]. Other singular string-like solutions were found for a global string by Cohen and Kaplan [34] and Gregory [35] in four dimensions. In six dimensions, Cohen and Kaplan [6] proposed a string-like solution whose singularity far from the brane is responsible for the compactification. Gregory found a string-like brane without singularity which has the same behavior of the GS model [7]. Moreover, a smooth braneworld which asymptotically converges to the GS model was obtained by Giovannini et al. [11]. In this model, the source is given by a local and Abelian vortex [11].

The metric factors (10) can be regarded as an exterior solution of the string-like brane of width \(\epsilon \). For \(\epsilon \rightarrow 0\), the brane is infinitely thin. An awkward property of the thin-string-like branes is that they do not satisfy the dominant energy condition, which turns this model a fairly exotic scenario [10]. In order to overcome these issues, some authors derived numerically the geometry from an Abelian vortex [11] and in a supersymmetric approach [12]. Here, we propose an extension of the thin-string-like solution and we investigate the modifications on the geometrical and physical properties of this scenario.

In this work, we consider the following warp factor [36]:

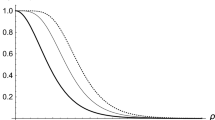
$$\begin{aligned} \sigma (\rho ) = \text {e}^{-(c\rho - \tanh {c\rho })}. \end{aligned}$$
(19)

It is noteworthy to mention two important features of this warp function in Eq. (19). First, as in the GS model, it behaves as \(\sigma (\rho )\approx \text {e}^{-c\rho }\) asymptotically [3, 4, 6–8, 10, 11]. Second, unlike the thin-string-like geometries [4, 8], it satisfies the regularity conditions. This last feature is due to the addition of the term \(\tanh {c \rho }\) that smoothens the warp factor near the origin [36]. The warp function has a bell-shape as sketched in Fig. 1. This agrees with the numerical solution generated by an Abelian vortex [11]. Therefore, we can realize this warp function as a near brane correction to the thin-string-like models [3, 4, 8, 9].

For the angular metric component, we have chosen the following ansatz:

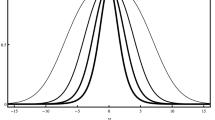
$$\begin{aligned} \gamma (\rho ) = \sigma (\rho )\beta (\rho ), \end{aligned}$$
(20)

where \(\beta (\rho )=\rho ^{2}\). Note that all the string-like regularity conditions are now satisfied. We have plotted the angular component (20) in Fig. 2, where we show that the function exhibits a smooth behavior near the brane. The \(\rho ^2\) term has a strong influence near the origin. Moreover, both the warp function and the angular component acquire a bell-shape. This feature is not present in the GS model [4]. However, the numerical solutions for the Abelian vortex model in six dimensions share similar profiles [11].

Fig. 1
figure 1

Warp function for some values of \(c\). The thin-string warp factor (subgraph) given by Eq. (10) is defined only for the exterior of the string

Full size image
Fig. 2
figure 2

Angular metric component for different values of \(c\). The subgraph refers to the thin-string angular metric component (10) for \(R_0 = 1.0\)

Full size image

The scalar curvature of \(\mathcal {M}_{6}\) has the expression

$$\begin{aligned} R&= c^2 \left( 10 \tanh {(c \rho )} \text {sech}^2{(c \rho )} - \frac{15}{2} \tanh ^4{(c \rho )}\right) \nonumber \\&\quad + 6 c \frac{\tanh ^2{(c \rho )}}{\rho }, \end{aligned}$$
(21)

which behavior is shown in Fig. 3. The curvature is everywhere smooth and asymptotically \(\mathcal {M}_{6}\) approaches the \(AdS_{6}\) case. In fact, considering the change of variable

$$\begin{aligned} z=z(\rho )=\int ^{\rho }{\sigma ^{-\frac{1}{2}}(\rho ')\mathrm{d}\rho '}, \end{aligned}$$
(22)

the metric (1) turns into

$$\begin{aligned} \mathrm{d}s^{2}_{6}=\sigma (z)\left( \mathrm{d}z^{2}+\eta _{\mu \nu }\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }+\beta (z)\mathrm{d}\theta ^{2}\right) . \end{aligned}$$
(23)

For large \(\rho \), the coordinate \(z\) behaves as \(z\approx \frac{2}{c}\text {e}^{\frac{c}{2}\rho }\). Then the string-cigar metric assumes the form

$$\begin{aligned} \mathrm{d}s^{2}_{6}\approx \left( \frac{a}{z}\right) ^{2}\left[ \mathrm{d}z^{2}+\eta _{\mu \nu }\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }+\left( \frac{2}{c}\ln {\frac{c}{2}z}\right) ^{2} \mathrm{d}\theta ^{2}\right] .\nonumber \\ \end{aligned}$$
(24)

Defining the coordinate \(x_{4}=\left( \frac{2}{c}\ln {\frac{c}{2}z}\right) \theta \), the metric (24) is changed to

$$\begin{aligned} \mathrm{d}s^{2}_{6}\approx & {} \left( \frac{a}{z}\right) ^{2}\left[ \left( 1-\left( \frac{\theta }{z}\right) ^{2}\right) \mathrm{d}z^{2}+\mathrm{d}x_{1}^{2}+\mathrm{d}x_{2}^{2}+\mathrm{d}x_{3}^{2}\right. \nonumber \\&\qquad \qquad \quad \left. - \mathrm{d}x_{4}^{2} - \frac{4\theta }{z}\mathrm{d}z\otimes \mathrm{d}\theta -\mathrm{d}t^{2}\right] . \end{aligned}$$
(25)

Therefore, the metric (25) recovers asymptotically the conformal form of the \(AdS_{6}\) manifold in the Poincaré patch (15). This ensures us that we may claim that \((\mathcal {M}_{6},\mathrm{d}s^{2}_{6})\) is an extension of the thin-string models near and far from the defect.

Fig. 3
figure 3

Bulk scalar curvature

Full size image

3 Sources properties

In this section, we study the components of the energy-momentum tensor as well as the value of the cosmological constant.

Using the metric ansatz (1), the Einstein equation (7) yields the components of the energy-momentum tensor in the form

$$\begin{aligned} t_{\theta }(\rho )= & {} \frac{5c^2}{\kappa _{6}}\left[ \text {sech}^{2}c\rho \left( 1 + \frac{4}{5} \tanh {c\rho }\right) -\frac{\text {sech}^{4} c \rho }{2} \right] ,\end{aligned}$$
(26)
$$\begin{aligned} t_{\rho }(\rho )= & {} \frac{5c^2}{\kappa _{6}}\left( \text {sech}^{2}c\rho + \frac{2}{5}\frac{\tanh ^{2}{c\rho }}{c\rho } -\frac{\text {sech}^{4} c \rho }{2} \right) ,\end{aligned}$$
(27)
$$\begin{aligned} t_{0}(\rho )= & {} t_{\theta }(\rho ) + \frac{5c}{2\kappa _6} \frac{\tanh ^{2}{c \rho }}{\rho } . \end{aligned}$$
(28)
Fig. 4
figure 4

Components of the energy-momentum tensor for \(c = 1.0\) (a) and \(c=4.0\) (b)

Full size image

For large \(\rho \), the components of the energy-momentum tensor vanish and the vacuum solution of the Einstein equation yields the relation between \(c\) and \(\Lambda \) given by Eq. (13). This equation determines the bulk to be asymptotically an \(AdS_{6}\) spacetime. Besides, it also means that, by varying \(c\), we can study the changes in the source and fields for different bulk cosmological constant values.

We have plotted in Fig. 4 the components of the energy-momentum tensor for \(\kappa _6 = 1\). It can be seen that, for \(i = \rho ,\theta \),

$$\begin{aligned} t_{0}(\rho ) + t_{i}(\rho )\geqslant & {} 0,\nonumber \\ t_{0}(\rho )\geqslant & {} 0 \quad \text {(weak energy condition)},\end{aligned}$$
(29)
$$\begin{aligned} t_{0}(\rho ) + \sum _{i} t_{i}(\rho )\geqslant & {} 0 \quad \text {(strong energy condition)}, \end{aligned}$$
(30)

and

$$\begin{aligned} t_{0}(\rho ) \geqslant | t_{i}(\rho ) | \quad \text {(dominant energy condition)}. \end{aligned}$$
(31)

Only the \(c = 1.0\) and \(c = 4.0\) cases are presented in Fig. 4. However, it is straightforward to prove that the conditions (29)–(31) are satisfied for all the (positive) values of \(c\). Since the hyperbolic functions in Eqs. (26)–(28) are limited from \(0\) to \(1\), all the terms of these equations are positive. Furthermore, the term \(\text {sech}^4(c\rho )\) is rather small, what directly proves the weak and the strong energy conditions. The term \(\frac{5c}{2\kappa _6}\frac{\tanh ^2(c\rho )}{c\rho }\) in Eq. (28) is responsible for the proof that the dominant energy condition (31) is satisfied. Firstly, from Eq. (28), it is obvious that \(t_0(\rho ) \ge t_{\theta }(\rho )\). If we write explicitly the expressions (26)–(28) in the inequality \(t_0(\rho ) \ge t_{\rho }(\rho )\), we are led to

$$\begin{aligned} \frac{4}{5}\text {sech}^2(c\rho )\tanh (c\rho ) \ge -\frac{1}{10}\frac{\tanh ^2(cp)}{c\rho }, \end{aligned}$$
(32)

which is satisfied, because the left side is always positive.

It is important to note that the near brane corrections, provided by the ansatz (19) and (20), lead to a displacement of the core of the source from the origin. Similar results have been obtained by Giovannini et al. [11] numerically for higher winding number Abelian vortices and for the string-cigar model [36]. Moreover, the brane width defined as \(\epsilon \approx \bar{\rho } - \rho _{\text {max}}\), where \(\bar{\rho }\) and \(\rho _{\text {max}}\) are the positions of the half-maximum and the maximum of \(t_0\), respectively, tends to zero when \(c\rightarrow \infty \). Therefore, the GS model can be seen as a \(c\rightarrow \infty \)-limit of this smoothed version.

4 Gravity localization

We now study the gravity localization on a \(3\)-brane embedded on this six-dimensional geometry. We consider a small perturbation \(h_{\mu \nu }\) in the background metric in the form

$$\begin{aligned} \mathrm{d}s^{2}_{6}=\sigma (\rho ,c)(\eta _{\mu \nu }+h_{\mu \nu })\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }+\mathrm{d}\rho ^{2}+\gamma (\rho ,c) \mathrm{d}\theta ^{2}.\nonumber \\ \end{aligned}$$
(33)

Imposing the transverse traceless gauge \(\nabla ^{\mu } h_{\mu \nu }\) = \(0\), the linearization of the Einstein equations yields the equation for the gravitational perturbation [4, 24],

$$\begin{aligned} \partial _{A} (\sqrt{-g_{6}} g^{AB} \partial _{B} h_{\mu \nu } ) = 0. \end{aligned}$$
(34)

Performing the well-known Kaluza–Klein decomposition [4]

$$\begin{aligned} h_{\mu \nu } (x^{\zeta }, \rho , \theta ) = \tilde{h}_{\mu \nu }(x^{\zeta })\sum _{m,l=0}^{\infty } \phi _{m,l}(\rho ) \text {e}^{i l \theta }, \end{aligned}$$
(35)

where \(l\) is an integer and \(0\le \theta \le 2\pi \), and imposing the mass condition

$$\begin{aligned} \square _{4} \tilde{h}_{\mu \nu } (x^{\zeta }) = m^{2} \tilde{h}_{\mu \nu } (x^{\zeta }), \end{aligned}$$
(36)

the radial modes satisfy the Sturm–Liouville equation

$$\begin{aligned}&\frac{\mathrm{d}^{2}}{\mathrm{d}\rho ^{2}} \phi (\rho ) + \left( \frac{1}{\rho } - \frac{5}{2}c\tanh ^{2} (c\rho )\right) \frac{\mathrm{d}}{\mathrm{d}\rho }\phi (\rho ) \nonumber \\&\quad + M^{2}(\rho ) \text {e}^{c \rho - \tanh c \rho } \phi (\rho ) = 0. \end{aligned}$$
(37)

The factor \(M^{2}(\rho )\) = \(\left( m^{2} - \frac{l^{2}}{\rho ^{2}}\right) \) is an effective mass containing orbital angular momentum contributions \(l\) and it behaves as a position dependent mass. Note that we have a degenerate KK spectrum, as in the GS model [4]. However, since \(\lim _{\rho \rightarrow \infty }{M^{2}(\rho )}=m^{2}\), the degeneracy is broken for large distances.

Due to the axial symmetry, we impose the Neumann boundary conditions on \(\phi _{m}\) [4, 36]

$$\begin{aligned} \phi '_{m}(0) = \phi '_{m} (\infty ) = 0. \end{aligned}$$
(38)

Furthermore, these modes satisfy the following orthonormality condition:

$$\begin{aligned} \int _{0}^{\infty } \sigma (\rho ) \sqrt{\gamma (\rho )} \phi ^{*}_{m} \phi _{n} \mathrm{d}\rho = \delta _{mn}. \end{aligned}$$
(39)

4.1 Massless mode

For \(M^{2}(\rho ) = 0\) (gravitational massless mode), a solution for Eq. (37) satisfying the boundary conditions (38) is the constant \(\phi (\rho ) = \phi _{0}\). However, from the orthornormality relation (39), we obtain a varying zero-mode function \(\psi _{0}\) [4, 24, 36],

$$\begin{aligned} \psi _0(\rho ) = \phi _0 \sigma (\rho )\beta ^{\frac{1}{4}}(\rho ), \end{aligned}$$
(40)

where \(\phi _0\) plays the role of a normalization constant given by

$$\begin{aligned} \phi _0^2 = \frac{1}{\int _0^{\infty } \sigma ^{\frac{7}{2}}(\rho )\beta (\rho )\mathrm{d}\rho }. \end{aligned}$$
(41)

In the next section we shall prove that \(\psi _{0}\) is in fact the massless mode using the Schrödinger approach.

Analysis of the massless mode graph, shown in Fig. 5, reveals new results. Differently from thin-strings models, the maximum of \(\psi _0\) is displaced from origin. It agrees with the fact that the brane core is not at \(\rho = 0\). As discussed in Sect. 3, the brane core approaches the origin when \(c\) increases. This behavior directly reflects on the zero-mode solution. This effect is due to the smooth correction near the origin induced by the \(\beta \) factor. This mode goes along with the energy-momentum tensor. As \(c\) increases, the maximum of the zero mode and the energy density tend to coincide.

Therefore, our smoothed model provides a near brane correction to the massless gravitational mode, smoothens the zero mode in the boundary of the core, and recovers the thin-string exponential behavior for large distances.

Fig. 5
figure 5

Gravitational massless mode

Full size image
Fig. 6
figure 6

Numerical solutions of Eq. (37) for \(m = 44.10\) (a) and \(m = 22.82\) (b). The sub-graphs are plots of the GS massive mode (44) for the same mass values, where \(C_1 = C_2 = 0.2\) (a) and \(C_1 = C_2 = 0.01\) (b)

Full size image

4.2 Massive modes

Solutions of Eq. (37) for \(M^2(\rho ) \ne 0\), called massive modes, are difficult to obtain analytically. Before embarking on a numerical analysis two different regimes are studied.

Firstly, we analyze the graviton massive modes near the brane (\(\rho \rightarrow 0\)). In this limit, the differential equation (37) is reduced to a Bessel equation

$$\begin{aligned} \frac{\mathrm{d}^{2}}{\mathrm{d} \rho ^{2}} \phi (\rho ) + \frac{1}{\rho } \frac{\mathrm{d}}{\mathrm{d} \rho } \phi (\rho ) + M^{2}(\rho )\phi (\rho ) = 0, \end{aligned}$$
(42)

which solutions satisfying the boundary conditions (38) are given by the Bessel functions of first kind \(J_{l}(m \rho )\). Furthermore, the boundary condition (38) excludes the \(l = 1\) solution; then p-waves are not allowed.

Asymptotically (\(\rho \rightarrow \infty \)), Eq. (37) becomes

$$\begin{aligned} \frac{\mathrm{d}^{2}}{\mathrm{d} \rho ^{2}} \phi (\rho ) - \frac{5 c}{2} \frac{\mathrm{d}}{\mathrm{d} \rho } \phi (\rho ) + m'^{2} \text {e}^{c \rho } \phi (\rho ) = 0, \end{aligned}$$
(43)

with a non-degenerate re-scaled mass \(m' = m/\sqrt{\text {e}}\). This equation is exactly the same as the GS model, of which the solution is [4]

$$\begin{aligned} \phi _{m^{\prime }} (\rho )&= \text {e}^{(5/4) c \rho } \left[ C_{1} J_{5/2} \left( \frac{2 m^{\prime }}{c} \text {e}^{(c/2) \rho } \right) \right. \nonumber \\&\quad \left. +C_{2} Y_{5/2}\left( \frac{2 m^{\prime }}{c} \text {e}^{(c/2) \rho } \right) \right] , \end{aligned}$$
(44)

where \(C_{1}\) and \(C_{2}\) are arbitrary constants and \(Y\) is the Bessel function of second kind.

Fig. 7
figure 7

Potential function \(\bar{U}(\rho )\) for the Schrödinger-like equation with \(l = 0\) (a) and \(l = 2\) (b)

Full size image

In order to obtain a complete domain solution, we integrated Eq. (37) numerically. For this purpose, we used the matrix method [37] with second order truncation error for the domain \(\rho \in [0,6]\). We have plotted in Fig. 6 numerical solutions for \(c = 1.0\), comparing with the analytical GS model solution (44). Near the origin, the solutions behave as a Bessel function, whereas far from the brane, they behave as the GS massive modes solutions. The main advantage of the numerical approach is that we obtain the full domain solution, so we may construe inside brane massive gravitons. In contrast to the thin-string model, the massive solutions are non-zero with a high amplitude near the brane.

4.3 Analog quantum potential

Another way to study massive modes is to turn the KK equation (37) into a Schrödinger-like equation. This formalism provides information as regards massive states that interact with the brane. Firstly, we perform a change of the independent variable, given in Eq. (22), which provides a conformally plane metric [24, 36]. Then we write \(\phi (z)\) as

$$\begin{aligned} \phi _m(z) = \frac{1}{\sigma (z)\beta ^{\frac{1}{4}}(z)} \psi _m(z), \end{aligned}$$
(45)

which turns Eq. (37) into a Schrödinger equation for the \(\psi _m(z)\) function

$$\begin{aligned} -\ddot{\psi }_m(z) + U(z) \psi _m(z) = m^{2} \psi _m(z), \end{aligned}$$
(46)

where the dots represent derivatives with respect to the \(z\) coordinate. The potential function has the form

$$\begin{aligned} U(z) = \frac{\ddot{\sigma }}{\sigma } + \frac{1}{2} \frac{\dot{\sigma }}{\sigma } \frac{\dot{\beta }}{\beta } - \frac{3}{16} \left( \frac{\dot{\beta }}{\beta }\right) ^{2} + \frac{1}{4} \frac{\ddot{\beta }}{\beta } + \frac{l^{2}}{\beta }. \end{aligned}$$
(47)

From Eq. (45), we conclude that the massless mode defined in Eq. (40) satisfies the analog Schrödinger equation for \(m = 0\). The potential can be rewritten in the \(\rho \) coordinate as

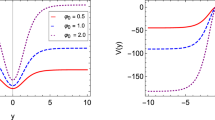
$$\begin{aligned} \bar{U}(\rho ;c,l)&= \text {e}^{-(c \rho - \tanh c \rho )} \left( - 2 c^{2} \tanh (c\rho ) \text {sech}^2(c\rho ) \right. \nonumber \\&\quad + \frac{3}{2} c^{2} \tanh ^{4}(c\rho ) - \frac{5c}{4}\frac{\tanh ^{2}(c \rho )}{\rho } - \frac{1}{4 \rho ^{2}} \nonumber \\&\quad +\left. \frac{l^{2}\text {e}^{(c \rho - \tanh c \rho )}}{\rho ^{2}} \right) . \end{aligned}$$
(48)

We have plotted the potential \(\bar{U}(\rho )\) given by Eq. (48) in Fig. 7. For \(l = 0\) we have a potential well near the origin, showing the possibility arises of bound states where massive gravitons may interact with the brane as resonant states [38, 39]. As \(c\) increases, a barrier is formed besides the origin. On the other hand, for \(l>1\), there is an infinite barrier avoiding any bound state. Therefore, massive gravitons with angular momentum \(l>1\) cannot interact with the brane, whereas, for \(l = 0\), resonant states (quasi-localized gravitational massive states highly coupled to the brane [40, 41]) are possible. The consequences of this interaction may be detected phenomenologically as a correction to the Newtonian potential [4, 40, 41]. It is expected since we have a degenerate massless spectrum in Eq. (37) and the four-dimensional graviton is identified with the s-waves (\(l=0\)).

It is important to note from the massless mode solution that the Neumann boundary conditions are satisfied around the brane core position. Moreover, for \(\rho \rightarrow 0\), \(\psi _0^{\prime } \rightarrow \infty \), which agrees with the infinite potential well (see Fig. 7a).

5 Conclusions and perspectives

We have studied the geometrical and physical properties of a six-dimensional thin-string braneworld extension considering a square dependence on radial extra coordinate on the angular metric component. We proposed a subtle warp function that agrees with the thin-string-like model far from the brane, yielding near brane corrections. The geometry possesses an axial symmetry about the origin and the curvature is well behaved. Although we have not been concerned with a specific physical model, the source of this geometry satisfies all the energy conditions. The energy density has a maximum displaced from the origin and a non-null thickness.

We also performed the gravity localization in this scenario. The massless mode is localized and, differently from thin-string models, also has a maximum displaced from the origin, which for great values of the cosmological constant tends to coincide with the energy density one. This shift of the core is due to the near brane smooth correction. Moreover, for large values of the cosmological constant, the model is reduced to a thin-string model slightly apart from the origin. More attention was given to massive modes. We firstly analyzed the graviton massive modes equation for its asymptotic regimes and showed that near brane solutions are expressed in terms of Bessel functions of the first kind for angular momentum values \(l \ne 1\). Far from the brane, we recover the Gherghetta–Shaposhnikov thin-string model without degenerate states. Numerical solutions of the equation for the massive modes revealed that, in contrast to the thin-string model, the massive solutions have a considerable amplitude near the brane, indicating the possibility of gravitational massive states interacting with the defect. This result was reinforced from a Schödinger approach, where we have studied the analog quantum potential. From this formalism we proved the massless mode, which must satisfy a Schödinger-like equation for \(m = 0\). We also concluded that massive states may interact with the brane only for \(l = 0\) which refers to four-dimensional gravitons.

As a future perspective, the KK spectrum can be achieved from the analog quantum potential by means of suitable numerical methods to predict corrections to the Newtonian potential.