Nonlinear electromagnetic quasinormal modes and Hawking radiation of a regular black hole with magnetic charge

Abstract

Based on a regular exact black hole (BH) from nonlinear electrodynamics (NLED) coupled to general relativity, we investigate the stability of such BH through the Quasinormal Modes (QNMs) of electromagnetic (EM) field perturbations and its thermodynamics through Hawking radiation. In perturbation theory, we can deduce the effective potential from a nonlinear EM field. The comparison of the potential function between regular and RN BHs could predict similar QNMs. The QNM frequencies tell us the effect of the magnetic charge $q$, the overtone $n$, and the angular momentum number $l$ on the dynamic evolution of NLED EM field. Furthermore we also discuss the cases of near-extreme conditions of such a magnetically charged regular BH. The corresponding QNM spectrum illuminates some special properties in the near-extreme cases. For the thermodynamics, we employ the Hamilton–Jacobi method to calculate the near-horizon Hawking temperature of the regular BH and reveal the relationship between the classical parameters of the black hole and its quantum effects.

1 Introduction

In the framework of a black hole, the research of singularity-free black holes has attracted considerable attention during the last decades. Fortunately physicists have found a new type of black-hole solutions without singularity in general relativity [1] and more general gravity theories to construct solutions without a singularity, such as string theory and exact conformal field theory [2, 3]. Especially with gravitation coupling to a suitable nonlinear electrodynamics (NLED) field, some regular metrics would be obtained [4–8]. Ayon-Beato, Garcia and Bronnikov successively found some static, spherically symmetric non-singular solutions [5–8]. It is also remarkable that all the NLED satisfy the zeroth and first laws of BH mechanics [9]. In the theory of NLED coupling to the Einstein equations, it is important to seek a suitable gauge-invariant Lagrangian $\mathcal{L}(F)$ ($F=F_{\mu \nu }F^{\mu \nu }$ is the electromagnetic tensor), and its energy-momentum tensor (EMT),

$$\begin{aligned} T_{\nu \mu }=\frac{1}{4\pi }\left[ \frac{\mathrm{d}\mathcal{L}(F)}{\mathrm{d}F}F_{\rho \mu }F^{\rho }_{\nu }-\frac{1}{4}g_{\mu \nu }\mathcal{L}(F)\right] , \end{aligned}$$

(1)

satisfying the symmetry $T^{0}_{0}=T^{1}_{1}$ [5, 10]. In this paper, we consider the stability of a specific regular BH solution, assuming

$$\begin{aligned} \mathcal{L}(F)=F\cosh ^{-2}\left( a\left| \frac{F}{2}\right| ^{1/4}\right) , \end{aligned}$$

(2)

in NLED theory. Here $a=|q|^{\frac{3}{2}}/2M$ ($M$ is the mass of BH). Without loss of generality, if there is no specific statement otherwise, we set $M=1$ in this paper. Then the static, spherically symmetric metric is described by [5, 7]

$$\begin{aligned} \mathrm{d}s^{2}=-f(r)\mathrm{d}t^{2}+f(r)^{-1}\mathrm{d}r^{2}+r^{2}\mathrm{d}\theta ^{2}+r^{2}\sin ^{2}\theta \mathrm{d}\phi ^{2}, \end{aligned}$$

(3)

where

$$\begin{aligned} f(r)=1-\frac{2M}{r}\left[ 1-\tanh \left( \frac{q^{2}}{2Mr}\right) \right] , \end{aligned}$$

(4)

where $q$ should obey Theorem 1 discussed in [5] (i.e., $q=q_{\mathrm{m}}\ne 0,q_{\mathrm{e}}=0$, where $q_{\mathrm{m}}$ is magnetic charge). About a decade ago, Mosquera Cuesta and Salim [11, 12] presented with NLED the gravitational redshift of super-strongly magnetized compact objects, such as pulsars and particular neutron stars that would rely definitely on the magnetic field permeating the magnetized objects. This is opposed to general relativity, where the gravitational redshift and background magnetic field are unrelated. Meanwhile they found that the gravitational redshift is related to the mass–radius ratio of the object, so that this NLED effect would also have impact on the metric of the black hole [11, 12]. The discussion of the effective metric of our regular spacetime indicates that the original metric is indeed revised by NLED moderately (see Appendix A). Since the discrepancy mainly concentrates on the area around $r=0$, we still consider the EM perturbation in the original spacetime in the following context.

A black hole can be described completely under perturbations, so that it is necessary to analyze the perturbations once one wants to know something about its stability [13]. After perturbation, BH will experience three stages (Initial oscillation–QNMs ringing–Ringdown), which can give us a glimpse into the interior region of black holes. The second stage named “quasinormal mode (QNM) ringing” contributes to gravitational wave (GW) detection. From a theoretical point of view, perturbations of a black hole spacetime can be performed in two ways: by adding fields to the black-hole spacetime or by perturbing the black-hole metric (the background) itself. The former way refers to physical particle fields such as scalar, Dirac, and electromagnetic (EM) fields; the latter one is the gravitational perturbation resulting in GWs. Many researches into regular BH QNMs have made great progress, focusing on scalar fields [14–17] and Dirac perturbations [18]. Usually the singularity of a regular black hole may vanish under the condition that gravitation be coupled to a suitable nonlinear electrodynamics (NLED) field; therefore we consider the QNMs of EM perturbations in specific regular spacetimes to be more meaningful.

The beginning of a QNMs calculation is to reduce the perturbation equations (which vary with the spin of the perturbation fields) into a two-dimensional wavelike form with decoupled angular variables. Once the variables are decoupled, the equation for radial and time variables usually has a Schrödinger-like form in a stationary background. Then the corresponding potential function $V(r)$ can be determined, which is the key to the numerical computation of the QNM frequencies (QNFs). Numerical methods for calculation of the QNFs have been developed for several years, and now mainly consist of the time domain method [19–21], the expansion method [22, 23], direct integration in the frequency domain [24], the WKB method [25–28], and the finite differential method [29, 30]. Since the WKB scheme has been shown to be more accurate for both the real and the imaginary parts of the dominant QNMs with $n\le l$ [31], we apply the WKB method to the QNF calculation and compare the results with the ones from the expansion method.

As important as the stability of BH, the thermodynamics of black holes is thought to be the connection between black-hole physics and quantum theory. Hawking radiation can be seen as quantum tunneling around the horizon, and the Hawking temperature of black holes can be deduced through the tunneling rate [32–37]. In order to find the effect of their classical parameters on Hawking radiation, we also study this topic for the magnetically charged regular BH in this paper.

The paper is organized as follows. In Sect. 2, we describe the nonlinear electromagnetic field equations in regular spacetimes and determine the shape of the potential. Since the regular spacetime asymptotically behaves as the Reissner–Nordström (RN) BH, we compare them. In Sect. 3 we use a sixth-order WKB method and expansion method to compute the QNFs of the regular solution and RN BH. Furthermore we apply the finite differential method to display intuitive images of the QNM perturbation. In Sect. 4, we investigate the strong charged cases for the spherically symmetric regular black hole and evaluate the QNMs through a third-order WKB method, since the sixth-order WKB method may break down if the potential is complicated [22, 23]. In order to further understand the magnetically charged regular BH, Sect. 5 shows the Hawking radiation of such a BH. Conclusions and future work are presented in Sect. 6.

2 The nonlinear electromagnetic field perturbation to the regular BH

The action proposed in Einstein-dual nonlinear electromagnetic theory is [38]

$$\begin{aligned} S=\frac{1}{16\pi }\int \mathrm{d}^{4}x\sqrt{-g}[R-\mathcal{L}(F)], \end{aligned}$$

(5)

where $R$ is the scalar curvature, $F=F_{\mu \nu }F^{\mu \nu }, F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }$ is the electromagnetic field. $\mathcal{L}(F)$ is the Lagrangian function of this theory, and it returns to the linear case (i.e., Maxwell field) at small $F$: $\mathcal{L}(F)\simeq F$ as $F\rightarrow 0$. The tensor $F_{\mu \nu }$ obeys Eq. [5],

$$\begin{aligned} \nabla _{\mu }(\mathcal{L}_{F}F^{\mu \nu })=0, \end{aligned}$$

(6)

with $\mathcal{L}_{F}=\mathrm{d}L/\mathrm{d}F$. We consider the background to be a spherically symmetric regular spacetime involving only a radial magnetic field (i.e., $\bar{A}_{3}=-q_{\mathrm{m}}\cos {\theta }$ and other components of $\bar{A}_{\mu }$ equal to zero) [39]. The zeroth-order solution of Eq. (6) is the solution of the background EM field in the regular static spacetime. Then we add the perturbation, $\delta A_{3}$, to the background EM field, yielding

$$\begin{aligned} A_{3}=\bar{A}_{3}+\delta A_3, \end{aligned}$$

(7)

where the NLED electromagnetic perturbation, $\delta A_3$, has a small value, which can be expressed as $\psi (t,r)P_{l}$ ($P_{l}=P_{l}(\cos \theta )$ is a Legendre function) after separation of the variables. According to $F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }$, $F^{\mu \nu }=F_{\alpha \beta }g^{\mu \alpha }g^{\beta \nu }$ and neglecting the second- and higher-order perturbed terms, we find the non-zero perturbed $F^{\mu \nu }$ and $F$ to be

$$\begin{aligned}&F^{03}=-F^{30}=-\frac{\text {csc}^{2}\theta P_{l}}{r^{2}f(r)}\frac{\partial \psi (t,r)}{\partial t},\nonumber \\&F^{13}=-F^{31}=\frac{\text {csc}^{2}\theta f(r)P_{l}}{r^{2}}\frac{\partial \psi (t,r)}{\partial r},\\&F^{23}=-F^{32}=\frac{\text {csc}^{2}\theta }{r^{4}}\left( q\text {sin}\theta +\psi (t,r)\frac{\mathrm{d}P_{l}}{\mathrm{d}\theta }\right) ,\nonumber \end{aligned}$$

(8)

$$\begin{aligned} F=\frac{2q^{2}}{r^{4}}+\frac{4q\text {csc}\theta \psi (t,r)}{r^{4}}\frac{\mathrm{d}P_{l}}{\mathrm{d}\theta }. \end{aligned}$$

(9)

Substituting Eq. (9) into Eq. (2) and assuming $\psi (t,r)=\phi (r)\exp (-i\omega t)$ yield $\mathcal{L}_{F}$:

$$\begin{aligned} \mathcal{L}_{F}=\bar{\mathcal{L}}_{F}+\delta \mathcal{L}_{F}, \end{aligned}$$

(10)

where $\bar{\mathcal{L}}_{F}$ is the $\mathcal{L}_{F}$ of the background EM field and $\delta \mathcal{L}_{F}$ is the perturbation term of $\mathcal L_{F}$. They are

$$\begin{aligned} \bar{\mathcal{L}}_{F}=-\frac{1}{2}\text {sech}^{2}\left( \frac{a\sqrt{q}}{r}\right) \left( -2+\frac{a\sqrt{q}}{r}\text {tanh}\left( \frac{a\sqrt{q}}{r}\right) \right) ,\nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned} \delta \mathcal{L}_{F}= & {} \frac{1}{8q}\bigg [\frac{a\sqrt{q}}{r}\text {csc}\theta \text {sech}^{4}\left( \frac{a\sqrt{q}}{r}\right) \nonumber \\&\times \left( -4\frac{a\sqrt{q}}{r}+2\frac{a\sqrt{q}}{r}\text {cosh}\left( \frac{a\sqrt{q}}{r}\right) \right. \nonumber \\&\left. -\,5\text {sinh}\left( 2\frac{a\sqrt{q}}{r}\right) \right) \frac{\mathrm{d}P_{l}}{\mathrm{d}\theta }\phi (r)\exp (-i\omega t)\bigg ]. \end{aligned}$$

(12)

Therefore, substituting the above quantities into Eq. (6) and defining $\phi (r)=B(r)R(r)$ (where $B(r)$ satisfies $B'(r)/B(r)=-\bar{\mathcal{L}}'_{F}/2\bar{\mathcal{L}}_{F}$), we obtain the main equation with the first order in the perturbation,

$$\begin{aligned} \left[ \frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}_{*}}+\omega ^{2}-V_{\mathrm{regular}}(r)\right] R(r)=0, \end{aligned}$$

(13)

where a prime represents $\mathrm{d}/\mathrm{d}r$, $\mathrm{d}/\mathrm{d}r_{*}=f(r)\mathrm{d}/\mathrm{d}r$, and

$$\begin{aligned}&V_{\mathrm{regular}}(r)\nonumber \\&\quad =\frac{l(l+1)f(r)}{r^{2}}-\frac{f^{3}\bar{\mathcal{L}}'_{F}(\bar{\mathcal{L}}_{F}f'+f\bar{\mathcal{L}}'_{F})(-3\bar{\mathcal{L}}'^{2}_{F}+2\bar{\mathcal{L}}_{F}\bar{\mathcal{L}}''_{F})}{8\bar{\mathcal{L}}^{4}_{F}} \nonumber \\&\qquad -\,\frac{f(r)}{4r^{4}\bar{\mathcal{L}}_{F}}\left\{ a^{2}ql(l+1)\text {sech}^{2}\left( \frac{a\sqrt{q}}{r}\right) \right. \nonumber \\&\qquad \times \left. \left[ -2+3\text {sech}^{2}\left( \!\frac{a\sqrt{q}}{r}\right) +5\frac{r}{a\sqrt{q}}\tanh \left( \!\frac{a\sqrt{q}}{r}\right) \!\right] \right\} . \end{aligned}$$

(14)

The RN BH is a result of the linear electromagnetic field, in which $q$ represents the electric charge $q_{\mathrm{e}}$. So it is meaningful to compare the effective potential function $V(r)$ with the RN solution. We use the same principle under the following replacement: $A_0=q/r$; $A_{3}=\delta A_3$; $F=-2q^{2}/r^{4}$; $\mathcal{L}(F)=F$, yielding

$$\begin{aligned} V_{\mathrm{RN}}(r)= & {} \frac{l(l+1)f_{\mathrm{RN}}(r)}{r^{2}}\nonumber \\&-\frac{f_{\mathrm{RN}}^{3}\bar{\mathcal{L}}'_{F}(\bar{\mathcal{L}}_{F}f_{\mathrm{RN}}'+f_{\mathrm{RN}}\bar{\mathcal{L}}'_{F})(-3\bar{\mathcal{L}}'^{2}_{F}+2\bar{\mathcal{L}}_{F}\bar{\mathcal{L}}''_{F})}{8\bar{\mathcal{L}}^{4}_{F}}. \end{aligned}$$

(15)

Note the following.

(1) Due to $\mathcal{L}(F)=F$, $\bar{\mathcal{L}}_{F}=1$, the above equation can be simplified as

$$\begin{aligned} V_{\mathrm{RN}}(r)=\frac{l(l+1)f_{\mathrm{RN}}(r)}{r^{2}}. \end{aligned}$$

(16)

(2) Actually, as a result of the linear electromagnetic field, there is a category of charged black holes named Kerr–Newman–Kusuya black holes [40–42], which represents a number of static or stationary rotating black holes with electric and magnetic charges. But using an equivalent charge $q_{\mathrm{h}}$ as discussed in Appendix C instead of $q_{\mathrm{e}}$, the spacetime of the Kerr–Newman–Kusuya black hole without rotation has the same expression as an ordinary RN solution. So we choose RN as a representative to be discussed in this paper.

Fig. 1

The potential function $V(r)$ of the regular metric and RN BH ($M=1$), for regular BH, $q=q_{\mathrm{m}}$, while $q=q_{\mathrm{e}}$ under the RN condition

Fig. 2

The comparison of QNMs frequencies from the regular BHs and RN BHs ($M=1$)

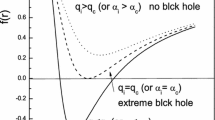
As predicted, the potential behavior of the regular solution is quite similar to the RN BH although the regular metric comes from NLED coupling to the Einstein equation, while the RN solution is deduced from linear EM theory. Figure 1 displays the effective potential of the regular metric and the RN solution. We find that their difference mainly is concentrated in the area near $r=0$, and they always tend to overlap each other once away from $r=0$. Therefore their QNM frequencies would also be very similar, which is reflected by Fig. 2 and Table 1.

3 QNMs for the nonlinear electromagnetic field perturbation

The NLED EM perturbation is governed by the wave equation,

$$\begin{aligned} \left[ \frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}_{*}}+\omega ^{2}-V(r,l)\right] \psi (t,r)=0, \end{aligned}$$

(17)

where $\psi (t,r)=\Phi (r)\mathrm{e}^{-i\omega t}$. The solution satisfies the following boundary conditions:

• 1. Pure ingoing waves at the event horizon $\Phi (r)\sim \mathrm{e}^{-i\omega r_{*}}$, $r_{*}\rightarrow -\infty$.

• 2. Pure outgoing waves at the spatial infinity $\Phi (r)\sim \mathrm{e}^{i\omega r_{*}}$,$r_{*}\rightarrow \infty$.

The WKB approximation can be used for the effective potential, which has the form of a potential barrier and takes constant values at the event horizon and spatial infinity. The method is based on matching the asymptotic WKB solutions at spatial infinity and the event horizon with a Taylor expansion near the top of the potential barrier through two turning points. Using the above potential functions, we calculate the QNMs frequencies through a sixth-order WKB approximation, which has been proven to be the most accurate method for finding the quasinormal spectrum with lower overtones [43].

Firstly, in order to illuminate the similarities of the QNMs from RN and such regular BH, it is necessary to compare their QNFs with some typical values. From Fig. 2, it can be found that their discrepancy keeps to a small range, which is consistent with the results in Table 1 and, more importantly, varying the parameters their QNF curves have the same shapes. So the relationship between QNMs of the regular metric and parameters (such as $q$, $l$, and $n$) may stand for the cases of an RN solution. Therefore in the following, we only figure out the QNMs of the regular BH.

Table 1 QNMs frequencies evaluated by expansion method ($n=0,M=1$ ignoring the $L^{-3}$ term)

Secondly, we calculate the QNMs frequencies with $n=0,1,2$, and for each overtone $n$ we choose $l=n+1,n+2,n+3$ to determine how the magnetic charge impacts the QNMs. Figure 3 shows the shapes of QNMs with different $n$ and $l$. For the real part of $\omega$, it increases with larger $q$ and $l$, however, it decreases slightly with higher overtone. This means the perturbation in the fundamental mode (i.e., $n=0$) with larger $q$ and $l$ leads to a more intense QNM oscillation. For the imaginary part of $\omega$, we find that:

(1) given $n,l$, $|\mathrm{Im}(\omega )|$ increases with stronger charge;

(2) given $q$, in the $n=0$ case the higher $l$ enhances $|\mathrm{Im}(\omega )|$, while in the $n=1,2$ cases $l$ has an inverse effect on $|\mathrm{Im}(\omega )|$. This can be seen as a property of fundamental QNM oscillations.

Overall, for such a regular BH the fundamental mode with lower charge and angular momentum number plays the dominant role in QNMs oscillation, since it exists for the longest time.

Fig. 3

The QNMs frequencies of the regular metric ($M=1$)

Next, we employ the expansion method to evaluate the QNM frequencies. It has been known for many years that QNMs are intimately linked to the existence and properties of unstable null orbits, and Dolan and Ottewill [22] developed a simple method for determining the QNMs frequency $\omega$, which can be expanded in inverse powers of $\hat{l}=l+1/2$.

According to the expansion method proposed by Dolan and Ottewill, the radial function $\Phi (r)$ can be redefined as

$$\begin{aligned} \Phi (r)=\upsilon (r)\mathrm{e}^{\int ^{r_{*}}\alpha (r)\mathrm{d}r_{*}}, \end{aligned}$$

(18)

where $\alpha (r)=i\omega b_\mathrm{c}k_\mathrm{c}(r)$ and

$$\begin{aligned} k_\mathrm{c}(r)=(r-r_\mathrm{c})\sqrt{\frac{k^{2}(r,b_\mathrm{c})}{(r-r_\mathrm{c})^{2}}},\quad k^{2}(r,b)=\frac{1}{b^{2}}-\frac{f(r)}{r^{2}}, \end{aligned}$$

(19)

with the condition

$$\begin{aligned} k^{2}(r_\mathrm{c},b_\mathrm{c})=\frac{\partial k^{2}(r,b_\mathrm{c})}{\partial r}\Bigg |_{r=r_\mathrm{c}}=0, \end{aligned}$$

(20)

yielding the wave equation

$$\begin{aligned}&\frac{\mathrm{d}^{2}\upsilon (r)}{\mathrm{d}r_{*}}+2\alpha (r)f(r)f'(r)\nonumber \\&\quad +\,[\omega ^{2}+\alpha ^{2}(r)-V(r)+f(r)\alpha '(r)]\upsilon (r)=0. \end{aligned}$$

(21)

For the fundamental mode $n=0$, $\omega$ and $\upsilon (r)$ can be expanded as

$$\begin{aligned} \omega =\sum \limits _{i=-1}^{\infty }\left( \frac{a_i}{\hat{l}^i}\right) ,\quad \ln v(r)=\sum \limits _{i=0}^{\infty }[\hat{l}^{-i}S_i(r)]. \end{aligned}$$

(22)

So the key advantage of the expansion method over many other approaches is that it furnishes simple approximations for the wave function (i.e., Eq. (18)) and it is more accurate in the case $l>n$. In order to illustrate the accuracy of the expansion method, we calculate some QNM frequencies with specific parameters and angular momentum numbers for the regular and RN metrics (cf. Table 1). The results show good agreement with those from the WKB approximation.

Finally in order to determine the QNMs oscillation shape, we adopt the finite difference method to study the dynamical evolution of the NLED field perturbation in the time domain and examine the stability of the regular black hole.

Firstly, we rewrite the wave equation in terms of the variables $\mu =t-r_{*}$ and $\nu =t+r_{*}$ ($\mathrm{d}r_{*}=\mathrm{d}r/f(r)$):

$$\begin{aligned} 4\frac{\partial ^{2}\Psi }{\partial \mu \partial \nu }+V(r)\Psi =0. \end{aligned}$$

(23)

This two-dimensional wave equation can be integrated numerically by using the finite difference method suggested in [29, 30]. It can be discretized as

$$\begin{aligned}&\psi (\mu +\delta \mu ,\nu +\delta \nu )\nonumber \\&\quad =\psi (\mu ,\nu +\delta \nu )+\psi (\mu +\delta \mu ,\nu )-\psi (\mu ,\nu )\nonumber \\&\qquad -\,\delta \mu \delta \nu V\left( \frac{2\nu -2\mu +\delta \nu -\delta \mu }{4}\right) \nonumber \\&\qquad \times \frac{\psi (\mu +\delta \mu ,\nu )+\psi (\mu ,\nu +\delta \nu )}{8}+\mathcal{O}(\epsilon ^{4}), \end{aligned}$$

(24)

where $\epsilon$ is an overall grid scale factor (i.e., $\delta \mu \sim \delta \nu \sim \epsilon$). Set a boundary condition $\psi (\mu ,\nu =\nu _{0})=0$ and suppose an initial perturbation as a Gaussian pulse, centered on $\nu _\mathrm{c}$ and with width $\sigma$ on $\mu =\mu _{0}$; thus

$$\begin{aligned} \psi (\mu =\mu _{0},\nu )=\mathrm{e}^{-\frac{(\nu -\nu _\mathrm{c})^{2}}{2\sigma ^{2}}}. \end{aligned}$$

(25)

The above equations indicate the key steps for a numerical calculation of the field dynamical evolution. Figure 4 is just the dynamical evolution of the NLED EM field in the background of the regular spacetime. As expected, the QNM oscillation of RN and the regular solution are almost the same (see the left subplot). The oscillation frequency increases with $q$ and $l$, and the decay speed becomes slightly faster with larger $q$ and $l$, which are in accordance with the results of WKB method.

Fig. 4

The dynamical evolution of NLED EM field in the background of the regular black-hole spacetime ($M=1$). The constants in the gaussian pulse are $\nu _\mathrm{c}=1$ and $\sigma =1$

Fig. 5

The comparison of QNMs frequencies of the regular metric and RN BH in near-extreme cases

4 Near-extreme cases

In this section, we consider the near-extreme cases around the extreme condition. When the inner horizon $r_{+}$ coincides with the outer horizon $r_{0}$, the extreme condition occurs. In order to maintain cosmic censorship [44, 45], the mass $M$ and $q$ should be confined by a certain relationship in order to keep $r_{+}\le r_{0}$. So we have

$$\begin{aligned}&f(r)=1-\frac{2M}{r}\left( 1-\tanh \frac{|q|^{2}}{2Mr}\right) =0, \end{aligned}$$

(26)

$$\begin{aligned}&f'(r)|_{r=r_{0}}=0. \end{aligned}$$

(27)

The second equation comes from the requirement that the temperature of a BH under the extreme condition should be zero. Through Eqs. (26) and (27), the location of the event horizon can be expressed explicitly as $r_{0} = 4Mq'/(q'-W(-q'\exp (q')))$, where $W(x)$ is a Lambert function and $q'=q^{2}/(2M)^{2}$. So we find a threshold quantity: $(q_\mathrm{c}\simeq 1.0554,r_{0}\simeq 0.8712)$. Then we plan to analyze the QNMs around the threshold charge $q_\mathrm{c}$. Due to the special function $\text {tanh}$ in $f(r)$, the potential function has a complicated form causing an endless computation and inaccurate sixth-order WKB results. Therefore we employ a Taylor expansion around $q_\mathrm{c}$ and calculate the QNMs by a third-order WKB approximation. Given the common parameters, Fig. 5 compares the QNMs of the regular BH with that of RN BH around extreme condition, and it indicates that in the near-extreme cases the regular BH after the NLED EM perturbation tends to stability faster than the RN BH.

Fig. 6

The QNMs frequencies of the regular BH with strong charge

Figure 6 describes the QNM frequencies of the regular BH around the extreme charge $q_\mathrm{c}$. Like the behavior of the weak charged cases, the real part of $\omega$ is enhanced by the increase of $q$ and $l$. But the imaginary part of $\omega$ behaves very differently from the weak charged conditions. It is found that the absolute value of $\mathrm{Im}(\omega )$ decreases with larger $q$ and lower overtone. The most important property is the effect of the angular momentum number, which increases the decay rate for the $n=0$ case but reduces the decay speed when $n=2$. Especially in the $n=1$ case, $|\mathrm{Im}(\omega )|$ has a similar shape to the one with $n=2$ at lower charge. As the charge approaches $q_\mathrm{c}$, the decay behavior is different from the cases of $n=0,2$. This may become the characteristic of such near-extreme BH perturbations.

For the near-extreme cases, we also employ the finite difference method to determine the dynamical evolution of an NLED EM perturbation. The same calculation procedures as mentioned in the previous section generate the results in Fig. 7. This figure shows that as $q$ increases the decay rate decreases, while the oscillation frequency increases, which is also in agreement with the WKB results.

Fig. 7

The dynamical evolution of NLED EM field in the background of the extreme regular black-hole spacetime. We set $M=1$. The constants in the gaussian pulse $\nu _\mathrm{c}=1$ and $\sigma =1$

5 Hawking radiation of the magnetically charged regular black hole

As an important issue of black-hole physics, Hawking radiation has been proven to support a new way to understand the thermodynamics of black holes. Moreover, recently an important relationship between QNMs and BH thermodynamics has been found [46–52], which can be helpful to explain BH QNMs in terms of quantum levels. Such works successfully interpreted the quantization of a QNM through an effective temperature [49, 50], and they found that as the electrons in the Bohr model the QNM frequency $\omega$ is also non-strictly continuous due to a quantum transition between two discrete energy levels. That is a brilliant interpretation of the Hawking radiation, but for our regular black hole it is difficult to find an analytic expression to calculate the discrete QNM frequency $\omega _{n}$ with $T_{\mathrm{eff}}$. So we apply a charged Hamilton–Jacobi equation, which is considered as an effective and simpler method for studying black-hole radiation, to study such regular black-hole Hawking radiation.

The charged Hamilton–Jacobi equation is given by [53]

$$\begin{aligned} g^{\mu \nu }\left( \frac{\partial S}{\partial x^{\mu }}+eA_{\mu }\right) \left( \frac{\partial S}{\partial x^{\nu }}+eA_{\nu }\right) +m^{2}=0, \end{aligned}$$

(28)

where $S$ is the action and $e$ is the charge of a Hawking radiation particle, especially, in a regular charged spacetime, $A_\mu =\delta ^3_\mu A_3=-q_\mathrm{m}\delta ^3_\mu \cos \theta$. Through variable separation the action can be written as

$$\begin{aligned} S=-\omega t+R(r)+Y(\theta ,\phi ). \end{aligned}$$

(29)

So in the regular black-hole spacetime, Eq. (28) can be rewritten as

$$\begin{aligned}&-\frac{\omega ^{2}}{f(r)}+f(r)\left( \frac{\mathrm{d}R}{\mathrm{d}r}\right) ^{2}+m^{2}+\frac{\lambda }{r^{2}}=0, \end{aligned}$$

(30)

$$\begin{aligned}&\left( \frac{\partial Y}{\partial \theta }\right) ^{2}+\frac{1}{\sin ^2\theta }\left( \frac{\partial Y}{\partial \phi }-e q_\mathrm{m}\cos \theta \right) ^{2}=\lambda . \end{aligned}$$

(31)

According to Eqs. (30) and (31), the radial function can be deduced from the partial equation,

$$\begin{aligned} \frac{\mathrm{d}R(r)}{\mathrm{d}r}=\pm \frac{\sqrt{\omega ^{2}-f(r)\left( m^{2}+\frac{\lambda }{r^{2}}\right) }}{f(r)}. \end{aligned}$$

(32)

Since our concern is the neighborhood around the horizon $r_{0}$, we can expand $f(r)$ as

$$\begin{aligned} f(r_{0})=f'(r_{0})(r-r_{0})+f''(r_{0})\frac{(r-r_{0})^{2}}{2}+\cdots . \end{aligned}$$

(33)

Fig. 8

The Hawking temperature varies with different masses of the black hole. The dashing, solid, dash-dotted lines are $r_{0}=1,2,3$, respectively

Fig. 9

$f(r)$ of the regular metric and the RN BH. From left to right $q=1,0.5,0.1$, respectively. Note for the regular BH $q=q_\mathrm{m}$, while $q=q_\mathrm{e}$ under the RN condition

Then the radial function is

$$\begin{aligned} R_{\pm }(r)=\pm \int \frac{\sqrt{\omega ^{2}-f'(r_{0})(r-r_{0})\left( m^{2}+\frac{\lambda }{r^{2}}\right) }}{f'(r_{0})(r-r_{0})}\mathrm{d}r. \end{aligned}$$

(34)

Applying the residue theorem to Eq. (34), the radial function $R(r)$ should be

$$\begin{aligned} R_{\pm }(r)=\pm \frac{i\pi \omega }{f'(r_{0})}. \end{aligned}$$

(35)

So the tunneling rate of Hawking radiation is [54, 55]

$$\begin{aligned} \Gamma =\frac{\exp (2\mathrm{Im}R_{+})}{\exp (2\mathrm{Im}R_{-})}=\exp \left( -4\pi \frac{\omega }{f'(r_{0})}\right) , \end{aligned}$$

(36)

and the Hawking temperature should be

$$\begin{aligned} T_{\mathrm{h}}=\frac{f'(r_{0})}{4\pi }=\frac{2M+(r_{0}-4M)\tanh ^{-1}\left( 1-\frac{r_{0}}{2M}\right) }{8M \pi r_{0}}, \end{aligned}$$

(37)

where $r_{0}$ can be determined by

$$\begin{aligned} q^{2}_\mathrm{m}=2Mr_{0}\tanh ^{-1}\left( \frac{2M-r_{0}}{2M}\right) . \end{aligned}$$

(38)

For the extreme BH, the Hawking temperature is zero. But in the weak charged cases, the Hawking temperature illuminates how the parameters, such as charge and mass of BH, have impact on the thermodynamics of a black hole. Figure 8 shows the shapes of $T_{\mathrm{h}}(M)$. In order to make the function $T_{\mathrm{h}}(M,r_{0})$ meaningful, the domain of the mass shifts to the right with increasing $r_{0}$. For the cases with $r_{0}=1,1.5,2$, the Hawking temperature has a maximum value. Meanwhile, the figure tells us the relationship among $q_\mathrm{m}, M$, and $T_{\mathrm{h}}$.

6 Conclusions

The regular BH discussed by us is one solution of nonlinear electrodynamics coupling with Einstein theory. Choosing different Lagrangian functions, $\mathcal{L}(F)$, various other regular solutions can be deduced [18]. All of them return to a Schwarzschild black hole when $q=0$. For non-zero $q$, they have no singularity – even at $r=0$, $f(r)$ is finite. Furthermore, it can be expanded into

$$\begin{aligned} f(r)=1-\frac{2M}{r}+\frac{q^{2}}{r^{2}}-\frac{q^{6}}{12(M^{2}r^{4})}+\mathcal{O}(q^{7}). \end{aligned}$$

(39)

In fact, all regular BHs can be expanded into a similar polynomial, so it can be noted that the regular metric asymptotically behaves as the RN BH. Figure 9 indicates the difference between the metric of regular BH and RN BH. It is apparent that the regular BHs with lower charge would be much more similar to RN spacetime except in the area around the singular point $r=0$. In our work, we consider the electromagnetic perturbation as a test field, which is so weak that the background spacetime can be regarded as a static gravitational field. Namely, what we researched is the limit case [56–60]. The results in the above sections have no divergence term, so the probe limit condition could be satisfied. In Appendix B, the general perturbation equations including gravitational and electromagnetic perturbation are derived (i.e. Eqs. (56) and (57)).

For the weak charged conditions, the magnetic charge $q$ should be confined by $q<q_\mathrm{c}$ to make sure that the regular spacetime has physical meaning. Considering the complicated expression of the potential function, we try to seek a more accurate QNM frequency through a higher-order Taylor expansion. From sixth-order WKB results Fig. 3 shows the behavior of the perturbation field evolution in detail.

For the near-extreme cases, it is meaningful to reveal how the perturbation behaves when the magnetic charge $q$ approaches $q_\mathrm{c}$. We find the distinguishing properties between the near-extreme case and weak charged conditions, which are mainly reflected in the relationship between the magnetic charge and the decay rate. There is a curve intersection in the $n=1$ case, and the effect of the angular momentum number $l$ on the perturbation field decay appears to be opposite between $n=0$ and $n=2$.

But in each case, we find that the fundamental mode with lower angular momentum number plays a dominant role in the perturbation field decay rate. This is also supported by the intuitive image from a finite difference method.

From the discussion of Hawking radiation, we find another useful property of regular BH. Although we do not determine how the magnetic charge impacts the temperature, this can evidently be deduced from Eq. (38).

As an important application of NLED theory, we choose this solution to understand the stability of initially global regular configurations. In one sense, it provides a new approach to improve general relativity. However, we also notice that there are some deficiencies of this metric. For instance the Lagrangian $\mathcal{L}(F)$ is not a monotonic function in the whole range of invariant $F$, but rather has some junctions where singularities appear [61–63]. This can be well shown using the effective metric [64]. Furthermore some researchers put forward more generic conditions [65] where the inner horizons of such regular black holes would be instable due to a mass inflation [66]. In addition to the specific regular solution discussed in this paper, there is another important non-singular solution for the gravitational collapse found in 2010 according to the relationship between the NLED gravitational redshift and the mass–radius ratio [67]. Furthermore some non-singular cosmologies can also be found with NLED [68, 69]. Therefore we plan to study these issues in our future work.

Appendices

Appendix A

Taking our regular black hole into consideration, the effective metric due to NLED can be derived from the equation [11]

$$\begin{aligned} g^{\mu \nu }_{\mathrm{eff}}=\mathcal{L}_{\mathrm{F}}g^{\mu \nu }-4\mathcal{L}_{\mathrm{FF}}F^{\mu }_{\alpha }F^{\alpha \nu }, \end{aligned}$$

(40)

where $\mathcal{L}_{\text {FF}}=\mathrm{d}^{2}L/\mathrm{d}F^{2}$. Then plugging Eqs. (3), (2), and (8) into Eq. (40) yields

$$\begin{aligned}&g^{00}_{\mathrm{eff}}=g^{00}+\frac{r\text {sech}^{2}\left( \frac{Q(r)}{2M}\right) \left( Q(r)+2M\text {sinh}\left( \frac{Q(r)}{M}\right) \right) \text {tanh}\left( \frac{Q(r)}{2M}\right) }{4M\left( r-2M+2M\text {tanh}\left( \frac{Q(r)}{2M}\right) \right) },\end{aligned}$$

(41)

$$\begin{aligned}&g^{11}_{\mathrm{eff}}=g^{11}-\frac{\text {sech}^{2}\left( \frac{Q(r)}{2M}\right) \left( Q(r)+2M\text {sinh}\left( \frac{Q(r)}{M}\right) \right) \text {tanh}\left( \frac{Q(r)}{2M}\right) \left( r-2M+2M\text {tanh}\left( \frac{Q(r)}{2M}\right) \right) }{4Mr},\end{aligned}$$

(42)

$$\begin{aligned}&g^{22}_{\mathrm{eff}}=g^{22}+\frac{\text {sech}^{4}\left( \frac{Q(r)}{2M}\right) \left[ -2Q^{2}(r)+Q^{2}(r)\text {cosh}\left( \frac{Q(r)}{M}\right) -M\text {sinh}\left( \frac{Q(r)}{M}\right) \left( 7Q(r)+4M\text {sinh}\left( \frac{Q(r)}{M}\right) \right) \right] }{16M^{2}r^{2}},\end{aligned}$$

(43)

$$\begin{aligned}&g^{33}_{\mathrm{eff}}=g^{33}-\frac{\text {csc}^{2}\theta \text {sech}^{4}\left( \frac{Q(r)}{2M}\right) \left[ \frac{q^{4}}{M^{2}r}\left( 2-\text {cosh}\left( \frac{Q(r)}{M}\right) \right) +2r\left( \text {cosh}\left( \frac{2Q(r)}{M}\right) -1\right) +\frac{7q^{2}}{M}\text {sinh}\left( \frac{Q(r)}{M}\right) \right] }{16r^{3}}, \end{aligned}$$

(44)

where $Q(r)=q^{2}/r$. The gravitational redshift is associated with the covariant form of effective metric, which can be derived from $g^{\mu \nu }_{\mathrm{eff}}g^{\mathrm{eff}}_{\nu \alpha }=\delta ^{\mu }_{\alpha }$. Then we get

$$\begin{aligned}&g^{\mathrm{eff}}_{00}=g_{00}+1+\frac{2M\left( \mathrm{tan}\left( \frac{Q(r)}{2M}\right) -1\right) }{r}\nonumber \\&\quad -\frac{4M\mathrm{cosh}\left( \frac{Q(r)}{2M}\right) \left( 2M\mathrm{tanh}\left( \frac{Q(r)}{2M}\right) +r-2M\right) }{r\left( 4M-Q(r)\mathrm{tanh}\left( \frac{Q(r)}{2}\right) \right) },\end{aligned}$$

(45)

$$\begin{aligned}&g^{\mathrm{eff}}_{11}=g_{11}-1+\frac{4M}{r+r\exp (Q(r)/M)}\nonumber \\&\quad \!+\frac{2Mr\left( 1\!+\!\mathrm{cosh}\left( \frac{Q(r)}{M}\right) \right) }{\left( 4M\!-\!Q(r)\mathrm{tanh}\left( \frac{Q(r)}{2M}\right) \right) \left( r\!-\!2M\!+\!2M\mathrm{tanh}\left( \frac{Q(r)}{2M}\right) \right) }, \end{aligned}$$

(46)

$$\begin{aligned}&g^{\mathrm{eff}}_{22}=g_{22}-\frac{1}{r^{2}}\nonumber \\&\quad +\frac{8M^{2}q^{3/2}r^{3}\left( 1\!+\!\mathrm{cosh}\left( \frac{Q(r)}{M}\right) \right) }{2\frac{\sqrt{q}}{r}\left[ 8M^{2}qr^{\frac{7}{2}}\!+\!q^{5}\left( 1-\frac{3}{1\!+\!\mathrm{cosh}\left( \frac{Q(r)}{M}\right) }\right) \right] -14Mq^{\frac{7}{2}}\mathrm{tanh}\left( \frac{Q(r)}{2M}\right) },\nonumber \\ \end{aligned}$$

(47)

$$\begin{aligned}&g^{\text {eff}}_{33}=g_{33}-\frac{\text {csc}^{2}\theta }{r^{2}}\nonumber \\&\quad \!+\frac{16M^{2}q^{\frac{3}{2}}r^{4}\text {cosh}^{2}\left( \frac{Q(r)}{2M}\right) }{2\sqrt{q}\left( q^{5}\!+\!8M^{2}qr^{\frac{7}{2}}\!-\!\frac{3q^{5}}{1\!+\!\text {cosh}\left( \frac{Q(r)}{M}\right) }\right) \!-\!14Mq^{\frac{7}{2}}\text {tanh}\left( \frac{Q(r)}{2M}\right) }.\nonumber \\ \end{aligned}$$

(48)

Figure 10 illuminates that the metric difference will be distinct around $r=0$ and tend to be eliminated with $r$ increasing, meanwhile in the stronger charged cases the discrepancy becomes more obvious.

Fig. 10

The discrepancy between the effective metric and original metric

Appendix B

Considering the process of NLED EM perturbation to the regular spacetime, it should obey the following equations:

$$\begin{aligned}&\delta G_{\mu \nu }=\delta T_{\mu \nu }, \end{aligned}$$

(49)

$$\begin{aligned}&\partial _{\nu } \delta \left( \sqrt{-g}\mathcal{L}_{F}F^{\mu \nu }\right) =0, \end{aligned}$$

(50)

which correspond to the first-order perturbation of the Einstein field equation and the NLED EM field equation (i.e., Eq. (6)) respectively, where $T_{\mu \nu }=-2\mathcal{L}_{F}g^{\alpha \beta }F_{\mu \alpha }F_{\nu \beta }+\frac{1}{2}g_{\mu \nu }\mathcal{L}$ [5]. Here the gravitational perturbations have been considered as $h_{\mu \nu }$, so we have

$$\begin{aligned} g_{\mu \nu }= & {} \bar{g}_{\mu \nu }+h_{\mu \nu }. \end{aligned}$$

(51)

Then

$$\begin{aligned} \delta G_{\mu \nu }= & {} \nabla ^{\beta }\nabla _{\mu }h_{\beta \nu }-\frac{1}{2}\nabla ^{2}h_{\mu \nu }\nonumber \\&-\frac{1}{2}\nabla _{\mu }\nabla _{\nu }h-\frac{1}{2}\bar{g}_{\mu \nu }\nabla ^{\alpha }\nabla ^{\beta }h_{\alpha \beta } \nonumber \\&+\frac{1}{2}\bar{g}_{\mu \nu }\nabla ^{2}h-\frac{\bar{R}}{2}h_{\mu \nu }-\frac{\bar{g}_{\mu \nu }}{2}\bar{R}_{\alpha \beta }h^{\alpha \beta }. \end{aligned}$$

(52)

According to Eq. (2) and assuming $A_{\mu }=\bar{A}_{\mu }+\delta A_{\mu }$, we get

$$\begin{aligned}&\delta F=-2h^{\alpha \beta }\bar{F}_{\alpha \mu }\bar{F}^{\mu }_{\beta }+2\bar{F}^{\mu \nu }(\partial _{\mu }\delta A_{\nu }-\partial _{\nu }\delta A_{\mu }),\end{aligned}$$

(53)

$$\begin{aligned}&\delta \mathcal{L}=\bar{\mathcal{L}}_{F}\delta F, \quad \delta \mathcal{L}_{F}=\bar{\mathcal{L}}_{FF}\delta F. \end{aligned}$$

(54)

Therefore

$$\begin{aligned} \delta T_{\mu \nu }= & {} \bigg (4\bar{\mathcal{L}}_{FF}\bar{F}^{b}_{\mu }\bar{F}_{\nu b}\bar{F}_{\alpha c}\bar{F}^{c}_{\beta }-\bar{g}_{\mu \nu }\bar{\mathcal{L}}_{F}\bar{F}_{\alpha c}\bar{F}^{c}_{\beta }\nonumber \\&+\frac{1}{2}\bar{g}_{\mu \alpha }\bar{g}_{\nu \beta }\bar{\mathcal{L}}\bigg )h^{\alpha \beta }+2\Big (\bar{g}_{\mu \nu }\bar{\mathcal{L}}_{F}\bar{F}^{\alpha \beta }\nonumber \\&-\,4\bar{F}^{\alpha \beta }\bar{\mathcal{L}}_{FF}\bar{F}^{b}_{\mu }\bar{F}_{\nu b}+\bar{\mathcal{L}}_{F}\bar{F}^{\alpha }_{\nu }\delta ^{\beta }_{\mu }-\bar{\mathcal{L}}_{F}\bar{F}^{\beta }_{\nu }\delta ^{\alpha }_{\mu }\nonumber \\&+\,\bar{\mathcal{L}}_{F}\bar{F}^{\alpha }_{\mu }\delta ^{\beta }_{\nu }-\bar{\mathcal{L}}_{F}\bar{F}_{\mu }^{\beta }\delta _{\nu }^{\alpha }\Big )\partial _{\alpha }\delta A_{\beta }. \end{aligned}$$

(55)

The general Einstein field equation with first-order perturbation can be expressed in the form

$$\begin{aligned}&\nabla ^{\beta }\nabla _{\mu }h_{\beta \nu }-\frac{1}{2}\nabla ^{2}h_{\mu \nu }-\frac{1}{2}\nabla _{\mu }\nabla _{\nu }h-\frac{1}{2}\bar{g}_{\mu \nu }\nabla ^{\alpha }\nabla ^{\beta }h_{\alpha \beta } \nonumber \\&\qquad +\,\frac{1}{2}\bar{g}_{\mu \nu }\nabla ^{2}h-\frac{\bar{R}}{2}h_{\mu \nu }-\frac{\bar{g}_{\mu \nu }}{2}\bar{R}_{\alpha \beta }h^{\alpha \beta }\nonumber \\&\quad =\,\bigg (4\bar{\mathcal{L}}_{FF}\bar{F}^{~b}_{\mu }\bar{F}_{\nu b}\bar{F}_{\alpha c}\bar{F}^{~c}_{\beta }-\bar{g}_{\mu \nu }\bar{\mathcal{L}}_{F}\bar{F}_{\alpha c}\bar{F}^{~c}_{\beta }\nonumber \\&\qquad +\frac{1}{2}\bar{g}_{\mu \alpha }\bar{g}_{\nu \beta }\bar{\mathcal{L}}\bigg )h^{\alpha \beta } +2\Big (\bar{g}_{\mu \nu }\bar{\mathcal{L}}_{F}\bar{F}^{\alpha \beta }-4\bar{F}^{\alpha \beta }\bar{\mathcal{L}}_{FF}\bar{F}^{~b}_{\mu }\bar{F}_{\nu b} \nonumber \\&\qquad +\,\bar{\mathcal{L}}_{F}\bar{F}^{~\alpha }_{\nu }\delta ^{\beta }_{\mu }-\bar{\mathcal{L}}_{F}\bar{F}^{~\beta }_{\nu }\delta ^{\alpha }_{\mu }+\bar{\mathcal{L}}_{F}\bar{F}^{~\alpha }_{\mu }\delta ^{\beta }_{\nu }\nonumber \\&\qquad -\,\bar{\mathcal{L}}_{F}\bar{F}_{\mu }^{~\beta }\delta _{\nu }^{\alpha }\Big )\partial _{\alpha }\delta A_{\beta }. \end{aligned}$$

(56)

Analogously the general NLED EM field equation with first-order perturbation can be deduced to be

$$\begin{aligned}&\frac{\partial }{\partial x^{\nu }}\bigg \{\sqrt{-\bar{g}}\bigg [-\frac{1}{2}\bar{\mathcal{L}}_{F}\bar{F}^{\mu \nu }h-\bigg (\bar{\mathcal{L}}_{F}\bar{F}^{~\nu }_{\alpha }+\bar{\mathcal{L}}_{F}\bar{F}^{~\eta }_{\alpha }\delta ^{\nu }_{\eta }\nonumber \\&\qquad +\,2\delta ^{\beta }_{\eta }\bar{\mathcal{L}}_{FF}\bar{F}^{\eta \nu }\bar{F}_{\alpha m}\bar{F}^{~m}_{\beta }\bigg )h^{\mu \alpha } +\Big (4\bar{\mathcal{L}}_{FF}\bar{F}^{\mu \nu }\bar{F}^{\alpha \beta }\nonumber \\&\qquad +\,\bar{\mathcal{L}}_{F}\bar{g}^{\mu \alpha }\bar{g}^{\nu \beta }-\bar{\mathcal{L}}_{F}\bar{g}^{\mu \beta }\bar{g}^{\nu \alpha }\Big )\partial _{\alpha }\delta A_{\beta }\bigg ] \bigg \}=0. \end{aligned}$$

(57)

Appendix C

According to the transformation which was proposed in [70], we discuss a source with electric and magnetic charges. The spacetime of the RN black hole with electric and magnetic charges can be expressed as [41, 42, 70]

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\left( 1-\frac{2Mr-(q^{2}_\mathrm{e}+q^{2}_\mathrm{m})}{r^{2}}\right) \mathrm{d}t^{2}+\frac{r^{2}}{\Delta }\mathrm{d}r^{2}+r^{2}\mathrm{d}\theta ^{2}\nonumber \\&+\,r^{2}\sin ^{2}\theta \mathrm{d}\phi ^{2}, \end{aligned}$$

(58)

where $\Delta =r^{2}+(q^{2}_\mathrm{e}+q^{2}_\mathrm{m})-2Mr$. The electromagnetic vector potential and event horizon $r=r_{0}$ are [40]

$$\begin{aligned}&\begin{aligned}&A=-\frac{q_\mathrm{e}}{r}\mathrm{d}t-q_\mathrm{m}\cos \theta \mathrm{d}\phi ;\\&r_{0}=M+\sqrt{M^{2}-(q_\mathrm{e}^{2}+q_\mathrm{m}^{2})}. \end{aligned} \end{aligned}$$

(59)

Since in this spacetime, electric and magnetic charges are concentrated on the black hole, it is meaningful to combine $q_\mathrm{e}$ and $q_\mathrm{m}$. Supposing that the densities of electric and magnetic charges satisfy $\rho _\mathrm{e}/\rho _\mathrm{m}=\cot \alpha$, where $\alpha$ is a real constant angle, the Maxwell equation can be written as

$$\begin{aligned} \nabla _{\nu }F^{\mu \nu }=4\pi \rho _\mathrm{e}u^{\mu },\quad \nabla _{\nu }F^{+\mu \nu }=4\pi \rho _\mathrm{m}u^{\mu }, \end{aligned}$$

(60)

where $F^{+\mu \nu }$ is the dual tensor of $F^{\mu \nu }$, $u^{\mu }$ is the 4-velocity in curved spacetime. In order to construct an equivalent charge and the electromagnetic tensor, firstly we rewrite the electromagnetic tensor [70, 71]

$$\begin{aligned} \hat{F}^{\mu \nu }=F^{\mu \nu }\cos \alpha +F^{+\mu \nu }\sin \alpha . \end{aligned}$$

(61)

This yields the equivalent Maxwell equation,

$$\begin{aligned}&\begin{aligned}&\nabla _{\nu }\hat{F}^{\mu \nu }=4\pi (\rho _{\mathrm{e}}\cos \alpha +\rho _{\mathrm{m}}\sin \alpha )u^{\mu },\\&\nabla _{\nu }\hat{F}^{\mu \nu }=4\pi (-\rho _{\mathrm{e}}\sin \alpha +\rho _{\mathrm{m}}\cos \alpha )u^{\mu }. \end{aligned} \end{aligned}$$

(62)

Let $\alpha$ satisfy

$$\begin{aligned} \rho _{\mathrm{e}}\cos \alpha +\rho _{\mathrm{m}}\sin \alpha =\rho _{\mathrm{h}},\quad \rho _{\mathrm{m}}\cos \alpha -\rho _{\mathrm{e}}\sin \alpha =0, \end{aligned}$$

(63)

so the equivalent charge density is $\rho _{\mathrm{h}}=\sqrt{\rho ^{2}_{\mathrm{e}}+\rho ^{2}_{\mathrm{m}}}$, and the equivalent charge becomes $q_{\mathrm{h}}^{2}=q_{\mathrm{e}}^{2}+q_{\mathrm{m}}^{2}$. Then the equivalent electromagnetic vector potential should be

$$\begin{aligned} \hat{A}=\frac{q_{\mathrm{h}}}{r}\mathrm{d}t. \end{aligned}$$

(64)

Therefore the line element of the RN black hole with electric and magnetic charges can be simplified to

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\left( 1-\frac{2M}{r}+\frac{q^{2}_\mathrm{h}}{r^{2}}\right) \mathrm{d}t^{2}+\left( 1-\frac{2M}{r}+\frac{q^{2}_\mathrm{h}}{r^{2}}\right) ^{-1}\mathrm{d}r^{2}\nonumber \\&+\,r^{2}(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}), \end{aligned}$$

(65)

which leads to the same expression as an ordinary RN solution, just letting $q_\mathrm{h}=q_\mathrm{e}$.