1 Introduction

As a simple system, the hydrogen atom with high precision measurements in atomic transitions is one of the best laboratories to test QED and new physics as well. Meanwhile, there is some discrepancy between the recent measurement of the muonic hydrogen Lamb shift and the corresponding proton radius and the CODATA value which is obtained from the spectroscopy of atomic hydrogen and electron–proton scattering [1, 2]. There are two possibilities to explain the discrepancy: 1—the theoretical calculation within the standard model is incomplete; 2—the existence of new physics beyond the standard model. There are attempts to explain the new physics by considering a new particle in MeV range where many stringent limits suppress its existence [3–5]. However, the effective new interactions do not necessarily need new particles to mediate the new interactions [6–8]. For instance, non-commutative (NC) space can induce new interactions in QED without adding new particles in the theory. Theoretical aspects of the non-commutative space have been extensively studied by many physicists [9–37]. Meanwhile, non-commutative standard model (NCSM) via two different approaches is introduced in [38–42] and its phenomenological aspects are explored in [43–69]. Here we would like to study the two-body bound state in non-commutative space to explore the differences in the electronic and muonic hydrogen spectrum. There are many studies on the hydrogen atom in the NC space-time [70–80]. However, the effect of NC space on the hydrogen atom at the lowest order is doubtful. Ho and Kao [70] have shown that there is not any correction on the space–space NC-parameter in this system. Since all fields live on the same non-commutative space the non-commutativity of a particle not only should be opposite to its antiparticle but also the NC-parameter of a charged particle should be opposite to any other particle of opposite charge. In fact, for the proton as a point particle \(\theta _p=-\theta _e\) and the corrections on the Coulomb potential coming from both particles cancel. However, the proton is not a point particle and the parameter of non-commutativity is an effective parameter and is not equal to \(-\theta _e\) [72]. Furthermore, even if the proton can be considered as a point particle, the space-time non-commutativity has some impact on the spectrum of the atom. Meanwhile, in the Lorentz-conserving NCQED the NC-parameter appears as \(\theta ^2\), which is equal for a point particle and its antiparticle. Therefore, it is reasonable to examine the hydrogen atom in the NC space. As \(\theta _{\mu \nu }\) has dimension \(-2\) one expects an energy shift proportional to \((\theta m^2)^2mc^2\alpha ^2\). In fact, in the NC space a larger energy shift for the muonic hydrogen is expected in comparison with the ordinary hydrogen, which is in agreement with the experimental data.

In Sect. 2 we explore the two-body bound state in NC space. In Sect. 3 we examine the \(1S\)–\(2S\) transition and the Lamb shift for hydrogen and muonic hydrogen and the \(g\)-factor for electron and muon. In Sect. 4 we give a brief review on the Lorentz-conserving NCQED and calculate the \(g\)-factor for electron and muon, the \(1S\)–\(2S\) transition and the Lamb shift for hydrogen and muonic hydrogen. In Sect. 5 we summarize our results.

2 Two-body bound state in non-commutative space-time

Since the NC-parameters for a point particle and its antiparticle are opposite, the NC-correction on the potential for the space–space part of the NC-parameter is zero at the lowest order. It can be shown that the Coulomb potential in the Schrödinger equation is proportional to \((\theta _p+\theta _e)_{ij}\), which is zero in the point particle limit of the proton [70, 81]. In the two references the starting point is the Schrödinger equation in the NC space. However, one can show how the NC field theory through the Bethe–Salpeter (BS)-equation leads to the Schrödinger equation with a modified potential [82, 83]. In fact, it is better to start from the NC field theory (NCFT) to avoid the mistake on the NC-contributions from each particle in the bound state. For instance, the correct potential in the NC Schrödinger equation can be explored in studying the kernel in the BS-equation for the corresponding NCFT. For this purpose examining the electron–proton scattering amplitude in the NCQED is adequate to derive the appropriate potential for the NCQM.

In a canonical non-commutative space, space-time coordinates are not numbers but operators which do not commute,

$$\begin{aligned} {[\hat{x}^{\mu },\hat{x}^{\nu }]}=i\theta ^{\mu \nu }=i\frac{C^{\mu \nu }}{\Lambda _{\tiny \mathrm{NC}}^2}, \end{aligned}$$
(1)

where \(\theta ^{\mu \nu }\) is the parameter of non-commutativity, \(C^{\mu \nu }\) is a constant and dimensionless antisymmetric tensor, and \(\Lambda _\mathrm{NC}\) is the non-commutative scale. Since the non-commutative parameter, \(\theta ^{\mu \nu }\), is constant and identifies a preferred direction in space, a canonical version of non-commutative space-time leads to the Lorentz symmetry violation. There are two versions of the construction of the NCQED [38–42]. In the first one in contrast with the ordinary QED a momentum dependent phase factor appears in the charged fermion–photon vertex as follows [84]:

$$\begin{aligned} ieQ\gamma _\mu \exp {(ip_\mu \theta ^{\mu \nu }p'_\nu )}, \end{aligned}$$
(2)

where \(p_\mu \) and \(p'_\nu \) are the incoming and outgoing momenta and \(\theta \) is the NC-parameter. Therefore, the electron–proton amplitude can be written as

$$\begin{aligned} \mathcal{{M}}_\mathrm{NC}=\mathcal{{M}}\exp ({ip_\mu (\theta _e)^{\mu \nu }p'_\nu })\exp ({ik_\mu (\theta _p)^{\mu \nu }k'_\nu }), \end{aligned}$$
(3)

where \(p\) (\(p'\)) and \(k\) (\(k'\)) are the incoming (outgoing) momenta of the electron and proton, respectively. One can easily see that the exponent in terms of the momentum transfer \(q\) in the center of mass is

$$\begin{aligned} -i(\vec {\theta }_e+\vec {\theta }_p).\vec {p}\times \vec {q} -ip_i(\theta _e^{i0}+\theta _p^{i0})q_0-i(p_0\theta _e^{0i}-k_0\theta _p^{0i})q_i, \end{aligned}$$
(4)

which for \(\theta _p=-\theta _e=\theta \) results in

$$\begin{aligned} i\left( \sqrt{m_e^2+\mathbf {p}^2}+\sqrt{m_p^2+\mathbf {p}^2}\right) \theta ^{0i}q_i. \end{aligned}$$
(5)

Therefore, for \(m^2_e\) and \(m^2_p\gg \mathbf {p}^2\), the non-relativistic potential in the NCQM is the Fourier transform of

$$\begin{aligned} \frac{e^2\exp [i(m_e+m_p)\theta ^{0i}q_i]}{q^2}, \end{aligned}$$
(6)

which leads to \(V_\mathrm{NC}=V(\vec {r}-(m_e+m_p)\vec {\theta }_t)\) where \(\vec {\theta }_t=(\theta _{10}, \theta _{20}, \theta _{30})\). In fact, to the lowest order of both \(\theta \) and \(\alpha \) the hydrogen atom only receives some contribution from the temporal part of the NC-parameter. Meanwhile, in [73, 74] a new correction due to the non-commutativity of the source at the lowest order of the space part of the NC-parameter is found. Nonetheless, it is of the order \(\alpha ^6\) and is not of the lowest order of \(\alpha \) too.

In the second approach, via Seiberg–Witten maps, the fields also depend on the non-commutative parameter. Using Seiberg–Witten maps, the non-commutative standard model and Feynman rules are fully provided in Refs. [38–40]. In this approach, the two-fermion–photon vertex is [39, 40]

$$\begin{aligned}&ieQ_{f}\gamma _{\mu }+\frac{1}{2}eQ_{f}[(p_\mathrm{out}\theta p_\mathrm{in})\gamma _{\mu }-(p_\mathrm{out}\theta )({p\!\!/}_\mathrm{in}-m_{f})\nonumber \\&\quad -({p\!\!/}_\mathrm{out}-m_{f})(\theta p_\mathrm{in})_{\mu }] , \end{aligned}$$
(7)

where \(Q\) is the fermion charge and \(p_\mathrm{in}\) and \(p_\mathrm{out}\) are incoming and outgoing momenta, respectively. Considering the proton as a point particle, the electron–proton scattering amplitude in the on-shell limit can be given as follows:

$$\begin{aligned} iM&= \bar{u}(p')\Bigg [-ie\gamma ^{\mu }-\frac{1}{2}e(p'\theta _{e} p)\gamma ^{\mu }\Bigg ]u(p)\nonumber \\&\times (- ig_{\mu \nu }/q^{2})\bar{\nu }(k)\Bigg [ie\gamma ^{\mu }+\frac{1}{2}e(k'\theta _{p} k)\gamma ^{\mu }\Bigg ]\nu (k'), \end{aligned}$$
(8)

where \(p\) (\(k\)) and \(p'\) (\(k'\)) are incoming and outgoing momenta of electron (proton), respectively. At the lowest order of \(\theta _{\mu \nu }\), (8) is the same as (3), which means in the second approach one has the same result as is given in (6). In fact, for point particles in the QED bound states such as positronium, there is no NC-correction at the lowest order of \(\alpha \) and \(\theta _{ij}\).

3 Hydrogen atom in non-commutative space-time

In a two-body bound state the point particles satisfy \(\theta _p=-\theta _e\) and the interaction potential only depends on the time part of the NC-parameter as is shown in (6). Nevertheless, the proton in the hydrogen atom is not a point particle and has an effective NC-parameter in terms of the NC-parameters of its contents [72] which is not equal to \(-\theta _e\). In fact, for the NC-parameter of the order of \(1\,\mathrm{TeV}\) neither the electron with energy of order \(eV\), nor the muon with \(\mathrm{keV}\)-energy in the hydrogen can probe inside the proton to see its non-commutativity. It should be noted that for the muon the Bohr radius is about \(\frac{m_e}{m_{\mu }}a_e\sim 2.5 \times 10^{-13} m\sim 3r_p\), which is comparable with the size of the proton. Meanwhile, for instance in the Lamb shift of muon-hydrogen the hadronic interactions are of the order of \(\alpha ^2\) smaller than the QED interaction of the muon with proton as a point particle. Thus, considering the NC-effects on the muon interaction with the proton contents leads to corrections of the order \(m_{\mu }^2\theta \alpha ^2\) smaller than what one finds in the main part of the interactions. Therefore, even in the muon-hydrogen the NC-corrections due to the finite size of the proton are negligible. In fact, at the low energy limit from the non-commutative point of view the proton is a macroscopic particle and \(\theta _\mathrm{proton}\simeq 0\). Therefore, in the non-relativistic limit and for the energy scale of atom, Eq. (4) leads to

$$\begin{aligned} -i\vec {\theta }_e.\vec {p}\times \vec {q} -ip_i\theta _e^{i0}q_0-ip_0\theta _e^{0i}q_i. \end{aligned}$$
(9)

Equation (9) for \(\theta ^{0i}= 0\) and \(\theta ^{ij}\ne 0\), has been already considered to find bound on the NC-parameter in hydrogen atom [71, 73–75]. The temporal part of the non-commutativity leads to a problem with the unitarity. However, in some cases it can be shown that the quantum mechanics is unitary for the temporal part of the NC-parameter [85, 86]. Nevertheless, we examine the temporal part (\(\theta ^{0i}\ne 0\) and \(\theta ^{ij}= 0\)) in the non-relativistic limit, where (9) leads to

$$\begin{aligned} \frac{e^2\exp [im_e\theta ^{0i}q_i]}{q^2}, \end{aligned}$$
(10)

or

$$\begin{aligned} V_\mathrm{NC}(\vec {r})=V(\vec {r}-m_e\vec {\theta }_t)-V(\vec {r})\simeq - \alpha m_{e}\frac{\overrightarrow{\theta }.\overrightarrow{r}}{r^{3}}. \end{aligned}$$
(11)

In (11) only the parallel part of \(\vec {\theta }\) with \(\vec {r}\) has some contribution to the NC-potential, that is,

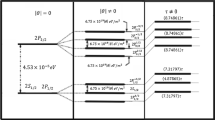
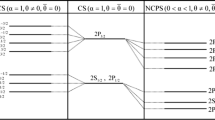
$$\begin{aligned} V_\mathrm{NC}(r)= -m_{e} \alpha \frac{|\vec {\theta }|\cos {\phi }}{r^{2}}, \end{aligned}$$
(12)

where \(\cos {\phi }\) is the angle between \(\vec {\theta }\) and \(\vec {r}\) and \(\alpha \) is the fine structure constant. Using the perturbation theory for the ground state leads to a zero energy shift for this state. However, for the excited states in the non-relativistic limit, the states \(^2S_{\frac{1}{2}}\) and \(^2P_{\frac{1}{2}}\) are degenerate. Therefore, the potential (12) splits these states into two states with an energy difference proportional to \(\langle R_{n0}\mid \frac{-m_e\alpha |\vec {\theta }|}{r^2}\mid R_{n1}\rangle \sim -m^3_e\alpha ^3 |\vec {\theta }|\). But one can surprisingly show that

$$\begin{aligned} \left\langle R_{20}\mid \frac{1}{r^2}\mid R_{21}\right\rangle =0, \end{aligned}$$
(13)

or up to the first order of \(|\vec {\theta }|\) the states \(2^2S_{\frac{1}{2}}\) and \(2^2P_{\frac{1}{2}}\) remain degenerate. Nonetheless, for \(n=3\) one has

$$\begin{aligned} \Delta E_\mathrm{NC}^\mathrm{H{\text {-}}atom}=\frac{2\sqrt{2}}{3}m^3_e\alpha ^3 |\vec {\theta }|. \end{aligned}$$
(14)

Here we consider the effects of the NC space-time on the physical quantities such as the 1S–3S transition, the Lamb shift in an atom, and the anomalous magnetic moment to fix the NC-parameter in accordance with the experimental uncertainties.

\(1S\)–\(3S\) transition: The obtained energy shift (14), from the temporal part of non-commutativity, leads to an additional contribution on the theoretical value of the \(1S\)–\(3S\) transition in the hydrogen atom as follows:

$$\begin{aligned} \Delta E_\mathrm{NC}^{1S{-}3S}=\frac{2\sqrt{2}}{3}m^3_e\alpha ^3 |\vec {\theta }|. \end{aligned}$$
(15)

The uncertainty of the experimental value for the \(1S\)–\(3S\) transition in the hydrogen atom is about \(13\, \mathrm{kHz}\) [87]

$$\begin{aligned} f_{1S{-}3S}=2{,}922{,}742{,}936.729 (13) \,\mathrm{MHz}. \end{aligned}$$
(16)

Therefore, for \(\Lambda =1.5\,\mathrm{TeV}\) one has

$$\begin{aligned} \Delta E_\mathrm{NC}^{1S{-}3S}\sim 30\, \mathrm{Hz}\ll 13\, \mathrm{kHz}. \end{aligned}$$
(17)

Lamb shift: For \(\Lambda =1.5\,\mathrm{TeV}\) the NC-correction to the Lamb shift for the electronic hydrogen is

$$\begin{aligned} \Delta E_\mathrm{NC}^{H_e}=\frac{2\sqrt{2}}{3}m^3_e\alpha ^3 |\vec {\theta }|\sim 30\, \mathrm{Hz}\ll 48\, \mathrm{kHz}, \end{aligned}$$
(18)

where \(48\, \mathrm{kHz}\) is the experimental accuracy of the \(n=3\) Lamb shift in the hydrogen atom [26]. Meanwhile, for the muonic hydrogen one has

$$\begin{aligned} \Delta E_\mathrm{NC}^{H_{\mu }}=\left( \frac{m_{\mu }}{m_e}\right) ^{3}\Delta E_\mathrm{NC}^{H_e}= 240\, \mathrm{MHz}\sim 2\times 10^{-4} \mathrm{meV}. \end{aligned}$$
(19)

g-2 for electron and muon: Since the NC-parameter has dimension \(-2\) the dimensionless quantity \(a=\frac{g-2}{2}\) should be corrected, at the lowest order in NC space, as \(C(\frac{\alpha }{2\pi })p_\mu \theta ^{\mu \nu }p'_\nu \), where \(C\) is a constant, which is obtained in [84, 89]. Therefore, for \(\Lambda =1.5\, \mathrm{TeV}\) the NC-correction on \(a\) for the electron is

$$\begin{aligned} \delta a_e=\frac{5}{6}\frac{\alpha }{2\pi }\frac{p^2}{\Lambda ^2} \simeq \frac{5}{6}\frac{\alpha }{2\pi }\frac{m_e^2}{\Lambda ^2}\sim 10^{-16}, \end{aligned}$$
(20)

and for the muon where in the E286 experiment we have a momentum of about \(3\, \mathrm{GeV}\) it is

$$\begin{aligned} \delta a_\mu =\frac{5}{6}\frac{\alpha }{2\pi }\frac{p^2}{\Lambda ^2} \simeq \frac{5}{6}\frac{\alpha }{2\pi }\left( \frac{3}{1{,}500}\right) ^2\sim 3\times 10^{-9}. \end{aligned}$$
(21)

4 Hydrogen atom in Lorentz-conserving non-commutative space-time

As the NC-parameter is a real and constant Lorentz tensor, there is, obviously, a preferred direction in a given particle Lorentz frame which leads to the Lorentz-symmetry violation. On the other hand, experimental inspections for Lorentz violation, including clock comparison tests, polarization measurements on the light from distant galaxies, analyses of the radiation emitted by energetic astrophysical sources, studies of matter–antimatter asymmetries for trapped charged particles and bound state systems [90–97], and so on, have thus far failed to produce any positive results. These experiments strictly bound the Lorentz-violating parameters, therefore, in the lower energy limit, the Lorentz symmetry is an almost exact symmetry of nature [98–101]. However, Carlson, Carone, and Zobin (CCZ) have constructed a Lorentz-conserving non-commutative quantum electrodynamics based on a contracted Snyder algebra [102]. In this class of NC theories, the parameter of non-commutativity is not a constant but an operator which transforms as a Lorentz tensor. In fact, (1) should be extended to

$$\begin{aligned} {[\hat{x}^{\mu },\hat{x}^{\nu }]}=i\hat{\theta }^{\mu \nu },\quad {[\hat{\theta }^{\alpha \beta },\hat{\theta }^{\mu \nu }]}=0,\quad [\hat{\theta }^{\mu \nu },\hat{x}^{\nu }]=0, \end{aligned}$$
(22)

where \(\hat{\theta }^{\mu \nu }\) is an operator. Consequently, according to the Weyl–Moyal correspondence, to construct the LCNC action the ordinary product should be replaced with the star product as follows:

$$\begin{aligned} f*g(x,\hat{\theta )}=f(x,\theta )exp(i/2\overleftarrow{\partial }_{\mu }\theta ^{\mu \nu }\overrightarrow{\partial }_{\nu })g(x,\theta ). \end{aligned}$$
(23)

In this formalism a sufficiently fast falling weight function \(W(\theta )\) has been used to construct the Lorentz-invariant Lagrangian in a non-commutative space as

$$\begin{aligned} \mathcal {L}(x)=\int \mathrm{d}^{6}\theta W(\theta )\mathcal {L}(\phi ,\partial \phi )_{*}, \end{aligned}$$
(24)

where the Lorentz-invariant weight function \(W(\theta )\) is introduced to suppresses the NC-cross section for energies beyond the NC-energy scale. In Ref. [103] the existence of an invariant normalized weight function is discussed and an explicit form for \(W(\theta )\) is given in terms of Lorentz-invariant combinations of \(\theta ^{\mu \nu }\)’s. The function \(W(\theta )\) can be used to define an operator trace as

$$\begin{aligned} Tr\hat{f}=\int \mathrm{d}^{4}x \mathrm{d}^{6}\theta W(\theta )f(x,\theta ), \end{aligned}$$
(25)

in which \(W(\theta )\) has the following properties:

$$\begin{aligned} \int \mathrm{d}^{6}\theta W(\theta ) = 1, \end{aligned}$$
(26)
$$\begin{aligned} \int \mathrm{d}^{6}\theta W(\theta )\theta ^{\mu \nu }=0, \end{aligned}$$
(27)
$$\begin{aligned} \int \mathrm{d}^{6}\theta W(\theta )\theta ^{\mu \nu }\theta ^{\kappa \Lambda }= \left\langle \frac{\theta ^{2}}{2}\right\rangle (g^{\mu \nu }g^{\mu \Lambda }-g^{\mu \Lambda }g^{\nu \kappa }), \end{aligned}$$
(28)

where

$$\begin{aligned} \langle \theta ^{2}\rangle =\int \mathrm{d}^{6}\theta W(\theta )\theta ^{\mu \nu }\theta _{\mu \nu }. \end{aligned}$$
(29)

As (27) shows, in the expansion of the Lagrangian (24) in terms of the NC-parameter the odd powers of \(\theta _{\mu \nu }\) vanish. In fact, to obtain the nonvanishing \(\theta \)-dependence terms, all fields should be expanded at least up to the second order of the NC-parameter. The Lorentz-conserving NCSM is fully introduced in [104, 105] and its fermionic part, we are interested in, is given as follows:

$$\begin{aligned}&S_\mathrm{fermion}= \int \mathrm{d}^{4}x (\overline{L}i{D\!\!/}L + \overline{R}i{D\!\!/}R)\nonumber \\&\qquad +\int \mathrm{d}^{6}\theta \int \mathrm{d}^{4}x W(\theta )\theta ^{\mu \nu }\theta ^{\kappa \Lambda } \left( -\frac{i}{8}\overline{L} \gamma ^{\rho }F^{0}_{\mu \kappa }F^{0}_{\Lambda \rho }D^{0}_{\nu }L\right. \nonumber \\&\qquad -\frac{i}{4}\overline{L}\gamma ^{\rho }F^{0}_{\mu \rho }F^{0}_{\nu \kappa }D^{0}_{\Lambda }L-\frac{1}{8}\overline{L}\gamma ^{\rho }(D^{0}_{\mu }F^{0}_{\kappa \rho })D^{0}_{\nu }D^{0}_{\Lambda }L \nonumber \\&\qquad \left. -\frac{i}{8}\overline{L} \gamma ^{\rho }F^{0}_{\mu \nu }F^{0}_{\kappa \rho }D^{0}_{\Lambda }L\right) \nonumber \\&\qquad \times \int \mathrm{d}^{6}\theta \int \mathrm{d}^{4}x W(\theta )\theta ^{\mu \nu }\theta ^{\kappa \Lambda } \left( -\frac{i}{8}\overline{R} \gamma ^{\rho }F^{0}_{\mu \kappa }F^{0}_{\Lambda \rho }D^{0}_{\nu }R\right. \nonumber \\&\qquad -\frac{i}{4}\overline{R}\gamma ^{\rho }F^{0}_{\mu \rho }F^{0}_{\nu \kappa }D^{0}_{\Lambda }R-\frac{1}{8}\overline{R}\gamma ^{\rho }(D^{0}_{\mu }F^{0}_{\kappa \rho })D^{0}_{\nu }D^{0}_{\Lambda }R\nonumber \\&\qquad \left. -\frac{i}{8}\overline{R} \gamma ^{\rho }F^{0}_{\mu \nu }F^{0}_{\kappa \rho }D^{0}_{\Lambda }R\right) , \end{aligned}$$
(30)

where \(L\) and \(R\) stand, respectively, for left and right handed fermions and \(F^{0}_{\mu \nu }\) is the ordinary field strength in the standard model. To find the LCNC-effects, at the lowest order, on the hydrogen atom we only consider the QED part of the NC-action (30) as follows:

$$\begin{aligned}&\int \mathrm{d}^{6}\theta \int \mathrm{d}^{4}x eQ_{f}\left( \overline{\nu }_{L}{A\!\!/}_{0}\nu _{L} \!-\!\frac{1}{8}\theta ^{\mu \nu }\theta ^{\kappa \Lambda }\overline{\nu }_{L}\gamma ^{\rho } \partial _{\mu }A_{0\kappa \rho }\partial _{\nu }\partial _{\Lambda }\nu _{L}\right. \nonumber \\&\quad \left. +\,\overline{e}{A\!\!/}_{0}e_{L}-\frac{1}{8}\theta ^{\mu \nu }\theta ^{\kappa \Lambda }\overline{e}\gamma ^{\rho }\partial _{\mu }A_{0\kappa \rho }\partial _{\nu }\partial _{\Lambda }e\right) , \end{aligned}$$
(31)

where \(A_{0\mu \nu } = \partial _{\mu }A_{0\nu }-\partial _{\nu }A_{0\mu }\) and the charged fermions interact with the photon via the following vertex:

$$\begin{aligned} ieQ_{f}\gamma ^{\mu }\left( 1+\frac{\langle \theta ^{2}\rangle }{96}\left( \frac{q^{4}}{4}-m_{f}^{2}q^{2}\right) \right) . \end{aligned}$$
(32)

In (32) the \(\theta \)-dependence appears as \(\langle \theta ^{2}\rangle \), which is similar for both particle and its antiparticle. In fact, in LCNC-QED in contrast with NCQED according to \(\theta _{f_-}= -\theta _{f_+}\), the particle vertex does not cancel the antiparticle vertex. Therefore, in an \(f_-\) \(f_+\) bound state the LCNC-effect via the \(f_-\) \(f_+\) scattering amplitude, in the low energy limit, leads to a potential in momentum space as

$$\begin{aligned} \widetilde{V}(q)=-\frac{e^{2}}{q^{2}}-\frac{e^{2}(m_{f^-}^{2}+m_{f^+}^{2})\langle \theta ^{2}\rangle }{96}, \end{aligned}$$
(33)

where to obtain (33), at low momentum transfer, the second term in (32) is ignored in comparison with the third one. However, the proton as a particle with internal structure does not see the NC space in those systems of which the momentum transfer is small such as a hydrogen-like atom. Therefore, the NC-potential in the hydrogen atom is

$$\begin{aligned} \widetilde{V}(q)= -\frac{e^{2}}{q^{2}}-\frac{e^{2}m_{e^-}^{2}\langle \theta ^{2}\rangle }{96}, \end{aligned}$$
(34)

or

$$\begin{aligned} V(r) =- \frac{e^{2}}{4\pi r}-\frac{e^{2}m_{e}^{2}\langle \theta ^{2}\rangle }{96}\delta (r). \end{aligned}$$
(35)

The NC-correction on the Coulomb potential in (35) is small and its expectation value directly gives the energy shift on the energy levels of the hydrogen atom as follows:

$$\begin{aligned} \Delta E_\mathrm{LCNC}^\mathrm{H{\text {-}}atom}&= - \langle \psi |\frac{e^{2}m_{e^-}^{2}\langle \theta ^{2}\rangle }{96}\delta (r)|\psi \rangle \nonumber \\&= -\frac{e^{2}m_{e^-}^{2}\langle \theta ^{2}\rangle }{96} |\psi _{nl}(r=0)|^{2} , \end{aligned}$$
(36)

where \( |\psi _{nl}(r=0)|^{2}=\frac{\alpha ^{3}m_{e^-}^{3}}{\pi n^{3}}\delta _{l0}\) leads to

$$\begin{aligned} \Delta E_\mathrm{LCNC}^\mathrm{H{\text {-}}atom}= - \frac{m_{e^-}^{5}\alpha ^{4}\langle \theta ^{2}\rangle }{24n^{3}} \delta _{l0}, \end{aligned}$$
(37)

or with \(\Lambda _\mathrm{LCNC}=(\frac{12}{\langle \theta ^{2}\rangle })^{4}\), (37) can be rewritten as

$$\begin{aligned} \Delta E_\mathrm{LCNC}^\mathrm{H{\text {-}}atom}= -\frac{m_{e^-}^{5}\alpha ^{4}}{2n^{3}}\frac{1}{\Lambda _\mathrm{LCNC}^{4}}\delta _{l0}. \end{aligned}$$
(38)

Here we fix the NC-parameter by the most precise experimental value in the hydrogen atom (i.e. \(1S\)–\(2S\) transition) then we find the effects of the NC space-time on the other physical quantities such as the Lamb shift in an atom and the anomalous magnetic moment.

\(1S\)–\(2S\) transition: The experimental value for \(1S\)–\(2S\) transition in the hydrogen atom [106] can fix the upper bound on the parameter \(\Lambda _\mathrm{LCNC}\) as follows:

$$\begin{aligned} \Delta E_\mathrm{LCNC}^{1S{-}2S}= \frac{7m_{e}^{5}\alpha ^{4}}{16}\frac{1}{\Lambda _\mathrm{LCNC}^{4}}\sim 34\, \mathrm{Hz}, \end{aligned}$$
(39)

which leads to

$$\begin{aligned} \Lambda _\mathrm{LCNC}\sim 0.2\, \mathrm{GeV}. \end{aligned}$$
(40)

Lamb shift: For \(\Lambda =0.5\, \mathrm{GeV}\) the NC-correction on the Lamb shift for electronic hydrogen is

$$\begin{aligned} \Delta E_\mathrm{NC}^{H_e}=\frac{m_{e}^{5}\alpha ^{4}}{16}\frac{1}{\Lambda _\mathrm{LCNC}^{4}}\sim 0.1\, \mathrm{Hz} \ll 3\, \mathrm{kHz}, \end{aligned}$$
(41)

where \(3\, \mathrm{kHz}\) is the experimental accuracy on the \(n=2\) Lamb shifts in the hydrogen atom [107]. Meanwhile, for the muonic hydrogen one has

$$\begin{aligned} \Delta E_\mathrm{NC}^{H_{\mu }}=\left( \frac{m_{\mu }}{m_e}\right) ^{5}\Delta E_\mathrm{NC}^{H_e}\simeq 40 \,\mathrm{GHz}\sim 0.03\, \mathrm{meV}. \end{aligned}$$
(42)

g-2 for electron and muon: As Eq. (32) shows, the NC-correction on \(a=\frac{g-2}{2}\) should be proportional to \(q^2\), which leads to a zero NC-correction on \(a\) at zero momentum transfer.

5 Summary

In this paper the two-body bound state has been studied by examining the scattering amplitude in the Lorenz-violated (LV) and Lorentz-conserving (LC) NCQED as given in (3) and (33), respectively. For a bound state of a particle with its antiparticle the NC-potential in LVNCQED, in contrast with LCNCQED, only depends on the space-time part of the NC-parameter; see (4). As the proton in a hydrogen atom is not a point particle, \(\theta _p\ne -\theta _e\). In fact, in \(ep\)-scattering in the low energy limit, the electron cannot probe inside the proton to see its NC-effects. In the Lorentz-violating NCQED for the hydrogen and the muonic hydrogen atom we have found:

  1. 1.

    In the \(1S\)–\(2S\) transition in the hydrogen atom the NC-effect is zero; see (13).

  2. 2.

    In \(1S\)–\(3S\) transition in the hydrogen atom the NC-parameter of the order of \(\Lambda _\mathrm{NC}=1.5\, \mathrm{\mathrm{TeV}}\) leads to a small correction on the theoretical value which is not detectable.

  3. 3.

    \(\Lambda _\mathrm{NC}=1.5\, \mathrm{TeV}\) leads to an NC-shift on the \(n=3\) Lamb shift about \(30\,\mathrm{Hz}\) which is far from the \(48\,\mathrm{kHz}\) current uncertainty on the Lamb shift in the hydrogen atom. As (19) shows an uncertainty of order of \(3\,\mathrm{kHz}\) in the Lamb shift of hydrogen leads to \((3\,\mathrm{kHz})(\frac{m_\mu }{m_e})^3=26\,\mathrm{GHz}\) which can only explain a small part of the current deviation between the experimental measurement and the theoretical prediction.

  4. 4.

    The NC-effect on the g-factors of electron and muon are \(a_e=10^{-16} \) and \(a_\mu =10^{-9}\), respectively. The obtained values for \(a_e\) and \(a_\mu \) are in agreement with the experimental measurements.

  5. 5.

    \(\Lambda _\mathrm{NC}=1.5\, \mathrm{TeV}\) which is found from the muon g-factor is a stringent bound in the atomic systems where the NC-parameter is usually of the order of a few \(\mathrm{GeV}\) [73, 74]. However, this bound cannot explain the discrepancy in measurement of the Lamb shift in muonic hydrogen.

In the Lorentz-conserving NCQED for the hydrogen and the muonic hydrogen atom we have found:

  1. 1.

    In the \(1S\)–\(2S\) transition in the hydrogen atom the NC-parameter has been fixed at about \(\Lambda _\mathrm{NC}=0.5\, \mathrm{GeV}\), which is the first bound on this parameter in an atomic system.

  2. 2.

    \(\Lambda _\mathrm{NC}=0.5\, \mathrm{GeV}\) leads to an NC-shift on the \(2s_{1/2}\)–\(2p_{1/2}\) transition in the hydrogen atom of about \(0.1\,\mathrm{Hz}\), which is far from the current \(3\,\mathrm{kHz}\) uncertainty on the Lamb shift in the hydrogen atom. As (42) shows, an uncertainty of order of \(3\,\mathrm{Hz}\ll 3\,\mathrm{kHz}\) in the Lamb shift of hydrogen leads to \((3\,\mathrm{Hz})(\frac{m_\mu }{m_e})^5=1{,}000\,\mathrm{GHz}\), which can explain the current difference between the experimental measurement and the theoretical prediction about \(0.3\, \mathrm{meV}\) [1, 2].

  3. 3.

    The NC-correction on \(a=\frac{g-2}{2}\) is proportional to \(q^2\), which is zero at the zero momentum transfer.