Radiative $\Omega _{Q}^{*}\rightarrow \Omega _{Q}\gamma$ and $\Xi _{Q}^{*}\rightarrow \Xi ^{\prime }_{Q}\gamma$ transitions in light cone QCD

Abstract

We calculate the magnetic dipole and electric quadrupole moments associated with the radiative $\Omega _{Q}^{*}\rightarrow \Omega _{Q}\gamma$ and $\Xi _{Q}^{*}\rightarrow \Xi ^{\prime }_{Q}\gamma$ transitions with $Q=b$ or $c$ in the framework of light cone QCD sum rules. It is found that the corresponding quadrupole moments are negligibly small, while the magnetic dipole moments are considerably large. A comparison of the results of the considered multipole moments as well as corresponding decay widths with the predictions of the vector dominance model is performed.

1 Introduction

In the recent years, there has been significant experimental progress on hadron spectroscopy. Many new baryons containing heavy bottom and charm quarks as well as many new charmonium like states are observed. Now, all heavy baryons with single heavy quark have been discovered in the experiments except the $\Omega ^*_b$ baryon with spin 3/2. In the case of doubly heavy baryons only the doubly charmed $\Xi _{cc}$ baryon has been discovered by SELEX Collaboration [1, 2] but the experimental attempts on the identification of other members of the doubly baryons as well as triply heavy baryons predicted by quark model are continued. Considering this progress and the facilities of experiments specially at LHC, it would be possible to study the decay properties of heavy baryons in the near future. Theoretical studies on electromagnetic, weak, and strong decays of heavy baryons receive special attention in the light of the experimental results.

In the present work we calculate the electromagnetic form factors of the radiative $\Omega _{Q}^{*}\rightarrow \Omega _{Q}\gamma$ and $\Xi _{Q}^{*}\rightarrow \Xi ^{\prime }_{Q}\gamma$ transitions in the framework of the light cone QCD sum rules as one of the best applicable non-perturbative tools to study hadron physics. Here, baryons with $*$ correspond to spin 3/2, while those without $*$ are spin-1/2 baryons. Using the electromagnetic form factors at the static limit ($q^2=0$), we obtain the magnetic dipole and electric quadrupole moments as well as the decay widths of the considered radiative decays. We compare our results with the predictions of the vector meson dominance model (VDM) [3], which uses the values of the strong coupling constants between spin-3/2 and spin-1/2 heavy baryons with vector mesons [4] to calculate the magnetic dipole and electric quadrupole moments of the transitions under consideration. The electromagnetic multipole moments of heavy baryons can give valuable information on their internal structure as well as their geometric shapes. Note that other possible radiative transitions among heavy spin-3/2 and spin-1/2 baryons with a single heavy quark, namely $\Sigma _{Q}^{*}\rightarrow \Sigma _{Q}\gamma$, $\Xi _{Q}^{*}\rightarrow \Xi _{Q}\gamma$, and $\Sigma _{Q}^{*}\rightarrow \Lambda _{Q}\gamma$, have been investigated in [5] using the same framework. Some of these radiative transitions have also been previously studied using chiral perturbation theory [6], heavy quark and chiral symmetries [7, 8], the relativistic quark model [9], and light cone QCD sum rules at leading order in HQET in [10].

The outline of the paper is as follows. In the next section, QCD sum rules for the electromagnetic form factors of the transitions under consideration are calculated. In the last section, we numerically analyze the obtained sum rules. This section also includes a comparison of our results with the predictions of VDM on the multipole moments as well as the corresponding decay widths.

2 Theoretical framework

The aim of this section is to obtain light cone QCD sum rules (LCQSR) for the electromagnetic form factors defining the radiative $\Omega _{Q}^{*}\rightarrow \Omega _{Q}\gamma$ and $\Xi _{Q}^{*}\rightarrow \Xi ^{\prime }_{Q}\gamma$ transitions. For this goal we use the following two-point correlation function in the presence of an external photon field:

$$\begin{aligned} \Pi _{\mu }(p,q)=i\int \mathrm{d}^{4}x\mathrm{e}^{ip\cdot x}\langle 0\mid T\{\eta (x)\bar{\eta }_{\mu }(0) \}\mid 0\rangle _{\gamma }, \end{aligned}$$

(1)

where $\eta$ and $\eta _{\mu }$ are the interpolating currents of the heavy flavored baryons with spin 1/2 and 3/2, respectively. The main task in the following is to calculate this correlation function once in terms of hadronic parameters called the hadronic side and in terms of photon distribution amplitudes (DAs) with increasing twist with the help of operator product expansion (OPE). By equating the coefficients of appropriate structures from the hadronic to the OPE side, we obtain LCQSR for the transition form factors. To suppress the contribution of the higher states and continuum, we apply Borel transformations with respect to the momentum squared of the initial and final baryonic states. For further pushing down those contributions, we also apply a continuum subtraction to both sides of the LCQSRs obtained.

2.1 Hadronic side

To obtain the hadronic representation, we insert complete sets of intermediate states having the same quantum numbers as the interpolating currents into the above correlation function. As a result of this we get

$$\begin{aligned} \Pi _{\mu }(p,q)&= \frac{\langle 0\mid \eta \mid 2(p,s')\rangle }{p^{2}-m_{2}^{2}}\langle 2(p,s')\mid 1(p+q,s)\rangle _\gamma \nonumber \\&\times \frac{\langle 1(p_+q,s)\mid \bar{\eta }_{\mu }\mid 0\rangle }{(p+q)^{2}-m_{1}^{2}}+\ldots , \end{aligned}$$

(2)

where the dots indicate the contributions of the higher states and continuum and $q$ is the photon’s momentum. In the above equation, $\langle 1(p+q,s)|$ and $\langle 2(p,s')|$ denote the heavy spin-3/2 and spin-1/2 states and $m_{1}$ and $m_{2}$ are their masses, respectively. To proceed, we need to know the matrix elements of the interpolating currents between the vacuum and the baryonic states. They are defined in terms of spinors and residues as

$$\begin{aligned} \begin{aligned} \langle 1(p+q,s)\mid \bar{\eta }_{\mu }(0)\mid 0\rangle&=\lambda _{1}\bar{u}_{\mu }(p+q,s), \\ \quad \langle 0 \mid \eta (0)\mid 2(p,s')\rangle&=\lambda _{2} u(p,s'), \end{aligned} \end{aligned}$$

(3)

where $u_{\mu }(p,s)$ is the Rarita–Schwinger spinor; and $\lambda _{1}$ and $\lambda _{2}$ are the residues of the heavy baryons with spin 3/2 and 1/2, respectively which are calculated in [5]. The matrix element $\langle 2(p,s')\mid 1(p+q,s)\rangle _\gamma$ is also defined as [11, 12]

$$\begin{aligned}&\langle 2(p,s')\mid 1(p+q,s)\rangle _\gamma \nonumber \\&\quad \!=\!e\bar{u}(p,s')\{G_{1}(q_{\mu } \not \!\varepsilon \!-\!\varepsilon _{\mu }\not \!q) \!+\!G_{2}[(\mathcal{P}\varepsilon )q_{\mu }\!-\!(\mathcal{P}q)\varepsilon _{\mu }]\gamma _{5}\nonumber \\&\qquad +G_{3}[(q\varepsilon )q_{\mu }-q^{2}\varepsilon _{\mu }]\gamma _{5} \} u_{\mu }(p+q,s), \end{aligned}$$

(4)

where the $G_i$ are electromagnetic form factors, $\varepsilon _{\mu }$ is the photon’s polarization vector and $\mathcal{P}=\frac{p+(p+q)}{2}$. In the above equation, the term proportional to $G_{3}$ is zero for the real photon which we consider in the present study. At $q^2=0$, the transition magnetic dipole moment $G_{M}$ and the electric quadrupole moment $G_{E}$ are defined in terms of the remaining electromagnetic form factors as

$$\begin{aligned} \begin{aligned} G_{M}&=\left[ (3m_{1}+m_{2})\frac{G_{1}}{m_{1}}+(m_{1}-m_{2})G_{2}\right] \frac{m_{2}}{3},\\ G_{E}&=(m_{1}-m_{2})\left[ \frac{G_{1}}{m_{1}}+G_{2}\right] \frac{m_{2}}{3}. \end{aligned} \end{aligned}$$

(5)

Now, we use Eqs. (4) and (3) in Eq. (2) and perform a summation over the spins of the Dirac and Rarita–Schwinger spinors. In the case of spin 3/2 this summation is written as

$$\begin{aligned} \sum _{s}u_{\mu }(p,s)\bar{u}_{\nu }(p,s)&= \frac{(\not \!p+m_)}{2m}\bigg \{-g_{\mu \nu } +\frac{1}{3}\gamma _{\mu }\gamma _{\nu }\nonumber \\&-\frac{2p_{\mu }p_{\nu }}{3m^{2}}-\frac{p_{\mu }\gamma _{\nu }-p_{\nu }\gamma _{\mu }}{3m}\bigg \}.\qquad \end{aligned}$$

(6)

Using Eqs. (3–6), in principle, one can straightforwardly calculate the hadronic side of the correlation function. But here appear two unwanted problems:

• There is pollution from spin-1/2 baryons, since the interpolating current $\eta _{\mu }$ couples with spin-1/2 baryons also.

• All Lorentz structures are not independent.

In order to solve the first problem, let us write the corresponding matrix element of the current $\eta _{\mu }$ between vacuum and $J=1/2$ states, which can be parameterized as

$$\begin{aligned} \langle 0|\eta _{\mu }|1(p+q,s)\rangle =[\alpha \gamma _{\mu }+\beta (p+q)_{\mu }]u(p+q,s). \end{aligned}$$

(7)

Multiplying both sides of this equation by $\gamma ^{\mu }$ and using $\gamma ^{\mu }\eta _{\mu }=0$ as well as the Dirac equation we get

$$\begin{aligned} \langle 0|\eta _{\mu }|1(p+q,s)\rangle =\alpha \left[ \gamma _{\mu }-\frac{4}{m_2} (p+q)_{\mu }\right] u(p+q,s). \end{aligned}$$

(8)

From this expression it follows that contributions of spin-1/2 states are either proportional to the $\gamma _{\mu }$ at the end or $(p+q)_{\mu }$. Taking into account this fact, from Eq. (6) it follows that only terms proportional to $g_{\mu \nu }$ contain contributions coming only from spin-3/2 states. This observation shows how spin-1/2 states’ contributions coupled to $\eta _{\mu }$ can be removed. The second problem can be solved if one orders the Dirac matrices in an appropriate way. In this work, we choose the ordering $\not \!\varepsilon \not \!q\not \!p\gamma _{\mu }$. After some calculations, for the hadronic side of the correlation function we get

$$\begin{aligned}&\Pi _\mu = e \lambda _{1} \lambda _{2} \frac{1}{p^2-m_{2}^2} \frac{1}{(p+q)^2-m_{1}^2} \nonumber \\&\quad \big [ [ \varepsilon _\mu (pq) - (\varepsilon p) q_\mu ] \{ -2 G_1 m_{1} - G_2 m_{1} m_{2} + G_2 (p+q)^2 \nonumber \\&\quad +\, [ 2 G_1 - G_2(m_{1}-m_{2}) ] \not \!p + m_{2} G_2 \not \!q - G_2 \not \!q\not \!p \} \gamma _5 \nonumber \\&\quad +\, [ q_\mu \not \!\varepsilon - \varepsilon _\mu \not \!q ] \{ G_1 (p^2 + m_{1} m_{2}) - G_1 (m_{1}+m_{2}) \not \!p \} \gamma _5 \nonumber \\&\quad +\, 2 G_1 [ \not \!\varepsilon (pq) - \not \!q (\varepsilon p) ] q_\mu \gamma _5 - G_1 \not \!\varepsilon \not \!q ( m_{2} + \not \!p ) q_\mu \gamma _5 \nonumber \\&\quad +\, \hbox {other structures with}~\gamma _\mu ~\hbox {at the end or which}\nonumber \\&\quad \hbox {are proportional to}~(p+q)_\mu \big ], \end{aligned}$$

(9)

where we need two invariant structures to calculate the form factors $G_{1}$ and $G_{2}$. In the present work, we select the structures $\not \!\varepsilon \not \!p\gamma _{5}q_{\mu }$ and $\not \!q\not \!p\gamma _{5}(\varepsilon p)q_{\mu }$ for $G_{1}$ and $G_{2}$, respectively. The advantage of these structures is that these terms do not receive contributions from contact terms.

2.2 OPE side

On the OPE side, the aforementioned correlation function is calculated in terms of the QCD degrees of freedom and photon DAs. To this aim, we substitute the explicit forms of the interpolating currents of the heavy baryons into the correlation function in Eq. (1) and use Wick’s theorem to obtain the correlation in terms of the quark propagators.

The interpolating currents for spin-3/2 baryons are taken as

$$\begin{aligned} \eta _{\mu }&= A\epsilon ^{abc}\left\{ \left( q_{1}^{a}C\gamma _{\mu }q_{2}^{b}\right) Q^{c} +\left( q_{2}^{a}C\gamma _{\mu }Q^{b}\right) q_{1}^{c}\right. \nonumber \\&\qquad \qquad \left. +\, \left( Q^{a}C\gamma _{\mu }q_{1}^{b}\right) q_{2}^{c}\right\} , \end{aligned}$$

(10)

where $q_{1}$ and $q_{2}$ stand for light quarks; $a$, $b$, and $c$ are color indices and $C$ is the charge conjugation operator. The normalization factor $A$ and light quark content of the heavy spin-3/2 baryons are presented in Table 1.

Table 1 The normalization factor $A$ and light quark content of heavy spin-3/2 baryons

The general form of the interpolating currents for the heavy spin-1/2 baryons under consideration can be written as (see for instance [13])

$$\begin{aligned} \eta&= - {B\over \sqrt{2}} \epsilon ^{abc} \left\{ \left( q_1^{aT} C Q^b \right) \gamma _5 q_2^c + \beta \left( q_1^{aT} C \gamma _5 Q^b \right) q_2^c \right. \nonumber \\&\quad \left. - \left[ \left( Q^{aT} C q_2^b \right) \gamma _5 q_1^c + \beta \left( Q^{aT} C \gamma _5 q_2^b \right) q_1^c \right] \right\} , \end{aligned}$$

(11)

where $\beta$ is an arbitrary parameter and $\beta =-1$ corresponds to the Ioffe current. The constant $B$ and quark fields $q_{1}$ and $q_{2}$ for the corresponding heavy spin-1/2 baryons are given in Table 2.

Table 2 The constant $B$ and light quark content of the heavy spin-1/2 baryons under consideration

The correlation function on the OPE side receives three different contributions: (1) perturbative contributions, (2) mixed contributions at which the photon is radiated from short distances and at least one of the quarks forms a condensate, and (3) non-perturbative contributions where a photon is radiated at long distances. The last contribution is parameterized by the matrix element $\langle \gamma (q)\mid \bar{q}(x_{1}) \Gamma q(x_{2})\mid 0\rangle$, which is expanded in terms of photon DAs with definite twists. Here $\Gamma$ is the full set of Dirac matrices $\Gamma _j = \{ 1,~\gamma _5,~\gamma _\alpha ,~i\gamma _5 \gamma _\alpha , ~\sigma _{\alpha \beta } /\sqrt{2}\}$.

The perturbative contribution at which the photon interacts with the quarks perturbatively is obtained by replacing the corresponding free quark propagator by

$$\begin{aligned} S^{ab}_{\alpha \beta } \Rightarrow \left\{ \int \mathrm{d}^4 y S^{\mathrm{free}} (x-y) \not \!A S^{\mathrm{free}}(y)\right\} ^{ab}_{\alpha \beta }, \end{aligned}$$

(12)

where the free light and heavy quark propagators are given as

$$\begin{aligned} S^{\mathrm{free}}_{q}&= \frac{i\not \!x}{2\pi ^{2}x^{4}}-\frac{m_{q}}{4\pi ^{2}x^{2}},\nonumber \\ S^{\mathrm{free}}_{Q}&= \frac{m_{Q}^{2}}{4\pi ^{2}}\frac{K_{1}(m_{Q}\sqrt{-x^2})}{\sqrt{-x^2}}-i \frac{m_{Q}^{2}\not \!x}{4\pi ^{2}x^2}K_{2}\left( m_{Q}\sqrt{-x^2}\right) ,\nonumber \\ \end{aligned}$$

(13)

with $K_{i}$ being the Bessel functions.

The non-perturbative contributions are obtained by replacing one of the light quark propagators that emits a photon by

$$\begin{aligned} S^{ab}_{\alpha \beta } \rightarrow - \frac{1}{4} \bar{q}^a \Gamma _j q^b ( \Gamma _j )_{\alpha \beta }, \end{aligned}$$

(14)

where a sum over $j$ is applied, and the remaining contributions by full quark propagators involving the perturbative as well as the non-perturbative parts. The full heavy and light quark propagators which we use in the present work are (see [14, 15])

$$\begin{aligned} S_Q (x)&= S_Q^{\mathrm{free}} (x) - i g_s \int \frac{\mathrm{d}^4 k}{(2\pi )^4} \mathrm{e}^{-ikx} \nonumber \\&\times \int _0^1 \mathrm{d}v \Bigg [\frac{\not \!k + m_Q}{( m_Q^2-k^2)^2} G^{\mu \nu }(vx) \sigma _{\mu \nu } \nonumber \\&+ \frac{1}{m_Q^2-k^2} v x_\mu G^{\mu \nu } \gamma _\nu \Bigg ], \nonumber \\ S_q(x)&= S_q^{\mathrm{free}} (x) - \frac{m_q}{4 \pi ^2 x^2} - \frac{\langle \bar{q} q \rangle }{12} \left( 1 - i \frac{m_q}{4} \not \!x \right) \nonumber \\&- \frac{x^2}{192} m_0^2 \langle \bar{q} q \rangle \left( 1 - i \frac{m_q}{6}\not \!x \right) \nonumber \\&-\, i g_s \int _0^1 \mathrm{d}u \left[ \frac{\not \!x}{16 \pi ^2 x^2} G_{\mu \nu } (ux) \sigma _{\mu \nu } \right. \nonumber \\&\left. -\, u x^\mu G_{\mu \nu } (ux) \gamma ^\nu \frac{i}{4 \pi ^2 x^2} \right. \nonumber \\&\left. -\, i \frac{m_q}{32 \pi ^2} G_{\mu \nu } \sigma ^{\mu \nu } \left( \ln \left( \frac{-x^2 \Lambda ^2}{4} \right) + 2 \gamma _E \right) \right] ,\nonumber \\ \end{aligned}$$

(15)

where $\Lambda$ is the scale parameter; we choose it at the factorization scale $\Lambda$ $=$ (0.5–1) GeV [16, 17].

In order to calculate the non-perturbative contributions, we need the matrix elements $\langle \gamma (q)\mid \bar{q} \Gamma _{i}q\mid 0\rangle$. These matrix elements are determined in terms of the photon DAs as [18]

$$\begin{aligned}&\langle \gamma (q) \vert \bar{q}(x) \sigma _{\mu \nu } q(0) \vert 0 \rangle = -i \mathrm{e}_q \bar{q} q (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \nonumber \\&\quad \times \int _0^1 \mathrm{d}u \mathrm{e}^{i \bar{u} qx} \left( \chi \varphi _\gamma (u) + \frac{x^2}{16} \mathbb {A} (u) \right) \nonumber \\&\quad -\frac{i}{2(qx)} \mathrm{e}_q \langle \bar{q} q \rangle \left[ x_\nu \left( \varepsilon _\mu - q_\mu \frac{\varepsilon x}{qx}\right) \right. \nonumber \\&\left. \quad - x_\mu \left( \varepsilon _\nu - q_\nu \frac{\varepsilon x}{q x}\right) \right] \int _0^1 \mathrm{d}u \mathrm{e}^{i \bar{u} q x} h_\gamma (u), \nonumber \\&\langle \gamma (q) \vert \bar{q}(x) \gamma _\mu q(0) \vert 0 \rangle \nonumber \\&\quad = \mathrm{e}_q f_{3 \gamma } \left( \varepsilon _\mu - q_\mu \frac{\varepsilon x}{q x} \right) \int _0^1 \mathrm{d}u \mathrm{e}^{i \bar{u} q x} \psi ^v(u),\nonumber \\&\langle \gamma (q) \vert \bar{q}(x) \gamma _\mu \gamma _5 q(0) \vert 0 \rangle \nonumber \\&\quad = - \frac{1}{4} \mathrm{e}_q f_{3 \gamma } \epsilon _{\mu \nu \alpha \beta } \varepsilon ^\nu q^\alpha x^\beta \int _0^1 \mathrm{d}u \mathrm{e}^{i \bar{u} q x} \psi ^a(u),\nonumber \\&\langle \gamma (q) | \bar{q}(x) g_s G_{\mu \nu } (v x) q(0) \vert 0 \rangle \nonumber \\&\quad = -i \mathrm{e}_q \langle \bar{q} q \rangle \left( \varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu \right) \int \mathcal{D}\alpha _i \mathrm{e}^{i (\alpha _{\bar{q}} + v \alpha _g) q x} \mathcal{S}(\alpha _i),\nonumber \\&\langle \gamma (q) | \bar{q}(x) g_s \tilde{G}_{\mu \nu } i \gamma _5 (v x) q(0) \vert 0 \rangle \nonumber \\&\quad = -i \mathrm{e}_q \langle \bar{q} q \rangle \left( \varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu \right) \int \mathcal{D}\alpha _i \mathrm{e}^{i(\alpha _{\bar{q}} + v \alpha _g) q x} \tilde{\mathcal{S}}(\alpha _i),\nonumber \\&\langle \gamma (q) \vert \bar{q}(x) g_s \tilde{G}_{\mu \nu }(v x) \gamma _\alpha \gamma _5 q(0) \vert 0 \rangle \nonumber \\&\quad = \mathrm{e}_q f_{3 \gamma } q_\alpha (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \int \mathcal{D}\alpha _i \mathrm{e}^{i (\alpha _{\bar{q}} + v \alpha _g) q x} \mathcal{A}(\alpha _i),\nonumber \\&\langle \gamma (q) \vert \bar{q}(x) g_s G_{\mu \nu }(v x) i \gamma _\alpha q(0) \vert 0 \rangle \nonumber \\&\quad = \mathrm{e}_q f_{3 \gamma } q_\alpha (\varepsilon _\mu q_\nu - \varepsilon _\nu q_\mu ) \int \mathcal{D}\alpha _i \mathrm{e}^{i (\alpha _{\bar{q}} + v \alpha _g) q x} \mathcal{V}(\alpha _i) ,\nonumber \\&\langle \gamma (q) \vert \bar{q}(x) \sigma _{\alpha \beta } g_s G_{\mu \nu }(v x) q(0) \vert 0 \rangle \nonumber \\&\quad = \mathrm{e}_q \langle \bar{q} q \rangle \left\{ \left[ \!\left( \varepsilon _\mu \!-\! q_\mu \frac{\varepsilon x}{q x}\right) \!\left( g_{\alpha \nu } \!- \!\frac{1}{qx} (q_\alpha x_\nu \!+\! q_\nu x_\alpha )\right) \! \right. \right. q_\beta \nonumber \\&\qquad -\, \left( \varepsilon _\mu - q_\mu \frac{\varepsilon x}{q x}\right) \left( g_{\beta \nu } - \frac{1}{qx} (q_\beta x_\nu + q_\nu x_\beta )\right) q_\alpha \nonumber \\&\qquad -\, \left( \varepsilon _\nu - q_\nu \frac{\varepsilon x}{q x}\right) \left( g_{\alpha \mu } - \frac{1}{qx} (q_\alpha x_\mu + q_\mu x_\alpha )\right) q_\beta \nonumber \\&\qquad +\, \left. \left( \varepsilon _\nu - q_\nu \frac{\varepsilon x}{q.x}\right) \left( g_{\beta \mu } - \frac{1}{qx} (q_\beta x_\mu + q_\mu x_\beta )\right) q_\alpha \right] \nonumber \\&\qquad \times \int \mathcal{D}\alpha _i \mathrm{e}^{i (\alpha _{\bar{q}} + v \alpha _g) qx} \mathcal{T}_1(\alpha _i) \nonumber \\&\qquad +\, \left[ \left( \varepsilon _\alpha - q_\alpha \frac{\varepsilon x}{qx}\right) \left( g_{\mu \beta } - \frac{1}{qx}(q_\mu x_\beta + q_\beta x_\mu )\right) \right. q_\nu \nonumber \\&\qquad -\, \left( \varepsilon _\alpha - q_\alpha \frac{\varepsilon x}{qx}\right) \left( g_{\nu \beta } - \frac{1}{qx}(q_\nu x_\beta + q_\beta x_\nu )\right) q_\mu \nonumber \\&\qquad -\, \left( \varepsilon _\beta - q_\beta \frac{\varepsilon x}{qx}\right) \left( g_{\mu \alpha } - \frac{1}{qx}(q_\mu x_\alpha + q_\alpha x_\mu )\right) q_\nu \nonumber \\&\qquad +\, \left. \left( \varepsilon _\beta - q_\beta \frac{\varepsilon x}{qx}\right) \left( g_{\nu \alpha } - \frac{1}{qx}(q_\nu x_\alpha + q_\alpha x_\nu ) \right) q_\mu \right] \nonumber \\&\qquad \times \int \mathcal{D} \alpha _i \mathrm{e}^{i (\alpha _{\bar{q}} + v \alpha _g) qx} \mathcal{T}_2(\alpha _i) \nonumber \\&\qquad + \,\frac{1}{qx} (q_\mu x_\nu - q_\nu x_\mu ) (\varepsilon _\alpha q_\beta - \varepsilon _\beta q_\alpha ) \!\int \! \mathcal{D} \alpha _i \mathrm{e}^{i (\alpha _{\bar{q}} + v \alpha _g) qx} \mathcal{T}_3(\alpha _i) \nonumber \\&\qquad + \,\left. \frac{1}{qx} (q_\alpha x_\beta \!-\! q_\beta x_\alpha ) (\varepsilon _\mu q_\nu \!-\! \varepsilon _\nu q_\mu ) \!\int \! \mathcal{D} \alpha _i \mathrm{e}^{i (\alpha _{\bar{q}} +v \alpha _g) qx} \mathcal{T}_4(\alpha _i) \right\} \!,\nonumber \\ \end{aligned}$$

(16)

where $\varphi _\gamma (u)$ is the leading twist 2, $\psi ^v(u)$, $\psi ^a(u)$, $\mathcal{A}$, and $\mathcal{V}$ are the twist 3; and $h_\gamma (u)$, $\mathbb {A}$, and $\mathcal{T}_i$ ($i=1,~2,~3,~4$) are the twist 4 photon DAs [18]. Here $\chi$ is the magnetic susceptibility of the quarks.

The measure $\int \mathcal{D} \alpha _i$ is defined as

$$\begin{aligned} \int \mathcal{D} \alpha _i \!=\! \int _0^1 \mathrm{d} \alpha _{\bar{q}} \int _0^1 \mathrm{d} \alpha _q \int _0^1 \mathrm{d} \alpha _g \delta (1-\alpha _{\bar{q}}-\alpha _q \!-\! \alpha _g).\nonumber \\ \end{aligned}$$

(17)

In order to obtain the sum rules for the form factors $G_{1}$ and $G_{2}$, we equate the coefficients of the structures $\not \!\varepsilon \not \!p\gamma _{5}q_{\mu }$ and $\not \!q\not \!p\gamma _{5}(\varepsilon p)q_{\mu }$ from both hadronic and OPE representations of the same correlation function. We apply the Borel transformations with respect to the variables $p^2$ and $(p+q)^2$ as well as continuum subtraction to suppress the contributions of the higher states and continuum. Finally, we obtain the following schematically written sum rules for the electromagnetic form factors $G_{1}$ and $G_{2}$:

$$\begin{aligned} G_{1}&= -\frac{1}{\lambda _{1}\lambda _{2}(m_{1}+m_{2})}\mathrm{e}^{\frac{m_{1}^{2}}{M_{1}^{2}}} \mathrm{e}^{\frac{m_{2}^{2}}{M_{2}^{2}}} [\mathrm{e}_{q_{1}}\Pi _{1}+\mathrm{e}_{q_{2}}\Pi _{1}(q_{1}\leftrightarrow q_{2})\nonumber \\&\quad +\mathrm{e}_{Q}\Pi '_{1}]\nonumber \\ G_{2}&= \frac{1}{\lambda _{1}\lambda _{2}}\mathrm{e}^{\frac{m_{1}^{2}}{M_{1}^{2}}}\mathrm{e}^{\frac{m_{2}^{2}}{M_{2}^{2}}} [\mathrm{e}_{q_{1}}\Pi _{2}+\mathrm{e}_{q_{2}}\Pi _{2}(q_{1}\leftrightarrow q_{2}) +\mathrm{e}_{Q}\Pi '_{2}],\nonumber \\ \end{aligned}$$

(18)

where the functions $\Pi _i[\Pi '_{i}]$ can be written as

$$\begin{aligned} \Pi _{i}[\Pi '_{i}]&= \int _{m_{Q}^{2}}^{s_{0}}\mathrm{e}^{\frac{-s}{M^{2}}}\rho _{i}(s)[\rho '_{i}(s)]\mathrm{d}s +\mathrm{e}^{\frac{-m_Q^2}{M^{2}}} \Gamma _{i}[\Gamma '_{i}], \end{aligned}$$

(19)

where $s_0$ is the continuum threshold and we take $M_1^2=M_2^2= 2M^2$ since the masses of the initial and final baryons are close to each other. The expressions for the spectral densities $\rho _{i}(s)[\rho '_{i}(s)]$ and the functions $\Gamma _{i}[\Gamma '_{i}]$ are very lengthy; hence, we do not present these explicit expressions here.

3 Numerical results

In this part, we numerically analyze the sum rules for the magnetic dipole $G_{M}$ and electric quadrupole $G_{E}$ obtained in the previous section. To this aim, we use the input parameters $\langle \bar{u} u \rangle (1~\mathrm{GeV}) = \langle \bar{d} d \rangle (1~\mathrm{GeV})= -(0.243)^3~\mathrm{GeV}^3$, $\langle \bar{s} s \rangle (1~\mathrm{GeV}) = 0.8 \langle \bar{u} u \rangle (1~\mathrm{GeV})$, $m_0^2(1~\mathrm{GeV}) = (0.8\pm 0.2)~\mathrm{GeV}^2$ [19], and $f_{3 \gamma } = - 0.0039~\mathrm{GeV}^2$ [18]. The values of the magnetic susceptibility are calculated in [20–22]. Here we use the value $\chi (1~\mathrm{GeV})=-4.4~\mathrm{GeV}^{-2}$ [22] for this quantity. The LCQSR for the magnetic dipole and electric quadrupole moments also include the photon DAs [18], whose expressions are given as

$$\begin{aligned} \varphi _\gamma (u)&= 6 u \bar{u} ( 1 + \varphi _2(\mu ) C_2^{\frac{3}{2}}(u - \bar{u}) ),\nonumber \\ \psi ^v(u)&= 3 (3 (2 u - 1)^2 -1 )+\frac{3}{64} (15 w^V_\gamma - 5 w^A_\gamma ) \nonumber \\&\times (3 - 30 (2 u - 1)^2 + 35 (2 u -1)^4 ),\nonumber \\ \psi ^a(u)&= (1- (2 u -1)^2)(5 (2 u -1)^2 -1) \nonumber \\&\times \frac{5}{2} \left( 1 + \frac{9}{16} w^V_\gamma - \frac{3}{16} w^A_\gamma \right) ,\nonumber \\ \mathcal{A}(\alpha _i)&= 360 \alpha _q \alpha _{\bar{q}} \alpha _g^2 \left( 1 + w^A_\gamma \frac{1}{2} (7 \alpha _g - 3)\right) ,\nonumber \\ \mathcal{V}(\alpha _i)&= 540 w^V_\gamma (\alpha _q - \alpha _{\bar{q}}) \alpha _q \alpha _{\bar{q}} \alpha _g^2,\nonumber \\ h_\gamma (u)&= - 10 (1 + 2 \kappa ^+) C_2^{\frac{1}{2}}(u - \bar{u}), \nonumber \\ \mathbb {A}(u)&= 40 u^2 \bar{u}^2 (3 \kappa - \kappa ^+ +1) \nonumber \\&+ 8 (\zeta _2^+ - 3 \zeta _2) [u \bar{u} (2 + 13 u \bar{u}) \nonumber \\&+ 2 u^3 (10 -15 u + 6 u^2) \ln (u) \nonumber \\&+ 2 \bar{u}^3 (10 - 15 \bar{u} + 6 \bar{u}^2) \ln (\bar{u})], \nonumber \\ \mathcal{T}_1(\alpha _i)&= -120 (3 \zeta _2 + \zeta _2^+)(\alpha _{\bar{q}} - \alpha _q) \alpha _{\bar{q}} \alpha _q \alpha _g, \nonumber \\ \mathcal{T}_2(\alpha _i)&= 30 \alpha _g^2 (\alpha _{\bar{q}} - \alpha _q) ((\kappa - \kappa ^+) + (\zeta _1 - \zeta _1^+)(1 - 2\alpha _g) \nonumber \\&+ \zeta _2 (3 - 4 \alpha _g)), \nonumber \\ \mathcal{T}_3(\alpha _i)&= - 120 (3 \zeta _2 - \zeta _2^+)(\alpha _{\bar{q}} -\alpha _q) \alpha _{\bar{q}} \alpha _q \alpha _g, \nonumber \\ \mathcal{T}_4(\alpha _i)&= 30 \alpha _g^2 (\alpha _{\bar{q}} - \alpha _q) ((\kappa + \kappa ^+) + (\zeta _1 + \zeta _1^+)(1 - 2\alpha _g) \nonumber \\&+ \zeta _2 (3 - 4 \alpha _g)),\nonumber \\ \mathcal{S}(\alpha _i)&= 30\alpha _g^2\{(\kappa \!+\! \kappa ^+)(1\!-\!\alpha _g)+(\zeta _1 \!+\! \zeta _1^+)(1 \!-\! \alpha _g)(1 \!-\! 2\alpha _g)\nonumber \\&+\zeta _2 [3 (\alpha _{\bar{q}} - \alpha _q)^2-\alpha _g(1 - \alpha _g)]\},\nonumber \\ \tilde{\mathcal{S}}(\alpha _i)&= -30\alpha _g^2\{(\kappa \!-\! \kappa ^+)(1\!-\!\alpha _g)\!+\!(\zeta _1 \!-\! \zeta _1^+)(1 \!-\! \alpha _g)(1 \!-\! 2\alpha _g)\nonumber \\&+\zeta _2 [3 (\alpha _{\bar{q}} - \alpha _q)^2-\alpha _g(1 - \alpha _g)]\}, \end{aligned}$$

(20)

where the constants inside the DAs are given by $\varphi _2(1~\mathrm{GeV}) = 0$, $w^V_\gamma = 3.8 \pm 1.8$, $w^A_\gamma = -2.1 \pm 1.0$, $\kappa = 0.2$, $\kappa ^+ = 0$, $\zeta _1 = 0.4$, $\zeta _2 = 0.3$, $\zeta _1^+ = 0$, and $\zeta _2^+ = 0$ [18].

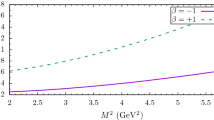
The sum rules for the electromagnetic form factors contain three more auxiliary parameters: the Borel mass parameter $M^2$, the continuum threshold $s_{0}$, and the arbitrary parameter $\beta$ entering the expressions of the interpolating currents of the heavy spin-1/2 baryons. Any physical quantities, like the magnetic dipole and electric quadrupole moments, should be independent of these auxiliary parameters. Therefore, we try to find “working regions” for these auxiliary parameters such that in these regions $G_{M}$ and $G_{E}$ are practically independent of these parameters. The upper and lower bands for $M^2$ are found requiring that not only the contributions of the higher states and continuum are less than the ground state contribution, but also the contributions of the higher twists are less compared to the leading twists. By these requirements, the working regions of Borel mass parameter are obtained as $15~\mathrm{GeV}^2\le M^{2}\le 30~\mathrm{GeV}^2$ and $6~\mathrm{GeV}^2\le M^{2}\le 12~\mathrm{GeV}^2$ for baryons containing b and c quarks, respectively. The continuum threshold $s_{0}$ is the energy square which characterizes the beginning of the continuum. If we denote the ground state mass by $m$, the quantity $\sqrt{s_0}-m$ is the energy needed to excite the particle to its first excited state with the same quantum numbers. The $\sqrt{s_0}-m$ is not well known for the baryons under consideration, but it should lie between $0.3~\mathrm{GeV}$ and $0.8~\mathrm{GeV}$. The dependence of the magnetic dipole moment $G_{M}$ and electric quadrupole moment $G_{E}$ on the Borel mass parameter at different fixed values of the continuum threshold and general parameter $\beta$ are depicted in Figs. 1, 2, 3, 4, 5, and 6 for the radiative transitions under consideration.

Fig. 1

Left: The dependence of the magnetic dipole moment $G_{M}$ for $\Omega ^{*-}_{b}\rightarrow \Omega ^{-}_{b}\gamma$ transition on the Borel mass parameter $M^{2}$. Right: The dependence of the electric quadrupole moment $G_{E}$ for $\Omega ^{*-}_{b}\rightarrow \Omega ^{-}_{b}\gamma$ transition on the Borel mass parameter $M^{2}$

Fig. 2

The same as Fig. 1, but for $\Omega ^{*0}_{c}\rightarrow \Omega ^{0}_{c}\gamma$

Fig. 3

The same as Fig. 1, but for $\Xi ^{*0}_{b}\rightarrow \Xi ^{\prime 0}_{b}\gamma$

Fig. 4

The same as Fig. 1, but for $\Xi ^{*+}_{c}\rightarrow \Xi ^{\prime +}_{c} \gamma$

Fig. 5

The same as Fig. 1, but for $\Xi ^{*-}_{b}\rightarrow \Xi ^{\prime -}_{b} \gamma$

Fig. 6

The same as Fig. 1, but for $\Xi ^{*0}_{c}\rightarrow \Xi ^{\prime 0}_{c} \gamma$

Note that, in all figures, we plot the absolute values of the physical quantities under study since it is not possible to predict the signs of the residues from the mass sum rules. From these figures, we see that the results weakly depend on the $M^2$ and $s_0$ in their working regions.

To determine the working regions for the general parameter $\beta$ at different radiative channels, we depict the dependence of the results on this parameter at different fixed values of the Borel mass parameter and continuum threshold in Figs. 7, 8, 9, 10, 11, and 12. Note that instead of $\beta$ we use $\cos \theta$, where $\beta =\tan \theta$. The interval $-1\le \cos \theta \le 1$ corresponds to $\beta$ between $-\infty$ to $+\infty$, which we shall consider in our calculations. The numerical results show that the values of $G_{E}$ are negligibly small and therefore we consider only the dependence of $G_{M}$ on $\beta$, in order to find its working region.

Fig. 7

Left: The dependence of the magnetic dipole moment $G_{M}$ for $\Omega ^{*-}_{b}\rightarrow \Omega ^{-}_{b}\gamma$ on $\cos \theta$. Right: The dependence of the electric quadrupole moment f $G_{E}$ for $\Omega ^{*-}_{b}\rightarrow \Omega ^{-}_{b}\gamma$ on $\cos \theta$

Fig. 8

The same as Fig. 7, but for $\Omega ^{*0}_{c}\rightarrow \Omega ^{0}_{c}\gamma$

Fig. 9

The same as Fig. 7, but for $\Xi ^{*0}_{b}\rightarrow \Xi ^{\prime 0}_{b}\gamma$

Fig. 10

The same as Fig. 7, but for $\Xi ^{*+}_{c}\rightarrow \Xi ^{\prime +}_{c}\gamma$

Fig. 11

The same as Fig. 7, but for $\Xi ^{*-}_{b}\rightarrow \Xi ^{\prime -}_{b}\gamma$

Fig. 12

The same as Fig. 7, but for $\Xi ^{*0}_{c}\rightarrow \Xi ^{\prime 0}_{c}\gamma$

From Figs. 7, 8, 9, 10, 11, and 12, we obtain the region $-0.25\le \cos \theta \le 0.5$ common for all radiative transitions under consideration, at which the dependence of the $G_{M}$ on $\cos \theta$ is relatively weak. In most of the figures related to the magnetic dipole moment, the Ioffe current which corresponds to $\cos \theta \simeq -0.71$ remains out of the reliable region.

Considering the working regions for the auxiliary parameters, the photon DAs, and other input parameters, we extract the values of the magnetic dipole moment $G_{M}$ and the electric quadrupole moment $G_{E}$ corresponding to the considered radiative transitions as presented in Table 3. For comparison, we also present the predictions of VDM [3] on $G_{M}$ and $G_{E}$ in this table. From this table we see that, considering the errors in our results, our predictions are comparable with those of the VDM on the magnetic dipole moment $G_{M}$ for all transitions except that $\Omega ^{*-}_{b}\rightarrow \Omega ^{-}_{b}\gamma$, for which our result is considerably small compared to that of VDM. In both models, the values of $G_{E}$ are negligibly small for all considered channels.

Table 3 The absolute values of the magnetic dipole moment $|G_{M}|$ and electric quadrupole moment $|G_{E}|$ for the corresponding radiative decays in units of the natural magneton. PW means present work and VDM refers to the vector dominance model

At the end of this section we would like to present the decay width for the radiative transitions under consideration. Considering the transition matrix element in Eq. (4) and definitions of the magnetic dipole and electric quadrupole moments in terms of the form factors $G_1$ and $G_2$, we get the following formula for the widths of the corresponding transitions:

$$\begin{aligned} \Gamma =3 \frac{\alpha }{32}\frac{(m_1^2-m_2^2)^3}{m_1^3m_2^2}(G_M^2+3G_E^2). \end{aligned}$$

(21)

Using the numerical values for the magnetic dipole and electric quadrupole moments as well as the QCD sum rules predictions for the baryon masses, viz. $\Omega ^{*}_{b}=(6.17\pm 0.15)~\mathrm{GeV}$, $\Omega ^{*}_{c}=(2.79\pm 0.19)~\mathrm{GeV}$, $\Xi ^{*}_{b}=(6.02\pm 0.17)~\mathrm{GeV}$, $\Xi ^{*}_{c}=(2.65\pm 0.20)~\mathrm{GeV}$, $\Omega _{b}=(6.11\pm 0.16)~\mathrm{GeV}$, $\Omega _{c}=(2.70\pm 0.20)~\mathrm{GeV}$, $\Xi ^{'}_{b}=(5.96\pm 0.17)~\mathrm{GeV}$, and $\Xi ^{'}_{c}=(2.56\pm 0.22)~\mathrm{GeV}$ [23, 24], we get the values for the widths as presented in Table 4. For comparison, we also depict the existing predictions from the VDM in the same table. Looking at this table we see that our results are overall comparable in orders of magnitudes with the results of [3] except for the $\Omega ^{*-}_{b}\rightarrow \Omega ^{-}_{b}\gamma$ channel, at which our result is roughly one order of magnitude smaller compared to that of [3]. When we compare our results with those of [25, 26], we see considerable differences in the orders of magnitudes between the two models’ predictions except for the $\Omega ^{*0}_{c}\rightarrow \Omega ^{0}_{c}\gamma$ and $\Xi ^{*+}_{c}\rightarrow \Xi ^{\prime +}_{c}\gamma$ channels where our predictions are in the same orders of magnitude as those of [25, 26]. The big differences between our results, [3], and [25, 26] may be attributed to the different baryon masses that are used since the width in Eq. (19) is very sensitive to the masses of the initial and final baryons.

Table 4 Widths of the corresponding radiative transitions in KeV

In summary, we have calculated the transition magnetic dipole moment $G_{M}$ and electric quadrupole moment $G_{E}$ as well as the decay width for the radiative $\Omega _{Q}^{*}\rightarrow \Omega _{Q}\gamma$ and $\Xi _{Q}^{*}\rightarrow \Xi ^{\prime }_{Q}\gamma$ transitions within the light cone QCD sum rule approach and compared the results with the predictions of the VDM. Considering the recent progress on the identification and spectroscopy of the heavy baryons, we hope it will be possible to study these radiative decay channels experimentally in the near future.