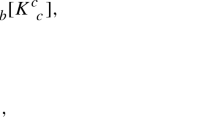Future dynamics in $f(R)$ theories

Abstract

The $f(R)$ gravity theories provide an alternative way to explain the current cosmic acceleration without invoking a dark energy matter component used in the cosmological modeling in the framework of general relativity. However, the freedom in the choice of the functional forms of $f(R)$ gives rise to the problem of the degeneracy among these gravity theories on theoretical and (or) observational grounds. In this paper we examine the question as to whether the future dynamics can be used to break the degeneracy between $f(R)$ gravity theories by investigating the dynamics of spatially homogeneous and isotropic dust flat models in two $f(R)$ gravity theories, namely the well-known $f(R) = R + \alpha R^{n}$ gravity and another by Aviles et al., whose motivation comes from the cosmographic approach to $f(R)$ gravity. We perform a detailed numerical study of the dynamics of these theories taking into account the recent constraints on the cosmological parameters made by the Planck Collaboration. We demonstrate that besides being useful for discriminating between these two $f(R)$ gravity theories, the future dynamics technique can also be used to determine the finite-time behavior as well as the fate of the Universe in the framework of these $f(R)$ gravity theories. There also emerges from our analysis the result that one still can have a dust flat FLRW solution with a big rip, if gravity is governed by $f(R) = R + \alpha R^n$. We also show that FLRW dust solutions with $f''<0$ do not necessarily lead to singularities.

1 Introduction

A wide range of cosmological observations coming from different sources, including the supernovae type Ia (SNe Ia) [1–3], the cosmic microwave background radiation (CMBR) [4, 5], and baryon acoustic oscillation (BAO) surveys [6–11], clearly indicate that the Universe is currently expanding with an accelerating rate. A fair number of models and frameworks have been proposed to account for this observed accelerated expansion. These approaches can be roughly grouped into two families. In the first, the so-called dark energy is invoked and the underlying framework of general relativity (GR) is kept unchanged. In this regard, the simplest way to account for the accelerating expansion of the Universe is through the introduction of a cosmological constant, $\Lambda$, into Einstein’s field equations. This is entirely consistent with the available observational data, but it faces difficulties such as the order of magnitude of the cosmological constant and its microphysical origin. In the second family, modifications of Einstein’s field equations are assumed as an alternative for describing the accelerated expansion. This latter group includes, for example, generalized theories of gravity based upon modifications of the Einstein–Hilbert action by taking nonlinear functions, $f(R)$, of the Ricci scalar $R$ or other curvature invariants (for reviews see Refs. [12–18]).

The fact that $f(R)$ theories can potentially be used to explain the observed accelerating expansion has given birth to a number of articles on these gravity theories, in which several features of $f(R)$ gravity have been discussed [19–42], including the stability conditions [43–47], compatibility with solar-system tests [48–56], energy conditions [57–64], nonlocal causal structure [65–68], and observational constraints from a diverse set of cosmological observations [69–81].

However, although the freedom in the choice of the functional forms of $f(R)$ has motivated many different suggestions of $f(R)$ gravity theories, which account for the accelerating expansion and are compatible with the solar-system tests, it also gives rise to the problem of how to constrain and break the degeneracy among these gravity theories on theoretical and/or observational grounds. In this regard, observational constraints on some $f(R)$ gravity from a diverse set of observations have been placed [69–81], and tests of the cosmological viability of some specific forms of $f(R)$ have been explored [82–87].

A pertinent question that arises here is whether the future dynamics can be used to break the degeneracy between $f(R)$ gravity theories. In this article, to proceed with the investigation on the potentialities, difficulties, and limitations of $f(R)$ gravity, we examine this question by investigating the future dynamics of Friedmann–Lemaître–Robertson–Walker (FLRW) dust flat model in two $f(R)$ gravity theories, namely the well-known $f(R) = R + \alpha R^{n}$ gravity, for which many results are available in the literature [88–91], and another by Aviles, Bravetti, Capozziello, and Luongo [92] (ABCL gravity for short), whose motivation comes from the cosmographic approach to $f(R)$ gravity [93–97]. We show that besides being helpful for discriminating between these $f(R)$ gravity theories, the future dynamics technique can also be used to determine the finite-time behavior as well as the fate of the FLRW flat universe in these $f(R)$ gravity theories. See the penultimate paragraph of this section for additional words of contextualization regarding the future dynamics in $f(R)$ gravity.

In the cosmological modeling in the framework of general relativity, until the observational discovery of the accelerating expansion virtually any textbook on cosmology describes the future dynamics of FLRW pressure-free dust models as follows. It expands forever if it has an Euclidean or hyperbolic spatial geometry, and expands and eventually recollapses if it has a spherical spatial geometry. However, the discovery of the accelerating expansion made apparent that these simple future forecasts had to be modified, since the negative-pressure dark energy component, invoked to account for the acceleration in the context of GR, plays a crucial role in the evolution of the Universe. Indeed, the dark energy (DE) is usually described in the framework of GR by the equation-of-state parameter $\omega = p/\rho$, which is the ratio of the DE pressure to its density. A value $\omega < -1/3$ is required for cosmic acceleration. When $-1 < \omega < -1/3$ the DE density decreases with the scale factor $a(t)$. However, if $\omega <-1$ the dark energy density becomes infinite in a finite-time, driving therefore the Universe to a future finite-time singularity, called big rip [98–100]. Subsequently, it was determined that this is not the only possible doomsday of a dark energy dominated universe. It may, for example, come to an end in a sudden singularity [101, 102] or a big freeze doomsday [103–105].

Afterwards, Nojiri et al. have grouped the finite-time future singularities for the perfect-fluid FLRW models into four types [106], called Type I (big rip), Type II (sudden), Type III (big freeze) and Type IV, depending on the future behavior of $a(t)$, $\rho$, $p$, and of the higher derivative of the Hubble parameter $H=\dot{a}/a$ (see also Ref. [107]).¹

In this paper we examine numerically the future dynamics of the FLRW flat dust model but, instead of assuming a perfect fluid with a dark energy component, we have assumed that gravity is governed by $f(R)$ gravity theories with dust. As a result we show that, differently from the perfect-fluid analytical results obtained in context of GR, one can have a big-rip singularity with a simple pressure-free dust fluid, if gravity is governed by $f(R) = R + \alpha R^n$. Furthermore, by using our numerical future dynamics scheme of this paper, we present an example of FLRW dust solution in which the ghost-like regimes ($f''<0)$ do not necessarily lead to singularity.

Before giving the outline of our paper, some additional words of clarification regarding the literature on the future dynamics in $f(R)$ gravity are in order. First, we mention that the possibility of a phantom (big-rip) behavior in these theories was previously pointed out in Ref. [114]. In this regard, we note that finite-time singularities in $f(R)$ gravity was investigated in Ref. [115], wherein by using a reconstruction technique, it was demonstrated that not only a big rip but all types of singularities (Type I–Type IV) can occur in these theories with no conflict with observational data.² Second, future dynamics in $f(R)$ gravity was previously considered in a number of articles [116–119]. However, their approaches are different from ours since they have considered a perfect-fluid matter source with $\rho , p$, and $\omega =p/\rho$, while here we consider simply a pressure-free dust. Furthermore, our analysis is numerical, while they have made an analytical approach to this issue.

Our paper is organized as follows. In Sect. 2 we give a brief review of $f(R)$ gravity theories, derive the field equations for the flat FLRW metric with dust matter content, state the initial conditions for the dynamical evolutions, and present the future dynamics in the context of the general relativity theory. In Sect. 3 we introduce the ABCL [92] Lagrangian, develop the necessary technique for solving the dynamical equations, and derive our numerical results regarding the ABCL $f(R)$ gravity. In Sect. 4 we use our method to study the polynomial Lagrangian $f(R)$ gravity and make a comparative analysis of these theories. Final remarks and main conclusions are presented in Sect. 5.

2 Prerequisites

In this section we briefly review $f(R)$ gravity, derive the field equations for the flat FLRW metric with dust matter content, state the initial conditions for all numerical analyses of this paper, and present the future dynamics for the particular Einstein’s gravity theory for later comparison with the dynamics in other gravity theories.

2.1 $f(R)$ gravity and field equations

We begin by recalling that the action that defines an $f(R)$ gravity theory can be written as

$$\begin{aligned} S=\frac{1}{2\kappa ^2}\int \mathrm{d}^4x\sqrt{-g}\,f(R) + S_m, \end{aligned}$$

(1)

where $\kappa ^2\equiv 8\pi G/c^4$, $g$ is the determinant of the metric $g_{ab}$, $f(R)$ is a function of the Ricci scalar $R$, and $S_m$ the standard action for the matter fields. Varying this action with respect to the metric we obtain the field equations

$$\begin{aligned} f'R_{ab} - \frac{f}{2}g_{ab} - \left( \nabla _{a}\nabla _{b}-g_{ab}\,\Box \, \,\right) f' = \frac{8\pi G}{c^{4}}T_{ab}\, ; \end{aligned}$$

(2)

here and in what follows a prime denotes differentiation with respect to $R$ and $\Box \equiv g^{ab}\,\nabla _{a}\nabla _{b}\,$. Clearly, for $f(R)=R+ \Lambda$ these field equations reduce to the Einstein equations with the cosmological constant, $\Lambda$, term.

Two important constraints, often used to simplify the calculations, come from the fact that the covariant divergence of both sides of Eq. 2 is null. This implies that the $0i$ and $00$ components of the field equations give rise to the following constraints:

$$\begin{aligned} E_{0i}&= f^{\prime }R_{0i}-\frac{f}{2}g_{0i}-(\nabla _{0}\nabla _{i}-g_{0i}\square )f^{\prime }=0, \end{aligned}$$

(3)

$$\begin{aligned} E_{00}&= f^{\prime }R_{00}-\frac{f}{2}g_{00}-(\nabla _{0}\nabla _{0}-g_{00}\square )f^{\prime } \nonumber \\&- \,\frac{8\pi G}{c^{4}}\,\,T_{00}=0. \end{aligned}$$

(4)

Clearly, Eq. (3) is identically satisfied, while the constraint given by Eq. (4) must be fulfilled throughout time evolution. We shall use this fact as a way of checking the accuracy of the numerical integration of the remaining equations of the dynamical system in the numerical analyses of the following sections.

In this work we focus on the flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric,

$$\begin{aligned} \mathrm{d}s^{2}=-c^2\mathrm{d}t^{2}+a(t)^{2}(\mathrm{d}x^{2}+\mathrm{d}y^{2}+\mathrm{d}z^{2}), \end{aligned}$$

(5)

which is supported by the recent observations [4, 5], and is consistent with the standard inflationary models. Thus, the non-vanishing component of the Ricci tensor and the Ricci scalar can be written in the form

$$\begin{aligned}&R^0_0=\frac{3}{c^2}( \dot{H}+H^2),\end{aligned}$$

(6)

$$\begin{aligned}&R_1^1=R_2^2=R_3^3=\frac{1}{c^2}(\dot{H}+3H^2), \end{aligned}$$

(7)

$$\begin{aligned}&R=\frac{6}{c^2}(\dot{H}+2H^2), \end{aligned}$$

(8)

where $H=\dot{a}/a$ and the over-dot denotes derivative with respect to the time $t$.

Since we are interested in dust of density $\rho$ with zero pressure ($p=0$), we have

$$\begin{aligned} \dot{\rho }=-3H\rho \quad \text{ and } \quad \rho =\frac{\rho _0}{a^3}; \end{aligned}$$

(9)

here and in what follows the subscript zero denotes present-day values of the cosmological parameters.

Taking into account Eqs. (6)–(9) the field equations (2) reduce to

$$\begin{aligned} -3(\dot{H} +H^2)f^\prime +\frac{fc^2}{2}+3Hf^{\prime \prime }\dot{R}=\frac{8\pi G\rho }{c^2}, \end{aligned}$$

(10)

$$\begin{aligned} f^\prime (\dot{H}+3H^2)-\frac{fc^2}{2}-2Hf^{\prime \prime }\dot{R}-f^{\prime \prime }\ddot{R}-\dot{R}^2f^{\prime \prime \prime }=0.\nonumber \\ \end{aligned}$$

(11)

One can easily show that Eq. (10) is nothing but the constraint Eq. (4), which for the dust flat FLRW models takes the form

$$\begin{aligned} E_{00}=-3(\dot{H} +H^2)f^\prime +\frac{fc^2}{2}+3Hf^{\prime \prime }\dot{R}-\frac{8\pi G\rho }{c^2}=0,\nonumber \\ \end{aligned}$$

(12)

which is in a suitable form for checking the accuracy of the numerical integration of the dynamical Eq. (11) for the $f(R)$ gravity theories we are concerned with in this paper.

2.2 Initial conditions

To study the future dynamics for the spatially flat FLRW dust models one needs to choose initial conditions for the numerical integration. In this work we use the numerical values of the cosmological parameters reported by the Planck Collaboration team [4, 5] along with the values of the cosmographic parameters given in Ref. [121]. In Table 1 we collect the values of the cosmological parameters we shall employ in our numerical analyses. Table 1 also contains details of the units and conventions we have adopted in this paper.

Table 1 Values of the cosmological parameters used as initial conditions in the numerical integrations. As a suitable choice of units, the length is the $Mpc$, the time unit $T=3.26158\times 10^{6}y$, and the mass unit is chosen as $M_\odot$, so that in these units the speed of light $c=1$, and Newton’s constant is $G=4.7863\times 10^{-20}\frac{Mpc^{3}}{M_{\odot }T}$. The values of the cosmological parameters, deceleration, and jerk parameters, are taken from the Planck results [4, 5] from Ref. [121]

To investigate the future dynamics in the following sections, we recall that for the flat FLRW models the dimensionless deceleration $(q)$ and jerk $(j)$ parameters [121] given in Table 1 are such that the relations

$$\begin{aligned}&q_{0}=-\frac{1}{H_{0}^{2}}(\dot{H}_0+H_0^2), \end{aligned}$$

(13)

$$\begin{aligned}&j_{0}=\frac{1}{H_{0}^{3}}(\ddot{H}_0+3H_0\dot{H}_0+H_0^3) . \end{aligned}$$

(14)

hold.

2.3 Dynamics in general relativity

For a later comparison with the dynamics in other gravity theories, we briefly present here the analysis for the spatially flat FLRW dust model in the Einstein theory with cosmological constant $\Lambda$, that is, for $f(R)=R+\Lambda$. In this case the field equations (12) and Eq. (11) reduce, respectively, to

$$\begin{aligned}&E_{00} = 3H^2 + \frac{\Lambda c^2}{2} - \frac{8\pi G}{c^2}\rho = 0,\end{aligned}$$

(15)

$$\begin{aligned}&-2\dot{H} - 3H^2 -\frac{\Lambda c^2}{2} = 0. \end{aligned}$$

(16)

The left panel in Fig. 1 shows the evolution of $H$ for spatially flat FLRW dust model in the Einstein theory, where the initial conditions given in Table 1 were employed in the numerical calculations. This panel also shows a de Sitter asymptotic behavior for $H$ for a non-vanishing cosmological constant $\Lambda$. The right panel shows the constraint equation (12), providing an assessment of the reliability of the numerical integration.

Fig. 1

Left panel time evolution of $H$ for spatially flat FLRW dust model in general relativity. Right panel the behavior of the constraint (12) making apparent the high level of accuracy in the numerical integration that has been obtained. The current values of the cosmological parameters as given by the Planck team [4, 5] were taken as initial conditions in the numerical integration

3 Dynamics in ABCL gravity

In this section we shall study the future dynamic of the spatially flat FLRW dust model in the $f(R)$ gravity recently suggested by A. Aviles et al. [92], referred to in this paper as ABCL gravity theory. This gravity theory has been obtained through an optimal Monte-Carlo fitting of cosmographic results and is given by

$$\begin{aligned} f(R)&= \frac{1}{2(a+b+c)e\pi R_0^2}\left\{ \Lambda R_0^2\left[ 2a\pi e^{R/R_0}\right. \right. \nonumber \\&\quad \left. \left. +e\left( 6b+(a+2c)\pi +8b\arctan \left( \frac{R}{R_0}\right) \right) \right] \right. \nonumber \\&\quad +eR\left[ 2R_0 \left( \,(a+b+c)\pi R_0-4b\Lambda \right) \right. \nonumber \\&\quad \left. +(2b-a\pi )\Lambda R\right] \nonumber \\&\quad \left. -2ce\pi \Lambda (R-R_0)^2\sin \left( \frac{2\pi R}{R_0}\right) \right\} , \end{aligned}$$

(17)

where $a$, $b$, and $c$ are free parameters, and $R_0$ is the present-day value of the Ricci scalar. Regardless of the values of these parameters for this theory one has

$$\begin{aligned}&f(R_0)=R_0+\Lambda , \end{aligned}$$

(18)

$$\begin{aligned}&f^\prime _0=1,\end{aligned}$$

(19)

$$\begin{aligned}&f^{\prime \prime }_0=0, \end{aligned}$$

(20)

where $f^{\prime }_{0} \equiv (\partial f/\partial R)_{R = R_{0}}$ and a similar notation is used for higher order derivatives. In addition to the constraints (18) and (19), which are required to ensure that both Einstein’s theory and Newton’s constant are recovered in the lowest order, we shall take into account that $f^{\prime \prime }\ge 0$, which is a condition to avoid the presence of ghosts [43, 122]. We also note that the conditions (18)–(20) also insure that (10) and (11) reduce to the Friedmann equations in the lower order.

In order to study the dynamics we will need

$$\begin{aligned}&\begin{aligned}&f^{\prime \prime \prime }_0=\Lambda \frac{2b+\pi (a-12c\pi )}{(a+b+c)\pi R_0^3},\\&f_0^{iv}=\frac{a\Lambda }{(a+b+c)R^4_0},\\&f_0^{v}={\frac{\Lambda a\pi -12b\Lambda +160\pi ^{4}c\Lambda }{(a +b+ c)\pi R_0^5}},\\&f_0^{vi}={\frac{\Lambda a\pi +60b\Lambda }{(a + b+ c)\pi R_0^6}},\\&f_0^{vii}={\frac{\Lambda a\pi -180b\Lambda -1344\pi ^{6}c\Lambda }{(a +b+ c)\pi R_0^7}},\\&f_0^{viii}=\frac{\Lambda a}{(a+b+c)R_0^8}. \end{aligned} \end{aligned}$$

(21)

Before proceeding to the numerical analysis for this gravity theory, we note that due care ought to be taken in using the initial conditions since $f^{\prime \prime }=0$ at $t=t_0$. Note that in Eqs. (10) and (11) the higher derivatives of the scalar factor are multiplied by $f^{\prime \prime }$. When $f^{\prime \prime }\ne 0$, we have a set of differential equations describing the dynamics. When $f^{\prime \prime }=0$ locally, at $t=t_0$ we have an entirely different set of differential equations obtained by (10) and (11). In what follows, to deal with this difficulty we first assume that the solution possesses a Taylor expansion about $t=t_0$ up to second order. Then we substitute this expansion into the field equations (10) and (11) in an order by order manner, which results in a perturbative solution up to some order. Second, instead of assuming the initial condition exactly at $t=t_0$, the initial condition is taken at $t=t_0+\epsilon$ ($\epsilon ^2 \lll 1$) through this perturbative scheme, for which now $f^{\prime \prime }(t_0+\epsilon )\ne 0$.

To carry out the outlined perturbative procedure, it is required to distinguish two different regimes in establishing the initial condition ($f'=(t_0+\epsilon )\ne 0$), namely one when at $t = t_0$, $f^{\prime \prime \prime } \ne 0$, and another when $t = t_0$, $f^{\prime \prime \prime }=0$. In the following we shall treat separately these two cases.

3.1 The case $f_0^{\prime \prime \prime }\ne 0$

Since for the ABCL gravity theory $f^{\prime \prime }(t_0)=0$, in order to find a suitable form for the field equations within a perturbative scheme, we first assume that the solution can be expanded in a Taylor series about $t=t_0$ up to second order. Thus, to obtain the terms of (10) and (11) we have

$$\begin{aligned}&H=H_0+\dot{H}_0(t-t_0)+\frac{1}{2}\ddot{H}_0(t-t_0)^2,\\&H^2=H_0^2+2H_0\dot{H}_0(t-t_0)+ ( \dot{H}_0^2+ H_0\ddot{H}_0)(t-t_0)^2,\\&\dot{H}=\dot{H}_0+\ddot{H}_0(t-t_0)+\frac{1}{2}\dddot{H}_0(t-t_0)^2,\\&\dot{R}^2=\dot{R}_0^2+2\dot{R}_0\ddot{R}_0(t-t_0)+ (\ddot{R}_0^2+\dot{R}_0\dddot{R}_0 )(t-t_0)^2,\\&\dot{R}=\dot{R}_0+\ddot{R}_0(t-t_0)+\frac{1}{2}\dddot{R}_0(t-t_0)^2,\\&\ddot{R}=\ddot{R}_0+\dddot{R}_0(t-t_0)+\frac{1}{2}\ddddot{R}_0(t-t_0)^2,\\&\rho =\rho _0-3H_0\rho _0(t-t_0)+\frac{1}{2}(9H_0^2-3\dot{H}_0)\rho _0(t-t_0)^2,\\&f=R_0+\Lambda +\dot{R}_0(t-t_0)+\frac{\ddot{R}_0}{2}(t-t_0)^2,\\&f^\prime =1+\frac{1}{2}f^{\prime \prime \prime }_0\dot{R}_0^2(t-t_0)^2,\\&f^{\prime \prime }=f^{\prime \prime \prime }_0\dot{R}_0(t-t_0)+\frac{1}{2}(f^{iv}_0\dot{R}_0^2+f^{\prime \prime \prime }_0\ddot{R}_0)(t-t_0)^2,\\&f^{\prime \prime \prime }=f^{\prime \prime \prime }_0+f_0^{iv}\dot{R}_0(t-t_0)+\frac{1}{2}(f^{v}_0\dot{R}_0^2+f_0^{iv}\ddot{R}_0)(t-t_0)^2. \end{aligned}$$

Then we substitute these terms into the field equations (10) and (11) in an order by order mode to have

• Zero order in $(t-t_0)$. Equations (10) and (11) give

  $$\begin{aligned}&3(H_0)^2+\frac{\Lambda c^2}{2}=\frac{8\pi G\rho _0}{c^2}, \end{aligned}$$

  (22)
  $$\begin{aligned}&-2\dot{H}_0-3(H_0)^2-\frac{\Lambda c^2}{2}-f_0^{\prime \prime \prime }\dot{R}_0=0. \end{aligned}$$

  (23)

• First order in $(t-t_0)$. Equations (10) and (11) yield

  $$\begin{aligned}&-3(\ddot{H}_0+2H_0\dot{H}_0)+\frac{c^2}{2}\dot{R}_0 +3 H_0f_0^{\prime \prime \prime } \dot{R}_0^2 \nonumber \\&\quad =\frac{8\pi G}{c^2}(-3H_0\rho _0), \end{aligned}$$

  (24)
  $$\begin{aligned}&(\ddot{H}_0+6H_0\dot{H}_0)-\frac{c^2}{2}\dot{R}_0 -f_0^{\prime \prime \prime }\dot{R}_0 (2H_0\dot{R}_0 +3\ddot{R_0}) \nonumber \\&\quad -f_0^{iv}(\dot{R}_0)^3=0. \end{aligned}$$

  (25)

From (22)–(25) one has

$$\begin{aligned} H_0^2&= \frac{1}{3}\left( \frac{8\pi G\rho _0}{c^2} -\frac{\Lambda c^2}{2}\right) ,\end{aligned}$$

(26)

$$\begin{aligned} \ddot{H}_0&= \frac{c^2}{6}\left( \frac{-2\dot{H}_0-3H_0^2-(\Lambda c^2)/2}{f_0^{'''}}\right) ^{1/2} -4H_0\dot{H}_0, \end{aligned}$$

(27)

$$\begin{aligned} \dddot{H}_0&= -4 \dot{H}_0^2-4H_0\ddot{H}_0 \nonumber \\&\quad -\frac{c^2}{6}\left( \frac{2\ddot{H}_0+6H_0\dot{H}_0+2H_0f_0^{\prime \prime \prime }\dot{R}_0^2+f_0^{iv}\dot{R}_0^3}{3f_0^{\prime \prime \prime }\dot{R}_0}\right) , \nonumber \\ \end{aligned}$$

(28)

where from Eq. (8) we have

$$\begin{aligned} \dot{R}_0=6(\ddot{H}_0+4H_0\dot{H}_0)/c^2. \end{aligned}$$

(29)

As mentioned, if $f^{\prime \prime }\ne 0$ the initial condition follows directly from Eqs. (10) and (11). Otherwise, if $f^{\prime \prime }_0=0$ at $t=t_0$, then the initial condition is chosen for $t$ near $t_0$, so that we can be sure that $f^{\prime \prime }(t)\ne 0$ and the dynamics is directly described by Eqs. (10) and (11). In this case, instead of taking $H_0$, $\dot{H}_0$, and $\ddot{H}_0$ the initial conditions are chosen at $t-t_0=\epsilon$; we have

$$\begin{aligned}&H=H_0+\dot{H_0}(t-t_0)+\frac{1}{2}\ddot{H}_0(t-t_0)^2,\end{aligned}$$

(30)

$$\begin{aligned}&\dot{H}=\dot{H}_0+\ddot{H}_0(t-t_0)+\frac{1}{2}\dddot{H}_0(t-t_0)^2,\end{aligned}$$

(31)

$$\begin{aligned}&\ddot{H}=\ddot{H}_0+\dddot{H}_0(t-t_0), \end{aligned}$$

(32)

where $\dot{H}_0$, $\ddot{H}_0$, $\dddot{H}_0$ satisfy the relations (26)–(28). We note that according to Eqs. (27) the initial value $\dot{H}_0$ ought to obey the constraint

$$\begin{aligned} \frac{-2\dot{H}_0-3H_0^2-(\Lambda c^2)/2}{f_0^{\prime \prime \prime }} <0. \end{aligned}$$

(33)

The left panel of Fig. 2 shows a representative numerical future dynamics of a spatially flat FLRW dust model in the ABCL gravity theory with $f_0^{\prime \prime \prime } \ne 0$. In this case, as indicated by $H(t)$, the universe would present a noteworthy expanding phase after an initial future decelerating period. The right panel in this figure shows the constraint $E_{00}=0$, given in Eq. (12); it fluctuates randomly and increases but is always smaller than $2\times 10^{-17}$, which is a strong indication of the correctness of the numerical solution.

Fig. 2

Left panel time evolution of $H$ for spatially flat FLRW dust model in the ABCL gravity theory with the initial conditions specified by Eqs. (30 31)–(32). The values of the free parameters were taken to be $a=107.9$, $b=-148.0$, and $c=40.0$, and the values of the cosmological parameters are the best fit values collected in Table 1 as given by the Planck team [4, 5]. They were taken as initial conditions in the numerical integration. Right panel the behavior of the constraint $E_{00}$ as given by (12), making apparent the degree of confidence of the numerical calculations. No singularities were found throughout the numerical evolution

Regarding the choice of the $a$, $b$, and $c$ used to find the numerical future dynamics solution, it is important to point out that the independence of Eqs. (18)–(20) allows some freedom in their choice. Although a more general phase space analysis, with its associated attractors, would be necessary to determine every possible future dynamics solution, here we have restricted our analysis to a set of values which are consistent with the present-day constraints on the cosmological parameters. This choice of values was also motivated by a similar procedure used in the study of the polynomial $f(R)$ gravity, which we study in details in Sect. 4.

3.2 The case $\mathbf {f_0^{\prime \prime \prime }=0}$

The condition $f_0'''=0$ can be achieved in the ABCL $f(R)$ gravity provided that the constraint

$$\begin{aligned} a = 12 \pi c - \frac{2b}{\pi } \end{aligned}$$

(34)

holds. Now, similarly to the previous section we assume that the solution can be expanded in a Taylor series $t=t_0$ up to second order. Then we substitute the Taylor series terms into the field equations (10) and (11) in an order by order manner. This gives the following:

• Zero order in $(t-t_0)$. Equations (10) and (11) give

  $$\begin{aligned}&3(H_0)^2+\frac{\Lambda c^2}{2}=\frac{8\pi G\rho _0}{c^2}, \end{aligned}$$

  (35)
  $$\begin{aligned}&-2\dot{H}_0=\frac{8\pi G\rho _0}{c^2} . \end{aligned}$$

  (36)

• First order in $(t-t_0)$. Equations (10)  and (11) yield

  $$\begin{aligned}&-2\dot{H}_0=\frac{8\pi G\rho _0}{c^2}, \end{aligned}$$

  (37)
  $$\begin{aligned}&f_0^{iv}\dot{R}_0^3+\frac{\dot{R}_0c^2}{3}-2H_0\dot{H}_0=0. \end{aligned}$$

  (38)

• Second order in $(t-t_0)$. Equations (10)  and (11) furnish

  $$\begin{aligned}&6\dot{H}_0\!+\!6H_0\ddot{H}_0\!+\!3H_0f_0^{iv}\dot{R}_0^3\!=\!\frac{8\pi G\rho _0}{c^2}\left( 9H_0^2-3\dot{H}_0\right) , \end{aligned}$$

  (39)
  $$\begin{aligned}&-2\dddot{H}_0-6\dot{H}_0^2-6H_0\ddot{H}_0-6f_0^{iv}\dot{R}_0^2\ddot{R}_0 \nonumber \\&\quad -2H_{0}f_0^{iv}\dot{R}^{3} - f_0^v\dot{R}_0^4=0, \end{aligned}$$

  (40)

Now, since $\dot{R}$ is given by Eq. (29) it is clear from Eq. (38) that $\ddot{H}_0$ is given by a third order algebraic equation. Thus, from Eqs. (35)–(40) one has

$$\begin{aligned}&H_0=\sqrt{\frac{8\pi G\rho _0}{3c^2}-\frac{\Lambda c^2}{6}},\\&\dot{H}_0=-\frac{4\pi G\rho _0}{c^2}, \end{aligned}$$

and

$$\begin{aligned} \ddot{H}_0\!=\!-4H_{0}\dot{H}_{0}+\frac{c^{2}}{6}\left[ \frac{1}{6f_{0}^{iv}}\root 3 \of {\Delta \,\left( f_{0}^{iv}\right) ^{2}}-\frac{2c^{2}}{3 \root 3 \of {\Delta \,\left( f_{0}^{iv}\right) ^{2}}} \right] , \end{aligned}$$

(41)

where

$$\begin{aligned} \Delta \!=\! 216H_{0}\dot{H}_{0}\!+\!12\sqrt{3}\,\left[ \frac{4\left( c^{2}/3\right) ^{3}\!+\!108\left( H_{0}\dot{H}_{0}\right) ^{2}f_{0}^{iv}}{f_{0}^{iv}}\right] ^{1/2}\!\!. \end{aligned}$$

(42)

We display in Fig. 3 another representative numerical solution (with a suitable choice of $a$, $b$, and $c$), but now for the case $f_0^{\prime \prime } = 0$. The left panel of the figure shows the dynamic evolution of this dust flat FLRW model tends asymptotically to a de Sitter space. Its asymptote approaches the de Sitter vacuum solution obtained by analytically solving Eq. (2) with no matter content, which returns a value $H=1.8476\times 10^{-4}$, i.e. the asymptote shown in Fig. 3. By carrying out a stability analysis having this solution as background, it is possible to show that this is an attractor solution with $f^{\prime \prime }>0$. The right panel of Fig. 3 makes it clear that the constraint on $E_{00}$ [Eq. (12)] is smaller than $2\times 10^{-13}$ during the evolution of the FLRW flat model. This makes apparent the accuracy of the numerical calculations performed in the study of the future dynamics in this case.

Fig. 3

Left panel time evolution of $H$ for spatially flat FLRW dust model in the ABCL gravity theory. The values of the free parameters were taken to be $a=157.0$, $b=-258.5$, and $c=-0.2$, which fulfills the constraint equation (34). The cosmological parameters were taken to be the best fit values collected in Table 1 as given by the Planck team [4, 5]. The dynamic evolution of the flat FLRW spacetime tends asymptotically to a de Sitter space. Right panel the behavior of the constraint $E_{00}$ as given by (12), which is smaller than $10^{-13}$ for all time $t$, making apparent the precision of the numerical calculation throughout the evolution of the model

4 Dynamics in ${f(R) = R + \alpha R^{n}}$

In this section we apply the same numerical scheme used in the previous section to study the well-known $f(R)$ gravity theory

$$\begin{aligned} f(R)=R+\alpha R^{n}. \end{aligned}$$

(43)

The above $f(R)$ has the special feature of presenting equivalent results to the $\Lambda$CDM model, when applied to a FLRW setting within a range of choices for the constants $\alpha$ and $n$. In this sense no observationally relevant prediction would distinguish these cases as established in [123].

As referred to in the end of Sect. 3.1, a straightforward calculation to guide the choice of parameters $\alpha$ and $n$ can be achieved by using the field equations (10) along with Eqs. (43), (13), and (14). Indeed, these equations allow one to write $\alpha$ as

$$\begin{aligned} \alpha \!=\!\frac{-2c^{2n-2}\,\left( 3\,H_0^{2}\!-\!8\pi G\rho _0/c^2\, \right) (1\!-\!q_0)^{2-2n}}{ \left( 6\,H_0^{2}\right) ^{n} \left( 2\,n-2\,q_0\!+\!1\!+\!2\,nq_0-{n}^{2}q_0\!-\!2\,{n}^{2}\!-\!nj_0\!+\!{n}^{2}j_0\!-\!n{q_0}^{2}\!+\!{q_0}^{2}\right) },\nonumber \\ \end{aligned}$$

(44)

where the observed values of parameters $H_0$, $q_0$, $j_0$, and $\rho _0$ and their uncertainties are given in Table 1.

Now, the standard error deviation

$$\begin{aligned} \Delta \alpha&= \left| \frac{\partial }{\partial H_0}\alpha \right| \Delta H_0+\left| \frac{\partial }{\partial \rho _0}\alpha \right| \Delta \rho _0\nonumber \\&\quad +\left| \frac{\partial }{\partial q_0}\alpha \right| \Delta q_0+\left| \frac{\partial }{\partial j_0}\alpha \right| \Delta j_0 \end{aligned}$$

(45)

gives rise to lower and upper bounds on the values of $\alpha$ for different values of $n$. In fact, making use of the uncertainties of the parameters $H_0$, $q_0$, $j_0$, and $\rho _0$ (Table 1) one can plot the curves in the panels of Fig. 4 to illustrate these bounds.³ They have been used to guide us making suitable choices of the values of the parameters $\alpha$ and $n$ below.

By applying the same analysis introduced in Sect. 3 and using again the main values at Table 1 as initial conditions for the FLRW dust flat models, we have, for $n>0$, many parameter choices leading to asymptotic de Sitter solutions, which is consistent with the results in the literature [88–91]. As an example, Fig. 5 depicts $H$ for of $n=0.2$ and $\alpha =-4.295\times 10^{-6}$, which are typical values between the above-mentioned bounds in the left panel of Fig. 4. In Fig. 5 we also show the behavior of the constraint $E_{00}$, which exhibits fluctuations around zero with rather small amplitudes, making apparent the degree of confidence of the numerical calculations. For this particular value of $\alpha$, $n$, and the initial conditions as given by the Planck team, the de Sitter analytical vacuum solution obtained by solving Eq. (2) gives $H=1.8431\times 10^{-4}$, in rather good agreement with the asymptotic values shown in Fig. 5. It is possible to show that this solution is an attractor over this phase space region, with $f^{\prime \prime }>0$, as is also the case for the example depicted before in Fig. 3.

Fig. 4

Left panel bounds on the values of $\alpha$ for different values of $n$ derived from Eqs. (44) and (45) taking into account the values of the cosmological parameters and associated uncertainties collected in Table 1. The depicted positive values of $n$ cover an interval used to compute Fig. 5. Right panel bounds on the values of $\alpha$ for negative $n$, showing the interval of $n$ used to calculate Fig. 6

Fig. 5

Left panel time evolution of $H$ for spatially flat FLRW dust model in the $f(R)$ theory defined by Eq. (43). It shows the case in which $n=0.2$ and $\alpha =-4.295\times 10^{-6}$. The initial conditions are the best fit values of the parameters collected in Table 1. Right panel the behavior of the constraint $E_{00}$ as given by (12), which is smaller than $10^{-22}$ for all time $t$, making explicit the precision of the numerical calculation throughout the evolution of the model

As for the $n<0$ case, many initial conditions lead to a big-rip singularity. This is a curvature singularity in the sense that it cannot be removed by a coordinate transformation. As an example, we show in Fig. 6 the time evolution of the Hubble parameter of the dust flat FLRW model for $n=-0.1$ and $\alpha =-4.557 \times 10^{-8}$, chosen by taking into account the right panel of Fig. 4. In this case, the analytical vacuum solution to the field equation (2) gives $H=1.8618\times 10^{-4}$. It is also possible to show that this solution is a repellor in this phase space region, rendering the divergent evolution shown in Fig. 6 an expected feature, complemented by our verification that it presents $f^{\prime \prime }<0$ asymptotically. As indicated by the right panel of Fig. 6, the numerical constraint $E_{00}$ noticeably increases as the solution approaches the physical singularity, which is expected from the outset, and then the numerical solution must be truncated.

It is also interesting to compare the future dynamics shown in Fig. 2, for ABCL gravity, with that of Fig. 6, for $f(R) = R+\alpha R^n$ with $n<0$. The dynamic depicted by Fig. 6 is a typical example of the run-away evolution that suddenly ends in a big-rip singularity. This evolution is usually understood in terms of the ghost-like behavior⁴ due to its transition to a regime where $f^{\prime \prime }<0$. On the other hand, Fig. 2 presents another run-away solution, which also develops a ghost-driven regime, but with no sudden singularity within the accuracy of the numerical analysis. Thus, even when $f^{\prime \prime }<0$ the evolution in one theory (ABCL gravity) presents the remarkable property of smoothing out the expected divergence. These different behaviors make apparent the richness of possible evolutions in the context of $f(R)$ gravity theories.

We can further examine the connection between big-rip singularities and ghost-like regimes ($f^{\prime \prime }<0$) through another example. In fact, by taking the same values for the parameters $n$ and $\alpha$ used for Fig. 6 along with a slightly different value for the Hubble parameter ($H_0=2.0\times 10^{-4}$, in units of Table 1), we have calculated the future dynamics of the FLRW dust flat models shown in Fig. 7. For this case, since $\dot{H}\rightarrow 0$ and $H\rightarrow 0$, from Eq. (8) one sees that the Ricci scalar tends to zero, and thus $f^{\prime \prime }\rightarrow -\infty$. This evolution illustrates a case where, in a limit strongly associated to ghost-dominated regimes ($f^{\prime \prime }\ll 0$), the solution actually evolves simply to Minkowski spacetime. To the best of our knowledge, this interesting dynamical behavior has not been highlighted so far in the literature. It also illustrates how a direct association of big-rip singularities, or even run-away solutions, with a ghost-like regime of the field equations can be misleading in the framework of $f(R)$ theories.

Fig. 6

Left panel time evolution of $H$ for spatially flat FLRW dust model in the $f(R)$ theory given by Eq. (43). It shows the illustrative case in which $n=-0.1$ and $\alpha =-4.557\times 10^{-8}$. The initial conditions were take to be the best fit values collected in Table 1 as given by the Planck team [4, 5]. Right panel the behavior of the constraint $E_{00}$ as given by (12). As expected, the constraint increases as the curvature singularity approaches, where the numerical solution must be halted

Fig. 7

Left panel time evolution of $H$ for spatially flat FLRW dust model in the $f(R)$ theory given by Eq. (43). As in Fig. 6, the values of the parameters were taken to be $n=-0.1$ and $\alpha =-4.557\times 10^{-8}$, but now a slightly different value for $H_0$. Other initial values are given by Table 1. It can be seen that Minkowski space is obtained asymptotically when $t\rightarrow \infty$, as $H\rightarrow 0 = \mathrm{const}$. Right panel the behavior of the constraint $E_{00}$ as given by (12), which clearly is smaller than $10^{-20}$ for all time $t$

5 Final remarks and conclusions

There have been a great deal of recent papers on $f(R)$ gravity motivated by the attempts to explain the current cosmic acceleration with no need of invoking a dark energy component. Despite the arbitrariness in the choice of different functional forms of $f(R)$, which call for ways of constraining the possible $f(R)$ gravity theories on physical grounds, several features of these gravity theories have been discussed in a number of recent articles. In this paper we have proceeded further with the investigation of potentialities and limitations of $f(R)$ gravity theories by examining whether the future dynamics can be used to break the degeneracy between two $f(R)$ gravity theories. To this end, by taking the recent constraints on the cosmological parameters made by the Planck team, we have performed a detailed numerical study of the future dynamics of spatially homogeneous and isotropic dust flat models in the framework of two gravity theories. As a first result, we have shown that besides being powerful for discriminating between the two $f(R)$ gravity theories, the future dynamics numerical technique introduced in this paper can also be used to determine the finite-time behavior of the FLRW flat dust models in these $f(R)$ gravity theories. Figure 8 collects the results of the future dynamics numerical analyses of the FLRW dust flat models in several cases. Curve $(a)$ shows the future evolution of this model in general relativity theory [$f(R)=R)$], while the other curves represent future dynamics of these FLRW models in several instances as follows. Curve $(b)$ is for ABCL theory, Eq. (17)] with $f^{\prime \prime \prime }\ne 0\,$; Curve $(c)$ for ABCL theory with $f^{\prime \prime \prime }=0\,$; Curve $(d)$ for $f(R)= R+\alpha R^n$ with positive $n\,$; Curve $(e)$ for $f(R)= R+\alpha R^n$ with negative $n\,$; Curve $(f)$ for $f(R)= R+\alpha R^n$ with negative $n$, but now with a slightly different value of the Hubble parameter. Figure 8 shows that, although with differences for $t\lesssim 1.5 Myr$, the ultimate fate of the Universe is a de Sitter model (with slightly different Hubble constant) for the cases $(a)$, $(c)$, and $(d)$. Clearly the case $(e)$ evolves to Minkowski space whereas the case $(f)$ develops a singularity. Thus, the future dynamics scheme developed in this paper is indeed a powerful tool to discriminate between these $f(R)$ gravity theories.

Fig. 8

Summary of future dynamics numerical analyses for explicit comparison. Except for $(f)$, they all correspond to the same initial best fit values of the cosmological parameters collected in Table 1 as given by the Planck team [4, 5]. a Standard FLRW dust flat solution in Einstein’s equations, which tends asymptotically to a de Sitter universe. b ABCL’s theory, Eq. (17), when initially $f^{\prime \prime \prime }\ne 0$, as discussed in Sect. 3.1. c A case when initial conditions satisfy $f^{\prime \prime \prime }=0$ in ABCL theory, as discussed in Sect. 3.2. d Future dynamics of FLRW dust flat model for $f(R) = R+\alpha R^n$ with $n>0$. e Same as d but now with $n<0$. f The same ($\alpha ,n$) as in e, but now with a slightly different value of the Hubble parameter $H_0$

The development of a big-rip singularity as shown in curve $(e)$ of Fig. 8 is consistent with the results found in the literature for $f(R) = R + \alpha R^{n}$ with negative $n$, and these are generally associated with ghost-like regimes ($f^{\prime \prime }<0$). In this regard, an interesting outcome of our analyses is the evolution given by curve $(b)$ of Fig. 8, where another ghost-driven regime follows a smooth accelerated evolution with no associated singularity.⁵ Along the same lines, we also note the interesting case presented by curve (f) in the same figure. This is a solution evolving to Minkowski spacetime for $f^{\prime \prime }$ negative and unbounded. Thus, our numerical analyses suggest that ghost-like regimes ($f^{\prime \prime }<0$) do not necessarily lead to singularities.

The discovery of the cosmological expansion along with earlier theoretical investigations concerning spatially homogeneous and isotropic models by Friedmann and Lemaître sparked the first scientific studies on the future dynamics and the ultimate fate of the Universe in the framework of Einstein’s theory of gravitation. It was shown that if the matter content of the Universe is a pressure-free dust, then the future of the Universe would depend only on the sign of the spatial curvature $k$. It would expand forever if $k=0$ or $k=-1$, and would expand and eventually recollapse if $k=1$. The discovery of the accelerating expansion made apparent that this simple future forecast for the Universe, in the framework of general relativity, could not hold anymore, since the negative-pressure dark energy (DE) component, invoked to account for the acceleration, plays a crucial role in the evolution of the Universe. Indeed, the dark energy is usually described by the equation-of-state parameter $\omega$, which is the ratio of the DE pressure to its density ($\omega = p/\rho$). It has been shown that if $\omega <-1$ the dark energy density (called phantom DE) becomes infinite in a finite-time, $t_s$ (say), driving therefore the universe to a future finite-time singularity, called a big rip, in which when $t \mapsto t_s, \;\,\text{ then }\;\ \rho \mapsto \infty ,\; a(t) \mapsto \infty \; \text{ and } \; |p| \mapsto \infty$.

Afterwards, it was understood that this is not the only possible doomsday of a dark energy dominated universe, and the finite-time future singularities were classified in four types [106], called Type I (big rip [113]), Type II (sudden [101, 102]), Type III (big freeze [103–105]), and Type IV, depending on the future behavior of $a(t)$, $\rho$, $p$, and of the higher derivative of the Hubble parameter $H=\dot{a}/a$.

In this paper we have examined numerically the future dynamics of the Universe but, instead of assuming a dark energy component, we have assumed that gravity is governed by $f(R)$ gravity theories and have kept a pressure-free dust as matter content. As a result, we have also shown that even if we do not invoke a dark energy component with $\omega < -1$ one still can have a pressure-free dust FLRW flat solution with a big rip, if gravity is governed by $f(R) = R + \alpha R^n$, as shown in Fig. 6.

Finally, by using the future dynamics scheme of this paper, we also show an example in which the ghost-like regimes ($f''<0)$ do not necessarily lead to singularity (Fig. 7). Thus, the future dynamics scheme we have developed in this paper is not only a powerful tool to discriminate between $f(R)$ gravity theories, but it has also permitted to shed some light on the ghost-like regime and its connection with singularities in the context of $f(R)$ gravity theories.

To close this article, some final words of clarification regarding the literature on the future dynamics in $f(R)$ gravity are in order. First, we note that the possibility of a big rip in $f(R)$ gravity was pointed out in Ref. [114], and the finite-time singularities in $f(R)$ gravity were investigated in Ref. [115], where it was demonstrated that all types of singularities (Type I–Type IV) can occur in these theories. For the specific $f(R)$ gravity theories and range of parameters used in our numerical analyses only the big-rip singularity occurs. Second, we emphasize that future dynamics in $f(R)$ gravity was previously considered in a number of articles [116–119]. Theirs approaches are different from ours since they have considered a perfect-fluid matter source with $\rho , p$ and $\omega =p/\rho$, while we have considered simply a pressure-free dust. Furthermore, our analysis is numerical, while they have made analytical studies.