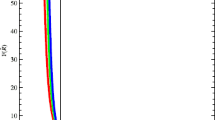Analysis of generalized ghost pilgrim dark energy in non-flat FRW universe

Abstract

This work is based on pilgrim dark energy conjecture which states that phantom-like dark energy possesses the enough resistive force to preclude the formation of black hole. The non-flat geometry is considered which contains the interacting generalized ghost pilgrim dark energy with cold dark matter. Some well-known cosmological parameters (evolution parameter ($\omega _{\Lambda }$) and squared speed of sound) and planes ($\omega _{\Lambda }$–$\omega _{\Lambda }'$ and statefinder) are constructed in this scenario. The discussion of these parameters is totally done through pilgrim dark energy parameter ($u$) and interacting parameter ($d^2$). It is interesting to mention here that the analysis of evolution parameter supports the conjecture of pilgrim dark energy. Also, this model remains stable against small perturbation in most of the cases of $u$ and $d^2$. Further, the cosmological planes correspond to $\Lambda$CDM limit as well as different well-known dark energy models.

1 Introduction

The accelerated expansion of the universe is one of the active topic in cosmology since its prediction [1]. It is suggested through different cosmological and astrological data arisen from well-known observational schemes [2–6] that this rapid expansion is due to an unknown force termed as dark energy (DE). Despite of many efforts from different observational and theoretical ways, the problem of DE is still not well settled due to its unknown nature. In order to justify the source of accelerating expansion (i.e., the nature of DE) of the universe, two different approaches have been adopted. One way is to modify the geometric part of Einstein-Hilbert action (termed as modified theories of gravity) for the discussion of expansion phenomenon [7–11]. The second approach is to propose the different forms of DE called dynamical DE models.

Upto now, different dynamical DE models have been proposed in two different contexts such as quantum gravity and general relativity. Holographic DE (HDE) model has been proposed in the framework of quantum gravity on the basis of holographic principle [12]. The density of HDE model has the following form [13]

$$\begin{aligned} \rho _{\Lambda }=3m^{2}m^2_pL^{-2}, \end{aligned}$$

where $m$ is a specific constant, $m_{p}=(8\pi G)^{-\frac{1}{2}}$ termed as reduced Planck mass and $L$ represent the infrared (IR) cutoff described the size of the universe. This density has been derived on the basis of idea of Cohen et al. [14] limit which is stated as the vacuum energy (or the quantum zero-point energy) of a system with size $L$ should always remain less than the mass of a black hole (BH) with the same size due to the formation of BH in quantum field theory. This idea is reconsidered by Wei [15] with the proposal of pilgrim dark energy (PDE).

According to Wei, the formation of BH can be avoided through appropriate resistive force which is capable to prevent the matter collapse. In this phenomenon, phantom-like DE can play important role which possesses strong repulsive force as compare to quintessence DE. The effective role of phantom-like DE onto the mass of the BH in the universe has also been observed in many different ways. The accretion phenomenon is one of them which favor the possibility of avoidance of BH formation due to presence of phantom-like DE in the universe. It has been suggested that accretion of phantom DE (which is attained through family of Chaplygin gas models [16–21]) reduces the mass of BH. On the other hand, there also exists a possibility of increasing of BH mass due to phantom energy accretion process which leads to the violation of cosmic censorship hypothesis [22]. Hence, this phenomenon is still unresolved.

It is strongly believed that the presence of phantom DE in the universe will force it towards big rip singularity. This represents that the phantom-like universe possesses ability to prevent the BH formation. The proposal of PDE model [15] also works on this phenomenon which states that phantom DE contains enough repulsive force which can resist against the BH formation. Wei [15] developed cosmological parameters for PDE model with Hubble horizon and provided different possibilities for avoiding the BH formation through PDE parameter. He adopted different possible theoretical and observational ways to make the BH free phantom universe. Also, PDE via reconstruction scheme is discussed in modified theory of gravity such as $f(T)$ gravity [23]. The behavior of cosmological parameters along with validity of generalized second law of thermodynamics are explored as well.

In addition, we worked on PDE models interacting with cold dark matter (CDM) and pointed different ways in order to meet the PDE phenomenon [24–26]. In this work, the generalized ghost version of PDE model so called GGPDE interacting with CDM is considered in non-flat universe. In this context, different cosmological parameters (EoS parameter and squared speed of sound) and planes ($\omega _{\Lambda }$–$\omega _{\Lambda }'$ and statefinder) are developed. The format of the paper is as follows. Section 2 contains the basic cosmological scenario, whereas Sect. 3 explores above mentioned cosmological parameters and planes. The concluding remarks of the results are given in the last section.

2 Non-flat FRW universe and basic equations

In this section, we provide the basic scenario of non-flat geometry of the universe as well as interacting scenario of GGPDE and CDM. The basic purpose of this work to visualize the effects of spatial curvature on PDE conjecture. It is found that different observational analysis favor the flat universe. However, there are arguments through observational schemes about the presence of small fraction of spatial fractional density in the total fractional energy contents of the universe. In non-flat FRW universe, the first Friedmann equation becomes

$$\begin{aligned} H^2+\frac{k}{a^{2}}&= \frac{1}{3m^2_{pl}}(\rho _m+\rho _\Lambda ), \end{aligned}$$

(1)

where $\rho _m$ and $\rho _\Lambda$ appear as CDM and GGPDE densities. Also, $k=-1,~0,~1$ describe open, flat and closed universes, respectively. In cosmological context, the total amount of energy density is calculated in terms of fractional energy density. Thus, Eq. (1) can be written in terms of fractional form as

$$\begin{aligned}&1+\Omega _{k}=\Omega _m+\Omega _\Lambda ,\quad \Omega _{k}=\frac{k}{a^2H^2},\quad \Omega _{m}=\frac{\rho _m}{3m^2_{pl}H^2},\nonumber \\&\quad \Omega _{\Lambda }=\frac{\rho _\Lambda }{3m^2_{pl}H^2}. \end{aligned}$$

(2)

It is well-known that dynamical DE models play an important role in describing the accelerated expansion of the universe. The Veneziano ghost DE is one of the dynamical DE model which is defined as follows [27–31]

$$\begin{aligned} \rho _\Lambda =\alpha H, \end{aligned}$$

where $\alpha$ is a constant with dimension [energy]$^3$. This model is proposed on the basis of Veneziano ghost of chromodynamics (QCD) which helps in solving the $U(1)$ problem in QCD. The Veneziano ghost (being unphysical in quantum field theory formulation in the Minkowski spacetime) provides non-trivial physical effects in FRW universe [32, 33]. Although, QCD ghost possesses small contribution in describing vacuum energy density which is proportional to $\Lambda ^{3}_\mathrm{QCD}H$ (here $\Lambda _\mathrm{QCD}\sim 100~\hbox {MeV}$ is the smallest QCD scale), but this contribution plays important role in the discussion of evolutionary universe. It is also investigated that this model also helps in alleviating two major problems of DE called fine tuning and cosmic coincidence problem [27–31, 34]. Many authors have investigated/tested this model through different cosmological parameters theoretically [35–39] and different observational schemes [40].

It is observed that the Veneziano ghost field in QCD of the form $H+O(H^2)$ has ability in producing enough vacuum energy to explain the accelerated expansion of the universe [41], but only leading term (i.e., $H$) involved in ordinary ghost DE model. It is suggested [42] that the contribution of the term $H^2$ in the ordinary ghost DE may be useful in describing the early evolution of the universe which is defined as follows

$$\begin{aligned} \rho _{\Lambda }=\alpha H+\beta H^2, \end{aligned}$$

here $\beta$ involves as a constant containing dimension [energy]$^2$ and corresponding energy density is called generalized ghost DE. Upto now, this model was investigated by different cosmological parameters such as EoS parameter, deceleration, $\omega _{\Lambda }{-}\omega '_{\Lambda }$, statefinder and squared speed of sound etc. [26, 43–46]. Its generalized version in terms of PDE is defined as follows [26]

$$\begin{aligned} \rho _{\Lambda }=(\alpha H+\beta H^2)^u, \end{aligned}$$

(3)

known as GGPDE.

We take interaction between GGPDE and CDM which follows the equations of continuity as

$$\begin{aligned} \dot{\rho }_{m}+3H\rho _{m}=\Gamma ,\quad \dot{\rho }_{\Lambda }+3H(\rho _{\Lambda }+p_{\Lambda })=-\Gamma , \end{aligned}$$

(4)

where $\Gamma$ is known as interaction term between CDM and GGPDE possessing dynamical behavior. The unknown nature of DE as well as CDM leads to the basic problem for the choice of interaction term. It is difficult to describe interaction via first principle. However, the continuity equation provides a clue about the form of interaction, i.e., it must be a function of the product of energy density and a term with units of time (such as Hubble parameter). With this idea, different forms for interaction have been proposed. We take the following form of this interaction term

$$\begin{aligned} \Gamma =3d^2H\rho _{m}, \end{aligned}$$

(5)

with $d^2$ serves as interaction parameter which exchanges the energy between CDM and DE components. This form of interaction term has been explored for energy transfer through different cosmological constraints. The sign of coupling constant decides the decay of energies either DE decays into CDM (when the interacting parameter is positive) or CDM decays into DE (when the interacting parameter is negative). The present analysis from different aspects imply that the phenomenon of DE decays into CDM which is more acceptable and favors the observational data.

3 Cosmological parameters

Here, we discuss the evolution of the Hubble parameter, the universe and stability of the interacting model GGPDE. For this purpose, we extract EoS parameter and squared speed of sound.

3.1 Hubble parameter

By using Eqs. (1)–(5), we obtain the differential equation in term of Hubble parameter as follows

$$\begin{aligned} \dot{H}(a)&= \Omega _{m0}H_{0}^2(-3(1-d^2)H(a)a^{-3(1-d^2)})\nonumber \\&+(2H(a))a^{-2} (2H(a)\nonumber \\&-\frac{u}{3}(\alpha H(a)+\beta H(a)^2)^{u-1}(\alpha +\beta H(a)))^{-1}. \end{aligned}$$

(6)

We solve it numerically for $H(a)$ and plot it against cosmic scale factor $a$ for three different values of $u=0.5,~-0.5,~1$ as shown in Figs. 1, 2 and 3. We chose initial condition $H(1)=74$ and other constant parameters are $d^2=0.02,~0.03,~0.04$ and $\Omega _{m0}=0.27,~H_0= 74,~\alpha = -1.05,~\beta = 2.25$. It can be observed through all plots for all values of interacting parameter $d^2$ that $H(a)$ shows increasing behavior which is consistent with the present day observations about the expanding of the universe. Also, it can be observed that the trajectories of $H(a)$ remains in the range $[74,75]$ which is consistent with the recent planck data as obtained by Ade et al. [47].

Fig. 1

Plot of $H$ versus $a$ for GGPDE in non-flat universe with $u=0.5$

Fig. 2

Plot of $H$ versus $a$ for GGPDE in non-flat universe with $u=-0.5$

Fig. 3

Plot of $H$ versus $a$ in non-flat universe with $u=1$

3.2 The equation of state parameter

In this scenario, EoS parameter takes the form

$$\begin{aligned} \omega _{\Lambda }&= -1-d^2((\Omega _m)(\Omega _{\Lambda })^{-1}\nonumber \\&-(u(\alpha + 2\beta (H(a))))(3(H(a)))^{-1}\Omega _{m0}\nonumber \\&\times H_0^2(-3 (1-d^2)H(a)a^{-3 (1-d^2)})\nonumber \\&+(2(H(a)))a^{-2})(2(H(a))\nonumber \\&-\frac{u}{3}(\alpha H(a)+\beta H(a)^2)^{u-1}(\alpha +\beta H(a)))^{-1}. \end{aligned}$$

(7)

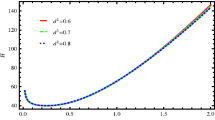
We analyze the behavior of EoS parameter corresponding to three different values of PDE parameter $u$, i.e., $u=0.5,~-0.5,~1$ and keeping the same values of other constant parameters as shown in Figs. 4, 5 and 6. In order to observe the effects of interaction parameter on PDE phenomenon, we take its three different values such as $d^2=0.02,~0.03,~0.04$. In Fig. 4 ($u=0.5$), it can be observed that the EoS parameter starts from phantom region (with comparatively large negative value) and goes towards lower negative value of phantom region for all cases of interacting parameter. For $u=-0.5$ (Fig. 5), it starts from quintessence phase and turns towards phantom region by crossing vacuum dominated era of the universe for the cases $(d^2=0.02,~0.03).$ However, it remains in the phantom region for $d^2=0.04$. Also, Fig. 6 provided that EoS parameter starts comparatively high value of phantom region and always remains in that region for all values of interacting parameter. It can also be observed that EoS parameter attains high phantom region with the increase of interacting parameter. The above discussion shows that all the models provides fully support the PDE phenomenon.

Fig. 4

Plot of $\omega _{\Lambda }$ versus $a$ for GGPDE in non-flat universe with $u=0.5$

Fig. 5

Plot of $\omega _{\Lambda }$ versus $a$ for GGPDE in non-flat universe with $u=-0.5$

Fig. 6

Plot of $\omega _{\Lambda }$ versus $a$ in non-flat universe with $u=1$

3.3 Stability analysis

Now, we use squared speed of sound for the stability analysis of the present interacting model. It is given by

$$\begin{aligned} \upsilon _{s}^2=\frac{\dot{p}}{\dot{\rho }}=\frac{p'}{\rho '}, \end{aligned}$$

(8)

By following [26], we obtain the following expression

$$\begin{aligned} \upsilon ^2_{s}&= -1+b-(3d^2(H(a)(\alpha +H(a)))^{-u}(1+a^2H(a)^2))a^{-2}\\&+(u H(a)(\alpha +2\beta H(a))(2a+3a^{3d^2}(-1+d^2)H_0^2 \Omega _{m0}))\\&\times (a^3(-6H(a)^2+u(H(a)(\alpha +\beta H(a)))^u))^{-1}+((2H(a)\\&-(u(H(a)(\alpha +\beta H(a)))^u(3H(a))^{-1})((3ad^2H(a)^2 \\&\times (\alpha (-2+ u)+2(-1+u)H(a))(2a+3a^{3 d^2}(-1+d^2)\\&\times H_0^2\Omega _{m0}))((\alpha + H(a))(6H(a)^2\!-\!u(H(a)(\alpha \!+\!\beta H(a)))^u))^{-1}\\&+(6d^2\times H(a)^2\times (H(a)(\alpha +H[a]))^{-u} (-3+a^2(-3H(a)^2\\&+(H(a)\times (\alpha +H(a)))^u))(2a+3a(3d^2)(-1+d^2)H_0^2\Omega _{m0}))\\&\times (6aH(a)^2 -au(H(a)(\alpha +\beta H(a)))^u)^{-1}+(3d^2uH(a)^3\\&\times (H(a)(\alpha +H(a)))^{-1-u}\times (\alpha +2H(a))(-3+a^2(-3H(a)^2\\&+(H(a)(\alpha +H(a)))^u)) \times (2a+ 3a(3d^2)(-1+d^2)H_0^2\Omega _{m0}))\\&\times (-6aH(a)^2 +au(H(a)\times (\alpha +\beta H(a)))^u)^{-1}-(6\beta u H(a)^4\\&\times (2a+3a^{3d^2}(-1+d^2)\times H_0^2\Omega _{m0})^2)(-6aH(a)^2 +au(H(a)\\&\times (\alpha +\beta H(a)))^u)^{-2}+(3u H(a)^3 \times (\alpha +2\beta H(a))(2a+3a^{3d^2}\\&\times (-1+d^2)H_0^2\Omega _{m0})^2)(-6 a H(a)^2+au(H(a)\\&\times (\alpha +\beta H(a)))^u)^{-2}+(3u H(a)^3 (\alpha +2\beta H(a))\times (-6H(a)^2\\&\times (\alpha +\beta H(a))+u(H(a)(\alpha +\beta H(a)))^u(\alpha (-1+u)\\&+\beta (-1+2u)H(a))) (2a+3a(3d^2)(-1+d^2)H_0^2\Omega _{m0})^2)\\&(a^2(\alpha +\beta H(a))(-6H(a)^2+u(H(a)(\alpha +\beta H(a)))^u)^3)^{-1}\\&+6ad^2(H(a)\times (\alpha +H(a)))^{-u}(H(a)+(3H(a)^2\\&\times (2a+ 3a^{3d^2}(-1+d^2)H_0^2\Omega _{m0}))\times (a^2(6H(a)^2\\&-u (H(a)(\alpha +\beta H(a)))^u)))-(u H(a)^2(\alpha +2\beta H(a))\\&\times (a^2u(H(a)(\alpha +\beta H(a)))^u(4a-9a^{3d^2}(-1+d^2)^2 \\&\times H_0^2\Omega _{m0})+3H(a)((2a+3a(3d^2)(-1+d^2)H_0^2 \Omega _{m0})^2\\&+2a^2H(a)(-4a+9a^{3d^2}(-1+d^2)^2 H_0^2\Omega _{m0}))))\\&\times (-6aH(a)^2+au(H(a)\times (\alpha +\beta H(a)))^u)^2))\\&\times (a u H(a)(2a+ 3a^{3d^2}(-1+d^2)H_0^2\Omega _{m0})). \end{aligned}$$

In order to analyze the behavior of squared speed of sound, we plot the $\upsilon ^2_{s}$ versus $a$ for its three different values, i.e., $u=0.5,~-0.5,~1$ as shown in Figs. 7, 8 and 9. In Fig. 7, it is observed that GGPDE remains stable against small perturbation at the present epoch as well as recent present epoch. It can be viewed from Fig. 8 ($u=-0.5$) that the GGPDE model exhibits stability for all values of interacting parameter in this scenario due to positive behavior of squared speed of sound. In case of $u=1$ (Fig. 9), the squared speed of sound also exhibits stability of the model for all cases of $d^2$.

Fig. 7

Plot of $\upsilon ^2_s$ versus $a$ for GGPDE in non-flat universe with $u=0.5$

Fig. 8

Plot of $\upsilon ^2_s$ versus $a$ for GGPDE in non-flat universe with $u=-0.5$

Fig. 9

Plot of $\upsilon ^2_s$ versus $a$ in non-flat universe with $u=1$

3.4 $\omega _{\Lambda }{-}\omega '_{\Lambda }$ analysis

The $\omega _{\Lambda }{-}\omega '_{\Lambda }$ plane is used to discuss the dynamical property of DE models, where $\omega '_{\Lambda }$ is the evolutionary form of $\omega _{\Lambda }$ (prime represents derivative with respect to $\ln a$). Caldwell and Linder [48] firstly proposed this method for analyzing the behavior of quintessence scalar field DE model. They pointed out that $\omega _{\Lambda }{-}\omega '_{\Lambda }$ plane for quintessence model with scalar field potential asymptotically approaching to zero, can be divided into two categories of thawing and freezing regions. In thawing region, EoS parameter begins nearly from $-1$ and increases with time while its evolution remains positive. In freezing region, EoS parameter remains negative and decreases with time while its evolution also remains negative. In other words, the thawing region is described as $\omega '_{\Lambda }>0$ for $\omega _{\Lambda }<0$ while freezing region as $\omega '_{\Lambda }<0$ for $\omega _{\Lambda }<0$. Later, this study was extended for examining the dynamical nature of various DE models such as more general form of quintessence [49], quintom [50], phantom [51], holographic [52], polytropic DE [53] and PDE [24–26] models. Differentiating $\Omega _{k}$ and $\Omega _{\Lambda }$ with respect to $x$ and after some manipulations, we get

$$\begin{aligned} \Omega '_k&= -2\Omega _k(1+((\Omega _k-(1+\Omega _k-\Omega _\Lambda )\nonumber \\&+3d^2(\Omega _\Lambda -(1+\Omega _k -\Omega _\Lambda )))(\alpha \nonumber \\&+\beta H))(2(\alpha +\beta H)-u\Omega _\Lambda (\alpha +2\beta H))^{-1}),\end{aligned}$$

(9)

$$\begin{aligned} \Omega '_k&= \Omega _\Lambda (((\Omega _k-(1+\Omega _k-\Omega _\Lambda )\nonumber \\&+3d^2(\Omega _\Lambda -(1+\Omega _k -\Omega _\Lambda )))(u(\alpha +\beta H)\nonumber \\&-\alpha -\beta H))(2(\alpha +\beta H)-u \Omega _\Lambda (\alpha + 2\beta H))^{-1})\nonumber \\ \end{aligned}$$

(10)

By taking the derivative of Eq. (7) and using the above expression, we get the evolutionary form of $\omega _{\Lambda }$ as follows

$$\begin{aligned} \omega '_{\Lambda }&= \frac{1}{a^5H(a)}((3ad^2H(a)^2(\alpha (-2+u)\!+\!2 (-1\!+\!u)H(a))\\&\times (2a+ 3a^{3d^2}(-1+d^2)H_0^2\Omega _{m0}))((\alpha +H(a))\\&\times (6H(a)^2 -u(H(a)\times (\alpha +\beta H(a)))^u))^{-1}\\&+(6d^2H(a)^2(H(a)(\alpha \!+\!H(a)))^{-u}(-3\!+\! a^2(-3H(a)^2 \\&+(H(a)(\alpha +H(a)))^u))(2a+3a^{3d^2}(-1+d^2)\\&\times H_0^2\Omega _{m0}))/(6aH(a)^2 -au(H(a)(\alpha +\beta H(a)))^u)\\&+(3d^2u\times H(a)^3(H(a)(\alpha \!+\!H(a)))^{-1-u}(\alpha \!+\!2H(a))\\&\times (-3+a^2\times (-3H(a)^2 +(H(a)(\alpha \!+\!H(a)))^u))\\&\times (2a\!+\!3a^{3d^2}(-1+d^2)\times H_0^2\Omega _{m0}))(-6aH(a)^2\\&+au (H(a)(\alpha +\beta H(a)))^u)^{-1}-(6\beta \times u H(a)^4\\&\times (2a+3a^{3d^2}(-1+d^2)H_0^2\Omega _{m0})^2)(-6 a H(a)^2+au\\&\times (H(a)(\alpha +\beta H(a)))^u)^{-2}\!+\!(3uH(a)^3(\alpha \!+\!2\beta H(a))\\&\times (2a+3a^{3d^2}(-1+d^2)H_0^2\Omega _{m0})^2)(-6aH(a)^2 +au\\&\times (H(a)(\alpha +\beta H(a)))^u)^{-2}+(3uH(a)^3(\alpha +2\beta H(a))\\&\times (-6H(a)^2(\alpha +\beta H(a))+u(H(a)(\alpha +\beta H(a)))^u \\&\times (\alpha (-1+u)+\beta (-1+2u)H(a)))(2a+3a^{3d^2}\\&\times (-1+d^2)\times H_0^2 \Omega _{m0})^2)(a^2(\alpha +\beta H(a))(-6H(a)^2\\&+u(H(a)(\alpha + \beta H(a)))^u)^3)^{-1}+6ad^2(H(a)\\&\times (\alpha +H(a)))^{-u} (H(a)+(3H(a)^2(2a+3a^{3d^2}\\&\times (-1+d^2)\times H_0^2\Omega _{m0}))(a^2(6H(a)^2-u (H(a)\\&\times (\alpha +\beta H(a)))^u))^{-1})-(u H(a)^2\times (\alpha +2\beta H(a))\\&\times (a^2u (H(a)(\alpha +\beta H(a)))^u(4a-9a^{3d^2}(-1+d^2)^2\\&\times H_0^2 \Omega _{m0})+3H(a)((2a+3a^{3d^2}(-1+d^2)H_0^2\Omega _{m0})^2\\&+2a^2H(a)\times (-4a+9a^{3d^2}(-1+d^2)^2H_0^2\Omega _{m0}))))\\&\times (-6aH(a)^2+au(H(a)\times (\alpha +\beta H(a)))^u)^{-2}). \end{aligned}$$

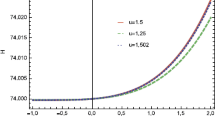
The $\omega _{\Lambda }{-}\omega '_{\Lambda }$ plane for the current DE model is constructed by plotting the $\omega '_{\Lambda }$ versus $\omega _{\Lambda }$ for three different values of $u$ as shown in Figs. 10, 11 and 12. The specific values of other constant are the same as above plots. Figures 10 and 12 provide thawing region while Fig. 11 exhibits freezing region. The $\Lambda$CDM limit, i.e., $(\omega _{\Lambda },\omega '_{\Lambda })=(-1,0)$ only achieved for $u=0.5$ with ($d^2=0$) as shown in Fig. 10. Hence, $\omega _{\Lambda }{-}\omega '_{\Lambda }$ plane provides consistent behavior with the present day observations in all cases of $u$.

Fig. 10

Plot of $\omega _{\Lambda }{-}\omega _{\Lambda }'$ for GGPDE in non-flat universe with $u=0.5$

Fig. 11

Plot of $\omega _{\Lambda }{-}\omega _{\Lambda }'$ for GGPDE in non-flat universe with $u=-0.5$

Fig. 12

Plot of $\omega _{\Lambda }{-}\omega _{\Lambda }'$ in non-flat universe with $u=1$

3.5 Statefinder parameters

The statefinder parameters depend upon two well-known basic geometric parameters such as Hubble and deceleration which measure expansion history of the universe. The deceleration parameter is defined as

$$\begin{aligned} q=-\frac{\ddot{a}}{aH^2}=-\left( 1+\frac{\dot{H}}{H^2}\right) . \end{aligned}$$

(11)

Notice that $\dot{a}>0$ represents the expansion of the universe which yields $H>0$ while $\ddot{a}>0$ exhibits accelerated expansion of the universe which provides negative deceleration parameter ($q<0$). Thus the negative value of deceleration parameter demonstrates accelerated expansion of the universe, its positive value shows decelerated phase of the universe while its zero value shows uniform expansion of the universe.

A large number of DE models have been proposed for elaborating the phenomenon of DE in the accelerated expansion of the universe. It is necessary to differentiate these models so that one can decide which one provides better explanation for the current status of the universe. Since various DE models exhibit the same present value of the deceleration and Hubble parameter, so these parameters could not be able to discriminate the DE models. For this purpose, Sahni et al. [54] introduced two new dimensionless parameters by combining the Hubble and deceleration parameters which are expressed as

$$\begin{aligned} r=\frac{\dddot{a}}{aH^3},\quad s=\frac{r-1}{3(q-\frac{1}{2})}. \end{aligned}$$

(12)

These parameters have geometrical diagnostic due to their total dependence on the expansion factor. The statefinders are useful in the sense that we can find the distance of a given DE model from $\Lambda$CDM limit. The well-known regions described by these cosmological parameters are as follows: $(r,s)=(1,0)$ indicates $\Lambda$CDM limit, $(r,s)=(1,1)$ shows CDM limit, while $s>0$ and $r<1$ represent the region of phantom and quintessence DE eras. For non-flat universe, the above parameters turn out to be

$$\begin{aligned} r=\frac{\dddot{a}}{aH^3},\quad s=\frac{r-\Omega _\mathrm{tot}}{3(q-\frac{\Omega _\mathrm{tot}}{2})}. \end{aligned}$$

(13)

Moreover, $r$ can be expressed in terms of Hubble parameter as

$$\begin{aligned} r=\frac{\ddot{H}}{H^3}-3q-2. \end{aligned}$$

(14)

With the help of Eqs. (11) and (14), one can write

$$\begin{aligned} r=2q^{2}+q-\frac{\dot{q}}{H}. \end{aligned}$$

(15)

By following the procedure of [25], we can get statefinders as

$$\begin{aligned} r&= 1+(a^2H(a)^2)^{-1}+3(2H(a)^2)^{-1}(\alpha H(a)+H(a)^2)^u\\&\times (-1-3d^2H(a)^2\times (\alpha H(a)+H(a)^2)^{-u}\\&\times (1+(a^2H(a)^2)^{-1}-(\alpha H(a)+H(a)^2)^u\\&\times (3H(a)^2)^{-1})-(u(\alpha +2\beta H(a))((2H(a))a^{-2}\\&-3a^{-3(1-d^2)} (1-d^2)\times H_0^2H(a)\Omega _{m0}))(3H(a)(2H(a)\\&- 3^{-1}u(\alpha +\beta H(a))(\alpha H(a)+\beta \times H(a)^2)^{-1+u}))^{-1})\\&\times (-3d^2H(a)^2(\alpha H(a)+H(a)^2)^{-u}(1+(a^2H(a)^2)^{-1}\\&-(\alpha H(a)+H(a)^2)^u(3H(a)^2)^{-1})+d^2(1-3H(a)^2\\&\times (\alpha H(a)+H(a)^2)^{-u}(1+(a^2H(a)^2)^{-1}-(\alpha H(a)\\&+H(a)^2)^u(3H(a)^2)^{-1}))-(u(\alpha +2 \beta H(a))\\&\times ((2H(a))a^{-2}-3a^{-3(1-d^2)}(1-d^2)H_0^2 H(a)\Omega _{m0}))\\&\times (3H(a)(2H(a)-3^{-1}u(\alpha +\beta H(a))(\alpha H(a)\\&+\beta H(a)^2)^{-1+u}))^{-1})-(2a^4H(a)^3)^{-1}(\alpha H(a)\\&+H(a)^2)^u((3ad^2H(a)^2(\alpha (-2 \!+\!u)\!+\!2(-1\!+\!u)H(a))\\&\times (2a+3a^{3d^2}(-1+d^2)H_0^2\Omega _{m0})) ((\alpha +H(a))(6H(a)^2 \\&-u(H(a)(\alpha +\beta H(a)))^u))^{-1} +(6d^2H(a)^2(H(a)\\&\times (\alpha +H(a)))^{-u}\times (-3+a^2(-3H(a)^2+(H(a)\\&\times (\alpha +H(a)))^u))(2a+3a^{3d^2}(-1+d^2)\times H_0^2 \Omega _{m0}))\\&\times (6aH(a)^2\!-\!au(H(a)(\alpha \!+\!\beta H(a)))^u)^{-1}\!+\!(3d^2uH(a)^3\\&\times (H(a)(\alpha +H(a)))^{-1-u} (\alpha +2H(a)) \end{aligned}$$

$$\begin{aligned}&\,\,\,\quad \times (-3+a^2(-3H(a)^2+(H(a)\times (\alpha +H(a)))^u))\\&\,\,\,\quad \times (2a+3a^{3 d^2}(-1+d^2)H_0^2\Omega _{m0}))(-6aH(a)^2+ au\\&\,\,\,\quad \times (H(a)(\alpha +\beta H(a)))^u)-(6\beta u H(a)^4(2a+ 3a(3d^2)\\&\,\,\,\quad \times (-1+d^2)H_0^2\times \Omega _{m0})^2)(-6aH(a)^2 +au(H(a)\\&\,\,\,\quad \times (\alpha +\beta H(a)))^u)^{-2}+(3uH(a)^3\times (\alpha +2\beta H(a))\\&\,\,\,\quad \times (2a+3a^{3d^2}(-1+d^2)H_0^2\Omega _{m0})^2)(-6 a H(a)^2\\&\,\,\,\quad +au(H(a)(\alpha \!+\!\beta H(a)))^u)^{-2}\!+\!(3uH(a)^3(\alpha \!+\!2\beta H(a))\\&\,\,\,\quad \times (-6H(a)^2\times (\alpha +\beta H(a))+u(H(a)(\alpha +\beta H(a)))^u \\&\,\,\,\quad \times (\alpha (-1+u)+\beta (-1+2u)\times H(a)))(2a+3a^{3d^2}\\&\,\,\,\quad \times (-1+d^2) H_0^2\Omega _{m0})^2)(a^2(\alpha +\beta H(a))(-6H(a)^2\\&\,\,\,\quad +u(H(a)(\alpha +\beta H(a)))^u)^3)^{-1}+ 6ad^2(H(a)\\&\,\,\,\quad \times (\alpha +H(a)))^{-u}(H(a)+(3 H(a)^2(2a+3a^{3d^2}\\&\,\,\,\quad \times (-1+d^2)H_0^2\Omega _{m0}))(a^2 (6H(a)^2-u(H(a)\\&\,\,\,\quad \times (\alpha +\beta H(a)))^u))^{-1})-(u H(a)^2(\alpha +2\beta H(a))\\&\,\,\,\quad \times (a^2u(H(a)(\alpha +\beta H(a)))^u\times (4a-9a(3d^2)\\&\,\,\,\quad \times (-1\!+\! d^2)^2H_0^2\Omega _{m0})+3H(a)((2a+3a^{3d^2} (-1+d^2)\\&\,\,\,\quad \times H_0^2\Omega _{m0})^2+2a^2H(a)(-4a+9a^{3d^2}(-1+d^2)^2\\&\,\,\,\quad \times H_0^2\Omega _{m0}))))(-6aH(a)^2 \!+\!au(H(a)(\alpha \!+\!\beta H(a)))^u)^{-2}), \end{aligned}$$

$$\begin{aligned} s&= -3d^2H(a)^2(\alpha H(a)+H(a)^2)^{-u}(1+1(a^2H(a)^2)^{-1}\\&-(\alpha H(a)+H(a)^2)^u\times (3H(a)^2))+d^2(1-3H(a)^2\\&\times (\alpha H(a)+H(a)^2)^{-u}(1+1(a^2H(a)^2)^{-1}-(\alpha H(a)\\&+H(a)^2)^u(3H(a)^2)^{-1}))-(u(\alpha +2\beta H(a))\\&\times ((2H(a))a^{-2}-3a^{-3(1-d^2)}(1-d^2)H_0^2H(a)\Omega _{m0}))\\&\times (3H(a)(2H(a)-3^{-1} u(\alpha +\beta H(a))\times (\alpha H(a)\\&+\beta H(a)^2)(-1+u)))^{-1}-((3ad^2 H(a)^2(\alpha (-2+u)\\&+2\times (-1+u)H(a))(2a+3a(3d^2)(-1+d^2)\\&H_0^2\Omega _{m0}))((\alpha +H(a)) (6H(a)^2-u(H(a)\\&\times (\alpha \!+\!\beta H(a)))^u))^{-1}\!+\!(6d^2H(a)^2(H(a)(\alpha \!+\! H(a)))^{-u}\\&\times (-3+a^2(-3H(a)^2+(H(a)(\alpha + H(a)))^u))\\&\times (2a+3a^{3d^2} (-1+d^2)H_0^2\Omega _{m0}))\times (6aH(a)^2\\&-au(H(a)(\alpha +\beta H(a)))^u)^{-1}+(3d^2uH(a)^3(H(a)\\&\times (\alpha +H(a)))^{-1-u}(\alpha +2H(a))(-3+ a^2(-3H(a)^2\\&+(H(a)(\alpha +H(a)))^u))(2a+3a^{3d^2}(-1+d^2)\\&\times H_0^2 \Omega _{m0}))(-6 a H(a)^2+au(H(a)(\alpha +\beta H(a)))^u)^{-1}\\&-(6\beta u H(a)^4(2a+3a^{3d^2}(-1+d^2)H_0^2 \Omega _{m0})^2)\\&\times (-6aH(a)^2+a u (H(a)(\alpha +\beta H(a)))u)^{-2} \end{aligned}$$

$$\begin{aligned}&\,\,\,\quad +(3uH(a)^3(\alpha +2\beta H(a))(2a+3a^{3d^2}(-1+d^2)\\&\,\,\,\quad \times H_0^2\Omega _{m0})^2)(-6aH(a)^2\!+\!au(H(a)(\alpha \!+\!\beta H(a)))^u)^{-2}\\&\,\,\,\quad +(3uH(a)^3 \times (\alpha +2\beta H(a))(-6H(a)^2 (\alpha +\beta H(a))\\&\,\,\,\quad +u(H(a)(\alpha \!+\!\beta H(a)))^u(\alpha (-1\!+\!u\!+\! \beta (-1\!+\!2u)H(a)))\\&\,\,\,\quad \times (2a+3a^{3d^2}(-1+d^2)H_0^2\Omega _{m0})^2)(a^2(\alpha +\beta \times H(a))\\&\,\,\,\quad \times (-6H(a)^2+u(H(a)(\alpha +\beta H(a)))^u)^3)^{-1}+6ad^2\\&\,\,\,\quad \times (H(a)(\alpha +H(a)))^{-u}(H(a)+(3H(a)^2(2a+3 a^{3d^2}\\&\,\,\,\quad \times (-1+d^2)H_0^2\Omega _{m0}))(a^2(6H(a)^2-u(H(a)\\&\,\,\,\quad \times (\alpha +\beta H(a)))^u))^{-1})-(u H(a)^2(\alpha +2\beta H(a))\\&\,\,\,\quad \times (a^2u(H(a)(\alpha + \beta H(a)))^u(4a-9a^{3d^2}(-1+d^2)^2\\&\,\,\,\quad \times H_0^2 \Omega _{m0})+3H(a)((2a+3a^{3d^2}(-1+d^2)\times H_0^2 \Omega _{m0})^2\\&\,\,\,\quad +2a^2H(a)(-4a+9a^{3d^2}(-1+d^2)^2H_0^2 \Omega _{m0}))))\\&\,\,\,\quad \times (-6aH(a)^2+au(H(a)(\alpha \!+\!\beta H(a)))^u)^{-2})(3a^4 H(a)\\&\,\,\,\quad \times (-1-3d^2H(a)^2(\alpha H(a)+H(a)^2)^{-u}\\&\,\,\,\quad \times (1+1(a^2H[a]^2)^{-1}\!-\! (\alpha H(a)\!+\! H(a)^2)^u(3H(a)^2)^{-1})\\&\,\,\,\quad -(u(\alpha +2 \beta H(a))((2 H(a))a^{-2}-3a^{-3(1-d^2)}\\&\,\,\,\quad \times (1-d^2)H_0^2H(a)\Omega _{m0}))(3H(a)\times (2H(a) -3^{-1}u\\&\,\,\,\quad \times (\alpha +\beta H(a))(\alpha H(a)+\beta H(a)^2)^{-1+u}))^{-1}))^{-1}. \end{aligned}$$

The $r{-}s$ plane corresponding to this scenario is shown in Figs. 13, 14 and 15. It is observed that the trajectories of $r{-}s$ plane for all cases of interacting parameter corresponds to $\Lambda$CDM model for $u=0.5$ as shown in Fig. 13. However, the trajectories of $r{-}s$ meet $\Lambda$CDM limit for only $d^2=0$ (in case of $u=-0.5$) and $d^2=0.02,~0.03$ (in case of $u=-0.5$) as shown in Figs. 14 and 15, respectively. Also, the trajectories coincide with the Chaplygin gas model in all cases of $u$.

Fig. 13

Plot of $r{-}s$ for GGPDE in non-flat universe with $u=0.5$

Fig. 14

$r{-}s$ for GGPDE in non-flat universe with $u=-0.5$

Fig. 15

$r{-}s$ in non-flat universe with $u=1$

4 Results and discussions

It is well-known that total energy density of the universe contains contribution of its different constituents in ratio of $\Omega _k<\Omega _m<\Omega _\Lambda$ (the cosmic curvature density $\Omega _k$ is found to be fractional). The early inflation era indicates that the universe is non-flat if the number of e-folding are small. It is predicted through many inflationary models that the order of spatial curvature ($|\Omega _k|$) in the universe should be less than $10^{-5}$ (but there are also exist some models which allow larger curvature) [55, 56]. Also, the bound on EoS parameter of different DE models was established in the non-flat scenario of the universe by using observations of SNe Ia, BAO and CMBR [57]. The range $(-0.2851,0.0099)$ of $\Omega _k$ at $95~\%$ confidence level was obtained with the help of WMAP 5 year data [56] which was improved upto $(-0.0181,0.0071)$ by using the data of BAO and SNe Ia. The range $-0.0133<\Omega _k<0.0084$ was obtained by using latest WMAP $7$-years [58].

An independent analysis of non-flat models based on time-delay measurements of two strong gravitational lens systems, combined with 7-year WMAP data, give consistent and nearly competitive constraints of $\Omega _k=0.003^{+0.005}_{-0.006}$ [59]. Recently, Ade et al. [47] (Planck data) found following constraints on $\Omega _k$

$$\begin{aligned} 100\Omega _{k}&= -4.2^{+4.3}_{-4.8} \qquad \text {(Planck+WP+highL)},\\ 100\Omega _{k}&= -0.10^{+4.8}_{-0.65},\quad \text {(Planck+lensing+WP+highL)} \end{aligned}$$

These constraints are improved substantially by the addition of BAO data which are

$$\begin{aligned} 100\Omega _{k}&= -0.05^{+0.65}_{-0.66} \qquad \text {(Planck+WP+highL+BAO)},\\ 100\Omega _{k}&= -1.0^{+1.8}_{-1.9},\quad \text {(Planck+lensing+WP+highL+BAO)} \end{aligned}$$

These limits are consistent with (and slightly tighter than) the results reported by Hinshaw et al. [60] from combining the 9-year WMAP data with high resolution CMB measurements and BAO data. Also, details about the curvature in the universe is given in the recent Planck data [47].

The above discussion motivate us to explore PDE phenomenon with generalized ghost DE model in non-flat FRW universe. For this purpose, two versatile cosmological parameters have been extracted such as EoS parameter and squared speed of sound for analyzing the behavior of evolution of the universe and stability of the model. Also, two cosmological planes have been constructed for providing the comparison of this model with other well-known DE models. The discussion of the developed parameters are summarized as follows:

• Two recent analysis have greatly improved the precision of the cosmic distance scale. Riess et al. [61] use HST observations of Cepheid variables in the host galaxies of eight SNe Ia to calibrate the supernova magnitude-redshift relation. Their “best estimate” of the Hubble constant, from fitting the calibrated SNe magnitude-redshift relation, is

  $$\begin{aligned} H_0&= 73.8\pm 2.4~\hbox {km}~\hbox {s}^{-1}\hbox { Mpc}^{-1} \qquad \text {(Cepheids+SNe Ia)}, \end{aligned}$$

  where the error is $1\sigma$ level and includes known sources of systematic errors. Freedman et al. [62], as part of the Carnegie Hubble Program, use Spitzer Space Telescope mid-infrared observations to recalibrate secondary distance methods used in the HST Key Project. These authors find

  $$\begin{aligned} H_0&= [74.3 \pm 1.5\text { (statistical)} \pm 2.1 \text { (systematic)}]\hbox { km}~\hbox {s}^{-1}~\\&\qquad \hbox {Mpc}^{-1}\text { (Carnegie HP)}, \end{aligned}$$

  It can be observed through all plots (Figs. 1, 2, 3) for all values of interacting parameter $d^2$ that $H(a)$ shows increasing behavior which is consistent with the above observations.

• In Fig. 4 ($u=0.5$), it can be observed that the EoS parameter starts from phantom region (with comparatively large negative value) and goes towards lower negative value of phantom region for all cases of interacting parameter. For $u=-0.5$ (Fig. 5), it starts from quintessence phase and turns towards phantom region by crossing vacuum dominated era of the universe for the cases ($d^2=0.02,~0.03$). However, it remains in the phantom region for $d^2=0.04$. Also, Fig. 6 provided that EoS parameter starts comparatively high value of phantom region and always remains in that region for all values of interacting parameter. It can also be observed that EoS parameter attains high phantom region with the increase of interacting parameter. Moreover, Ade et al. [47] (Planck data) have put the following constraints on the EoS parameter

  $$\begin{aligned} \omega _{\Lambda }&= -1.13^{+0.24}_{-0.25} \qquad \text {(Planck+WP+BAO)},\\ \omega _{\Lambda }&= -1.09\pm 0.17, \qquad \text {(Planck+WP+Union 2.1)}\\ \omega _{\Lambda }&= -1.13^{+0.13}_{-0.14},\qquad \text {(Planck+WP+SNLS)},\\ \omega _{\Lambda }&= -1.24^{+0.18}_{-0.19},\qquad (\text {Planck+WP}+H_0). \end{aligned}$$

  by implying different combination of observational schemes at $95~\%$ confidence level. It can be seen from Figs. 4, 5 and 6 that the EoS parameter also meets the above mentioned values for all cases of interacting parameter which shows consistency of our results. The above discussion shows that all the models provides fully support the PDE phenomenon.

• In Fig. 7, it is observed that GGPDE remains stable against small perturbation at the present epoch as well as recent present epoch. It can be viewed from Fig. 8 ($u=-0.5$) that the GGPDE model exhibits stability for all values of interacting parameter in this scenario due to positive behavior of squared speed of sound. In case of $u=1$ (Fig. 9), the squared speed of sound also exhibits stability of the model for all cases of $d^2$.

• The $\omega _{\Lambda }{-}\omega '_{\Lambda }$ plane for the current DE model is constructed by plotting the $\omega '_{\Lambda }$ versus $\omega _{\Lambda }$ for three different values of $u$ as shown in Figs. 10, 11 and 12. The specific values of other constant are the same as above plots. Figures 10 and 12 provide thawing region while Fig. 11 exhibits freezing region. The $\Lambda$CDM limit, i.e., $(\omega _{\Lambda },\omega '_{\Lambda })=(-1,0)$ only achieved for $u=0.5$ with ($d^2=0$) as shown in Fig. 10. Also, Ade et al. [47] have obtained the following constraints on $w_{\Lambda }$ and $w'_{\Lambda }$:

  $$\begin{aligned} \omega _{\Lambda }&= -1.13^{+0.24}_{-0.25} \qquad \text {(Planck+WP+BAO)},\\ \omega '_{\Lambda }&< 1.32,\qquad \text {(Planck+WP+BAO)} \end{aligned}$$

  at $95~\%$ confidence level. Also, other data with different combinations of observational schemes such as (Planck+WP+Union 2.1) and (Planck+WP+SNLS) favor the above constraints. In the present case, the trajectories of $\omega '_{\Lambda }$ against $\omega _{\Lambda }$ also meet the above mentioned values for all cases of interacting parameter which shows consistency of our results as shown in Figs. 10, 11 and 12. Hence, $\omega _{\Lambda }{-}\omega '_{\Lambda }$ plane provides consistent behavior with the present day observations in all cases of $u$.

• The $r-s$ plane corresponding to this scenario is shown in Figs. 13, 14 and 15. It is observed that the trajectories of $r-s$ plane for all cases of interacting parameter corresponds to $\Lambda$CDM model for $u=0.5$ as shown in Fig. 13. However, the trajectories of $r-s$ meet $\Lambda$CDM limit for only $d^2=0$ (in case of $u=-0.5$) and $d^2=0.02,~0.03$ (in case of $u=-0.5$) as shown in Figs. 14 and 15, respectively. Also, the trajectories coincide with the Chaplygin gas model in all cases of $u$.