1 Introduction

The dynamics of particles (massive or massless, charged or neutral) around a black hole is among the most important and interesting problems of the black hole astrophysics. These studies not only help us to understand the geometrical structure of spacetimes but also shed light on the high energy phenomenon occurring near the black hole such as formation of jets (which involve escaping particles) and accretion disks (particles orbiting in circular orbits). Due to the presence of strong gravitational and electromagnetic fields, charged particles in general do not follow stable orbits and inter-particle collisions are most common. The aftermath of these collisions among numerous particles lead to various interesting astrophysical phenomenon. There are numerous pieces of astrophysical evidence that a magnetic field might be present in the nearby surrounding of the black holes [1, 2] which support the large scale jets. These jets are most likely the source of cosmic rays and high energy particles coming from nearby galaxies. The origin of this magnetic field is probably the existence of a plasma in the vicinity of a black hole in the form of an accretion disk or a charged gas cloud [3, 4]. The relativistic motion of particles in the conducting matter in the accretion disk can generate the regular magnetic field inside the disk. Therefore near the event horizon of a black hole, it is expected that there exists a very strong magnetic field. To an approximation, it is presumed that this field does not affect the geometry of the black hole but it does affect the motion of the charged particles moving around the black hole [5, 6].

More importantly, a rotating black hole may provide sufficient energy to the particle moving around it due to which the particle may escape to spatial infinity. This physical effect appears to play a crucial role in the ejection of high energy particles from accretion disks around black holes. In the process of ejection of high energy particles, besides the rotation of the black hole, the magnetic field plays an important role [7, 8]. Note that if the black hole is carrying electric charge producing a static electric field (also called Coulomb field), then the mere rotation of the black hole itself induces the magnetic field. Acceleration of the particle by the black hole is generally explained in [9]. Other interesting processes around black holes may include evaporation and phantom energy accretion onto black holes [10–13].

During the motion of a charged particle around a magnetized black hole, it remains under the influence of both gravitational and electromagnetic forces which makes the situation complicated [14, 15]. In the present article, it is considered that a charged particle is orbiting in the innermost stable circular orbit (ISCO) of a slowly rotating Kerr black hole and is suddenly hit by a radially incoming neutral particle. The aftermath of a collision will depend on the energy of the incoming particle which may result in one of the three possible outcomes: the charged particle may escape to infinity; be captured by the black hole, or keep orbiting in ISCO. However, predicting the nature of outcome is compounded by the facts that the particle is charged and interacts with the magnetic field and is frame dragged by the Kerr black hole. It should be noted that the present work is altogether different from the BSW mechanism where two particles (with non-zero angular momentum and high energies) arrive from spatial infinity and collide near the event horizon to generate surplus energy in the center of mass frame [16]. In the literature, the motion of charged particles in ISCO around various black holes has been studied ([17–22] and see references therein).

Here we consider a slowly rotating Kerr black hole which is surrounded by an axially symmetric magnetic field homogeneous at infinity. An almost similar problem was studied for weakly charged rotating black holes in [23]. The main conclusion is that, if the magnetic field is present, then the ISCO is located closer to the black hole horizon. In general, the effect of the black hole rotation on the motion of a neutral particle is the same as the effect of the magnetic field on the motion of a charged particle [24, 25].

To study the escape velocity of a particle from the vicinity of the black hole, in this paper we first consider a neutral particle moving around a slowly rotating Kerr black hole in the absence of a magnetic field and colliding with another particle. For simplicity we consider the motion in the equatorial plane only. Then we consider the same problem for a charged particle in the presence of a magnetic field. We focus on the question under what circumstances the particle can escape from the strong gravitational field to infinity. The magnetic field is homogeneous far from the black hole and the gravitational field is ignorable. Thus, far from the black hole the charged particle moves in a homogeneous magnetic field. If the magnetic field is absent then the equations of motion are fairly simple and can be solved analytically. When a particle moving in a non-uniform magnetic field in the absence of the black hole its motion is chaotic [26, 27]. We are extending previous work [24] for the slowly rotating Kerr black hole.

The outline of the paper is as follows: In Sect. 2 we explain our model and derive an expression for the escape velocity of the neutral particle. In Sect. 3 we derive the equations of motion of the charged particle moving around a slowly rotating weakly magnetized Kerr black hole. In Sect. 4 we give the dimensionless form of the equations. Trajectories for escape energy and escape velocity of the particle are discussed in Sects. 5 and 6, respectively. Summary and conclusion are presented in Sect. 7. Throughout we use the sign convention \((+,-,-,-)\) and units where \(c=1,G=1\).

2 Escape velocity for a neutral particle

We start with the simple case of calculating the escape velocity when the particle is neutral and the magnetic field is absent. The Kerr metric is given by [28]

$$\begin{aligned}&\mathrm{d}s^{2}=\frac{\Delta -a^{2}\sin ^{2}\theta }{\rho ^{2}}\mathrm{d}t^{2}+\frac{4Mar\sin ^{2}\theta }{\rho ^{2}}\mathrm{d}\phi \mathrm{d}t\nonumber \\&\qquad \qquad -\,\frac{\rho ^{2}}{\Delta }\mathrm{d}r^{2} -\rho ^{2}\mathrm{d}\theta ^{2}-\frac{A\sin ^{2}\theta }{\rho ^{2}}\mathrm{d}\phi ^{2}, \nonumber \\&\Delta \equiv r^{2}-2Mr+a^{2}, \ \ \rho ^{2}\equiv r^{2}+a^{2}\cos ^{2}\theta , \nonumber \\&A \equiv (r^{2}+a^{2})^{2}-a^{2}\Delta \sin ^{2}\theta , \end{aligned}$$
(1)

where \(M\) is the mass and \(a\) is the spin of the black hole and interpreted as the angular momentum per unit mass of the black hole \(a=\frac{L}{M}\). The horizons of the Kerr metric are obtained by solving

$$\begin{aligned} \Delta (r)=r^{2}+a^{2}-2Mr=0. \end{aligned}$$
(2)

From the above equation we get two values of \(r\):

$$\begin{aligned} r_{+}=M+\sqrt{M^{2}-a^{2}}, \quad r_{-}=M-\sqrt{M^{2}-a^{2}}. \end{aligned}$$
(3)

Note that \(\Delta >0\) for \(r>r_{+}\) and \(r<r_{-}\) and \(\Delta <0\) for \(r_{-}<r<r_{+}\) [29]. The region \(r=r_{+}\) represents the event horizon while \(r_-\) is termed the Cauchy horizon. Further \(r=0\) and \(\theta =\frac{\pi }{2}\) is the location of a curvature ring-like singularity in the Kerr spacetime.

In the literature, slowly rotating Kerr black holes have been investigated for numerous astrophysical processes including retro-MACHOS [30], particle acceleration via the BSW mechanism [31], thin accretion disk and accretion rates [32, 33], to list a few. Hence we consider the slowly rotating black hole and neglect the terms involving \(a^{2}\). The line element in (1) becomes

$$\begin{aligned} \mathrm{d}s^2&= \left( 1-\frac{r_{\mathrm{g}}}{r}\right) \mathrm{d}t^2+\frac{4aM\sin ^{2}\theta }{r}\mathrm{d}\phi \mathrm{d}t\nonumber \\&-\frac{1}{1-\frac{r_{\mathrm{g}}}{r}}\mathrm{d}r^2-r^2\mathrm{d}\theta ^2-r^2\sin ^2\theta \mathrm{d}\phi ^2. \end{aligned}$$
(4)

Here \(r_{\mathrm{g}}=2M\) is the gravitational radius of the slowly rotating Kerr black hole just like the Schwarzschild black hole (note that for a slowly rotating Kerr and Schwarzschild black hole the horizon occurs at \(r=r_{\mathrm{g}}\)). Clearly the metric (4) is stationary but non-static since \(\mathrm{d}t\rightarrow -\mathrm{d}t\), changes the signature of the metric. The metric is also axially symmetric (invariance under \(\mathrm{d}\theta \rightarrow -\mathrm{d}\theta \)).

In terms of Lagrangian mechanics (\(\mathcal {L}=g_{\mu \nu }\dot{x}^\mu \dot{x}^\nu \)), the \(t\) and \(\phi \) coordinates are cyclic, which leads to two conserved quantities, namely energy and angular momentum, with the corresponding Noether symmetry generators

$$\begin{aligned} \xi _{(t)}= \xi _{(t)}^\mu \partial _\mu =\frac{\partial }{\partial t}, \qquad \xi _{(\phi )}=\xi _{(\phi )}^\mu \partial _\mu =\frac{\partial }{\partial \phi }. \end{aligned}$$
(5)

This shows that the black hole metric is invariant under time translation and rotation around the symmetry axis. The corresponding conserved quantities are the energy \(\mathcal {E}\) per unit mass and azimuthal angular momentum \(L_{z}\) per unit massFootnote 1

$$\begin{aligned} \dot{t}&=\frac{r^{3}\mathcal {E}+aL_{z}r_{\mathrm{g}}}{r^{2}(r-r_{\mathrm{g}})},\nonumber \\ \dot{\phi }&=\frac{1}{r^{2}}\left( \frac{ar_{\mathrm{g}}\mathcal {E}}{(r-r_{\mathrm{g}})}+\frac{L_{z}}{\sin ^{2}\theta }\right) . \end{aligned}$$
(6)

From the astrophysical perspective, it is well known that particles orbit a rotating black hole in the equatorial plane [34]. Therefore we choose \(\theta =\frac{\pi }{2}\) to get

$$\begin{aligned} \dot{t}&=\frac{r^{3}\mathcal {E}+aL_{z}r_{\mathrm{g}}}{r^{2}(r-r_{\mathrm{g}})},\nonumber \\ \dot{\phi }&=\frac{1}{r^{2}}\left( \frac{ar_{\mathrm{g}}\mathcal {E}}{(r-r_{\mathrm{g}})}+L_{z}\right) . \end{aligned}$$
(7)

Throughout this paper the over dot represents differentiation with respect to proper time \(\tau \).

Using the normalization condition, \(u^{\mu }u_{\mu }=1\), we get the equation of motion

$$\begin{aligned} \dot{r}^{2}=\frac{(\mathcal {E} r^{2}- aL_{z})^2}{r^{4}}-\frac{r^{2}-r_{\mathrm{g}}r}{r^{4}}(r^{2}+L_{z}^{2}-2a\mathcal {E} L_{z}). \end{aligned}$$
(8)

At the turning points \(\dot{r}=0\), Eq. (8) is quadratic in \(\mathcal {E}\) whose solution is

$$\begin{aligned} \mathcal {E}=\frac{aL_{z}r_{\mathrm{g}}\pm \sqrt{r^{5}(r-r_{\mathrm{g}})+L_{z}^{2}(r^{4}-r^{3}r_{\mathrm{g}}+a^{2}r_{\mathrm{g}}^{2})}}{r^{3}}, \end{aligned}$$
(9)

which gives \(\mathcal {E}=V_\text {eff}\), the effective potential. The condition \(\dot{r}=0\) is termed the turning point because it gives the location at which an incoming particle turns around from the neighborhood of the gravitating source [35]. As we are considering only the positive energy we will consider only the positive sign before the square root in Eq. (9) for all the further calculation. Equations (8) and (9) hold for equatorial plane only. It can be seen from (9) that \(\mathcal {E}\rightarrow 1\) for \(r\rightarrow \infty \). Therefore the minimum energy for the particle to escape from the vicinity of the black hole is \(1\).

Consider a particle in ISCO, where \(r_{\mathrm{o}}\) is the local minimum (which is also the convolution point) of the effective potential [29]. The corresponding energy and azimuthal angular momentum are given by [29, 36] after neglecting terms involving \(a^{2}\); we have

$$\begin{aligned} L_{z\mathrm{o}}=\pm \frac{\sqrt{r_{\mathrm{g}}}\left( r_{\mathrm{o}}\pm a\sqrt{\frac{2r_{\mathrm{g}}}{r_{\mathrm{o}}}}\right) }{\sqrt{2r_{\mathrm{o}}-3r_{\mathrm{g}}\mp 2a\sqrt{\frac{2r_{\mathrm{g}}}{r_{\mathrm{o}}}}}}, \end{aligned}$$
(10)
$$\begin{aligned} \mathcal {E}_{\mathrm{o}}=\frac{1-\frac{r_{\mathrm{g}}}{r}\mp \frac{a}{r}\sqrt{\frac{r_{\mathrm{g}}}{2r}}}{\sqrt{1-\frac{3r_{\mathrm{g}}}{2r}}\mp \frac{a}{r}\sqrt{\frac{2r_{\mathrm{g}}}{r}}}. \end{aligned}$$
(11)

Now consider the particle in the ISCO which collides with another incoming particle. After collision between these particles, three cases are possible for the motion of the particle: (i) bound motion, (ii) capture by the black hole, (iii) escape to infinity. The result will depend on the collision process. For a small change in energy and momentum, the orbit of the particle will be slightly perturbed. For a large change in energy and angular momentum, the particle can either be captured by the black hole or escape to infinity.

After the collision the particle should have new values of energy and momentum \(\mathcal {E}\), \(L_{z}\), and the total angular momentum \(L^{2}\). We simplify the problem by applying the following conditions: (i) the azimuthal angular momentum is fixed, (ii) the initial radial velocity remains the same after the collision. Under these conditions only the energy of the particle can determine its motion. After collision the particle acquires an escape velocity \((v_{\bot })\) in an orthogonal direction of the equatorial plane [37]. The square of the total angular momentum of the particle after a collision is given by

$$\begin{aligned} L^{2}=r^{4}\dot{\theta ^{2}}+r^{4}\sin ^{2}\theta \dot{\phi }^{2}. \end{aligned}$$
(12)

Putting the value of \(\dot{\phi }\) from Eq. (6) in Eq. (12) we have

$$\begin{aligned} L^{2}=r^{2}v_{\perp }^{2}+\sin ^{2}\theta \left( \frac{ar_{\mathrm{g}}\mathcal {E}_{\mathrm{o}}}{r-r_{\mathrm{g}}}+\frac{L_{z\mathrm{o}}}{\sin ^{2}\theta }\right) ^{2}. \end{aligned}$$
(13)

Here we denote \(v\equiv -r\dot{\theta }_{\mathrm{o}}\). Note that \(L^2\) is not the integral of motion. It is conserved for \(a=0\), i.e. in the spherically symmetric case. However, now the metric is axially symmetric, therefore only the \(L_z\) component is conserved. In a flat spacetime, all three components \(L_x\), \(L_y\), \(L_z\) are conserved, and so is the square of the total angular momentum. The angular momentum \(L_{z\mathrm{o}}\) and energy \(\mathcal {E}_{\mathrm{o}}\) appearing in (13) are given by (10) and (11), which provide the necessary corrections due to the spin of the black hole.

From Eqs. (9) and (13), the angular momentum and the energy of the particle after the collision become

$$\begin{aligned}&L^{2}=r_{\mathrm{o}}^{2}v_{\perp }^{2}+\left( \frac{ar_{\mathrm{g}}\mathcal {E}_{\mathrm{o}}}{r_{\mathrm{o}}-r_{\mathrm{g}}}+L_{z\mathrm{o}}\right) ^{2},\end{aligned}$$
(14)
$$\begin{aligned}&\mathcal {E_\text {new}}=\frac{aLr_{\mathrm{g}}+\sqrt{r_{\mathrm{o}}^{5}(r_{\mathrm{o}}-r_{\mathrm{g}}) +L^{2}(r_{\mathrm{o}}^{4}-r_{\mathrm{o}}^{3}r_{\mathrm{g}}+a^{2}r_{\mathrm{g}}^{2})}}{r_{\mathrm{o}}^{3}}.\nonumber \\ \end{aligned}$$
(15)

These values of the angular momentum and energy are greater than their values before the collision. Physically it means that the energy of the particle exceeds its rest mass energy. We have mentioned above that all the orbits with \(\mathcal {E}_\text {new}\ge 1\) are unbounded in the sense that the particle escapes to infinity. Conversely for \(\mathcal {E}_\text {new}<1\), the particle cannot escape to infinity (the orbits are always bounded).

Therefore the particle escapes to infinity if \(\mathcal {E}_\text {new}\ge 1\), or

$$\begin{aligned} v_{\perp }\ge \pm \frac{r(r_{\mathrm{g}}-r)(L_{z}(r-r_{\mathrm{g}})+ar_{\mathrm{g}}(\mathcal {E}_{\mathrm{o}}-1))+\sqrt{r^{2}r_{\mathrm{g}}(r-r_{\mathrm{g}})^{2}(r^{3} +r_{\mathrm{g}}(a^{2}-r^{2}-2a^{2}\mathcal {E}_{\mathrm{o}}))}}{r^{2}(r-r_{\mathrm{g}})^{2}}. \end{aligned}$$
(16)

The particle escape condition is \(|v|\ge v_{\perp }\), i.e. the magnitude of the velocity should be greater than any orthogonal velocity.

3 Charged particle around the slowly rotating magnetized Kerr black hole

Here we investigate the motion of a charged particle (electric charge \(q\)) in the presence of a magnetic field in the exterior of the slowly rotating Kerr black hole. The Killing equation is

$$\begin{aligned} \square \xi ^{\mu }=0, \end{aligned}$$
(17)

where \(\xi ^{\mu }\) is a Killing vector. Note that (17) follows from the result: a Killing vector in a vacuum spacetime generates a solution of the Maxwell equations i.e. \(F_{\mu \nu }=-2\xi _{\mu ;\nu }\). From \(F^{\mu \nu }_{~~;\nu }=0\), it follows that \(-2\xi ^{\mu ;\nu }_{~~;\nu }=0\). Thus (17) coincides with the Maxwell equation for the 4-potential \(A^{\mu }\) in the Lorenz gauge \(A^{\mu }_{\ \ ;\mu }=0\). The special choice for \(A^{\mu }\) is [2, 23]

$$\begin{aligned} A^{\mu }= \left( a\mathcal {B},0,0,\frac{\mathcal {B}}{2} \right) , \end{aligned}$$
(18)

where \(\mathcal {B}\) is the magnetic field strength. The \(4\)-potential is invariant under the symmetries which correspond to the Killing vectors, i.e.,

$$\begin{aligned} L_{\xi }A_{\mu }=A_{\mu ,\nu }\xi ^{\nu }+A_{\nu }\xi ^{\nu }_{,\mu }=0. \end{aligned}$$
(19)

A magnetic field vector is defined as

$$\begin{aligned} \mathcal {B}^{\mu }=-\frac{1}{2}\mathrm{e}^{\mu \nu \lambda \sigma }F_{\lambda \sigma }u_{\nu }, \end{aligned}$$
(20)

where

$$\begin{aligned} \mathrm{e}^{\mu \nu \lambda \sigma }=\frac{\epsilon ^{\mu \nu \lambda \sigma }}{\sqrt{-g}},\ \ \epsilon _{0123}=1,\ \ g=\mathrm{det}(g_{\mu \nu }). \end{aligned}$$
(21)

In (21) \(\epsilon ^{\mu \nu \lambda \sigma }\) is the Levi-Civita symbol and the Maxwell tensor is defined as

$$\begin{aligned} F_{\mu \nu }=A_{\nu ;\mu }-A_{\mu ;\nu }. \end{aligned}$$
(22)

For a local observer at rest we have

$$\begin{aligned}&u^{\mu }=\left( \frac{1}{\sqrt{(1-\frac{r_{\mathrm{g}}}{r})+\frac{4aM\sqrt{\left( 1-\frac{r_{\mathrm{g}}}{r}\right) }}{r^{2}\sin \theta }}},0,0,\nonumber \right. \\&\quad \left. \frac{1}{r\sin \theta \sqrt{\left( 1+\frac{4aM}{r^{2}\sin \theta \sqrt{\left( 1-\frac{r_{\mathrm{g}}}{r}\right) }}\right) }}\right) . \end{aligned}$$
(23)

From (20)–(23) we obtain the components of the magnetic field,

$$\begin{aligned} \mathcal {B}^{\mu }&= \mathcal {B}\left( 0,\cos \theta \left( \frac{\bigg (1-\frac{r_{\mathrm{g}}}{r}\bigg )}{\sqrt{\bigg (1-\frac{r_{\mathrm{g}}}{r}\bigg )+ \frac{2r_{\mathrm{g}}a\sqrt{\bigg (1-\frac{r_{\mathrm{g}}}{r}\bigg )}}{r^{2}\sin \theta }}}\right) \right. \nonumber \\&\left. +\,\,\frac{r_{\mathrm{g}}a\sin \theta \cos \theta }{r} \!\left( \!\frac{\bigg (1-\frac{r_{\mathrm{g}}}{r}\bigg )}{r\sin \theta \!\sqrt{\bigg (\!1\!+\!\frac{2r_{\mathrm{g}}a}{r^{2}\sin \theta \!\sqrt{\bigg (\!1-\frac{r_{\mathrm{g}}}{r}\!\bigg )}}\!\bigg )}} \!\right) \!,\right. \nonumber \\&\left. -\frac{\sin \theta \bigg (1-\frac{r_{\mathrm{g}}}{r}\bigg )}{r\sqrt{\bigg (1-\frac{r_{\mathrm{g}}}{r}\bigg )+\frac{2r_{\mathrm{g}}a\sqrt{\bigg (1-\frac{r_{\mathrm{g}}}{r}\bigg )}}{r^{2}\sin \theta }}},0\right) . \end{aligned}$$
(24)

For the equatorial plane only, the third component of the magnetic field will survive. Hence Eq. (24) becomes

$$\begin{aligned} \mathcal {B}^{\mu }&= \mathcal {B}\left( 0,0, -\frac{\left( 1-\frac{r_{\mathrm{g}}}{r}\right) }{r\sqrt{\left( 1-\frac{r_{\mathrm{g}}}{r}\right) +\frac{2r_{\mathrm{g}}a\sqrt{\left( 1-\frac{r_{\mathrm{g}}}{r}\right) }}{r^{2}}}},0\right) . \end{aligned}$$
(25)

The Lagrangian of the particle of mass \(m\) and charge \(q\) moving in an external magnetic field in a curved spacetime is [38]

$$\begin{aligned} \mathcal {L}=\frac{1}{2}g_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }+\frac{qA_{\mu }}{m}\dot{x}^{\mu }, \end{aligned}$$
(26)

and the generalized 4-momentum of the particle is \(P_{\mu }=mu_{\mu }+qA_{\mu }\). The constants of motion are

$$\begin{aligned} \dot{t}&=\frac{r^{3}\mathcal {E}+aL_{z}r_{\mathrm{g}}}{r^{2}(r-r_{\mathrm{g}})}-2aB, \nonumber \\ \dot{\phi }&=\frac{1}{r^{2}}\left( \frac{ar_{\mathrm{g}}\mathcal {E}}{(r-r_{\mathrm{g}})}+\frac{L_{z}}{\sin ^{2}\theta }\right) -B. \end{aligned}$$
(27)

For the equatorial plane \(\theta =\frac{\pi }{2}\) the above integrals of motion become

$$\begin{aligned} \dot{t}&=\frac{r^{3}\mathcal {E}+aL_{z}r_{\mathrm{g}}}{r^{2}(r-r_{\mathrm{g}})}-2aB, \nonumber \\ \dot{\phi }&=\frac{1}{r^{2}}\left( \frac{ar_{\mathrm{g}}\mathcal {E}}{(r-r_{\mathrm{g}})}+L_{z}\right) -B. \end{aligned}$$
(28)

Here we denote

$$\begin{aligned} B\equiv \frac{q\mathcal {B}}{2m}. \end{aligned}$$
(29)

Using the values of \(\dot{t}\) and \(\dot{\phi }\) and neglecting the terms involving \(a^{2}\), Eq. (26) yields

$$\begin{aligned} \mathcal {L}&= \frac{1}{2r^{2}(r-r_{\mathrm{g}})^{2}}[4Br^{2}L_{z}(r_{\mathrm{g}}-r)+L_{z}^{2}(r_{\mathrm{g}}-r) \nonumber \\&+\,r^{2}(Br_{\mathrm{g}}(3Br^{2}+2a\mathcal {E})r(\mathcal {E}^{2}-3B^{2}r^{2}-\dot{r}^{2}))]. \end{aligned}$$
(30)

By using the above Lagrangian in the Euler–Lagrange equation, which is defined as

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau }\left( \frac{\partial \mathcal {L}}{\partial \dot{x}}\right) -\frac{\partial \mathcal {L}}{\partial {x}}=0, \end{aligned}$$
(31)

we get

$$\begin{aligned} \ddot{r}&= \frac{Ba\mathcal {E}r_{\mathrm{g}}}{r(r-r_{\mathrm{g}})} +\frac{1}{2r^{4}(r-r_{\mathrm{g}})}[6B^{2}r^{6}-2L_{z}^{2}(r-r_{\mathrm{g}})^{2} \nonumber \\&+\,r^{3}r_{\mathrm{g}}(-\mathcal {E}^{2}+6B^{2}rr_{\mathrm{g}}+\dot{r}^{2}-12B^{2}r^{2})]. \end{aligned}$$
(32)

Following the procedure of Sect. 2, using the normalization condition, \(u^{\mu }u_{\mu }=1\), and using the value of the new constants of motion, see (28), we obtain

$$\begin{aligned} \mathcal {E}&= \frac{1}{r_{\mathrm{o}}^{6}(r_{\mathrm{o}}-r_{\mathrm{g}})}[2aBr_{\mathrm{o}}^{7}+ar_{\mathrm{g}}r_{\mathrm{o}}^{3}(2Br_{\mathrm{o}}^{2}(r_{\mathrm{g}}-2r_{\mathrm{o}})\nonumber \\&+\,L_{z}(r_{\mathrm{g}}-r_{\mathrm{o}})) \nonumber \\&\pm \,(a^{2}r_{\mathrm{o}}^{6}(r_{\mathrm{o}}-r_{\mathrm{g}})^{2}(r_{\mathrm{g}}(L_{z}+2Br_{\mathrm{o}}^{2})-2Br_{\mathrm{o}}^{3})^{2} \nonumber \\&+\,r_{\mathrm{o}}^{9}(r_{\mathrm{o}}-r_{\mathrm{g}})^{3}(r_{\mathrm{o}}^{2}+(L_{z}+Br_{\mathrm{o}}^{2})^{2}))^{\frac{1}{2}}]. \end{aligned}$$
(33)

If (33) is satisfied initially (at the time of collision), then it is always valid (throughout the motion), provided that \(r(\tau )\) is controlled by (32).

The system (26)–(33) is invariant with respect to reflection \((\theta \rightarrow \pi -\theta )\). This transformation retains the initial position of the particle and changes \((v_{\perp }\rightarrow -v_{\perp })\) as it is defined by \(v_{\perp }\equiv -r\dot{\theta _{\mathrm{o}}}\). Therefore, it is sufficient to consider only the positive value of \((v_{\perp })\).

4 Dimensionless form of the dynamical equations

To perform the numerical analysis, it is convenient to convert Eqs. (32) and (33) to dimensionless form by introducing the following dimensionless quantities:

$$\begin{aligned} \sigma =\frac{\tau }{r_{\mathrm{g}}},\ \rho =\frac{r}{r_{\mathrm{g}}},\ \ell =\frac{L_{z}}{r_{\mathrm{g}}},\ b=Br_{\mathrm{g}}. \end{aligned}$$
(34)

Equation (33) now becomes

$$\begin{aligned} \mathcal {E}_{\mathrm{o}}&= \frac{1}{\rho _{\mathrm{o}}^{6}(\rho _{\mathrm{o}}-1)}[a\rho _{\mathrm{o}}^{3}(1-\rho _{\mathrm{o}})(\ell -2b\rho _{\mathrm{o}}^{2}(\rho _{\mathrm{o}}-1)) \nonumber \\&+\,(\rho _{\mathrm{o}}^{6}(\rho _{\mathrm{o}}-1)^{2}(a^{2}(\ell -2b\rho _{\mathrm{o}}^{2}(\rho _{\mathrm{o}}-1))^{2}) \nonumber \\&+\,\rho _{\mathrm{o}}^{3}(\rho _{\mathrm{o}}-1)(\rho _{\mathrm{o}}^{2}+(\ell +b\rho _{\mathrm{o}}^{2})^{2}) )^{\frac{1}{2}}]. \end{aligned}$$
(35)

The magnetic field is zero at \(\rho \rightarrow \infty \). Therefore from Eq. (35) as \(\rho \rightarrow \infty \), we have \(\mathcal {E}\rightarrow 1\).

The dimensionless form of Eq. (32) is

$$\begin{aligned} \frac{\mathrm{d}^{2}\rho }{\mathrm{d}\sigma ^{2}}&= \frac{1}{2\rho ^{4}(\rho -1)}\bigg [\rho ^{3}(2a\mathcal {E}b+6\mathcal {E}^{2}b^{2}\rho (\rho -1)^{2})\nonumber \\&-\,2\ell (\rho -1)^{2}+\rho ^{3}\frac{\mathrm{d}\rho }{\mathrm{d}\sigma }\bigg ]. \end{aligned}$$
(36)

We solved Eq. (36) numerically by using the built in command NDSolve of Mathematica. As ISCO exists at \(r=3r_{\mathrm{g}}\), and using \(\rho =\frac{r}{r_{\mathrm{g}}}\) and \(\sigma =\frac{\tau }{r_{\mathrm{g}}}\), our initial conditions for solving (36) become \(\rho (1)=3\) and \(\dot{\rho }(1)=3\). We get the interpolating function \(\rho (\sigma )\) as the solution of the Eq. (36) which we plotted in Fig. 1 against \(\sigma \). In Fig. 2 we have plotted the radial velocity (derivative of the interpolating function) vs. \(\sigma \), which shows that the particle will escape to infinity according to the initial conditions.

Fig. 1
figure 1

The graph for \(\rho (\sigma )\) vs. \(\sigma \). Here \(\mathcal {E}=1, q=1, b=0.5, \ell =2,\) and \(a=0.1\)

Full size image
Fig. 2
figure 2

The graph for \(\rho '(\sigma )\) (radial velocity) vs. \(\sigma \). Here \(\mathcal {E}=1, q=1, b=0.5, \ell =2,\) and \(a=0.1\)

Full size image

As is the case of a neutral particle, we assume that the collision does not change the azimuthal angular momentum of the particle but it changes the transverse velocity \(v>0\). Due to this, the angular momentum and the energy of the particle will change as \(\ell \rightarrow \ell _{t}\) and \(\mathcal {E}_{\mathrm{o}}\rightarrow \mathcal {E}\), respectively, which is given by

$$\begin{aligned} \ell _{t}^{2}=\rho ^{2}v_{\perp }^{2}+\rho ^{4}\bigg [\frac{1}{\rho ^{2}}\bigg (\frac{a\mathcal {E}_{\mathrm{o}}}{2(\rho -1)}+\ell \bigg )-b\bigg ]^{2}, \end{aligned}$$
(37)
$$\begin{aligned} \mathcal {E}&= \frac{1}{\rho _{\mathrm{o}}^{6}(\rho _{\mathrm{o}}-1)}[a\rho _{\mathrm{o}}^{3}(1-\rho _{\mathrm{o}})(\ell _{t}-2b\rho _{\mathrm{o}}^{2}(\rho _{\mathrm{o}}-1)) \nonumber \\&+\,\,(\rho _{\mathrm{o}}^{6}(\rho _{\mathrm{o}}-1)^{2}(a^{2}(\ell _{t}-2b\rho _{\mathrm{o}}^{2}(\rho _{\mathrm{o}}-1))^{2}) \nonumber \\&+\,\,\rho _{\mathrm{o}}^{3}(\rho _{\mathrm{o}}-1)(\rho _{\mathrm{o}}^{2}+(\ell _{t}+b\rho _{\mathrm{o}}^{2})^{2}) )^{\frac{1}{2}}]. \end{aligned}$$
(38)

Here \(\ell _{t}\) is the dimensionless form of \(L\) given by Eq. (13). For the unbound motion \(\mathcal {E}\ge 1\). By solving (38) and putting \(\mathcal {E}=1\), we get the escape velocity of the particle as given by

$$\begin{aligned}&v_{\perp }=\pm \frac{1}{4\rho ^{2}(\rho -1)}\nonumber \\&\quad \times \bigg [4(\rho -1)\bigg [\sqrt{a^{2}\rho ^{2}+\rho ^{4}(\rho -1)-2ab\rho ^{4}(\rho -1)(2\rho -1)} \nonumber \\&\quad -\,a\rho +\rho (\rho -1)(b\rho ^{2}+(\ell -b\rho ^{2})^{2})\bigg ]\nonumber \\&\quad +\,a\rho \mathcal {E}_{\mathrm{o}}[4(\rho -1)(\ell -b\rho ^{2})] \bigg ]. \end{aligned}$$
(39)

We now discuss the behavior of the particle when it escapes to asymptotic infinity. For simplicity we consider the particle initially in ISCO. The parameters \(\ell \) and \(b\) are defined in terms of \(\rho _{\mathrm{o}}\) and only \(\mathcal {E}\) specifies the motion of the particle. We can express the parameters \(\ell \) and \(b\) in terms of \(\rho _{\mathrm{o}}\) by simultaneously solving the equations \(\frac{\mathrm{d}\mathcal {E}_{\mathrm{o}}}{\mathrm{d}\rho }=0\) and \(\frac{\mathrm{d}^{2}\mathcal {E}_{\mathrm{o}}}{\mathrm{d}\rho ^{2}}=0\), for \(\ell \) and \(b\). But the first derivative and second derivative of the effective potential are very complicated and we cannot find the explicit expression for \(\ell \) and \(b\) in terms of \(\rho \).

5 Trajectories for escape energy

Here we investigate the dynamics of the particle for the positive energy \(\mathcal {E}_{+}\). Particles with negative energy exist only inside the static limit surface \((r_{st}=2m)\) orbiting in the retrograde orbits and do not have the chance to escape. The equation for the rotational (angular) variable \(\phi \) is

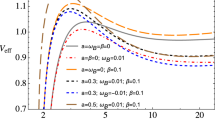
$$\begin{aligned} \frac{\mathrm{d}\phi }{\mathrm{d}\sigma }=\frac{\ell }{\rho ^{2}}-b+\frac{a\mathcal {E}}{\rho ^{3}(1-\rho )}. \end{aligned}$$
(40)

The Lorentz force acting on the massive charged particle is attractive when \(\mathrm{d}\phi /\mathrm{d}\sigma <0\) and vice versa. All of Figs. (3, 4, 5, 6, 7, 8) correspond to Eq. (35). In Fig. 3, the shaded region corresponds to an unbound motion, while the unshaded region refers to bounded trajectories of the particle. The curved line represents the minimum energy required for the particle to escape from the vicinity of the black hole. It can be seen from Fig. 4 that for large values of the angular momentum, the plot is similar to the effective potential of a Schwarzschild black hole [24]. In Fig. 4, \(\mathcal {E}_\text {max}\) corresponds to an unstable circular orbit and \(\mathcal {E}_\text {min}\) refers to ISCO.

Fig. 3
figure 3

The effective potential \(\mathcal {E}\) as a function of \(\rho \) for \(\ell =5\), \(b=0.5\), and \(a=0.1\)

Full size image
Fig. 4
figure 4

The effective potential against \(\rho \) for \(\ell =20\), \(b=0.5\), and \(a=0.1\). In this figure \(\mathcal {E}_\mathrm{max}\) corresponds to an unstable circular orbit and \(\mathcal {E}_\mathrm{min}\) corresponds to a stable circular orbit

Full size image
Fig. 5
figure 5

The effective potential \(\mathcal {E}\) as a function of radial coordinate \(\rho \) for different values of the angular momentum \(\ell \)

Full size image
Fig. 6
figure 6

The effective potential \(\mathcal {E}\) against radial coordinate \(\rho \) for different values of the negative angular momentum \(\ell \)

Full size image
Fig. 7
figure 7

The effective potential \(\mathcal {E}\) vs. \(\rho \) for \(\ell =-10\) and \(\ell =10\)

Full size image
Fig. 8
figure 8

The effective potential \(\mathcal {E}\) against \(\rho \) for different values of the magnetic field

Full size image

The effective potential \(\mathcal {E}\) of a particle moving in a slowly rotating Kerr spacetime is plotted as a function of radial coordinate \(\rho \) for different values of the angular momentum \(\ell \) in Fig. 5. We can see from Fig. 5 that for large values of the angular momentum, the maxima is shifting upward. For a particle to be captured by the black hole it is required that the energy which should be greater than this maxima. If its energy is less than this maxima there are two possibilities for a particle either it will escape to infinity or it might start moving in ISCO. If energy of the particle \(\mathcal {E}<1\) then it will stay in some stable orbit and if \(\mathcal {E}>1\) then it will escape to infinity. In Fig. 5 we plotted effective potential against \(\rho \) for different value of the angular momentum. For \(\ell >0\) the Lorentz force is repulsive. Hence it can be concluded from Fig. 5 that the possibility of a particle to escape after a collision from the vicinity of the black hole is greater for a larger value of \(\ell _{+}\) as compare to the lesser value of it. For \(\ell <0\) the Lorentz force is attractive. Therefore, the possibility of a particle to escape after a collision is less for a larger value of \(\ell _{-}\) as compared to smaller value of \(\ell _{-}\), represented in Fig. 6. The graph for \(\ell =0\) and \(b=0\) in Fig. 6 corresponds to a photon as there is no stable region. Moreover, we compare the effective potential for \(\ell =10\) and \(\ell =-10\) in Fig. 7. It can be seen that the stability is larger for \(\ell =-10\). Therefore it is concluded that for the attractive Lorentz force \((\ell =-10)\), the particle requires more energy to escape. It can be seen from Fig. 8 that with the increase in the strength of the magnetic field, the local minimum of the effective potential is shifting toward the horizon. This local minimum corresponds to ISCO, which is in agreement with the result of [23].

6 Trajectories for the escape velocity

For all the figures of the escape velocity we have denoted \(v_{\perp }\equiv v_\text {esc}\). From Eq. (38) we calculate the escape velocity by substituting \(\mathcal {E}=1\). Figures 9, 10, 11, and 12 correspond to Eq. (39). In Fig. 9, the shaded region corresponds to the escape velocity of the particle and the solid curve represents the minimum velocity required to escape from the vicinity of the black hole to infinity. The unshaded region represents the bound motion around the black hole. In Fig. 10 the shaded region corresponds to the escape velocity of the particle and the solid curve represents the minimum velocity required to escape from the vicinity of the black hole. The unshaded region represents the bound motion around the black hole.

Fig. 9
figure 9

The escape velocity against \(\rho \) for \(\ell =5\), \(b=0.5\) and \(a=0.1\)

Full size image
Fig. 10
figure 10

The escape velocity against \(\rho \) for \(\ell =5\), \(b=0.5\) and \(a=0.1\)

Full size image
Fig. 11
figure 11

The escape velocity \(v_\mathrm{esc}\) against \(\rho \) for different values of the magnetic field \(b\)

Full size image
Fig. 12
figure 12

The escape velocity \(v_\mathrm{esc}\) against \(\rho \) for different values of the angular momentum \(\ell \)

Full size image

In Fig. 11 we plotted the escape velocity of a particle moving in ISCO as a function of radial coordinate \(\rho \) for different values of the magnetic field \(b\). It can be seen from Fig. 11 that due to the presence of the magnetic field in the vicinity of the black hole the escape velocity of the particle increases. Therefore we can say that in the presence of the magnetic field \(b\), the possibility of the particle to escape is greater than in the case when the magnetic field is absent i.e. \(b=0\). We plot the escape velocity against \(\rho \) in Fig. 12 for different values of the angular momentum \(\ell \). We can see from Fig. 12 that the escape velocity is increasing for large values of \(\ell \). Hence we can conclude that if the particle has a larger value of the angular momentum \(\ell \), then it can easily escape to infinity as compared to the particle with a smaller value of the angular momentum \(\ell \), regardless of the magnetic field.

7 Discussion

We have studied the dynamics of a neutral and a charged particle around the slowly rotating Kerr black hole which is immersed in a magnetic field. Therefore the particle is under the influence of both gravitational and electromagnetic forces. We have obtained the equations of motion by using Lagrangian formalism. We have derived the expression for the magnetic field present in the vicinity of a slowly rotating Kerr black hole. We have calculated the minimum energy for a particle to escape from ISCO to infinity. With zero spin i.e. \(a=0\), our results reduce to the case of the Schwarzschild black hole [15].

The behavior of the effective potential and escape velocity against magnetic field and angular momentum are discussed in detail. It is shown in Figs. 4, 9, and 10 under what conditions particle can escape from the vicinity of the black hole to spatial infinity. For larger values of the angular momentum, the behavior of the effective potential is similar to that of the Schwarzschild black hole [15]. It is concluded that the magnetic field largely affects the motion of the particle in the vicinity of the black hole. This effect decreases far away from the black hole. It is found that as the value of the magnetic field parameter is increased, the local minimum of the effective potential shifted towards the horizon, as shown in Fig. 8. This indicates that the ISCO shrinks as the strength of the magnetic field increases. It is concluded from Figs. 5 and 12 that if the particle has a large value angular momentum \(\ell _{+}\), then it can escape easily as compared to a particle with smaller angular momentum \(\ell _{+}\). Figure 7 shows that for an attractive Lorentz force \((\ell _{-})\) the stability is larger in comparison with a repulsive Lorentz force \((\ell _{+})\).

The escape velocity \(v_\mathrm{esc}\), for different values of the magnetic field \(b\) is plotted in Fig. 11. It is found that due to the presence of the magnetic field in the vicinity of the black hole the escape velocity of the particle increases. Therefore we found that the possibility of the particle to escape from the vicinity of the black hole to infinity is greater in the presence of a magnetic field as compared to the case when the magnetic field is absent, \(b=0\).