pp elastic scattering at LHC energies

Abstract

Using a unified analytic representation for the elastic scattering amplitudes of pp scattering valid for all energies above 20 GeV, the behavior of observables in the LHC collisions in the range $\sqrt{s} =$ 2.76–14 TeV is discussed. After the precise description of $\mathrm{d}\sigma /\mathrm{d}t$ at 7 TeV, we discuss the energy dependence of the amplitudes and expect that the proposed analytical forms give equally good predictions for the future experiments.

1 Introduction

Elastic scattering is described by one single complex function depending on two kinetic variables: the incident center of mass energy $\sqrt{s}$ and momentum transfer $\vec {q}$. In high energy pp( p̄ ) scattering, the scattering amplitude is usually represented as $T(s,t)$, where $t$ is the four momentum transfer squared. More than a decade ago, Ferreira and Pereira analyzed all available elastic scattering data for energies above 20 GeV [1, 2] and all $|t|$, identifying properties of the amplitudes (zeros, signs, magnitudes), with proper attention given to the real part, which plays a critical role in differential cross sections for mid and large $|t|$ ranges.

Recently, this analysis was extended [3] to the LHC-TOTEM elastic scattering 7 TeV data [4], and also the behavior of proposed amplitudes was re-examined in the whole energy region from 20 GeV to 14 TeV to determine the precise energy dependence of the model parameters [5], and it was applied to the cosmic energy domain with calculation of p-air cross sections [6]. From this analysis, an analytic representation of scattering amplitudes as a function of $\sqrt{s}$ and $t$ was established. In the present work we apply these analytical forms to investigate in detail the LHC energy region from 2.76 to 14 TeV.

We stress that we establish explicitly disentangled real and imaginary amplitudes based on a QCD motivated model, and not just fit pure phenomenological expressions to observables. Besides, since the so-called impact parameter representation $(s,\vec {b})$ and its Fourier transform in $(s,\vec {q})$ space are both represented by simple analytical forms, we are able to control unitarity and dispersion relation constraints and provide a geometric interpretation of the interaction range. The regularity that we obtain in our treatment of the data and associated reasonable physical interpretation of the consequences give reliability to our proposal of disentanglement of the amplitudes [5].

The present work is organized as follows. In the next section, we describe briefly the amplitudes and their energy dependences in both $t$- and $b$-representations. In Sect. 3 we apply these amplitude to describe observables and discuss their energy dependence, and also we investigate consequences for very high energies of the form of the amplitudes in $b$-space. In Sect. 4 we make use of the properties of our amplitudes and observables for the LHC range, particularly for $\sqrt{s}=$ 8 TeV, where preliminary information on $\mathrm{d}\sigma /\mathrm{d}t$ starts to become available. The last section is devoted to a further discussion of our results and perspectives, together with a geometric interpretation in the $b$-space representation.

2 Analytic representation of the amplitudes

2.1 Impact parameter representation

The Fourier transform of the momentum transfer $\vec {q}$ amplitudes to the $\vec {b}$-space defines the impact parameter (or simply $b$-space) representation. Since the impact parameter variable $\vec {b}$ is not observable, the treatments of data are made usually in $(s,t)$ space, except for integrated cross sections. However, the $b$-space description gives insight in geometric aspects of the collision, since in the classical limit the variable $b$ reduces to the physical impact parameter. Besides, it plays an important role in the eikonal representation, where unitarity constraints are more simply formulated. On the other hand, the dispersion relation (causality) constraint is properly dealt with in $t$-space. In the following discussion, we do not consider the effects of spin or polarization.

The amplitudes for the description of pp scattering in the stochastic vacuum model (SVM) [7, 8] are originally constructed through profile functions in $b$-space and here we describe this formalism first. The dimensionless $(s,b)$ amplitudes due to the nuclear interaction are written

$$\begin{aligned} \widetilde{T}_{K}(s,\vec {b})=\frac{\alpha _{K}}{2\beta _{K}}\mathrm{e}^{-{b^{2}}/{ 4\beta _{K}}}+\lambda _{K}\widetilde{\psi }_{K}(s,b), \end{aligned}$$

(1)

with the characteristic shape function

$$\begin{aligned} \widetilde{\psi }_{K}(s,b)=\frac{2\mathrm{e}^{\gamma _{K}-\sqrt{\gamma _{K}^{2}+{b^{2} }/{a_{0}}}}}{a_{0}\sqrt{\gamma _{K}^{2}+{b^{2}}/{a_{0}}}}\Big [1-\mathrm{e}^{\gamma _{K}-\sqrt{\gamma _{K}^{2}+{b^{2}}/{a_{0}}}}\Big ]. \end{aligned}$$

(2)

The label $K$ $=R,I$ indicates either the real or the imaginary part of the complex amplitude.

The fixed quantity $a_0=1.39 \text{ GeV }^{-2}$ is related to the square of the correlation length $a$ of the correlation function of the gluon condensate, with $a=(0.2\sim 0.3)$ fm, as measured in hadronic interactions and in lattice QCD, with our best choice 0.27 fm. In the large $b$ behavior of the profile function of the SVM there appears the dimensionless combination $b^2/a_0$ where $a_0 = [a/(3\pi /8)]^2$, which fixes the value of $a_0$ appearing in Eq. (2). The quantity $3\pi /8$ is a feature of the correlation function [7, 8].

The Gaussian form of the first term in Eq. (1) is similar to the usual formalism of reggeon exchanges [9]. The second term, referred to as shape function, represents contributions from the perturbed vacuum structure around the protons at larger $b$ values. It is zero at $b=0$ and is normalized as

$$\begin{aligned} \frac{1}{2\pi }\int \mathrm{d}^{2}\vec {b}\ \tilde{\psi }_{K}\left( b,s\right) =1. \end{aligned}$$

(3)

In Eq. (1) we have introduced four energy dependent parameters for each amplitude, $\alpha _{K}$, $\beta _{K}$, $\gamma _{K}$, $\lambda _{K}$, with $\gamma _{K}$ dimensionless, while $\alpha _{K}$, $\gamma _{K}$ and $\beta _{K}$ are like GeV$^{-2}$.

In the small and mid $b$ ranges there is a superposition of the contributions of the two parts, which we may call, respectively, Regge phenomenology and loop–loop interaction. The resulting parameter values are determined describing with accuracy the imaginary and real amplitudes as a whole, there is no case of double counting effects, and each part is duly represented, if one thinks of each one separately. Actually Eq. (1) represents an extension of the parametrization of results of the SVM, opening possibilities of introducing proper $s$ and $t$ dependences.

Although $b$ is not exactly the physical impact parameter, nor observable, the $b$-space representation permits a geometrical interpretation of the behavior of the amplitude. For large $b$, which corresponds to peripheral collisions, the amplitudes fall down with a Yukawa-like tail,

$$\begin{aligned} \sim \frac{1}{b}\mathrm{e}^{-b/b_{0}}, \end{aligned}$$

(4)

which reflects the effects of virtual partons (the modified gluon field) at large distance in the SVM. A feature of the $b$-space representation is that it can be directly related to the eikonal formalism, as shown below.

We introduce the eikonal function $\chi \left( s,b\right)$ through

$$\begin{aligned} i\sqrt{\pi }~(1-\mathrm{e}^{i\chi (s,\vec {b})})~\equiv \widetilde{T}(s,\vec {b})= \widetilde{T}_{R}(s,\vec {b})+i\widetilde{T}_{I}(s,\vec {b}), \end{aligned}$$

(5)

with

$$\begin{aligned} \chi (s,\vec {b})=\chi _{R}(s,\vec {b})+i\chi _{I}(s,\vec {b}). \end{aligned}$$

(6)

Separating real and imaginary parts, we have

$$\begin{aligned}&1-\cos \chi _{R}\ \mathrm{e}^{-\chi _{I}} =\frac{1}{\sqrt{\pi }}\widetilde{T}_{I}(s, \vec {b}), \end{aligned}$$

(7)

$$\begin{aligned}&\sin \chi _{R}\ \mathrm{e}^{-\chi _{I}} =\frac{1}{\sqrt{\pi }}\widetilde{T}_{R}(s, \vec {b}). \end{aligned}$$

(8)

From Eq. (8) we have immediately

$$\begin{aligned} \mathrm{e}^{-2\chi _{I}}\ge \frac{1}{\pi }\widetilde{T}_{R}^{2}(s,\vec {b}), \end{aligned}$$

(9)

and thus the general unitarity constraint is written

$$\begin{aligned} \frac{\widetilde{T}_{R}^{2}}{\pi }\le \mathrm{e}^{-2\chi _{I}(s,\vec {b})}\le ~1, \end{aligned}$$

(10)

or

$$\begin{aligned} 0\le \chi _{I}\le -\frac{1}{2}\log (\widetilde{T}_{R}^{2}/\pi ). \end{aligned}$$

Our solution, at all energies, satisfies this bound condition.

Satisfying a monotonic behavior of the scattering amplitudes, our solutions are restricted to the branch where $\chi _{R}\ge 0,$ and thus, in turn, we have

$$\begin{aligned} 0~\le ~\widetilde{T}_{I}(s,\vec {b})\le \sqrt{\pi },\ ~\forall ~s,b. \end{aligned}$$

(11)

Under these conditions, our analysis shows that for a fixed $\sqrt{s}$, the function $\widetilde{T}_{I}(s,\vec {b})$ is monotonically decreasing in $b$. The maximum of the imaginary amplitude, $\widetilde{T}_{I}(s,\vec {b}=0)$, tends to its limiting value $\sqrt{\pi }$ for asymptotic large energies [5].

In terms of the $\widetilde{T}_{K}(s,\vec {b})$ amplitudes, the elastic, total, and inelastic cross sections are written, respectively,

$$\begin{aligned}&\sigma _{\mathrm {el}}(s)=\frac{(\hbar c)^{2}}{\pi }\int \mathrm{d}^{2}\vec {b}~| \widetilde{T}(s,\vec {b})|^{2} \equiv \int \mathrm{d}^{2}\vec {b}~\frac{\mathrm{d}\widetilde{ \sigma }_{\mathrm {el}}(s,\vec {b})}{\mathrm{d}^{2}\vec {b}},\nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned}&\sigma (s)=\frac{2}{\sqrt{\pi }}(\hbar c)^{2}\int \mathrm{d}^{2}\vec {b}~\widetilde{T} _{I}(s,\vec {b})~ \equiv \int \mathrm{d}^{2}\vec {b}~\frac{\mathrm{d}\widetilde{\sigma }_{ \mathrm {tot}}(s,\vec {b})}{\mathrm{d}^{2}\vec {b}},\nonumber \\ \end{aligned}$$

(13)

and

$$\begin{aligned} \sigma _{\mathrm {inel}}&= \sigma -\sigma _{\mathrm {el}} =(\hbar c)^{2}\int \mathrm{d}^{2}\vec {b}~\Bigg (\frac{2}{\sqrt{\pi }}\widetilde{T}_{I}(s,\vec {b})\nonumber \\&-\frac{1 }{\pi }|\widetilde{T}(s,\vec {b})|^{2}\Bigg )\equiv \int \mathrm{d}^{2}\vec {b}~\frac{d\widetilde{\sigma }_{\mathrm {inel}}(s,\vec { b})}{\mathrm{d}^{2}\vec {b}}. \end{aligned}$$

(14)

In terms of the eikonal function, we write

$$\begin{aligned}&\frac{\mathrm{d}\widetilde{\sigma }_{\mathrm {el}}(s,\vec {b})}{\mathrm{d}^{2}\vec {b}} =1-2\cos \chi _{R}\mathrm{e}^{-\chi _{I}}+\mathrm{e}^{-2\chi _{I}},\end{aligned}$$

(15)

$$\begin{aligned}&\frac{\mathrm{d}\widetilde{\sigma }(s,\vec {b})}{\mathrm{d}^{2}\vec {b}} =2\left( 1-\cos \chi _{R}\mathrm{e}^{-\chi _{I}}\right) \end{aligned}$$

(16)

$$\begin{aligned}&\frac{\mathrm{d}\widetilde{\sigma }_{\mathrm {inel}}(s,\vec {b})}{\mathrm{d}^{2}\vec {b}} =1-\mathrm{e}^{-2\chi _{I}}. \end{aligned}$$

(17)

2.2 $t$-space representation

The comparison with $\mathrm{d}\sigma /\mathrm{d}t$ data and determination of parameters are made with the amplitudes in $t$-space. The quantities $\Psi _{K}(\gamma _{K}(s),t=-\vec {q}_{T}^{2})$ obtained by the Fourier transform of Eq. (1) are written

$$\begin{aligned} T_{K}^{N}(s,t)=\alpha _{K}(s)\mathrm {e}^{-\beta _{K}(s)|t|}+\lambda _{K}(s)\Psi _{K}(\gamma _{K}(s),t), \end{aligned}$$

(18)

with $K=R,I$, and the shape functions in $t$-space take the form

$$\begin{aligned} \Psi _{K}(\gamma _{K}(s),t)=&2~\mathrm {e}^{\gamma _{K}}~\left[ {\frac{\mathrm {e}^{-\gamma _{K}\sqrt{ 1+a_{0}|t|}}}{\sqrt{1+a_{0}|t|}}}-\mathrm {e}^{\gamma _{K}}~{\frac{\mathrm{e}^{-\gamma _{K}\sqrt{4+a_{0}|t|}}}{\sqrt{4+a_{0}|t|}}}\right] \!,\nonumber \\ \end{aligned}$$

(19)

with the property

$$\begin{aligned} \Psi _{K}(\gamma _{K}(s),t=0)=1, \end{aligned}$$

(20)

which corresponds to Eq. (3).

The expression (18) represents the nuclear amplitude due to the non-perturbative QCD interactions that dominate the low and mid $|t|$ regions. To describe elastic $\mathrm{d}\sigma /\mathrm{d}t$ data for all $|t|$, we should account for contributions from perturbative processes. We thus add a term representing the perturbative three-gluon exchange amplitude [10, 11], which may appear in the large $|t|$ region, and the complete nuclear amplitudes are then written

$$\begin{aligned}&T_{K}^{N}(s,t)\rightarrow T_{K}^{N}(s,t)\nonumber \\&\quad =\alpha _{K}(s)\mathrm {e}^{-\beta _{K}(s)|t|}+ \lambda _{K}(s)\Psi _{K}(\gamma _{K}(s),t)\nonumber \\&\qquad +\,\delta _{K,R}R_{ggg}\left( t\right) , K=R,I, \end{aligned}$$

(21)

where the Kronecker delta symbol $\delta _{K,R}$ is introduced since we define $R_{ggg}\left( t\right)$ as the real contribution from the perturbative three-gluon exchange amplitude. The effect of the tail term $R_{ggg}\left( t\right)$, producing a universal (not energy dependent) $|t|^{-8}$ form for large $|t|$ in $\mathrm{d}\sigma /\mathrm{d}t$, was studied in the analysis of the experiments at CERN-ISR, CERN-SPS [1, 2], 1.8 TeV [12] and 7 TeV [3]. We write

$$\begin{aligned} R_{ggg}(t)\equiv \pm 0.45~t^{-4}(1-\mathrm{e}^{-0.005\left| t\right| ^{4} })(1-\mathrm{e}^{-0.1\left| t\right| ^{2}}), \end{aligned}$$

(22)

where the last two factors cut off this term smoothly in the non-perturbative domain, and the signs $\pm$ refer to the pp and p${\bar{\mathrm {p}}}$ amplitudes, respectively. Although the cut-off factors written in Eq. (22) have been adequate for all cases that were examined, their detailed forms in the transition range $(2.5~<~|t|~<~4)$   GeV$^{2}$ must be examined with data.

For a complete analysis of elastic scattering, we must also take into account the contribution from the Coulomb interaction. The complete amplitudes $T_{R}(s,t)$ and $T_{I}(s,t)$, with dimensions GeV$^{-2}$, contain the nuclear and the Coulomb parts as

$$\begin{aligned} T_{R}(s,t)=T_{R}^{N}(s,t)+\sqrt{\pi }F^{C}(t)\cos (\alpha \Phi ), \end{aligned}$$

(23)

and

$$\begin{aligned} T_{I}(s,t)=T_{I}^{N}(s,t)+\sqrt{\pi }F^{C}(t)\sin (\alpha \Phi ), \end{aligned}$$

(24)

where $\alpha$ is the fine-structure constant, $\Phi (s,t)$ is the Coulomb phase and $F^{C}(t)$ is related with the proton form factor

$$\begin{aligned} F^{C}(t)~=(-/+)~\frac{2\alpha }{|t|}~F_{\mathrm {proton}}^{2}(t), \end{aligned}$$

(25)

for the pp$/$p${\bar{\mathrm {p}}}$ collisions. The proton form factor is taken as

$$\begin{aligned} F_{\mathrm {proton}}(t)=[t_{0}/(t_{0}+|t|)]^{2}, \end{aligned}$$

(26)

where $t_{0}=0.71\$GeV$^{2}$. Note that the strong interaction parts of the amplitudes are smooth and regular functions of $s$ and $t$, while the Coulomb amplitude is relevant in the very forward range $|t|<10^{-2}~\mathrm { {GeV}^{2}}$.

In our normalization the elastic differential cross section is written

$$\begin{aligned} \frac{\mathrm{d}\sigma (s,t)}{\mathrm{d}t}&= (\hbar c)^2[T_I^2(s,t)+ T_R^2(s,t)]\nonumber \\&= \frac{\mathrm{d}\sigma ^I(s,t)}{\mathrm{d}t} + \frac{\mathrm{d}\sigma ^R(s,t)}{\mathrm{d}t}, \end{aligned}$$

(27)

and the total pp cross section is given by the optical theorem

$$\begin{aligned} \sigma = (\hbar c)^2~ 4\sqrt{\pi } ~ T_{I}^{N}(s,t=0). \end{aligned}$$

(28)

The analysis of all pp elastic scattering data for $\sqrt{s}$ from 20 GeV to 7 TeV leads to a separate identification of the real and imaginary parts contributing to Eq. (27). The energy dependence of the eight parameters is given below, with $\sqrt{s}$ in TeV, and GeV$^{-2}$ in the units of the parameters that are not dimensionless ($\gamma _I$ and $\gamma _R$ are dimensionless).

$$\begin{aligned} \alpha _I(s)&= 11.0935+1.35479\log \sqrt{s},\end{aligned}$$

(29)

$$\begin{aligned} \beta _I(s)&= 4.44606586+0.3208411\log \left( \sqrt{s}/{30.4469}\right) \nonumber \\&+\,0.0613381 \left[ \log ^2\left( \sqrt{s}/30.4469\right) +0.5 \right] ^{1/2},\end{aligned}$$

(30)

$$\begin{aligned} \alpha _R(s)&= 0.208528+0.0419028~\log \sqrt{s},\end{aligned}$$

(31)

$$\begin{aligned} \beta _R(s)&= 1.1506+0.12584~\log \sqrt{s}+ 0.017002~\log ^2\sqrt{s},\nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned} \gamma _I(s)&= 10.025+0.79097~\log \sqrt{s}+0.088~\log ^2\sqrt{s},\end{aligned}$$

(33)

$$\begin{aligned} \gamma _R(s)&= 10.401+1.4408~\log (\sqrt{s})\nonumber \\&+\,0.16659~\log ^2(\sqrt{s}), \end{aligned}$$

(34)

$$\begin{aligned} \lambda _I(s)&= 14.02008\!+\!3.23842~\log \sqrt{s}+0.444594~\log ^2\sqrt{s},\nonumber \\ \end{aligned}$$

(35)

$$\begin{aligned} \lambda _R(s)&= 3.31949+0.743706~\log \sqrt{s}. \end{aligned}$$

(36)

The peculiar (not so simple) expression for $\beta _{I}(s)$ is constructed in order to satisfy both the low-energy phenomenology and the unitarity constraints at all energies, as given in Eq. (11), and this leads to the asymptotic behavior $\widetilde{T}_I(s,b=0) \rightarrow \sqrt{\pi }$. For very high energy and considerations of asymptotic behavior, it is useful to use the simpler form for $\beta _I(s)$

$$\begin{aligned} \beta _I(s) = 0.382179 \log (\sqrt{s})+ 3.14055. \end{aligned}$$

(37)

The first term in Eq. (18) can be written in the usual notation of Regge phenomenology, with the dimensionless scattering amplitude $A(s,t)$

$$\begin{aligned}&A(s,t) ~ > \rightarrow [4 \sqrt{\pi }\times 11.09\times 10^{6} \mathrm{e}^{-3.14|t|}]\nonumber \\&\quad \times [1+0.061 \log (s/1 \mathrm{TeV^2})] \times (s/1 \mathrm{TeV^2})^{1-0.19 |t|}, \end{aligned}$$

(38)

where $|t|$ is in $\text{ GeV }^2$ and $\sqrt{s}$ in TeV, with a $t$-dependent residue and a trajectory with intercept 1 and angular coefficient 0.19 GeV$^{-2}$. The log term corresponds to a double pole, arising from the derivative with respect to the trajectory [9].

These expressions give a high precision representation for all data [1–3, 5, 12], with coherent and reliable identification of the real and imaginary amplitudes. Properties and consequences for the energy range above 1 TeV are discussed in the present paper, with particular attention to the experimental LHC energies. Cosmic ray energies up to $\sqrt{s} =$ 100 TeV and asymptotic behavior have been discussed elsewhere [6].

2.3 Forward amplitudes and associated observables

In the very forward direction, where the elastic pp and p${\bar{\mathrm {p}}}$ scattering amplitudes can be approximated by pure exponential forms, the differential cross section is written

$$\begin{aligned} \frac{\mathrm{d}\sigma }{\mathrm{d}t}&\rightarrow \pi \left( \hbar c\right) ^{2}~~\Big \{\Big [ \frac{\rho \sigma }{4\pi \left( \hbar c\right) ^{2}}~{\mathrm{e}^{B_{R}t/2}+F^{C}(t)\cos {(\alpha \Phi )}\Big ]^{2}}\nonumber \\&+\,\Big [\frac{\sigma }{4\pi \left( \hbar c\right) ^{2}}~{\mathrm{e} ^{B_{I}t/2}+F^{C}(t)\sin {(\alpha \Phi )}\Big ]^{2}\Big \},} \end{aligned}$$

(39)

where $t\equiv -|t|$ and we must allow different values for the slopes $B_{I}$ and $B_{R}$ of the imaginary and real amplitudes. With $\sigma$ in millibarns and $|t|$ in GeV$^{2}$, we have $\left( \hbar c\right) ^{2}~=~0.3894$. Since we work with $B_{R}\ne B_{I}$, treatment of the Coulomb interference requires a more general expression for the Coulomb phase, which has been developed before [3].

The limits of the amplitudes for small $|t|$ give the total cross section $\sigma$, the ratio $\rho$ of the real to imaginary amplitudes, and the slopes $B_{R,I}$ at $t=0$ through

$$\begin{aligned} \sigma (s)&= 4\sqrt{\pi } \left( \hbar c\right) ^{2}~[\alpha _{I}(s)+\lambda _{I}(s)], \end{aligned}$$

(40)

$$\begin{aligned} \rho (s)&= \frac{T_{R}^{N}(s,t=0)}{T_{I}^{N}(s,t=0)}=\frac{\alpha _{R}(s)+ \lambda _{R}(s)}{\alpha _{I}(s)+\lambda _{I}(s)}, \end{aligned}$$

(41)

$$\begin{aligned} B_{K}(s)&= \frac{2}{T_{K}^{N}(s,t)}\frac{\mathrm{d}T_{K}^{N}(s,t)}{\mathrm{d}t}\Big |_{t=0}=~ \frac{2}{\alpha _{K}(s)+\lambda _{K}(s)}\nonumber \\&\times \,\Big [\alpha _{K}(s)\beta _{K}(s)+\frac{1}{8}\lambda _{K}(s)a_{0}\Big (6\gamma _{K}(s)+7\Big )\Big ]. \nonumber \\ \end{aligned}$$

(42)

Using the energy dependences given in Eqs. (29–36) we can write the practical expressions for the four quantities

$$\begin{aligned}&\sigma (s)=69.3286+12.6800\log \sqrt{s}+1.2273\log ^{2}\sqrt{s}\,\end{aligned}$$

(43)

$$\begin{aligned}&B_{I}(s)=16.2472+1.53921\log \sqrt{s}+0.174759\log ^{2}\sqrt{s}\,\end{aligned}$$

(44)

$$\begin{aligned}&B_{R}(s)=22.835+2.862\log \sqrt{s}+0.329721\log ^{2}\sqrt{s}\, \end{aligned}$$

(45)

and

$$\begin{aligned} \rho (s)=\frac{3.528018+0.7856088\log \sqrt{s}}{25.11358+4.59321\log \sqrt{s} +0.444594\log ^{2}\sqrt{s}}, \end{aligned}$$

(46)

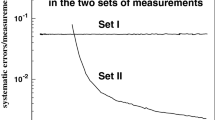
where $\sqrt{s}$ is in TeV, $\sigma$ in millibarns, $B_{I}$ and $B_{R}$ are in $\text{ GeV }^{-2}$; $\rho$ is dimensionless, passes through a maximum at about 1.8 TeV, and decreases at higher energies, with asymptotic value zero. The ratio $B_{R}/B_{I}$ is always larger than one, as expected from the dispersion relations [13]. The ratio $B_{R}/B_{I}$ as a function of the energy is shown in Fig. 1. There is a finite asymptotic value $B_{R}/B_{I}\rightarrow 1.887$.

Fig. 1

The slopes of real and imaginary amplitudes vary with the energy with a $\log ^{2}$ dependence as given by Eqs. (44) and (45). At all energies $B_{R}>B_{I}$, as predicted by the dispersion relations [13]. In the figure, the ratio $B_{R}/B_{I}$ is plotted as a function of the energy, indicating the finite asymptotic limit

This treatment of pp forward scattering has been applied to the calculation of p-air cross sections measured in Extended Air Showers studies in cosmic ray experiments. Covering the range from 1 to 100 TeV in pp energies, our input amplitudes are used as a basis of Glauber calculations, giving a good description [6] of all cosmic ray data.

3 Observables in the range from 1.8 to 14 TeV

3.1 Differential cross sections and amplitudes

In Fig. 2 we show the predictions for $\mathrm{d}\sigma /\mathrm{d}t$ for the LHC energies 2.76, 8, 13, and 14 TeV. We first observe that the dip and the bump peak displace to the left as the energy increases and in this figure these displacements follow almost straight lines, as indicated by marks with black circles and open squares. For the sake of convenience, we list the values of parameters for these energies in Table 1, where $\gamma _{I}, \lambda _{I}, \alpha _{R}$ and $\gamma _{R}$ are substituted by more commonly used quantities $\sigma ,\rho$ together with the slope parameters $B_{I}$ and $B_{R}$. In Table 2 we show the values of several quantities obtained in the numerical calculation of the amplitudes and of observables in the elastic process. Some characteristic features are exhibited below in plots.

Fig. 2

The lines show the values of $\mathrm{d}\sigma /\mathrm{d}t$ obtained for energies of LHC experiments. The 7 TeV case, presented before [3], is obviously very close to the 8 TeV curve. The positions of dips and bump peaks at different energies, marked with dots and squares, can be connected with straight lines. The inset shows the low $|t|$ range, with Coulomb interaction effects included

Table 1 Values of parameters that build the amplitudes for all $|t|$, for the energies of LHC pp collisions

Table 2 Some derived quantities that characterize the structure of amplitudes and cross sections: positions of zeros, dip, and $|t|_{\mathrm { peak}}$ at highest point of bump in $\mathrm{d}\sigma /\mathrm{d}t$; ratio $R$ of values of $\mathrm{d}\sigma /\mathrm{d}t$ at $|t|_{\mathrm {peak}}$ and $|t|_{\mathrm { dip}}$; position and height of the inflection; inelastic and integrated elastic cross sections

In Fig. 3 we use the energy $\sqrt{s}=8$ TeV as an example to show the imaginary and real amplitudes $T_I^N(s,t)$, $T_R^N(s,t)$ as functions of $|t|$ as predicted by Eq. (21). For all energies the characteristic features are the two zeros of the real part, and the single zero of the imaginary part appearing in the plotted range (a second zero of $T_I^N$ would appear in a much larger $|t|$, outside experimental visibility). The interplay of the imaginary and real amplitudes at mid values of $|t|$ is responsible for the dip–bump structure of the differential cross section, which was shown before [3] for $\sqrt{ s}=7$ TeV and is exemplified for 8 TeV in the next section. For $|t|\ge 1.5\,\text{ GeV }^2$ the real part becomes dominant, with positive sign. The inset shows the small $|t|$ range, in log scale, normalized to one at $|t|=0$. The straight exponential slopes are shown in dashed lines, with the dramatic difference between the real and imaginary amplitudes. Soon the exact amplitudes leave the straight line and curve down, searching for their respective zeros. As shown in the next section, the consequences for the behavior of $\mathrm{d}\sigma /\mathrm{d}t$ at 8 TeV will be visible for $|t|$ larger than about 0.2 GeV$^2$.

Fig. 3

Plots of the real and imaginary parts of elastic pp scattering amplitude at 8 TeV, as functions of $|t|$. The general behavior is the same for all energies, with one and two zeros respectively for the imaginary and real parts. The behavior for small $|t|$ is shown in the inset, indicating the difference of slopes $B_R$ and $B_I$ at the origin, and the deviations of the exponential forms that occur as $|t|$ increases, each amplitude going towards its zero. A second zero of the imaginary part occurs at much higher $|t|$

The difference in slopes $B_{R}$ and $B_{I}$ that is required by dispersion relations [13] is often neglected. The real part is small for small $|t|$, due to the small value of $\rho$, but it becomes influential or dominant for mid and large $|t|$. The amplitudes must be treated as functions for the whole $|t|$ range. Our unique analytical form connects all regions and controls the behavior both at small and large $|t|$. Thus, for example, the value of $\rho$ is very important for the shape of the dip–bump structure.

The regular energy dependence of the positions of the zeros and of dips and peaks of bumps is shown in Fig. 4. We see that all these characteristic quantities move towards smaller $|t|$ with increasing energy, following forms like

$$\begin{aligned} A+\frac{1}{a+b \log \sqrt{s}+c \log ^2\sqrt{s} }, \end{aligned}$$

(47)

possibly with finite asymptotic limits $A$. Particularly interesting is the displacement of the first real zero $Z_R^{(1)}$, which at very high energies behaves as above, with $A=0$ and $c=0$, according to a theorem by $A$. Martin [14]. This behavior is obviously connected with a fast increase of the slope $B_R$.

Fig. 4

a Positions of the zeros of the amplitudes, and of the dip and peak at the bump of $\mathrm{d}\sigma /\mathrm{d}t$. There appears one zero in the imaginary and two in the real amplitude. A second imaginary zero occurring at very large $|t|$ is outside the physically accessible range. All quantities move towards small values with increasing energies. The dips tend to coincide with the imaginary zero at high energies. The remarkable dip–bump structure in pp scattering occurs in the interval between the imaginary zero and the second real zero. The first real and the imaginary zero move towards smaller $|t|$, indicating the $\log ^2\sqrt{s}$ increase of the real and imaginary slopes. The dots are put to help the connection of values of the quantities for different energies. b There is a regular and fast increase of the ratio $R=[\mathrm{d}\sigma /\mathrm{d}t] \mathrm {peak} /[\mathrm{d}\sigma /\mathrm{d}t] \mathrm {dip}$, with increasing sharpness of the dip–bump structure although the distance $|t|_{\mathrm {peak}}-|t|_{\mathrm {dip}}$ between them varies very little. These symptoms come from the increasing proximity of $|t|_{\mathrm {dip}}$ and $Z_I$, and to the convergence to finite asymptotic limits of both $|t|_{\mathrm {peak}}$ and $|t|_{\mathrm {dip}}$

It is interesting to observe the relative positions of the dip and the peak of the bump in $\mathrm{d}\sigma /\mathrm{d}t$ and the zeros of the imaginary and real parts, shown in Fig. 4. This question has been discussed a long time ago [1, 2]. The figure shows that $Z_I$ and the dip position tend to the (apparently) common finite limit. Dips and peaks are always located between $Z_I$ and $Z_R^{(2)}$. All energy dependences are simple and can easily be parameterized.

It is interesting to note that the ratio between the maximum of the mid-$|t|$ bump (called peak) and the dip minimum

$$\begin{aligned} R=[\mathrm{d}\sigma /\mathrm{d}t]_{\mathrm {peak}}/[\mathrm{d}\sigma /\mathrm{d}t]_{\mathrm {dip}} \end{aligned}$$

(48)

increases with energy rather rapidly (see Fig. 4b), like $\sim \ln ^{2}\sqrt{s}$, while the distance $|t|_{\mathrm {peak}}-|t|_{\mathrm { dip}}$ remains practically constant (Fig. 4a).

In Fig. 5 we plot $\mathrm{d}\sigma /\mathrm{d}t$ for 2.76 and 8 TeV, showing that the characteristic dip–bump structure of $\mathrm{d}\sigma /\mathrm{d}t$ occurs in the interval between the imaginary zero and the second real zero.

Fig. 5

The dip–bump structure in the differential cross section is determined by the interplay of the regularly increasing modulus (magnitude) of the imaginary part and the regularly decreasing modulus (magnitude) of the real part. At all energies both dip and peak of the bump are located between $Z_I$ and $Z_R^{(2)}$. This behavior is shown in this figure for the energies 2.76 and 8 TeV. As the energy increases $|t|_{\mathrm {dip}}$ approaches $Z_I$ from the right to the left. Figure 4 illustrates these properties again, in another way

3.2 Integrated quantities, ratios, and asymptotic limits

The integrated elastic cross section due to the imaginary amplitude can be represented by

$$\begin{aligned} \sigma _{\mathrm {el}}^{I}(s)&= \int _{0}^{\infty }\mathrm{d}t~T_{I}(s,t)^{2}~\mathrm{d}t\nonumber \\&= 15.3366+4.15903\log \sqrt{s}+0.43405\log ^{2}\sqrt{s}, \nonumber \\ \end{aligned}$$

(49)

with $\sqrt{s}$ in TeV and $\sigma _{\mathrm {el}}^{I}(s)$ in mb. The accuracy of this representation is very good, particularly for energies equal and above 7 TeV. The ratio with the total cross section has a finite asymptotic limit at high energies $\sigma _{\mathrm {el}}^{I}/\sigma \rightarrow 0.354$. This result is very important for a geometrical description of pp scattering, as it means that a pp collision does not follow a black disk form at high energies (see below).

For the contribution of the real part to the elastic cross section the quantity that is related to the exponential behavior in the forward direction and that presents a finite asymptotic ratio with $\sigma$ requires an extra factor $1/\rho ^{2}$. We have the representation

$$\begin{aligned}&\frac{1}{\rho ^{2}}\sigma _{\mathrm {el}}^{R}(s)=\frac{1}{\rho ^{2}} \int _{0}^{\infty }\mathrm{d}t~T_{R}(s,t)^{2}~\mathrm{d}t \nonumber \\&\quad =10.2037+2.47691\log \sqrt{s}+0.23108\log ^{2}\sqrt{s}. \end{aligned}$$

(50)

The asymptotic ratio is now $(1/\rho ^{2})(\sigma _{\mathrm {el}}^{R}/\sigma )\rightarrow 0.188$. These ratios participate in the geometric interpretation in $b$-space representations.

The dimensionless ratios

$$\begin{aligned} \sigma /(16\pi B_{K}), K=I, R, \end{aligned}$$

(51)

are related to $\sigma _{\mathrm {el}}^{I}/\sigma$ and $(1/\rho ^{2})\sigma _{\mathrm {el}}^{R}/\sigma$ when the amplitudes are of pure exponential forms with $B_{I}$ and $B_{R}$ slopes. The imaginary part is studied to investigate the occurrence of black disk behavior (assuming zero real part), where the ratios $\sigma _{\mathrm {el}}^{I}/\sigma$ and $\sigma /(16\pi B_{I})$ are both equal to 1/2. As shown in Fig. 6 our solutions lead to values about 1/3 for the imaginary part case, which is a more realistic expectation [15, 16] than the black disk hypothesis.

Fig. 6

Ratio between integrated (imaginary part) elastic cross section and total cross section and ratio between total cross section and imaginary slope as a function of energy. On the RHS, the same for the real sector. The asymptotic limits are approached very slowly: observe the extended energy scale. For each part (imaginary or real) the two kinds of ratio would be equal if the amplitudes were of purely exponential form. We may observe that the ratio of ratios in each sector ($I$ or $R$) is about the same, namely $0.359/0.354 \approx 0.190/0.188 \approx 1.01$

3.3 Geometric scaling and ratio of cross sections

In Fig. 7a, we plot $\mathrm{d}^{2}\sigma _{\mathrm {inel}}/\mathrm{d}\vec {b} ^{2}$ defined in Eq. (14) as a function of $b$ for $\sqrt{s}=$ 2.76 and 14 TeV. The behavior at very high energies ( $\sqrt{s}=10^{4}, 10^{5}$ and $10^{6}$ TeV) is also shown. We clearly see the increase of effective radius of the interaction range with increasing energy. In Fig. 7b, we plot the same quantities with respect to the variable

$$\begin{aligned} x\equiv \frac{b}{\sqrt{\sigma \left( s\right) /2\pi }}. \end{aligned}$$

(52)

This figure shows clearly that there exists a universal function $\xi \left( x\right)$ such that

$$\begin{aligned} \mathrm{d}^{2}\sigma _{\mathrm {inel}}/\mathrm{d}\vec {b}^{2}\rightarrow \xi \left( x\right) \end{aligned}$$

(53)

for $\sqrt{s}\gg 10^{4}$ TeV. An important point is that $\xi \left( x\right)$ is far from the Heaviside step function, rather possessing a considerably diffused surface. In this asymptotic limit, we can safely set $\cos \chi _{R}\rightarrow 1$ so that the total cross section is [5]

$$\begin{aligned} \frac{\mathrm{d}^{2}\sigma \left( s,b\right) }{\mathrm{d}\vec {b}^{2}}\rightarrow 2\left( 1- \sqrt{1-\xi (x)}\right) . \end{aligned}$$

(54)

Note that $0\le \xi \le 1$ means $\left( 1-\xi \right) \le \sqrt{1-\xi },$ so that $\xi \left( x\right) \ge 1-\sqrt{1-\xi \left( x\right) }$ for all $x$ where the equality holds if and only if $\xi =0$ or $\xi =1$. Therefore, whenever the function $\xi$ is different from a sharp-cut Heaviside theta function $\theta \left( 1-x\right) ,\$ we have

$$\begin{aligned} \frac{\int _{0}^{\infty }x~\xi (x)~\mathrm{d}x}{2\int _{0}^{\infty }x~\left( 1-\sqrt{ 1-\xi (x)}\right) ~\mathrm{d}x}>\frac{1}{2}. \end{aligned}$$

(55)

For our amplitudes, as shown in Fig. 7, $\xi$ clearly does not converge to a sharp-cut $\theta \$function, preserving an appreciable diffused surface for asymptotic energies. Therefore, we have

$$\begin{aligned} \frac{\sigma _{\mathrm {inel}}}{\sigma \left( s\right) }>\frac{1}{2}, \end{aligned}$$

(56)

or

$$\begin{aligned} \frac{\sigma _{\mathrm {el}}\left( s\right) }{\sigma \left( s\right) }<\frac{1 }{2}. \end{aligned}$$

(57)

This means that our amplitudes do not show the black disk behavior at very large energies, deviating from the well-known result for a black disk $\sigma _{\mathrm {el}}/\sigma \left( s\right) \rightarrow 1/2$. From the above discussion, we can also easily see that the more diffused surface $\xi \left( x\right)$ has, the less the ratio $\sigma _{\mathrm {el}}\left( s\right) /\sigma \left( s\right)$ becomes. In fact, for our case this ratio is close to $1/3$ (see also [15, 16]). Note that this is a somewhat different scenario compared to [17, 18], where $\xi \left( x\right)$ would not have surface diffuseness.

Fig. 7

a Plots of $\mathrm{d}^{2} \sigma _{\mathrm {inel}}/\mathrm{d}\vec {b}^{2}$ as a function of $b$ for $\sqrt{s}=$ 2.76, 14 TeV and for three very high energies indicated in this figure; b the same quantity plotted as a function of the scaled variable $x=b/\sqrt{\sigma \left( s\right) /2 \pi }$, showing the convergence to a unique function, $\xi \left( x\right)$, which has a finite surface diffuseness

4 Comparison with data and predictions

Our description [3] of the elastic scattering data at 7 TeV from the TOTEM Collaboration [4] reproduces $N$ = 165 points in $\mathrm{d}\sigma /\mathrm{d}t$ with an impressive squared average relative deviation $<\chi ^2>=0.31$. Characteristic quantities at this energy, shown in Tables 1 and 2, are $\sigma =98.65$ mb, $\sigma _{\mathrm {el}}=25.39$ mb, $B=19.90$ GeV$^{-2}$, which compare extremely well with the values published by TOTEM [4], $\sigma =98.6 \pm 2.2$ mb, $\sigma _{ \mathrm {el}}=25.4 \pm 1.1$ mb, $B=19.9 \pm 0.3$ GeV$^{-2}$.

After the successful description of the 7 TeV data [3], we now present comparison and predictions for other LHC energies.

4.1 Inelastic and total cross sections

For the inelastic cross section we assume the difference $\sigma _{\mathrm { inel}}=\sigma -\sigma _{\mathrm {el}}$ and then we have 73.26 mb at 7 TeV. Published values of the TOTEM Collaboration using different methods are $73.15 \pm 1.26$ [4], $73.7 \pm 3.4$ [19], and $72.9 \pm 1.5$ [20]. The ALICE Collaboration [21] gives $\sigma _{\mathrm {inel}}= 73.2 \pm 5.3$ mb, and the ATLAS Collaboration $\sigma _{\mathrm {inel}}= 69.4 \pm 2.4 \pm 6.9$ mb [22]. We are not able to understand the CMS results [23] in terms of pure $\sigma _{\mathrm {inel}}$ due to non-informed missing contributions. In these measurements there are extrapolations to using Monte Carlo models to include diffractive events of low mass. Of course all these results are compatible with our calculations.

A measurement to be compared with our predictions is the $\sqrt{ s}=2.76$ TeV value of ALICE Collaboration, which gives $\sigma _{\mathrm {inel}} = 62.8 \pm 4.2$ mb, while our tables give the compatible value 63.11 mb.

The analysis of compatibility for the 1.8 TeV measurements of $\sigma _{ \mathrm {inel}}$ by CDF and E811 in Fermilab [24] suggests the value $(1+\rho ^2)\sigma _\mathrm{inel}=(60.3 \pm 2.3$ mb, which with our $\rho$ value gives $\sigma _\mathrm{inel}=(59.1 \pm 2.3$ mb. Our table gives 58.89 mb for 1.8 TeV, once more in very good agreement (Table 3).

Table 3 Characteristic values of $b$-space amplitudes and eikonal functions. These quantities are related to the saturation of the unitarity bounds. Thus $\widetilde{T}_I(b=0)$ approaches the bound $\sqrt{\pi }=1.77$ as $\sqrt{s}$ increases

Finally, at 57 TeV the Auger Cosmic Ray experiment [25], using other models for the pp input, evaluates $\sigma _{\mathrm {inel}} = 92 \pm 14.8$ mb, while our extrapolation gives 101 mb. We have discussed this measurement [6] together with other CR extended air showers (EAS) experiments, using our amplitudes as inputs and a basic Glauber method to connect pp and p-air processes. Our calculation reproduces well all CR data for p-air cross sections with $\sqrt{s}$ (in the pp system) up to 100 TeV.

For 8 TeV we have predictions $\sigma =101.00$ mb, $\sigma _{\mathrm {el} }=26.18$ mb, $\sigma _{\mathrm {inel}}=74.82$ mb , $\sigma _{\mathrm {el} }/\sigma =0.26$ shown in the tables. The measurements by TOTEM [26] give for the same quantities $\sigma =101.7 \pm 2.9$ mb, $\sigma _{\mathrm {el }}=27.1 \pm 1.4$ mb, $\sigma _{\mathrm {inel}}=74.7 \pm 1.7$ mb, $\sigma _{ \mathrm {el}}/\sigma =0.266\pm 0.006$. Of course these numbers are very encouraging, indicating also good expectations for $\mathrm{d}\sigma /\mathrm{d}t$ at this energy.

The data and our curve for $\sigma _{\mathrm {inel}}(s)$ are shown in Fig. 8. All this information shows that our formulas for the energy dependence of $\sigma (s)$ and $\sigma _{\mathrm {inel}}(s)$ in pp scattering work very well.

Fig. 8

Our calculations for pp inelastic cross sections and the data above $\sqrt{s}= 1$ TeV, which cover the energies 1.8 TeV [24], 2.76 TeV [21], 7 TeV [4, 19–22], 8 TeV [26], and 57 TeV [25]

4.2 Expected data for $\mathrm{d}\sigma /\mathrm{d}t$ at 8 TeV

The preliminary data for $\mathrm{d}\sigma /\mathrm{d}t$ at 8 TeV, shown in talks by members of the TOTEM Collaboration [27, 28], are encouraging for the application of our method of analysis. We recall that in the treatment of the 7 TeV data, we obtained precise description, with average $\langle \chi ^2\rangle = 0.34$ for 165 data points in the whole $|t|$ interval of measurements.

In Fig. 9 we shown our calculation for $\mathrm{d}\sigma /\mathrm{d}t$ covering the whole $|t|$ range of the preliminary information, using the amplitudes defined in Sect. 3. The characteristic features of the forward peak and of the dip–bump structure are expected to represent accurately the angular dependence. Numerical values for characteristic features are given in Tables 1 and 2.

Fig. 9

Predicted representation for $\mathrm{d}\sigma /\mathrm{d}t$ in the whole $|t|$ range of observations at 8 TeV made in LHC by the TOTEM Collaboration [27, 28]

This is the description of the global $\mathrm{d}\sigma /\mathrm{d}t$ data at 8 TeV, which promises to be more complete and regular than the 7 TeV data, except for not reaching larger $|t|$ values. In the following we discuss the forward region in more detail.

In Fig. 10 we plot the calculations in the small $|t|$ range, including the influence of the Coulomb phase [3]. The calculation with the Coulomb phase put equal to zero is represented by the dashed line, showing that its influence is small. Our specific calculation of the Coulomb phase takes into account the difference in values of the $B_R$ and $B_I$ slopes. Other calculations for the interference phase [29, 30] also show that its influence is small, reducing $\mathrm{d}\sigma /\mathrm{d}t$ by a few percent.

Fig. 10

Calculation of $\mathrm{d}\sigma /\mathrm{d}t$ in the forward range at 8 TeV. The solid lines correspond to the full calculation with our amplitudes. a In the LHS a $\log |t|$ scale is used to represent in detail the forward range; the dashed line is obtained with Coulomb phase put equal to zero; the dotted line represents the hadronic interaction. b In the RHS the dashed line represents the calculation with pure exponential amplitudes, with the real and imaginary parts entering with their corresponding slopes; the dotted line shows the usual description of the foreword peak in the form $\mathrm{d}\sigma /\mathrm{d}t= \mathrm{d}\sigma /\mathrm{d}t|_{t=0} ~ \exp {(-B|t|)}$

Our values for $B_I$ and $B_R$ given in Table 1 lead to the $\mathrm{d}\sigma /\mathrm{d}t$ effective slope at 8 TeV,

$$\begin{aligned} B=\frac{B_I+\rho ^2 B_R}{1+\rho ^2}, \end{aligned}$$

(58)

equal to $B=20.405~\text{ GeV }^{-2}$.

Our predictions seem to be in accordance with the eye-guided reading of the preliminary data of $\mathrm{d}\sigma /\mathrm{d}t$ that appear in presentations of the TOTEM group in workshops, at least at the qualitative level. At 7 TeV our expressions perform extremely well when compared to the published experimental information, and we expect that the same will happen at 8, 13, and 14 TeV.

4.3 Other models

The complete identification of the real and imaginary parts of the complex pp elastic amplitude is fundamental for the knowledge of the dynamics of the collision, being an essential bridge between the observed quantities and fundamental QCD dynamical processes. Our determination, though consistent and complete, depends on the analytical forms used for the representation. It is thus important to compare our predictions with the results obtained with other input assumptions.

The important Yukawa-like behavior of the amplitudes in $b$-space based on the behavior of the loop-loop interaction for large $b$ in the SVM, which is incorporated in our input amplitudes in Eq. (2), is confirmed in a recent treatment of the pp interaction through Wilson correlation functions [31].

The representation of amplitudes in $b$-space from the ISR to the SPS energies shows at $b=0$ a slow increase with the energy [32, 33], remaining below saturation, which seems to be approached asymptotically, as can be seen in the present work for the LHC energies and also in studies at higher cosmic ray energies [6]. With parameters adjusted to describe the energy dependence in the 23–546 GeV range [34], the model predicts characteristic quantities of pp forward scattering for the range 7–14 TeV, with results for the total cross section and the slope parameter that agree very well with the numbers given in Table 1, and in particular with the TOTEM values at 7 TeV.

The model proposed by Bourrely, Soffer, and Wu (hereafter called the BSW model) [35] gives explicitly the full $s,t$ dependence of the elastic scattering amplitudes and is appropriate for the comparison with our results. Important similarities and differences were discussed in detail in the 7 TeV case [3], and we now compare the predictions for 14 TeV. Figure 11 shows that the dip–bump structure occurs in similar $|t|$ regions, but there is a difference in $\mathrm{d}\sigma /\mathrm{d}t$ by a factor larger than 2. This difference results from the larger magnitudes (with negative signs) of both real and imaginary parts in the BSW model, as can be observed in the second part of the figure. The second real zero occurs for a larger $|t|$ in the BSW calculation.

Fig. 11

Calculation of $\mathrm{d}\sigma /\mathrm{d}t$ at 14 TeV compared with the predictions of the BSW model. The solid lines correspond to the full calculations with our amplitudes. a In the LHS are shown the differential cross sections. b In the RHS are shown the real and imaginary parts of the amplitudes

To raise interest on measurements at higher $|t|$, in Fig. 12 the 14 TeV plot is extended to very large $|t|$ pointing out the possible smooth connection with the supposedly universal tail at 27.4 GeV [36]. We recall the situation with similar plot drawn in the 7 TeV case [3], where the measurements reached larger $|t| \approx 2.5 \text{ GeV }^2$ and the conjecture of the universality of the tail at such high energy encounters motivation. The broad dip in the region of 6 GeV$^2$ in the BSW calculation is due to a zero in its imaginary amplitude, as was also indicated at 7 TeV.

Fig. 12

Calculations predicting $\mathrm{d}\sigma /\mathrm{d}t$ for large $|t|$ at 14 TeV, including the perturbative tail term in our real amplitude, plotted with the data [36] at 27.4 GeV for very large $|t|$

The structure of the pp and ${\mathrm{p}{\bar{\mathrm{p}}}}$ interactions studied by $O$. Selyugin [37], based on the analysis of different sets of Parton distribution functions and introducing a $t$-dependence in the generalized Parton distributions, gives a good representation of $\mathrm{d}\sigma /\mathrm{d}t$ data in large energy range, up to the LHC Totem experiment at 7 TeV. We include in Fig. 11 the $t$ dependences of $\mathrm{d}\sigma /\mathrm{d}t$ and the amplitudes in this model for 14 TeV. It is important to observe the similarity with our results in the forms of the amplitudes, which differ essentially only in the real part for large $|t|$, with different locations of the second zero. The similarity, which must be investigated at all energies, reinforces the expectation of the present work, that is, to find a realistic and accurate disentanglement of the elastic amplitudes.

Recently, Csörgö et al. applied the multiple diffraction calculation of the Glauber–Valesco Model [38] to the TOTEM results for 7 TeV and fitted the parameters of the partonic charge form factor, obtaining a good representation for the scattering cross section, including the dip–bump structure [39]. Parametrizing the partonic distribution function for each energy, the Glauber–Valesco model also describes the lower energy data from ISR and FNAL. The model leads to the conclusion that at LHC energies the pp interaction is not that of sharp-edged black-discs, but it presents a considerable tail in the profile function [40, 41]. These observations are essentially the same as in predictions of our work [3, 5, 6].

In addition, more detailed measurements of the inelastic pp cross section in LHC experiments [42–44], especially of diffractive-dissociation processes (DD), yield very important information on the dynamics of the interaction, as discussed by Lipari and Lusignoli [45]. These studies and ours are complementary in the sense that, while our approach is based on the field theoretical model of interaction between two geometrical objects, their approach applies the multiple diffractive model and introduces parametrizations of the partonic form factor of the proton. A detailed comparison of the two approaches, together with the identification of the presence of diffraction in the inelastic part in our formalism, will give more precise insight on the physical roles behind the features of our description. Studies in this direction are under investigation.

5 Final remarks and comments

In this paper we present predictions for observables of pp elastic scattering above $\sqrt{s}=1$ TeV up to coming LHC energies in terms of analytic forms for the real and imaginary parts of the complex scattering amplitude. The representation proposes a separate identification of the two parts, which are both constructed respecting unitarity and dispersion relation constraints and precisely determine their influences in the observed quantities.

The amplitudes have simple analytical forms, which can be directly evaluated with few operations with elementary functions. The shape of the dip–bump behavior results from a delicate interplay of the imaginary and real amplitudes. All intervening quantities and derived properties are connected by smooth energy dependences.

The zeros of the real and imaginary parts have very regular displacements, converging to finite limits as the energy increases. There is a remarkable connection between the positions of the zeros and positions and heights of dips and bumps and inflections in $\mathrm{d}\sigma /\mathrm{d}t$.

The slopes $B_I$ and $B_R$ at the origin, with their characteristic difference in values, together with the ratio $\rho$, are essential quantities that participate in the definition, through the unique analytical forms of the amplitudes, of the properties of the observed $\mathrm{d}\sigma /\mathrm{d}t$ in the whole $t$ range. Their values are thus fixed with high accuracy. It is very important that the slopes show a quadratic dependence in $\log {s}$, instead of the linear dependence suggested by Regge phenomenology.

The integrated elastic cross sections are evaluated in their separate parts, obtained from the real and imaginary amplitudes, and they are also represented by simple parabolic forms in $\log {s}$.

The properties of ratios (with respect to the total cross section) of slopes and of integrated elastic cross sections, which tend to finite asymptotic limits, are studied, showing that the hypothesis of a black disk limit in the behavior of the pp interaction seems to be excluded by phenomenology.

In Sect. 4 we give predictions, presented in Tables 1 and 2, in equations and in figures. Taking into account previous publications at 1.8 and 7 TeV, the present paper gives explicit predictions of the cross sections at 2.76, 8, 13, and 14 TeV, with no free numbers. More precise future data may confirm our predictions more firmly.

We also discuss the geometrical interpretation of our amplitudes, showing that the effective interaction radius in $b$-space increases with the energy. Our amplitudes obey a geometric scaling in asymptotic energies and indicate that the profile function $\mathrm{d}^{2}\sigma _{\mathrm {inel}}/\mathrm{d}^{2}\vec {b}$ tends to a universal (energy independent) function with respect to the scaling variable, $x\sim b/\sqrt{\sigma }$. This universal function exhibits a considerable diffused surface, indicating a scenario different from the commonly accepted black disk. At LHC energies, the saturation seems to start (the central value of $\mathrm{d}^{2}\sigma _{\mathrm {inel}}/\mathrm{d}^{2}\vec {b}$ is almost unity), but the asymptotic profile is still far and only can be reached for $\sqrt{s}>10^{4}$ TeV. The connection between the diffused surface of long range and inelastic diffractive processes will be an interesting line of investigation.

We believe that our analytic representation of the scattering amplitudes will serve as important guidance, not only for the future measurements in LHC, but also for a theoretical understanding of the intermediate region of the partonic saturation phenomena.