Searching for extra dimensions in Large Hadron Collider (LHC) experiments via a Kaluza–Klein (KK) graviton mode is an extensive area of collider research. In particular the recent ATLAS experiment put some stringent lower bound on the lightest KK graviton mass in the context of Randall–Sundrum warped geometry model via the dilepton decay of the KK graviton. The Randall–Sundrum model has become phenomenologically popular because of its promise to resolve the fine-tuning problem in connection with the Higgs mass without introducing any hierarchical parameter. This model is defined on a slice of \(\mathbf{AdS_{5}}\) with the bulk being an Einstein–anti-de Sitter spacetime. Recent conflict between the ATLAS data and Randall–Sundrum model in estimating the lightest KK graviton mass motivate us here to extend the bulk beyond Einstein–anti-de Sitter to a string loop corrected Gauss–Bonnet anti-de Sitter space and explore the graviton search experiment again to look for a possible stringy signature in collider physics.

In this work we have first explored the phenomenological features of string modified warped geometry in the presence of 5D Gauss–Bonnet coupling and gravidilaton coupling in a 5D bulk. Here the 5D warped geometry model has been proposed by making use of the following sets of assumptions as building blocks:

  • The Einstein gravity sector is modified by the introduction of a Gauss–Bonnet correction [1–11] and a string two-loop correction [4–6] originating from the holographic dual \(\mathbf{CFT_{4}}\) disk amplitude in type II B string theory or its low energy supergravity theory [12–15].

  • The well-known \(\mathbf{S^{1}/Z_{2}}\) orbifold compactification is considered.

  • We considered that the system is embedded in 5D AdS bulk where the background warped metric has a Randall–Sundrum (RS) like structure with \(\mathbf{AdS_{5}\times S^{5}}\) geometry [16, 17].

  • The compactification radius/modulus is assumed to be independent of four-dimensional coordinates (by Poincaré invariance) as well as an extra-dimensional coordinate [6].

  • The strength of the gravidilaton interaction is determined by dilaton degrees of freedom which are assumed to be confined within the bulk.

  • Additionally, the dilaton field also interacts with the 5D bulk cosmological constant \(\Lambda _{5}\) via dilaton coupling.

  • The Higgs field is localized at the visible brane and the hierarchy problem is resolved via Planck to TeV scale warping.

  • The modulus can be stabilized by introducing a scalar in the \(\mathbf{AdS_{5}}\) bulk without any fine-tuning following the Goldberger–Wise mechanism [7, 18–20].

  • It is assumed that the requirement of the solution of the gauge hierarchy problem (or equivalently naturalness problem/fine-tuning problem) is still obeyed as this resolution was one of the main goals of involving such warped geometry model in the perturbative limit of our proposed setup.

  • Additionally while determining the value of the model parameters from the proposed setup we also require that the bulk curvature is less than the five-dimensional Planck scale \(M_{5}\) so that the classical solution can be trusted [21–23].

In the present article first we compute the warping solution in the presence of 5D Gauss–Bonnet as well as gravidilaton coupling and the two-loop higher genus string loop correction. Further using the solution we have discussed the detailed phenomenological features of the lightest Kaluza–Klein graviton mass in the light of the constraint obtained from the ATLAS dilepton search. We further compare our results with the results obtained from the well-known Randall–Sundrum model and comment on the present status of both of them in the light of present collider constraints. In this analysis we use the combined phenomenological bounds on Gauss–Bonnet coupling \(\alpha _{5}\) obtained from Higgs diphoton and dilepton decay channels [24] and from Higgs mass from the ATLAS [25] and CMS [26] data within \(5\sigma \) C.L. This bound lies below the upper bound of the viscosity–entropy ratio [27] and satisfies the unitarity bound [27–33] on the GB coupling. We have also discussed the explicit dependence and the phenomenological feature of the lightest Kaluza–Klein graviton mass on the 5D Gauss–Bonnet coupling, gravidilaton coupling and the two-loop higher genus string loop correction by scanning our analysis throughout the allowed parameter space in the perturbative regime of the proposed setup.

We start our discussion with the following 5D action of the two brane warped geometry model given by [6]:

$$\begin{aligned} \displaystyle S&= \int d^{5}x \left[ \sqrt{-g_{(5)}}\left\{ \frac{M^{3}_{5}}{2}R_{(5)}+\frac{\alpha _{5}M_{5}}{2}(1-A_{1}e^{\theta _{1}\phi (y)})\right. \right. \nonumber \\&\times \left[ R^{ABCD(5)}R^{(5)}_{ABCD}-4R^{AB(5)}R^{(5)}_{AB}+R^{2}_{(5)}\right] \nonumber \\&\left. \displaystyle +\,\frac{g^{AB(5)}}{2}\partial _{A}\phi (y)\partial _{B}\phi (y)-2\Lambda _{5}e^{\theta _{2}\phi (y)}\right\} \nonumber \\&\left. +\,\displaystyle \sum ^{2}_{i=1}\sqrt{-g^{(i)}_{(5)}}\left[ \mathcal{L}^{field}_{i}-V_{i}\right] \delta (y-y_{i})\right] \end{aligned}$$
(1)

with \(A,B,C,D=0,1,2,3,4\) (extra dimension) and a conformal two-loop string coupling constant \(A_{1}\). Here \(i\) signifies the brane index, \(i=1\ (\text {hidden})\), \(2(\text {visible})\), and \(\mathcal{L}^{field}_{i}\) is the Lagrangian for the fields on the \(i\)th brane where the \(i\)th brane tension is \(V_{i}\) and \(\phi (y)\) represents the dilaton field which is dynamical in the bulk with respect to the extra-dimensional coordinate ‘y’. The background metric describing a slice of the \(\mathbf{AdS_{5}}\) is given by

$$\begin{aligned} \displaystyle ds^{2}_{5}=g_{AB}dx^{A}dx^{B}=e^{-2A(y)}\eta _{\alpha \beta }dx^{\alpha }dx^{\beta }+r^{2}_{c}dy^{2} \end{aligned}$$
(2)

where \(r_{c}\) is the dimensionless quantity in Planck units representing the compactification radius of the extra dimension. Here the orbifold points are \(y_{i}=[0,\pi ]\) and the periodic boundary condition is imposed in the closed interval \(-\pi \le y\le \pi \).

Varying the action stated in Eq. (1) and neglecting the back reaction of all the other brane/bulk fields except gravity and the dilaton, the five-dimensional bulk Einstein equation turns out to be

$$\begin{aligned}&\displaystyle \sqrt{-g_{(5)}}\left[ G^{(5)}_{AB}+\frac{\alpha _{5}}{M^{2}_{5}}\left( 1-A_{1}e^{\theta _{1}\phi (y)}\right) H^{(5)}_{AB}\right] \nonumber \\&\quad =-\frac{e^{\theta _{2}\phi (y)}}{M^{3}_{5}}\left[ \Lambda _{5} \sqrt{-g_{(5)}}g^{(5)}_{AB}+\sum ^{2}_{i=1}V_{i}\sqrt{-g^{(i)}_{(5)}} g^{(i)}_{\alpha \beta }\delta ^{\alpha }_{A}\delta ^{\beta }_{B}\delta (y-y_{i})\right] \nonumber \\ \end{aligned}$$
(3)

where the five-dimensional Einstein tensor and the Gauss–Bonnet tensor are given by

$$\begin{aligned} \begin{array}{llll} G^{(5)}_{AB}=\left[ R^{(5)}_{AB}-\frac{1}{2}g^{(5)}_{AB}R_{(5)}\right] , \end{array} \end{aligned}$$
(4)
$$\begin{aligned}&H^{(5)}_{AB}=2R^{(5)}_{ACDE}R_{B}^{CDE(5)}-4R_{ACBD}^{(5)}R^{CD(5)}\nonumber \\&\qquad \qquad -\,4R_{AC}^{(5)}R_{B}^{C(5)}+2R^{(5)}R_{AB}^{(5)}-\frac{1}{2}g^{(5)}_{AB}\nonumber \\&\qquad \qquad \times \left( R^{ABCD(5)}R^{(5)}_{ABCD}\!-\!4R^{AB(5)}R^{(5)}_{AB}\!+\!R^{2}_{(5)}\right) . \end{aligned}$$
(5)

Similarly varying Eq. (1) with respect to the dilaton field the gravidilaton equation of motion turns out to be

$$\begin{aligned}&\displaystyle \frac{\theta _{2}}{M^{2}_{5}}\sum ^{2}_{i=1}V_{i}\sqrt{-g^{(i)}_{(5)}}e^{\theta _{2}\phi (y)}\delta (y-y_{i}) \nonumber \\&\quad \!=\!\sqrt{\!-g_{(5)}}\left\{ \!\alpha _{5}A_{1}\theta _{1}\left[ R^{ABCD(5)}R^{(5)}_{ABCD}\!-\!4R^{AB(5)}R^{(5)}_{AB}\!+\!R^{2}_{(5)}\right] \right. \nonumber \\&\qquad \left. \displaystyle +\,2\frac{\Lambda _{(5)}}{M^{2}_{5}}\theta _{2}e^{\theta _{2}\phi (y)}+\frac{\Box _{(5)} \phi (y)}{M_{5}}\right\} \end{aligned}$$
(6)

where the five-dimensional D’Alembertian operator is defined as

$$\begin{aligned} \Box _{(5)}\phi (y)=\frac{1}{\sqrt{-g_{(5)}}}\partial _{A}\left( \sqrt{-g_{(5)}}\partial ^{A}\phi (y)\right) . \end{aligned}$$
(7)

To solve Eq. (3) and Eq. (6) we assume that the dilaton is weakly coupled to gravity (weak coupling \(\theta _{1}\)) and the bulk cosmological constant (weak coupling \(\theta _{2}\)) since the Gauss–Bonnet coupling is an outcome of perturbative correction to gravity at the quadratic order. Now including the well-known \(\mathbf{Z_{2}}\) orbifolding symmetry at the orbifold points, \(y_{i}=[0,\pi ]\), for perturbative regime of solution due to the presence of very weak couplings \(\theta _{1}\), \(\theta _{2}\) and \(\alpha _{(5)}\) we can neglect the contribution from first two terms in the right hand side of Eq. (6) in the bulk. The contribution from the left hand side in Eq. (6) automatically vanishes within bulk. Finally we are left with only the last term in the right hand side of Eq. (6) from which we get the following solution of the dilaton degrees of freedom within the bulk [6]:

$$\begin{aligned} \displaystyle \phi (y)=c_{1}|y|+c_{2} \end{aligned}$$
(8)

where \(c_{1}\) and \(c_{2}\) are integration constants, to be determined from the value of \(\phi (y)\) at the boundaries. We write the dimensionless exponent of the dilaton factors by substituting Eq. (8) at the orbifold point \(y_{i}=\pi \):

$$\begin{aligned} \begin{aligned}&\displaystyle \chi _{1}=\theta _{1}\phi (\pi )=\theta _{1}(c_{1}|\pi |+c_{2}),\\&\displaystyle \chi _{2}=\theta _{2}\phi (\pi )=\theta _{2}(c_{1}|\pi |+c_{2}), \end{aligned} \end{aligned}$$
(9)

where we redefine the exponents by using the symbols \(\chi _{1}\) and \(\chi _{2}\). In the present context we have chosen that the two different dilaton couplings are connected through \(\theta _{1}=-\theta _{2}\), for which we have

$$\begin{aligned} \displaystyle \chi _{1}=-\chi _{2}=\theta _{1}(c_{1}|\pi |+c_{2}). \end{aligned}$$
(10)

For numerical estimations we take the dilation couplings \(\theta _{1},\theta _{2}\) to be small to keep them within the perturbative regime of the solution and we set the arbitrary integration constants \(c_{1},c_{2}\) to a desired value for which the dimensionless exponents of the dilaton factors are fixed at

$$\begin{aligned} \lim _{\theta _{1}\rightarrow weak}e^{-\chi _{1}}=\lim _{\theta _{1}\rightarrow weak} e^{\chi _{2}}=e^{11}. \end{aligned}$$
(11)

Such a value of the dimensionless exponent of the dilaton factor produces a large enhancement even for a small value of the dilaton coupling parameters \(\theta _{1},\theta _{2}\) and moderate values for \(\phi (0)\) and \(\phi (\pi )\). In our subsequent calculation this enhancement factor will play a significant role. As we will see later such a choice is inspired by the requirement of Planck to TeV scale warping as well as to keep the mass of the first excited state of the Kaluza–Klein mode graviton above the bound set by LHC, which is \(1.01\) TeV, as can be seen from Table 1. Thus this choice sets a bound on the dilaton coupling consistent with the LHC constraint.

Table 1 Comparative study between the lower limit of the lightest Kaluza–Klein graviton mass for the \(n=1\) mode from the proposed theoretical model, the well-known Randall–Sundrum (RS) model, and the LHC ATLAS dilepton search in 7 TeV proton–proton collisions. To study the outcome from our proposed setup we fix the model parameters as follows: Gauss–Bonnet coupling \(\alpha _{5}=5\times 10^{-7}\) (which is consistent with the solar system constraint [41], combined constraint from the Higgs mass and favored decay channels \(H\rightarrow (\gamma \gamma ,\tau \bar{\tau })\) [24] using ATLAS [25] and CMS [26] data), and string two-loop correction \(A_{1}=0.05\) with \(M_{Pl}\approx 10^{19}GeV\) and Higgs mass \(m_{H}=125\) GeV (within the \(5\sigma \) statistical C.L. of ATLAS and CMS). Throughout the analysis additionally we have maintained another constraint between the gravidilaton coupling and the dilaton coupling with the 5D cosmological constant in AdS spacetime, \(\theta _{2}=-\theta _{1}\). This implies at the leading order approximation \(\theta _{2}\phi (\pi )=-\theta _{1}\phi (\pi )=11\) at the visible brane
Full size table

In the presence of a dilaton the solution of the five-dimensional bulk Einstein–Gauss–Bonnet equation of motion at leading order in the GB coupling (\(\alpha _{5}\)) turns out to be [6]

$$\begin{aligned}&A(y)=k_{\pm }r_{c}|y|\nonumber \\&\quad \!=\!\sqrt{\frac{3M^{2}_{5}}{16\alpha _{5}(1\!-\!A_{1}e^{\theta _{1}\phi (y)})} \left[ 1\!\pm \!\sqrt{\left( 1\!+\!\frac{4\alpha _{5}(1\!-\!A_{1}e^{\theta _{1}\phi (y)}) \Lambda _{5}e^{\theta _{2}\phi (y)}}{9M^{5}_{5}}\right) }\right] }r_{c}|y|.\nonumber \\ \end{aligned}$$
(12)

Also the localized brane tension can be computed as

$$\begin{aligned} \displaystyle V^{\pm }_{2}&= -V^{\mp }_{1}=\pm 24 k_{\pm }M^{3}_{(5)}e^{-\theta _{2}\phi (y)}\nonumber \\&\times \left[ 1-\frac{\alpha _{5} \left( 1-A_{1}e^{\theta _{1}\phi (y)}\right) }{3M^{2}_{5}}k^{2}_{\pm }r^{2}_{c}\right] . \end{aligned}$$
(13)

where the brane tensions \(V_{1}\) and \(V_{2}\) are localized at the position of the orbifold fixed points, \(y_{i}=[0,\pi ]\), where the hidden and visible branes are placed, respectively. However, it is clearly observed from Eq. (12) and Eq. (13) that within the bulk both the warp factor and the brane tension vary with the extra-dimensional coordinate ’y’ due to the presence of the dynamical dilaton degrees of freedom within the bulk. Here we have discarded the other branch of the solution of \(k_\mathbf{+}\) (+ve branch), which diverges in the limit \(\alpha _{5}\rightarrow 0\), bringing in ghost fields [11, 34–38]. So we concentrate only on the -ve branch of the solution, which we call \(k_{-}:=k_\mathbf{M}\).

In the limits \(\alpha _{5}\rightarrow 0\), \(A_{1}\rightarrow 0\), \(\theta _{1}\rightarrow 0\), and \(\theta _{2}\rightarrow 0\) we retrieve asymptotically the same result as in the case of the RS model with [16, 17]

$$\begin{aligned} k_\mathbf{M}\rightarrow k_{RS}=\sqrt{-\frac{\Lambda _{5}}{24M^{3}_{5}}} \end{aligned}$$
(14)

and the barne tension is given by

$$\begin{aligned} V^{-}_{2}\rightarrow V^{RS}_{2}=24M^{3}_{5}k_{RS} \end{aligned}$$
(15)

with \(\Lambda _{5}<0\).

Now expanding Eq. (12) in the perturbation series order by order around \(\alpha _{5}\rightarrow 0\), \(A_{1}\rightarrow 0\), \(\theta _{1}\rightarrow 0\), and \(\theta _{2}\rightarrow 0\) we can write

$$\begin{aligned}&\displaystyle k_\mathbf{M}=k_{RS}~e^{\frac{\theta _{2}\phi (y)}{2}}\nonumber \\&\quad \sqrt{\left[ 1+\frac{8\alpha _{5} k^{2}_{RS}}{M^{2}_{5}(1-A_{1}e^{\theta _{1}\phi (y)})} \left\{ 1-2e^{(\theta _{1}+\theta _{2})\phi (y)}A_{1}+e^{(2\theta _{1}+\theta _{2})\phi (y)}A^{2}_{1}+\cdots \right\} +\mathcal{O}\left( \frac{\alpha ^{2}_{5}k^{4}_{RS}}{M^{4}_{5}}\right) +\cdots \right] }. \end{aligned}$$
(16)

For the graviton, the Kaluza–Klein mass spectra for the \(n\)th excited state in the presence of gravidilatonic and Gauss–Bonnet coupling by applying Neumann (\(-\)) and Dirichlet (+) boundary conditions at the orbifold point \(y_{i}=\pi \) where the visible brane is placed, can be written as [6, 39]:

$$\begin{aligned} \displaystyle m^\mathbf{G}_{n}=\left( n+\frac{1}{2}\mp \frac{1}{4}\right) \pi k_\mathbf{M}(\pi )~e^{-k_\mathbf{M}r_{c}\pi } \end{aligned}$$
(17)

in the presence of the Gauss–Bonnet coupling and string loop corrections. For the numerical estimations we use the +ve Dirichlet branch throughout the article. Furthermore the modified 4D effective Planck mass in the presence of the Gauss–Bonnet coupling can be expressed in terms of the 5D mass scale as [6]

$$\begin{aligned} \displaystyle M^{2}_{Pl}=\frac{M^{3}_{5}}{k_\mathbf{M}}\left( 1-e^{-2k_\mathbf{M}r_{c}\pi }\right) . \end{aligned}$$
(18)

Now using Eq. (16) on Eq. (18) the 5D quantum gravity scale at the position of the visible brane \(y=\pi \) turns out to be

$$\begin{aligned} \displaystyle M_{5}&= \root 3 \of {Z_\mathbf{T}}M_{Pl}~e^{\frac{\theta _{2}\phi (\pi )}{6}}\left[ 1+\frac{8\alpha _{5}Z^{\frac{4}{3}}_\mathbf{T}e^{-\frac{\theta _{2}\phi (\pi )}{3}}}{(1-A_{1}e^{\theta _{1}\phi (\pi )})}\right. \nonumber \\&\times \left\{ 1-2e^{(\theta _{1}+\theta _{2})\phi (\pi )}A_{1}+e^{(2\theta _{1}\!+\!\theta _{2})\phi (\pi )}A^{2}_{1}\!+\!\cdots \right\} \nonumber \\&\left. \displaystyle +\,\mathcal{O}\left( \alpha ^{2}_{5}Z^{\frac{8}{3}}_\mathbf{T}e^{-\frac{2\theta _{2}\phi (\pi )}{3}}\right) +\cdots \right] ^{\frac{1}{6}} \end{aligned}$$
(19)

where we use the fact that \(e^{-2k_\mathbf{M}r_{c}\pi }<<1\) approximation holds good in Eq. (18). Here additionally we use the fact that \(k_{RS}=Z_\mathbf{T}M_{PL}\), where \(Z_\mathbf{T}\) is a dimensionless tuning parameter. Now for the sake of clarity one can write \(Z_\mathbf{T}\) as

$$\begin{aligned} \begin{array}{l} \displaystyle Z_\mathbf{T}=\frac{M_{5}}{M_{Pl}}\epsilon _{RS} \end{array} \end{aligned}$$
(20)

where we introduce an additional parameter, \(\epsilon _{RS}=\frac{k_{RS}}{M_{5}}\), with the restriction on the parameter, \(0.01<\epsilon _{RS}<0.1\), as used in [21, 40]. This requirement emerges from the fact that the bulk curvature must be smaller than the Planck scale so that the classical solutions for the bulk metric given by the proposed model can be trusted. On the other hand, string theory also supports this favored range within the background of the Klebanov–Strassler throat geometry motivated \(D3\)–\(\overline{D3}\) brane–antibrane setup [23]. It is important to mention here that only for the RS model \(Z_\mathbf{T}\approx \epsilon _{RS}\), as the \(M_{5}\sim M_{Pl}\) approximation holds good in an RS setup. Further substituting Eq. (20) in Eq. (19) we found the simplified expression for the 5D quantum gravity scale in terms of \(\epsilon _{RS}\), which turns out to be

$$\begin{aligned} \displaystyle M_{5}&= \sqrt{\epsilon _{RS}}M_{Pl}~e^{\frac{\theta _{2}\phi (\pi )}{4}}\left[ 1+\frac{8\alpha _{5}\epsilon ^{2}_{RS}}{(1-A_{1}e^{\theta _{1}\phi (\pi )})}\right. \nonumber \\&\times \left\{ 1-2e^{(\theta _{1}+\theta _{2})\phi (\pi )}A_{1}+e^{(2\theta _{1}+\theta _{2})\phi (\pi )}A^{2}_{1}+\cdots \right\} \nonumber \\&\left. +\mathcal{O}\left( \alpha ^{2}_{5}\epsilon ^{4}_{RS}\right) +\cdots \right] ^{\frac{1}{4}}. \end{aligned}$$
(21)

On the other hand to solve the hierarchy problem the brane localized Higgs mass can be written as

$$\begin{aligned} \begin{array}{l} \displaystyle m_{H}\approx m_\mathbf{CUT}~e^{-k_\mathbf{M} r_{c}\pi } \end{array} \end{aligned}$$
(22)

where we introduce a new parameter \(m_\mathbf{CUT}\), defined as

$$\begin{aligned} m_\mathbf{CUT}= M_{Pl}; \end{aligned}$$
(23)

it physically represents the cut-off scale of the theory, above which new physics beyond the standard model is expected to appear. A natural choice for this would be the Planck or quantum gravity scale beyond which the standard model will not be valid.

Now using Eq. (16) we introduce a new parameter, \(\epsilon _\mathbf{M}\), defined as

$$\begin{aligned} \displaystyle \epsilon _\mathbf{M}&= \frac{k_\mathbf{M}}{M_{5}}\approx Z^{\frac{2}{3}}_\mathbf{T}~e^{\frac{\theta _{2}\phi (\pi )}{3}} \left[ 1+\frac{8\alpha _{5}Z^{\frac{4}{3}}_\mathbf{T}e^{-\frac{\theta _{2}\phi (\pi )}{3}}}{(1-A_{1}e^{\theta _{1}\phi (\pi )})}\right. \nonumber \\&\quad \times \left\{ 1-2e^{(\theta _{1}+\theta _{2})\phi (\pi )}A_{1}+e^{(2\theta _{1}+\theta _{2})\phi (\pi )}A^{2}_{1}+\cdots \right\} \nonumber \\&\qquad \left. \displaystyle +\mathcal{O}\left( \alpha ^{2}_{5}Z^{\frac{8}{3}}_\mathbf{T}e^{-\frac{2\theta _{2}\phi (\pi )}{3}}\right) +\cdots \right] ^{\frac{1}{3}}\nonumber \\&\displaystyle \quad =\epsilon _{RS}~e^{\frac{\theta _{2}\phi (\pi )}{2}}\left[ 1+\frac{8\alpha _{5} \epsilon ^{2}_{RS}}{(1-A_{1}e^{\theta _{1}\phi (\pi )})}\right. \nonumber \\&\qquad \times \left\{ 1-2e^{(\theta _{1}+\theta _{2})\phi (\pi )}A_{1}+e^{(2\theta _{1}+\theta _{2})\phi (\pi )}A^{2}_{1}+\cdots \right\} \nonumber \\&\qquad \left. +\mathcal{O}\left( \alpha ^{2}_{5}\epsilon ^{4}_{RS}\right) +\cdots \right] ^{\frac{1}{2}}. \end{aligned}$$
(24)

Further using Eq. (24) and Eq. (22) in the graviton Kaluza–Klein mass spectra as stated in Eq. (17), the first Kaluza–Klein excitation (\(n=1\)) becomes

(25)

where we again use the fact that \(e^{-2k_\mathbf{M}r_{c}\pi }<<1\) and the lightest graviton mass for the Randall–Sundrum model is given by

$$\begin{aligned} (m^\mathbf{G}_{1})_\mathbf{RS}=x_{1}\epsilon ^{\frac{2}{3}}_{RS}m_{H} \end{aligned}$$
(26)

where \(x_{1}=7\pi /4\) be the root of the Bessel function of order 1 as obtained from Eq. (17). Here in Eq. (25) we introduce a new parameter, \(\mathbf{\Theta }_\mathbf{T}\), given by

(27)

which signifies the multiplicative uplifting factor of the lightest Kaluza–Klein graviton mass spectra for the proposed model compared to the lightest graviton mass for the Randall–Sundrum model.

The five-dimensional action describing the interaction between bulk graviton and visible Standard Model fields dominated by fermionic contribution on the brane is given by

$$\begin{aligned} \displaystyle \mathcal{S}_\mathbf{SM-\mathbf G}=-\frac{\mathcal{K}_{(5)}}{2}\int d^{5}x\sqrt{-g_{(5)}}\mathbf{T}^{\alpha \beta }_\mathbf{SM}(x)\mathbf{h}_{\alpha \beta }(x,y)\delta (y-\pi )\nonumber \\ \end{aligned}$$
(28)

where \(\mathbf{T}^{\alpha \beta }_\mathbf{SM}(x)\) represents the energy momentum or stress energy tensor containing all informations of Standard Model matter fields on the visible brane and \(h_{\alpha \beta }(x,y)\) be the bulk graviton degrees of freedom. In this context \(\mathcal{K}_{(5)}:=\frac{2}{M^{\frac{3}{2}}_{(5)}}\) is the coupling strength describing the tensor fluctuation in the context of graviton phenomenology. After substituting the Kaluza–Klein expansion for graviton degrees of freedom:

$$\begin{aligned} \begin{array}{l} \displaystyle \mathbf{h}_{\alpha \beta }(x,y)=\sum ^{\infty }_{n=0}\mathbf{h}^{(n)}_{\alpha \beta }(x)~\frac{\chi ^{(n)}_\mathbf{G}(y)}{\sqrt{r_{c}}}. \end{array} \end{aligned}$$
(29)

and rescaling the fields appropriately, the effective four dimensional action turns out to be

$$\begin{aligned}&\displaystyle \mathcal{S}_\mathbf{SM-\mathbf G}=-\frac{\mathcal{K}_{(5)}}{2}\int d^{5}x~r_{c}~e^{-4A(y)} \mathbf{T}^{\alpha \beta }_\mathbf{SM}(x)\nonumber \\&\qquad \qquad \quad \times \sum ^{\infty }_{n=0}\mathbf{h}^{(n)}_{\alpha \beta }(x)\frac{\chi ^{(n)}_\mathbf{G}(y)}{\sqrt{r_{c}}}\delta (y-\pi )\nonumber \\&\quad \displaystyle =-\frac{\sqrt{r_{c}}\mathcal{K}_{(5)}}{2}\int d^{4}x~e^{-4A(\pi )} \mathbf{T}^{\alpha \beta }_\mathbf{SM}(x)\sum ^{\infty }_{n=0}\mathbf{h}^{(n)}_{\alpha \beta }(x)\chi ^{(n)}_\mathbf{G}(\pi )\nonumber \\&\quad \displaystyle =-\frac{\sqrt{k_\mathbf{M}}r_{c}\mathcal{K}_{(5)}}{2}\int d^{4}x~ \mathbf{T}^{\alpha \beta }_\mathbf{SM}(x)\nonumber \\&\qquad \times \left[ \mathbf{h}^{(0)}_{\alpha \beta }(x) + e^{k_\mathbf{M}r_{c}\pi }\sum ^{\infty }_{n=1}\mathbf{h}^{(n)}_{\alpha \beta }(x)\right] \nonumber \\&\quad \displaystyle =-\frac{r_{c}}{k_{RS}M_{Pl}}~e^{-\frac{\theta _{2}\phi (\pi )}{2}} \left[ 1+\frac{8\alpha _{5} k^{2}_{RS}}{M^{2}_{5}(1-A_{1}e^{\theta _{1}\phi (\pi )})}\right. \nonumber \\&\qquad \times \left\{ 1-2e^{(\theta _{1}+\theta _{2})\phi (\pi )}A_{1}+e^{(2\theta _{1}+\theta _{2})\phi (\pi )}A^{2}_{1}+\cdots \right\} \nonumber \\&\qquad \left. \displaystyle +\mathcal{O}\left( \frac{\alpha ^{2}_{5} k^{4}_{RS}}{M^{4}_{5}}\right) +\cdots \right] ^{-\frac{1}{2}}\displaystyle \int d^{4}x~ \mathbf{T}^{\alpha \beta }_\mathbf{SM}(x)\nonumber \\&\qquad \times \left[ \mathbf{h}^{(0)}_{\alpha \beta }(x) + e^{k_\mathbf{M}r_{c}\pi }\sum ^{\infty }_{n=1}\mathbf{h}^{(n)}_{\alpha \beta }(x)\right] . \end{aligned}$$
(30)

It is evident from Eq. (30) that, while the zero mode couples to the brane fields with the usual gravitational coupling \({\sim }1/M_{Pl}\), which we have taken as unity, the couplings of the KK modes are \({\sim } e^{k_\mathbf{M}r_{c}\pi } / M_{Pl} \sim \mathrm{TeV}^{-1}\), which is much larger than the coupling of the massless graviton. Though such a feature is also observed for the graviton KK modes in the usual RS model, here the graviton KK mode coupling depends on the GB coupling \(\alpha _{5}\). In the present context the values of \(k_\mathbf{M}\) though increase with \(\alpha _{5}\); the enhancement of the graviton KK mode mass causes the overall decrease in the detection cross section. Thus the absence of any signature of graviton KK modes, as reported by ATLAS data in dilepton decay processes, may be explained by the GB coupling in warped geometry models.

In Table 1 we present a comparative study between the lower limit of the lightest Kaluza–Klein graviton mass for the \(n=1\) mode from the proposed theoretical model, the well-known Randall–Sundrum (RS) model and the LHC ATLAS dilepton search in the 7 TeV proton–proton collision experiment. Additionally we show that the 5D mass scale of the proposed model is lying within the window \(1.56M_{Pl}<M_{5}<4.95M_{Pl}\) for \(0.01<\epsilon _{RS}<0.1\). For the RS model, the lower limit of the graviton KK mode mass lying within the window, \(0.22 ~\mathrm{TeV}<m^{G,\mathbf{RS}}_{1}<1.02~\mathrm{TeV}\) for \(0.01<\epsilon _{RS}<0.1\). On the other hand the latest data from ATLAS predicts the graviton KK mode mass lying within \(1.01~\mathrm{TeV}<m^{G,\mathbf{ATLAS}}_{1}<2.22~\mathrm{TeV}\) for \(0.01<\epsilon _{RS}<0.1\). This implies a serious conflict between the graviton KK modes as predicted in the RS model and the result reported by the ATLAS Collaboration. For the proposed model the lightest bound of the KK graviton mass is estimated as \(1.68 ~\mathrm{TeV}<m^{G,\mathbf{RS}}_{1}<16.82~\mathrm{TeV}\), which is above the recent lower bound of the KK graviton mass measured through the LHC ATLAS dilepton search and lies within the parameter space for the future probing region of LHC. By taking into consideration the enhancement of the coupling between SM fields and graviton, it may be observed from Table 1 that, for \(\epsilon _{RS}=0.07\) or higher, the lower bound of the graviton KK mode exceeds that predicted from the ATLAS data.

To study the various hidden phenomenological features within the super-Planckian regime of the UV cut-off scale from our proposed setup the scanned parameter space is given by

$$\begin{aligned} \begin{aligned}&\alpha _{5}=\mathcal{O}((4.8-5.1)\times 10^{-7}),\\&|A_{1}|\sim \mathcal{O}(0.01-0.09),\\&\theta _{2}=-\theta _{1},\\&\chi _{1}={\theta _{1}\phi (\pi )}\sim -11,\\&\chi _{2}={\theta _{2}\phi (\pi )}\sim 11, \\&for~~m_{H}\sim \mathcal{O}((125-126)~GeV). \end{aligned} \end{aligned}$$
(31)

This bound on the GB coupling \(\alpha _{5}\) is also consistent with the solar system constraint [41], the combined constraint from the Higgs mass, and the favored decay channels \(H\rightarrow (\gamma \gamma ,\tau \bar{\tau })\) [24] using ATLAS [25] and CMS [26] data within the \(5\sigma \) statistical C.L. Additionally, the parameter space mentioned in Eq. (31) is a necessary ingredient to increase/uplift the lower bound of the lightest KK graviton mass constrained from the LHC ATLAS dilepton search. It is important to mention here that the bound on the 5D Gauss–Bonnet coupling obtained from Eq. (31) is below the upper cut-off on the coupling obtained from the Kubo formula, i.e. \(\alpha _{5}<1/4\) [4, 5, 27], obtained in the context of the \(\mathbf{AdS_{5}/CFT_{4}}\) correspondence.

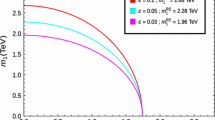
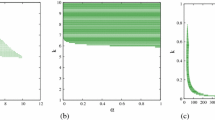
In Fig. 1 we show the variation of the lightest Kaluza–Klein graviton mass from the proposed model (represented by a red curve) and the Randall–Sundrum (RS) model (represented by a blue curve) with respect to the phenomenological parameter \( \epsilon _{RS}=\frac{k_{RS}}{M_{5}}\), within the range \(0.01<\epsilon _{RS}<0.10\) as stated in Eq. (31). We also show the present status of the lower limit of the lightest Kaluza–Klein graviton mass for the LHC ATLAS dilepton search by the green curve in Fig. 1. Here the allowed region is in the upper half of the green curve. The rest of the region below the green curve phenomenologically is ruled out. We have also explored the phenomenological feature of the lightest Kaluza–Klein graviton mass with respect to the dilaton coupling \(\chi _{2}=\theta _{2}\phi (\pi )\) with the 5D \(\mathbf{AdS_{5}}\) cosmological constant \(\Lambda _{5}\) at the wall of the visible brane for the proposed theoretical setup in Fig. 2. We also show the present status of the allowed region for the lower limit of the lightest Kaluza–Klein graviton mass for the LHC ATLAS dilepton search by the yellow shaded region in Fig. 2. This will constrain the parameter \(\chi _{2}\) within \(\chi _{2}\sim \mathcal{O}(6\)–\(12.8)\). This is also consistent with the present theoretical analysis as the proposed setup predicts \(\chi _{2}\sim 11\) as mentioned in Eq. (31). For both branches the lightest Kaluza–Klein graviton mass increases exponentially by increasing the dilaton coupling \(\chi _{2}=\theta _{2}\phi (\pi )\) and fixing the other parameters within the allowed parameter space stated in Eq. (31). Next in Fig. 3a and b we present the characteristic feature of the lightest Kaluza–Klein graviton mass with respect to the 5D Gauss–Bonnet coupling (\(\alpha _{5}\)) for the proposed theoretical setup for \(\epsilon _{RS}=0.01\) and \(\epsilon _{RS}=0.10\), respectively. For both cases the lightest Kaluza–Klein graviton mass increases by increasing the 5D Gauss–Bonnet coupling (\(\alpha _{5}\)) and fixing the other parameters stated in Eq. (31). We also show the present status of the lower limit of the lightest Kaluza–Klein graviton mass for the LHC ATLAS dilepton search by a point in Fig. 3a and b both. To uplift/increase the lower bound of the lightest Kaluza–Klein graviton mass estimated from the proposed theoretical setup compared to the LHC dilepton search by proposing the 5D Gauss–Bonnet coupling (\(\alpha _{5}\)) within \(\alpha _{5}\sim \mathcal{O}((4.8\)–\(5.1)\times 10^{-7})\), as explicitly mentioned in Table 1. Finally, in Fig. 4a and b we explicitly show the behavior of the lightest Kaluza–Klein graviton mass with respect to the string two-loop coupling \(A_{1}\) by fixing the rest of the parameters for the proposed theoretical setup for \(\epsilon _{RS}=0.01\) and \(\epsilon _{RS}=0.10\), respectively. For both cases the lightest Kaluza–Klein graviton mass decreases by increasing the string two-loop coupling \(A_{1}\) and fixing the other parameters stated in Eq. (31). We also show the present status of the lower limit of the lightest Kaluza–Klein graviton mass for the LHC ATLAS dilepton search by a point in these figures.

Fig. 1
figure 1

Variation of the lightest Kaluza–Klein graviton mass \(m^{G}_{1}\) for the \(n=1\) mode from the proposed model (red curve) and Randall–Sundrum (RS) model (blue curve) with respect to the phenomenological parameter \( \epsilon _{RS}=\frac{k_{RS}}{M_{5}}\) within the range \(0.01<\epsilon _{RS}<0.10\). We also show the present status of the lower limit of the lightest Kaluza–Klein graviton mass for the LHC ATLAS dilepton search by the green curve as depicted in Table 1. Here for this plot we fix the model parameters as follows: \(\alpha _{5}=5\times 10^{-7}\), \(A_{1}=0.05\), \(\theta _{2}=-\theta _{1}\), \(\theta _{2}\phi (\pi )\sim 11\), and \(\theta _{1}\phi (\pi )\sim -11\). Here the allowed region is in the upper half of the green curve. The rest of the region (below the green curve) is ruled out

Full size image
Fig. 2
figure 2

Variation of the lightest Kaluza–Klein graviton mass \(m^{G}_{1}\) for \(n=1\) mode with respect to the dilaton coupling \(\chi _{2}=\theta _{2}\phi (\pi )\) for the proposed theoretical setup for \(0.01<\epsilon _{RS}<0.10\) at the wall of the TeV brane. We also show the present status of the allowed region for the lower limit of the lightest Kaluza–Klein graviton mass for the LHC ATLAS dilepton search by the yellow shaded region bounded by the black colored line drawn for \(\epsilon _{RS}=0.10\) and \(\epsilon _{RS}=0.01\), respectively. Here for this plot we fix \(A_{1}=0.05\), \(\theta _{2}=-\theta _{1}\), and \(\alpha _{5}\sim 5\times 10^{-7}\). Additionally, the white region bounded by the red and blue curves represents the future probing region for LHC. Also the black dotted region represents the overlapping area between the parameter space obtained from the proposed model and the present LHC ATLAS dilepton search

Full size image
Fig. 3
figure 3

Variation of the lightest Kaluza–Klein graviton mass \(m^{G}_{1}\) with respect to 5D Gauss–Bonnet coupling \(\alpha _{5}\) for the \(n=1\) mode with a \(\epsilon _{RS}=0.01\) and b \(\epsilon _{RS}=0.1\) for the proposed theoretical setup at the wall of the TeV brane. We also show the present status of the lower limit of the lightest Kaluza–Klein graviton mass for the LHC ATLAS dilepton search by the black colored point drawn for \(\epsilon _{RS}=0.10\) and \(\epsilon _{RS}=0.01\), respectively. For this plot we fix \(A_{1}=0.05\), \(\theta _{2}=-\theta _{1}\), \(\theta _{2}\phi (\pi )\sim 11\), and \(\theta _{1}\phi (\pi )\sim -11\). Additionally, we show the amount of the uplift of the lower bound of the lightest Kaluza–Klein graviton mass compared to the result obtained from the LHC ATLAS dilepton search

Full size image
Fig. 4
figure 4

Variation of the lightest Kaluza–Klein graviton mass \(m^{G}_{1}\) with respect to the string two-loop coupling \(A_{1}\) for \(n=1\) mode with a, \(\epsilon _{RS}=0.01\), and b, \(\epsilon _{RS}=0.1\), for the proposed theoretical setup at the wall of the TeV brane. We also show the present status of the lower limit of the lightest Kaluza–Klein graviton mass for the LHC ATLAS dilepton search by the black colored point drawn for \(\epsilon _{RS}=0.10\) and \(\epsilon _{RS}=0.01\), respectively. Here for this plot we fix \(\theta _{2}=-\theta _{1}\), \(\theta _{2}\phi (\pi )\sim 11\), and \(\theta _{1}\phi (\pi )\sim -11\). Additionally, we show the amount of the uplift of the lower bound of the lightest Kaluza–Klein graviton mass compared to the result obtained from the LHC ATLAS dilepton search

Full size image

To summarize, we say that the perturbative two-loop higher genus correction to Einstein gravity in the presence of a stringy type IIB gravidilatonic interaction can also be examined through collider experimental tests by studying the hidden phenomenological features of the lightest KK mode from the graviton mass spectrum. Using the prescription mentioned in this paper one can directly check the validity and justifiability of higher order gravity or any modified gravity model in the presence of stringy higher genus corrections and also constrain the associated parameter space which involves various couplings with such higher order gravity corrections. Thus, in this work, by applying the requirements from the latest data we have also elaborately analyzed the multiparameter space dependence on the lightest Kaluza–Klein graviton mass by studying the flow of the running through the crucial parameters proposed in this article. This analysis therefore determines the allowed parameter space for the proposed model and brings out the phenomenological constraint on the value of the stringy parameters in the context of the recent LHC experiment by scanning the multiparameter space within a phenomenologically feasible range.