Quasinormal modes of Lovelock black holes

Abstract

The quasinormal modes of metric perturbations in asymptotically flat black hole spacetimes in the Lovelock model are calculated for different spacetime dimensions and higher orders of curvature. It is analytically established that in the asymptotic limit $l\rightarrow \infty$, the imaginary parts of the quasinormal frequencies become constant for tensor, scalar as well as vector perturbations. Numerical calculation shows that this indeed is the case. Also, the real and imaginary parts of the quasinormal modes are seen to increase as the order of the theory $k$ increases. The real part of the modes decreases as the spacetime dimension $d$ increases, indicating the presence of lower frequency modes in higher dimensions. Also, it is seen that the modes are roughly isospectral at very high values of the spacetime dimension $d$.

1 Introduction

Quasinormal modes (QNMs) are damped oscillatory modes of a field that perturbs the spacetime metric in the vicinity of a black hole. They depend only on the parameters of the black hole, and not on the nature of the perturbing field. This makes them ideal tools to study the physics of black holes, which are otherwise impossible to observe by their very definition. The long-lived modes in asymptotically flat spacetimes surrounding black holes are expected to be observed in future by gravitational wave detectors. Different models of gravity predict different “quasinormal signatures” of their respective spacetimes and the experimental observation of these modes may well put to rest the problem of selecting the most suitable model for gravity from existing (numerous) ones.

The research on QNMs is decades old with an extensive literature (for example, [1–14] and references therein). The quasinormal behavior in first order theories of gravity such as the General Theory of Relativity (GTR) is particularly well studied with its asymptotic behavior firmly established both numerically and analytically [15]. The asymptotic quasinormal modes of perturbations in GTR have their real parts approach a constant value, while the imaginary parts increase indefinitely. These modes are significant from the standpoint of quantum theories of gravity since they help us to compute the area spectrum and subsequently the entropy of the black hole event horizons, which, in GTR, are known to be equally spaced. The asymptotic behavior of the modes, observed numerically, can help one analytically determine the precise form of these modes in terms of the parameters of the theory later. This has been demonstrated in [15], where the decision to compute the monodromy along the Stokes line was made because of the asymptotic behavior mentioned above. Thus it would be highly interesting to see how the quasinormal modes behave asymptotically in any model of gravity that one considers.

The connection between geodesic stability and quasinormal modes in black hole spacetimes has been known for a long time; see [5, 6, 16–18] among others. These studies reveal the connection between quasinormal modes of black hole spacetimes and the dynamics of null particles in an unstable circular orbit around the black hole, with its energy slowly leaking out. The relation is most clearly established in [16] for any static, spherically symmetric and asymptotically flat spacetime, according to which the quasinormal frequencies $\omega _\mathrm{asy}$ in the asymptotic limit $(l\rightarrow \infty )$ is given by

$$\begin{aligned} \omega _\mathrm{asy}=\varOmega _c l-i\left( n+\frac{1}{2}\right) |\lambda |, \end{aligned}$$

(1)

where $\varOmega _c$ and $\lambda$ are the angular velocity at the unstable null geodesic and the principal Lyapunov exponent which is related to the time scale of energy decay in the orbit.

The actual number of spacetime dimensions is predicted to be higher than four by string theory and it has led to attempts to develop models of gravity in higher dimensions. In these higher dimensional spacetimes, GTR no longer is the most general model of gravity. Generalizations of GTR are naturally attempted by adding higher order curvature correction terms to the Einstein–Hilbert action. Among such generalizations to GTR, the Lovelock model [19, 20], considered as a natural generalization of the GTR to higher dimensions and orders of curvature, is particularly interesting since it yields field equations of second order that are free of ghosts. The Lovelock Lagrangian consists of dimensionally continued curvature terms of orders one and above. The resulting theories are labeled by the order of the maximum-order term, $k$, which in turn is determined by the dimension of the spacetime $d$, by $k=[\frac{d-1}{2}]$ where $[x]$ denotes the integer part of $x$. Black hole solutions to the theory in general contain many branches that depend on the values of the higher order coupling constants [21]. It is well known [22] that the metric perturbations to the most general, asymptotically flat Lovelock spacetime are unstable in the ultraviolet region. Therefore it is necessary to impose further constraints to select a suitable set of Lovelock theories which would permit stable perturbations. Such maximally symmetric, asymptotically flat as well as AdS spacetimes have been known for a long time [23].

In this work, we compute the quasinormal modes of metric perturbations to the metric of such maximally symmetric spacetimes using the sixth order WKB method [24]. We analytically determine the asymptotic form of these modes using the above-mentioned null geodesic method. The paper is organized as follows: in Sect. 2, we describe the essential details of the null geodesic method used to compute the asymptotic form of the modes. In Sect. 2.1, we describe the class of Lovelock theories for which the modes are computed and the WKB expression of numerical computation. The relation between the asymptotic quasinormal modes and the null geodesic parameters is expressed in Sect. 2.2. The results of the calculation are discussed in Sect. 3. We summarize the main results of the work in Sect. 4.

2 Geodesic stability

Consider the general stationary and spherically symmetric metric

$$\begin{aligned} \mathrm{d}s^{2}=f(r)\mathrm{d}t^{2}-\frac{1}{g(r)}\mathrm{d}r^{2}-r^{2}\mathrm{d}\varOmega _{d-2}^2, \end{aligned}$$

(2)

where $f(r)$ and $g(r)$ are solutions of the Lovelock field equations [21]. $\mathrm{d}\varOmega _{d-2}^2$ represents the metric of the spherically symmetric background. For this metric, we have the Lagrangian in the form [25]

$$\begin{aligned} 2{\mathcal L}=f(r){\dot{t}}^2-\frac{1}{g(r)}{\dot{r}}^2-r^2{\dot{\varphi }}^2, \end{aligned}$$

(3)

where a dot represents the derivative with respect to proper time and $\varphi$ is an angular coordinate. For this system, the coordinate angular velocity $\varOmega _c$ and the principal Lyapunov exponent $\lambda$ for circular null geodesics take the form [16]

$$\begin{aligned}&\!\!\!\varOmega _c=\frac{\dot{\varphi }}{\dot{t}}=\left( \frac{f'_c}{2r_c}\right) ^{1/2},\end{aligned}$$

(4)

$$\begin{aligned}&\!\!\!\lambda =\frac{1}{\sqrt{2}}\sqrt{-\frac{r_c^2}{f_c} \left( \frac{\mathrm{d}^2}{\mathrm{d}r_*^2}\frac{f}{r^2}\right) _{r=r_c}}, \end{aligned}$$

(5)

where the subscript $c$ means that the evaluation is done at the critical radius, $r=r_c$, which satisfies the relation $2f-rf'=0$. $r_c$ can be viewed as the innermost circular timelike geodesic, since circular timelike geodesics satisfy $2f-rf'>0$. $r_*$ is the tortoise coordinate which satisfies the relation $\mathrm{d}r_*=\frac{\mathrm{d}r}{\sqrt{g(r)f(r)}}$.

2.1 The equations of perturbation and the WKB method

The action for the class of Lovelock theories, a subset of which are studied in this work, is written in terms of the Riemann curvature $R^{ab}=d\omega ^{ab}+\omega _{c}^{a}\omega ^{cb}$ and the vielbein $e^{a}$ as [20, 23, 26]

$$\begin{aligned} I_{G}=\kappa \int \sum _{p=0}^{k}\alpha _{p}L^{(p)}, \end{aligned}$$

(6)

where $\alpha _{p}$ are positive coupling constants and $L^{(p)}$, given by

$$\begin{aligned} L^{(p)}=\epsilon _{a_{1}\cdots a_{d}}R^{a_{1}a_{2}}\cdots R^{a_{2p-1}a_{2p}}e^{a_{2p+1}}\cdots e^{a_{d}}, \end{aligned}$$

(7)

are the $p$th order dimensionally continued terms in the Lagrangian, $\epsilon _{a_{1}\cdots a_{d}}$ being the Levi-Civita symbol. $\kappa$ is a parameter related to the gravitational constant $G_k$ by $\kappa =\frac{1}{2(d-2)!\varOmega _{d-2}G_{k}}$, $\varOmega _{d-2}$ being the volume of the $(d-2)$ dimensional spherically symmetric tangent space with unit curvature.

The resulting field equations are of the form

$$\begin{aligned}&\!\!\!\epsilon _{ba_{1}\cdots a_{d-1}}{\bar{R}}^{a_{1}a_{2}}\cdots {\bar{R}}^{a_{2k-1}a_{2k}}e^{a_{2k+1}}\cdots e^{a_{d-1}} =0, \end{aligned}$$

(8)

$$\begin{aligned}&\!\!\!\epsilon _{aba_{3}\cdots a_{d}}{\bar{R}}^{a_{3}a_{4}}\cdots {\bar{R}}^{a_{2k-1}a_{2k}}T^{a_{2k+1}}e^{a_{2k+2}}\cdots e^{a_{d-1}} =0. \end{aligned}$$

(9)

Here, ${\bar{R}}^{ab}:=R^{ab}+\frac{1}{R^{2}}e^{a}e^{b}$.

The quasinormal behavior in a similar class of asymptotically AdS Lovelock theories possessing a unique cosmological constant has recently been studied [27]. It is well known [22] that the theories in which all the higher order coupling constants $\alpha _{p}$ are positive permit asymptotically flat spacetime solutions that suffer from dynamical instability against metric perturbations. In the present work, we consider a special case. We consider the class of theories with $\alpha _{p}$ given by

$$\begin{aligned} \alpha _{p}=\frac{1}{d-2k}\delta ^{k}_{p} \end{aligned}$$

(10)

The static and spherically symmetric black hole solutions of the theory, written in Schwarzschild-like coordinates, take the form

$$\begin{aligned} \mathrm{d}s^{2}=f(r)\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{f(r)}+r^{2}\mathrm{d}\varOmega _{d-2}^{2}, \end{aligned}$$

(11)

where $f(r)$ is given by

$$\begin{aligned} f(r)=1-\left( \frac{2G_kM}{r^{d-2k-1}}\right) ^{1/k}, \end{aligned}$$

(12)

$M$ being the mass of the black hole. It is to be noted that only the cases in which $d-2k-1 \ne 0$ yield black hole solutions [23] with their event horizons $r_h$ located at $(2G_kM)^{\frac{1}{d-2k-1}}$. It is noted that for the case of $d=4$ and $k=1$, we get the Schwarzschild geometry of GTR. We can therefore consider these spacetimes as natural generalizations of the former to the case of higher order theories in higher dimensions.

The master equations obeyed by the metric perturbations for the general Lovelock theory were derived in [21].

The master equation satisfied by the tensor metric perturbation $\delta g_{ij}=r^{2}\phi (t,r)h_{ij}(x^{i})$, after separating the variables $\phi (r,t)=\chi (r)e^{-i\omega t}$, takes the form [21]

$$\begin{aligned}&\!\!\!-f^{2}\chi ^{{\prime \prime }}-\left( f^{2}\frac{T^{{\prime \prime }}}{T^{{\prime }}} +\frac{2f^{2}}{r}+ff^{{\prime }}\right) \chi ^{{\prime }}\nonumber \\&\quad +\frac{(2\kappa +\gamma _{t})f}{(n-2)r}\frac{T^{{\prime \prime }}}{T^{{\prime }}}\chi =\omega ^{2}\chi , \end{aligned}$$

(13)

where the function $T(r)$, for the most general class of Lovelock theories given by (6) with all the constants $\alpha _p$ being positive, is given by the expression

$$\begin{aligned}&T(r)\equiv r^{n-1}\partial _{\psi }W[\psi ]=r^{n-1}\nonumber \\&\quad \times \left( 1+\sum \limits _{m=2}^{k}\left[ a_{m}\left\{ \prod \limits _{p=1}^{2m-2}(n-p)\right\} \psi ^{m-1}\right] \right) . \end{aligned}$$

(14)

We write $\varPsi (r)=\chi (r)r\sqrt{T^{{\prime }}(r)}$ and define the tortoise coordinate $r^{*}$ by $\mathrm{d}r^{*}=\mathrm{d}r/f(r)$ to transform (13) to the form

$$\begin{aligned} \frac{\mathrm{d}^{2}\varPsi }{\mathrm{d}r^{*2}}+(\varOmega ^{2}-V(r))\varPsi =0, \end{aligned}$$

(15)

Here, $V(r)=V_t(r)$, the effective potential for tensor perturbations. The tortoise coordinate $r^{*}$ is defined by $\mathrm{d}r^{*}=\mathrm{d}r/f(r)$. Similar expressions for the vector and scalar type perturbations can be derived easily. The effective potentials $V(r)$ for tensor ($V_t(r)$), vector ($V_v(r)$) and scalar ($V_s(r)$) perturbations are given below:

$$\begin{aligned} V(r)=\left\{ \begin{array}{ll} V_{t}(r)=\frac{(2\kappa +\gamma _{t})f}{(n-2)r}\frac{\mathrm{d}\ln {T^{{\prime }}}}{\mathrm{d}r}+\frac{1}{r\sqrt{T^{{\prime }}}}f\frac{\mathrm{d}}{\mathrm{d}r}\left( f\frac{\mathrm{d}}{\mathrm{d}r}r\sqrt{T^{{\prime }}}\right) ,\\ V_v(r)=r\sqrt{T^{'}}f\partial _r \left( f\partial _r\frac{1}{r\sqrt{T^{'}}}\right) +\frac{f}{r}\left( \frac{\gamma _v}{n-1}-\kappa \right) \frac{T^{'}}{T},\\ V_s(r)=2\gamma _sf\frac{(rNT)^{'}}{nr^2NT}-f\left( \frac{1}{N}\partial _r (f\partial _rN)+\frac{1}{T}\partial _r(f\partial _rT)\right) \\ \quad +2f^2\left( \frac{N^{'2}}{N^{2}}+\frac{T^{'2}}{T^2}+ \frac{N^{'}T^{'}}{NT}\right) . \end{array} \right. \nonumber \\ \end{aligned}$$

(16)

Here, $\gamma _{t}=l(l+d-3)-2$, $\gamma _{v}=l(l+d-3)-1$, and $\gamma _{s}=l(l+d-3)$ are the eigenvalues for the tensor, vector, and scalar harmonics, respectively. The functions $T(r)$ and $N(r)$, for the class of theories given by (10), are given by

$$\begin{aligned} T(r)&= \left( \prod _{p=1}^{2k-2}(d-p-2)\right) \left( \frac{2G_kM}{r^{d-1}} \right) ^{1-\frac{1}{k}},\nonumber \\ N(r)&= \frac{2\gamma _s-2(d-2)f+(d-2)rf'}{r\sqrt{T'}}. \end{aligned}$$

(17)

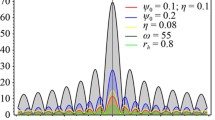
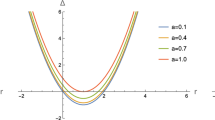
Figure 1 represents the typical variation of the effective potential $V(r)$ outside the event horizon for all types of perturbations. The different plots are drawn for different values of $k$ which is the tunable parameter for the set of theories studied in this work. It is noted that the potential is barrier-like for all values of $k$. The height of the barrier is seen to be a decreasing function of the order parameter $k$.

Fig. 1

Effective potential $V(r)$ vs. $r$ for different $k$, from $k=2$ (top) to $k=5$ (bottom), with $d=17$ and $l=7$

We now apply the WKB method in order to compute the QNMs of the metric perturbations that obey (15). The third order WKB formula for QNMs was derived by Iyer and Will [13] and was extended to the sixth order by Konoplya [24]. We use the sixth order formula derived in [24] since it gives better accuracy for lower modes.

The sixth order formula for computing the QNM $\varOmega$ for perturbations obeying (15) is given by

$$\begin{aligned} \frac{Q_0}{\sqrt{2Q_0^{\prime \prime }}}-\varLambda _2-\varLambda _3- \varLambda _4-\varLambda _5-\varLambda _6=i\left( n+\frac{1}{2}\right) , \end{aligned}$$

(18)

where $n$ is the overtone number and we have used the notation $Q(x)=\varOmega ^2-V(x)$. $Q_0=Q(x_0)$, where $x_0$ is the tortoise coordinate at which the potential attains its peak. Also, prime $(')$ represents differentiation with respect to the tortoise coordinate $x$. The expressions for the correction terms $\varLambda _2, \varLambda _3,\varLambda _4,\varLambda _5$, and $\varLambda _6$ are given in [24] and [28].

2.2 Asymptotic quasinormal modes in terms of null geodesic parameters

In order to find an approximate analytic expression for the quasinormal modes in the asymptotic limit $l\rightarrow \infty$, we drop the higher order terms in (18) and write

$$\begin{aligned} \frac{Q_0}{\sqrt{2Q_0^{\prime \prime }}}=i\left( n+\frac{1}{2}\right) . \end{aligned}$$

(19)

It can be seen that in the limit $l\rightarrow \infty$, the effective potentials $V(r)$ for all three types of perturbations, given by (16), reduce to much simpler forms so that simple expressions are obtained for the corresponding functions $Q_0$ as follows:

$$\begin{aligned} Q_0\simeq \varOmega ^2-Cl^2\frac{f}{r^2}, \end{aligned}$$

(20)

where the values of the parameter $C$ for tensor ($C_t$), vector ($C_v$) and scalar ($C_s$) perturbations in $d$ dimensions for the Lovelock theory of order $k$ take the form

$$\begin{aligned} C=\left\{ \begin{array}{ll} C_{t}=\frac{1}{d-4}\Biggl [(d-4)-(k-1)\left( \frac{d-1}{k}\right) \Biggr ],\\ C_v=\frac{1}{d-3}\Biggl [(d-3)-(k-1)\left( \frac{d-1}{k}\right) \Biggr ],\\ C_s=\frac{1}{d-2}\Biggl [(d-2)-(k-1)\left( \frac{d-1}{k}\right) \Biggr ]. \end{array} \right. \end{aligned}$$

(21)

Substituting (21) and (20) into (19), we get the following expression for the quasinormal modes in the limit $l\rightarrow \infty$:

$$\begin{aligned} \varOmega _\mathrm{asy}=l\sqrt{C}\sqrt{\frac{f_c}{r_c^2}} -i\frac{\left( n+\frac{1}{2}\right) }{\sqrt{2}} \sqrt{-\frac{r_c^2}{f_c}\left[ \frac{\mathrm{d}^2}{\mathrm{d}r_*^2} \left( \frac{f}{r^2}\right) \right] _{r=r_c}},\nonumber \\ \end{aligned}$$

(22)

with $C$ taking appropriate values depending on the type of perturbation under consideration. The connection between $\varOmega _\mathrm{asy}$ and the null geodesic parameters is clear from (4), (5), and (22). Clearly, the real parts of the modes vary linearly with $l$ while the imaginary parts are independent of $l$. Thus, for the same value of $n$, the imaginary parts of the modes should approach a constant. Also, given a sufficiently high value of the parameter $d$, we have $C_t\simeq C_v\simeq C_s$, which means that the metric perturbations of the spacetime given by (11) should be isospectral if one considers Lovelock theories given by (6) in very high dimensions.

3 Results and discussion

We use (18) to compute the QNMs $\varOmega$ for various combinations of spacetime dimension $d$ and the order parameter $k$. The calculation is done for different values of the mode number $n$. We have tabulated the low-lying modes for $l=2$ in Tables 1, 2, and 3. The parameter $l$ is given values from 6 to 80 and selected values of the QNMs are tabulated in Tables 4, 5, and 6. Tables 8, 9, and 10 show the QNMs for various values of the order $k$. In Table 7, we compare the values of QNMs obtained using the eikonal approximation and the sixth order WKB method. In all tables and figures in this work, $\omega$ stands for $\varOmega G_kM$, where $\varOmega$ is the QNM calculated using (18).

Table 1 Low-lying modes for tensor perturbations for various dimensions (in units of $10^{-6}$)

Table 2 Low-lying modes for vector perturbations for various dimensions (in units of $10^{-6}$)

Table 3 Low-lying modes for scalar perturbations for various dimensions (in units of $10^{-6}$)

Table 4 QNMs of tensor perturbations for $n=1$ (in units of $10^{-6}$)

Table 5 QNMs of vector perturbations for $n=1$ (in units of $10^{-6}$)

Table 6 QNMs of scalar perturbations for $n=1$ (in units of $10^{-6}$)

Table 7 Comparison between the eikonal approximation and the numerical values of QNMs ($d=10$, $k=2$ and $n=1$) (in units of $10^{-6}$)

Table 8 QNMs for Tensor perturbations for various values of $k$ with $d=17$ and $l=7$ (in units of $10^{-14}$)

Table 9 QNMs for vector perturbations for various values of $k$ with $d=17$ and $l=7$ (in units of $10^{-14}$)

Table 10 QNMs for scalar perturbations for various values of $k$ with $d=17$ and $l=7$ (in units of $10^{-14}$)

Figures 2, 3, and 4 are log–log plots of the QNMs for tensor, vector and scalar modes respectively, which show the behavior of the modes as the parameter $l$ varies from relatively low values to high values. From the plots, we observe a behavior that is consistent with that suggested by the null geodesic method. We see that the imaginary parts of the modes tend to become a constant at high values of $l$, just as suggested by (22). The behavior of the imaginary parts for lower values of $l$ is similar to that in an earlier work [29] which also shows a convergent pattern for $\hbox {Im}~\omega$ as $l$ increases.

Fig. 2

Tensor modes for $k=2$ and $d=8$, for $n=5$ (top) and $n=3$ (bottom). The plotted points within each curve are for $l=10$ (left) to $l=80$ (right)

Fig. 3

Vector modes for $k=2$ and $d=8$, for $n=5$ (top) and $n=3$ (bottom). The plotted points within each curve are for $l=10$ (left) to $l=80$ (right)

Fig. 4

Scalar modes for $k=2$ and $d=8$, for $n=5$ (top) and $n=3$ (bottom). The plotted points within each curve are for $l=10$ (left) to $l=80$ (right)

Figures 5, 6, and 7 show the variation of logarithm of the absolute values of the real parts of the QNMs with spacetime dimension $d$. As observed from the plots, the real parts decrease as $d$ increases, indicating modes with lower frequency in higher dimensions. For any value of $d$, the real parts increase with increasing values of $l$.

Fig. 5

Variation of $\ln |\hbox {Re}(\omega )|$ vs. $d$ for $k=2$ for tensor modes. Here, $n=5$. The curves are for $l=10$ (bottom) to $l=50$ (top)

Fig. 6

Variation of $\ln |\hbox {Re}(\omega )|$ vs. $d$ for $k=2$ for vector modes. Here, $n=5$. The curves are for $l=10$ (bottom) to $l=50$ (top)

Fig. 7

Variation of $\ln |\hbox {Re}(\omega )|$ vs. $d$ for $k=2$ for scalar modes. Here, $n=5$. The curves are for $l=10$ (bottom) to $l=50$ (top)

Figures 8, 9, 10, 11, 12, and 13 show the variation of logarithm of the absolute values of the real and imaginary parts of the QNMs with the order parameter $k$. As observed from the plots, the real parts as well as the imaginary parts increase as $k$ increases.

Fig. 8

Variation of $\ln |\hbox {Re}(\omega )|$ vs. $k$ for $d=17$ and $l=7$ for tensor modes. The curves are for $n=0$ (top) to $n=2$ (bottom)

Fig. 9

Variation of $\ln |\hbox {Im}(\omega )|$ vs. $k$ for $d=17$ and $l=7$ for tensor modes. The curves are for $n=0$ (bottom) to $n=2$ (top)

Fig. 10

Variation of $\ln |\hbox {Re}(\omega )|$ vs. $k$ for $d=17$ and $l=7$ for vector modes. The curves are for $n=0$ (top) to $n=2$ (bottom)

Fig. 11

Variation of $\ln |\hbox {Im}(\omega )|$ vs. $k$ for $d=17$ and $l=7$ for vector modes. The curves are for $n=0$ (bottom) to $n=2$ (top)

Fig. 12

Variation of $\ln |\hbox {Re}(\omega )|$ vs. $k$ for $d=17$ and $l=7$ for scalar modes. The curves are for $n=0$ (top) to $n=2$ (bottom)

Fig. 13

Variation of $\ln |\hbox {Im}(\omega )|$ vs. $k$ for $d=17$ and $l=7$ for scalar modes. The curves are for $n=0$ (bottom) to $n=2$ (top)

4 Conclusion

In summary, we have studied the quasinormal modes of metric perturbations of tensor, vector and scalar type for asymptotically flat black hole spacetimes for a particular class of theories in the Lovelock model. These theories are specified by the action given by (6) with the higher order coupling constants given by (10). We used the sixth order WKB formula for the quasinormal modes [24] in order to compute the QNMs for various values of $d$ and $k$. We also used the connection between null geodesic parameters and the asymptotic quasinormal modes of static and spherically symmetric spacetimes, established in [16], to deduce an analytic form for the asymptotic modes in the limit $l \rightarrow \infty$. Numerical analysis indicates that the asymptotic behavior of the QNMs in higher order theories is indeed consistent with the theory, as can be seen easily from Table 7. We observe that the imaginary parts of the modes attain a constant value for very high values of the parameter $l$, just as suggested by the null geodesic method. We calculated the quasinormal modes of perturbations for different orders of the Lovelock theory and found that the real as well as imaginary parts of the modes increase with increasing values of $k$. We also find that the real parts of the modes decrease with increase in the spacetime dimension $d$. The theory also suggests that the modes should be approximately isospectral at high values of $d$. This is seen to hold roughly at $d\ge 10$, especially in the case of imaginary parts. The quasinormal behavior revealed in this study helps us understand better the dynamics of fields in the vicinity of black holes in higher order theories of gravity.