Abstract
A study of \(\upchi _{{\mathrm {b}}}\) meson production at LHCb is performed on proton–proton collision data, corresponding to 3.0\(\text { fb}^{-1}\)of integrated luminosity collected at centre-of-mass energies \(\sqrt{s}\) = 7 and 8 \(\mathrm {\,TeV}\). The fraction of \(\Upsilon \mathrm {(nS)}\) mesons originating from \(\upchi _{{\mathrm {b}}}\) decays is measured as a function of the \(\Upsilon \) transverse momentum in the rapidity range \(2.0 < y^{\Upsilon } < 4.5\). The radiative transition of the \(\upchi _{{\mathrm {b}}}\mathrm {(3P)}\) meson to \(\Upsilon \mathrm {(3S)}\) is observed for the first time. The \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) mass is determined to be
where the first uncertainty is statistical and the second is systematic.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The production of quarkonia states in high-energy hadron collisions is described in the framework of non-relativistic quantum chromodynamics (NRQCD), as two-step process: a heavy quark–antiquark pair is first created perturbatively at short distances, then it evolves non-perturbatively into quarkonium at long distances. The NRQCD framework makes use of a combination of colour-singlet and colour-octet mechanisms [1–5]. Recent calculations [6–10] support the leading role of the colour-singlet mechanism. The comparison of experimental data for prompt production of S-wave quarkonia, e.g. \({\mathrm {J}/\uppsi }\) or \(\Upsilon \mathrm {(1S)}\) mesons, with theory predictions requires knowledge of feed-down contributions from P-wave quarkonia states, e.g. radiative \(\upchi _{{\mathrm {b}}} \!\rightarrow \Upsilon {\upgamma } \) decays. This contribution could significantly influence the interpretation of the measured polarization of S-wave vector quarkonia. In addition, measurements of the relative production rates of P-wave to S-wave quarkonia, as well as the tensor-to-vector ratios, provide valuable information on colour-octet matrix elements [10–12].
The production of P-wave charmonia, jointly referred to as \(\upchi _{{\mathrm {c}}}\) states, has been studied by the CDF [13], HERA-B [14], LHCb [15–17], CMS [18], and ATLAS [19] collaborations; measurements involving \(\upchi _{{\mathrm {b}}}\) states have been performed by the CDF [20], ATLAS [21], CMS [22] and LHCb [23, 24] experiments.
This paper presents a measurement of the fractions of \(\Upsilon \) mesons originating from radiative decays of \(\upchi _{{\mathrm {b}}}\) mesons. Depending on the relative orientation of the quark spins, the \(\upchi _{{\mathrm {b}}}\) states can be either scalar, vector or tensor mesons, denoted by \(\upchi _{{\mathrm {b}} \mathrm {J}}\) with total angular momentum \(\mathrm {J}=0,1,2\). The fractions of \(\Upsilon \mathrm {(nS)}\) decays originating from \(\upchi _{{\mathrm {b}}}\mathrm {(mP)}\) decays, where \(\mathrm {n}\) and \(\mathrm {m}\) are radial quantum numbers of the bound states are defined as
where \(\mathcal{B} _{1(2)}\) denotes the branching fraction for the decay \(\upchi _{{\mathrm {b}} 1(2)}\mathrm {(mP)}\!\rightarrow \Upsilon \mathrm {(nS)} {\upgamma } \). Possible contributions from \(\upchi _{{\mathrm {b}} 0}\mathrm {(mP)}\!\rightarrow \Upsilon \mathrm {(nS)} {\upgamma } \) decays are neglected because of the small branching fraction for the corresponding radiative decays [25].
The results presented in this paper supersede earlier LHCb measurements [23, 24]. In particular, the full data sample collected by LHCb at \(\sqrt{s} =7\) and 8\(\mathrm {\,TeV}\) has been used and the measured fractions \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}_{\Upsilon \mathrm {(nS)}}\) are reported for all six kinematically allowed transitions: \(\upchi _{{\mathrm {b}}}\mathrm {(1P)} \!\rightarrow \Upsilon \mathrm {(1S)} {\upgamma } \), \(\upchi _{{\mathrm {b}}}\mathrm {(2P)} \!\rightarrow \Upsilon \mathrm {(1S)} {\upgamma } \), \(\upchi _{{\mathrm {b}}}\mathrm {(2P)} \!\rightarrow \Upsilon \mathrm {(2S)} {\upgamma } \), \(\upchi _{{\mathrm {b}}}\mathrm {(3P)} \!\rightarrow \Upsilon \mathrm {(1S)} {\upgamma } \), \(\upchi _{{\mathrm {b}}}\mathrm {(3P)} \!\rightarrow \Upsilon \mathrm {(2S)} {\upgamma } \) and \(\upchi _{{\mathrm {b}}}\mathrm {(3P)} \!\rightarrow \Upsilon \mathrm {(3S)} {\upgamma } \) in bins of transverse momentum of the \(\Upsilon \) mesons in the rapidity range \(2.0<y<4.5\). The last transition, which is usually not considered in theory predictions, is observed for the first time. A precise measurement of the mass of the \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) meson, which was recently observed by the ATLAS [21], D0 [26] and LHCb [24] collaborations, is also performed.
2 The LHCb detector and data samples
The LHCb detector [27] is a single-arm forward spectrometer covering the pseudorapidity range \(2<\eta <5\), designed for the study of heavy-flavoured particles. The detector includes a high-precision tracking system consisting of a silicon-strip vertex detector surrounding the interaction region, a large-area silicon-strip detector located upstream of a dipole magnet with a bending power of about \(4\mathrm{\,Tm}\), and three stations of silicon-strip detectors and straw drift tubes placed downstream of the magnet. The combined tracking system provides a momentum measurement with a relative uncertainty that varies from 0.4 % at low momentum to 0.6 % at 100\({\mathrm {\,GeV}/c}\), and an impact parameter measurement with a resolution of 20\({\,\upmu \mathrm{m}}\) for charged particles with large transverse momentum, \(p_\mathrm{T}\). Different types of charged hadrons are distinguished using information from two ring-imaging Cherenkov detectors (RICH) [28]. Photon, electron and hadron candidates are identified by a calorimeter system consisting of scintillating-pad (SPD) and preshower (PS) detectors, an electromagnetic calorimeter (ECAL) and a hadronic calorimeter [29]. Muons are identified by a system composed of alternating layers of iron and multiwire proportional chambers [30]. The trigger [31] consists of a hardware stage, based on information from the calorimeter and muon systems, followed by a software stage, which applies a full event reconstruction.
Candidate events used in this analysis must pass the hardware trigger, with the specific requirement that the product of the \(p_\mathrm{T}\) of two muon candidates be greater than \((1.3{\mathrm {\,GeV}/c})^2\) and \((1.6{\mathrm {\,GeV}/c})^2\) for data collected at \(\sqrt{s} =7\) and 8\(\mathrm {\,TeV}\), respectively. The first stage of the software trigger selects candidate events with two well-reconstructed tracks with hits in the muon system, \(p_\mathrm{T}\) greater than 500\({\mathrm {\,MeV}/c}\) and momentum greater than 6\({\mathrm {\,GeV}/c}\) for each track. The two tracks are required to originate from a common vertex and to have an invariant mass greater than 2.7\({\mathrm {\,GeV}/c^2}\). Events are required to pass a second software trigger stage, where the previous trigger decision is confirmed using improved track reconstruction algorithms, and the requirement that the invariant mass of the dimuon pair exceeds 4.7\({\mathrm {\,GeV}/c^2}\) is applied.
The data samples used in this paper have been collected by the LHCb detector in \(\mathrm {p} \) \(\mathrm {p} \) collisions at \(\sqrt{s} =7\) and 8\(\mathrm {\,TeV}\) with integrated luminosities of 1.0\(\text { fb}^{-1}\)and 2.0\(\text { fb}^{-1}\), respectively. Simulated samples are used to determine signal efficiencies. In these samples, \(\Upsilon \) and \(\upchi _{{\mathrm {b}}}\) mesons are produced unpolarized. The effect of the unknown initial polarization on the efficiencies, and therefore on the results, is taken into account as a systematic uncertainty. In the simulation, \(\mathrm {p} \) \(\mathrm {p} \) collisions are generated using Pythia [32] with a specific LHCb configuration [33]. Decays of hadrons are described by EvtGen [34], in which final-state radiation is generated using Photos [35]. The interaction of the generated particles with the detector and its response are implemented using the Geant4 toolkit [36, 37] as described in Ref. [38]. A comparison of the distributions of the relevant variables used in this analysis is performed on data and simulated samples, in order to assess the reliability of the simulation in computing signal efficiencies and good agreement is found.
3 Event selection and signal extraction
This analysis proceeds through the reconstruction of \(\Upsilon \mathrm {(nS)}\) candidates via their dimuon decays and their subsequent pairing with a photon candidate to reconstruct \(\upchi _{{\mathrm {b}}} \!\rightarrow \Upsilon {\upgamma } \) decays.
The \(\Upsilon \) candidates are selected from pairs of oppositely charged tracks identified as muons and originating from a common vertex. The muons are required to have \(p_\mathrm{T}\) larger than 1\({\mathrm {\,GeV}/c}\). Good track quality is ensured by requiring a \(\chi ^2 \) per degree of freedom, \(\chi ^2/\mathrm {ndf}\), of the track fit to be less than 4 [39]. A multivariate estimator, based on information from the tracking, muon and RICH systems, as well as compatibility with the hypothesis of a minimum ionizing particle in the calorimeter system [40–42], is used to improve the muon identification purity. The identification efficiency for muons from \(\Upsilon \rightarrow {\upmu ^+\upmu ^-} \) decays rises from 75 % to 98 % as the transverse momentum of the muon increases from 1\({\mathrm {\,GeV}/c}\) to 3\({\mathrm {\,GeV}/c}\). A good quality of the two-prong common vertex is ensured by requiring the p-value of the common vertex fit to be greater than 0.5 %. To improve the dimuon mass resolution and to suppress combinatorial background from muons originating in semileptonic decays of heavy-flavoured hadrons, the dimuon vertex is refitted using the position of the reconstructed \(\mathrm {p} \) \(\mathrm {p} \) collision vertex as an additional constraint [43]. The p-value for this fit is required to be larger than 0.05 %. When several collision vertices are reconstructed in the event, the one closest to the dimuon vertex is used.
The invariant mass distributions for selected dimuon candidates in the kinematic range of transverse momentum \(6<p_{\mathrm {T}}^{{\upmu ^+\upmu ^-}}<40{\mathrm {\,GeV}/c} \) and rapidity \(2.0<y^{{\upmu ^+\upmu ^-}}<4.5\) are shown in Fig. 1 for data collected at \(\sqrt{s} =7\) and 8\(\mathrm {\,TeV}\). Three clear peaks are visible, corresponding to the \(\Upsilon \mathrm {(1S)}\), \(\Upsilon \mathrm {(2S)}\) and \(\Upsilon \mathrm {(3S)}\) signals (low-mass to high-mass). The yields of the \(\Upsilon \mathrm {(nS)}\) signals are determined using an extended maximum likelihood fit to the unbinned dimuon mass distributions. The fit function is parameterised as the sum of three signal components and combinatorial background. Each \(\Upsilon \) signal has been modelled with a modified Gaussian function with power-law tails on both sides. The combinatorial background is modelled with an exponential function. The tail parameters of the signal functions are fixed using simulated events, whereas the mean and resolution are allowed to vary in the fit. The fit results are superimposed in Fig. 1 and fitted signal yields are summarized in Table 1. The peak positions and mass resolutions are found to be in good agreement for the data collected at \(\sqrt{s} =7\) and 8\(\mathrm {\,TeV}\), and in agreement with the known \(\Upsilon \mathrm {(nS)}\) masses [25] and the resolutions expected from simulated samples.
Invariant mass distributions for selected dimuon candidates in the kinematic range \(6<p_{\mathrm {T}}^{{\upmu ^+\upmu ^-}}<40{\mathrm {\,GeV}/c} \) and \(2.0<y^{{\upmu ^+\upmu ^-}}<4.5\) for ( left) data collected at \(\sqrt{s} =7\,\mathrm {TeV}\) and ( right) \(8\,\mathrm {TeV}\). The three peaks on each plot correspond to the \(\Upsilon \mathrm {(1S)}\), \(\Upsilon \mathrm {(2S)}\) and \(\Upsilon \mathrm {(3S)}\) signals (low-mass to high-mass). The result of the fit, described in the text, is illustrated with a red solid line, while the background component is shown with a blue dashed line
Muon pairs with invariant mass in the intervals \(9310<m_{{\upmu ^+\upmu ^-}}<9600{\mathrm {\,MeV}/c^2} \), \(9860<m_{{\upmu ^+\upmu ^-}}<10\,155{\mathrm {\,MeV}/c^2} \) and \(10\,220<m_{{\upmu ^+\upmu ^-}}<10\,520{\mathrm {\,MeV}/c^2} \) are used as \(\Upsilon \mathrm {(1S)}\), \(\Upsilon \mathrm {(2S)}\) and \(\Upsilon \mathrm {(3S)}\) candidates, respectively, when reconstructing \(\upchi _{{\mathrm {b}}}\) particles. The selected \(\Upsilon \) candidates are combined with photons reconstructed using the electromagnetic calorimeter and identified using a likelihood-based estimator, constructed from variables that rely on calorimeter and tracking information [16, 29, 44, 45]. Candidate photon clusters must not be associated with the position of any reconstructed track extrapolated to the calorimeter. The photon selection is further refined by using information from the PS and SPD detectors. The photon transverse energy is required to be greater than 600\(\mathrm {\,MeV}\).
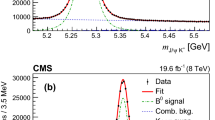
Distributions of the corrected mass \(m_{\Upsilon \mathrm {(nS)} {\upgamma }}\) for the selected \(\upchi _{{\mathrm {b}}}\) candidates ( black points) decaying into ( top row) \(\Upsilon \mathrm {(1S)}\), ( middle row) \(\Upsilon \mathrm {(2S)}\) and ( bottom row) \(\Upsilon \mathrm {(3S)}\), in the transverse momentum ranges given in the text, for ( left) \(\sqrt{s} =7\,\mathrm {TeV}\) and (right) \(8\,\mathrm {TeV}\) data. Each plot shows also the result of the fit ( solid red curve), including the background (dotted blue curve) and the signal ( dashed green and magenta curves) contributions. The magenta dashed curve corresponds to the \(\upchi _{{\mathrm {b}} 1}\) signal and the green dashed curve to the \(\upchi _{{\mathrm {b}} 2}\) signal
The \(\upchi _{{\mathrm {b}}}\) signals are searched for in the invariant mass of \(\Upsilon {\upgamma } \) combinations. To improve the \(\Upsilon \mathrm {(nS)} {\upgamma } \) mass resolution and to remove any residual bias, the corrected mass
is used, where \(m_{\Upsilon \mathrm {(nS)}}\) is the known mass of the \(\Upsilon \mathrm {(nS)}\) meson [25]. The resolution improves by a factor between two and four with respect to the one obtained by simply computing the invariant mass of the \(\Upsilon {\upgamma } \) pair. The distributions of the corrected masses \(m_{\Upsilon \mathrm {(nS)} {\upgamma }}\) are shown in Fig. 2 for \(\Upsilon \mathrm {(1S)}\), \(\Upsilon \mathrm {(2S)}\) and \(\Upsilon \mathrm {(3S)}\) candidates in the transverse momentum ranges \(14<p_{\mathrm {T}}^{\Upsilon \mathrm {(1S)}}<40{\mathrm {\,GeV}/c} \), \(18<p_{\mathrm {T}}^{\Upsilon \mathrm {(2S)}}<40{\mathrm {\,GeV}/c} \) and \(24<p_{\mathrm {T}}^{\Upsilon \mathrm {(3S)}}<40{\mathrm {\,GeV}/c} \).
The yields of \(\upchi _{{\mathrm {b}}}\mathrm {(mP)}\) mesons are determined from an extended maximum likelihood fit to the unbinned \(m_{\Upsilon \mathrm {(nS)} {\upgamma }}\) distributions. The fit model consists of the sum of signal components for all kinematically allowed \(\upchi _{{\mathrm {b}}}\mathrm {(mP)} \!\rightarrow \Upsilon \mathrm {(nS)} {\upgamma } \) decays and combinatorial background. Neglecting a possible contribution due to \(\upchi _{{\mathrm {b}} 0}\mathrm {(mP)}\!\rightarrow \Upsilon \mathrm {(nS)} {\upgamma } \) decays, the signal from each \(\upchi _{{\mathrm {b}}}\mathrm {(mP)} \) multiplet is parameterised as the sum of two overlapping Crystal Ball (CB) functions [46] with high-mass tails. The peak positions are separated by the known mass-splitting between the tensor and vector states in the \(\upchi _{{\mathrm {b}}}\mathrm {(1P)}\) and \(\upchi _{{\mathrm {b}}}\mathrm {(2P)}\) multiplets [25]. For the \(\upchi _{{\mathrm {b}}}\mathrm {(3P)}\) multiplet the expected splitting of \(10.5{\mathrm {\,MeV}/c^2} \) [47, 48] is used. The tail parameters of the CB functions and the resolutions are fixed to the values determined using simulated samples. The yield fractions \(N_{\upchi _{{\mathrm {b}} 2}}/N_{\upchi _{{\mathrm {b}} 1}}\) of the tensor and vector states in each \(\upchi _{{\mathrm {b}}}\mathrm {(mP)}\) multiplet are assumed to be equal to 0.5 according to expectations from Refs. [11, 47]. For the \(\upchi _{{\mathrm {b}}}\mathrm {(1P)}\) and \(\upchi _{{\mathrm {b}}}\mathrm {(2P)}\) cases, this choice agrees with direct measurements of the relative productions of \(\upchi _{{\mathrm {b}} 2}\mathrm {(1P)}/\upchi _{{\mathrm {b}} 1}\mathrm {(1P)} \) and \(\upchi _{{\mathrm {b}} 2}\mathrm {(2P)}/\upchi _{{\mathrm {b}} 1}\mathrm {(2P)} \) [22, 49]. This assumption is necessary for the determination of signal yields, since the \(\upchi _{{\mathrm {b}} 1}\) and \(\upchi _{{\mathrm {b}} 2}\) states cannot be resolved given the limited invariant mass resolution for the \(\Upsilon \mathrm {(nS)} {\upgamma } \) system. The impact of this assumption is quantified as a systematic uncertainty. With this parameterisation for the twelve \(\upchi _{{\mathrm {b}}}\) signal components, the free parameters are the three masses of the \(\upchi _{{\mathrm {b}} 1}\) states and the six overall yields of \(\upchi _{{\mathrm {b}} 1}\) and \(\upchi _{{\mathrm {b}} 2}\) signals. The combinatorial background is parameterised as the product of an exponential and polynomial functions up to the fourth order. The fit results are superimposed on Fig. 2 and the signal yields are summarized in Table 2.
To perform a precise measurement of the \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) mass, the data samples collected at \(\sqrt{s} =7\) and 8\(\mathrm {\,TeV}\) are combined. A fit to the combined sample of \({\upchi _{{\mathrm {b}}}\mathrm {(3P)} \!\rightarrow \Upsilon \mathrm {(3S)} {\upgamma } }\) decays gives
where the uncertainty is statistical only.
For the determination of the \(\upchi _{{\mathrm {b}}}\) signal yields in \(p_{\mathrm {T}}^{\Upsilon }\) bins, the masses of the \(\upchi _{{\mathrm {b}} 1}\) states in the fits are fixed to the values obtained in the fits to the full \(p_\mathrm{T}\) ranges. For each \(p_{\mathrm {T}}^{\Upsilon }\) bin the fractions \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}_{\Upsilon \mathrm {(nS)}}\), defined by Eq. (1), are calculated separately for \(\sqrt{s}\) =7 and 8\(\mathrm {\,TeV}\) data samples as
where \(\varepsilon _{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}\) and \(\varepsilon _{\Upsilon \mathrm {(nS)}}\) denote the total efficiencies, and \(N_{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}\) and \(N_{\Upsilon \mathrm {(nS)}}\) are the fitted yields for the \(\upchi _{{\mathrm {b}}}\mathrm {(mP)}\) and \(\Upsilon \mathrm {(nS)}\) states for the respective \(p_{\mathrm {T}}^{\Upsilon }\) bin. The ratio of the efficiencies \(\varepsilon _{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}\) and \(\varepsilon _{\Upsilon \mathrm {(nS)}}\) is largely determined by the reconstruction efficiency for photons from \(\upchi _{{\mathrm {b}}}\) decays. It is close to 25 % for \(\upchi _{{\mathrm {b}}}\) mesons with transverse momentum larger than 20\({\mathrm {\,GeV}/c}\), and it drops to approximately 10 % for the lowest \(p_\mathrm{T}\) considered in this analysis. The dominant sources of inefficiency are the geometrical acceptance of the electromagnetic calorimeter, photon conversions in the detector material, the accidental overlap of clusters in the ECAL and the selection requirement on the photon transverse energy. The measurements are performed in six bins of \(p_{\mathrm {T}}^{\Upsilon \mathrm {(1S)}}\) in the range \(6<p_{\mathrm {T}}^{\Upsilon \mathrm {(1S)}}<40{\mathrm {\,GeV}/c} \), five bins of \(p_{\mathrm {T}}^{\Upsilon \mathrm {(2S)}}\) in the range \(18<p_{\mathrm {T}}^{\Upsilon \mathrm {(2S)}}<40{\mathrm {\,GeV}/c} \) and two bins of \(p_{\mathrm {T}}^{\Upsilon \mathrm {(3S)}}\) in the range \(24<p_{\mathrm {T}}^{\Upsilon \mathrm {(3S)}}<40{\mathrm {\,GeV}/c} \).
4 Systematic uncertainties
The systematic uncertainties on the fractions \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}_{\Upsilon \mathrm {(nS)}}\), calculated using Eq. (3), are related to the determination of the signal yields and the evaluation of the efficiency ratios. The main contributions to the former are due to fit modelling, whereas the photon reconstruction efficiency and the knowledge of the initial state polarization dominate the uncertainty on the ratios of efficiencies \(\varepsilon _{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}/\varepsilon _{\Upsilon \mathrm {(nS)}}\). The contributions due to other effects largely cancel in these ratios.
Based on studies from Refs. [23, 50–52] the systematic uncertainty associated with the \(\Upsilon \) signal yields determination is taken to be 0.7 % for all \(p_{\mathrm {T}}^{\Upsilon }\) bins.
In the \(\upchi _{{\mathrm {b}}}\) fit model several sources of uncertainty are taken into account. The yield ratio \(N(\upchi _{{\mathrm {b}} 2})/N(\upchi _{{\mathrm {b}} 1})\), which is fixed in the fit to be 0.5 as predicted by theory, is varied from 0.3 to 1.0. These limits are obtained by following the prescription of Ref. [11], where the experimentally measured cross-section ratio of \(\upchi _{{\mathrm {c}}}\) mesons is rescaled to predict the corresponding ratio for \(\upchi _{{\mathrm {b}}}\) mesons. The ratio of cross-sections is then converted to a ratio of yields by taking into account the \(\upchi _{{\mathrm {b}} 1}\) and \(\upchi _{{\mathrm {b}} 2}\) radiative branching fractions and reconstruction efficiencies. For the \(\upchi _{{\mathrm {b}}}\mathrm {(1P)}\) and the \(\upchi _{{\mathrm {b}}}\mathrm {(2P)}\) mesons, the variation obtained agrees within uncertainties with the direct measurements of relative productions of \(\upchi _{{\mathrm {b}} 2}\mathrm {(1P)} \) and \(\upchi _{{\mathrm {b}} 1}\mathrm {(1P)} \) mesons and \(\upchi _{{\mathrm {b}} 2}\mathrm {(2P)} \) and \(\upchi _{{\mathrm {b}} 1}\mathrm {(2P)} \) mesons [49]. The corresponding systematic uncertainty on \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}_{\Upsilon \mathrm {(nS)}}\) varies between 0.1 % and 15 % across \(p_{\mathrm {T}}^{\Upsilon }\) bins. The systematic uncertainty due to a slight dependence of the mass fit results on \(p_{\mathrm {T}}^{\Upsilon }\) is estimated by taking the minimum and the maximum values of the \(\upchi _{{\mathrm {b}} 1} \) masses, repeating the fit and taking the maximum difference in the yields. The assigned uncertainty varies between 0.3 % and 20 % for various \(p_{\mathrm {T}}^{\Upsilon }\) bins. The smaller values corresponds to the low-Q transitions: \(\upchi _{{\mathrm {b}}}\mathrm {(1P)} \!\rightarrow \Upsilon \mathrm {(1S)} {\upgamma } \), \(\upchi _{{\mathrm {b}}}\mathrm {(2P)} \!\rightarrow \Upsilon \mathrm {(2S)} {\upgamma } \) and \(\upchi _{{\mathrm {b}}}\mathrm {(3P)} \!\rightarrow \Upsilon \mathrm {(3S)} {\upgamma } \). To assess the systematic uncertainty related to possible mismodelling of the mass resolution, the mass resolution is varied by \(\pm 10\,\%\) around the values obtained using simulated samples, and the difference between the obtained \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}_{\Upsilon \mathrm {(nS)}}\) is treated as the corresponding systematic uncertainty. The maximum deviation in the results obtained from varying by \(\pm 1\) the order of the polynomial function used in the fit model to describe the combinatorial background, is assigned as the systematic uncertainty associated with the background parameterisation. For the \(\upchi _{{\mathrm {b}}}\mathrm {(3P)}\) case, a systematic uncertainty stems from the assumption on the mass splitting between \(\upchi _{{\mathrm {b}} 2}\mathrm {(3P)}\) and \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) states. This parameter is varied in the range between 9 and 12\({\mathrm {\,MeV}/c^2}\). The obtained uncertainty for \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(3P)}}_{\Upsilon \mathrm {(3S)}}\) is found to be much smaller than the one obtained for \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(3P)}}_{\Upsilon \mathrm {(1S)}}\) and \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(3P)}}_{\Upsilon \mathrm {(2S)}}\). The assigned uncertainty on \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(3P)}}_{\Upsilon \mathrm {(nS)}}\) varies between 0.1 % and 2 %.
The uncertainty due to possible imperfections in the simulation in the determination of the photon reconstruction efficiency is studied by comparing the relative yields between data and simulation for \({{\mathrm {B}} ^+} \rightarrow {{\mathrm {J}/\uppsi }} \mathrm {K}^{*+}\) and \({{\mathrm {B}} ^+} \rightarrow {{\mathrm {J}/\uppsi }} \mathrm {K}^{+}\) decays, where the \(\mathrm {K}^{*+}\) meson is reconstructed using the \(\mathrm {K}^+{{\uppi } ^0} \) final state [23, 45, 53–55]. According to these studies, a systematic uncertainty of 3 % is assigned for photons in the kinematical range considered in this analysis. This uncertainty is dominated by the knowledge of the ratio of the branching fractions for \({{\mathrm {B}} ^+} \rightarrow {{\mathrm {J}/\uppsi }} \mathrm {K}^{*+}\) and \({{\mathrm {B}} ^+} \rightarrow {{\mathrm {J}/\uppsi }} \mathrm {K}^{+}\) decays.
Another source of systematic uncertainty is associated with the unknown polarization of \(\upchi _{{\mathrm {b}}}\) and \(\Upsilon \) states. The polarization of \(\Upsilon \) mesons for \(p_{\mathrm {T}}^{\Upsilon }>10{\mathrm {\,GeV}/c} \) and in the central rapidity region \(|y^{\Upsilon }|<1.2\) has been found to be small by the CMS collaboration [56]. Therefore in this paper we assume zero polarization of \(\Upsilon \) mesons and no systematic uncertainty is assigned due to this effect. The systematic uncertainty related to the unknown polarization of \(\upchi _{{\mathrm {b}}}\) mesons was estimated following Refs. [14, 17]. For each \(p_{\mathrm {T}}^{\Upsilon }\) bin, the ratios of efficiencies \(\varepsilon _{\upchi _{{\mathrm {b}} 1}}/\varepsilon _{\Upsilon }\) and \(\varepsilon _{\upchi _{{\mathrm {b}} 2}}/\varepsilon _{\Upsilon }\) are recomputed using various possible polarizations scenarios for \(\upchi _{{\mathrm {b}} 1}\) and \(\upchi _{{\mathrm {b}} 2}\) mesons. The maximum deviation of the efficiency ratio with respect to the one obtained with unpolarized production of \(\upchi _{{\mathrm {b}} 1}\) and \(\upchi _{{\mathrm {b}} 2}\) states is taken as the systematic uncertainty. The assigned uncertainty on \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}_{\Upsilon \mathrm {(nS)}}\) varies between 0.9 % and 9 % for various \(p_{\mathrm {T}}^{\Upsilon }\) bins.
Systematic uncertainties due to external experimental inputs, e.g. the \(\Upsilon \) mass or the mass splitting of \(\upchi _{{\mathrm {b}}}\mathrm {(1P)}\) and \(\upchi _{{\mathrm {b}}}\mathrm {(2P)}\) multiplets, are negligible. The systematic uncertainties on the \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}_{\Upsilon \mathrm {(nS)}}\) measurements are summarized in Table 3.
Systematic uncertainties on the measurement of the \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) mass are due to the ECAL energy scale, the fit model and the \(\Upsilon \mathrm {(3S)}\) mass [25]. The first of these is studied by comparing the reconstructed invariant mass of photons in \({{\uppi } ^0} \!\rightarrow {\upgamma } {\upgamma } \) decays with the known mass of the neutral pion [57–59], which gives an uncertainty of 1.0\({\mathrm {\,MeV}/c^2}\) in \(\upchi _{{\mathrm {b}}}\mathrm {(3P)} \!\rightarrow \Upsilon \mathrm {(3S)} {\upgamma } \) decays. The effects of possible mismodelling of the mass resolution and background models are found to be 0.8\({\mathrm {\,MeV}/c^2}\) and 0.3\({\mathrm {\,MeV}/c^2}\), respectively. Other significant contributions to the systematic uncertainty are related to the assumptions on \(N(\upchi _{{\mathrm {b}} 2})/N(\upchi _{{\mathrm {b}} 1})\), and to the mass splitting between \(\upchi _{{\mathrm {b}}}\) multiplet components. The effect of the unknown value for the mass-splitting is tested by varying \(m_{\upchi _{{\mathrm {b}} 2}\mathrm {(3P)}}-m_{\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}}\) in the fit in a range between 9 and 12\({\mathrm {\,MeV}/c^2}\), preferred by theory [47, 48]; the obtained deviation of 0.4\({\mathrm {\,MeV}/c^2}\) is assigned as the corresponding systematic uncertainty. The \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) mass exhibits a linear dependence on the assumed fraction of \(\upchi _{{\mathrm {b}} 1}\) decays and varies from \(10\,509\) to \(10\,513\) \({\mathrm {\,MeV}/c^2}\), when the \(\upchi _{{\mathrm {b}} 2}/\upchi _{{\mathrm {b}} 1} \) yield ratio changes from 0.3 to 1.0. The determination of the \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) mass is further checked using the large \(\upchi _{{\mathrm {b}}}\mathrm {(1P)} \rightarrow \Upsilon \mathrm {(1S)} {\upgamma } \) signal, where the measured \(\upchi _{{\mathrm {b}} 1}\mathrm {(1P)}\) mass agrees with the known \(\upchi _{{\mathrm {b}} 1}\mathrm {(1P)}\) mass [25] to better than 0.5\({\mathrm {\,MeV}/c}\), separately for \(\sqrt{s} =7\) and 8\(\mathrm {\,TeV}\) data. No additional systematic uncertainty is assigned. The systematic uncertainties on the \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) mass measurement are summarized in Table 4.
5 Results and conclusion
The measured fractions \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}_{\Upsilon \mathrm {(nS)}}\) are presented in Fig. 3 and Tables 5 and 6. The results are dominated by the statistical uncertainties, and show no dependence on the \(\mathrm {p} \) \(\mathrm {p} \) collision energy. A measurement of the \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(3P)}}_{\Upsilon \mathrm {(3S)}}\) fraction is performed for the first time. The large value of this fraction impacts the interpretation of experimental data on \(\Upsilon \) production and polarization. When data on \(\Upsilon \) production and polarization are compared with theory predictions, as well as when different theory predictions are compared among themselves, it is often implicitly assumed that the fraction of \(\Upsilon \mathrm {(3S)}\) mesons produced by feed down from higher states is small. The large measured value of \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(3P)}}_{\Upsilon \mathrm {(3S)}}\) indicates that these assumptions need to be revisited.
Fractions \(\mathcal {R}^{\upchi _{{\mathrm {b}}}\mathrm {(mP)}}_{\Upsilon \mathrm {(nS)}}\) as functions of \(p_{\mathrm {T}}^{\Upsilon }\). Points with blue open ( red solid) symbols correspond to data collected at \(\sqrt{s} =7(8)\,\mathrm {TeV}\), respectively. For better visualization the data points are slightly displaced from the bin centres. The inner error bars represent statistical uncertainties, while the outer error bars indicate statistical and systematic uncertainties added in quadrature
In conclusion, the fractions of \(\Upsilon \) mesons originating from \(\upchi _{{\mathrm {b}}}\) radiative decays are measured using a data sample collected by LHCb at centre-of-mass energies of 7 and 8\(\mathrm {\,TeV}\), as a function of the \(\Upsilon \) transverse momentum in the kinematic range \(2.0<y^{\Upsilon }<4.5\). The results presented in this paper supersede previous LHCb measurements [23] by increasing the statistical precision and exploiting more decay modes and higher transverse momentum regions. The measurement of the \(\Upsilon \mathrm {(3S)}\) production fraction due to radiative \(\upchi _{{\mathrm {b}}}\mathrm {(3P)}\) decays is performed for the first time.
Assuming the mass splitting \(m_{\upchi _{{\mathrm {b}} 2}\mathrm {(3P)}}-m_{\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}}=10.5{\mathrm {\,MeV}/c^2} \), the mass of \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) state is measured to be
where the first uncertainty is statistical and the second systematic. This result is compatible and significantly more precise than the event yield average mass of \(\upchi _{{\mathrm {b}} 1}\mathrm {(3P)}\) and \(\upchi _{{\mathrm {b}} 2}\mathrm {(3P)}\) states of \(10\,530 \pm 5\pm 17{\mathrm {\,MeV}/c^2} \) and \(10\,551 \pm 14\pm 17{\mathrm {\,MeV}/c^2} \), reported by the ATLAS [21] and D0 [26] experiments, respectively.
References
V.G. Kartvelishvili, A.K. Likhoded, S.R. Slabospitsky, \(D\) meson and \(\psi \) meson production in hadronic interactions. Sov. J. Nucl. Phys. 28, 678 (1978)
E.L. Berger, D. Jones, Inelastic photoproduction of \(J/\psi \) and \(\Upsilon \) by gluons. Phys. Rev. D23, 1521 (1981)
R. Baier, R. Rückl, Hadronic production of \(J/\psi \) and \(\Upsilon \): transverse momentum distributions. Phys. Lett. B102, 364 (1981)
E. Braaten, S. Fleming, Color octet fragmentation and the \(\psi ^{\prime }\) surplus at the Fermilab Tevatron. Phys. Rev. Lett. 74, 3327 (1995). arXiv:hep-ph/9411365
G.T. Bodwin, E. Braaten, G.P. Lepage, Rigorous QCD analysis of inclusive annihilation and production of heavy quarkonium. Phys. Rev. D51, 1125 (1995). arXiv:hep-ph/9407339
B. Gong, J.-X. Wang, Next-to-leading-order QCD corrections to \(J/\psi \) polarization at tevatron and large-hadron-collider energies. Phys. Rev. Lett. 100, 232001 (2008). arXiv:0802.3727
J. Campbell, F. Maltoni, F. Tramontano, QCD corrections to \(J/\psi \) and \(\Upsilon \) production at hadron colliders. Phys. Rev. Lett. 98, 252002 (2007). arXiv:hep-ph/0703113
P. Artoisenet et al., \(\Upsilon \) production at fermilab tevatron and LHC energies. Phys. Rev. Lett. 101, 152001 (2008). arXiv:0806.3282
J.-P. Lansberg, On the mechanisms of heavy-quarkonium hadroproduction. Eur. Phys. J. C61, 693 (2009). arXiv:0811.4005
Y.-Q. Ma, K. Wang, K.-T. Chao, QCD radiative corrections to \(\chi _{cJ}\) production at hadron colliders. Phys. Rev. D83, 111503 (2011). arXiv:1002.3987
A.K. Likhoded, A.V. Luchinsky, S.V. Poslavsky, Production of \(\chi _{b}\)-mesons at LHC. Phys. Rev. D86, 074027 (2012). arXiv:1203.4893
A. K. Likhoded, A. V. Luchinsky, S. V. Poslavsky, Hadronic production of \(\chi _{c}\)-mesons at the LHC. arXiv:1305.2389
CDF collaboration, A. Abulencia et al., Measurement of \(\sigma _{\chi _{c2}}{\cal B}(\chi _{c2} \rightarrow {\rm J}/\psi \gamma )/\sigma _{\chi _{c 1}} {\cal B}(\chi _{c 1} \rightarrow J/\psi \gamma )\) in \(p\bar{p}\) collisions at \(\sqrt{s}\) = 1.96 TeV. Phys. Rev. Lett. 98 (2007) 232001. arXiv:hep-ex/0703028
HERA-B collaboration, I. Abt et al., Production of the charmonium states \(\chi _{c 1}\) and \(\chi _{c 2}\) in proton nucleus interactions at \(\sqrt{s}=41.6\,\text{ GeV }\). Phys. Rev. D79, 012001 (2009). arXiv:0807.2167
LHCb collaboration, R. Aaij et al., Measurement of the cross-section ratio \(\sigma (\chi _{c2})/\sigma (\chi _{c1})\) for prompt \(\chi _c\) production at \(\sqrt{s}=7\) TeV. Phys. Lett. B714, 215 (2012). arXiv:1202.1080
LHCb collaboration, R. Aaij et al., Measurement of the ratio of prompt \(\chi _{c}\) to \(J/\psi \) production in \(pp\) collisions at \(\sqrt{s}=7\) TeV. Phys. Lett. B718, 431 (2012). arXiv:1204.1462
LHCb collaboration, R. Aaij et al., Measurement of the relative rate of prompt \(\chi _{c0}\), \(\chi _{c1}\) and \(\chi _{c2}\) production at \(\sqrt{s}=7\) TeV, JHEP 10, 115 (2013). arXiv:1307.4285
CMS collaboration, S. Chatrchyan et al., Measurement of the relative prompt production rate of \(chi(c2)\) and \(chi(c1)\) in \(pp\) collisions at \(\sqrt{s}=7\) TeV, Eur. Phys. J. C72, 2251 (2012). arXiv:1210.0875
ATLAS collaboration, G. Aad et al., Measurement of \(\chi _{c1}\) and \(\chi _{c2}\) production with \(\sqrt{s}\) = 7 TeV \(pp\) collisions at ATLAS. JHEP 1407, 154 (2014). arXiv:1404.7035
CDF collaboration, T. Affolder et al., Production of \(\Upsilon (1S)\) mesons from \(\chi _b\) decays in \(p\bar{p}\) collisions at \(\sqrt{s} = 1.8\,\text{ TeV }\). Phys. Rev. Lett. 84, 2094 (2000). arXiv:hep-ex/9910025
ATLAS collaboration, G. Aad et al., Observation of a new \(\chi _b\) state in radiative transitions to \(\Upsilon (1S)\) and \(\Upsilon (2S)\) at ATLAS. Phys. Rev. Lett. 108, 152001 (2012). arXiv:1112.5154
CMS collaboration, Measurement of the \(\chi _{b2}/\chi _{b1}\) production cross section ratio in \(pp\) collisions at \(\sqrt{s}= 8\,\text{ TeV }\) (2013) (CMS-PAS-BPH-13-005)
LHCb collaboration, R. Aaij et al., Measurement of the fraction of \(\Upsilon (1S)\) originating from \(\chi _b(1P)\) decays in \(pp\) collisions at \(\sqrt{s}=7\) TeV. JHEP 11, 031 (2012). arXiv:1209.0282
LHCb collaboration, Observation of \(\chi _b(3P)\) state at LHCb in pp collisions at \(\sqrt{s}=7\,\text{ TeV }\) (LHCb-CONF-2012-020)
Particle Data Group, J. Beringer et al., Review of particle physics. Phys. Rev. D86, 010001 (2012) (2013 partial update for the 2014 edition)
D0 collaboration, V. M. Abazov et al., Observation of a narrow mass state decaying into \(\Upsilon (1S) + \gamma \) in \(p\bar{p}\) collisions at \(\sqrt{s} = 1.96\) TeV. Phys. Rev. D86, 031103 (2012). arXiv:1203.6034
LHCb collaboration, A. A. Alves Jr. et al., The LHCb detector at the LHC. JINST 3, S08005 (2008)
M. Adinolfi et al., Performance of the LHCb RICH detector at the LHC. Eur. Phys. J. C73, 2431 (2013). arXiv:1211.6759
R. Aaij et al., Performance of the LHCb calorimeters (LHCb-DP-2013-004) (in preparation)
A.A. Alves Jr et al., Performance of the LHCb muon system. JINST 8, P02022 (2013). arXiv:1211.1346
R. Aaij et al., The LHCb trigger and its performance in 2011. JINST 8, P04022 (2013). arXiv:1211.3055
T. Sjöstrand, S. Mrenna, P. Skands, PYTHIA 6.4 physics and manual. JHEP 05, 026 (2006). arXiv:hep-ph/0603175
I. Belyaev et al., Handling of the generation of primary events in Gauss, the LHCb simulation framework, in Nuclear Science Symposium Conference Record (NSS/MIC), vol. 1155 (IEEE, 2010)
D.J. Lange, The EvtGen particle decay simulation package. Nucl. Instrum. Methods A462, 152 (2001)
P. Golonka, Z. Was, Photos Monte Carlo: a precision tool for QED corrections in Z and W decays. Eur. Phys. J. C45, 97 (2006). arXiv:hep-ph/0506026
Geant4 collaboration, J. Allison et al., Geant4 developments and applications. IEEE Trans. Nucl. Sci. 53, 270 (2006)
Geant4 collaboration, S. Agostinelli et al., Geant4: a simulation toolkit. Nucl. Instrum. Methods A506, 250 (2003)
M. Clemencic et al., The LHCb simulation application, Gauss: design, evolution and experience. J. Phys. Conf. Ser. 331, 032023 (2011)
R. Arink et al., Performance of the LHCb outer tracker. JINST 9, P01002 (2014). arXiv:1311.3893
A. Powell, Particle identification at LHCb, in 35th International Conference on High Energy Physics, Paris (22–28 July 2010), pp. 020
H. Terrier, I. Belyaev, Particle identification with LHCb calorimeters, in Technical Report, CERN-LHCb-2003-092, CERN, Geneva (2003)
F. Archilli et al., Performance of the muon identification at LHCb. JINST 8, P10020 (2013). arXiv:1306.0249
W.D. Hulsbergen, Decay chain fitting with a Kalman filter. Nucl. Instrum. Methods A552, 566 (2005). arXiv:physics/0503191
O. Deschamps et al., Photon and neutral pion reconstruction, in Technical Report CERN-LHCb-2003-091, CERN, Geneva (2003)
LHCb collaboration, R. Aaij et al., Evidence for the decay \(B^0 \rightarrow J/\psi \omega \) and measurement of the relative branching fractions of \(B^0_s\) meson decays to \(J/\psi \eta \) and \(J/\psi \eta ^\prime \). Nucl. Phys. B867, 547 (2013). arXiv:1210.2631
T. Skwarnicki, A study of the radiative cascade transitions between the \(\Upsilon ^{\prime }\) and \(\Upsilon \) resonances. PhD thesis, Institute of Nuclear Physics, Krakow (1986) (DESY-F31-86-02)
W. Kwong, J.L. Rosner, \(D\)-wave quarkonium levels of the \(\Upsilon \) family. Phys. Rev. D38, 279 (1988)
L. Motyka, K. Zalewski, Mass spectra and leptonic decay widths of heavy quarkonia. Eur. Phys. J. C4, 107 (1998). arXiv:hep-ph/9709254
LHCb collaboration, R. Aaij et al., Measurement of the \(\chi _b(3P)\) mass and of the relative rate of \(\chi _{b1}(1P)\) and \(\chi _{b2}(1P)\) production. arXiv:1409.1408 (submitted to JHEP)
LHCb collaboration, R. Aaij et al., Measurement of \(\Upsilon \) production in \(pp\) collisions at \(\sqrt{s}=7\) TeV. Eur. Phys. J. C72, 2025 (2012). arXiv:1202.6579
LHCb collaboration, R. Aaij et al., Production of \(J/\psi \) and \(\Upsilon \) mesons in \(pp\) collisions at \(\sqrt{s}=8\) TeV. JHEP 06, 064 (2013). arXiv:1304.6977
LHCb collaboration, R. Aaij et al., Measurement of \(\Upsilon \) production in \(pp\) collisions at \(\sqrt{s} = 2.76\) TeV. Eur. Phys. J. C74, 2835 (2014). arXiv:1402.2539
LHCb collaboration, R. Aaij et al., Observations of \(B^0_s \rightarrow \psi (2S)\eta \) and \(B^0_{(s)} \rightarrow \psi (2S)\pi ^+\pi ^-\) decays. Nucl. Phys. B871, 403 (2013). arXiv:1302.6354
LHCb collaboration, R. Aaij et al., Observation of \(B^0_s\rightarrow \chi _{c1}\phi \) decay and study of \(B^0\rightarrow \chi _{c1,2}K^{*0}\) decays. Nucl. Phys. B874, 663 (2013). arXiv:1305.6511
LHCb collaboration, R. Aaij et al., Evidence for the decay \(X(3872)\rightarrow \psi (2S)\gamma \). Nucl. Phys. B886, 665 (2014). arXiv:1404.0275
CMS collaboration, S. Chatrchyan et al., Measurement of the \(\Upsilon (1S)\), \(\Upsilon (2S)\) and \(\Upsilon (3S)\) polarizations in \(pp\) collisions at \(\sqrt{s}=7\,\text{ TeV }\), Phys. Rev. Lett. 110, 081802 (2013). arXiv:1209.2922
I. Belyaev, D. Savrina, R. Graciani, A. Puig, Kali: the framework for fine calibration of the LHCb electromagnetic calorimeter. J. Phys. Conf. Ser. 331, 032050 (2011)
D. Savrina, Measurement of the branching fractions of the \(B^0_s \rightarrow J/\psi \eta \), \(B^0_s\rightarrow J/\psi \eta ^{\prime }\) and \(B^0\rightarrow J/\psi \omega ^{0}\) decays in the LHCb experiment. PhD thesis, Institute for Theoretical and Experimental Physics, Moscow (2013) (CERN-THESIS-2013-229)
I.M. Belyaev, D.Y. Golubkov, V.Y. Egorychev, D.V. Savrina, Calibration of the LHCb electromagnetic calorimeter using the technique of neutral pion invariant mass reconstruction. Instrum Exp Tech 57(1), 33 (2014)
Acknowledgments
We thank K.-T. Chao, H. Han, V. G. Kartvelishvili, J.-P. Lansberg A. K. Likhoded, A. V. Luchinsky, S. V. Poslavsky and H.-S. Shao for inspiring and fruitful discussions on P-wave bottomonia production. We express our gratitude to our colleagues in the CERN accelerator departments for the excellent performance of the LHC. We thank the technical and administrative staff at the LHCb institutes. We acknowledge support from CERN and from the national agencies: CAPES, CNPq, FAPERJ and FINEP (Brazil); NSFC (China); CNRS/IN2P3 (France); BMBF, DFG, HGF and MPG (Germany); SFI (Ireland); INFN (Italy); FOM and NWO (The Netherlands); MNiSW and NCN (Poland); MEN/IFA (Romania); MinES and FANO (Russia); MinECo (Spain); SNSF and SER (Switzerland); NASU (Ukraine); STFC (United Kingdom); NSF (USA). The Tier1 computing centres are supported by IN2P3 (France), KIT and BMBF (Germany), INFN (Italy), NWO and SURF (The Netherlands), PIC (Spain), GridPP (United Kingdom). We are indebted to the communities behind the multiple open source software packages on which we depend. We are also thankful for the computing resources and the access to software R&D tools provided by Yandex LLC (Russia). Individual groups or members have received support from EPLANET, Marie Skłodowska-Curie Actions and ERC (European Union), Conseil général de Haute-Savoie, Labex ENIGMASS and OCEVU, Région Auvergne (France), RFBR (Russia), XuntaGal and GENCAT (Spain), Royal Society and Royal Commission for the Exhibition of 1851 (United Kingdom).
Author information
Authors and Affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Funded by SCOAP3 / License Version CC BY 4.0.
About this article
Cite this article
Aaij, R., Adeva, B., Adinolfi, M. et al. Study of \(\upchi _{{\mathrm {b}}}\) meson production in \(\mathrm {p} \) \(\mathrm {p} \) collisions at \(\sqrt{s}=7\) and \(8{\mathrm {\,TeV}} \) and observation of the decay \(\upchi _{{\mathrm {b}}}\mathrm {(3P)} \rightarrow \Upsilon \mathrm {(3S)} {\upgamma } \) . Eur. Phys. J. C 74, 3092 (2014). https://doi.org/10.1140/epjc/s10052-014-3092-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-014-3092-z