Event-by-event mean $\varvec{p}_{\mathbf {T}}$ fluctuations in pp and Pb–Pb collisions at the LHC

Abstract

Event-by-event fluctuations of the mean transverse momentum of charged particles produced in pp collisions at $\sqrt{s}$ $=$ 0.9, 2.76 and 7 TeV, and Pb–Pb collisions at $\sqrt{s_\mathrm{NN}}$ $=$ 2.76 TeV are studied as a function of the charged-particle multiplicity using the ALICE detector at the LHC. Dynamical fluctuations indicative of correlated particle emission are observed in all systems. The results in pp collisions show little dependence on collision energy. The Monte Carlo event generators PYTHIA and PHOJET are in qualitative agreement with the data. Peripheral Pb–Pb data exhibit a similar multiplicity dependence as that observed in pp. In central Pb–Pb, the results deviate from this trend, featuring a significant reduction of the fluctuation strength. The results in Pb–Pb are in qualitative agreement with previous measurements in Au–Au at lower collision energies and with expectations from models that incorporate collective phenomena.

Introduction

The study of event-by-event fluctuations was proposed as a probe of the properties of the hot and dense matter generated in high-energy heavy-ion collisions [1–9]. The occurrence of a phase transition from the Quark-Gluon Plasma to a Hadron Gas or the existence of a critical point in the phase diagram of strongly interacting matter may go along with critical fluctuations of thermodynamic quantities such as temperature. This could be reflected in dynamical event-by-event fluctuations of the mean transverse momentum $\big ( \left\langle p_\mathrm{T}\right\rangle \big )$ of final-state charged particles.

Event-by-event $\left<p_\mathrm{T}\right>$ fluctuations have been studied in nucleus-nucleus (A–A) collisions at the Super Proton Synchrotron (SPS) [10–14] and at the Relativistic Heavy-Ion Collider (RHIC) [15–20], where dynamical fluctuations have been observed. Fluctuations of $\left<p_\mathrm{T}\right>$ were found to decrease with collision centrality, as generally expected in a dilution scenario caused by superposition of partially independent particle-emitting sources. In detail, however, deviations from a simple superposition scenario have been reported. In particular, with respect to a reference representing independent superposition – i.e. a decrease of fluctuations according to $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $^{-0.5}$, where $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ is the average charged-particle density in a given interval of collision centrality and pseudorapidity ($\eta$) – the observed fluctuations increase sharply from peripheral to semi-peripheral collisions, followed by a shallow decrease towards central collisions [18]. A number of possible mechanisms have been proposed to explain this behavior, such as string percolation [21] or the onset of thermalization and collectivity [22, 23], but no strong connection to critical behavior could be made. It was recently suggested [24, 25] that initial state density fluctuations [26] could affect the final state transverse momentum correlations and their centrality dependence.

Fluctuations of $\left<p_\mathrm{T}\right>$ arise from many kinds of correlations among the $p_\mathrm{T}$ of the final-state particles, such as resonance decays, jets, or quantum correlations. To account for these contributions from conventional mechanisms similar studies can be performed in pp, where such correlations are also present. The results from pp could thus be used to construct a model-independent baseline to search for non-trivial fluctuations in A–A which manifest themselves in a modification of the fluctuation pattern with respect to the pp reference.

In this paper, we present results of a multiplicity-dependent study of event-by-event $\left<p_\mathrm{T}\right>$ fluctuations of charged particles in pp collisions at $\sqrt{s}$ $=$ 0.9, 2.76 and 7 TeV, and Pb–Pb collisions at $\sqrt{s_\mathrm{NN}}$ $=$ 2.76 TeV measured with ALICE at the LHC. The experimental data are compared to different Monte Carlo (MC) event generators.

ALICE detector and data analysis

The data used in this analysis were collected with the ALICE detector at the CERN Large Hadron Collider (LHC)  [27] during the Pb–Pb run in 2010 and the pp runs in 2010 and 2011.

For a detailed description of the ALICE apparatus see [28]. The analysis is based on $19\times 10^6$ Pb–Pb events at $\sqrt{s_\mathrm{NN}}$ $=$ 2.76 TeV, and $6.9\times 10^6$, $66\times 10^6$ and $290\times 10^6$ pp events at $\sqrt{s}$ $=$ 0.9, 2.76 and 7 TeV, respectively. The standard ALICE coordinate system is used, in which the nominal interaction point is the origin of a right-handed Cartesian coordinate system. The $z$-axis is along the beam pipe, the $x$-axis points towards the center of the LHC, $\varphi$ is the azimuthal angle around the $z$-axis and $\theta$ is the polar angle with respect to this axis. The detectors in the central barrel of the experiment are operated inside a solenoidal magnetic field with $B=0.5$ T. About half of the Pb–Pb data set was recorded with negative ($B_z<0$) and positive ($B_z>0$) field polarity, respectively.

A minimum bias (MB) trigger condition was applied to select collision events. In pp, this trigger was defined by at least one hit in the Silicon Pixel Detector (SPD) or in one of the two forward scintillator systems VZERO-A ($2.8 < \eta < 5.1$) and VZERO-C ($-3.7 < \eta < -1.7$). In Pb–Pb, the MB trigger condition is defined as a coincidence of hits in both VZERO detectors.

In this analysis, the Time Projection Chamber (TPC) [29] is used for charged-particle tracking in $|\eta |<0.8$. In the momentum range selected for this analysis, $0.15<p_\mathrm{T}<2$ GeV/$c$, the momentum resolution $\sigma (p_\mathrm{T})/p_\mathrm{T}$ is better than 2 %. The tracking efficiency is larger than 90 % for $p_\mathrm{T}>0.3$ GeV/$c$ and drops to about 70 % at $p_\mathrm{T}=0.15$ GeV/$c$.

Primary vertex information is obtained from both the Inner Tracking System (ITS) and the TPC. Events are used in the analysis when at least one accepted charged-particle track contributes to the primary vertex reconstruction. It is required that the reconstructed vertex is within $\pm 10$ cm from the nominal interaction point along the beam direction to ensure a uniform pseudo-rapidity acceptance within the TPC. Additionally, the event vertex is reconstructed using only TPC tracks. The event is rejected if the $z$-position of that vertex is different by more than 10 cm from that of the standard procedure.

In Pb–Pb, at least 10 reconstructed tracks inside the acceptance are required. The contamination by non-hadronic interactions is negligible in the event sample that fulfills the aforementioned selection criteria. The centrality in Pb–Pb is estimated from the signal in the VZERO detectors using the procedure described in [30, 31].

The charged-particle tracks used for this analysis are required to have at least 70 out of a maximum of 159 reconstructed space points in the TPC, and the maximum $\chi ^2$ per space point in the TPC from the momentum fit must be less than 4. Daughter tracks from reconstructed secondary weak-decay topologies (kinks) are rejected. The distance of closest approach (DCA) of the extrapolated trajectory to the primary vertex position is restricted to less than 3.2 cm along the beam direction and less than 2.4 cm in the transverse plane. The number of tracks in an event that are accepted by these selection criteria is denoted by $N_\mathrm{acc}$.

Event-by-event measurements of the mean transverse momentum are subject to the finite reconstruction efficiency of the detector. While efficiency corrections can be applied on a statistical basis to derive the inclusive $\left<p_\mathrm{T}\right>$ of charged particles in a given kinematic acceptance range, such an approach is not adequate for event-by-event studies. The event-by-event mean transverse momentum is therefore approximated by the mean value $M_\mathrm{EbE}(p_\mathrm{T})_k$ of the transverse momenta $p_{\mathrm{T},i}$ of the $N_\mathrm{acc},_k$ accepted charged particles in event $k$:

$$\begin{aligned} M_\mathrm{EbE}(p_\mathrm{T})_k=\frac{1}{N_\mathrm{acc},_k} \sum _{i=1}^{N_\mathrm{acc},_k} p_{\mathrm{T},i}. \end{aligned}$$

(1)

Event-by-event fluctuations of $M_\mathrm{EbE}(p_\mathrm{T})_k$ in heavy-ion collisions are composed of statistical and dynamical contributions. The two-particle transverse momentum correlator $C = \langle \Delta p_{\mathrm{T},i}, \Delta p_{\mathrm{T},j} \rangle$ is a measure of the dynamical component $\sigma _\mathrm{dyn}^2$ of these fluctuations and therefore well suited for an event-by-event analysis [13, 18, 32]. The correlator $C_{m}$ is the mean of covariances of all pairs of particles $i$ and $j$ in the same event with respect to the inclusive $M(p_\mathrm{T})_m$ in a given multiplicity class $m$ and is defined as

$$\begin{aligned} C_m&= \frac{1}{\sum _{k=1}^{n_{\mathrm{ev},m}}{N_{k}^\mathrm{pairs}}} \cdot \nonumber \\&\quad \sum _{k=1}^{n_{\mathrm{ev},m}} \sum _{i=1}^{N_\mathrm{acc},_{k}} \sum _{j=i+1}^{N_\mathrm{acc},_{k}}\! (p_{\mathrm{T},i} \!-\! M(p_\mathrm{T})_m )\cdot \,(p_{\mathrm{T},j} \!-\! M(p_\mathrm{T})_m), \nonumber \\ \end{aligned}$$

(2)

where $n_{\mathrm{ev},m}$ is the number of events in multiplicity class $m$, $N_{k}^\mathrm{pairs} = 0.5 \cdot N_\mathrm{acc},_{k} \cdot (N_\mathrm{acc},_{k}-1)$ is the number of particle pairs in event $k$ and $M(p_\mathrm{T})_m$ is the average $p_\mathrm{T}$ of all tracks in all events of class $m$:

$$\begin{aligned} M(p_\mathrm{T})_m&= \frac{1}{\sum _{k=1}^{n_{\mathrm{ev},m}}N_\mathrm{acc},_k} \sum _{k=1}^{n_{\mathrm{ev},m}}\sum _{i=1}^{N_\mathrm{acc},_k} p_{\mathrm{T},i}\nonumber \\&= \frac{1}{\sum _{k=1}^{n_{\mathrm{ev},m}}N_\mathrm{acc},_k} \sum _{k=1}^{n_{\mathrm{ev},m}} N_\mathrm{acc},_k \cdot M_\mathrm{EbE}(p_\mathrm{T})_k. \end{aligned}$$

(3)

By construction, $C_m$ vanishes in the case of uncorrelated particle emission, when only statistical fluctuations are present.

The results in this paper are presented in terms of the dimensionless ratio $\sqrt{C_m}/M(p_\mathrm{T})_m$ which quantifies the strength of the dynamical fluctuations in units of the average transverse momentum $M(p_\mathrm{T})_m$ in the multiplicity class $m$.

The correlator is computed in intervals of the event multiplicity $N_\mathrm{acc}$. In pp collisions, intervals of $\Delta N_\mathrm{acc}$ = 1 are used for the calculation of $C_m$ and $M(p_\mathrm{T})_m$. In Pb–Pb collisions, $C_m$ is calculated in the multiplicity intervals $\Delta N_\mathrm{acc}$ = 10 for $N_\mathrm{acc} < 200$, $\Delta N_\mathrm{acc}$ = 25 for $200 \le N_\mathrm{acc} < 1000$ and $\Delta N_\mathrm{acc}$ = 100 for $N_\mathrm{acc} \ge$ 1000. To account for the steep increase of $M(p_\mathrm{T})_m$ with multiplicity in peripheral collisions, the calculation of the correlator in (2) uses values for $M(p_\mathrm{T})_m$ which are calculated in bins of $\Delta N_\mathrm{acc}$ = 1 for $N_\mathrm{acc}<1000$. At higher multiplicities, $M(p_\mathrm{T})$ changes only moderately and $M(p_\mathrm{T})_m$ is calculated in the same intervals as $C_m$, i.e. $\Delta N_\mathrm{acc}$ = 100.

Additionally, the Pb–Pb data are also analyzed in 5 % intervals of the collision centrality. The results are shown in bins of the mean number of participating nucleons $\langle N_\mathrm{part} \rangle$ as derived from the centrality percentile using a Glauber MC calculation [30]. For the results presented as a function of the mean charged-particle density $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$, the mean value $\left<N_\mathrm{acc}\right>$ in each centrality bin is associated with the measured value for $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ from [30]. A linear relation between $\langle N_\mathrm{acc} \rangle$ and $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ is observed over the full centrality range, allowing interpolation to assign a value for $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ to any interval of $N_\mathrm{acc}$. In pp, $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ is calculated for each interval of $N_\mathrm{acc}$ employing the full detector response matrix from MC and unfolding of the measured $N_\mathrm{acc}$ distributions following the procedure outlined in [33].

The systematic uncertainties are estimated separately for each collision system (Pb–Pb and pp) and at each collision energy. The relative uncertainties on $\sqrt{C_m}/M(p_\mathrm{T})_m$ are generally smaller than those on $C_m$ because most of the sources of uncertainties lead to correlated variations of $M(p_\mathrm{T})_m$ and $C_m$ that tend to cancel in the ratio $\sqrt{C_m}/M(p_\mathrm{T})_m$. Therefore, all quantitative results shown below are presented in terms of $\sqrt{C_m}/M(p_\mathrm{T})_m$. The contributions to the total systematic uncertainty on $\sqrt{C_m}/M(p_\mathrm{T})_m$ in pp and Pb–Pb collisions are summarized in Table 1. Ranges are given when the uncertainties depend on $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ or centrality.

Table 1 Contributions to the total systematic uncertainty on $\sqrt{C_{m}} / M(p_\mathrm{T})_m$ in pp and Pb–Pb collisions. Ranges are given when the uncertainties depend on $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ or centrality

The largest contribution to the total systematic uncertainty results from the comparison of $\sqrt{C_m}/M(p_\mathrm{T})_m$  from full MC simulations employing a GEANT3 [34] implementation of the ALICE detector setup [35] to the MC generator level. Processing the events through the full simulation chain alters the result for $\sqrt{C_m}/M(p_\mathrm{T})_m$ with respect to the MC generator level by up to 6 % in high multiplicity pp collisions. This includes effects of tracking efficiency dependence on the transverse momentum. The studies in pp are performed using the Perugia-0 tune of PYTHIA6 [36, 37], similar results are obtained with PHOJET [38]. HIJING [39] is used for Pb–Pb collisions, where the differences are slightly smaller, reaching up to 4 % in most central collisions.

Since these deviations are in general dependent on the event characteristics assumed in the model, in particular on the nature of the underlying particle correlations, no correction of experimental results is performed. Instead, these deviations are added to the systematic data uncertainties to allow for a comparison of the experimental results to model calculations on the MC event generator level.

Another major contribution to the total systematic uncertainty emerges from the difference between the standard analysis using only TPC tracks and an alternative analysis employing a hybrid tracking scheme. The hybrid tracking combines TPC and ITS tracks when ITS detector information is available, and thus provides more powerful suppression of secondary particles (remaining contamination 4–5 %) as compared to the standard TPC-only tracking ($\sim$12 %). The TPC, on the other hand, features very stable operational conditions throughout the analyzed data sets. The differences between the results from the two analyses reach 5 % in $\sqrt{C_m}/M(p_\mathrm{T})_m$.

At the event level, minor contributions to the total systematic uncertainty arise from the cut on the maximum distance of the reconstructed vertex to the nominal interaction point along the beam axis. In the standard analysis global tracks that combine TPC and ITS track segments are used for the vertex calculation. Alternatively, we studied also the results when only TPC tracks or only tracklets from the SPD are used to reconstruct the primary vertex. The effect from using the different vertex estimators is negligible in Pb–Pb collisions. In pp collisions, this effect is small with the exception of the lowest multiplicity bin, where it reaches 2 % in $\sqrt{C_m}/M(p_\mathrm{T})_m$. Additionally, the cut on the difference between the $z$-positions of the reconstructed vertices obtained from global tracks and TPC-only tracks is varied. This shows a sizable effect only in peripheral Pb–Pb and low-multiplicity pp collisions (2–3 % in $\sqrt{C_m}/M(p_\mathrm{T})_m$).

In addition, variations of the following track quality cuts are performed: the number of space points per track in the TPC, the $\chi ^{2}$ per degree of freedom of the momentum fit, and the DCA of each track to the primary vertex, both along the beam direction and in the transverse plane. Neither of these contributions to the total systematic uncertainty exceeds 3 % in $\sqrt{C_m}/M(p_\mathrm{T})_m$.

The difference between the results obtained from Pb–Pb data taken at the two magnetic field polarities is included into the systematic uncertainties. The effect is small (0.5 % in $\sqrt{C_m}/M(p_\mathrm{T})_m$). The corresponding uncertainty in pp is assumed to be the same as in Pb–Pb collisions. Finally, the effect of finite centrality intervals in Pb–Pb, and the corresponding variation of $M(p_\mathrm{T})$ within these intervals, is taken into account by including the difference between the analyses in 5 and 10 % centrality intervals [30, 31] into the systematic uncertainty. The total uncertainty on $\sqrt{C_m}/M(p_\mathrm{T})_m$ for each data set was obtained by adding in quadrature the individual contributions in Table 1.

Results in pp collisions

The relative dynamical fluctuation $\sqrt{C_m}/M(p_\mathrm{T})_m$ as a function of the average charged-particle multiplicity $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ in pp collisions at $\sqrt{s}$ $=$ 0.9, 2.76 and 7 TeV is shown in Fig. 1. The non-zero values of $\sqrt{C_m}/M(p_\mathrm{T})_m$ indicate significant dynamical event-by-event $M(p_\mathrm{T})$ fluctuations. The fluctuation strength reaches a maximum of 12–14 % in low multiplicity collisions and decreases to about 5 % at the highest multiplicities. No significant beam energy dependence is observed for the relative fluctuation $\sqrt{C_m}/M(p_\mathrm{T})_m$.

Fig. 1

Relative fluctuation $\sqrt{C_m}/M(p_\mathrm{T})_m$ as a function of $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ in pp collisions at $\sqrt{s}$ $=$ 0.9, 2.76 and 7 TeV

The beam energy dependence of relative dynamical mean transverse momentum fluctuations in pp collisions was studied at lower collision energies by the Split Field Magnet (SFM) detector at the Intersection Storage Rings (ISR). The SFM experiment measured relative fluctuations in inclusive pp collisions at $\sqrt{s}$ $=$ 30.8, 45, 52, and 63 GeV [40]. The fluctuations are expressed by the quantity $R$ that is extracted from the multiplicity dependence of the event-by-event $M(p_\mathrm{T})$ dispersion. The measure $R=\left[ D( M_\mathrm{EbE}(p_\mathrm{T})_k)/M(p_\mathrm{T})\right] _{n\rightarrow \infty }$ is obtained from an extrapolation of the multiplicity-dependent dispersion $D( M_\mathrm{EbE}(p_\mathrm{T})_k)$ to infinite multiplicity, normalized by the inclusive mean transverse momentum. It is an alternative approach to extract dynamical transverse momentum fluctuations in inclusive pp collisions.

To allow for a comparison to ISR results, an inclusive analysis of ALICE pp data is performed. The relative fluctuation $\sqrt{C}/M(p_\mathrm{T})$ is computed at each collision energy as in (2), however, without subdivision into multiplicity classes $m$. Monte Carlo studies of pp collisions at $\sqrt{s}$ $=$ 7 TeV using PYTHIA8 have shown that results for $R$ and $\sqrt{C}/M(p_\mathrm{T})$ agree within 10–15 %. The ALICE results for the inclusive $\sqrt{C}/M(p_\mathrm{T})$ as a function of $\sqrt{s}$ are shown in Fig. 2, along with the ISR results for $R$ from [40]. No significant dependence of the relative transverse momentum fluctuations on the collision energy is observed over this large energy range.

The results in pp at $\sqrt{s}$ $=$ 7 TeV are compared with results from different event generators. In particular, PYTHIA6 (tunes Perugia-0 and Perugia-11), PYTHIA8.150 and PHOJET have been used.

Fig. 2

Relative dynamical mean transverse momentum fluctuations in pp collisions as a function of $\sqrt{s}$. The ALICE results for $\sqrt{C}/M(p_\mathrm{T})$ are compared to the quantity $R$ measured at the ISR (see text and [40])

It has been pointed out that high-multiplicity events in pp collisions at LHC energies are driven by multi-parton interactions (MPIs) [41]. This picture is also suggested by recent studies of the event sphericity in pp collisions [42]. MPIs are independent processes on the perturbative level. However, the color reconnection mechanism between produced strings may lead to correlations in the hadronic final state. Color reconnection is also the driving mechanism in PYTHIA for the increase of $\left<p_\mathrm{T}\right>$ as a function of $N_\mathrm{ch}$ [43, 44].

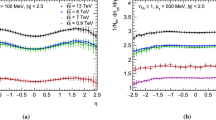
The default PYTHIA6 Perugia-11 tune including the color-reconnection mechanism is compared to results of the same tune without color-reconnection (NOCR). Figure 3 shows model calculations for $\left<p_\mathrm{T}\right>$ $_m$ as a function of $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ in $0.15<p_\mathrm{T}<2$ GeV/$c$ and $|\eta |<0.8$ in pp collisions at $\sqrt{s}$ $=$ 7 TeV. The MC generators yield qualitatively different results for the multiplicity dependence, in particular PHOJET and the NOCR version of PYTHIA6 Perugia-11 show only little increase of $\left<p_\mathrm{T}\right>$ $_m$ with multiplicity. Good agreement between PYTHIA8 and ALICE results in pp collisions at $\sqrt{s}$ $=$ 7 TeV was demonstrated [44], albeit in a different $\eta$ and $p_\mathrm{T}$ interval.

Results for the relative dynamical fluctuation measure $\sqrt{C_m}/M(p_\mathrm{T})_m$ in pp at $\sqrt{s}$ $=$ 7 TeV are compared to model calculations in Fig. 4. The data exhibit a clear power-law dependence with $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ except for very small multiplicities. A power-law fit of $\sqrt{C_m}/M(p_\mathrm{T})_m$ $\propto$ $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $^{b}$ in the interval $5<$ $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $<30$ yields $b= -0.431 \pm 0.001$ (stat.) $\pm 0.021$ (syst.). The deviation of the power-law index from $b=-0.5$ indicates that the observed multiplicity dependence of $M(p_\mathrm{T})$ fluctuations in pp does not follow a simple superposition scenario, contrary to what might be expected for independent MPIs. All PYTHIA tunes under study agree with this finding to the extent that they exhibit a similar power-law index as the data. This is also true for the NOCR calculation which excludes the color reconnection mechanism in its present implementation in PYTHIA as a dominant source of correlations beyond the independent superposition scenario.

Fig. 3

Results for $\left<p_\mathrm{T}\right>$ $_m$ as a function of $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ in pp collisions at $\sqrt{s}$ $=$ 7 TeV from different event generators

Fig. 4

Left Relative dynamical fluctuation $\sqrt{C_m}/M(p_\mathrm{T})_m$ for data and different event generators in pp collisions at $\sqrt{s}$ $=$ 7 TeV as a function of $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$. Right Ratio models to data. The red error band indicates the statistical and systematic data uncertainties added in quadrature

Results in Pb–Pb collisions

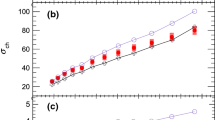
Results for the relative dynamical fluctuation $\sqrt{C_m}/M(p_\mathrm{T})_m$ in Pb–Pb collisions at $\sqrt{s_\mathrm{NN}}$ $=$ 2.76 TeV as a function of $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ are shown in Fig. 5. As for pp collisions, significant dynamical fluctuations as well as a strong decrease with multiplicity are observed. Also shown in Fig. 5 is the result of a HIJING [39] simulation (version 1.36) without jet-quenching. A power-law fit in the interval $30<$ $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $<1500$ describes the HIJING results very well, except at low multiplicities, and yields $b= -0.499 \pm 0.003$ (stat.) $\pm 0.005$ (syst.). The approximate $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $^{-0.5}$ scaling reflects the basic property of HIJING as a superposition model of independent nucleon-nucleon collisions. The HIJING calculation, in particular the multiplicity dependence, is in obvious disagreement with the data.

Fig. 5

Relative dynamical fluctuation $\sqrt{C_m}/M(p_\mathrm{T})_m$ as a function of $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ in pp and Pb–Pb collisions at $\sqrt{s_\mathrm{NN}}$ $=$ 2.76 TeV. Also shown are results from HIJING and power-law fits to pp (solid line) and HIJING (dashed line) (see text)

In peripheral collisions $\big ( \!\left\langle \mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right\rangle < 100 \big )$, the Pb–Pb results are in very good agreement with the extrapolation of a power-law fit to pp data at $\sqrt{s}$ $=$ 2.76 TeV in the interval $5<$ $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $<25$, with $b= -0.405 \pm 0.002$ (stat.) $\pm 0.036$ (syst.). This is remarkable because significant differences in $\left<p_\mathrm{T}\right>$ are observed between pp and Pb–Pb in this multiplicity range [44]. At larger multiplicities, the Pb–Pb results deviate from the pp extrapolation. An enhancement in $100<$ $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $<500$ is followed by a pronounced decrease at $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $>$ 500, corresponding to centralities $<$ 40 %, which indicates a strong reduction of fluctuations towards central collisions.

Measurements of mean transverse momentum fluctuations in central A–A collisions at the SPS [13] and at RHIC [18] are compared to the ALICE result in Fig. 6. As in pp, there is no significant dependence on $\sqrt{s_\mathrm{NN}}$ observed over a wide range of collision energies.

Fig. 6

Mean transverse momentum fluctuations in central heavy-ion collisions as a function of $\sqrt{s_\mathrm{NN}}$. The ALICE data point is compared to data from the CERES [13] and STAR [18] experiments. For STAR only statistical uncertainties are available

Figure 7 shows a comparison of the ALICE results for $\sqrt{C_m}/M(p_\mathrm{T})_m$ to measurements in Au–Au collisions at $\sqrt{s_\mathrm{NN}}$ $=$ 200 GeV by the STAR experiment at RHIC [18]. In the peripheral region, the STAR data show very similar scaling with $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ as the ALICE data, as shown on the left panel of Fig. 7. Also shown are the fit to pp data at $\sqrt{s}$ $=$ 2.76 TeV from Fig. 5 and the result of a power-law fit to the STAR data in $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $<$ 200 where the power is fixed to $b=-0.405$. Good agreement of the ALICE and STAR data with the fits is observed in peripheral collisions. The decrease of fluctuations in central collisions is similar in ALICE and STAR, however, no significant enhancement in semi-central events is observed in the STAR data. In the right panel of Fig. 7, the results for $\sqrt{C_m}/M(p_\mathrm{T})_m$ in ALICE and STAR are shown as a function of the mean number of participating nucleons $\langle N_\mathrm{part} \rangle$. In this representation, the measurements of $\sqrt{C_m}/M(p_\mathrm{T})_m$ from ALICE and STAR are compatible within the rather large experimental uncertainties on $\langle N_\mathrm{part} \rangle$ in STAR. A power-law fit $\sqrt{C_m}/M(p_\mathrm{T})_m$ $\propto$ $\langle N_\mathrm{part} \rangle$ $^{b}$ to the ALICE data in the interval $10<$ $\langle N_\mathrm{part} \rangle$ $<40$ yields $b= -0.472 \pm 0.007$ (stat.) $\pm 0.037$ (syst.). The agreement between ALICE and STAR data as a function of $\langle N_\mathrm{part} \rangle$ points to a relation between the observed fluctuation patterns and the collision geometry.

Fig. 7

Left Relative dynamical fluctuation $\sqrt{C_m}/M(p_\mathrm{T})_m$ as a function of $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ in Pb–Pb collisions at $\sqrt{s_\mathrm{NN}}$ $=$ 2.76 TeV from ALICE compared to results from STAR in Au–Au collisions at $\sqrt{s_\mathrm{NN}}$ $=$ 200 GeV [18]. Also shown as dashed lines are results from power-law fits to the data (see text). Right same data as a function of $\langle N_\mathrm{part} \rangle$

Transverse momentum correlations and fluctuations may be modified as a consequence of collective flow in A–A collisions. It should be noted, however, that event-averaged radial flow and azimuthal asymmetries are not expected to give rise to strong transverse momentum fluctuations in azimuthally symmetric detectors [13, 16]. On the other hand, $M(p_\mathrm{T})$ fluctuations may occur due to fluctuating initial conditions that are also related to event-by-event fluctuations of radial flow and azimuthal asymmetries. We compare our results to calculations from the AMPT model [45] which has been demonstrated to give a reasonable description of inclusive and event-averaged bulk properties in Pb–Pb collisions at LHC energies [46, 47], in particular of the measured elliptic flow coefficient $v_2$. Figure 8 shows the ratio of $\sqrt{C_m}/M(p_\mathrm{T})_m$ in data and models to the result of a fit of $A\cdot$ $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $^{-0.5}$ to the HIJING simulation in the interval $30<$ $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $<1500$. For $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $<$ 30, HIJING agrees well with the results from pp and Pb–Pb. At larger multiplicities, none of the models shows quantitative agreement with the Pb–Pb data. The default AMPT calculation gives rise to increased fluctuations on top of the underlying HIJING scenario exceeding those observed in the data, except for very peripheral collisions. In contrast, the AMPT calculation with string melting, where partons after rescattering are recombined by a hadronic coalescence scheme, predicts smaller fluctuations. On the other hand, both AMPT versions exhibit a pronounced fall-off in central collisions which is in qualitative agreement with the data.

Fig. 8

Relative dynamical fluctuation $\sqrt{C_m}/M(p_\mathrm{T})_m$ normalized to $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $^{-0.5}$ (see text) as a function of $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ in pp and Pb–Pb collisions at $\sqrt{s_\mathrm{NN}}$ $=$ 2.76 TeV. The ALICE data are compared to results from HIJING and AMPT

In a recent approach [24], initial spatial fluctuations of glasma flux tubes have been related to mean transverse momentum fluctuations of final state hadrons via their coupling to a collective flow field. A comparison of these calculations to data from ALICE and STAR is shown in [24]. Good agreement is found in the semi-central and central region, where the data deviate from the pp extrapolation.

Summary and conclusions

First results on event-by-event fluctuations of the mean transverse momentum of charged particles in pp and Pb–Pb collisions at the LHC are presented. Expressed in terms of the relative dynamical fluctuation $\sqrt{C_m}/M(p_\mathrm{T})_m$, little energy dependence of the mean transverse momentum fluctuations is observed in pp at $\sqrt{s}$ $=$ 0.9, 2.76 and 7 TeV. The results are also compatible with similar measurements at the ISR. For the first time, mean transverse momentum fluctuations in pp are studied as a function of $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$. A characteristic decrease of $\sqrt{C_m}/M(p_\mathrm{T})_m$ following a power law is observed. The decrease is weaker than expected from a superposition of independent sources. The nature of such sources in pp is subject to future studies, but a connection to the concept of multi-parton interactions is suggestive. Model studies using PYTHIA however indicate that there is no strong sensitivity of transverse momentum fluctuations to the mechanism of color reconnection.

In peripheral Pb–Pb collisions $\big ( \left\langle \mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right\rangle < 100 \big )$, the dependence of $\sqrt{C_m}/M(p_\mathrm{T})_m$ on $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ is very similar to that observed in pp collisions at the corresponding collision energy. At larger multiplicities, the Pb–Pb data deviate significantly from an extrapolation of pp results and show a strong decrease for $\left<\mathrm{d}N_\mathrm{ch}/\mathrm{d}\eta \right>$ $>$ 500. The results for the most central collisions are of the same magnitude as previous measurements at the SPS and at RHIC. The centrality dependence of $\sqrt{C_m}/M(p_\mathrm{T})_m$ is compatible with that observed in Au–Au at $\sqrt{s_\mathrm{NN}}$ $=$ 200 GeV.

The Pb–Pb data can not be described by models based on independent nucleon-nucleon collisions such as HIJING. Models which include initial state density fluctuations and their effect on the development of collectivity in the final state are in qualitative agreement with the data. This suggests a connection between the observed fluctuations of transverse momentum and azimuthal correlations, and their relation to fluctuations in the initial state of the collision.