1 Introduction

Similar to black holes, wormholes in \(2+1\) dimensions also constitute informative objects to help us learn more about their higher-dimensional counterparts. The same is also true for thin-shell wormholes (TSWs) [1] which are constructed from an energy-momentum at the throat through a cut-and-paste technique satisfying the proper junction conditions. We recall that the history of TSWs started with Visser’s construction in a \(3+1\)-dimensional flat Minkowski spacetime [1]. At the same time he extended the idea to the Schwarzschild spacetime [2]. In his book [3] and work with Poisson [4] he introduced into physics the terminology of TSWs first. In the latter work they considered also the stability of a TSW. Ever since, there have been extensive attempts to understand the various features of the new kind of wormholes. For a short list of such attempts we refer the reader to [5–17] and references cited therein. Among the works on TSWs we see generalizations to higher [18–20] and lower [21–23] dimensions, and extensions to Lovelock gravity [24–27]. The theory has also been considered in cylindrical symmetry [28–34], dilaton theory [35], and so on. The common feature of all these extensions is that the bulk spacetimes are all static. We are well aware of the difficulties in rotating thin-shell wormholes (RTSWs). For this reason we restrict ourselves in this study to the relatively simpler case of \(2+1\) dimensions. The absence of gravitational degrees of freedom, namely, Weyl curvature in the lower dimension enforces us to add new physical parameters such as cosmological constant, electric / magnetic charge, scalar charge, and rotation. Our aim in this study is to consider RTSWs in \(2+1\) dimensions. The metric function contains the square of the angular momentum \(\mathbf {J}^{2}\), which does not distinguish the cases of \(\pm \mathbf {J}\) for angular momentum. We recall that rotating TSWs constructed from a Kerr black hole in \(3+1\) dimensions have been considered in [36] and their geodesics have been analyzed in [37]. Also rotational effects for collapsing thin shells in \(2+1\) and \(4+1\) dimensions have been considered in detail in [38, 39], respectively.

In our analysis of TSWs we observe that the off-diagonal components of the extrinsic curvature tensor \(k_{ij}\) and related components of the surface energy-momentum at the throat \(S_{ij}\) vanish in the case that we assume counter-rotating components of shells at the throat. The gas pressures from the upper and lower shells cancel each other to modify the equation of state to the extent that it becomes equivalent to a static case. We may draw a rough analogy with the rotating Earth. Due to the non-inertial effects curly geodesics of winds, i.e. the Coriolis effect matching at the equator, are counter-circular in different hemispheres. If the two hemispheres of our Earth were counter-rotating instead of corotating the curly motions should be identical. Counter-rotation at the throat in the case of TSWs allows us to choose a simpler surface energy-momentum tensor and study the stability condition. We can choose, for instance, a linear gas (LG) equation of state (EoS) at the junction in which the pressure is linearly related to the mass density. For such a LG the counter-rotating components make the TSW more stable. Increasing the angular momentum magnitude, i.e. the relative rotation, stabilizes the TSW further. Our next attempt toward a stable TSW is to assume a velocity dependent perturbation of the LG. It is observed that our stability argument is restricted by the linear perturbation alone in which at the equilibrium radius (\(R_{0}\)) we have the initial conditions \(\dot{R} _{0}=\ddot{R}_{0}=0.\) Once we assume that \(\dot{R}_{0}\ne 0,\) the perturbed throat grows exponentially to make the TSW unstable. This behavior is proved explicitly.

2 Rotating thin-shell wormhole

The \(2+1\)-dimensional rotating Bañados–Teitelboim–Zanelli (RBTZ) black hole solution is [40, 41]

$$\begin{aligned} \mathrm{d}s^{2}=-f(r)\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{f( r) }+r^{2}( \mathrm{d}\varphi +N^{\varphi }(r) \mathrm{d}t) ^{2}, \end{aligned}$$
(1)

in which

$$\begin{aligned} f(r) =-M+\frac{r^{2}}{\ell ^{2}}+\frac{J^{2}}{4r^{2}} \end{aligned}$$
(2)

and

$$\begin{aligned} N^{\varphi }(r) =-\frac{J}{2r^{2}}. \end{aligned}$$
(3)

Herein \(\Lambda =\pm 1/\ell ^{2}\) and \(M\) and \(J\) are the mass and angular momentum of the RBTZ black hole. We note that in order to have two horizons \( 0\le \frac{J}{\ell }\le M\). To construct the thin-shell wormhole we use the method of cut-and-paste introduced in [1–5]. According to this method we take two copies of the bulk, \(\mathcal {M}_{\pm }=\{ x^{\mu }|t\ge T(\tau ) \text { and }r\ge R(\tau )\} \), with the line elements

$$\begin{aligned} \mathrm{d}s_{\pm }^{2}=-f_{\pm }(r)\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{f_{\pm }(r) } +r^{2}(\mathrm{d}\varphi +N_{\pm }^{\varphi }(r) \mathrm{d}t)^{2}, \end{aligned}$$
(4)

and we paste them at an identical hypersurface \(\Sigma _{\pm }=\Sigma =\left\{ x^{\mu }|t=T\left( \tau \right) \text { and }r=R\left( \tau \right) \right\} .\) For convenience we move to a corotating frame by introducing \( \mathrm{d}\varphi +N_{\pm }^{\varphi }\left( R\right) \mathrm{d}t=\mathrm{d}\psi \) on each side separately. The line elements in both sides become

$$\begin{aligned} \mathrm{d}s_{\pm }^{2}&= -f_{\pm }(r)\mathrm{d}t^{2} \nonumber \\&+\frac{\mathrm{d}r^{2}}{f_{\pm }\left( r\right) }+r^{2}\left[ \mathrm{d}\psi +\left( N_{\pm }^{\varphi }\left( r\right) -N_{\pm }^{\varphi }\left( R\right) \right) \mathrm{d}t \right] ^{2}. \end{aligned}$$
(5)

The product manifold is complete with one boundary at the hypersurface \( \Sigma \) which we shall call the throat. On the throat the line element is given by

$$\begin{aligned} \mathrm{d}s_{\Sigma }^{2}=-\mathrm{d}\tau ^{2}+R^{2}\mathrm{d}\psi ^{2}. \end{aligned}$$
(6)

To satisfy the Israel junction conditions [42–46], first of all we have \(f_{+}(R)=f_{-}(R)=f\left( R\right) \) followed by

$$\begin{aligned} -f(R)\dot{T}^{2}+\frac{\dot{R}^{2}}{f\left( R\right) }=-1, \end{aligned}$$
(7)

in which a \(dot\) stands for the derivative with respect to the proper time \( \tau .\) Next, the Einstein equations (Israel junction conditions) on the hypersurface become

$$\begin{aligned} k_{i}^{j}-k\delta _{i}^{j}=-8\pi \mathrm{GS}_{i}^{j}, \end{aligned}$$
(8)

in which \(k_{i}^{j}=K_{i}^{j\left( +\right) }-K_{i}^{j\left( -\right) },\) \( k=tr\left( k_{i}^{j}\right) \), and

$$\begin{aligned} K_{ij}^{\left( \pm \right) }=-n_{\gamma }^{\left( \pm \right) }\left( \frac{ \partial ^{2}x^{\gamma }}{\partial X^{i}\partial X^{j}}+\Gamma _{\alpha \beta }^{\gamma }\frac{\partial x^{\alpha }}{\partial X^{i}}\frac{\partial x^{\beta }}{\partial X^{j}}\right) _{\Sigma } \end{aligned}$$
(9)

is the extrinsic curvature with embedding coordinate \(X^{i}\). Also the normal unit vector is defined as

$$\begin{aligned} n_{\gamma }^{\left( \pm \right) }=\pm \left( -\dot{R},\dot{T},0\right) . \end{aligned}$$
(10)

The surface energy-momentum tensor of the throat is chosen to be a perfect fluid type gas with

$$\begin{aligned} S_{ij}=\left( \sigma +P\right) u_{i}u_{j}+Pg_{ij}. \end{aligned}$$

Here \(\sigma \) is the energy density of the shell, \(P\) is the tangential pressure at the throat and \(u_{i}\) is the shell’s velocity. We note that in a rotating system in both sides of the throat \(u_{\psi }=0\) and therefore \( S_{\tau \psi }=0\), which means that \(S_{i}^{j}=\mathrm{diag}\left( -\sigma ,P\right) \). The extrinsic curvature components are then found to be

$$\begin{aligned} K_{\tau }^{\tau \left( \pm \right) }=\pm \frac{2\ddot{R}+f^{\prime }}{2\sqrt{ \dot{R}^{2}+f}}, \end{aligned}$$
(11)
$$\begin{aligned} K_{\tau }^{\psi \left( \pm \right) }=\mp \frac{N_{\pm }^{\varphi }\left( R\right) }{R}, \end{aligned}$$
(12)

and

$$\begin{aligned} K_{\psi }^{\psi \left( \pm \right) }=\pm \frac{\sqrt{\dot{R}^{2}+f}}{R}. \end{aligned}$$
(13)

As a result

$$\begin{aligned} k_{i}^{j}=\left( \begin{array}{ll} \frac{2\ddot{R}+f^{\prime }}{\sqrt{\dot{R}^{2}+f}} &{} -\frac{\left[ N_{+}^{\varphi }\left( R\right) +N_{-}^{\varphi }\left( R\right) \right] }{R}\\ -\frac{\left[ N_{+}^{\varphi }\left( R\right) +N_{-}^{\varphi }\left( R\right) \right] }{R} &{} \frac{2\sqrt{\dot{R}^{2}+f}}{R} \end{array}\right) . \end{aligned}$$
(14)

Having diagonal \(S_{i}^{j}\) implies that \(N_{+}^{\varphi }\left( R\right) +N_{-}^{\varphi }\left( R\right) =0,\) which consequently admits \( J_{+}+J_{-}=0.\) This in turn implies that the upper shell and the lower shell are counter-rotating, i.e. they spin in opposite directions. This configuration is depicted in Fig. 1. (We should add that thin shells in \(3+1\) dimensions with counter-rotating Kerr black holes have been constructed before in [47].) On the other hand, since \(J^{2}\) appears in \(f\), it does not create any problem in having the other conditions satisfied. Therefore

$$\begin{aligned} -\frac{2\sqrt{\dot{R}^{2}+f}}{R}=8\pi G\sigma \end{aligned}$$
(15)

and

$$\begin{aligned} \frac{2\ddot{R}+f^{\prime }}{\sqrt{\dot{R}^{2}+f}}=8\pi GP \end{aligned}$$
(16)

are the only Israel equations left to be satisfied. With the assumption \( J_{+}+J_{-}=0,\) therefore the problem becomes equivalent to the static (i.e. non-rotating) case. At the equilibrium state where \(R=R_{0}\) with \(\dot{R} _{0}=\ddot{R}_{0}=0\) one gets

$$\begin{aligned} \sigma _{0}=-\frac{2\sqrt{f_{0}}}{8\pi GR_{0}} \end{aligned}$$
(17)

and

$$\begin{aligned} P_{0}=\frac{f_{0}^{\prime }}{8\pi G\sqrt{f_{0}}}. \end{aligned}$$
(18)

One observes easily that the energy conditions are not satisfied since \( \sigma _{0}<0.\) The rest of the paper investigates the role of the angular momentum on the stability of the TSW.

Fig. 1
figure 1

Rotating thin-shell wormhole made by counter-rotating perfect fluids

Full size image

3 Angular momentum and stability

From (15) one finds

$$\begin{aligned} \dot{R}^{2}+f-\frac{\left( 8\pi G\sigma \right) ^{2}R^{2}}{4}=0, \end{aligned}$$
(19)

which can be written as

$$\begin{aligned} \dot{R}^{2}+V_\mathrm{eff}\left( R\right) =0 \end{aligned}$$
(20)

with \(V_\mathrm{eff}=f-\frac{\left( 8\pi G\sigma \right) ^{2}R^{2}}{4}.\) Also, from (15) and (16), it is a simple task to show that

$$\begin{aligned} \sigma +P=-R\sigma ^{\prime }. \end{aligned}$$
(21)

If we try to perturb the TSW from its equilibrium point, this relation must be satisfied. To keep our analysis as general as possible, we consider \( P=\xi \left( \sigma \right) \) in which \(\xi \) is a well-defined function of \( \sigma \). One can show that \(V_\mathrm{eff}\left( R_{0}\right) =V_\mathrm{eff}^{\prime }\left( R_{0}\right) =0\) and therefore the first nonzero term of the expansion of \(V_\mathrm{eff}\left( R\right) \) about \(R_{0}\) is \(V_\mathrm{eff}^{\prime \prime }\left( R_{0}\right) \) given by

$$\begin{aligned} V_\mathrm{eff}^{\prime \prime }\left( R_{0}\right) =f_{0}^{\prime \prime }-\frac{ f_{0}^{\prime 2}R_{0}^{2}+2\xi _{0}^{\prime }f_{0}\left( 2f_{0}-f_{0}^{\prime }R_{0}\right) }{2f_{0}R_{0}^{2}}, \end{aligned}$$
(22)

in which \(\xi _{0}^{\prime }=\left. \frac{\mathrm{d}\xi }{\mathrm{d}\sigma }\right| _{\sigma _{0}}\) and where using quantities with a subindex \(0\) implies they are calculated at the throat \(R=R_{0}.\) The equation of motion of the throat, for a small perturbation, becomes

$$\begin{aligned} \dot{R}^{2}+\frac{V_\mathrm{eff}^{\prime \prime }\left( R_{0}\right) }{2}\left( R-R_{0}\right) ^{2}\,\tilde{=}\,0 \end{aligned}$$
(23)

or, equivalently,

$$\begin{aligned} \ddot{x}+\frac{V_\mathrm{eff}^{\prime \prime }\left( R_{0}\right) }{2}x\,\tilde{=}\,0 \end{aligned}$$
(24)

in which \(x=R-R_{0}.\) Therefore for \(V_\mathrm{eff}^{\prime \prime }\left( R_{0}\right) >0\) the motion of the throat is oscillatory with angular frequency \(\omega =\sqrt{\frac{V_\mathrm{eff}^{\prime \prime }\left( R_{0}\right) }{ 2}}\), which implies that the TSW is stable. On the other hand if \(V_\mathrm{eff}^{\prime \prime }\left( R_{0}\right) <0\) the motion is of exponential type and hence the throat upon effecting the perturbation is unstable. In the following sections we shall consider a specific EoS i.e. \(\xi \left( \sigma \right) \), and for fixed values of mass and \(\ell ^{2}\) we study the effect of the angular momentum \( J \) on the stability of the wormhole.

3.1 Linear gas

The EoS of a LG is given by \(\frac{\mathrm{d}\xi }{\mathrm{d}\sigma }=\beta \) in which \(\beta \) is a constant parameter. One observes that for the cases

$$\begin{aligned} \frac{\left( 2f_{0}f_{0}^{\prime \prime }-f_{0}^{\prime 2}\right) R_{0}^{2}}{ 2f_{0}\left( 2f_{0}-f_{0}^{\prime }R_{0}\right) }<\beta \quad \text {for }\frac{2f_{0}}{f_{0}^{\prime }}>R_{0} \end{aligned}$$
(25)

and

$$\begin{aligned} \frac{2f_{0}R_{0}^{2}f_{0}^{\prime \prime }-f_{0}^{\prime 2}R_{0}^{2}}{ 2f_{0}\left( 2f_{0}-f_{0}^{\prime }R_{0}\right) }>\beta \quad \text {for }\frac{2f_{0}}{f_{0}^{\prime }}<R_{0} \end{aligned}$$
(26)

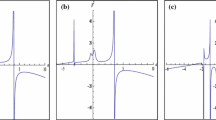
\(V_\mathrm{eff}^{\prime \prime }\left( R_{0}\right) >0\) and the equilibrium is stable. In Fig. 2 we plot the stability region with respect to \(\beta \) and \( R_{0}.\) In the same figure the result for different \(J\) are compared. As one can see, increasing the value of \(J\) increases the region of stability. Therefore the RTSW supported by a perfect fluid with an EoS of the form of LG becomes more stable. Let us comment that different EoS may also be investigated but in this work LG is enough to show the contribution of the angular momentum.

Fig. 2
figure 2

A plot of the regions of stability with respect to \(R_{0}\) and \(\beta \) for \(\ell =1.0\), \(M=1.0\), and various values for the angular momentum \(J.\) The value of \(J\) is given from top to bottom by \( J=0.0,0.2,0.4,0.6,0.8,1.0,1.2\), and \(1.4.\) We note that for \(J=1.0\) the bulk possesses a degenerate horizon (extremal black hole) and for \(J>1\) the bulk solution is not a black hole. The stability region for each case is shown with an arrow. According to this figure, one concludes that the bigger the angular momentum, the more stable the RTSW is

Full size image

3.2 Small velocity dependent perturbation

In this section we apply the small velocity perturbation method which is based on the assumption that the EoS of the fluid supporting the wormhole after the perturbation is the same as when the wormhole is at its equilibrium. From this assumption one finds from (15) and (16)

$$\begin{aligned} \frac{P}{\sigma }=-\frac{Rf^{\prime }}{2f}, \end{aligned}$$
(27)

which yields the equation of motion for the throat after the small speed perturbation as

$$\begin{aligned} \frac{2\ddot{R}+f^{\prime }}{\dot{R}^{2}+f}=\frac{f^{\prime }}{f}. \end{aligned}$$
(28)

Equivalently this amounts to

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau }\ln ( \dot{R}^{2}+f) =\frac{\mathrm{d}}{\mathrm{d}R}\ln \left( f\right) , \end{aligned}$$
(29)

which admits

$$\begin{aligned} \dot{R}^{2}=\dot{R}_{0}^{2}f. \end{aligned}$$
(30)

Using the explicit form of \(f\) upon integration yields

$$\begin{aligned} \ln \left( \frac{2R^{2}\sqrt{f}+\ell \left( \frac{2R^{2}}{\ell ^{2}} -M\right) }{2R_{0}^{2}\sqrt{f_{0}}+\ell \left( \frac{2R_{0}^{2}}{\ell ^{2}} -M\right) }\right) =\frac{2\dot{R}_{0}}{\ell }\left( \tau -\tau _{0}\right) . \end{aligned}$$
(31)

Perhaps it would be much easier to comment on \(R\) if we could find a closed form for it but even in this form one can see that the motion is not oscillatory. This means that although the speed of the throat does not increase dramatically with respect to \(R\) the equilibrium is not stable.

4 Conclusion

For a TSW in 2+1-dimensions it is observed that by pasting two counter-rotating shells at the throat the off-diagonal elements of the surface energy tensor \(S_{i}^{j}\) (and the related \(K_{i}^{j}\)) vanish. That is, although \(S_{\tau }^{\tau }\) and \(S_{\psi }^{\psi }\) are not affected the gluing procedure sets \(S_{\tau }^{\psi }=S_{\psi }^{\tau }=0.\) This amounts to the mutual cancelation of the upper and lower pressure components of the fluid, leaving only the pressure component \(S_{\psi }^{\psi }\ne 0.\)

The effect of the rotation on the geometry, however, remains intact as it depends on the square of the angular momentum (\(\mathbf {J}^{2}\)). The stability of a counter-rotating TSW for a gas of linear equation of state turns out to make the TSW more stable. For very fast rotation the stability region grows much larger in the parameter space. For a velocity dependent perturbation, however, it is shown that the TSW is no more stable. That is, after a perturbation of the throat radius (\(R_{0}\)) that depends on the initial speed (\(\dot{R}_{0}\ne 0 \)), no matter how small, it does not return to the equilibrium radius \(R_{0}\) again. Although our work is confined to the simple \(2+1\)-dimensional spacetime it is our belief that similar behaviors are exhibited also by the higher-dimensional TSWs.