1 Introduction

Entanglement is a pure quantum property which is associated with a quantum non-separability of parts of a composite system. Entangled states became a powerful tool for studying principal questions both in quantum theory and in quantum computation and information theory [1–5]. Recently a two-qubit photonic quantum processor was proposed that implements two consecutive quantum gates on the same pair of polarization-encoded qubits [12]. It is believed that the complete understanding of the nature of quantum entanglement still requires a detailed consideration of a variety of relatively simple cases, not only in nonrelativistic quantum mechanics, but in QFT as well. This explains recent interest to study quantum entanglement and entropy of quantum states in QFT systems with an unstable vacuum; in particular, with strong external backgrounds that may create particles from the vacuum, see e.g. [6–11]. In all these cases models with exact solutions could be very useful. In the present article, we are going to use exact solutions of a relativistic quantum mechanical problem to study how one can affect the entanglement measure of a two-qubit system consisting of two photons moving in the same direction with different frequencies and any of the two possible linear polarizations each, with the help of an applied external magnetic field. The interaction between the magnetic field and the photons in the model is performed through intermediate electrons that interact both with the photons and the magnetic field. An experimental realization of this theoretical scheme could be the following. Let us suppose that a beam consisting of the two photons propagating from a sender to a recipient crosses a region filled with free electrons subjected to an action of the magnetic field. Thereby the possibility of creating an indirect interaction between the external magnetic field and the photon beam appears. After leaving the region filled with the electrons, the photons will, in the general case, be registered in an entangled state, if their initial state was separable, or in an entangled state with a modified initial entanglement measure, if the initial state was already entangled. The theoretical support for this scheme is based on exact solutions of quantum equations of motion that describe the interaction of an electron subjected to an external magnetic field (or a medium of electrons not interacting with each other) with a quantized field of two photons with different frequencies and arbitrary linear polarizations. These exact solutions were studied in Refs. [13–17]. In Sect. 2 we apply results of this study to the case under consideration. In Sect. 3, by using the wave functions obtained in Sect. 2, we calculate the entanglement measures (the information and the Schmidt ones) of the photon beam as functions of the applied magnetic field and parameters of the electron medium. To illustrate the proposed idea, these calculations are done in the lowest order with respect to a small parameter, which naturally appears in the problem as a product of the fine-structure constant and density of the electron medium. It should be noted that a preliminary consideration of a similar problem was presented in [18].

2 Two-qubit photon beam interacting with an electron placed in constant uniform magnetic field

Consider a system of photons (in what follows: the photon beam) moving in the same direction \(\mathbf {n}\) and interacting with a Dirac electron. At the same time whole the system is placed in an external constant and uniform magnetic field \(\mathbf {B}=B\mathbf {n}\) parallel to the photon beam. In fact, this external field affects directly only the electron, but then, due to the electron–photon interaction, it affects photons as well. The quantum motion of such a system was studied in detail in Refs. [13–17]. Solving the problem in the volume box \(V=L^{3}\), one obtains quantum states for a photon beam interacting with a free electron gas with a given particle density \(\rho =V^{-1}\).

Below we describe a class of solutions of this kind that correspond to a photon beam that consists of two photons with different frequencies, each one with two possible polarizations. The system under consideration is described by the following Hamiltonian:

$$\begin{aligned}&{\hat{H}}={\hat{H}_{\gamma }}+{\gamma ^{0}} \left( \varvec{\gamma }{\hat{\mathbf{P}}}\right) +{m\gamma }^{0},\, {\hat{\mathbf{P}}}={\hat{\mathbf{p}}}+e\left[ {\hat{\mathbf{A}}}(\mathbf {r}) +\mathbf {A}^{\mathrm {ext}}(\mathbf {r})\right] \mathbf {,}\nonumber \\&\quad \mathbf {r} =\left( x,y,z\right) . \end{aligned}$$
(1)

Here \(\hat{H}_{\gamma }\) is the Hamiltonian of the two free transversal photons that move in the \(\mathbf {n}\) direction; \(\gamma ^{\mu }=\left( \gamma ^{0},\varvec{\gamma }\ \right) \) are Dirac gamma matrices [19]; \({\hat{\mathbf{A}}}(\mathbf {r})\) is the operator-valued vector potential of the photons in the Coulomb gauge, \(\hat{A}_{0}=0\), \(\mathrm{div } {\hat{\mathbf{A}}}(\mathbf {r})=0\); \(\mathbf {r}\) is the electron coordinate; \({\hat{\mathbf{p}}}=-i\varvec{\nabla }\) is the electron momentum operator, and \(\mathbf {A}^{\mathrm {ext}}(\mathbf {r})\) is the vector potential of the magnetic field in the Landau gauge (\(A_{x}^{\mathrm {ext}}=-By,\ A_{0} ^{\mathrm {ext}}=A_{y}^{\mathrm {ext}}=A_{z}^{\mathrm {ext}}=0\)), \(B>0\) magnitude of the magnetic field, \(e>0\) is the absolute value of the electron charge, and \(m\) is the electron mass. Following the original work, we represent solutions in the Heavyside system of units.Footnote 1 Provided that \(\mathbf {n}\) is chosen along the \(z\) axis, \(\mathbf {n}=(0,0,1),\) the momenta of the photons from the beam are

$$\begin{aligned}&\mathbf {k}_{s}=2\pi L^{-1}\left( 0,0,m_{s}\right) =\kappa _{s}\mathbf {n} ,\ s=1,2,\ \kappa _{s}=\kappa _{0}m_{s},\nonumber \\&\quad \kappa _{0}=2\pi L^{-1},\ m_{s} \in \mathbb {N}\ , \end{aligned}$$
(2)

so that

$$\begin{aligned}&\hat{H}_{\gamma }=\sum _{s=1,2\mathbf {;}\lambda }\kappa _{s}a_{s,\lambda } ^{+}a_{s,\lambda },\nonumber \\&{\hat{\mathbf{A}}}(\mathbf {r})=\sum _{s=1,2\mathbf {;} \lambda }\frac{1}{e}\sqrt{\frac{\varepsilon }{2\kappa _{s}}}\left[ a_{s,\lambda }\mathrm{e}^{i\kappa _{s}z}+a_{s,\lambda }^{+}\mathrm{e}^{-i\kappa _{s}z}\right] \mathbf {e} _{\lambda }\,. \end{aligned}$$

Here \(V=L^{3}\) is the quantization box volume, \(\mathbf {e}_{\lambda },\) \(\lambda =1,2\) are real polarization vectors, \((\mathbf {e}_{\lambda } \mathbf {e}_{\lambda ^{^{\prime }}})=\delta _{\lambda ,\lambda ^{\prime }} \), \(\left( \mathbf {ne}_{\lambda }\right) =0\) and \(\varepsilon =e^{2}/L^{3}.\) The photon creation and annihilation operators \(a_{s},{\lambda }^{+}\) and \(a_{s},{\lambda }\) are labeled by \(s\) and \(\lambda \) and obey the Bose type commutation relations. The only nonzero relations are

$$\begin{aligned}&a_{s^{^{\prime }},\lambda ^{^{\prime }}}a_{s,{\lambda }}^{+}-a_{s,{\lambda } }^{+}a_{s^{^{\prime }},\lambda ^{^{\prime }}}\\&\quad =\delta _{s,{s^{^{\prime }}}} \delta _{\lambda ,{\lambda ^{^{\prime }}}}\, , {s},\,{s^{\prime }}=1,2,\ \ \lambda ,\lambda ^{\prime }=1,2. \end{aligned}$$

The quantity \(\varepsilon \) characterizes the strength of the interaction between the charge and the plane-wave field. If we interpret \(\rho =V^{-1}=L^{-3}\) as the electron density, then \(\varepsilon =e^{2}\rho \). The dimensionality of \(\varepsilon \) is \([\varepsilon ]=l^{-3}\) (where \(l\) is the dimensionality of length). Being written with \(\hbar \) and \(c\) restored, it has the form

$$\begin{aligned} \varepsilon =\alpha \rho =\frac{\alpha \kappa _{0}^{3}}{8\pi ^{3}},\ \ \alpha =\frac{e^{2}}{\hbar c}=1/137, \end{aligned}$$
(3)

where \(\alpha \) is the fine-structure constant.

The motion of an electron in the magnetic field can be represented as an oscillator motion, described by new Bose creation, \(a_{0}^{+}\), and annihilation, \(a_{0}\), operators,

$$\begin{aligned} \sqrt{2}a_{0}^{+}=\eta -{\partial _{\eta }},\, \sqrt{2}a_{0} =\eta +{\partial _{\eta }}, \quad \eta =\frac{eBy-p_{x}}{\sqrt{eB}}. \end{aligned}$$
(4)

The operators \(a_{0}\) and \(a_{0}^{+}\) commute with every photon operator \(a_{k,\lambda }\) and\(\ a_{k,\lambda }^{+}\).

Using a canonical transformation, one can diagonalize the total Hamiltonian (1) in such a way that it is reduced to two terms that describe two subsystems—a subsystem of a quasielectron and a subsystem of quasiphotons—that do not interact between themselves,

$$\begin{aligned}&\hat{H}=\tilde{H}_{\gamma }+\tilde{H}_{e},\ \ \tilde{H}_{e}=r_{0}c_{0} ^{+}c_{0}+\frac{m^{2}}{2(np)}-\frac{\omega }{2},\nonumber \\&\tilde{H}_{\gamma }=\sum _{s=0,1,2;\lambda }r_{s\lambda }c_{s,\lambda } ^{+}c_{s,\lambda }+\tilde{H}_{\gamma 0},\nonumber \\&\tilde{H}_{\gamma 0}=-\sum _{s,k=0,1,2;\lambda ,\lambda ^{\prime }}r_{k\lambda ^{\prime }}|v_{s\lambda ,k\lambda ^{\prime }}|^{2}+\frac{\epsilon \left( \kappa _{1}+\kappa _{2}\right) }{2\kappa _{1}\kappa _{2}}, \end{aligned}$$
(5)

where

$$\begin{aligned} \epsilon =\frac{\varepsilon }{(np)}\ge 0,\ \ \omega =\frac{eB}{(np)} \ge 0,\ (np)=p_{0}-p_{z}>0, \end{aligned}$$
(6)

\(p_{0}\) is the electron energy, and \(p_{z}\) is \(z\)-projection of the electron momentum, such that for the electron states \((np)>0\). The quantities \(r_{k\lambda }\) are positive roots of the equation

$$\begin{aligned} \sum _{s=1,2}\frac{\epsilon }{r_{k\lambda }^{2}-\kappa _{s}^{2}}=1+\frac{\left( -1\right) ^{\lambda -1}\omega }{r_{k\lambda }},\ \ r_{0\lambda }=r_{0} \delta _{\lambda 1}. \end{aligned}$$
(7)

The matrices \(v_{s\lambda ,k\lambda ^{\prime }}\) are involved in the above-mentioned canonical transformation, which, when written in matrix form, reads

$$\begin{aligned}&a=uc-vc^{+},\, a^{+}=c^{+}u^{+}-cv^{+};\ \ c=u^{+}a+v^{T}a^{+}, \nonumber \\&\quad c^{+} =a^{+}u+av^{*}; uu^{+}-vv^{+}=1,\, vu^{T}-uv^{T}=0. \end{aligned}$$
(8)

This linear uniform canonical transformation [20] relates the initial creation and annihilation operators \(a_{k,\lambda }\) and\(\ a_{k,\lambda } ^{+},\ k=0,1,2,\) \(a_{0,\lambda }=a_{0}\delta _{\lambda 1}\), to the new creation and annihilation operators \(c_{k,\lambda }\) and\(\ c_{k,\lambda }^{+} ,\ k=0,1,2\), \(c_{0,\lambda }=c_{0}\delta _{\lambda 1}\). The free photon operators \(a_{s,\lambda }^{+}\) and \(a_{s,\lambda }\), \(s=1,2\),\(\ \lambda =1,2,\) are transformed to new quasiphoton operators \(c_{s,\lambda }^{+}\) and \(c_{s,\lambda }\), \(s=1,2\),\(\ \lambda =1,2,\) and the electron creation and annihilation operators \(a_{0}^{+}\) and \(a_{0}\) are transformed to the corresponding quasielectron operators \(c_{0}^{+}\) and \(c_{0}\).

For our purposes it is necessary to write here explicitly only the matrices \(u_{s\lambda ,k\lambda ^{\prime }}\) and \(v_{s\lambda ,k\lambda ^{\prime }}\) that correspond to the transformation of the photon operators, i.e., the matrices with the indices \(s,k=1,2\), and\(\ \lambda =1,2\). These matrices have the form

$$\begin{aligned}&u_{s\lambda ,k\lambda ^{\prime }}=\left[ \left( \sqrt{\frac{r_{k\lambda ^{\prime }}}{\kappa _{s}}}+\sqrt{\frac{\kappa _{s}}{r_{k\lambda ^{\prime }}} }\right) \frac{\left( -1\right) ^{\lambda ^{\prime }-1}\delta _{\lambda ,1}-i\delta _{\lambda ,2}}{2(r_{k\lambda ^{\prime }}^{2}-\kappa _{s}^{2})}\right] q_{k\lambda ^{\prime }},\nonumber \\&v_{s\lambda ,k\lambda ^{\prime }}=\left[ \left( \sqrt{\frac{r_{k\lambda ^{\prime }}}{\kappa _{s}}}-\sqrt{\frac{\kappa _{s}}{r_{k\lambda ^{\prime }}} }\right) \frac{\left( -1\right) ^{\lambda ^{\prime }-1}\delta _{\lambda ,1}-i\delta _{\lambda ,2}}{2(r_{k\lambda ^{\prime }}^{2}-\kappa _{s}^{2})}\right] q_{k\lambda ^{\prime }},\nonumber \\&q_{k\lambda }=\left[ \frac{\left( -1\right) ^{\lambda }\omega }{r_{k\lambda }^{3}\epsilon }+2\sum _{s=1,2}(r_{k\lambda }^{2}-\kappa _{s}^{2} )^{-2}\right] ^{-1/2}. \end{aligned}$$
(9)

Stationary states of the system have the form \(\Psi =\Psi _{\gamma } \otimes \Psi _{e},\) where \(\Psi _{\gamma }\) are state vectors of the quasiphotons,

$$\begin{aligned} \Psi _{\gamma }=\prod _{\lambda _{1}=1,2}\frac{(c_{1,\lambda _{1}}^{+} )^{N_{1,\lambda _{1}}}}{\sqrt{N_{1,\lambda _{1}}!}}\left| 0_{1}\right\rangle _{c}\otimes \prod _{\lambda _{2}=1,2}\frac{(c_{2,\lambda _{2}}^{+})^{N_{2,\lambda _{2}}}}{\sqrt{N_{2,\lambda _{2}}!}}\left| 0_{2}\right\rangle _{c}, \end{aligned}$$
(10)

\(c_{s\lambda }\left| 0_{s}\right\rangle _{c}=0\),\(\ s=1,2\),\(\ \forall \lambda ,\ \)and \(\Psi _{e}\) are state vectors of the quasielectrons, the explicit forms of which are not important for our purposes.

3 Entanglement in two-qubit photon beam

Here, to illustrate the proposed idea, we consider the case where the parameter \(\epsilon \) is small. That is why, in what follows, we ignore terms of the order \(o\left( \epsilon \right) \) as \(\epsilon \rightarrow 0.\)

In this approximation, for \(k=1,2\), we obtain

$$\begin{aligned}&r_{k\lambda }=\kappa _{k}+\epsilon \nonumber \\&\quad \frac{\left[ 2\kappa _{k}^{2}-\left( \kappa _{1}^{2}+\kappa _{2}^{2}\right) \right] }{(-1)^{\lambda -1} 2\omega \left[ 2\kappa _{k}^{2}-\left( \kappa _{1}^{2}+\kappa _{2}^{2}\right) \right] +\kappa _{k}\left[ 5\kappa _{k}^{2}-3\left( \kappa _{1}^{2}+\kappa _{2}^{2}\right) \right] +\frac{\kappa _{1}^{2}\kappa _{2}^{2}}{\kappa _{k}}}. \end{aligned}$$
(11)

3.1 Photons with antiparallel polarizations

Consider now the state vector (10) with only two quasiphotons, one of the first kind, and another of the second kind, and with antiparallel polarizations, which we take as \(\lambda _{1}=2\) and \(\lambda _{2}=1\). Such a state vector corresponds to \(N_{1,1}=N_{2,2}=0\) and \(N_{1,2}=N_{2,1}=1\) and has the form

$$\begin{aligned} \Psi _{\gamma }\left( \downarrow ,\uparrow \right) =c_{1,2}^{+}c_{2,1} ^{+}\left| 0\right\rangle _{c},\ \ \ \ \left| 0\right\rangle _{c}=\left| 0_{1}\right\rangle _{c}\otimes \left| 0_{2}\right\rangle _{c}. \end{aligned}$$
(12)

From the point of view of quasiphotons this is a separable state. However, if an observer analyzes this state by using tools that register free photons (to be consistent we have to suppose that in the region where such measurements is performed the magnetic field and the electron density are zero) he/she will observe an entangled two free photon state. The corresponding state vector can be obtained from Eq. (12) by expressing all the quasiphoton operators and vacuum vectors in terms of the corresponding free photon quantities. In this consideration, we disregard all the terms of the order \(o\left( \epsilon \right) \). One can easily verify that in this approximation, one can merely replace the quasiphoton vacuum \(\left| 0_{s}\right\rangle _{c}\) by the corresponding free photon vacuum \(\left| 0\right\rangle _{s} \), \(a_{s,\lambda }\left| 0_{s}\right\rangle =0\), so that

$$\begin{aligned} \Psi _{\gamma }\left( \downarrow ,\uparrow \right) =c_{1,2}^{+}c_{2,1} ^{+}\left| 0\right\rangle _{c}\simeq c_{1,2}^{+}c_{2,1}^{+}\left| 0\right\rangle \!,\ \ \left| 0\right\rangle =\left| 0_{1}\right\rangle \otimes \left| 0_{2}\right\rangle \!. \end{aligned}$$
(13)

The operators \(c_{1,2}^{+}\ \)and \(c_{2,1}^{+}\) have to be expressed in terms of the free photon operators using the canonical transformations (8) and (9),

$$\begin{aligned}&c_{1,2}^{+}=\sum _{s=1,2;\lambda =1,2}a_{s,\lambda }^{+}u_{s\lambda }, \ \ c_{2,1}^{+}=\sum _{s=1,2;\lambda =1,2}a_{s,\lambda }^{+}\tilde{u}_{s\lambda },\ u_{s\lambda }\\&\quad =u_{s\lambda ,12},\ \tilde{u}_{s\lambda }=u_{s\lambda ,21}. \end{aligned}$$

Thus,

$$\begin{aligned} \Psi _{\gamma }\left( \downarrow ,\uparrow \right) \simeq \sum _{s,s^{\prime },\lambda ,\lambda ^{\prime }}u_{s\lambda }\tilde{u}_{s^{\prime }\lambda ^{\prime } }a_{s,\lambda }^{+}a_{s^{\prime },\lambda ^{\prime }}^{+}\left| 0\right\rangle . \end{aligned}$$
(14)

Then one can see that in the approximation under consideration we have to ignore terms of the form \(u_{1\lambda }\tilde{u}_{1\lambda ^{\prime } }a_{1,\lambda }^{+}a_{1,\lambda ^{\prime }}^{+}\) and \(u_{2\lambda }\tilde{u}_{2\lambda ^{\prime }}a_{2,\lambda }^{+}a_{2,\lambda ^{\prime }}^{+}\) in the right hand side of Eq. (14). Thus, we obtain

$$\begin{aligned} \Psi _{\gamma }\left( \downarrow ,\uparrow \right) =\sum _{\lambda ,\lambda ^{\prime }}\left[ u_{1\lambda }\tilde{u}_{2\lambda ^{\prime }}+u_{2\lambda ^{\prime }}\tilde{u}_{1\lambda }\right] a_{1,\lambda }^{+}a_{2,\lambda ^{\prime } }^{+}\left| 0\right\rangle \!. \end{aligned}$$
(15)

Introducing the computational basis

$$\begin{aligned}&\left| \left( \lambda -1\right) \left( \lambda ^{\prime }-1\right) \right\rangle =a_{1,\lambda }^{+}a_{2,\lambda ^{\prime }}^{+}\left| 0\right\rangle ,\ \left| \vartheta _{1}\right\rangle =\left| 00\right\rangle ,\\&\left| \vartheta _{2}\right\rangle =\left| 01\right\rangle ,\ \left| \vartheta _{3}\right\rangle =\left| 10\right\rangle ,\ \left| \vartheta _{4}\right\rangle =\left| 11\right\rangle , \end{aligned}$$

we rewrite the vector (15) as

$$\begin{aligned}&\Psi _{\gamma }\left( \downarrow ,\uparrow \right) =\sum _{\lambda ,\lambda ^{\prime }}\left[ u_{1\lambda }\tilde{u}_{2\lambda ^{\prime }}+u_{2\lambda ^{\prime }}\tilde{u}_{1\lambda }\right] \left| \left( \lambda -1\right) \left( \lambda ^{\prime }-1\right) \right\rangle \nonumber \\&\quad =\sum _{j=1}^{4}\upsilon _{j}\left| \vartheta _{j}\right\rangle ,\ \ \ \sum _{i=1}^{4}|\upsilon _{i}|^{2}=1,\nonumber \\&\upsilon _{1}=u_{11}\tilde{u}_{21}+u_{21}\tilde{u}_{11}=u_{11,12} u_{21,21}+u_{21,12}u_{11,21},\nonumber \\&\upsilon _{2}=u_{11}\tilde{u}_{22}+u_{22}\tilde{u}_{11}=u_{11,12} u_{22,21}+u_{22,12}u_{11,21},\nonumber \\&\upsilon _{3}=u_{12}\tilde{u}_{21}+u_{21}\tilde{u}_{12}=u_{12,12} u_{21,21}+u_{21,12}u_{12,21},\nonumber \\&\upsilon _{4}=u_{12}\tilde{u}_{22}+u_{22}\tilde{u}_{12}=u_{12,12} u_{22,21}+u_{22,12}u_{12,21}. \end{aligned}$$
(16)

The entanglement measure of the system under consideration can be calculated as the information entropy \(E_{I}\left( \Psi \right) \) (the von Neumann entropy with Boltzmann constant that is equal to \(1/\ln 2\)) of the reduced density operator \(\hat{\rho }^{\left( 1\right) }\) of the subsystem of the first photon (the same results we obtain calculating the von Neumann entropy of the reduced operator \(\hat{\rho }^{\left( 2\right) }=\mathrm {tr}_{1} \hat{R}\) of the subsystem of the second photon) [21],

$$\begin{aligned} E_{I}\left( \Psi \right) =-\mathrm {tr}\left( \hat{\rho }^{\left( 1\right) }\log _{2}\hat{\rho }^{\left( 1\right) }\right) =-\sum _{a=1,2}\lambda _{a} \log _{2}\lambda _{a}, \end{aligned}$$
(17)

where \(\lambda _{a},\) \(a=1,2,\) are eigenvalues of \(\hat{\rho }^{\left( 1\right) }\). In what follows, we call \(E_{I}\left( \Psi \right) \) the information measure. The eigenvalues \(\lambda _{a}\) and the information measure \(E_{E}\left( \Psi \right) \) have the following form:

$$\begin{aligned}&\lambda _{a}=\frac{1}{2}\left[ \rho _{11}^{\left( 1\right) }+\rho _{22}^{\left( 1\right) }+\left( -1\right) ^{a}y\right] ,\ \ y=\root + \of {\left( \rho _{11}^{\left( 1\right) }-\rho _{22}^{\left( 1\right) }\right) ^{2}+4\left| \rho _{12}^{\left( 1\right) }\right| ^{2}},\nonumber \\&E_{I}\left( \Psi \right) =-\frac{1}{\ln 4}\left[ \left( 1-y\right) \ln \left( \frac{1-y}{2}\right) +\left( 1+y\right) \ln \left( \frac{1+y}{2}\right) \right] . \end{aligned}$$
(18)

To obtain the quantity \(E_{I}\left( \Psi \right) \) in our specific case, we use the explicit form of the matrices \(u\) from Eq. (9) and of the square roots \(r_{k\lambda }\) from Eq. (11) to calculate the quantities \(\upsilon _{i}\). The latter are

$$\begin{aligned} \upsilon _{1}=-(a+b),\ \ \upsilon _{2}=-i(a-b),\ \ \upsilon _{3}=-\upsilon _{2},\ \ \upsilon _{4}=\upsilon _{1}, \end{aligned}$$
(19)

where

$$\begin{aligned} \begin{aligned} a&=\frac{\left( \sqrt{\frac{\kappa _{1}}{r_{21}}}+\sqrt{\frac{r_{21} }{\kappa _{1}}}\right) \left( \sqrt{\frac{\kappa _{2}}{r_{12}}}+\sqrt{\frac{r_{12}}{\kappa _{2}}}\right) }{4\left( r_{12}^{2}-\kappa _{2} ^{2}\right) \left( r_{21}^{2}-\kappa _{1}^{2}\right) \sqrt{\frac{2}{\left( r_{21}^{2}-\kappa _{1}^{2}\right) ^{2}}+\frac{2}{\left( r_{21}^{2}-\kappa _{2}^{2}\right) ^{2}}-\frac{\omega }{r_{21}^{3}\epsilon }}\sqrt{\frac{2}{\left( r_{12}^{2}-\kappa _{1}^{2}\right) ^{2}}+\frac{2}{\left( r_{12}^{2}-\kappa _{2}^{2}\right) ^{2}}+\frac{\omega }{r_{12}^{3}\epsilon }} },\\ b&=\frac{\left( \sqrt{\frac{\kappa _{1}}{r_{12}}}+\sqrt{\frac{r_{12} }{\kappa _{1}}}\right) \left( \sqrt{\frac{\kappa _{2}}{r_{21}}}+\sqrt{\frac{r_{21}}{\kappa _{2}}}\right) }{4\left( r_{12}^{2}-\kappa _{2} ^{2}\right) \left( r_{21}^{2}-\kappa _{1}^{2}\right) \sqrt{\frac{2}{\left( r_{21}^{2}-\kappa _{1}^{2}\right) ^{2}}+\frac{2}{\left( r_{21}^{2}-\kappa _{2}^{2}\right) ^{2}}-\frac{\omega }{r_{21}^{3}\epsilon }}\sqrt{\frac{2}{\left( r_{12}^{2}-\kappa _{1}^{2}\right) ^{2}}+\frac{2}{\left( r_{12}^{2}-\kappa _{2}^{2}\right) ^{2}}+\frac{\omega }{r_{12}^{3}\epsilon }}}. \end{aligned} \end{aligned}$$
(20)

Then we obtain the quantity \(y\) from Eq. (18) in the approximation under consideration as

$$\begin{aligned}&y\left( \downarrow ,\uparrow \right) =4\left| \left( a^{2} -b^{2}\right) \right| =\left| 1-2\frac{\omega }{\epsilon }\left[ \frac{\left( r_{12}-\kappa _{1}\right) ^{2}}{\kappa _{1}}-\frac{\left( r_{21}-\kappa _{2}\right) ^{2}}{\kappa _{2}}\right] \right| \nonumber \\&\quad =1-\epsilon \Phi \left( \downarrow ,\uparrow \right) ,\ \ 0\le \epsilon \Phi \left( \downarrow ,\uparrow \right) <1,\nonumber \\&\Phi \left( \downarrow ,\uparrow \right) =\omega \frac{\left( \omega ^{2}\left( \kappa _{2}-\kappa _{1}\right) +2\omega \left( \kappa _{2} ^{2}+\kappa _{1}^{2}\right) +\left( \kappa _{2}^{3}-\kappa _{1}^{3}\right) \right) }{2\kappa _{1}\kappa _{2}\left( \omega -\kappa _{1}\right) ^{2}\left( \omega +\kappa _{2}\right) ^{2}}. \end{aligned}$$
(21)

The asymptotic behavior of the information measure \(E_{I}\left( \Psi _{\gamma }\left( \uparrow ,\downarrow \right) \right) \) as \(\epsilon \rightarrow 0\) reads

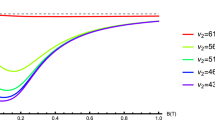
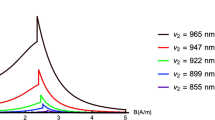
$$\begin{aligned} E_{I}\left( \Psi _{\gamma }\left( \downarrow ,\uparrow \right) \right) \!=\!\frac{\Phi \left( \downarrow ,\uparrow \right) }{2\ln 2}\left[ \epsilon \!\left( 1\!-\!\ln \left( \Phi \left( \downarrow ,\uparrow \right) /2\right) \right) \!-\!\epsilon \ln \epsilon \right] . \end{aligned}$$
(22)

We have calculated the entanglement measure for different values of cyclotron frequencies \(\omega =0\div 0.5\) THz achievable in a laboratory. For this study we selected the photon angular frequencies starting with the red light \(\kappa _{1}=2{,}500\) THz and calculated \(E_{I}\left( \Psi _{\gamma }\left( \downarrow ,\uparrow \right) \right) \) as a function of \(\Delta \kappa =\kappa _{2}-\kappa _{1}\) ranging from red to ultraviolet. The result is shown in Fig. 1 as a surface plot, where the color gradient represents the values of the entanglement measure.

Fig. 1
figure 1

Information measure \(E_{I}\left( \Psi _{\gamma }\left( \downarrow ,\uparrow \right) \right) \) as a function of \(\omega \) and \(\Delta \kappa ,~\)for \(\epsilon =0.1\)

Full size image

It is also known that for a pure bipartite qudit state one can recognize entanglement by evaluating the so-called Schmidt measure \(E_{S}\left( \Psi \right) ,\) which is the trace of the squared reduced density operators [22],

$$\begin{aligned} E_{S}\left( \Psi \left( \downarrow ,\uparrow \right) \right) =-\mathrm {tr} \left[ \left( \hat{\rho }^{\left( 1\right) }\right) ^{2}\right] =-\sum _{a=1,2}\lambda _{a}^{2}. \end{aligned}$$
(23)

The Schmidt measure can be considered as an alternative to the information entanglement measure. In the case under consideration

$$\begin{aligned} E_{S}\left( \Psi _{\gamma }\left( \downarrow ,\uparrow \right) \right)&=1-\left[ \left( \rho _{11}^{\left( 1\right) }\right) ^{2}+\left( \rho _{22}^{\left( 1\right) }\right) ^{2}+2\ \left| \rho _{12}^{\left( 1\right) }\right| ^{2}\right] \nonumber \\&=1-\left[ 2\left( \left| v_{1}\right| ^{2}+\left| v_{2}\right| ^{2}\right) ^{2}+8\left| \upsilon _{1}\upsilon _{2}\right| ^{2}\right] \nonumber \\&=1-16\left( a^{4}+b^{4}\right) =2\epsilon \Phi \left( \downarrow ,\uparrow \right) . \end{aligned}$$
(24)

The Schmidt measure calculated for parameters chosen above has a quite similar behavior to the information measure and is presented in Fig. 2.

Fig. 2
figure 2

Schmidt measure \(E_{S}\left( \Psi _{\gamma }\left( \downarrow ,\uparrow \right) \right) \) as a function of \(\omega \) and \(\Delta \kappa ,~\)for \(\epsilon =0.1\)

Full size image

3.2 Photons with parallel polarizations aligned along the magnetic field

Let us consider a state (10) with two quasiphotons, one of the first kind, and another one of the second kind and with parallel polarizations \(\lambda _{1}=1\) and\(\ \lambda _{2}=1\). Such a state vector corresponds to \(N_{1,1}=N_{2,1}=1\), \(N_{1,2}=N_{2,2}=0\) and has the form

$$\begin{aligned} \Psi _{\gamma }\left( \uparrow ,\uparrow \right) =c_{1,1}^{+}c_{2,1} ^{+}\left| 0\right\rangle _{c},\ \ \ \ \left| 0\right\rangle _{c}=\left| 0_{1}\right\rangle _{c}\otimes \left| 0_{2}\right\rangle _{c}. \end{aligned}$$
(25)

With the help of the same arguments that were used in the case of antiparallel polarizations, we obtain for \(\Psi _{\gamma }\left( \uparrow ,\uparrow \right) \) the representation (16) with

$$\begin{aligned} \begin{aligned}&\vartheta _{1}=u_{11,11}u_{21,21}+u_{21,11}u_{11,21},\\&\vartheta _{2}=u_{11,11}u_{22,21}+u_{22,11}u_{11,21},\\&\vartheta _{3}=u_{12,11}u_{21,21}+u_{21,11}u_{12,21},\\&\vartheta _{4}=u_{12,11}u_{22,21}+u_{22,11}u_{12,21}. \end{aligned} \end{aligned}$$
(26)

Using the explicit form of the matrices \(u\) from Eq. (9) and square roots \(r_{k\lambda }\) from Eq. (11), we can calculate the quantities \(\upsilon _{i}\). They are

$$\begin{aligned} \upsilon _{1}=a+b,\ \upsilon _{2}=-i\upsilon _{1},\ \upsilon _{3}=-i\upsilon _{1},\ \upsilon _{4}=-\upsilon _{1}, \end{aligned}$$
(27)

where

$$\begin{aligned} a&=\frac{\left( \sqrt{\frac{r_{11}}{\kappa _{2}}}+\sqrt{\frac{\kappa _{2} }{r_{11}}}\right) \left( \sqrt{\frac{r_{21}}{\kappa _{1}}}+\sqrt{\frac{\kappa _{1}}{r_{21}}}\right) }{4\left( r_{11}^{2}-\kappa _{2}^{2}\right) \left( r_{21}^{2}-\kappa _{1}^{2}\right) \sqrt{\frac{2}{\left( r_{11} ^{2}-\kappa _{1}^{2}\right) ^{2}}+\frac{2}{\left( r_{11}^{2}-\kappa _{2} ^{2}\right) ^{2}}-\frac{\omega }{r_{11}^{3}\epsilon }}\sqrt{\frac{2}{\left( r_{21}^{2}-\kappa _{1}^{2}\right) ^{2}}+\frac{2}{\left( r_{21}^{2}-\kappa _{2}^{2}\right) ^{2}}-\frac{\omega }{r_{21}^{3}\epsilon }}},\nonumber \\ b&=\frac{\left( \sqrt{\frac{r_{11}}{\kappa _{1}}}+\sqrt{\frac{\kappa _{1} }{r_{11}}}\right) \left( \sqrt{\frac{r_{21}}{\kappa _{2}}}+\sqrt{\frac{\kappa _{2}}{r_{21}}}\right) }{4\left( r_{11}^{2}-\kappa _{1}^{2}\right) \left( r_{21}^{2}-\kappa _{2}^{2}\right) \sqrt{\frac{2}{\left( r_{11} ^{2}-\kappa _{1}^{2}\right) {}^{2}}+\frac{2}{\left( r_{11}^{2}-\kappa _{2} ^{2}\right) {}^{2}}-\frac{\omega }{r_{11}^{3}\epsilon }}\sqrt{\frac{2}{\left( r_{21}^{2}-\kappa _{1}^{2}\right) {}^{2}}+\frac{2}{\left( r_{21}^{2} -\kappa _{2}^{2}\right) {}^{2}}-\frac{\omega }{r_{21}^{3}\epsilon }}}. \end{aligned}$$
(28)

Then we obtain the quantity \(y\)

$$\begin{aligned} y&= \sqrt{4\left| \upsilon _{1}i\upsilon _{1}+\left( -i\upsilon _{1}\right) \left( -\upsilon _{1}\right) \right| ^{2}}\\&= 4\left| \upsilon _{1} ^{2}\right| =4\left| \left( a+b\right) ^{2}\right| =1. \end{aligned}$$

One can easily see that in this case, both the information and the Schmidt entanglement measure of the state \(\Psi _{\gamma }\left( \uparrow ,\uparrow \right) \) are zero

$$\begin{aligned} E_{I}(\Psi _{\gamma }\left( \uparrow ,\uparrow \right) )=0,\ E_{S}\left( \Psi _{\gamma }\left( \uparrow ,\uparrow \right) \right) =0. \end{aligned}$$

The same result holds true for the state

$$\begin{aligned} \Psi _{\gamma }\left( \downarrow ,\downarrow \right) =c_{1,2}^{+}c_{2,2} ^{+}\left| 0\right\rangle _{c},\ \ \ \ \left| 0\right\rangle _{c}=\left| 0_{1}\right\rangle _{c}\otimes \left| 0_{2}\right\rangle _{c}, \end{aligned}$$

with two quasiphotons, one of the first kind, and another one of the second kind and with parallel polarizations \(\lambda _{1}=2\),\(\ \lambda _{2}=2\),

$$\begin{aligned} E_{I}(\Psi _{\gamma }\left( \downarrow ,\downarrow \right) )=E_{S}\left( \Psi _{\gamma }\left( \downarrow ,\downarrow \right) \right) =0. \end{aligned}$$

4 Concluding remarks

Considering a relevant quantum mechanical model, we have demonstrated that a two-qubit system that consists of two photons moving in the same direction with different frequencies, and with any of two possible linear polarizations, can be entangled in a controlled way by applying an external magnetic field in an electron medium. Then we succeeded to express the corresponding entanglement measures (the information and the Schmidt ones) via the parameters characteristic of the problem, such as photon frequencies, magnitude of the magnetic field, and the parameters of the electron medium. We have found that, in the general case, the entanglement measures depend on the magnitude of the applied magnetic field and hence can be controlled by the latter. As a rule, the entanglement increases with increasing the magnetic field (with increasing the cyclotron frequency). It should be noted that we did not consider resonance cases where the cyclotron frequency approaches the photon frequencies. Obviously, the entanglement depends on the parameters that specify the electron medium such as the electron density and electron energy and momentum. We did not study this dependence in this work; these characteristics were fixed by choosing a natural, small parameter in our calculations. The obtained results allow us to see how the entanglement measures depends on the fixed parameters that characterize the system under consideration, i.e., on the choice of initial states of the photons and on photon frequencies. We have come to the following observations: if the both photon polarizations coincide with themselves and with the direction of the magnetic field, then no entanglement occurs. The entanglement takes place if at least one of the photon polarizations is aligned against the direction of the magnetic field. In this respect, we have a direct analogy with the Pauli interaction between spin and a magnetic field. However, it seems that this interaction depends also on the photon frequency and the resulting entanglement effect depends on the both photon frequencies, or on the first photon frequency and the difference between the frequencies.

We understand that our study is based on exact solutions of the model problem—an electron interacting with a quantized field of two photons and with a constant uniform magnetic field. First of all, the constant uniform magnetic field is an idealization, which cannot be realized experimentally. However, such an idealization allows exact solutions and is often used in QED. Sometimes, one can verify that local space-time processes do not depend essentially on the asymptotic behavior of the external field. More realistic results could be obtained if magnetic fields vanishing at space-time infinity were used. In calculating the entanglement measures, we have also used the first-order approximation in the natural parameter \(\epsilon =\frac{\rho }{137(np)}\), supposing that it is small, \(\epsilon \sim 0,1.\) In fact, this imposes restrictions on the electron density \(\rho \) and electron energy and momentum, \((np)=p_{0}-p_{z}.\) However, this approximation was enough for our semi-qualitative preliminary study of the problem. All the above-mentioned approximations would have to be carefully estimated in order for realistic numbers to occur in an experimental realization of the controlled entanglement of photons by a magnetic field that might be extracted.

Finally, we stress that the principal aim of our study was to demonstrate a possibility for entangling photon beams with the help of an external magnetic field. In contrast with the well-known possibilities of doing this by using crystal devices, the present way allows one to change easily and continuously the entanglement measure. We do not discuss in the article how one can experimentally measure the entanglement measure. This is an important general problem, which, however, is beyond the scope of our study. In each specific case, it requires significant efforts to realize such experiments. Important results in this direction can be found in Refs. [8–11]. Descriptions of some experiments that use NMR methods and allow one to detect quantum entanglement can be found in the book [5] (see Sect. 6.3 therein).