Shadowing in multiparton proton–deuteron collisions

Abstract

We study the screening effect for the multiparton interactions (MPI) for proton–deuteron collisions in the kinematics where one parton belonging to the deuteron has small $x_1$, so the leading twist shadowing is present, while the second parton ($x_2$) is involved in the interaction in the kinematics where shadowing effects are small. We find that the ratio of the shadowing and the impulse approximation terms is approximately a factor of 2 larger for MPI than for the single parton distributions. We also calculate the double parton antishadowing (DPA) contribution to the cross section due to the independent interactions of the partons of the projectile proton with two nucleons of the deuteron and find that shadowing leads to a strong reduction of the DPA effect. For example, for the resolution scale $Q_1^2 \sim 4$ $\text{ GeV }^2$ of the interaction with parton $x_1$ we find that shadowing reduces the DPA effect by $\sim$30 %. It is argued that in the discussed kinematics the contribution of the interference diagrams, which correspond to the interchange of partons between the proton and neutron, constitutes only a small correction to the shadowing contributions.

1 Introduction

Recently there was a renewed interest in the theoretical studies of the multiparton interactions (MPI) in which at least two partons of one of the colliding particles are involved in the proton–nucleus collisions [1–7]. To a large extent this is due to the first experimental studies of $pA$ collisions at the LHC [8–11]. It was suggested in [1–4] that MPI would be easier to observe experimentally in $pA$ collisions than in $pp$ collisions since they are parametrically enhanced in the $pA$ case by a factor $A^{1/3}$ [1]. General formulas for this cross section were derived in [2] within perturbative QCD (pQCD) in the impulse approximation (that is, neglecting deviations of the nuclear parton distribution functions (pdf) from the additive sum of the nucleon pdfs). The analysis demonstrated connection of the pQCD treatment with the parton model calculation of [1] for the large $A$ limit and uncorrelated nucleon distribution in the nucleus. The calculation of [2] employed the formalism developed in Refs. [12–15], which is based on the use of the generalized double parton distributions in momentum space introduced in Ref. [12]. The calculation was done explicitly in the impulse approximation. It was argued in Refs. [5–7] that the impulse approximation is not a complete answer and one must include also the so-called interference diagrams, although no explicit estimates of their relative strength was performed. In Ref. [2] the arguments were presented that interference diagrams become important for small x due to the leading twist (LT) nuclear shadowing phenomenon.

The main aim of the paper is to calculate explicitly the interference corrections to the impulse approximation due to the nuclear shadowing for the case of proton–deuteron scattering based on the theory of the leading twist shadowing phenomena (for a recent review see [16]) which successfully predicted gluon shadowing for the coherent photoproduction of $J/\psi$ recently observed at the LHC [17, 18]. We will focus on the limit when one of partons in the deuteron has small enough $x$, so that nuclear shadowing is present for the deuteron pdf while the second parton is probed in the kinematics where shadowing effects are absent. We will demonstrate that in this limit nuclear shadowing induced interference is present already on the level of diagrams where one of the nucleons is active in the amplitude and two in the conjugated amplitude (or vise versa), and that it has the same magnitude as the enhancement of MPI due to the interaction with two nucleons in the impulse approximation. In our analysis we will neglect a small effect of antishadowing in the deuteron pdfs at $x \sim 0.1$ which is present due to the momentum sum rule; see the discussion in [16]. We also consider the interference for the case when just one parton of the proton is interchanged with one parton of the neutron and argue that this interference effect is much smaller than the leading twist shadowing interference.

While the actual experiments are done with the heavy nuclei, we believe that the deuteron case provides a simple “laboratory” for the studying possible mechanisms of shadowing in four jet production processes. In the case of heavy nuclei, the combinatorics of the shadowing diagrams is much more complicated. It will be considered elsewhere.

The shadowing in the multijet production differs significantly from the LT shadowing for nuclear pdfs since the two partons belonging to the projectile proton are typically located in a very small transverse area of the radius $\sim$ $0.5 fm$. As a result they scatter off two different but very close in the impact parameter space nucleons that may be rather strongly correlated. This is especially true for the case of scattering off the deuteron which is a highly correlated system. Hence the analysis presented here can serve as the stepping stone to a discussion of similar effects for MPI with heavy nuclei.

In the current experimental studies one usually starts with a trigger on a hard process of large virtuality—say a dijet with $p_t$’s larger than 50 $\div$ 100 GeV and one next looks for a second hard subprocess in the underlying event. Since the LT nuclear shadowing for $p_t \ge$ 100 GeV/c is very small we will focus here on consideration of the MPI in which one of the subprocesses has large enough x or large virtuality so that the leading twist nuclear shadowing can be neglected in this case. The paper is organized as follows. In Sect. 2 we apply the general expressions relating double hard four jet cross section for the collision of hadrons $A$ and $B$ in terms of $_2$GPDs (Eq. 3) to obtain a compact expression for the double parton antishadowing contribution (DPA) taking into account the finite transverse size of the gluon GPD in the nucleon. In Sect. 3 we summarize first the theory of the LT shadowing for the deuteron pdfs and next use it to calculate the shadowing correction to the MPI rate for the case when x of one of the partons of the deuteron participating in collision is large and another is small. We demonstrate that the shadowing in the case of MPI is a factor of 2 stronger than in the case of the deuteron pdfs. At the same time an additional contribution to MPI due to the pQCD evolution induced correlations in the proton wave function reduces this enhancement. In Sect. 4 we present the numerical results. We find that the shadowing effect is smaller but of the same magnitude as DPA for modest virtualities ($Q^2\sim 4~\text{ GeV }^2$). We show explicitly that the double parton shadowing is negligible when both of the partons have large $x$, confirming the results of Ref. [2]. In Sect. 5 we estimate the contribution of the interference diagrams corresponding to the situation when a parton “1” (“2”) in the amplitude belongs to the proton (neutron) and in the conjugated amplitude to the neutron (proton). We argue that these contributions are small compared to the shadowing mechanisms. Our conclusions are presented in Sect. 6. In the appendix we consider correspondence of the Glauber series for the inelastic $pA$ scattering and combinatorics of MPI.

2 Impulse approximation for the proton–deuteron scattering

2.1 Leading term

Let us first consider the case when both partons of the nucleus involved in the interaction belong to the same nucleon—the impulse approximation (see Fig. 1).

Fig. 1

Impulse approximation

This is the dominant contribution in the deuteron case, though it becomes subleading for heavy nuclei [1, 2]. The corresponding cross section is, obviously, twice the cross section of the MPI $pp$ scattering (we neglect here the difference of the quark distributions in proton and neutron). It is given by

$$\begin{aligned} \sigma _\mathrm{imp 4}(pD) = 2 \sigma _\mathrm{imp 4}(pN). \end{aligned}$$

(1)

Thus, introducing the so-called $\sigma _\mathrm{eff}(pD)$ we can write

$$\begin{aligned} \frac{1}{\sigma _\mathrm{eff \,pA}}&= \frac{\sigma _\mathrm{imp 4}}{\sigma _1\sigma _2}\nonumber \\&= 2\int \frac{d^2\Delta _t}{(2\pi )^2} F_{2g}(\Delta ^2,x_{1})F_{2g}(\Delta ^2,x_{2})F_{2g}(\Delta ^2,x_{1p})\nonumber \\&\times F_{2g}(\Delta ^2,x_{2p})(1+N), \end{aligned}$$

(2)

where $\sigma _1,\sigma _2$ are the elementary cross sections of production of jets in the parton–parton interaction; the factor $F_{2g}$ is the two gluon form factor of nucleon [19]. The factor $1+N$ parameterizes the enhancement of the observed cross section as compared to the calculation in the mean field approximation.

A significant positive contribution to $N$ originates from the pQCD evolution induced parton–parton correlations—the $1\otimes 2$ processes [12–15] which enhance the cross section as compared to the one calculated assuming dominance of the collisions of two independent pairs of partons—the $2 \otimes 2$ processes. Our numerical studies found $1+N\sim 2.2$ for $pp$ scattering in quasi-symmetric kinematics, which is consistent with the LHC data for $x\sim 0.001\div 0.01$. In the kinematics we consider here—one large $p_t$ pair of $p_t \sim 30$ GeV/c jets and another pair with moderate $p_t$’s of the order $2, 3, 10$ GeV/c, the mechanisms of Refs. [12–14] lead to an expectation of $N\sim 0.3, 0.6, 1.0$, respectively. Note that these values of $N$ are slightly larger than the corresponding values in $pp$ collisions at the LHC for the same hard transverse scales, since the c.m. energy in $pA$ collisions is smaller ($\sqrt{s}=5~$ TeV) and the corresponding $x$ are larger by a factor of 1.3 than in $pp$ collisions for $\sqrt{s}= 8~$TeV.

2.2 Antishadowing contribution

The second contribution, which becomes dominant in the case of scattering off heavy nuclei, results from the process in which two partons from a incoming proton interact with two different nucleons of the deuteron. The corresponding diagram is depicted in Fig. 2.

Fig. 2

Double parton antishadowing correction

It can be calculated using the general expression relating double hard four jet cross section for the collision of hadrons $A$ and $B$ in terms of $_2$GPDs,

$$\begin{aligned} \frac{d\sigma ^{AB}_{4jet}}{d\hat{t}_1d\hat{t}_2}&= \int \frac{ d^2\vec \Delta }{(2\pi )^2} \frac{d\hat{\sigma }_1(x_1',x_1)}{d\hat{t}_1}\frac{d\hat{\sigma }_2(x_2',x_2)}{d\hat{t}_2} \, \,\nonumber \\&_2G_{A}(x_1',x_2',\vec \Delta )\,_2G_{B}(x_1,x_2,\vec \Delta ), \end{aligned}$$

(3)

where in our case $G_A, G_B$ are the $2$ parton GPDs of the nucleon and the deuteron [12]. Here $x_1'=x_{1p},x_2'=x_{2p}$ are the light-cone fractions for the partons of the projectile nucleon, and $x_1, x_2$ are the light-cone fractions for the target nucleon/nucleons. It was demonstrated in [2] that this contribution can be written through the two-body nuclear form factor. In the case of scattering off the deuteron (diagram of Fig. 2) this form factor is easily calculated and expressed through the deuteron form factor (since in this case there is a simple relation between two-body and single-body form factors). Indeed, the contribution of the corresponding diagram is given by (cf. Fig. 2 and Eqs. 19–21 in [2])

$$\begin{aligned} \frac{\sigma _\mathrm{DPA}}{\sigma _1\sigma _2}&= 2\times \int \frac{d^4\Delta }{(2\pi ))^4}F_{2g}(\Delta _t,x_1)F_{2g}(\Delta _t,x_2)F_{2g}(\Delta _t,x_{1p})F_{2g}(\Delta _t,x_{2p})\nonumber \\&\times \int \frac{d^4k}{(2\pi )^4} \frac{\Gamma (p/2 +k, p/2 -k)\Gamma (p/2 +k-\Delta , p/2 -k+\Delta )}{((p/2+k)^2-m^2)((p/2+k-\Delta )^2-m^2)((p/2-k)^2-m^2)((p/2-k+\Delta )^2-m^2)}. \end{aligned}$$

(4)

The factors $\Gamma$ are the two vertex functions depicted in Fig. 2. We can now integrate in a standard way over $k^0,\Delta ^0$ and use the fact that the corresponding denominators are dominated by nonrelativistic kinematics: $k^0,\Delta ^0\sim \vec k^2/M$ and the longitudinal transfer $\Delta _z=0$. After performing the integration we immediately obtain

$$\begin{aligned} \frac{\sigma _\mathrm{DPA}}{\sigma _1\sigma _2}&= 2\times \int \frac{d^2\Delta _t }{(2\pi ))^2}F_{2g}(\Delta _t,x_1)\nonumber \\&F_{2g}(\Delta _t,x_2))F_{2g}(\Delta _t,x_{1p})F_{2g}(\Delta _t,x_{2p})S(\vec \Delta ^2). \end{aligned}$$

(5)

We define here the deuteron form factor as (see e.g. [16]):

$$\begin{aligned} S(\vec \Delta ^2)= \int \frac{d^3k}{(2\pi )^3 8M}\frac{\Gamma (\vec k^2)\Gamma ((\vec k-\vec \Delta )^2)}{(A^2+\vec k^2)(A^2+(\vec k-\vec \Delta )^2)}, \end{aligned}$$

(6)

where the $\Gamma$ is the deuteron to two nucleons vertex, and

$$\begin{aligned} A^2=m^2-M^2/4. \end{aligned}$$

(7)

Here $M$ is the deuteron mass, $m$ is the nucleon mass, and the momenta of nucleons in the deuteron are $\vec p/2\,{+}\,\vec k$, and $\vec p/2\,{-}\,\vec k$. Here we used the fact that the deuteron is a nonrelativistic system, so the form factors $\Gamma$ depend only on the differences of the spatial components of the nucleon momenta. Using the relation between the vertex functions and wave functions of the deuteron we can rewrite the latter expression in terms of the deuteron nonrelativistic wave functions as

$$\begin{aligned} S\left( \Delta ^2\right)&= \int d^3 \vec {p} \Bigg [u(\vec {p})u(\vec {p}+\vec {\Delta }) +\, w(\vec {p})w(\vec {p}+\vec {\Delta })\nonumber \\&\times \left( \frac{3}{2}\frac{(\vec {p}\cdot (\vec {p}+\vec {\Delta }))^2}{p^2 (p+\vec {\Delta })^2}-\frac{1}{2}\right) \Bigg ], \qquad \end{aligned}$$

(8)

where $u$ and $w$ are the $S$-wave and $D$-wave components of the deuteron wave function respectively (here in difference from Eq. 6 we give the expression for the spin-1 deuteron).

Note that Eqs. 5, 6 accurately take into account the finite transverse size of the nucleon GPDs which is numerically rather important (see Sect. 4).

At the same time we neglected in this calculation the nucleon Fermi motion effect which shifts the x-argument of the bound nucleon pdfs. The reason is that this effects is a very small correction which enters only on the level of the terms $\propto \vec k^2/m^2$ which are very small for the deuteron, cf. the discussion in [2].

Finally, let us mention that we must multiply this expression by $1+N_L$, where $N_L$ is the enhancement of 4 jet cross section relative to mean field approximation in the given kinematics due to parton correlations. In our kinematics this number is very small. Indeed, in difference from the case of $pp$ collisions the $\Delta$ dependence of the nucleus and nucleon factors in the corresponding equation is very different. As a result one does not have in this case an enhancement factor of $\sim 2$ from $1\otimes 2$ which is present in the $pp$ case. In addition, the transverse integral is dominated by the same deuteron form factor both in $1\otimes 2$ and $2\otimes 2$ contributions, leading to $N_L\sim N/5\le 0.1$ (see Sect. 4) for $Q^2\le 10$ GeV$^2$, and reaching $20\,\%$ for $Q^2\sim 10$ GeV$^2$.

3 Single shadowing: one to two processes

3.1 Leading twist shadowing for the deuteron pdfs

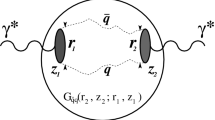
Before discussing the shadowing for MPI in the deuteron it is worth recalling the picture of the LT shadowing for the case of the deuteron pdfs. It was demonstrated in [20] that the shadowing correction to the deuteron pdf can be expressed in the model independent way through the diffractive nucleon pdfs. In the reference frame where deuteron is fast, the process can be pictured as the hard interaction in $| in>$-state with a small $x$ parton in which the nucleon in the final state carries most of its initial momentum fraction—$(1 - x_{I\!\!P})$, while in the final state the diffractive system which carries the light-cone fraction $x_{I\!\!P}$ combines with the second nucleon into a nucleon with momentum fraction $1 + x_{I\!\!P}$; see Fig. 3.

Fig. 3

Shadowing in DIS off the deuteron

As a result one finds for the shadowing correction (see Eq. 98 and Fig.28 in Ref. [16])

$$\begin{aligned}&\Delta f_D(x,Q^2) = 2f_N(x,Q^2)-f_D(x,Q^2),\end{aligned}$$

(9)

$$\begin{aligned}&\Delta f_D= 2\int \frac{d^2 q_t dx_{I\!\!P}}{(2\pi )^3}S(\vec {q}~^2))F^{D(4)}(\beta ,Q^2,x_{I\!\!P},q_t), \end{aligned}$$

(10)

where $\beta =x/x_{I\!\!P}$ and $F^{D(4)}(\beta ,Q^2,x_{I\!\!P},q_t)$ is the diffractive pdf. It is easy to see that the shadowing originates from configurations where two nucleons are roughly behind each other. For these configurations shadowing is large as long as the effective cross section of the rescattering:

$$\begin{aligned} \sigma _2\approx 16\pi {\int _x^{0.1}dx_{I\!\!P} \beta F_j^{D(4)}(\beta , Q^2,x_{I\!\!P},t_{min})\over xf_{j/N}(x,Q^2)}, \end{aligned}$$

(11)

is comparable to the pion–nucleon cross section which is the case for the gluon channel for $x \le 10^{-3}$, $Q^2\le \text{10 } \text{ GeV }^2$.

The leading twist shadowing theory [16, 20] predicted reduction of the gluon pdfs in the gluon channel for $x\sim 10^{3}, Q^2 \sim \text{ few } \text{ GeV }^2, A= 200$ by a factor 0.5–0.6 which agrees well with the $J/\psi$ coherent photoproduction data [17, 18]. It is worth emphasizing that the expressions for shadowing contribution to the deuteron pdfs can be derived both using pretty cumbersome approach of the original paper of Gribov [21] or using Abramovski–Gribov–Kancheli (AGK) cutting rules [22] in combination with the QCD factorization theorems for diffraction scattering and for inclusive scattering [16]. The dominance of the soft Pomeron dynamics for the hard diffraction is now confirmed by the HERA data—$\alpha _{I\!\!P}$ for hard diffraction is the same as for soft processes [16, 23]. So we are applying AGK rules effectively for the soft dynamics where it appears to be well justified.¹

3.2 Single shadowing for MPI

The DPA contribution which we considered above corresponds to collisions where two nucleons of the deuteron are located at small relative transverse distance of the order of the nucleon transverse gluon size—$\sim 0. 5 fm$. For such two nucleon configuration LT nuclear shadowing is large since the effective cross section of the rescattering interaction is large. Hence it may strongly reduce the DPA effect. The shadowing term corresponds to the diagrams which are an analog of the LT shadowing diagrams for the deuteron pdf with an extra blob corresponding to the non-screened second interaction (Fig. 4).

Fig. 4

Shadowing correction to 4 jet production in pD scattering

The screening contribution requires that the first nucleon experiences the diffractive interaction, while the second hard blob is a generic hard nucleon–nucleon interaction. Similar to the DIS case this diagram gives negative contribution to the cross section.

As usual only the diagrams with elastic $I\!\!P$—$nucleon$—$I\!\!P$ vertex contribute, since we work in conventional two nucleon approximation for the deuteron when all other components of the deuteron wave function are neglected.

Hence the shadowing is described by four diagrams one of which is depicted in Fig. 4. The combinatorial factor of 2 arises since the parton “1” can belong to either of two nucleons. Another factor of 2 is due to the possibility to attach the Pomeron line to the first nucleon either in the initial or in the final state. The shadowing contribution can be written as

$$\begin{aligned} \frac{\sigma _{SS}}{\sigma _1\sigma _2}&= -4\int \frac{d^4qd^4\Delta d^4k}{(2\pi )^{12}} \frac{F^{D(4)}(\beta ,Q_1^2,q^2_t,x_{I\!\!P},\vec \Delta _t)}{G_N(x_1,Q_1^2)}\frac{1}{((p/2+k)^2-m^2)((p/2+k-q+\Delta )^2-m^2)}\nonumber \\&\times \frac{F_{2g}(\Delta _t,x_{1p})F_{2g}(\Delta _t,x_{2p})F_{2g}(\Delta _t,x_2)}{((p/2-k)^2-m^2)((p/2-k-\Delta )^2-m^2)((p/2-k-\Delta +q)^2-m^2)}+(1\leftrightarrow 2), \end{aligned}$$

(12)

with the factor of 4 reflecting the presence of four diagrams. The Pomeron exchanges carry three-momenta $\vec q =(\vec q_t,q_z)$ and $\vec q+\vec \Delta$.

We carry the integration over $q_0,k_0,\Delta _0$ in exactly the same way as in the previous section, where we calculated the diagram of Fig. 2, taking into account that the vector $\vec \Delta$ is transverse. Using Eq. 6 for the deuteron form factor we can rewrite Eq. 12 as

$$\begin{aligned} \frac{\sigma _{SS}}{\sigma _1\sigma _2}&= -4\int \frac{d^2q_td^2\Delta _t dx_{I\!\!P}}{(2\pi )^5} \displaystyle {\frac{F^{D(4)}(\beta ,Q_1^2,q^2_t,x_{I\!\!P},\vec \Delta _t)}{G_N(x_1,Q_1^2)}}\nonumber \\&\times \, S((\vec q+\vec \Delta )^2) F_{2g}(\Delta _t,x_{1p})F_{2g}(\Delta _t,x_{2p})F_{2g}(\Delta _t,x_2))\nonumber \\&+\,(1\leftrightarrow 2). \end{aligned}$$

(13)

Overall, we can see from a comparison of Eqs. 10 and 13 that in the limit when the radius of the deuteron is very large, one could neglect the $q_t$ dependence of all other factors; the ratio of shadowing and impulse approximation terms in the case of the MPI is a factor of 2 larger than for the case of DIS. This reflects the enhancement of the central collisions in the MPI, which we mentioned above. Note that we implicitly use here the AGK relation between the cross section for the total MPI cross section and for the cross section for the inelastic final state depicted in Fig. 4. In principle, one could first obtain the expression for the small x parton distribution in the impact parameter space as a function of the transverse distance between the nucleons (cf. [16] where GPDs for the nuclei at small x are calculated) and next calculate the $\rho$ distribution of the second parton, ultimately deriving $_2$ GPD for the deuteron and calculating the MPI cross section using the $b$ space representation [24, 25]. However, similar to the case of DPA the expressions in the momentum space representation are more compact.

4 Numerical estimates

4.1 Antishadowing

For numerical estimates it is convenient to approximate the deuteron form factor calculated with a realistic deuteron wave functions by a sum of two exponentials [26]

$$\begin{aligned} S(\vec \Delta ^2)=0.6\exp (-K^2_{1D}\vec \Delta ^2)+0.4\exp (-K^2_{2D}\vec \Delta ^2), \end{aligned}$$

(14)

where

$$\begin{aligned} K^2_{1D}=22.7~\text{ GeV }^{-2},\quad K^2_{2D}=127~\text{ GeV }^{-2}. \end{aligned}$$

(15)

The momentum dependence of the two gluon form factor can be extracted [19] from the $J/\psi$ photoproduction data. The exponential fit gives

$$\begin{aligned} F_{2g}(\vec \Delta ^2,x)=\exp (-\vec \Delta ^2B_N(x))), \end{aligned}$$

(16)

where

$$\begin{aligned} B_N\approx 1.43 +0.14\mathrm{Log}[x_0/x]\,\,\, \mathrm{GeV}^{-2}. \end{aligned}$$

(17)

and $x_0=0.1$. For understand better qualitative features of the interplay between the distance scales related to the deuteron and to the nucleon GPDs we shall use below a simplified form of the deuteron form factor

$$\begin{aligned} S(\vec \Delta ^2)=\exp (-K^2_{D}\vec \Delta ^2), \end{aligned}$$

(18)

while in the numerical calculations we will use Eq. 14. (the radius $K^2_{D}$ is related to the electric radius of the deuteron as $K^2_{D}= (2/3) R^2_{D\, e.m.}$.) Performing the integration in Eq. 2 we obtain for the leading term

$$\begin{aligned} \frac{\sigma _\mathrm{imp4}}{(\sigma _1\sigma _2)}=\frac{1}{2\pi }\frac{(1+N)}{K(x_1,x_2,x_{1p},x_{2p})}, \end{aligned}$$

(19)

where

$$\begin{aligned} K(x_1,x_2,x_{1p},x_{2p})&= B_N(x_1)+B_N(x_2)\nonumber \\&+B_N(x_{1p})+B_N(x_{2p}). \end{aligned}$$

(20)

The function $K$ is determined by the two gluon form factors of the nucleon. It is independent of the deuteron wave function. The answer for the DPA correction to the cross section is obtained by taking integral over $\vec {\Delta }$ in Eq. 5 using parametrization 18:

$$\begin{aligned} \frac{\sigma _{DPA}}{\sigma _1\sigma _2}=\frac{1}{2\pi } \frac{1}{K^2_{D}+K(x_1,x_2,x_{1p},x_{2p})}. \end{aligned}$$

(21)

Using parametrization 14 for the deuteron form factor, we obtain the DPA correction of the order $8\,\%$ when all $x$’s are $\sim 0.01$ (neglecting $N_L$) and slowly decreasing with a further decrease of x’s. This is in very good agreement with a more explicit calculation using a expression 8 for the form factor and the Paris deuteron wave functions, which gives $7.3\,\%$. Note here that neglecting the nucleon finite size as compared to the deuteron size (putting $B_N$ to zero in Eq. 21) would result in an overestimate of the discussed contribution to the cross section by 25 $\div$ 30 %.

4.2 Single shadowing

We now use the simple parametrization for the nucleon diffractive pdf $F_D$ [16],

$$\begin{aligned} F^{4(D)}D(\beta ,Q^2,x_{I\!\!P},q_t)&= B_D\exp (-B_Dq^2_t)\nonumber \\&\times \, F^{3(D)}(\beta ,Q^2,x_{I\!\!P}), \end{aligned}$$

(22)

where $\beta =x_1/x_{I\!\!P}$. In the limit of small x when we can neglect $t_{\min }=-m^2_Nx^2_{I\!\!P}/(1-x_{I\!\!P})$, integral over longitudinal and transverse degrees of freedom in Eq. 10 decouple. In this limit, Eq. 10, for the shadowing correction, can be rewritten as (we can neglect $x_{I\!\!P}$ in the argument of the deuteron form factor)

$$\begin{aligned}&\Delta G(x,Q^2)= -I(x,Q^2)B_D(\frac{0.6}{K^2_{1D}+B_D} +\frac{0.4}{K^2_{2D}+B_D})\nonumber \\&\quad = -S\cdot I(x,Q^2)=-0.166 I(x,Q^2), \end{aligned}$$

(23)

where we defined

$$\begin{aligned} I(x,Q^2)=\int ^{0.1}_x dx_{I\!\!P} \beta F_3(\beta ,Q^2,x_{I\!\!P}) /8 \pi ^2. \end{aligned}$$

(24)

and $S$ is the integral over transverse momenta:

$$\begin{aligned} S=B_D\left( \frac{0.6}{K^2_{1D}+B_D}+\frac{0.4}{K^2_{2D}+B_D}\right) \end{aligned}$$

(25)

Here $B_D \text{=7 } \text{ GeV }^{-2}$ is the slope of diffractive structure function of the nucleon based on the HERA experimental data which indicates that $B_D$ practically does not depend on $x_{I\!\!P}$ [23]. In this approximation the function $I(x,Q^2)$ can be easily determined from numerical results for $\Delta G(x,Q^2)$ [16].

Now we can use expression 13 for the single parton shadowing in four jet production to calculate the value of the shadowing effect. For the exponential parametrization we can write

$$\begin{aligned}&F^{4(D)}(\beta ,Q^2,x_{I\!\!P},q_t,\Delta _t)= B_D\exp (-q_t^2B_D/2\nonumber \\&\quad -(q_t+\Delta _t)^2 B_D/2) F_3(\beta ,Q^2,x_{I\!\!P}). \end{aligned}$$

(26)

Hence the shadowing correction is

$$\begin{aligned} \frac{\sigma _{SS}}{\sigma _1\sigma _2}=-{4(I(x_1,Q_1^2)U(x_1,x_2,x_{1p},x_{2p})+I(x_2,Q_2^2)U(x_2,x_1,x_{1p},x_{2p}))\over 4\pi }.\nonumber \\ \end{aligned}$$

(27)

Here the longitudinal function $I$ is given by Eq. 24 and the transverse integrals $U$ are obtained by using Eq. 13, and explicit Gaussian parametrization for the form factor.

The ratio $K=\sigma _{SS}/\sigma _{DPA}$ is presented in Fig. 5 as a function of $x_1$ and $Q_1^2$ for the LHC kinematics of production of two jets with $p_t = Q$ and $4Q^2=x_1x_{1p}s$, $s=2.5\times 10^7$ GeV$^2$. The second $x_2=0.1, Q_2^2=1,000$ GeV$^2$ being fixed to stick to the kinematics under discussion. In Fig. 6 we also present the ratio of the shadowing correction for this kinematics and the full impulse approximation result.

Fig. 5

The ratio $K$ of shadowing and DPA corrections to the four jet production cross section as a function of $x_1\equiv x$ for hard scales $Q_1^2=4, 10, 100$ GeV$^2$, $Q_2^2=1,000$ GeV$^2$. We put $x_2=0.1$ and $x_{1p}=4Q_1^2/(x_1s), x_{2p}=4Q_2^2/(x_2s)\sim 0.0016$

Fig. 6

The ratio of shadowing correction to DPA and full impulse cross section as a function of x for hard scales $Q_1^2=4, 10, 100$ GeV$^2$. $Q_2^2=1000$ GeV$^2$. We put $x_2=0.1$ and $x_{1p}=4Q_1^2/(x_1s), x_{2p}=4Q_2^2/(x_2s)\sim 0.0016$

For typical $x_1\sim 0.001,x_2\sim 0.05$ in LHC kinematics we find shadowing of order $30\,\%$ relative to DPA for low $Q_1^2\sim 4$ GeV$^2$. We also see from Fig. 5 that the shadowing contribution to the cross section decreases with the increase of the transverse scale.

Note also that the account for the finite size of the nucleon reduces the absolute value of the correction by $\sim 10\,\%$. The same reduction occurs also for the DPA, so the ratio of shadowing and DPA contributions is practically not sensitive to the finite nucleon radius.

In the limit of very small $x_1 \le 10^{-3}$ and $x_2$ large one maybe close to the black disk regime and the LT approximation would break down. Still our calculation indicate that in this limit suppression effect should be large—$\sim 0.5$. relative to DPA.

It is instructive to compare the shadowing correction to the total differential cross section of the four jet production in $pD$ collision in the impulse approximation to the shadowing correction to deuteron structure functions. The integral over the longitudinal momenta is the same for both corrections and hence their ratio is given then by the ratio of the transverse integrals, which is of the order 1. Indeed, the ratio of shadowing and impulse contributions can be rewritten as

$$\begin{aligned} \frac{\sigma _{SS}}{\sigma _\mathrm{imp4}}=\frac{\Delta G_N(x_1,Q_1^2)}{G_N(x_1,Q_1^2}\frac{2}{1+N}\frac{U\cdot K}{S}, \end{aligned}$$

(28)

where we used Eqs. 23, 25. Thus we see that the shadowing correction for DPI is proportional to the shadowing correction to the deuteron gluon PDF, the proportionality coefficient being the product of the factor $2/(1+N)$ and the ratio of the transverse integrals. The latter one is always close to 1. For a logarithmic parametrization of $B_N$ the transverse factor $U\cdot K/S$ does not depend on $x_1$ (only on the hard scales). The factor 2/(1+N) also depends on $x_1$ only weakly, at least for $x_1\ge 0.001$, and it is close to 1 for large $Q_1^2$, while it is of the order 1.5 at $Q\sim$ few GeV in the chosen kinematics [14].

Altogether we see that the $x$-dependence of the ratio (28) is the same as for the shadowing correction for the corresponding deuteron pdf, but the absolute value depends on the ratio of the transverse integrals (which is of the order of one) and the value of $N$. As a result the ratio is of the order of $2/(1+N)$. The factor 2 shows that there is a different combinatorics in MPI in pD scattering and in the DIS scattering of the deuteron, i.e. one does not obtain the screening correction simply by substituting the nuclear pdf (that includes shadowing) instead of nucleon pdf in the impulse approximation equations. Finally, let as note that the ratio $\sigma _\mathrm{DPA}/\sigma _\mathrm{imp4}$ of DPA and impulse approximation is x-independent and depends only on hard scales. It is equal to

$$\begin{aligned} \sigma _\mathrm{DPA}/\sigma _\mathrm{imp4}\sim (0.16 \div 0.18)/(1+N), \end{aligned}$$

(29)

where 0.18 corresponds to the hard scale 4 GeV$^2$ and 0.16 to the 100 GeV$^2$ scale. So the ratio slowly decreases with the change of the hard scale, mostly due to the change of N, decreasing from $\sim 1$ at the hard scale $10$ GeV to $\sim$0.3 at $2$ GeV, due to the dynamical dependence of N on the scale, found in [13, 14]. The $1\otimes 2$ contributions to DPA is small. Indeed, as was already mentioned above, there is no factor $2$ that is present in the $pp$ collisions due to the asymmetric kinematics. Also, the integral over $\vec \Delta$ for the $1\otimes 2$ term in the $pp$ collisions is proportional to $4B_N/2B_N$, enhancing $1\otimes 2$ contributions by a factor of 2 relative to the $2\otimes 2$ contribution. This enhancement, however, is absent in DPA, where the corresponding ratio is $(K_D+4B_N)/(K_D+2B_N)\sim 1.1$. Altogether this results in a strong suppression of the $1\otimes 2$ contribution in DPA, so it can be safely neglected. A similar effect for heavy nuclei was discussed in Ref. [2].

5 Two nucleon interference

It was emphasized in Refs. [5, 6] that in addition to the impulse approximation mechanism and the double nucleon interaction mechanism considered above there exists a contribution due to the interchange of partons between the nucleons—so that the parton “1” (“2”) in $|in >$ and $<out |$ states belongs to the different nucleons. This is in addition to the interference in nuclear shadowing mechanism, which was discussed in Sect. 3. It was suggested in [5, 6] that such a contribution may give a significant contribution to the cross section, though no numerical estimates were presented so far. A typical contribution of this kind is depicted in Fig. 7 where filled circles represent interactions with two partons of the projectile. $\alpha _i$ are the light-cone fractions carried by proton and neutron and the scale is chosen so that $\alpha _1 + \alpha _2=2$, cf. discussion in [2].

The interference mechanism is present only for the case when either two (anti)quarks or two gluons are involved in the hard processes and it is absent in the mixed case allowing to avoid completely the interference contribution [5, 6]. To estimate its magnitude as compared to the shadowing effects in the kinematics discussed in the paper we need to consider effects related to the difference of the momentum scales in the deuteron and nucleon as well as the pQCD effects related to the presence of the large scale in the problem. We will consider them in turn.

Fig. 7

Parton interference mechanism. The filled circles represent interactions with two partons of the projectile

5.1 Overlap due to the momentum flow

It was argued in Ref. [2] that the interference mechanism is strongly suppressed even in the case of the processes involving (say) two gluons of the nucleus if $x_1-x_2$ is large enough. In the case of the deuteron it is possible to elaborate the arguments of [2]. It is straightforward to see that the integration over the momenta of nucleons in the initial and final states leads to the factor $F_D(\vec {r})$, where $F_D$ is the deuteron body form factor defined in Eq. 8, and $\vec {r}= ((x_1-x_2)m_N, \vec {\Delta })$ is the 3D momentum transfer to the nucleon of the deuteron calculated in the nonrelativistic limit. Hence in the limit we consider when one $x$ is small and second is far away from the shadowing region there exists a range of $x_1$

$$\begin{aligned} x_1 \ge \sqrt{{3\over 2}} {1\over R_D m_N} \sim 0.1, \end{aligned}$$

(30)

where interference is very strongly suppressed by the deuteron form factor independent of the details of the dynamics.

Let us now discuss the interference contribution for smaller $x_1$ and compare it to the DPA contribution. First, there are generic small factors which are related the dominance of the two nucleon configurations in the deuteron wave function (accuracy of this approximation is discussed below).

Consider now the dynamical overlap in the final state. Let us now demonstrate that the overlap integral calculated neglecting color and spin effects is similar to the case of double nucleon interaction. We consider for simplicity the case when $x_1$ is small and the effect of suppression due to the longitudinal momentum transfer can be neglected. Also we introduce $\phi ^2_N(k_t)$—the transverse momentum distribution of partons at the low Q-scale which is normalized to one (we do not write explicitly its dependence on $x_i$. The factor $\int d^2\Delta G_N^4(\Delta ) S_D(\Delta )$ in the expression for the DPA contribution is changed to

$$\begin{aligned}&R\equiv \int \Psi _D(p)\Psi _D(p+ \tilde{\Delta }) \phi _N^2(\tilde{\Delta })\phi _N(k_1) \phi _N(k_2) G_N^2(\Delta )\nonumber \\&\quad \qquad \times \, d^2 \tilde{\Delta } d^2k_1d^2k_2d^2p. \end{aligned}$$

(31)

where $\tilde{\Delta } = - k_1+k_2+\Delta$. The integral over $p$ gives a deuteron form factor $S_D(\tilde{\Delta })$ which converges on the scale much lower than the parton transverse momentum scale, so in the rest of the integrand we can substitute $\Delta \rightarrow k_1-k_2$ and obtain, using Eq. 8:

$$\begin{aligned}&R = \int S_D(\tilde{\Delta }) \phi _N^2(\tilde{\Delta }) d^2 \tilde{\Delta } \int \phi _N(k_1) \phi _N(k_2) G_N^2(k_1-k_2)\nonumber \\&\quad \qquad \times \, d^2k_1d^2k_2. \end{aligned}$$

(32)

Taking Gaussian transverse momentum distribution for partons in the nucleon: $\phi _N^2= (1/ \lambda \pi ) \exp (-k_t^2/\lambda )$ with $\lambda = \left<k_t^2\right> \sim 0.25~\text{ GeV }^2$ we can easily perform integrations and find that numerically $R$ is close to the corresponding factor in the expression for the DPA. Note here that we considered parton interchange at a very low scale $Q^2 \sim 0.25~\text{ GeV }$. Choosing a more realistic scale $\ge 1~\text{ GeV }^2$ will lead to a significant reduction of $R$. The $Q^2$ evolution to the scale $\sim p_t^2(\mathrm{jet})$ leads to an additional suppression which will be discussed below. Hence to account of the spatial overlap leads to suppression of interference, so it will be at most of the order of DPA contribution.

5.2 Suppression of interference in LLA

It was demonstrated in [27] that for the contributions involving the parton interchange are suppressed in generic hadron–hadron collisions. The reason is that, if there is a parton interchange in the projectile/target or both, the large logarithm is lost, which is due to the integration over transverse momenta. As a result such diagrams are not double collinear enhanced and do not contribute in the LLA (the authors of [27] call this type of diagrams the ladder cross talk). The physical reason is that in order to get a large logarithm from the integration over transverse momenta in the ladder the partons in the initial and final states must be at the same impact parameter. While this occurs automatically for diagonal pairing, this generally does not happen for pairing of arbitrary partons. There is an additional small factor due to the longitudinal color delocalization in such exchange as the color interchange creates a color dipole of length comparable to the nucleon size and hence carrying a significant excitation energy [14]. The only way to avoid losing transverse logarithm is to consider the $1\otimes 2$ processes. The interference for the $1\otimes 2$ processes was studied recently by Gaunt [28], In this case two partons which interact with the deuteron are created in the split of a single parton of the projectile nucleon. They are located at the same impact parameter. Hence such interference diagrams contributing in the LLA (double collinearly enhanced). However, the contribution of this mechanism may become sizable only at very small x, near the black disk regime limit. Indeed, the contribution of $1\otimes 2$ mechanism to the DPA is small in the discussed x-range. Thus the interference contributions considered in [28] are actually a small correction to already small correction to DPA due to $1\otimes 2$ processes.

Indeed, it was showed in Sect. 2B that the contribution of $1\otimes 2$ mechanism to DPA is $\sim 5 (10, 20)\,\%$ for $Q^2=2 (10, 100)~\text{ GeV }^2$, respectively. For our kinematics typical $x$ are of the order 0.1 or larger. In this case the interference is negligible relative to the full $1\otimes 2$ contribution [28]. Hence the overall upper limit on the interference based on these considerations is much smaller than the shadowing effect which we calculated above.

At the same time it follows from the analysis in [28] that significant contribution of interference to $1\otimes 2$ can appear potentially, even for symmetric kinematics for very small $x$, since they are effectively defined by values of $x$ where the split occurs. Only then it can become comparable to shadowing. This case needs further study. In particular a more detailed analysis of the ladder cross talk effect [29] is desirable.

5.3 Color suppression for a single interchange in the deuteron

We explained above that the interference contributions are small in the LLA. Here we shall show that there are additional suppression mechanisms that will reduce interference further, even beyond the LLA. Let us now show that the interchange of two partons between neutron and proton in the deuteron, in the case when no exchange occurs in the projectile proton, leads to the color suppression by a factor $d_c$, where $d_c$ is the dimension of the SU(3) irreducible representation to which the parton belongs. Such a suppression is a reflection of the well-known property of the suppression of nonplanar diagrams as compared to planar ones. For simplicity we shall consider the interaction of two partons of the deuteron with two partons of the projectile due to single gluon exchanges in the t-channel. Indeed, consider for example the case of two baryons, $q^{i_1}q^{i_2}q^{i_3}...q^{i_{N_c}}$. Their wave functions in the color space are $\frac{1}{\sqrt{N_c!}}\epsilon ^{i_1i_2...}q_{1i_1}q_{2i_2}q_{3i_3}...$ for the first nucleon and $\frac{1}{\sqrt{N_c!}}\epsilon ^{j_1j_2j_3...}q_{(N_c+1)j_1}q_{(N_c+2)j_2}...$ for the second one. Consider the color factor from the projectile nucleon. For simplicity assume that two dijets originate from quark–quark scattering. The color factor that we obtain from contracting the same quark in the amplitude and the conjugated amplitude is $\mathrm {tr}(t^at^{a'})\cdot \mathrm {tr}(t^bt^{b'})$, where we sum over the final jet indices. The color factor from the projectile nucleon gives $\frac{1}{4}\delta ^{aa'}\delta ^{bb'}$. Consider now the factor originating from the deuteron block:

$$\begin{aligned} t^{a}_{si_1}q_{2i_2}...\epsilon ^{i_1i_2...} t^{b}_{s_1p_1}q_{(N_c+2)q}q_{(N_c+3)r}...\epsilon ^{pqr...}. \end{aligned}$$

(33)

The corresponding factor in the conjugated amplitude in the diagonal case is

$$\begin{aligned} t^{a'}_{si'}q_{2j'}q_{3k'}...\epsilon ^{i'j'k'...} t^{b'}_{s_1p'}q_{(N_c+2)q'}q_{(N_c+3)r'}...\epsilon ^{p'q'r'...}. \end{aligned}$$

(34)

Taking the product we obtain

$$\begin{aligned} \frac{1}{4N^2_c}\mathrm {tr}(t^at^{a'})\mathrm {tr}(t^bt^{b'})=\delta ^{aa'}\delta ^{bb'}\frac{1}{4N_c^2}. \end{aligned}$$

(35)

Combining color factors coming from the projectile and deuteron blocks we finally obtain

$$\begin{aligned} \frac{1}{4N_c^2}(N^2_c-1)^2. \end{aligned}$$

(36)

Consider now the interference term. In this case quarks “1” and “$N_c+1$” are interchanged between two nucleons in the conjugated amplitude, while having the same initial state (here for simplicity we consider two nucleons consisting of $N_c$ quarks with $N_c$ flavors). Hence the nucleon wave functions in the conjugated amplitude are $\frac{1}{\sqrt{N_c!}}\epsilon ^{ijk...}q_{(N_c+1)i}q_{(2)j}q_{(3)k}...$ for the first nucleon and $\frac{1}{\sqrt{N_c!}}\epsilon ^{pqr...}q_{1p}q_{(N_c+2)q}q_{(N_c+3)r}...$ for the second one. Then the color factor originating from the deuteron block is

$$\begin{aligned} \frac{1}{N_c!} t^{a'}_{si'}q_{(N_c+2)j'}q_{(N_c+3)k'}\epsilon ^{i'j'k'...} t^{b'}_{s_1p'}q_{2q'}q_{3r'}...\epsilon ^{p'q'r'...}. \end{aligned}$$

(37)

Calculating the product we obtain

$$\begin{aligned} \frac{1}{N_c}(t^at^{b'})_{s's_1} \otimes \frac{1}{N_c}(t^bt^{a'})_{s_1's}. \end{aligned}$$

(38)

Taking the trace over indices of the final jets we obtain

$$\begin{aligned} \mathrm {tr}(t^at^{b'}t^{b}t^{a'}). \end{aligned}$$

(39)

Combining with the color factor coming from the proton block we obtain

$$\begin{aligned} \frac{1}{N_c^2}\mathrm {tr}(t^at^bt^bt^a)=\frac{1}{N_c^2}c_F^2N_c=\frac{1}{N_c^2}(N^2_c-1)^2\frac{1}{4N_c}, \end{aligned}$$

(40)

which is $1/N_c$ smaller than in the diagonal case. The same calculation can be done for two dijets originating from the scattering off two gluons. For simplicity let us take the gluon part of the first nucleon wave function as a color singlet $g_1^ag_2^a$, where gluon $g_1$ participates in the scattering process and the second one is a spectator, while the second nucleon has wave function $g_3^ag_4^a$. Repeating the calculation for the quark case, we find that the factor originating from the projectile nucleon is $N_c^2\delta ^{aa'}\delta ^{bb'}$. For the deuteron contribution for the diagonal case we get $\mathrm {tr}(T^aT^{a'})tr(T^bT^{b'})=N_c^2\delta ^{aa'}\delta ^{bb'}$, where the matrices $T$ are the generators in the adjoint representation. Combining the factors coming from the projectile nucleon and the target deuteron we obtain for the diagonal case

$$\begin{aligned} N^4_c(N^2_c-1)^2. \end{aligned}$$

(41)

In the same way for the interference contribution we obtain $\mathrm{ tr}(T^aT^bT^{b'}T^{a'})$, and after combining with the upper block of the diagram we get

$$\begin{aligned} c_V^2N_c^2(N_c^2-1)=N^4_c(N_c^2-1), \end{aligned}$$

(42)

which corresponds to the $1/(N^2_c-1)$ suppression. From these two examples it is clear that if we interchange the partons in the conjugated amplitude, the interchanged parton being in irreducible representation of $\mathrm{SU}(3)$ with dimension $d_c$, we obtain the $1/d_c$ suppression. Similar arguments for the spin variables for the chiral states give a suppression $1/d_s$, where $d_s$ is the number of spin states. Thus, altogether we obtain a factor of 1/6 suppression for the quark, and a factor of 1/16 suppression for the gluon interference.

5.4 Color suppression for a double interchange

Consider now double interference; in this case using the same arguments we see that if we interchange the partons both in the nuclear part (between two nucleons) and in the upper part of the diagram, we get the product of two traces, i.e. for quark case we obtain

$$\begin{aligned} \mathrm {tr}(t^at^bt^{b'}t^{a'})\cdot \mathrm tr(t^{a'}t^{b'}t^{b}t^{a})\sim \frac{1}{2}\mathrm tr(t^{a'}t^{b'}t^{b}t^{a'}t^{b'}t^{b}). \end{aligned}$$

(43)

where the last equality is in the large $N_c$ limit. It is easy to see that in this limit the trace is $\sim N^2_c$, and thus the double interchange increases the color suppression to $1/d_c^2$, in the notations of the previous subsection. Note finally that such color suppressions were included in the estimate of the interference in LLA discussed in Subsect. 5.2.

5.5 Accuracy of the two nucleon approximation for the deuteron

Finally, we assumed above that the deuteron in both initial and conjugated amplitudes consists of two nucleons. Since the deuteron block for $\Delta =0$ corresponds to the intermediate state for the deuteron wave function which is not a two-nucleon state we can use the information as regards the deuteron structure to estimate the probability of the non-nucleonic (exotic) component of the deuteron wave function, $P_\mathrm{ex}$ as well. The exotic components are expected to have a small probability since the $NN\pi$ configurations are suppressed by the chiral nature of the pion [30], while the lowest mass two baryon intermediate state is $\Delta \Delta$, which has a mass gap of $\sim 2(m_{\Delta } - 2m_N \sim \text{600 } \text{ MeV }$ with the ground state. As a result one expects that the probability of the non-nucleonic component in the deuteron is $P_\mathrm{ex} \le (1\div 2)\cdot 10^{-3}$ [30]. The experimental limit on the probability of the non-nucleonic components in the short-range correlations (SRC) in nuclei coming from the Jlab and BNL experiments is $\sim$0.1; for a review see [31]. Since the structure of SRC in the deuteron and heavier nuclei is found to be very similar and the probability of SRC in the deuteron is $\approx 0.04$ the current data lead to the upper limit for the exotic admixture $P_\mathrm{ex} (D) < 4\times 10^{-3}$. Note here that a likely candidate for the dominant exotic component for the deuteron wave function, the lightest baryon intermediate state—$\Delta \Delta$—cannot be generated via interchange of two gluons.

A complementary way to look at the problem is to consider the singularities in the t-channel for the parton interchange—in the case of the two gluon interchange the closest singularity is presumably a gluonium state which has a mass $m_\mathrm{gluonium}$ $\sim$1.5 GeV and hence corresponds to exceedingly small inter-nucleon distances, which occur in the deuteron with probability on the scale of $10^{-3}$. Note also that this argument does not include a small factor due to the requirement that both nucleons after interchange of partons remain nucleons rather than some excited states, since typically the color is delocalized in such exchanges at the distance scale of the order on the nucleon size.

Overall we see that the interference mechanism contribution is negligible in the leading twist LLA approximation, unless we consider kinematics region close to the black disk regime, where the interference effects may be significant, but this region is clearly beyond the scope of this paper. In addition, we have seen that there are additional suppression mechanisms, like color/spin suppression, overlap of momentum flows (Subsect. 5.1) that likely diminish the interference mechanism in an independent way. More studies are necessary for the $x, Q^2$ range for the black disk limit. Going beyond the LLA is also highly desirable both for $pp$ and $pA$ scattering. The case of large A will be considered elsewhere.

6 Conclusion

We calculated the contributions of DPA and the nucleon shadowing to the four jet MPI cross section in the proton–deuteron collisions in the limit when one of the probes has small $x$ and another has $x,Q^2$ in the range where shadowing is small. We have demonstrated that shadowing increases with the decrease of $x$, and decreases rapidly with the increase of hard scale. For large $p_t$ of one of the probes corresponding to a typical jet trigger in $pA$ collisions at the LHC and small $p_t$ of the other probe we obtain a correction of the order of $30\,\%$. This contribution is not reduced to the substitution of the deuteron pdf instead of the nucleon pdf in the impulse approximation formula—it is twice as large as such a naive guess. There is a reduction by the factor $1/(1+N)$, which may be of order 1/2, depending on kinematics, due to a completely different mechanism of $1\otimes 2$ enhancement of the four jet cross section. We also provided arguments for the dominance of the leading twist shadowing one nucleon–two nucleon interference mechanism over the contribution due to the interchange of partons between two nucleons in the kinematics discussed ($x_1\le 0.1,x_2\ge 0.1,Q_1^2$ few GeV$^2$). In particular, we demonstrated that in the LLA used in our analysis the interference diagrams are strongly suppressed. Further studies of interference beyond LLA and in different kinematic domains are desirable. This is especially true in the region of small $Q^2$ and $x$, in proximity to the black disk regime. Our analysis will serve as a starting point to a more complicated calculation of shadowing in the case of heavy nuclei for similar kinematics. Further studies will be necessary for calculations of the shadowing in the kinematics when both $x$’s of the partons from the nucleus are small and hence more complicated diagrams contribute to the nuclear shadowing.

Appendix A: Correspondence with the Glauber model of \(pA\) scattering

It is easy to see that the structure of the double scattering term is very close to that for the double scattering term for the total cross section of $pA$ scattering in the Glauber model. This similarity holds for any nuclear wave functions, as the two-body form factor which enters in both cases is the same. Since the relevant expressions for the heavy nucleus case were derived before in [1] it is convenient to check the correspondence taking the limit of large A, and neglecting nucleon–nucleon correlations.

The ratio of the double and single scattering terms in the Glauber series for the total cross section of $hA$ scattering,

$$\begin{aligned} \sigma _\mathrm{tot}^{hA}\!=\! \int d^2b 2(1\!-\! \exp (\!-\!\sigma _\mathrm{tot}T(b)/2) = \sigma _1 -\sigma _2 + \sigma _3 - ... , \end{aligned}$$

(A1)

is given by

$$\begin{aligned} \sigma _2/ \sigma _1= {1\over 4} \sigma _\mathrm{tot} \int T^2(b)d^2b/A. \end{aligned}$$

(A2)

This expression differs from the ratio of the cross section of the production of four jets in the interaction with two and one nucleons (Eqs. 2,  5) by the factor of ${1\over 4}$ and substitution $\sigma _\mathrm{tot}\rightarrow \pi R^2_\mathrm{int}$. The factor of 4 could be understood on the basis of the AGK cutting rules [22], which state that the double cut diagram enters with the extra factor of 2 as compared to the shadowing correction to the total cross section. Another factor of 2 reflects the combinatorics of emission of “pair one” from either the first or the second nucleon.

Using this observation it is straightforward to find the expressions for the double interaction contribution if the expression for the shadowing for the total cross section is known (including the effects of nucleon–nucleon correlations).

For example, in the case of the scattering off the deuteron contribution of the diagram 2 to $G_2(x_1,x_2, \vec {\Delta } )$ is given by (for the discussion of proton–deuteron four jet production in the coordinate space representation, see [5–7])

$$\begin{aligned} {_2G}^{D}(x_1,x_2,\vec {\Delta })= 2 G_N(x_1,\vec {\Delta })G_N(x_2,\vec {\Delta })\cdot S_D(\vec {\Delta }). \end{aligned}$$

(A3)

Here $S_D(\vec {\Delta })$ is the standard deuteron form factor defined above (Eq. 6), which enters in the Glauber double scattering term. The factor of 2 in Eq. A3 is due to combinatorics (the factor of A(A-1)). This is just the result obtained in Sect. II—Eq. 5.

Similarly, one can obtain the expressions for the triple MPIs matching the corresponding expressions of Ref. [1].