1 Introduction

The transition from a radiation-dominated phase to a matter-dominated phase is crucial in order to understand the formation of structures in the Universe [1, 2]. In the standard cold-dark-matter (CDM) scenario, the dark-matter (DM) component decouples from the primordial plasma very early, beginning to collapse deep in the radiative phase. This allows one to form the gravitational potential wells into which the baryons fall after decoupling. The scenario is very successful in predicting the large scale structure of the Universe. However, there are some disturbing tensions at smaller scales, one of them being the predicted large number of small structures which do not fit observations [3, 4]. Such tensions leave the door open for alternative DM scenarios.

One of the possibilities is to consider a warm-dark-matter (WDM) model, attributing a low, non-vanishing temperature to the dark component [5]. This small temperature does not spoil the advantages of the CDM scenario at large scales but it may, at the same time, reduce the excess of power in the spectrum on small scales. This problem, to be treated exactly, implies the consideration of the collisional Boltzmann–Einstein system, including the baryon–photon interaction and the thermodynamics of the WDM.

In the present work we will develop a greatly simplified approach that takes into account out-of-equilibrium features of the system. To do so, we will use the Reduced Relativistic Gas (RRG) model [6, 7]. This model is based on the assumption that all particles have equal kinetic energies. The use of the RRG model substantially simplifies the formalism, such that all the complexity of the Boltzmann–Einstein system can be reduced to an effective equation of state (EoS) that interpolates between a pure radiative fluid and a pressureless matter fluid. Remarkably, the EoS of such a system is given by a simple algebraic formula [8, 9] (see also [6] for a detailed derivation), which enables one to solve the Friedmann equation exactly (for the equilibrium case) and to obtain an explicit and transparent picture of the transition between the radiation phase in the early Universe and the dust phase in the late Universe. Indeed, the deviation from the Maxwell relativistic EoS is very small and therefore the quality of the RRG-based approximation can be evaluated as excellent [6].

Although the interaction (Thomson scattering) between baryons and photons establishes an equilibrium, equivalent to a perfect fluid description of the combined photon–baryon system on the macroscopic level, the interaction ceases to be effective as the decoupling era is approaching. This implies the existence of an out-of-equilibrium period when the mean free collision time is no longer negligible compared with the Hubble time. We shall characterize such a period by a phenomenological out-of-equilibrium parameter and investigate its influence on the cosmological dynamics. Even after decoupling the electrons remain coupled to the photons which implies that baryonic matter extracts energy from the CMB such that the electron temperature remains of the order of the temperature of the photons [10, 11]. This leads to tiny spectral distortions of the CMB. Within the RRG framework we take into account temperature effects both for the DM and for the baryons which results in (small) non-vanishing pressure contributions of these components and we study the influence of the corresponding “warmness” parameters on the evolution of the Universe. In a first step we shall find an analytic solution for the homogeneous and isotropic background dynamics of the four-component model of (“thermal”) baryons, photons, WDM and a cosmological constant. The mere existence of such a solution can be seen as a merit of our method since it maps the complicated astrophysical processes of the complete Boltzmann–Einstein system of equations on a much simpler structure. Of course, it remains to be shown that this simplified structure really reproduces essential features of the underlying microphysics.

In a next step, using the tight-coupling approximation [10], we look for the implications of the out-of equilibrium and warmness parameters on the position of the first acoustic peak of the CMB spectrum. We demonstrate that the so-called monopole mode, which defines this position, is modified due to the interaction. Comparison with the \(\Lambda \)CDM model, assuming the latter grosso modo to represent a reliable reference, we obtain upper limits for the mentioned phenomenological parameters which turn out to be of the order of \(10^{-4}\). Interestingly, for the DM warmness parameter this is in agreement with previous estimations based on results for large scale structures in the universe [7].

The paper is organized as follows. In the next section, Sect. 2, we construct and work out the equations for the coupled system of baryons and radiation. The balance equations for our four-component model are solved exactly which provides us with an explicit expression for the Hubble parameter in terms of the scale factor. In Sect. 3 we use the tight-coupling approximation to study the influence of the interaction and warmness parameters on the position of the first acoustic peak of the CMB spectrum. Finally, in the last section, Sect. 4 we draw our conclusions and discuss further perspectives of the RRG model.

2 Basic equations of the interacting RRG model

We consider a four-component cosmic model consisting of baryons, photons, DM and a cosmological constant. Both baryons and DM are described as a relativistic gas of massive particles. Furthermore, we include an interaction between baryons and photons in a phenomenological manner. Microscopically, photons and baryons interact via Thomson scattering which establishes an equilibrium between them. As a consequence, both components are treated as perfect fluids with the same temperature. Here, we take into account, in a phenomenological manner, the possibility of small deviations from this equilibrium. Moreover, the baryon pressure, although small, is not assumed to be zero exactly.

The dynamics of the photon–baryon system is then described by the following system of equations:

$$\begin{aligned} \frac{d\rho _{b}}{dt} + 3H(\rho _{b}+P_{b})&= \gamma _{rb} \rho _{r} - \gamma _{br}\rho _{b},\end{aligned}$$
(1)
$$\begin{aligned} \frac{d\rho _{r}}{dt} + 3H(\rho _{r}+P_{r})&= - \gamma _{rb} \rho _{r} + \gamma _{br}\rho _{b}. \end{aligned}$$
(2)

Here, \(\rho _{b}\) and \(\rho _{r}\) are the energy densities of baryonic matter and of radiation, respectively, while \(P_{b}\) and \(P_{r}\) are the corresponding pressures and \(H = a^{-1}da/dt\) is the Hubble rate with \(a\) being the scale factor of the Robertson–Walker metric. The quantities \(\gamma _{rb}\) and \(\gamma _{br}\) denote the rates by which energy is transferred from radiation to baryons and from baryons to radiation, respectively. The particle numbers of the components are assumed to be conserved. A similar interacting system was discussed in Ref. [12] and applied to cosmological vacuum energy decay, particle annihilation and the evolution of a population of evaporating black holes. Here, we simplify the system (1) and (2) by introducing a state of equilibrium for which one has

$$\begin{aligned} \overline{\gamma }_{rb} \rho _{r} - \overline{\gamma }_{br}\rho _{b} = -\left( \overline{\gamma }_{br} - \frac{\rho _{r}}{\rho _{b}}\,\overline{\gamma }_{rb}\right) \rho _{b} = 0, \end{aligned}$$
(3)

where the bars indicate the equilibrium values of the corresponding quantities.

Deviations from equilibrium are mapped onto a single constant parameter \(\xi \) according to the simple approximation

$$\begin{aligned} \gamma _{br} - \frac{\rho _r}{\rho _b}\,\gamma _{rb} = \xi H. \end{aligned}$$
(4)

In this case, the relevant set of basic equations can be written as

$$\begin{aligned}&\frac{d\rho _b}{dt} + 3H(\rho _b + P_b) \,=\, -\xi H \rho _{b},\end{aligned}$$
(5)
$$\begin{aligned}&\frac{d\rho _r}{dt} + 3H(\rho _r + P_r) \,=\, \xi H \rho _{b}.\end{aligned}$$
(6)
$$\begin{aligned}&\frac{d\rho _{D}}{dt} + 3H(\rho _{D}+P_{D})\,=\, 0.\end{aligned}$$
(7)
$$\begin{aligned}&\frac{d\rho _{\Lambda }}{dt} \,=\, 0, \end{aligned}$$
(8)

where \(\rho _{D}\) and \(P_{D}\) are energy density and pressure, respectively, of the DM component and \(\rho _{\Lambda }\) is the density of the dark energy (cosmological constant, in our case).

Within our simplified fluid description, the phenomenological parameter \(\xi \) quantifies the net effect of potential out-of-equilibrium processes including the final stage of decoupling and the subsequent energy transfer from photons to electrons which results in a baryon temperature that is considerably higher than the corresponding temperature of a noninteracting nonrelativistic gas. Of course, this can only be a very rough approximation to the kinetic theory based exact treatment.

The pressures of the warm components and radiation in the above equations are described by the simplified equation of state [6]

$$\begin{aligned} P_{i}&= \frac{\rho _{i}}{3}\,\Big (1-\frac{\rho ^2_{di}}{\rho _{i}^2}\Big ),\end{aligned}$$
(9)
$$\begin{aligned} P_{r}&= \frac{\rho _{r}}{3}, \end{aligned}$$
(10)

where \(i=b,D\), i.e., \(i\) corresponds to baryonic matter or dark matter, respectively, and \(\rho _{di}=\rho _{i1}(1+z)^{3}\) is the mass (static energy) density. Let us stress that the main RRG relation (9) reproduces the EoS of the relativistic Maxwell distribution with a very good precision and can be used as a reliable and simple approximation for describing the warm matter components in the Universe [6, 8, 9]. The new aspect of the present work is the interaction which we introduced phenomenologically in Eqs. (5) and (6).

It is easy to see that Eq. (5) can be solved independently of Eq. (6). Using (9), we can cast Eq. (5) in the form of a Bernoulli differential equation, which can easily be solved to give

$$\begin{aligned} \rho _{b}(a)&= \sqrt{\frac{\rho _{b1}^2}{1+\xi }\,a^{-6} + \Big (\rho _{b0}^{2}-\frac{\rho _{b1}^2}{1+\xi }\Big )a^{-2(4+\xi )}}\end{aligned}$$
(11)
$$\begin{aligned}&= \frac{\rho _{b1}}{\sqrt{1+\xi }} \,a^{-3} \, \Big [1 + b^2 a^{-2 -2 \xi }\Big ]^{1/2}\ , \end{aligned}$$
(12)

where

$$\begin{aligned} \rho _{b1} = \frac{\rho _{b0}\sqrt{1+\xi }}{\sqrt{1+b^{2}}} \quad \text{ and } \quad b^{2}=\frac{\rho _{b0}^{2}}{\rho _{b1}^{2}}(1+\xi )-1. \end{aligned}$$

Here, \(\rho _{b0}\) and \(\rho _{b1}\) are integration constants which have a clear physical interpretation [6] in case of \(\xi =0\). For the present moment, with \(a=1\), we have \(\rho _{b}(1) = \rho _{b0}\), while the ratio between \(\rho _{b1}\) and \(\rho _{b0}\) measures the warmness of the baryonic matter constituent. The same role is played by the parameter \(b\) in a different parametrization. An interaction term \(\xi \ne 0\) just renormalizes the corresponding values.

For \(\xi =0\) we consistently recover the ideal relativistic gas RRG case from (12). In this limit the solution is a square root of the sum of the squares of the dust-like and radiation-like terms. Notice that this form is different from the simple sum of the dust and radiation components. In order to see this explicitly, consider the case when the dust component is dominating, which means \(\rho _{b0}(1+z)^3 \gg \rho _{r0}(1+z)^4\). Then we can rewrite Eq. (12) as

$$\begin{aligned} \rho _{ideal}(a)&= \frac{\rho _{b0}}{\sqrt{1+b^{2}}} a^{-3} \Big [1 + b^2 a^{-2}\Big ]^{1/2} \nonumber \\&\approx \frac{\rho _{b0}}{\sqrt{1+b^{2}}} a^{-3} + \frac{\rho _{b0}b^{2}}{2\sqrt{1+b^{2}}}\, a^{-5}\,. \end{aligned}$$
(13)

Obviously, the last term in (13) has a scaling behavior which is distinct from the one of the radiation with a small dust component. It is easy to see that at the intermediate stages the difference is even greater. Indeed, Eq. (11) shows that for \(\xi =0\) the gas is close to radiation for a very large positive redshift and to dust when the redshift approaches \(-1\). One can see that the relativistic gas is cooling down with the expansion of the Universe, such that its radiation-like part becomes weaker.

For \(\xi > 0\) we have a similar behavior in the distant past but, as to be expected, the relativistic gas cools down faster and the radiation component is decreasing less rapidly than in the ideal gas case. Physically this means the gas of massive particles heats up the radiation.

On the contrary, for \(\xi < 0\) Eq. (11) indicates an opposite effect. The relativistic gas of massive particles is absorbing energy from the radiation and cools down slower compared to the ideal gas case. Moreover, starting from some negative value of \(\xi \) the gas may not cool down at all and even start to heat up when the Universe expands.

Using the solution (12) in Eq. (6) for the radiation component, the latter takes the form

$$\begin{aligned}&\frac{d\rho _{r}(a)}{da}+\frac{4\rho _{r}}{a} = \frac{\sqrt{1 + b^2\,a^{-2-2\xi }}}{\sqrt{1 + b^{2}}} \,\times \,\frac{\xi \,\rho _{bm0}}{a^4}, \end{aligned}$$
(14)

which has an analytic solution

$$\begin{aligned} f_{r}(a)&= \frac{\rho _{r}(a)}{\rho _{r0}} = \Big [1+\frac{\rho _{b0}}{\rho _{r0}}\,G(\xi ,b,1)\Big ]a^{-4}\nonumber \\&- \frac{\rho _{b0}}{\rho _{r0}}\,\, G(\xi ,b,a), \end{aligned}$$
(15)

where \(\rho _{r0}\) is the present value of \(\rho _{r}\) and the function \(\,G(\xi ,b,a)\,\) is defined as

$$\begin{aligned} G(\xi ,b,a)&= \frac{a^{-3} }{\sqrt{1+b^{2}}} \left[ (1+\xi )\,_2F_{1}(\alpha ,\beta ,\gamma ,\zeta )\right. \nonumber \\&\left. -\sqrt{1+b^{2}a^{-2-2\xi }}\right] . \end{aligned}$$
(16)

Here, \(\,_2F_{1}(\alpha ,\beta ,\gamma ,\zeta )\,\) is the hypergeometric function, which has a branch-cut discontinuity in the complex \(\zeta \) plane running from \(1\) to \(\infty \) and is defined as

$$\begin{aligned} _{2}F_{1}(\alpha ,\beta ,\gamma ,\zeta ) \,=\, \sum _{k=0}^{\infty }\frac{(\alpha )_{k}(\beta )_{k}}{(\gamma )_{k}}\, \frac{\zeta ^{k}}{k!}, \end{aligned}$$
(17)

where \((\alpha )_{k}\) is the Pochhammer symbol. For our case we find that

$$\begin{aligned}&\alpha =-\frac{1}{2 + 2 \xi },\end{aligned}$$
(18)
$$\begin{aligned}&\beta = \frac{1}{2},\end{aligned}$$
(19)
$$\begin{aligned}&\gamma =1-\frac{1}{2 + 2\xi },\end{aligned}$$
(20)
$$\begin{aligned}&\zeta = - \frac{b^{2}}{a^{(2 + 2\xi )}}. \end{aligned}$$
(21)

When \(\xi =0\) then \(-\alpha =\beta -\gamma =\frac{1}{2}\) and in this case there is a simple form for the hypergeometric function, i.e. \((1-\zeta )^{\frac{1}{2}}\) [13], where \(\zeta \) is given by Eq. (21). Thus the solution for \(\xi =0\) corresponds to Eq. (2) of Ref. [14]. Finally, Eq. (7) for the DM energy density is decoupled from the other components, and its solution is given by

$$\begin{aligned} f_{D}(a)=\frac{\rho _{D}}{\rho _{D0}} = \frac{a^{-3}}{\sqrt{1+b_{1}^{2}}}\sqrt{1+\frac{b_{1}^{2}}{a^{2}}}, \end{aligned}$$
(22)

with \(b_{1}^{2}=(\rho _{D0}^{2}-\rho _{D1}^{2})/\rho _{D1}^{2}\).

Combining Eqs. (12), (15), and (22) and restricting ourselves to the spatially flat case, the Hubble parameter for our model is explicitly given by

$$\begin{aligned} E(a)&= \frac{H^{2}}{H_{0}^{2}} = \big [ \Omega _{b0}f_{b}(a) \!+\! \Omega _{r0}f_{r}(a)\! +\! \Omega _{D0}f_{D}(a) \nonumber \\&\qquad \qquad +\, (1\!-\!\Omega _{b0}-\Omega _{r0}-\Omega _{D0})\big ], \end{aligned}$$
(23)

where the \(\Omega _{i0}\) (now here \(i = b, r, D, \Lambda \)) represent the ratios of the present-time values of the energy densities and the critical energy density. The explicit knowledge of the Hubble rate of the interacting four-component system can be considered as a main advantage of our simplified approach. (For a different analytic approach see [15].)

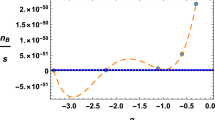
It is useful to characterizes the dynamics of our model with the help of the redshift dependence of the deceleration parameter

$$\begin{aligned} q(z)&= \frac{1+z}{H}\, \frac{dH}{dz}\,-\,1, \qquad z = \frac{1}{a} - 1, \end{aligned}$$
(24)

which results in the plots of Fig. 1. As already mentioned, positive values of \(\xi \) cause a faster cooling of the baryon temperature compared with that of an isolated Boltzmann gas, for negative values of \(\xi \) the baryon fluid absorbs energy from the photon gas and the matter temperature is higher than the corresponding ideal gas temperature.

Fig. 1
figure 1

Redshift dependence of the deceleration parameter \(q(z)\) for different values of \(\xi \). From top to bottom \(\xi =0.7,0.1,0,-0.1\). The transition redshift for a wide range of values of the \(\xi \) parameter lies in the region \(z <1\). As mentioned in the text, for negative values of \(\xi \) the gas is absorbing energy from the radiation. In all cases we have used the values \(\Omega _{b0}=0.04\), \(b=0.0001\), \(b_{1}=0.0001\) and \(\Omega _{D0}= 0.25\). Notice that for a better qualitative visualization we have chosen much higher values of \(|\xi |\) than admitted by our analysis in Sect. 3

Full size image

The fractional density parameters for arbitrary times are defined as

$$\begin{aligned} \Omega _{i} = \frac{\rho _{i}}{\rho _{c}} = \frac{8 \pi G \rho _{i}}{3H^{2}}. \end{aligned}$$
(25)

These density parameters are plotted in Fig. 2 for all four components, assuming a small positive value of \(\xi \).

Fig. 2
figure 2

Dependence of the density parameters on the scale factor for all four components. This figure shows the transition from a radiation-dominated phase to a DM-dominated phase as well as a subsequent transition to a final period where the cosmological constant dominates. In all case we have used the values \(\Omega _{b0}=0.04\), \(b=0.001\), \(b_{1}=0.01\), \(\xi =10^{-2}\) and \(\Omega _{D0}= 0.25\)

Full size image

Let us emphasize that our model admits analytical solutions for the entire homogeneous and isotropic background dynamics, including interaction and warmness effects. This should definitely be a very welcome feature for the sake of reconstruction of the history of the Universe by using observational data. Along with practical advantages of analytic expressions, it is well known that, in the use of numerical solutions, any additional derivative or integration results in new correlations and this increases the error in the final result. This aspect is important in both parametric and nonparametric approaches. For details on this issue see Refs. [16–18].

3 The tight-coupling approximation

In general, the study of anisotropies in the CMB requires to use a system of thousands of coupled equations [1] (Boltzmann hierarchy). However, progress has been made by implementing numerical codes as CAMB [19]. Even so, to study the implications of a given cosmological model for the CMB is a task that involves the Boltzmann equations together with the perturbed Einstein equations. This objective is beyond the scope of our paper. Instead, we shall resort to the tight-coupling approximation which we believe to be a reasonable simplification in the present context.

Thus, we assume that before recombination, photons and baryons are tightly coupled since Thomson scattering happens much faster than the expansion of the Universe. Quantitatively, this is described in terms of the optical depth \(\tau \),

$$\begin{aligned} \tau&\equiv \int _{\eta }^{\eta _{0}}{d\eta ' n_{e} \sigma _{T} a} \,\,\gg \,\,1, \end{aligned}$$
(26)

where \(n_{e}\) is the electron number density and \(\sigma _{T}\) denotes the Thomson cross section. Originally this approximation was implemented by Peebles and Yu [20] (see also Hu and Sugiyama [21]).

Following Ref. [1], the only nonnegligible momenta \(\Theta _{l}\) in the Boltzmann hierarchy in the limit \(\tau \gg 1\) are the monopole \((l=0)\) and the dipole \((l=1)\). All the higher momenta are suppressed. As a result one obtains an equation for the density contrast with the help of which it is possible to derive an expression for the position of the first acoustic peak. In the standard model this position is well determined by the fit given by Hu and Sugiyama [21]. Although it is strictly valid only for the \(\Lambda \)CDM model, we can use this fit her as well because values \(\xi <10^{-3}\) are suggested from observational constraints on the sound horizon \(r_{s}\). This is shown in Fig. 3, where we have included measurements of \(r_{s}\) made by WMAP [22] and Planck [23]. For values \(\xi > 0.05\) the sound horizon is outside the observational limits for a wide range of values of the matter density parameters. In this context it is important to note that in our approach the influence of the interaction parameter \(\xi \) on the first acoustic peak is entirely due to the dependence of the Hubble parameter on \(\xi \). Because of the supposed small value of \(\xi \), the contribution of the interaction term to the tight-coupling equations is considered to be small and will be neglected here.

In order to make the presentation clear, let us recall the derivation of the equation for the density contrast in the tight-coupling approximation. We shall follow here Ref. [24] and use the uniform curvature gauge. Then the perturbation equations for the baryons are given by [24]

$$\begin{aligned}&\dot{D_{b}} \,=\, -kV_{b},\end{aligned}$$
(27)
$$\begin{aligned}&\dot{V_{b}} + H V_{b} \,=\, k\Psi + \frac{\dot{\tau }}{R}(V_{r}-V_{b}), \end{aligned}$$
(28)

where \(V_k\) and \(D_k\) are gauge invariant velocity and density perturbations for the fluid \(k\) (we use the notation of [25]), over-dot indicates a derivative with respect at the conformal time \(\eta \) and \(\dot{\tau }=an_{e} \sigma _{T}\) is the differential optical depth. Quite similarly, the equations for the photons are

$$\begin{aligned}&\dot{D_{r}} \,=\, -\frac{4}{3} k V_{r},\end{aligned}$$
(29)
$$\begin{aligned}&\dot{V_{r}} \,=\, 2k\Psi + \frac{1}{4} k D_{r} - \dot{\tau }(V_{r}-V_{b})\,. \end{aligned}$$
(30)

The relations between the variables \(D\) and \(V\) of the uniform curvature gauge and those of the longitudinal gauge are given by [25]

$$\begin{aligned} D_{b,r}&= \delta ^{long}_{b,r} - 3(1+w_{b,r})\Psi ,\end{aligned}$$
(31)
$$\begin{aligned} V_{b,r}&= v^{long}_{b,r}, \end{aligned}$$
(32)

where the superscript “long” refers to the longitudinal gauge, \(\delta ^{long}_{b,r}\) are the corresponding fractional density perturbations for baryons and photons, respectively, and the quantities \(w_{b,r}\) denote their EoS parameters. The velocity potentials \(v^{long}_{b,r}\) are related to the four-velocities by

$$\begin{aligned} U^{\alpha }_{b,r}&= \big ((1-\Psi ),\,v^{long ,i}_{b,r}\big )\, \end{aligned}$$

and \(\Psi \) is the Newtonian potential. The last terms on the right-hand sides of (28) and (30) can be associated with the collision term for Thomson scattering of the Boltzmann equation. The details of this derivation can be followed in Ref. [26]. Now we rewrite (30) as

$$\begin{aligned} V_{r}-V_{b}&= \frac{2k}{\dot{\tau }}\, \Big (\Psi + \frac{D_{r}}{8}\Big ) \,-\, \frac{1}{\dot{\tau }}\,\dot{V_{b}}\,. \end{aligned}$$
(33)

The tight-coupling regime is characterized by a high rate of collision between baryons and photons. Therefore, an expansion with respect to \(\dot{\tau }^{-1}\) is a reasonable approximation. In zeroth order, we get

$$\begin{aligned} V_{b} = V_{r}\, \quad \Rightarrow \quad \dot{V}_{b} = \dot{V}_{r}\,. \end{aligned}$$
(34)

This is the first step of an iteration approach, first presented by Peebles and Yu [20]. Furthermore, using Eq. (34) in Eqs. (27)–(29) we get

$$\begin{aligned} D_{r}&= \frac{4}{3} D_{b}\,. \end{aligned}$$
(35)

This relation characterizes an adiabatic evolution. Since \(\xi \ll 1\), the adiabatic approximation is justified. In fact, due to the small value of \(\xi \), all non-adiabatic contributions, typical for an interacting model, become negligible at the first-order approximation. Of course, for larger \(\xi \) the situation can be different.

By using Eqs. (34–35) in Eq. (28), we arrive at

$$\begin{aligned} \ddot{D_{b}} + \frac{R}{1+R} H \dot{D_{b}} + \frac{k^{2}}{3(1+R)}D_{b} \,=\, -\frac{2+R}{1+R} k^{2} \Psi \,. \end{aligned}$$
(36)

To achieve the common form given in the literature for the above equation, the speed sound should be defined as

$$\begin{aligned} c_{s}^{2}&= \frac{1}{\sqrt{3(1+R)}}, \end{aligned}$$
(37)

where \(R\) is the photon–baryon momentum-density ratio that can be written as [26]

$$\begin{aligned} R=\frac{(P_{b}+\rho _{b})V_{b}}{(P_{r}+\rho _{r})V_{r}} = \frac{P_{b}+\rho _{b}}{P_{r}+\rho _{r}} \approx \frac{3\rho _{b}}{4\rho _{r}}. \end{aligned}$$
(38)

Due to the presence of the pressure \(P_{b}\), the ratio \(R\) in (38) does not exactly coincide with the standard ratio \(R = (3/4)\rho _{b}/\rho _{r}\). Numerically, it is possible show that the difference between both expressions is less than \(10\%\) and we shall use the approximation in the last part of (38) in the following.

Equation (36) with (37) and (38) is the second-order differential equation for a forced, damped harmonic oscillator which governs the acoustic oscillations of the photon–baryon fluid. The oscillation period is determined by the sound speed and hence by the baryon and photon densities. In our case it is given by the solutions (11) and (15) for baryons and photons, respectively. Via these solutions, the interaction parameter \(\xi \) influences the sound speed.

To solve Eq. (36), we suppose \(R\) to be slowly varying over an oscillation period inside of the sound horizon. Making use of the WKB method [1], we obtain the general solution, which can be written as

$$\begin{aligned} D_{b}(k,\eta )&= D_{b0} \,\Big (\frac{1}{1+R}\Big )^{1/4} \cos (kr_{s}) \,-\, E(k,\eta ), \end{aligned}$$
(39)

where

$$\begin{aligned}&E(k,\eta ) = (1+R)^{-1/4} \int _{0}^{\eta }d\beta \nonumber \\&\quad \times \Big [ \frac{2+R}{(1+R)^{3/4}} \,\, \frac{\sin \left[ k r_{s}(\eta )-kr_{s}(\beta )\right] }{kc_{s}}\,\, k^{2} \Psi \Big ]. \end{aligned}$$
(40)

In the limit when the first term in Eq. (39) dominates, the peaks and troughs should appear at the extremals of \(\cos (kr_{s})\). Following Refs. [1, 10, 27], the location of the first peak is conveniently fit as

$$\begin{aligned} k_{1,peak} \,=\, \frac{5\pi }{2r_{s}}\, \big (1+0.217 \Omega _{D}h^{2}\big )\,. \end{aligned}$$
(41)

The sound horizon \(r_{s}\) at decoupling, which appears in Eqs. (39) and (40), is defined as the comoving distance that a wave can travel prior to decoupling:

$$\begin{aligned} r_{s}&= \int _{0}^{a_{dec}}{\frac{c_{s}\,da}{a^2\,H(a)}} \,=\, \int _0^{a_{dec}}{\frac{da}{a^{2} H(a) \sqrt{3(1+R)}}}\,. \end{aligned}$$
(42)

Here, \(a_{dec}\) is the scale factor at the time of decoupling.

In Fig. 3 we depict the sound horizon at decoupling as a function of the interaction parameter \(\xi \) for three different values of the matter density parameter. One can see that values less than \(\xi \le 0.5 \times 10^{-2}\) are numerically compatible with observational constraints of the last dataset of PLANCK [22]: \(r_{s}=144\pm 0.71\). Furthermore, Fig. 4 shows that the difference between \(\Lambda CDM\) and our model is very small for a value of \(\xi = 10^{-3}\). However, the difference increases for a greater value of the interaction parameter.

Fig. 3
figure 3

The sound horizon at decoupling as function of the interaction parameter. The two horizontal lines show the observational constraints given by the measurements of PLANCK and WMAP [22, 23]. We have multiplied the error by 2 to be conservative. In all figures we used \(b_{1}=0.0001\) and \(\Omega _{b0}=0.05\)

Full size image
Fig. 4
figure 4

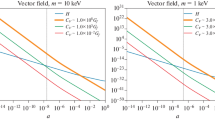
The position \(k_{1,peak}\) of the first acoustic peak (cf. Eq. (41)) as function of the density parameters. The solid lines represent our model and the dashed lines the \(\Lambda \)CDM model. For the values \(\xi \approx 10^{-4}\), \(b \approx 10^{-4}\) and \(b_{1} \approx 10^{-4}\) (upper left panel) our model is indistinguishable from the \(\Lambda \)CDM model. When the value of \(\xi \) increases to \(10^{-3}\) (upper right panel) the difference between the models is already evident. In the lower panels we consider the influence of the WDM parameter \(b_{1}\) for the fixed values \(\xi =10^{-4}\) and \(b=10^{-4}\). For \(b_{1}=10^{-2}\) for example (bottom left), the departure from the \(\Lambda \)CDM model is dramatic, implying a high degeneracy of the \(\Omega _{D0}\) parameter. Already for \(b_{1}= 0.5 \times 10^{-3}\) (bottom right) the differences are substantial. In all case we used \(h=0.7\) and the point represent the measure from PLANCK (\(k_{1,peak}= 0.05628 \pm 0.00028\)) [22, 23] with best fit of the density parameters given by \(\Omega _{\Lambda }=0.685^{+0.018}_{-0.016}\) and \(\Omega _{D0}=0.315^{+0.016}_{-0.018}\)

Full size image

4 Conclusions

We generalized a previously constructed, simplified RRG-based cosmological model [6, 8, 9], made of WDM, a cosmological constant, baryons and photons by taking into account an out-of-equilibrium interaction within the baryon–photon fluid. Such interaction, characterized here by a single phenomenological parameter \(\xi \), is supposed to be relevant before decoupling when the scattering rate ceases to be much higher than the Hubble rate and deviations from equilibrium are expected. We found an exact analytic solution for the homogeneous and isotropic background which encodes the impact of this parameter on the dynamics as well as warmness effects of both DM and baryons. This solution interpolates the cosmic evolution from an early radiation-dominated phase, followed by a transition to matter dominance until a final de Sitter stage.

In a second step, using the tight-coupling approximation, we considered perturbations in the photon–baryon fluid on this background and studied the influence of the out-of equilibrium and warmness parameters on the position of the first acoustic peak of the CMB spectrum. We found that both the parameter \(\xi \) and the DM warmness parameter \(b_{1}\) have to be of the order of \(10^{-4}\) or less to be compatible with observational data and with the \(\Lambda \)CDM model. As far as \(\xi \) is concerned, this can be seen as a confirmation of the perfect-fluid approach for the interacting photon–baryon system since deviations from equilibrium do not seem to be important. If \(b_{1}\) considerably exceeds the value \(10^{-4}\) there is a degeneracy in the DM density such that almost all values of the DM parameter \(\Omega _{D0}\) respecting the flat condition are compatible with \(\Omega _{b0} \sim 0.05\). The restriction on \(b_{1}\) is in agreement with the results obtained for the equilibrium RRG model using the large scale structures data [7]. On the other hand, even a small degree of warmness may potentially be useful to cure problems of the CDM paradigm, such as the cusps in the density profiles of galaxies and the excess of galactic satellites [3, 4]. An important procedure to break the degeneracy with the \(\Lambda \)CDM model for \(b_{1} \le 10^{-4}\) is to inspect the non-linear regime. This implies to adapt the usual computations used for CDM to the case where there is a departure from coldness, equivalent to the appearance of a pressure component. We hope to perform a corresponding analysis in future work.