Abstract
We find the entire form of the amplitude of two fermion strings (with different chiralities), a massless scalar field and one closed string Ramond–Ramond (RR) in IIA superstring theory, which is different from its IIB one. We make use of a very particular gauge fixing and explore several new couplings in IIA. All infinite \(u\)-channel scalar poles and \(t,s\)-channel fermion poles are also constructed. We find a new form of the higher derivative corrections to two fermion-two scalar couplings and show that the first simple \((s+t+u)\)-channel scalar pole for the \(p+2=n\) case can be obtained by having new higher derivative corrections to Supersymmetric Yang–Mills (SYM) couplings at third order of \(\alpha '\). We find that the general structure and the coefficients of the higher derivative corrections to two fermion-two scalar couplings are completely different from the derived \(\alpha '\) higher derivative corrections of type IIB.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
D\(_p\)-branes (with \(p\) as the spatial dimension of a D\(_p\)-brane) are the fundamental objects in superstring theory [1–4]. It is well known that a BPS brane does carry the so-called Ramond–Ramond Footnote 1 charge. We recommend several important papers to work with superstring perturbation theory [5] or to deal with holomorphic string amplitudes [6]. We also refer to several fascinating papers on the mathematical structures and hidden symmetries of the scattering amplitudes [7–10].
For various reasons, one needs to deal with the branes’ dynamics. In an interesting paper [11], various transitions of open/closed strings have been comprehensively explained. In order to highlight several dual prescriptions of the branes, we refer the interested reader to a review of string dualities [12]. For completeness, let us just remind the reader that some specific examples, such as the \(D0/D4\) system [13], the description of the world volume of BPS branes from the super-gravity side and eventually the realization of the AdS brane world [14] have already been shown.
If we are able to explore either bosonic or supersymmetric effective actions of BPS branes in the low energy limit by the scattering approach, then we might hope very much to indeed learn about the brane dynamics. In Myers’ paper [15] by taking into account several D\(_p\)-brane configurations in fact it is well explained how to employ bosonic actions. Although it is very difficult to completely discover supersymmetric effective actions [16], in this paper we try to make progress in our understandings of these particular actions.
Having considered several important papers (to include an effective action of a single bosonic brane [17] and its supersymmetrized version [18–22]), one may be able to follow what has been achieved.
The aim of this paper is to show that the S-matrix of the mixed closed/open string amplitudes of type IIA is entirely different from type IIB and in fact several new couplings will come out from direct computations of conformal field theory techniques of type IIA. In addition we want to show that the derived corrections of type IIB do not work for type IIA.
Basically we have shown that in the computations of the S-matrix of one RR \((C)\), two fermions and one scalar of type IIB, there are infinite u-channel scalar/gauge poles. For the same amplitude in type IIA (with different chirality) we will see that all infinite u-channel gauge poles will disappear.
Another interesting point is that unlike IIB, here in IIA we do not have any \(\alpha '\) corrections to two fermions, one gauge, and one scalar field.
The very interesting point which comes out of long computations of \(\langle V_{C}V_{\phi } V_{\bar{\psi }}V_{\psi }\rangle \) of type IIA is that not only the general structure of higher derivative corrections of two fermions-two scalars of IIA are different from IIB but also their coefficients are different.
We find these corrections at third order of \(\alpha '\). It is also of high importance to focus on the point that several new couplings could be explored in type IIA of this paper.
To deal with effective field theory, one must know the Myers terms, the Wess–Zumino, and the Chern–Simons actions, [23, 24]. The pull-back, the so-called Taylor expansion and essentially the all-order Myers terms of BPS/non-BPS branes have already been constructed in [25].
Some nice work in favor of the entire low energy actions has been carried out [26–28]. One can introduce some of the basic papers of mixed closed/open BPS branes where various motivations/applications to scattering theory/mathematical physics and similar results on BPS branes have been involved [29–39]. It is also explained in [13] how to dissolve the branes with lower dimensions inside higher dimensional ones by taking some of the higher derivative \(\alpha '\) corrections [40]. To be precise, if we take the \(D(-1)/D3\) system, then the description of its \(N^2\) entropy could be explained, if and only if \(\alpha '\) higher derivative corrections of the known Myers terms had been derived. In [40, 41] some arguments in favor of the applications to recent couplings are given.
Keeping in mind either the Myers terms or the new WZ actions [23, 42–46], we are willing to find new couplings and in particular new higher derivative corrections of two fermions (with different chirality)-two scalars up to third order of \(\alpha '\) by producing the first simple \((t+s+u)\)-channel scalar pole (just for \(p+2=n\) with \(n\) the index of RR field strength) of our S-matrix \(\langle V_{C} V_{\phi } V_{\bar{\psi }}V_{\psi } \rangle \). These corrections might accord to some crucial rule in F-theory [47] or M-theory [13, 40, 41].
Let us make some remarks. As we will observe, in the explicit form of the RR vertex operator (in ten dimensions of non-compact space), we did not include winding modes. Thus it is important to highlight that applying direct computations of CFT is much better than making use of T-duality to the old amplitudes of type IIB. We have argued in [48] that in order to be sure that all the terms of the related S-matrix appear in its final form and to derive the correct form of the higher derivative \(\alpha '\) corrections with exact coefficients, we should carry out direct CFT computations at each level of the amplitude.
Notice that for mixed open-closed amplitudes, computations should be made by taking the path integral method and all scalar/gauge/fermion (open) propagators should be derived by CFT techniques. Meanwhile it is discussed that, in the case of RR, one has to use both \((\alpha _n,\tilde{\alpha }_n)\) oscillators. The authors of [49] explained that one can work out both oscillators by dealing with open strings and RR could be taken by definition as open strings’ composite states.
To the best of our knowledge this means that we can define background fields as some functions of SYM. It is also described in Myers paper [15] that to make sense of all super-gravity fields, we need to employ the Taylor expansion for the effective field theory. It is also described in [50, 51] that the presence of BPS quantum effects of the open strings might shed new light on understanding the host brane curvature.
The organization of this paper is as follows. First we make some points on the notations. Then we move on to explore the complete form of the \(\langle V_{C} V_{\phi } V_{\bar{\psi }}^{\dot{\gamma }}V_{\psi }^{\dot{\delta }} \rangle \) of type IIA. Then we expand the amplitude and make use of the low energy limit to be able to reconstruct all-order vertices and we find several new couplings in field theory of type IIA. These couplings can be discovered just by comparing them with this S-matrix of type IIA. Finally, we produce all \(u\)-channel scalar poles and \(t,s\)-channel fermion poles, and we make various comments (for further details see Appendix A and B of [25, 42]).
2 Notations and analysis of \(\langle V_{\bar{\psi }}V_{\psi }V_{\phi }\rangle \)
The goal of this section is to provide necessary details to obtain the exact and complete form of a mixed and technically five point (physically four point) amplitude involving two fermions with different chiralities, a massless scalar and a closed string RR in the bulk in type IIA superstring theory. To do so, of course we need to apply conformal field theory (CFT) techniques. The computations of this particular case in IIB has been done in a recent paper [48] but as we will see various things change in higher point functions of string theory. For completeness we want to emphasize some of the string computations in various string theories [23, 42, 43, 52–57]. It is important to mention that the three point function including two fermions (with the same chirality) and one gauge (scalar) field in IIB is done in [48, 58] and since the correlation function for two spin operators and a fermion field (a Wick-like rule) is not changed [59, 60], we expect that the same result for the three point function holds for IIA (with different chiralities) as well.
It is worth trying to address an important technical issue, namely to be able to have various S-matrices of a closed and several open strings (fermions and/or currents), the so-called Wick-like rule should have been generalized. This generalization was carried out in [23, 25, 45, 46].
We just point out to the related vertex operators in IIA:
where the on-shell conditions for the scalar are \(k^2=k.\xi =0\) and for the fermions are \(q^2=q_a \gamma ^a \bar{u}^{\dot{\gamma }}= u^{\dot{\delta }}q_b \gamma ^b=0 \). Now \(u^{\dot{\delta }}\) should be regarded as the wave function of the fermion and one could use the charge conjugation matrix \(C^{\alpha \beta }\) to work with the spin indices. We refer to [48] for the meanings of the traces and for some other details.
2.1 The complete form of \(\left( RR \bar{\psi }^{\dot{\gamma }} \psi ^{\dot{\delta }}\phi \right) \) in type IIA
In this section we are going to work with the world volume of BPS branes to be able to find the comprehensive form to all orders of \(\alpha '\) of the S-matrix of two fermions (with different chirality of RR ), a massless scalar field, and a closed string RR. Having settled on that, this amplitude just makes sense in IIA, thus all the corrections that we have found in IIB [48] cannot be applied to IIA.
Let us clarify more details. We need to begin with the following vertices for this particular amplitude:

The definitions of the RR’s field strength in IIA and projection operator are

It is also recommended to work with holomorphic functions as follows:
which is why we apply doubling tricks to our calculations [25].
It is understood that the amplitude does not depend on the picture of BPS branes, and we prefer to carry out the computations in the following picture:
We just look for the ordering of \(\text{ Tr }\,(\lambda _1\lambda _2\lambda _3)\). If we think of the given vertices, then we realize that the S-matrix has to be divided into two different parts. We first find its first part.
To this aim we have to discover the correlator of four spin operators (in ten dimensions) with different chiralities [61, 62] as follows:
the next step is to actually substitute the above correlator inside the amplitude and one can read off its S-matrix as

\(\frac{\mu _p \pi ^{-1/2}}{4}\) is a normalization constant, and we have used the definitions \(x_{ij}=x_i-x_j, x_4=z=x+iy, x_5=\bar{z}=x-iy\) where
Notice that now the amplitude is SL(2,R) invariant and for simplicity we use the standard Mandelstam variables
We also need to apply a very distinguished gauge fixing \((x_1=0,x_2=1,x_3=\infty )\).
After gauge fixing one can derive the following form for the first part of the amplitude in IIA:

To have the complete part of the amplitude to all orders in \(\alpha '\) one has to perform integrations just on the position of the closed string RR (see [25, 63]). Without any further work we write the all-order solution of the first part of our amplitude:

with
As is clear from the above only \(L_3\) has infinite singularities in the \(u\)-channels, and depending on whether \(\mu \) takes either the world volume or the transverse direction we could have a gauge for \(n=p\) or scalar poles for the \(n=p+2\) case. More importantly, our S-matrix involves as many contact interactions. Needless to say that the expansion is just done by sending all Mandelstam variables to zero (for a comprehensive review of the expansions see [23]).
We are about to find the second part of the amplitude. There is a subtle issue for this part, as follows. If we substitute the second part of the vertex operator of the scalar inside the amplitude then we observe that one has to derive the correlator of four spin operators with different chiralities and one current in ten dimensions of space-time.
Thus the second part of the S-matrix is given by

in which
In [48] we have explained the method of deriving the correlation function of four spin operators and one current but let us summarize it very briefly once more. To do so the first step is to indeed consider the OPE,
and, in addition, we need to substitute the above relation into our original correlator \(\langle :\psi ^a\psi ^i(x_1):S_{\dot{\gamma }}(x_2):S_{\dot{\delta }}(x_3):S_{\alpha }(x_4):S_{\beta }(x_5):\rangle \) and use the correlation of four spin operators with different chiralities (5) (see also [62]). The other steps could easily be followed by taking the other different permutations and finally adding all the terms. It is also of high importance to mention that the following correlator must have been considered as well:
Finally, we should reconstruct different combinations of various gamma matrices and take advantage of Appendices A.1, A.3, B.3 and in particular section 6 of [62]. Indeed we have checked that our amplitude produces all the desired singularities associated to various channels, and more significantly the S-matrix keeps track of the SL(2,R) invariance. All these points are showing us that we have obtained the correct and ultimate form of the correlation function of four spin operators (with different chiralities) and one current. We also emphasize that the integrals are evaluated on the location of RR and a particular gauge fixing (likewise the gauge fixing of the first part of the amplitude) has been taken.
The final form of the second part of the S-matrix of \(RR\bar{\Psi }\Psi \Phi \) is given as follows:

such that
where \(L_4,L_5,L_6\) are
Let us turn to the parts of the amplitude in IIA. Since we are dealing with massless strings, we have just a low energy expansion and if we would send all Mandelstam variables to zero, then we would see that \(L_1,L_2,L_4\) have no singularities. Indeed these functions are responsible for an infinite contact interaction of two fermions with different chiralities and one RR and one massless scalar field. Therefore to be able to work with singular terms and at the level of poles one can easily ignore them. The first part of the amplitude has just infinite \(u\)-channel poles (as is obvious from the expansion of \(L_3\)).
Thus all terms in the second part of the amplitude carrying the \(L_4\) coefficient are just contact terms. Notice also the fact that the second terms of \( \mathcal{A}_{21}\) and \( \mathcal{A}_{23}\) are related to an infinite number of \(t\)-channel poles and one has to add them to reproduce all \(t\)-channel poles in field theory side of IIA. More importantly the second terms of \( \mathcal{A}_{22}\) and \( \mathcal{A}_{24}\) are related to an infinite number of \(s\)-channel poles and we need to add them to reproduce all \(s\)-channel poles on the field theory side of IIA, accordingly.
Note that all terms accompanying the coefficient of \(L_3\) in \( \mathcal{A}_{25}\), \( \mathcal{A}_{26}\), \( \mathcal{A}_{27}\), and \( \mathcal{A}_{28}\) themselves do include just infinite \(u\)-channel poles where in field theory we make it clear what kinds of poles (either gauge or scalar) can be propagated. In fact the trace and kinematic relation of closed string RR imposes on the amplitude whether a gauge or massless scalar must be propagated.
On the other hand the coefficient of the first part of \( \mathcal{A}_{25}\), which is \(sL_6\), tells us that this part of the amplitude has a double pole in the \(t\) and \((t+s+u)\) channels and appropriately the coefficient of the first part of\( \mathcal{A}_{26}\), which is \(-tL_6\), gives us the information as regards having a double pole \(s\) and \((t+s+u)\) channels and finally \(-tL_6\) (\(-sL_6\)) inside \( \mathcal{A}_{29}\) clarifies that we do have a double pole in \(s\) and \((t+s+u)\) (\(t\) and \((t+s+u)\)) channels where one has to add them to the other double poles.
Note that each part of our amplitude is totally anti symmetric with respect to interchanging the fermions and this is a test in favor of our long computations. The other fact which is highly important is that unlike type IIB superstring theory here we do have double poles.
Neither do we have single nor infinite massless \((t+s+u)\)-channel poles in the first part of the amplitude; therefore those corrections that have been derived in IIB, including infinite corrections to two fermions-two scalar fields and to two fermions, one scalar, and one gauge field, are not applicable to two fermions, one RR, and one scalar of IIA at all.
Here we are going to highlight an important comment as follows.
Given the above reasons, one can reveal that the closed form of the correlators of this amplitude and the final result of our amplitude is completely different from the same S-matrix in IIB and it is quite obvious that one cannot obtain the complete form of the IIA S-matrix by applying T-duality to the results of IIB [42, 43].
In fact, due to the presence of the momentum of RR in the transverse direction \(p^i\) and the fact that we are working in non-compact direction and winding modes do not appear in the RR vertex operator, we understand that the terms coming with \(p^i\) should be derived by just explicit computations and cannot be found by a duality transformation (compare \(CA AA\) with \(C\phi AA\)). Hence we must apply direct CFT methods even for fermionic amplitudes.
To deal with all contact interactions, one needs to make use of the low energy expansion by sending (\(t,s,u \rightarrow 0\)) so that the momentum conservation in world volume holds, \(t+s+u=-p^ap_a\). One can find the \( L_3\) expansion comprehensively:
where \(-sL_5\) could easily be derived from \(-tL_5\) by interchanging t and s, with the following coefficients:
in the next section we first produce all infinite \(u\)-channel scalar poles, more importantly we try to formulate some remarks about double poles that are allowed in type IIA, given the complete form of our S-matrix.
2.2 New couplings in type IIA and their third order \(\alpha '\) corrections
In this section we are going to make several important remarks on type IIA superstring theory. First, by applying direct computations in string theory (having found our complete S-matrix), we obtain several new couplings in IIA with their \(\alpha '\) corrections; second, we want to explore new corrections in IIA.
Basically we will show that the higher derivative corrections of two fermions-two scalars of IIB are not consistent with IIA and in fact not only the coefficients of those corrections of IIA are different from IIB but also the S-matrix imposes the requirement that the general structure of those IIA corrections is entirely different from IIB.
The third reason is as follows. In IIB we had for the S-matrix
and since we do not have any of the those terms in IIA, we expect not to have any single correction of two fermions, one scalar, and one gauge field of IIA. Namely the following corrections of IIB
are not applicable to IIA:
Let us start exploring the new corrections of type IIA.
For this section we must consider \(\mathcal{A}_{25} \) and \(\mathcal{A}_{26} \) (which are antisymmetric with respect to interchanging t and s), and add them to \(\mathcal{A}_{29} \). In fact \((\gamma _\lambda )\) in \((\gamma _\lambda C)_{\alpha \beta }\) can have just component in the transverse direction \(\lambda =i\), in such a way that after adding all the terms and extracting the traces, the final form of our S-matrix will be given by
So it is antisymmetric with respect to interchanging two fermions and it means that the amplitude of one RR, two fermion with the same chirality is zero as we expected, so we just work with the expansion of \(tL_6\) as follows:
It is clear from the above expansion that unlike IIB in type IIA for one RR and two fermions and one scalar we have several poles, involving double poles and new couplings. In particular, we do have simple poles in the \((s+t+u)=-p^a p_a\) channels for type IIA.
The effective field theory of IIA suggests that we have a double pole in \(t+s+u\) and \(s\) channels and they need to be reconstructed for the \(p+2=n\) case by the following rule.
The effective field theory has also the following poles:
note that the off-shell scalar \(\phi \) can be both \(\phi ^{(1)}\) and \(\phi ^{(2)}\). The vertex of \(V_i(C_{p+1},\phi )\) could be extracted from
to be \(V_i(C_{p+1},\phi )= (2\pi \alpha ')\mu _p {1\over (p+1)!} (\varepsilon )^{a_0\cdots a_{p}} H^{i}_{a_0\cdots a_{p}}\), and the scalar propagator is also derived from the kinetic term of the scalar fields to be
where k is the momentum of the off-shell scalar field.
Note that the vertex of \(V_j(\phi ,\bar{\psi }_1,\psi _2)\) including an off-shell scalar field, one on-shell and one off-shell fermion field, where each one lives in a different brane, can be decomposed as follows:
The fermion propagator could be derived from the fermions’ kinetic term and we have to note that this off-shell fermion is the fermion that is glued to one external scalar and one on-shell external fermion so that, if we apply the momentum conservation, then we can write down this propagator:
Finally we need to find the vertex of an on-shell scalar and one on-shell/an off-shell fermion \(V(\bar{\psi }_2,\psi _1,\phi ^{(1)})\), which could be explored from their kinetic terms as below:
Having replaced all above vertices and making use of this rule, we have \(\mathcal{A} =V_i(C_{p+1},\phi )G_{ij}(\phi )V_j(\phi ,\bar{\psi }_1,\psi _2)\) \( G(\psi _2)V(\bar{\psi }_2,\psi _1,\phi ^{(1)})\), and we are able to exactly obtain the following result:
which is exactly the first term of the expansion, so we could precisely produce the double pole. Note that we have also used \(k_{3a}\gamma ^a u=0\), which is the equation of motion for the fermion field. In order to produce the second term in the expansion of \(t L_6\), one has to consider the following rule with some new couplings:
where we have derived the fermion propagator and the \(V(\bar{\Psi }_2,\Psi _1,\phi ^1)\) could be once more derived by taking into account the fermions’ kinetic term as follows: \(V(\bar{\Psi }_2,\) \(\Psi _1,\phi ^1)=T_p (2\pi \alpha ') u^{\dot{\delta }} \gamma ^j \xi _{1j}\). On the other hand in order to look for the second pole in the \(tL_6\) expansion, the S-matrix imposes the requirement that a new WZ coupling in type IIA should appear:
Now if we choose \(\beta _1\) to be
and make use of the given vertices and the rule \(\mathcal{A}=V(C_{p+1},\bar{\Psi }_1,\Psi _2)G(\Psi _2)V(\bar{\Psi }_2,\Psi _1,\phi ^1),\) we can obtain the following amplitude on the field theory side:
which is precisely the second pole of the expansion of \(tL_6\).
The next question to address is how we can produce the third term of the expansion of \(t L_6\), which is a simple massless fermion pole. The answer is as follows.
The third pole could be looked for by proposing the same rule as of (23), however, the fermion propagator and the vertex of two fermions and one scalar field do not receive any correction; therefore, to produce that pole, one has to explore the higher derivative corrections to one RR-(p+1) form field and to \(\bar{\Psi }_2\) and \(\Psi _1\) as below:
Now by performing integration by parts and using the constraint \(s+t+u=-p^ap_a\), we can precisely obtain the correct form of a new WZ coupling in the presence of its correction at second order of \(\alpha '\):
Keeping fixed the fermion propagator and the vertex of two fermion fields and one scalar field and in particular substituting (26) in \(\mathcal{A}=V(C_{p+1},\bar{\Psi }_1,\Psi _2)G(\Psi _2)V(\bar{\Psi }_2,\Psi _1,\) \(\phi ^1),\) we are actually able to discover the amplitude in field theory,
which is exactly the third pole of the \(t L_6\) expansion and we have considered the equations of motion for fermion fields as well.
Consider the \(-sL_6\) expansion,
by interchanging the fermions \(\Psi _1 \) and \(\Psi _2\) and taking \(t \leftrightarrow s\), one can precisely show that the first, second, and third poles could be produced by the described field theory. On the other hand we now add the last terms of \(tL_6\) and \(-s L_6\) to get to final result of the string amplitude for the \(p+2=n\) case:
As we can see apart from the RR field strength, the amplitude carries three momenta. One may argue that this simple \((t+s+u)\)-pole (which has to be just a scalar pole), could be produced by the obtained couplings of two fermions-two scalars of type IIB [48]; however, we show that those corrections cannot hold in type IIA.
In order to be able to generate the poles in (29), one must consider the rule
where we have shown that \(V^{\alpha }_i(C_{p+1},\phi )\) and the scalar propagator will not receive any corrections; thus we need to look for the corrections to \(V^{\beta }_{j}(\phi ,\bar{\Psi },\Psi ,\phi _1)\) of type IIA.
It is shown in [48] that the corrections of two on-shell fermions and an on-shell/ an off-shell scalar of type IIB are
while if we consider (31), extract all the desired orderings for \(V^{\beta }_{j}(\phi ,\bar{\Psi },\Psi ,\phi _1)\) and apply the fermions’ equation of motion we find
Now if we replace (32) inside (30), then we obviously find that the final result is completely different from the given S-matrix in (29). This confirms that the corrections of type IIB do not work for type IIA.
The method of finding the corrections of BPS and non-BPS branes has been comprehensively explained in [43]; let us propose the following corrections of type IIA at third order of \(\alpha '\):
work out (33) and specially apply standard field theory techniques to the above couplings; then we are able to obtain the following vertex:
Having replaced the scalar propagator \(G_{\alpha \beta }^{ij}(\phi ) =\) \(\frac{-i\delta _{\alpha \beta }\delta ^{ij}}{T_p(2\pi \alpha ')^2(t+s+u)}\) (\(k\) is the off-shell scalar’s momentum), the vertex of an off-shell scalar and one RR (p \(+\) 1) form field \(V_i(C_{p+1},\phi )= (2\pi \alpha ')\mu _p {1\over (p+1)!} (\varepsilon )^{a_0\cdots a_{p}} H^{i}_{a_0\cdots a_{p}}\) and (34)–(30) we get the final result for the field theory amplitude:
This is precisely the first simple \((t+s+u)\) channel we were looking for.
Note that to get to the above result we have taken momentum conservation and made use of the fermions’ equations of motion. Let us end this section by making an extremely important message about the couplings that appeared in the second line of (33). Basically we need to apply the on-shell conditions and the fact that we have sent \(p^ap_a\) to zero value, that is, \((t+s+u)=0\) is also largely used. It would be interesting to find higher derivative corrections of two on-shell fermions and an off-shell/an on-shell scalar of type IIA to all orders in \(\alpha '\) and also to observe whether or not the universal conjecture, made and checked for type IIB, works for type IIA superstring theory.
Although it is seen that bosonic amplitudes of type IIB and even fermionic amplitudes of type IIB follow a universal conjecture on higher derivative corrections to all orders of \(\alpha '\) [43] (as several checks are made in [23, 42]), it is not clear to us that it so happens for fermionic amplitudes of type IIA; therefore we hope to answer some of these deep questions in favor of exploring all corrections of superstring theory in near future.
3 All-order \(u\)-channel massless scalar poles for the \(p+2=n\) case
One may argue that depending on whether \((\lambda ^\mu C) _{\alpha \beta }\) in the first part of the amplitude is carried on in the world volume or transverse we could have a gauge or scalar field \(u\)-channel pole; however, the coefficient of \((p.\xi )\) comes from the interaction of closed string RR with a scalar where the scalar comes from the Taylor expansion. This clarifies that the first part of the amplitude can have just a scalar pole and no massless gauge pole is allowed. We should highlight the fact that all contact interactions of the second term of \(\mathcal{A}_{25}\) are overlooked as in this section we would like to obtain just all massless scalar singularities. However, there are already several publications that deal with contact terms in string theory [25, 42].
Thus \(\mu \) should have been in the transverse direction for the first part of our amplitude. Therefore one might extract the related traces to actually write down all infinite massless scalar u-channel poles:
A normalization constant \(\frac{\mu _p \pi ^{-1/2}}{4}\) is also used.
We have already shown that \(T_p (2\pi \alpha ')\text{ Tr }\,\left( {\bar{\Psi }}\gamma ^aD_a\Psi \right) \) (fermion fields’ kinetic term) does not receive any correction and indeed all the kinetic terms inside the DBI action have no correctionFootnote 2 [23, 25, 42]. One off-shell scalar and two on-shell fermions \(V_{\beta }^{j}(\phi ,{\bar{\Psi }},\Psi )\) could be found by extracting the connection or commutator inside the kinetic term of the fermions,
In field theory we need to work out either pull-back ways, a Taylor expansion (see [25]), or we have to deal with new Wess–Zumino couplings which are all-order corrections to the Myers action [15].
To be able to produce all singularities, we also need to find the scalar propagator for which it has been fixed and received no correction (it should be extracted from the scalar field’s kinetic term \(-T_p \text{ Tr }\,\left( \frac{(2\pi \alpha ')^2}{2} D_a \phi ^i D^a\phi _i\right) \) as follows:
The important point here is that the connections must be dropped out.
We also need to employ all-order corrections to the Taylor expansion of one RR, an off-shell, and an on-shell scalar field,
where these corrections have been derived in [48]. If we apply field theory techniques to those corrections, then the vertex of a RR \(p+1\) form field, one on-shell/one off-shell scalar field \(V_{\alpha }^{i}(C_{p+1},\phi _1,\phi )\) to all orders in \(\alpha '\) can be extracted as follows:
Now if we replace the above equations by the following rule:
then we are able to precisely generate all massless \(u\)-channel scalar poles in type IIA. Therefore not only RR field induced all order corrections to an on-shell/ an off-shell scalar field in type IIB string theory [48] but also it imposed the same corrections to type IIA string theory and from this point of view it is a universal phenomenon which does work for both BPS and non-BPS actions [23, 25, 42, 43, 64, 65].
We now turn to see whether or not we do have an infinite number of \(u\)-channel gauge poles in type IIA.
One may think that due to the following trace in the second term of \(\mathcal{A}_{25}\):

and because of \((\lambda ^a C) _{\alpha \beta }\), we do have infinite u-channel gauge poles for IIA. However, if we add the second terms of \( \mathcal{A}_{25}\), \( \mathcal{A}_{26}\) and both \( \mathcal{A}_{27}\) and \( \mathcal{A}_{26}\) and also use various identities, then we can clearly observe that unlike the closed form of the correlators \(\langle V_{C}V_{\bar{\psi }}V_{\psi } V_{\phi }\rangle \) of type IIB, here for type IIA we have no longer any massless gauge poles left over.
Let us provide several physical reasons in favor of the above discussion. The first reason is as follows. If we consider the second term of \( \mathcal{A}_{26}\), then the trace imposes us that this part is not vanished for \(p+2=n\) case and then just RR \(C_{p+1}\) can have a non-zero value, while if we want to have a gauge pole we need to have a \(C_{p-1}\) form field to have a non-zero Chern–Simons coupling \( i\frac{(2\pi \alpha ')^2\mu _p}{p!}\int d^{p+1}\sigma \text{ Tr }\,\left( \partial _i C_{(p-1)}\wedge F \phi ^i\right) \). The second reason is that we have shown in the type IIB case [48] that all gauge poles should be produced by the following terms:
meanwhile, if we take the second part of \( \mathcal{A}_{25}\), then we are left with \(\bar{u}^{\dot{\gamma }} (\gamma _i)_{\dot{\gamma }\dot{\delta }} u^{\dot{\delta }}\) which is inconsistent with the above poles. The third reason is that for \(\lambda =i\) (\(\lambda =b\)) in \( \mathcal{A}_{28}\) we would have a \(C_p\) (\(C_{p-2}\)) form field, whereas both \(C_p\) (or \(C_{p-2}\)) cannot be acted upon, neither by the field strength of the gauge field nor by a covariant derivative of the scalar field to give rise to all \(p+1\) indices of the world volume so Chern–Simons terms cannot hold for these two relevant cases.
Finally the last reason is that we cannot expect to be able to produce any contact terms by \((\varepsilon )^{a_0\cdots a_{p-2}} C_{a_0\cdots a_{p-2}} {\bar{\Psi }}\gamma ^a D_a \Psi \) coupling as a sum of the indices cannot cover all \(p+1\) world volume directions. Hence there are no gauge poles for this amplitude of type IIA. Therefore neither the rule for type IIB, \( V_{\alpha }^{a}(C_{p-1},\phi _1,A)G_{\alpha \beta }^{ab}(A) V_{\beta }^{b}(A,{\bar{\Psi }}_1,\Psi _2) \), nor the following corrections of type IIBFootnote 3 will hold for type IIA anymore.
4 An infinite number of fermion poles for the \(p+2=n\) case
It is discussed in [48] that due to saturation of the super-ghost charge to the S-matrix, we cannot have any gauge/scalar, tachyon or graviton/closed string poles. Therefore to be able to construct all \(t,s\)-channel poles, one must consider the fermion poles.
All the second terms of \(A_{21},A_{23}\) (\(A_{22},A_{24}\)) are exactly related to an infinite number of t(s)-channel poles of our S-matrix; meanwhile, all the first terms of \(A_{21},A_{22},A_{23},A_{24}\) correspond to various contact interactions for the different \(p,n\) cases.
We first reconsider all s(t)-channel fermion poles of our S-matrix as follows:

As we can see the amplitude is antisymmetric with respect to interchanging the fermions. Now one could replace the expansions of \((-sL_5) \) and \((tL_5) \), extract the related traces, and simplify the amplitude more. Thus proceeding, we are able to write down all \(t\),(\(s\))-channel fermion poles of the string amplitude; however, due to the antisymmetric property of the fermion poles, here we are just going to write down all infinite s-channel fermion poles and obviously in the end one could produce an infinite number of t-channel fermion poles by just changing the fermions so all infinite s-channel fermion poles in string theory should be given by
Notice that we have overlooked all the terms carrying the coefficients of \(L_4\) because they are just for a contact interaction.
It is discussed in detail that to be able to produce all infinite s-channel fermion poles one has to use a particular rule.Footnote 4
It is crucial to mention that the kinetic term of the fermion fields is indeed fixed, so there is no correction to this term and if we use that, then one can derive the fermion propagator:
where the momentum conservation in the world volume has been used; the next step is to extract the covariant derivative of the fermion field,
and apply standard field theory techniques to write the needed vertex of an on-shell/an off-shell fermion and one on-shell scalar field \(V_{\beta }(\bar{\Psi },\Psi _3,\phi _1)\),
We have discussed Chern–Simons terms and Wess–Zumino terms including RR and an arbitrary scalar or gauge fields and one can generalize those couplings/actions to their supersymmetrized version as followsFootnote 5
In addition, the vertex operator of one on-shell closed string Ramond–Ramond \((p+1)\)-form and an on-shell/an off-shell fermion field is also needed (\(V_{\alpha }(C_{p+1},\bar{\Psi }_2,\Psi )\)) which must be found by using (49).Footnote 6
Now given the above rule and vertices, one can feasibly show that the first simple s-channel fermion pole is actually produced in field theory, however, as we might understand, there are an infinite fermion poles. An interesting point is that the above rule holds for an infinite number of fermion poles as well, but the only point is to impose an infinite number of higher derivative corrections to (\(V_{\alpha }(C_{p+1},\bar{\Psi }_2,\Psi )\)):
It is important to mention that neither a simple fermion pole nor two fermion-one scalar vertex received any correction as they have been obtained from the fixed kinetic term of open strings.
In (50), one could replace the partial derivative by a covariant derivative and ignore the connection terms, however, in order to see whether those connections can still be kept in the covariant derivative, one must go to a six or higher point function, which is beyond the reach of this paper.
Let us write down the complete and all-order \(\alpha '\) corrections of \(V_{\alpha }(C_{p+1},\Psi _2,\bar{\Psi })\) as follows:
fermions equations of motion were also used. Having used the above all-order \(\alpha '\) vertex and keeping fixed the other vertices, we are precisely able to actually generalize and construct all-order poles in field theory. This obviously clarifies that the presence of just a closed string RR \(p+1\) form field has resulted in infinite corrections to two fermions in both the IIA and IIB cases, and for this specific case the corrections remain invariant.
It is very worthwhile to mention that this idea (producing an infinite number of poles with considering an RR field and by applying all infinite higher derivative corrections to open strings) is an important result where its importance will become apparent in various higher point BPS and non-BPS branes so that certainly we do not need to have any knowledge about world-sheet integrals and all singularities of higher point functions can easily be derived.
Now having compared field theory coupling with all infinite S-matrix elements, we are going to construct all-order \(\alpha '\) corrections (without any ambiguities) to two fermions and one scalar and one closed string RR \(p+1\) form field in type IIA and finally fix its coefficient. We first replace the desired expansions inside the S-matrix and consider the following coupling:
Comparing with S-matrix elements, one could find all-order \(\alpha '\) corrections of the above coupling in type IIB as follows:
Note that, in the above all-order corrections, the connection terms must be dropped, but we expect those commutators hold in higher point functions. Note that the partial derivative on fermion in transverse direction must be moved to RR by taking integration by parts.
5 Conclusions
We have used the direct CFT methods to actually find the complete and closed form of the amplitude of two fermions with different chiralities (in type IIA superstring theory), a massless scalar field and one closed string Ramond–Ramond field. Indeed due to various reasons it is very important to have the entire correlators that appeared in \(\langle V_{C}V_{\bar{\psi }}^{\dot{\gamma }}V_{\psi }^{\dot{\delta }} V_{\phi }\rangle \) of the IIA case. Probably one can mention that the most important reason to have the complete result of the S-matrix is to find the \(\alpha '\) corrections in different theories.
We have shown that there are infinite massless scalar poles \(u\)-channels of type IIA for \(p+2=n\) case. Unlike the same amplitude of \(\rangle V_{C}V_{\bar{\psi }} V_{\psi } V_{\phi }\rangle \) of type IIB, here in IIA we have explicitly shown that there is no gauge pole. All infinite fermionic poles at \(t,s\)-channels with their all-order \(\alpha '\) corrections are also explored.
Unlike the IIB amplitude, explicit computations gave rise to the fact that in IIA the couplings between two fermions/one gauge and one scalar and their corrections do not exist anymore.
The explicit form of the amplitude clearly imposed the requirement that several new couplings should accompany the effective field theory of type IIA, while those couplings did not appear in type IIB.
The other important result is that the first simple \((t+s+u)\)-channel scalar pole has clarified for us that the new forms of the higher derivative corrections of two fermions (with different chirality) and an on-shell/an off-shell scalar should be written. In fact in order to reconstruct the \((t+s+u)\)-channel scalar pole, one has to explore the new corrections at the order of \(\alpha '^3\) [see (33)] where the general structure of these corrections and most significantly their coefficient is different from IIB corrections and it is a very crucial fact in favor of applying direct CFT methods.
Notes
From now on denoted RR.
See their fixed form:
$$\begin{aligned}&-T_p (2\pi \alpha ')\text{ Tr }\,\left( \frac{(2\pi \alpha ')}{2} D_a \phi ^i D^a\phi _i-\frac{(2\pi \alpha ')}{4}F_{ab}F^{ba}-{\bar{\Psi }}\gamma ^aD_a\Psi \right) .\nonumber \\ \end{aligned}$$(36)We have
$$\begin{aligned}&i\frac{(2\pi \alpha ')^2\mu _p}{p!}\int d^{p+1}\sigma \,\sum _{n=-1}^{\infty }b_n(\alpha ')^{n+1}\text{ Tr }\,\nonumber \\&\times \left( \partial _i C_{(p-1)} \wedge \partial ^{a_0}\cdots \partial ^{a_n}F \partial _{a_0}\cdots \partial _{a_n}\phi ^i\right) .\, \end{aligned}$$(42)We have
$$\begin{aligned} \mathcal{A}&= V_{\alpha }(C_{p+1}, \bar{\Psi }_2,\Psi )G_{\alpha \beta }(\Psi ) V_{\beta }(\bar{\Psi },\Psi _3,\phi _1). \end{aligned}$$(45)Notice that we write the above coupling in such a way that the integrations should be taken over the whole world volume space, that is, the total indices should cover all \(p+1\) directions of space-time and one must keep in mind the fermions’ equations of motion
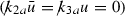 .
.- $$\begin{aligned} V_{\alpha }(C_{p+1},\bar{\Psi }_2,\Psi )&= i\frac{(2\pi \alpha ')\mu _p}{(p+1)!} H^i_{a_0\cdots a_{p}} \gamma ^i_{\dot{\gamma }} \bar{u}^{\dot{\gamma }} (\varepsilon )^{a_0\cdots a_{p}}\,\text{ Tr }\,\left( \lambda _2\lambda ^{\alpha }\right) .\, \nonumber \\ \end{aligned}$$(49)
References
J. Polchinski, Dirichlet-Branes and Ramond-Ramond charges. Phys. Rev. Lett. 75, 4724 (1995). arXiv:hep-th/9510017
E. Witten, Bound states of strings and p-branes. Nucl. Phys. B 460, 335 (1996). arXiv:hep-th/9510135
J. Polchinski, in Lectures on D-branes. arXiv:hep-th/9611050
C.P. Bachas, Lectures on D-branes. arXiv:hep-th/9806199
E. Witten, More On Superstring Perturbation Theory. arXiv:1304.2832 [hep-th]
E. Witten, Notes On Holomorphic String And Superstring Theory Measures Of Low Genus. arXiv:1306.3621 [hep-th]
E. D’Hoker, M.B. Green, Zhang-Kawazumi invariants and superstring amplitudes. arXiv:1308.4597 [hep-th]
E. Hatefi, SuperYang-Mills, Chern-Simons couplings and their all order \(\alpha ^{\prime }\) corrections in IIB superstring theory. arXiv:1310.8308 [hep-th], to appear in PRD
N. Arkani-Hamed, J. Trnka, The amplituhedron. arXiv:1312.2007 [hep-th]
N. Arkani-Hamed, J. Trnka, Into the amplituhedron. arXiv:1312.7878 [hep-th]
M. Ademollo, A. D’Adda, R. D’Auria, E. Napolitano, P. Di Vecchia, F. Gliozzi, S. Sciuto, Unified dual model for interacting open and closed strings. Nucl. Phys. B 77, 189 (1974)
J. Polchinski, String duality: a colloquium. Rev. Mod. Phys. 68, 1245 (1996). [ hep-th/9607050]
E. Hatefi, A.J. Nurmagambetov, I.Y. Park, \(N^3\) entropy of \(M5\) branes from dielectric effect. Nucl. Phys. B 866, 58 (2013). [ arXiv:1204.2711 [hep-th]]
E. Hatefi, A.J. Nurmagambetov, I.Y. Park, ADM reduction of IIB on \({\cal H}^{p, q}\) to dS braneworld. JHEP 1304, 170 (2013). [ arXiv:1210.3825 [hep-th]]
R.C. Myers, Dielectric-branes. JHEP 9912, 022 (1999). [ hep-th/9910053]
P.S. Howe, U. Lindstrom, L. Wulff, On the covariance of the Dirac-Born-Infeld-Myers action. JHEP 0702, 070 (2007). [ hep-th/0607156]
R.G. Leigh, Dirac-Born-infeld action from Dirichlet sigma model. Mod. Phys. Lett. A 4, 2767 (1989)
M. Cederwall, A. von Gussich, B.E.W. Nilsson, A. Westerberg, The Dirichlet super three-brane in ten-dimensional type IIB supergravity. Nucl. Phys. B 490, 163 (1997). [ hep-th/9610148]
M. Aganagic, C. Popescu, J.H. Schwarz, D-brane actions with local kappa symmetry. Phys. Lett. B 393, 311 (1997). [ hep-th/9610249]
M. Aganagic, C. Popescu, J.H. Schwarz, Gauge invariant and gauge fixed D-brane actions. Nucl. Phys. B 495, 99 (1997). [ hep-th/9612080]
M. Cederwall, A. von Gussich, B.E.W. Nilsson, P. Sundell, A. Westerberg, Nucl. Phys. B 490, 179 (1997). [ hep-th/9611159]
E. Bergshoeff, P.K. Townsend, Nucl. Phys. B 490, 145 (1997). [ hep-th/9611173]
E. Hatefi, On effective actions of BPS branes and their higher derivative corrections. JHEP 1005, 080 (2010). [ arXiv:1003.0314 [hep-th]]
E. Hatefi, Shedding light on new Wess-Zumino couplings with their corrections to all orders in alpha-prime. JHEP 1304, 070 (2013). [ arXiv:1211.2413 [hep-th]]
E. Hatefi, On higher derivative corrections to Wess-Zumino and Tachyonic actions in type II super string theory. Phys. Rev. D 86, 046003 (2012). [ arXiv:1203.1329 [hep-th]]
P. Koerber, A. Sevrin, The NonAbelian D-brane effective action through order alpha-prime**4. JHEP 0210, 046 (2002). [ hep-th/0208044]
A. Keurentjes, P. Koerber, S. Nevens, A. Sevrin, A. Wijns, Towards an effective action for D-branes. Fortsch. Phys. 53, 599 (2005). [ hep-th/0412271]
F. Denef, A. Sevrin, J. Troost, NonAbelian Born-Infeld versus string theory. Nucl. Phys. B 581, 135 (2000). [ hep-th/0002180]
A. Hashimoto, I.R. Klebanov, Scattering of strings from D-branes. Nucl. Phys. Proc. Suppl. 55B, 118 (1997). hep-th/9611214
I.R. Klebanov, L. Thorlacius, The Size of p-branes, Phys. Lett. B 371, 51 (1996). hep-th/9510200
S.S. Gubser, A. Hashimoto, I.R. Klebanov, J.M. Maldacena, Gravitational lensing by \(p\)-branes, Nucl. Phys. B 472, 231 (1996). hep-th/9601057
C. Bachas, D-Brane dynamics, Phys. Lett. B 374, 37 (1996). hep-th/9511043
W. Taylor, Lectures on D-branes, gauge theory and M(atrices). hep-th/9801182
C. Vafa, Lectures on strings and dualities. hep-th/9702201
M. Billo, M. Frau, F. Lonegro, A. Lerda, N = 1/2 quiver gauge theories from open strings with R-R fluxes. JHEP 0505, 047 (2005). hep-th/0502084
M. Billo, P. Di Vecchia, M. Frau, A. Lerda, I. Pesando, R. Russo, S. Sciuto, Microscopic string analysis of the D0–D8 brane system and dual R-R states. Nucl. Phys. B 526, 199 (1998). hep-th/9802088
E. Hatefi, Three point tree level amplitude in superstring theory. Nucl. Phys. Proc. Suppl. 216, 234 (2011). [ arXiv:1102.5042 [hep-th]]
S. de Alwis, R. Gupta, E. Hatefi, F. Quevedo, Stability, tunneling and flux changing de Sitter transitions in the large volume string scenario, JHEP 1311, 179 (2013) [ arXiv:1308.1222 [hep-th]]
A. Hashimoto, I.R. Klebanov, Decay of excited D-branes. Phys. Lett. B 381, 437 (1996). [ hep-th/9604065]
E. Hatefi, A.J. Nurmagambetov, I.Y. Park, Near-extremal black-branes with n*3 entropy growth. Int. J. Mod. Phys. A 27, 1250182 (2012). [ arXiv:1204.6303 [hep-th]]
J. McOrist, S. Sethi, M-theory and type IIA flux compactifications. JHEP 1212, 122 (2012). [ arXiv:1208.0261 [hep-th]]
E. Hatefi, I.Y. Park, More on closed string induced higher derivative interactions on D-branes. Phys. Rev. D 85, 125039 (2012). [ arXiv:1203.5553 [hep-th]]
E. Hatefi, I.Y. Park, Universality in all-order \(\alpha ^{\prime }\) corrections to BPS/non-BPS brane world volume theories. Nucl. Phys. B 864, 640 (2012). [ arXiv:1205.5079 [hep-th]]
E. Hatefi, On D-brane anti D-brane effective actions and their corrections to all orders in alpha-prime, JCAP 1309, 011 (2013) [ arXiv:1211.5538]
M.R. Garousi, E. Hatefi, On Wess-Zumino terms of Brane-Antibrane systems. Nucl. Phys. B 800, 502 (2008). [ arXiv:0710.5875 [hep-th]]
M.R. Garousi, E. Hatefi, More on WZ actions of non-BPS branes. JHEP 0903, 08 (2009). [ arXiv:0812.4216 [hep-th]]
C. Vafa, Evidence for F theory. Nucl. Phys. B 469, 403 (1996). hep-th/9602022
E. Hatefi, Closed string Ramond-Ramond proposed higher derivative interactions on fermionic amplitudes in IIB. Nucl. Phys. B 880, 1 (2014). arXiv:1302.5024 [hep-th]
M. Billo, M. Frau, F. Fucito, A. Lerda, Instanton calculus in R-R background and the topological string. JHEP 0611, 012 (2006). [ hep-th/0606013]
I.Y. Park, Scattering on D3-branes, Phys. Lett. B 660, 583 (2008) arXiv:0708.3452 [hep-th]
I.Y. Park, Open string engineering of D-brane geometry, JHEP 0808, 026 (2008) arXiv:0806.3330 [hep-th]
E. Hatefi, More on Ramond-Ramond, SYM, WZ couplings and their corrections in IIA. arXiv:1403.7167 [hep-th]
C. Kennedy, A. Wilkins, Ramond-Ramond couplings on brane-antibrane systems. Phys. Lett. B 464, 206 (1999). hep-th/9905195
L.A. Barreiro, R. Medina, 5-field terms in the open superstring effective action. JHEP 0503, 055 (2005). hep-th/0503182
R. Medina, F.T. Brandt, F.R. Machado, The open superstring 5-point amplitude revisited. JHEP 0207, 071 (2002). hep-th/0208121
L.A. Barreiro, R. Medina, JHEP 1210, 108 (2012). arXiv:1208.6066 [hep-th]
A. Bilal, Nucl. Phys. B 618, 21 (2001). [ hep-th/0106062]
J. Polchinski, in String Theory, vol. 2 (Cambridge University Press, Cambridge 1998)
H. Liu, J. Michelson, *-trek 3: The search for Ramond-Ramond couplings. Nucl. Phys. B 614, 330 (2001). [ hep-th/0107172]
V.A. Kostelecky, O. Lechtenfeld, W. Lerche, S. Samuel, S. Watamura, Conformal techniques, bosonization and tree level string amplitudes. Nucl. Phys. B 288, 173 (1987)
D. Friedan, E.J. Martinec, S.H. Shenker, Conformal invariance, supersymmetry and string theory. Nucl. Phys. B 271, 93 (1986)
D. Haertl, O. Schlotterer, Higher loop spin field correlators in various dimensions. Nucl. Phys. B 849, 364 (2011). arXiv:1011.1249 [hep-th]
A. Fotopoulos, On (alpha’)**2 corrections to the D-brane action for non-geodesic world-volume embeddings. JHEP 0109, 005 (2001). hep-th/0104146
E. Hatefi, All order \(\alpha ^{\prime }\) higher derivative corrections to non-BPS branes of type IIB Super string theory. JHEP 1307, 002 (2013). arXiv:1304.3711 [hep-th]
E. Hatefi, Selection rules and RR couplings on non-BPS branes, JHEP 1311, 204 (2013). [ arXiv:1307.3520]
Acknowledgments
I would like to thank E. Witten, Joe Polchinski, L. Alvarez-Gaume, E. Martinec, N. Arkani-Hamed, I. Klebanov, J. Schwarz, C. Vafa, J. Maldacena, L. Rastelli, W. Siegel, L. Bonora, K.S. Narain, and N. Lambert for valuable discussions/comments and for their great remarks. It is true that without their knowledge I was not able to finish up the last stages of this paper. It is also a fact that almost all of the computations of this paper were done during my visits to the Simons center for geometry and physics at Stony Brook, Institute for advanced study at Princeton, NJ, University of California at Berkeley, KITP, Center for the Fundamental Laws of Nature at Harvard University and at Caltech. I would like to thank for the great hospitality of those universities/institutes and in particular acknowledge Nima Arkani-Hamed, P. Horava, C. Vafa, O. Ganor, Mike Douglas and J. Schwarz.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Funded by SCOAP3 / License Version CC BY 4.0.
About this article
Cite this article
Hatefi, E. SYM, Chern–Simons, Wess–Zumino couplings and their higher derivative corrections in IIA superstring theory. Eur. Phys. J. C 74, 2949 (2014). https://doi.org/10.1140/epjc/s10052-014-2949-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-014-2949-5



 .
.