Analysis of the $Z_c(4020)$, $Z_c(4025)$, $Y(4360)$, and $Y(4660)$ as vector tetraquark states with QCD sum rules

Abstract

In this article, we distinguish the charge conjugations of the interpolating currents, calculate the contributions of the vacuum condensates up to dimension-10 in the operator product expansion, and we study the masses and pole residues of the $J^{PC}=1^{-\pm }$ hidden charmed tetraquark states with the QCD sum rules. We suggest a formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_c)^2}$ with the effective mass ${\mathbb {M}}_c=1.8~\hbox {GeV}$ to estimate the energy scales of the QCD spectral densities of the hidden charmed tetraquark states, which works very well. The numerical results disfavor assigning the $Z_c(4020)$, $Z_c(4025)$, and $Y(4360)$ as the diquark–antidiquark (with the Dirac-spinor structure $C-C\gamma _\mu$) type vector tetraquark states, and they favor assigning the $Z_c(4020)$, $Z_c(4025)$ as the diquark–antidiquark type $1^{+-}$ tetraquark states. While the masses of the tetraquark states with symbolic quark structures $c{\bar{c}}s{\bar{s}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ favor assigning the $Y(4660)$ as the $1^{--}$ diquark–antidiquark type tetraquark state, more experimental data are still needed to distinguish its quark constituents. There are no candidates for the positive charge conjugation vector tetraquark states; the predictions can be confronted with the experimental data in the future at the BESIII, LHCb and Belle-II.

1 Introduction

Recently, the BESIII collaboration studied the process $e^+e^- \rightarrow (D^{*} {\bar{D}}^{*})^{\pm } \pi ^\mp$ at a center-of-mass energy of $4.26~\hbox {GeV}$ using a $827\,\hbox {pb}^{-1}$ data sample obtained with the BESIII detector at the Beijing Electron Positron Collider, and observed a structure $Z^{\pm }_c(4025)$ near the $(D^{*} {\bar{D}}^{*})^{\pm }$ threshold in the $\pi ^\mp$ recoil mass spectrum [1]. The measured mass and width of the $Z^{\pm }_c(4025)$ are $(4026.3\pm 2.6\pm 3.7)~\hbox {MeV}$ and $(24.8\pm 5.6\pm 7.7)~\hbox {MeV}$, respectively [1]. Later, the BESIII collaboration studied the process $e^+e^- \rightarrow \pi ^+\pi ^- h_c$ at center-of-mass energies from $3.90~\hbox {GeV}$ to $4.42~\hbox {GeV}$, and they observed a distinct structure $Z_c(4020)$ in the $\pi ^\pm h_c$ mass spectrum; the measured mass and width of the $Z_c(4020)$ are $(4022.9\pm 0.8\pm 2.7)~\hbox {MeV}$ and $(7.9\pm 2.7\pm 2.6)~\hbox {MeV}$, respectively [2]. No significant signal of the $Z_c(3900)$ was observed in the $\pi ^\pm h_c$ mass spectrum [2]; the $Z_c(3900)$ and $Z_c(4020)$ maybe have different quantum numbers.

At first sight, the S-wave $D^{*} {\bar{D}}^{*}$ systems have the quantum numbers $J^{PC}=0^{++}$, $1^{+-}$, $2^{++}$, while the S-wave $\pi ^\pm h_c$ systems have the quantum numbers $J^{PC}=1^{--}$, so the $Z_c(4025)$ and $Z_c(4020)$ are different particles. On the other hand, it is also possible for the P-wave $D^{*} {\bar{D}}^{*}$ ($h_c\pi$) systems to have the quantum numbers $J^{PC}=1^{--}$ ($1^{+-}$). We cannot exclude the possibility that the $Z_c(4025)$ and $Z_c(4020)$ are the same particle with the quantum numbers $J^{PC}=1^{--}$ or $1^{+-}$. There have been several tentative assignments of the $Z_c(4025)$ and $Z_c(4020)$, such as the re-scattering effects [3, 4], molecular states [5–10], tetraquark states [11], etc. The $Z_c(4025)$ and $Z_c(4020)$ are charged charmonium-like states, their quark constituents must be $c{\bar{c}}u{\bar{d}}$ or $c{\bar{c}}d{\bar{u}}$ irrespective of the diquark–antidiquark type or meson–meson type substructures.

In 2013, the BESIII collaboration studied the process $e^+e^- \rightarrow \pi ^+\pi ^-J/\psi$ and observed the $Z_c(3900)$ in the $\pi ^\pm J/\psi$ mass spectrum with the mass $(3899.0\pm 3.6\pm 4.9)~\hbox {MeV}$ and width $(46\pm 10\pm 20) \,\hbox {MeV}$, respectively [12]. Later the $Z_c(3900)$ was confirmed by the Belle and CLEO collaborations [13, 14]. Also in 2013, the BESIII collaboration studied the process $e^+e^- \rightarrow \pi ^{\mp } \left( D {\bar{D}}^*\right) ^{\pm }$ and observed the $Z_c(3885)$ in the $(D {\bar{D}}^*)^{\pm }$ mass spectrum with the mass $(3883.9 \pm 1.5 \pm 4.2)~\hbox {MeV}$ and width $(24.8 \pm 3.3 \pm 11.0)~\hbox {MeV}$, respectively [15]. The angular distribution of the $\pi Z_c(3885)$ system favors assigning the $Z_c(3885)$ with $J^P=1^+$ [15]. We tentatively identify the $Z_c(3900)$ and $Z_c(3885)$ as the same particle according to the uncertainties of the masses and widths [16], one can consult Ref. [16] for more articles on the $Z_c(3900)$. The possible quantum numbers of the $Z_c(3900)$ or $Z_c(3885)$ are $J^{PC}=1^{+-}$. There is a faint possibility that the $Z_c(3900)$ and $Z_c(4020)$ are the same axial-vector meson with $J^{PC}=1^{+-}$ according to the masses.

In 2007, the Belle collaboration measured the cross section for the process $e^+e^- \rightarrow \pi ^+ \pi ^- \psi ^{\prime }$ between threshold and $\sqrt{s}=5.5~\hbox {GeV}$ using a $673~\hbox {fb}^{-1}$ data sample collected with the Belle detector at KEKB, and they observed two structures $Y(4360)$ and $Y(4660)$ in the $\pi ^+ \pi ^- \psi ^{\prime }$ invariant mass distributions at $(4361\pm 9\pm 9)~\hbox {MeV}$ with a width of $(74\pm 15\pm 10)~\hbox {MeV}$ and $(4664\pm 11\pm 5)~\hbox {MeV}$ with a width of $(48\pm 15\pm 3)~\hbox {MeV}$, respectively [17]. The quantum numbers of the $Y(4360)$ and $Y(4660)$ are $J^{PC}=1^{--}$, which are unambiguously listed in the Review of Particle Physics now [18]. In 2008, the Belle collaboration studied the exclusive process $e^+e^- \rightarrow \Lambda _c^+ \Lambda _c^-$ and observed a clear peak $Y(4630)$ in the $\Lambda _c^+ \Lambda _c^-$ invariant mass distribution just above the $\Lambda _c^+ \Lambda _c^-$ threshold, and they determined the mass and width to be $\left( 4634^{+8}_{-7}{}^{+5}_{-8}\right) ~\hbox {Mev}$ and $\left( 92^{+40}_{-24}{}^{+10}_{-21}\right) ~\hbox {MeV}$, respectively [19]. The $Y(4660)$ and $Y(4630)$ may be the same particle according to the uncertainties of the masses and widths (also the decay properties [20]). There have been several tentative assignments of the $Y(4360)$ and $Y(4660)$, such as the conventional charmonium states [21–24], baryonium state [25], molecular states or hadro-charmonium states [26–31], tetraquark states [32–38], etc. One can consult Refs. [39–43] for more articles on the $X$, $Y$, and $Z$ particles.

In this article, we study the diquark–antidiquark type vector tetraquark states in detail with the QCD sum rules, and we explore possible assignments of the $Z_c(4020)$, $Z_c(4025)$, $Y(4360)$, and $Y(4660)$ in the tetraquark scenario. In Ref. [16], we extend our previous works on the axial-vector tetraquark states [44], distinguish the charge conjugations of the interpolating currents, calculate the contributions of the vacuum condensates up to dimension-10 and discard the perturbative corrections in the operator product expansion, study the $C\gamma _5-C\gamma _\mu$ type axial-vector hidden charmed tetraquark states with the QCD sum rules. We explore the energy scale dependence of the charmed tetraquark states in detail for the first time, and we tentatively assign the $X(3872)$ and $Z_c(3900)$ (or $Z_c(3885)$) as the $J^{PC}=1^{++}$ and $1^{+-}$ tetraquark states, respectively [16]. In calculations, we observe that the tetraquark masses decrease monotonously with increase of the energy scales, the energy scale $\mu =1.5~\hbox {GeV}$ is the lowest energy scale to reproduce the experimental values of the masses of the $X(3872)$ and $Z_c(3900)$, and it serves as an acceptable energy scale for the charmed mesons in the QCD sum rules [16].

In Refs. [45, 46], we study the $C\gamma _\mu -C$ and $C\gamma _\mu \gamma _5-C\gamma _5$ type tetraquark states with the QCD sum rules by carrying out the operator product expansion to the vacuum condensates up to dimension-10 and setting the energy scale to be $\mu =1~\hbox {GeV}$. In Refs. [11, 32–34, 47, 48], the authors carry out the operator product expansion to the vacuum condensates up to dimension-8 to study the vector tetraquark states with the QCD sum rules, but they do not show the energy scales or do not specify the energy scales at which the QCD spectral densities are calculated. In Refs. [11, 32–34, 45–48], some higher dimension vacuum condensates involving the gluon condensate, mixed condensate and four-quark condensate are neglected, which maybe impair the predictive ability. The terms associated with $\frac{1}{T^2}$, $\frac{1}{T^4}$, $\frac{1}{T^6}$ in the QCD spectral densities manifest themselves at small values of the Borel parameter $T^2$, we have to choose large values of the $T^2$ to warrant convergence of the operator product expansion and appearance of the Borel platforms. In the Borel windows, the higher dimension vacuum condensates play a less important role. In summary, the higher dimension vacuum condensates play an important role in determining the Borel windows therefore the ground state masses and pole residues, so we should take them into account consistently.

In this article, we extend our previous works [16] to study the vector tetraquark states, distinguish the charge conjugations of the interpolating currents, calculate the contributions of the vacuum condensates up to dimension-10 and discard the perturbative corrections, study the masses and pole residues of the $C-C\gamma _\mu$ type vector hidden charmed tetraquark states with the QCD sum rules. Furthermore, we explore the energy-scale dependence in detail so as to obtain some useful formulas, and we make tentative assignments of the $Z_c(4020)$, $Z_c(4025)$, $Y(4360)$, and $Y(4660)$ as the $J^{PC}=1^{-+}$ or $1^{--}$ tetraquark states. The scalar and axial-vector heavy-light diquark states have almost degenerate masses from the QCD sum rules [49, 50], the $C\gamma _\mu -C$ and $C\gamma _\mu \gamma _5-C\gamma _5$ type tetraquark states have degenerate (or slightly different) masses [45, 46], as the pseudoscalar and vector heavy-light diquark states have slightly different masses.

The article is arranged as follows: we derive the QCD sum rules for the masses and pole residues of the vector tetraquark states in Sect. 2; in Sect. 3, we present the numerical results and discussions; Sect. 4 is reserved for our conclusion.

2 QCD sum rules for the vector tetraquark states

In the following, we write down the two-point correlation functions $\Pi _{\mu \nu }(p)$ in the QCD sum rules,

$$\begin{aligned}&\Pi _{\mu \nu }(p)=i\int \mathrm{d}^4x e^{ip \cdot x} \left\langle 0|T\left\{ J_\mu (x)J_\nu ^{\dagger }(0)\right\} |0\right\rangle ,\end{aligned}$$

(1)

$$\begin{aligned}&J^1_\mu (x)=\frac{\epsilon ^{ijk}\epsilon ^{imn}}{\sqrt{2}}\left\{ s^j(x)C c^k(x) {\bar{s}}^m(x)\gamma _\mu C {\bar{c}}^n(x)\right. \nonumber \\&\left. +\,ts^j(x)C\gamma _\mu c^k(x){\bar{s}}^m(x)C {\bar{c}}^n(x)\right\} , \end{aligned}$$

(2)

$$\begin{aligned}&J^2_\mu (x)=\frac{\epsilon ^{ijk}\epsilon ^{imn}}{2}\left\{ u^j(x)C c^k(x) {\bar{u}}^m(x)\gamma _\mu C {\bar{c}}^n(x)\right. \nonumber \\&+\,d^j(x)C c^k(x) {\bar{d}}^m(x)\gamma _\mu C {\bar{c}}^n(x)\nonumber \\&+\,tu^j(x)C\gamma _\mu c^k(x){\bar{u}}^m(x)C {\bar{c}}^n(x)\nonumber \\&\left. +\,td^j(x)C\gamma _\mu c^k(x){\bar{d}}^m(x)C {\bar{c}}^n(x)\right\} , \end{aligned}$$

(3)

$$\begin{aligned}&J^3_\mu (x)=\frac{\epsilon ^{ijk}\epsilon ^{imn}}{\sqrt{2}}\left\{ u^j(x)C c^k(x) {\bar{d}}^m(x)\gamma _\mu C {\bar{c}}^n(x)\right. \nonumber \\&\left. +\,tu^j(x)C\gamma _\mu c^k(x){\bar{d}}^m(x)C {\bar{c}}^n(x)\right\} , \end{aligned}$$

(4)

where $J_\mu (x)=J_\mu ^1(x),\,J_\mu ^2(x),\,J_\mu ^3(x)$, $t=\pm 1$, the $i$, $j$, $k$, $m$, $n$ are color indices, the $C$ is the charge conjugation matrix. Under the charge conjugation transform $\widehat{C}$, the currents $J_\mu (x)$ have the properties,

$$\begin{aligned} \begin{aligned}&\widehat{C}J^{1/2}_{\mu }(x)\widehat{C}^{-1}=\pm J^{1/2}_\mu (x) \quad \hbox {for}\ t=\pm 1, \\&\widehat{C}J^{3}_{\mu }(x)\widehat{C}^{-1}=\pm J^{3}_\mu (x)\mid _{u\leftrightarrow d}\quad \hbox {for}\ t=\pm 1, \end{aligned} \end{aligned}$$

(5)

which originate from the charge conjugation properties of the pseudoscalar and axial-vector diquark states,

$$\begin{aligned} \begin{aligned}&\widehat{C}\left[ \epsilon ^{ijk}q^j C c^k\right] \widehat{C}^{-1}=\epsilon ^{ijk}\bar{q}^j C {\bar{c}}^k, \\&\widehat{C}\left[ \epsilon ^{ijk}q^j C\gamma _\mu c^k\right] \widehat{C}^{-1}=\epsilon ^{ijk}\bar{q}^j \gamma _\mu C {\bar{c}}^k. \end{aligned} \end{aligned}$$

(6)

We choose the neutral currents $J^1_\mu (x)$ and $J^2_\mu (x)$ with $t=-$ to interpolate the $J^{PC}=1^{--}$ diquark–antidiquark type tetraquark states $Y(4660)$ and $Y(4360)$, respectively. There are two structures in $\pi ^+\pi ^-$ invariant mass distributions at about $0.6~\hbox {GeV}$ and $1.0~\hbox {GeV}$ in the $\pi ^+ \pi ^-\psi ^{\prime }$ mass spectrum, which may be due to the scalar mesons $f_0(600)$ and $f_0(980)$, respectively [17]. In the two-quark scenario, $f_0(600)=(u\overline{u}+d\overline{d})/\sqrt{2}$ and $f_0=s\overline{s}$ in the ideal mixing limit, while in the tetraquark scenario, the $f_0(600)$ and $f_0(980)$ have the symbolic quark structures $ud{\bar{u}}{\bar{d}}$ and $(us{\bar{u}}{\bar{s}}+ ds{\bar{d}}{\bar{s}})/\sqrt{2}$, respectively. The $Y(4660)$ couples to the current $J^1_\mu (x)$ while the $Y(4360)$ couples to the current $J^2_\mu (x)$. However, we cannot exclude the possibility that the $Y(4660)$ has the symbolic quark structure $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$, in that case the decay $Y(4660)\rightarrow f_0(600)\psi ^{\prime }$ is Okubo–Zweig–Iizuka (OZI) allowed. We choose the charged vector current $J^3_\mu (x)$ with $t=\pm$ to interpolate the $Z_c(4020)$ and $Z_c(4025)$, the results for the scalar and tensor currents will be presented elsewhere. At present, we cannot exclude the possibility that the $Z_c(4020)$ and $Z_c(4025)$ are the same vector particle.

We can insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators $J_\mu (x)$ into the correlation functions $\Pi _{\mu \nu }(p)$ to obtain the hadronic representation [51–53]. After isolating the ground state contributions of the vector tetraquark states, we get the following results:

$$\begin{aligned} \Pi _{\mu \nu }(p)&= \frac{\lambda _{Y/Z}^2}{M_{Y/Z}^2-p^2}\left( -g_{\mu \nu } +\frac{p_\mu p_\nu }{p^2}\right) +\cdots , \end{aligned}$$

(7)

where the pole residues $\lambda _{Y/Z}$ are defined by

$$\begin{aligned} \langle 0|J_\mu (0)|Y/Z(p)\rangle =\lambda _{Y/Z} \,\varepsilon _\mu , \end{aligned}$$

(8)

the $\varepsilon _\mu$ are the polarization vectors of the vector tetraquark states $Z_c(4020)$, $Z_c(4025)$, $Y(4360)$, $Y(4660)$, etc.

In the following, we take the current $J_\mu (x)=J^1_\mu (x)$ as an example and briefly outline the operator product expansion for the correlation functions $\Pi _{\mu \nu }(p)$ in perturbative QCD. We contract the $c$ and $s$ quark fields in the correlation functions $\Pi _{\mu \nu }(p)$ with the Wick theorem, and we obtain the results

$$\begin{aligned} \Pi _{\mu \nu }(p)&= \frac{i\epsilon ^{ijk}\epsilon ^{imn} \epsilon ^{i^{\prime }j^{\prime }k^{\prime }} \epsilon ^{i^{\prime }m^{\prime }n^{\prime }}}{2} \nonumber \\&\times \int \mathrm{d}^4x e^{ip \cdot x}\times \left\{ \mathrm{Tr}\left[ C^{kk^{\prime }}(x) CS^{jj^{\prime }T}(x)C\right] \right. \nonumber \\&\times \left. \mathrm{Tr}\left[ \gamma _\nu C^{n^{\prime }n}(-x)\gamma _\mu C S^{m^{\prime }mT}(-x)C\right] \right. \nonumber \\&\left. +\,\mathrm{Tr}\left[ \gamma _\mu C^{kk^{\prime }}(x)\gamma _\nu CS^{jj^{\prime }T}(x)C\right] \right. \nonumber \\&\left. \times \,\mathrm{Tr}\left[ C^{n^{\prime }n}(-x) C S^{m^{\prime }mT}(-x)C\right] \right. \nonumber \\&\mp \,\mathrm{Tr}\left[ \gamma _\mu C^{kk^{\prime }}(x) CS^{jj^{\prime }T}(x)C\right] \nonumber \\&\left. \times \,\mathrm{Tr}\left[ \gamma _\nu C^{n^{\prime }n}(-x) C S^{m^{\prime }mT}(-x)C\right] \right. \nonumber \\&\left. \mp \,\mathrm{Tr}\left[ C^{kk^{\prime }}(x)\gamma _\nu CS^{jj^{\prime }T}(x)C\right] \right. \nonumber \\&\left. \times \,\mathrm{Tr}\left[ C^{n^{\prime }n}(-x)\gamma _\mu C S^{m^{\prime }mT}(-x)C\right] \right\} , \end{aligned}$$

(9)

where the $\mp$ correspond to $C=\pm$, respectively, the $S_{ij}(x)$ and $C_{ij}(x)$ are the full $s$ and $c$ quark propagators, respectively,

$$\begin{aligned}&S_{ij}(x)= \frac{i\delta _{ij}\!\not \!{x}}{ 2\pi ^2x^4} -\frac{\delta _{ij}m_s}{4\pi ^2x^2}-\frac{\delta _{ij}\langle {\bar{s}}s\rangle }{12} +\frac{i\delta _{ij}\!\not \!{x}m_s \langle {\bar{s}}s\rangle }{48}\nonumber \\&\qquad \qquad \quad -\frac{\delta _{ij}x^2\langle {\bar{s}}g_s\sigma Gs\rangle }{192}+\frac{i\delta _{ij}x^2\!\not \!{x} m_s\langle {\bar{s}}g_s\sigma Gs\rangle }{1152}\nonumber \\&\qquad \qquad \quad -\frac{ig_s G^{a}_{\alpha \beta }t^a_{ij}(\!\not \!{x} \sigma ^{\alpha \beta }+\sigma ^{\alpha \beta } \!\not \!{x})}{32\pi ^2x^2} \!-\!\frac{i\delta _{ij}x^2\!\not \!{x}g_s^2\langle {\bar{s}} s\rangle ^2}{7776} \nonumber \\&\qquad \qquad \quad -\frac{\delta _{ij}x^4\langle {\bar{s}}s \rangle \langle g_s^2 GG\rangle }{27648}-\frac{1}{8}\langle {\bar{s}}_j\sigma ^{\mu \nu }s_i \rangle \sigma _{\mu \nu } \nonumber \\&\qquad \qquad \quad -\frac{1}{4}\langle {\bar{s}}_j\gamma ^{\mu }s_i\rangle \gamma _{\mu }+\cdots ,\end{aligned}$$

(10)

$$\begin{aligned}&C_{ij}(x)=\frac{i}{(2\pi )^4}\int d^4k e^{-ik \cdot x} \left\{ \frac{\delta _{ij}}{\!\not \!{k}-m_c}\right. \nonumber \\&\qquad \qquad \quad \left. -\frac{g_sG^n_{\alpha \beta }t^n_{ij}}{4}\frac{\sigma ^{\alpha \beta }(\!\not \!{k}+m_c)+(\!\not \!{k}+m_c) \sigma ^{\alpha \beta }}{(k^2-m_c^2)^2}\right. \nonumber \\&\qquad \qquad \quad \left. +\frac{g_s D_\alpha G^n_{\beta \lambda }t^n_{ij}(f^{\lambda \beta \alpha }+f^{\lambda \alpha \beta }) }{3(k^2-m_c^2)^4}\right. \nonumber \\&\qquad \qquad \quad \left. -\frac{g_s^2 (t^at^b)_{ij} G^a_{\alpha \beta }G^b_{\mu \nu }(f^{\alpha \beta \mu \nu }\!+\!f^{\alpha \mu \beta \nu }\!+\!f^{\alpha \mu \nu \beta }) }{4(k^2-m_c^2)^5}\right. \nonumber \\&\qquad \qquad \quad \left. +\cdots \right\} ,\nonumber \\&f^{\lambda \alpha \beta }=(\!\not \!{k}+m_c) \gamma ^\lambda (\!\not \!{k}+m_c)\gamma ^\alpha (\!\not \!{k}+m_c) \gamma ^\beta (\!\not \!{k}+m_c),\nonumber \\&f^{\alpha \beta \mu \nu }=(\!\not \!{k}+m_c) \gamma ^\alpha (\!\not \!{k}+m_c)\gamma ^\beta (\!\not \!{k}+m_c) \gamma ^\mu (\!\not \!{k}+m_c)\nonumber \\&\qquad \qquad \quad \times \gamma ^\nu (\!\not \!{k}+m_c), \end{aligned}$$

(11)

and $t^n=\frac{\lambda ^n}{2}$, the $\lambda ^n$ is the Gell-Mann matrix, $D_\alpha =\partial _\alpha -ig_sG^n_\alpha t^n$ [53], then compute the integrals both in the coordinate and momentum spaces, and obtain the correlation functions $\Pi _{\mu \nu }(p)$ therefore the spectral densities at the level of quark–gluon degrees of freedom. In Eq. (10), we retain the terms $\langle {\bar{s}}_j\sigma _{\mu \nu }s_i \rangle$ and $\langle {\bar{s}}_j\gamma _{\mu }s_i\rangle$ originate from the Fierz rearrangement of the $\langle s_i {\bar{s}}_j\rangle$ to absorb the gluons emitted from the heavy quark lines to form $\langle {\bar{s}}_j g_s G^a_{\alpha \beta } t^a_{mn}\sigma _{\mu \nu } s_i \rangle$ and $\langle {\bar{s}}_j\gamma _{\mu }s_ig_s D_\nu G^a_{\alpha \beta }t^a_{mn}\rangle$ so as to extract the mixed condensate and four-quark condensates $\langle {\bar{s}}g_s\sigma G s\rangle$ and $g_s^2\langle {\bar{s}}s\rangle ^2$, respectively. One can consult Ref. [16] for some technical details in the operator product expansion.

Once analytical results are obtained, we can take the quark-hadron duality below the continuum threshold $s_0$ and perform Borel transform with respect to the variable $P^2=-p^2$ to obtain the following QCD sum rules:

$$\begin{aligned} \lambda ^2_{Y/Z}\, \exp \left( -\frac{M^2_{Y/Z}}{T^2}\right) = \int _{4m_c^2}^{s_0}\mathrm{d}s\, \rho (s) \, \exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(12)

where

$$\begin{aligned} \rho (s)&= \rho _{0}(s)+\rho _{3}(s) +\rho _{4}(s)+\rho _{5}(s)\nonumber \\&+\rho _{6}(s)+\rho _{7}(s) +\rho _{8}(s)+\rho _{10}(s), \end{aligned}$$

(13)

where 0, 3, 4, 5, 6, 7, 8, 10 denote the dimensions of the vacuum condensates, the explicit expressions of the spectral densities $\rho _i(s)$ are presented in the appendix. In this article, we carry out the operator product expansion to the vacuum condensates up to dimension-10 and discard the perturbative corrections, and we assume vacuum saturation for the higher dimension vacuum condensates. The higher dimension vacuum condensates are always factorized to lower condensates with vacuum saturation in the QCD sum rules, factorization works well in large $N_c$ limit. In reality, $N_c=3$, and some (not much) ambiguities maybe come from the vacuum saturation assumption. The condensates $\langle \frac{\alpha _s}{\pi }GG\rangle$, $\langle {\bar{s}}s\rangle \langle \frac{\alpha _s}{\pi }GG\rangle$, $\langle {\bar{s}}s\rangle ^2\langle \frac{\alpha _s}{\pi }GG\rangle$, $\langle {\bar{s}} g_s \sigma Gs\rangle ^2$, and $g_s^2\langle {\bar{s}}s\rangle ^2$ are the vacuum expectations of the operators of the order ${\mathcal {O}}(\alpha _s)$. The four-quark condensate $g_s^2\langle {\bar{s}}s\rangle ^2$ comes from the terms $\langle {\bar{s}}\gamma _\mu t^a s g_s D_\eta G^a_{\lambda \tau }\rangle$, $\langle {\bar{s}}_jD^{\dagger }_{\mu }D^{\dagger }_{\nu } D^{\dagger }_{\alpha }s_i\rangle$ and $\langle {\bar{s}}_jD_{\mu }D_{\nu }D_{\alpha }s_i\rangle$, rather than comes from the perturbative corrections of $\langle {\bar{s}}s\rangle ^2$ (see Ref. [16] for the technical details). The condensates $\langle g_s^3 GGG\rangle$, $\langle \frac{\alpha _s GG}{\pi }\rangle ^2$, $\langle \frac{\alpha _s GG}{\pi }\rangle \langle {\bar{s}} g_s \sigma Gs\rangle$ have the dimensions 6, 8, 9, respectively, but they are the vacuum expectations of the operators of the order ${\mathcal {O}}( \alpha _s^{3/2})$, ${\mathcal {O}}(\alpha _s^2)$, ${\mathcal {O}}( \alpha _s^{3/2})$, respectively, and they are discarded. We take the truncations $n\le 10$ and $k\le 1$ in a consistent way, the operators of the orders ${\mathcal {O}}( \alpha _s^{k})$ with $k> 1$ are discarded. Furthermore, the numerical values of the condensates $\langle g_s^3 GGG\rangle$, $\langle \frac{\alpha _s GG}{\pi }\rangle ^2$, $\langle \frac{\alpha _s GG}{\pi }\rangle \langle {\bar{s}} g_s \sigma Gs\rangle$ are very small, and they are neglected safely.

Differentiating Eq. (12) with respect to $\frac{1}{T^2}$, then eliminating the pole residues $\lambda _{Y/Z}$, we obtain the QCD sum rules for the masses of the vector tetraquark states,

$$\begin{aligned} M^2_{Y/Z}= \frac{\int _{4m_c^2}^{s_0} \mathrm{d}s\frac{\mathrm{d}}{\mathrm{d} \left( -1/T^2\right) }\rho (s)\exp \left( -\frac{s}{T^2}\right) }{\int _{4m_c^2}^{s_0}\mathrm{d}s\rho (s)\exp \left( -\frac{s}{T^2}\right) }. \end{aligned}$$

(14)

We can obtain the QCD sum rules for the vector tetraquark states $c{\bar{c}}u{\bar{d}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ with the simple replacements

$$\begin{aligned}&m_s\rightarrow 0, \nonumber \\&\langle {\bar{s}}s\rangle \rightarrow \langle \bar{q}q\rangle , \\&\langle {\bar{s}}g_s\sigma G s\rangle \rightarrow \langle \bar{q}g_s\sigma Gq\rangle ,\nonumber \end{aligned}$$

(15)

the QCD sum rules for the $c{\bar{c}}u{\bar{d}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ are degenerate in the isospin limit.

3 Numerical results and discussions

The vacuum condensates are taken to have the standard values $\langle \bar{q}q \rangle =-(0.24\pm 0.01~\hbox {GeV})^3$, $\langle {\bar{s}}s \rangle =(0.8\pm 0.1)\langle \bar{q}q \rangle$, $\langle \bar{q}g_s\sigma G q \rangle =m_0^2\langle \bar{q}q \rangle$, $\langle {\bar{s}}g_s\sigma G s \rangle =m_0^2\langle {\bar{s}}s \rangle$, $m_0^2=(0.8 \pm 0.1)~\hbox {GeV}^2$, $\langle \frac{\alpha _s GG}{\pi }\rangle =(0.33~\hbox {GeV})^4$ at the energy scale $\mu =1~\hbox {GeV}$ [51–55]. The quark condensate and mixed quark condensate evolve with the renormalization group equation, $\langle \bar{q}q \rangle (\mu )=\langle \bar{q}q \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )} \right] ^{\frac{4}{9}}$, $\langle {\bar{s}}s \rangle (\mu )\!=\!\langle {\bar{s}}s \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{4}{9}}$, $\langle \bar{q}g_s \sigma Gq \rangle (\mu )\!=\!\langle \bar{q}g_s \sigma Gq \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{27}}$ and $\langle {\bar{s}}g_s \sigma Gs \rangle (\mu )=\langle {\bar{s}}g_s \sigma Gs \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{27}}$.

In the article, we take the $\overline{MS}$ masses $m_{c}(m_c)=(1.275\pm 0.025)~\hbox {GeV}$ and $m_s(\mu =2~\hbox {GeV})=(0.095\pm 0.005)~\hbox {GeV}$ from the Particle Data Group [18], and we take into account the energy-scale dependence of the $\overline{MS}$ masses from the renormalization group equation,

$$\begin{aligned} m_c(\mu )&= m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}},\nonumber \\ m_s(\mu )&= m_s(2~\mathrm{{GeV}} )\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(2~\mathrm{{GeV}})} \right] ^{\frac{4}{9}},\\ \alpha _s(\mu )\!&= \!\frac{1}{b_0t}\left[ 1\!-\!\frac{b_1}{b_0^2}\frac{\log t}{t} \!+\!\frac{b_1^2(\log ^2{t}\!-\!\log {t}\!-\!1)\!+\!b_0b_2}{b_0^4t^2}\right] \!,\nonumber \end{aligned}$$

(16)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =213\,\hbox {MeV}$, $296~\hbox {MeV}$, and $339\,\hbox {MeV}$ for the flavors $n_f=5$, $4$, and $3$, respectively [18].

In Ref. [16], we observe that the energy scale $\mu =(1.1{-}1.6)~\hbox {GeV}$ is an acceptable energy scale of the QCD spectral densities in the QCD sum rules for the hidden and open charmed mesons, as it can reproduce the experimental values $M_D=1.87~\hbox {GeV}$ and $M_{J/\psi }=3.1~\hbox {GeV}$ with suitable Borel parameters. However, such energy scale and truncation in the operator product expansion cannot reproduce the experimental values of the decay constants $f_{D}$ and $f_{J/\psi }$. In calculation, we observe that the masses of the axial-vector tetraquark states decrease monotonously with increase of the energy scales of the QCD spectral densities, the energy scale $\mu =1.5~\hbox {GeV}$ is the lowest energy scale to reproduce the experimental values of the masses of the $X(3872)$ and $Z_c(3900)$ (or $Z_c(3885)$), and it serves as an acceptable energy scale (not the universal energy scale) for the tetraquark states [16]. On the other hand, it is hard to obtain the true values of the pole residues $\lambda _{X/Y/Z}$ of the tetraquark states, so we focus on the masses to study the tetraquark states, and the predictions of the pole residues may be not as robust. If the $Z_c(4020)$ and $Z_c(4025)$ are the vector tetraquark states, we can choose the threshold parameters $\sqrt{s_0}=(4.3{-}4.8)~\hbox {GeV}$ and energy scales $\mu =(1.5{-}3.0)~\hbox {GeV}$ tentatively, and we search for the ideal parameters, such as the threshold parameters, energy scales and Borel parameters.

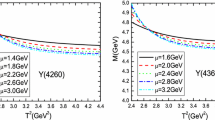
In Fig. 1, the masses of the vector $c{\bar{c}}u{\bar{d}}$ tetraquark states are plotted with variations of the Borel parameters $T^2$, energy scales $\mu$, and continuum threshold parameters $\sqrt{s_0}$. From the figure, we can see that the masses decrease monotonously with increase of the energy scales, the parameters $\sqrt{s_0}\le 4.5\,\hbox {GeV}$ and $\mu \le 1.5~\hbox {GeV}$ can be excluded, as the predicted masses $M_{Z}\gg (\hbox {or }{>})\sqrt{s_0}=4.5~\hbox {GeV}$ for the values of the Borel parameters at a large interval. We have to choose larger threshold parameters or (and) energy scales, the resulting masses are larger than $4.3~\hbox {GeV}$ for the parameters $\sqrt{s_0}\ge 4.5~\hbox {GeV}$ and $\mu =3.0~\hbox {GeV}$. The predictions based on the QCD sum rules disfavor assigning the $Z_c(4020)$ and $Z_c(4025)$ as the diquark–antidiquark type vector tetraquark states. We cannot satisfy the relation $\sqrt{s_0}=M_Z+0.5~\hbox {GeV}$ with reasonable $M_Z$ compared to the experimental data.

Fig. 1

The masses of the vector $c{\bar{c}}u{\bar{d}}$ tetraquark states with variations of the Borel parameters $T^2$, energy scales $\mu$, and threshold parameters $\sqrt{s_0}$, where the horizontal lines denote the threshold parameters $\sqrt{s_0}=4.5~\hbox {GeV}$ and $4.7~\hbox {GeV}$, respectively; the $C=\pm$ denote the charge conjugations

The BESIII collaboration observed the $Z^{\pm }_c(4025)$ and $Z^{\pm }_c(4020)$ in the following processes [1, 2]:

$$\begin{aligned}&e^+ e^- \rightarrow Z^{\pm }_c(4025)\pi ^{\mp }\nonumber \\&\quad \rightarrow (D^*{\bar{D}}^*)^{\pm } (0^{++},1^{+-},2^{++},0^{-+},1^{--},2^{-+},3^{--})\,\pi ^{\mp }, \nonumber \\&e^+ e^- \rightarrow Z^{\pm }_c(4020)\pi ^{\mp }\nonumber \\&\quad \rightarrow (h_c\pi )^{\pm }(1^{--},0^{++},1^{+-},2^{++})\,\pi ^{\mp }, \end{aligned}$$

(17)

where we present the possible quantum numbers $J^{PC}$ of the $(D^*{\bar{D}}^*)^{\pm }$ and $(h_c\pi )^{\pm }$ systems in the brackets. If the $Z^{\pm }_c(4025)$ and $Z^{\pm }_c(4020)$ are the same particle, the quantum numbers are $J^{PC}=1^{--}$, $0^{++}$, $1^{+-}$, $2^{++}$. On the other hand, the $Z^{\pm }_c(4025)\pi ^{\mp }$ and $Z^{\pm }_c(4020)\pi ^{\mp }$ systems have the quantum numbers $J^{PC}=1^{--}$, then the surviving quantum numbers of the $Z^{\pm }_c(4025)$ and $Z^{\pm }_c(4020)$ are $J^{PC}=1^{--}$, $1^{+-}$, and $2^{++}$. The predictions based on the QCD sum rules reduce the possible quantum numbers of the $Z_c(4025)$ and $Z_c(4020)$ to $J^{PC}=1^{+-}$ and $2^{++}$.

The strong decays

$$\begin{aligned} Y(4260)/\gamma ^*(4260)\rightarrow Z_c^{\pm }(4025/4020)(2^{++})\,\pi ^{\mp } \end{aligned}$$

(18)

take place through relative D-wave, and they are kinematically suppressed in the phase-space. The $2^{++}$ assignment is disfavored, but it is not excluded.

In the following, we list the possible strong decays of the $Z^{\pm }_c(4025)$ and $Z^{\pm }_c(3900)$ in the case of the $J^{PC}=1^{+-}$ assignment.

$$\begin{aligned} Z^{\pm }_c(4025)(1^{+-})&\rightarrow h_c(\mathrm{1P})\pi ^{\pm }, \, J/\psi \pi ^{\pm }, \, \eta _c \rho ^{\pm }, \, \eta _c(\pi \pi )_\mathrm{P}^{\pm },\!\!\nonumber \\&\chi _{c1}(\pi \pi )_\mathrm{P}^{\pm }, \,(D{\bar{D}}^*)^{\pm }, \,(D^*{\bar{D}}^*)^{\pm },\!\! \nonumber \\ Z^{\pm }_c(3900)(1^{+-}) \!&\rightarrow \! h_c(\mathrm{1P})\pi ^{\pm }, \, J/\psi \pi ^{\pm }, \, \eta _c \rho ^{\pm }, \, \eta _c(\pi \pi )_\mathrm{P}^{\pm }, \!\!\nonumber \\&\chi _{c1}(\pi \pi )_\mathrm{P}^{\pm }, \end{aligned}$$

(19)

where the $(\pi \pi )_\mathrm{P}$ denotes the P-wave $\pi \pi$ systems have the same quantum numbers of the $\rho$. We take the $Z_c(4025)$ and $Z_c(4020)$ as the same particle in the $J^{PC}=1^{+-}$ assignment, and we will denote them as $Z_c(4025)$. In Ref. [16], we observe that the $Z_c(3900)$ couples to the axial-vector current $J_{1^{+-}}^{\mu }$. Now we perform Fierz rearrangement both in the color and Dirac-spinor spaces and obtain the following result:

$$\begin{aligned} J_{1^{+-}}^{\mu }\!&= \!\frac{\epsilon ^{ijk}\epsilon ^{imn}}{\sqrt{2}}\!\left\{ u^jC\gamma _5 c^k {\bar{d}}^m\gamma ^\mu C {\bar{c}}^n\!-\! u^jC\gamma ^\mu c^k{\bar{d}}^m\gamma _5 C {\bar{c}}^n\! \right\} \!\!,\!\!\! \nonumber \\&= \frac{1}{2\sqrt{2}}\left\{ \,i{\bar{c}}i\gamma _5 c\,{\bar{d}}\gamma ^\mu u-i{\bar{c}} \gamma ^\mu c\,{\bar{d}}i\gamma _5 u\right. \!\!\!\!\nonumber \\&\left. +\,{\bar{c}} u\,{\bar{d}}\gamma ^\mu \gamma _5 c-{\bar{c}} \gamma ^\mu \gamma _5u\,{\bar{d}}c\right. \nonumber \\&\left. -\, i{\bar{c}}\gamma _\nu \gamma _5c\, {\bar{d}}\sigma ^{\mu \nu }u+i{\bar{c}}\sigma ^{\mu \nu }c\, {\bar{d}}\gamma _\nu \gamma _5u \right. \nonumber \\&\left. - \,i {\bar{c}}\sigma ^{\mu \nu }\gamma _5u\,{\bar{d}}\gamma _\nu c+i{\bar{c}}\gamma _\nu u\, {\bar{d}}\sigma ^{\mu \nu }\gamma _5c\right\} , \end{aligned}$$

(20)

the components such as ${\bar{c}}i\gamma _5 c\,{\bar{d}}\gamma ^\mu u$, ${\bar{c}} \gamma ^\mu c\,{\bar{d}}i\gamma _5 u$, etc. couple to the meson–meson pairs, the strong decays

$$\begin{aligned} Z^{\pm }_c(3900)(1^{+-}) \rightarrow h_c(\mathrm{1P})\pi ^{\pm }, \, J/\psi \pi ^{\pm }, \, \eta _c \rho ^{\pm }, \, \eta _c(\pi \pi )_\mathrm{P}^{\pm },\!\!\!\!\nonumber \\ \end{aligned}$$

(21)

are OZI super-allowed, we take the decays to the $(\pi \pi )_\mathrm{P}^{\pm }$ final states as OZI super-allowed according to the decays $\rho \rightarrow \pi \pi$. The BESIII collaboration observed no evidence of the $Z_c(3900)$ in the process $e^+e^- \rightarrow \pi ^+\pi ^- h_c$ at center-of-mass energies from $3.90~\hbox {GeV}$ to $4.42~\hbox {GeV}$ [2]. We expect to observe the $Z_c^{\pm }(3900)$ in the $h_c(\mathrm{1P})\pi ^{\pm }$ final states when a large amount of events are accumulated. The $Z_c(4025)$ and $Z_c(3900)$ have the same quantum numbers and analogous strong decays but different masses and quark configurations.

Now we take a short digression to discuss the interpolating currents consist of four quarks. The diquark–antidiquark type current with special quantum numbers couples to a special tetraquark state, while the current can be re-arranged both in the color and Dirac-spinor spaces, and it is changed to a current as a special superposition of color singlet–singlet type currents. The color singlet–singlet type currents couple to the meson–meson pairs. The diquark–antidiquark type tetraquark state can be taken as a special superposition of a series of meson–meson pairs, and it embodies the net effects. The decays to its components (meson–meson pairs) are OZI super-allowed, the kinematically allowed decays take place easily.

We can search for the $Z^{\pm }_c(4025)(1^{+-})$ in the final states $h_c(\mathrm{1P})\pi ^{\pm }$, $J/\psi \pi ^{\pm }$, $\eta _c \rho ^{\pm }$, $\eta _c(\pi \pi )_\mathrm{P}^{\pm }$, $\chi _{c1}(\pi \pi )_\mathrm{P}^{\pm }$. In Ref. [56], we observe that the $Z_c(4025)$ couples to the axial-vector current $J_{1^{+-}}^{\mu \nu }$. We perform Fierz rearrangement both in the color and Dirac-spinor spaces and obtain the following result:

$$\begin{aligned} J_{1^{+-}}^{\mu \nu }\!&= \!\frac{\epsilon ^{ijk} \epsilon ^{imn}}{\sqrt{2}}\!\left\{ u^jC\gamma ^\mu c^k {\bar{d}}^m\gamma ^\nu C {\bar{c}}^n\!-\!u^jC\gamma ^\nu c^k{\bar{d}}^m\gamma ^\mu C {\bar{c}}^n \!\right\} \!\!,\!\!\! \nonumber \\&= \frac{1}{2\sqrt{2}}\left\{ i{\bar{d}}u\, {\bar{c}}\sigma ^{\mu \nu }c +i{\bar{d}}\sigma ^{\mu \nu }u \,{\bar{c}}c+i{\bar{d}}c\, {\bar{c}}\sigma ^{\mu \nu }u \right. \! \nonumber \\&+\,i{\bar{d}}\sigma ^{\mu \nu }c \,{\bar{c}}u-{\bar{c}}\sigma ^{\mu \nu }\gamma _5c\,{\bar{d}}i\gamma _5u-{\bar{c}}i\gamma _5 c\,{\bar{d}}\sigma ^{\mu \nu }\gamma _5u\nonumber \\&-\,{\bar{c}}\sigma ^{\mu \nu }\gamma _5u\,{\bar{d}}i\gamma _5c -{\bar{d}}i\gamma _5 c\,{\bar{c}}\sigma ^{\mu \nu }\gamma _5u\nonumber \\&+\,i\epsilon ^{\mu \nu \alpha \beta }{\bar{c}}\gamma ^\alpha \gamma _5c\, {\bar{d}}\gamma ^\beta u-i\epsilon ^{\mu \nu \alpha \beta }{\bar{c}} \gamma ^\alpha c\, {\bar{d}}\gamma ^\beta \gamma _5u\nonumber \\&\left. +\,i\epsilon ^{\mu \nu \alpha \beta }{\bar{c}}\gamma ^\alpha \gamma _5u\, {\bar{d}}\gamma ^\beta c-i\epsilon ^{\mu \nu \alpha \beta }{\bar{c}}\gamma ^\alpha u\, {\bar{d}}\gamma ^\beta \gamma _5c\right\} .\nonumber \\ \end{aligned}$$

(22)

The scattering states $J/\psi \pi ^{+}$, $\eta _c \rho ^{+}$, $\eta _c(\pi \pi )_\mathrm{P}^{+}$, $\chi _{c1}(\pi \pi )_\mathrm{P}^{+}$, $(DD^*)^+$ couple to the components ${\bar{c}}\sigma ^{\mu \nu }\gamma _5c\,{\bar{d}}i\gamma _5u$, ${\bar{c}}i\gamma _5 c{\bar{d}}\sigma ^{\mu \nu }\gamma _5u$, ${\bar{c}}i\gamma _5 c\,{\bar{d}}\sigma ^{\mu \nu }\gamma _5u$, $\epsilon ^{\mu \nu \alpha \beta }{\bar{c}}\gamma ^\alpha \gamma _5c\, {\bar{d}}\gamma ^\beta u$, ${\bar{c}}\sigma ^{\mu \nu }\gamma _5u\,{\bar{d}}i\gamma _5c$, respectively. The strong decays

$$\begin{aligned}&Z^{\pm }_c(4025)(1^{+-})\nonumber \\&\quad \rightarrow J/\psi \pi ^{\pm } ,\, \eta _c \rho ^{\pm }, \, \eta _c(\pi \pi )_\mathrm{P}^{\pm }, \chi _{c1}(\pi \pi )_\mathrm{P}^{\pm }, \, (DD^*)^\pm , \end{aligned}$$

(23)

are OZI super-allowed. In this article, we take the decays to the $(\pi \pi )_\mathrm{P}^{\pm }/(\pi \pi \pi )_\mathrm{P}^{0}$ final states as OZI super-allowed according to the decays $\rho \rightarrow \pi \pi /\omega \rightarrow \pi \pi \pi$.

We can also search for the neutral partner $Z^{0}_c(4025)(1^{+-})$ in the following strong and electromagnetic decays:

$$\begin{aligned} Z^{0}_c(4025)(1^{+-})&\rightarrow h_c(\mathrm{1P})\pi ^{0}, \, J/\psi \pi ^{0}, \, J/\psi \eta , \,\eta _c \rho ^{0},\nonumber \\&\eta _c \omega , \, \eta _c(\pi \pi )_\mathrm{P}^{0}, \, \chi _{cj}(\pi \pi )_\mathrm{P}^{0},\nonumber \\&\eta _c(\pi \pi \pi )_\mathrm{P}^{0}, \, \chi _{cj}(\pi \pi \pi )_\mathrm{P}^{0},\nonumber \\&\eta _c \gamma , \, \chi _{cj} \gamma , \, (DD^*)^0, \end{aligned}$$

(24)

where the $(\pi \pi \pi )_\mathrm{P}$ denotes the P-wave $\pi \pi \pi$ systems with the same quantum numbers as the $\omega$.

On the other hand, if the $Z_c(4025)$ and $Z_c(4020)$ are different particles, we can search for the $Z^{\pm }_c(4025/4020)(0^{++})$ and $Z^{\pm }_c(4025/4020)(2^{++})$ in the following strong decays:

$$\begin{aligned} Z^{\pm }_c(4025/4020)(0^{++})&\rightarrow \eta _c\pi ^{\pm }, \, J/\psi \rho ^{\pm }, \, J/\psi (\pi \pi )_\mathrm{P}^{\pm },\,\nonumber \\&\chi _{c1}\pi ^{\pm },\, D{\bar{D}}\, ,\, D^*{\bar{D}}^*, \nonumber \\ Z^{\pm }_c(4025/4020)(2^{++})&\rightarrow \eta _c\pi ^{\pm }, \, J/\psi \rho ^{\pm }, \, J/\psi (\pi \pi )_\mathrm{P}^{\pm },\nonumber \\&\chi _{c1}\pi ^{\pm },\, D{\bar{D}},\, D^*{\bar{D}}^*. \end{aligned}$$

(25)

The strong decays

$$\begin{aligned} Y(4260)/\gamma ^*(4260)&\rightarrow Z_c^{\pm }(4025/4020)(0^{++})\,\pi ^{\mp } \end{aligned}$$

(26)

cannot take place. The $0^{++}$ assignment is excluded.

Now, we explore the possibility of assigning the $Y(4360)$ and $Y(4660)$ as the diquark–antidiquark type vector tetraquark states. We utilize the often used energy scale $\mu \!=\!\sqrt{m_D^2\!-\!m_c^2}\approx 1~\hbox {GeV}$ in the QCD sum rules for the $D$ mesons, and we suggest a formula to estimate the energy scales of the QCD spectral densities in the QCD sum rules for the hidden charmed tetraquark states,

$$\begin{aligned} \mu&= \sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_c)^2}, \end{aligned}$$

(27)

where the effective mass of the $c$-quark ${\mathbb {M}}_c=1.8~\hbox {GeV}$. The heavy tetraquark system could be described by a double-well potential with two light quarks $q^{\prime }\bar{q}$ lying in the two wells, respectively. In the heavy quark limit, the $c$ (and $b$) quark can be taken as a static well potential, which binds the light quark $q$ to form a diquark in the color antitriplet channel. The heavy tetraquark states are characterized by the effective heavy quark masses ${\mathbb {M}}_Q$ (or constituent quark masses) and the virtuality $V=\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ (or bound energy which is not as robust). It is natural to take the energy scale $\mu =V$. The energy scales are estimated to be $\mu =1.5~\hbox {GeV}$ for the $X(3872)$ and $Z_c(3900)$ [16], $\mu =3.0~\hbox {GeV}$ for the $Y(4660)$, and $\mu =2.5~\hbox {GeV}$ for the $Y(4360)$. The formula also works well for the scalar hidden charmed (and double charmed) tetraquark states, and we can use the formula to improve the predictions [57–60]. Furthermore, we study the possible applications in the QCD sum rules for the molecular states [61–63]. From Fig. 1, we can see that the energy scales $\mu =2.5~\hbox {GeV}$ and $3.0\,\hbox {GeV}$ lead to slightly different masses for the threshold parameters $\sqrt{s_0}=4.7\,\hbox {GeV}$ or larger than $4.7\,\hbox {GeV}$. In this article, we set the energy scale $\mu =3.0\,\hbox {GeV}$ to study the vector tetraquark states.

In Fig. 2, the contributions of the pole terms are plotted with variations of the threshold parameters $\sqrt{s_0}$ and Borel parameters $T^2$ at the energy scale $\mu =3.0\,\hbox {GeV}$. From the figure, we can see that the values $\sqrt{s_0}\le 4.8 \, \hbox {GeV}$ are too small to satisfy the pole dominance condition and result in reasonable Borel windows. In Fig. 3, the contributions of different terms in the operator product expansion are plotted with variations of the Borel parameters $T^2$ for the threshold parameters $\sqrt{s_0}=5.1\,\hbox {GeV}$ and $5.0\,\hbox {GeV}$ in the channels $c{\bar{c}}s{\bar{s}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ respectively at the energy scale $\mu =3.0\,\hbox {GeV}$. From the figure, we can see that the contributions of the vacuum condensates of dimension-0, 5, 6 change quickly with variations of the Borel parameters at the region $T^2< 3.2\,\hbox {GeV}^2$, which does not warrant platforms for the masses. In this article, the value $T^2\ge 3.2\,\hbox {GeV}^2$ is chosen tentatively, in that case the convergent behavior in the operator product expansion is very good, as the perturbative terms make the main contributions. The Borel parameters, continuum threshold parameters and the pole contributions are shown explicitly in Table 1. The two criteria (pole dominance and convergence of the operator product expansion) of the QCD sum rules are fully satisfied, so we expect to make reasonable predictions. In the QCD sum rules for the light tetraquark states, the two criteria are difficult to satisfy [64].

Fig. 2

The pole contributions with variations of the Borel parameters $T^2$ and threshold parameters $\sqrt{s_0}$, where the $A$, $B$, $C$, $D$, $E$, and $F$ denote the threshold parameters $\sqrt{s_0}=4.8$, 4.9, 5.0, 5.1, 5.2, and $5.3\,\hbox {GeV}$, respectively; the (I) and (II) denote the $c{\bar{c}}s{\bar{s}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ tetraquark states, respectively; the $C=\pm$ denote the charge conjugations; the horizontal lines denote the pole contributions of $50~\%$

Fig. 3

The contributions of different terms in the operator product expansion with variations of the Borel parameters $T^2$, where the 0, 3, 4, 5, 6 ,7, 8, and 10 denotes the dimensions of the vacuum condensates; the (I) and (II) denote the $c{\bar{c}}s{\bar{s}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ tetraquark states, respectively; the $C=\pm$ denote the charge conjugations

Table 1 The Borel parameters, continuum threshold parameters, pole contributions, masses, and pole residues of the vector tetraquark states

Taking into account all uncertainties of the input parameters, finally we obtain the values of the masses and pole residues of the vector tetraquark states, which are shown explicitly in Figs. 4 and 5 and Table 1. The prediction $M_{c{\bar{c}}s{\bar{s}} (1^{--})}=4.70^{+0.14}_{-0.10}\,\hbox {GeV}$ is consistent with the experimental data $M_{Y(4660)}=(4664\pm 11\pm 5)\,\hbox {MeV}$ within uncertainties [18], and the prediction $M_{c{\bar{c}}u{\bar{d}} (1^{--})}$ or $M_{c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2} (1^{--})}$ $=4.66^{+0.17}_{-0.10}\,\hbox {GeV}$ is much larger than the upper bound of the experimental data $M_{Y(4360)}=(4361\pm 9\pm 9)~\hbox {MeV}$ [18]. The present predictions favor assigning the $Y(4660)$ as the $J^{PC}=1^{--}$ diquark–antidiquark type tetraquark state, the masses $M_{c{\bar{c}}s{\bar{s}}}$ and $M_{c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2} }$ are both consistent with the experimental data $M_{Y(4660)}$ within uncertainties. By precisely measuring the $\pi ^+\pi ^-$ mass spectrum in the final state $\pi ^+\pi ^-\psi ^{\prime }$, we can distinguish the $f_0(600)$ and $f_0(980)$; therefore we can disentangle the quark constituents of the $Y(4660)$. On the other hand, we can also take the $Y(4360)$ as the $c{\bar{c}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ mixed state, as the $c{\bar{c}}$ component can reduce the mass so as to reproduce the experimental value at about $4.4\,\hbox {GeV}$.

Fig. 4

The masses with variations of the Borel parameters $T^2$, where the horizontal lines denote the experimental value of the mass of the $Y(4660)$; the (I) and (II) denote the $c{\bar{c}}s{\bar{s}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ tetraquark states, respectively; the $C=\pm$ denote the charge conjugations

Fig. 5

The pole residues with variations of the Borel parameters $T^2$, where the (I) and (II) denote the $c{\bar{c}}s{\bar{s}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ tetraquark states, respectively; the $C=\pm$ denote the charge conjugations

From Table 1, we can also see that there is an energy gap of about $(70$–$90)\,\hbox {MeV}$ between the central values of the $C=+$ and $C=-$ vector tetraquark states, which can be confronted with the experimental data in the future. In Ref. [16], we observe that there is a small energy gap, smaller than $40\,\hbox {MeV}$ between the central values of the $C=+$ and $C=-$ axial-vector tetraquark states, which is consistent with the value $10\,\hbox {MeV}$ from the constituent diquark model [65, 66].

In this article, we construct the $C-C\gamma _\mu$ type diquark–antidiquark currents to interpolate the vector tetraquark states. The scalar and axial-vector heavy-light diquark states have almost degenerate masses from the QCD sum rules [49, 50], the $C\gamma _\mu -C$ and $C\gamma _\mu \gamma _5-C\gamma _5$ type tetraquark states have degenerate (or slightly different) masses [45, 46]. On the other hand, we can also construct the $C\gamma _\alpha -\partial _\mu -C\gamma ^\alpha$ and $C\gamma _5-\partial _\mu -C\gamma _5$ type diquark–antidiquark currents to interpolate the vector tetraquark states, the $C\gamma _\alpha -C\gamma ^\alpha$ and $C\gamma _5-C\gamma _5$ type diquark–antidiquark currents couple to the scalar tetraquark states with the masses about $3.85\,\hbox {GeV}$ [56]. If the contribution of an additional P-wave to the mass is about $0.5\,\hbox {GeV}$, the masses of the vector tetraquark states couple to the $C\gamma _\alpha -\partial _\mu -C\gamma ^\alpha$ and $C\gamma _5-\partial _\mu -C\gamma _5$ type interpolating currents are about $4.35\,\hbox {GeV}$, which happens to be the value of the mass $M_{Y(4360)}$. In Refs. [38, 67] Zhang and Huang take the $C\gamma _5-\partial _\mu -C\gamma _5$ type diquark–antidiquark currents to study the $Y(4360)$ and $Y(4660)$ with the symbolic quark structures $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ and $c{\bar{c}}s{\bar{s}}$, respectively, and they obtain the values $M_{Y(4360)}=(4.32\pm 0.20)\,\hbox {GeV}$ and $M_{Y(4660)}=(4.69\pm 0.36)\,\hbox {GeV}$, which are consistent with the rough estimation $M_{Y(4360)}=4.35\,\hbox {GeV}$. The present predictions $M_{c{\bar{c}}u{\bar{d}}(1^{-+})}=4.57^{+0.12}_{-0.08}\,\hbox {GeV}$ and $M_{c{\bar{c}}u{\bar{d}} (1^{--})}=4.66^{+0.17}_{-0.10}\,\hbox {GeV}$ disfavor assigning the $Z_c(4025)$ and $Z_c(4020)$ as the $J^{PC}=1^{--}$ tetraquark states, and they favor assigning the $Y(4360)$ as the $C\gamma _\alpha -\partial _\mu -C\gamma ^\alpha$ and $C\gamma _5-\partial _\mu -C\gamma _5$ type $J^{PC}=1^{--}$ tetraquark states.

Now we perform Fierz rearrangement to the vector currents $J_{1^{--},{\bar{d}}u}^{\mu }$, $J_{1^{-+},{\bar{d}}u}^{\mu }$, $J_{1^{--},{\bar{s}}s}^{\mu }$, $J_{1^{-+},{\bar{s}}s}^{\mu }$ both in the color and Dirac-spinor spaces, and we obtain the following results:

$$\begin{aligned} J_{1^{--},{\bar{d}}u}^{\mu }&= \frac{\epsilon ^{ijk}\epsilon ^{imn}}{\sqrt{2}}\left\{ u^jC c^k {\bar{d}}^m\gamma ^\mu C {\bar{c}}^n-u^jC\gamma ^\mu c^k{\bar{d}}^m C {\bar{c}}^n \right\} , \nonumber \\&= \frac{1}{2\sqrt{2}}\left\{ \,{\bar{c}} \gamma ^\mu c\,{\bar{d}} u-{\bar{c}} c\,{\bar{d}}\gamma ^\mu u+i{\bar{c}}\gamma ^\mu \gamma _5 u\,{\bar{d}}i\gamma _5 c \right. \nonumber \\&\left. -i{\bar{c}} i\gamma _5 u\,{\bar{d}}\gamma ^\mu \gamma _5c- i{\bar{c}}\gamma _\nu \gamma _5c\, {\bar{d}}\sigma ^{\mu \nu }\gamma _5u\right. \nonumber \\&\left. +\,i{\bar{c}}\sigma ^{\mu \nu }\gamma _5c\, {\bar{d}}\gamma _\nu \gamma _5u \!-\! i{\bar{d}}\gamma _\nu c\, {\bar{c}}\sigma ^{\mu \nu }u\!+\!i {\bar{d}}\sigma ^{\mu \nu }c \,{\bar{c}}\gamma _\nu u \,\right\} \!,\nonumber \\ \end{aligned}$$

(28)

$$\begin{aligned} J_{1^{-+},{\bar{d}}u}^{\mu }&= \frac{\epsilon ^{ijk}\epsilon ^{imn}}{\sqrt{2}}\left\{ u^jC c^k {\bar{d}}^m\gamma ^\mu C {\bar{c}}^n+u^jC\gamma ^\mu c^k{\bar{d}}^m C {\bar{c}}^n \right\} , \nonumber \\&= \frac{1}{2\sqrt{2}}\left\{ \,i{\bar{c}}i\gamma _5 c\,{\bar{d}}\gamma ^\mu \gamma _5 u -i{\bar{c}} \gamma ^\mu \gamma _5 c\,{\bar{d}}i\gamma _5 u\right. \nonumber \\&\left. \!\!-\,{\bar{c}}\gamma ^\mu u\,{\bar{d}} c+{\bar{c}} u\,{\bar{d}}\gamma ^\mu c\!+\!i{\bar{c}}\sigma ^{\mu \nu } c\, {\bar{d}}\gamma _\nu u\!-\! i{\bar{c}}\gamma _\nu c\, {\bar{d}}\sigma ^{\mu \nu } u\right. \nonumber \\&\left. - i{\bar{d}}\gamma _\nu \gamma _5 c\, {\bar{c}}\sigma ^{\mu \nu }\gamma _5u+i {\bar{d}}\sigma ^{\mu \nu }\gamma _5 c \,{\bar{c}}\gamma _\nu \gamma _5 u \,\right\} ,\end{aligned}$$

(29)

$$\begin{aligned} J_{1^{--},{\bar{s}}s}^{\mu }&= \frac{\epsilon ^{ijk}\epsilon ^{imn}}{\sqrt{2}}\left\{ s^jC c^k {\bar{s}}^m\gamma ^\mu C {\bar{c}}^n-s^jC\gamma ^\mu c^k{\bar{s}}^m C {\bar{c}}^n \right\} , \nonumber \\&= \frac{1}{2\sqrt{2}}\left\{ \,{\bar{c}} \gamma ^\mu c\,{\bar{s}} s-{\bar{c}} c\,{\bar{s}}\gamma ^\mu s+i{\bar{c}}\gamma ^\mu \gamma _5 s\,{\bar{s}}i\gamma _5 c \right. \nonumber \\&\left. -i{\bar{c}} i\gamma _5 s\,{\bar{s}}\gamma ^\mu \gamma _5c- i{\bar{c}}\gamma _\nu \gamma _5c\, {\bar{s}}\sigma ^{\mu \nu }\gamma _5s\right. \nonumber \\&\left. +\,i{\bar{c}}\sigma ^{\mu \nu }\gamma _5c\, {\bar{s}}\gamma _\nu \gamma _5s - i{\bar{s}}\gamma _\nu c\, {\bar{c}}\sigma ^{\mu \nu }s+i {\bar{s}}\sigma ^{\mu \nu }c \,{\bar{c}}\gamma _\nu s \right\} ,\nonumber \\ \end{aligned}$$

(30)

$$\begin{aligned} J_{1^{-+},{\bar{s}}s}^{\mu }&= \frac{\epsilon ^{ijk}\epsilon ^{imn}}{\sqrt{2}}\left\{ s^jC c^k {\bar{s}}^m\gamma ^\mu C {\bar{c}}^n+s^jC\gamma ^\mu c^k{\bar{s}}^m C {\bar{c}}^n \right\} , \nonumber \\&= \frac{1}{2\sqrt{2}}\left\{ \,i{\bar{c}}i\gamma _5 c\,{\bar{s}}\gamma ^\mu \gamma _5 s-i{\bar{c}} \gamma ^\mu \gamma _5 c\,{\bar{s}}i\gamma _5 s-{\bar{c}}\gamma ^\mu s\,{\bar{s}} c\right. \nonumber \\&\left. +\,{\bar{c}} s\,{\bar{s}}\gamma ^\mu c\!+\!i{\bar{c}}\sigma ^{\mu \nu } c\, {\bar{s}}\gamma _\nu s - i{\bar{c}}\gamma _\nu c\, {\bar{s}}\sigma ^{\mu \nu } s\right. \nonumber \\&\left. - i{\bar{s}}\gamma _\nu \gamma _5 c\, {\bar{c}}\sigma ^{\mu \nu }\gamma _5s+i {\bar{s}}\sigma ^{\mu \nu }\gamma _5 c \,{\bar{c}}\gamma _\nu \gamma _5 s \right\} , \end{aligned}$$

(31)

where the subscripts $1^{-\pm }$ and ${\bar{d}}u$ (${\bar{s}}s$) are added to show the $J^{PC}$ and light quark constituents, respectively. Then we obtain the OZI super-allowed decays by taking into account the couplings to the meson–meson pairs,

$$\begin{aligned} Y(cu{\bar{c}}{\bar{d}})(1^{--})&\rightarrow J/\psi a_0(980), \,\chi _{c0} \rho , \, \chi _{c1} \rho , \,J/\psi \pi , \nonumber \\&J/\psi a_1(1260), \, DD_{1}(2420),\, D^*D_{1}(2420),\nonumber \\ Y(cu{\bar{c}}{\bar{d}})(1^{-+})&\rightarrow \eta _c \pi , \,\eta _c a_1(1260), \,\chi _{c1} \pi , \,h_c \rho , \,\nonumber \\&J/\psi b_1(1235),D^*D_{0}(2400),\, D^*D_{1}(2420),\nonumber \\\end{aligned}$$

(32)

$$\begin{aligned} Y(4660)(1^{--})&\rightarrow J/\psi f_0(980), \,J/\psi f_0(600), \,J/\psi (\pi \pi )_S,\nonumber \\&\psi ^{\prime } f_0(980), \,\psi ^{\prime } f_0(600), \,\psi ^{\prime } (\pi \pi )_S,\nonumber \\&\chi _{c0} \phi (1020), \, \chi _{c0} (KK)_{S}, \,\chi _{c1} \phi (1020), \nonumber \\&\chi _{c1} (KK)_{S}, \,J/\psi h_1(1380)/f_1(1510),\nonumber \\&J/\psi \eta , \, D_sD_{s1}(2460)/D_{s1}(2536),\nonumber \\&D_s^*D_{s1}(2460)/D_{s1}(2536),\nonumber \\ Y(cs{\bar{c}}{\bar{s}})(1^{-+})&\rightarrow \eta _c h_1(1380)/f_1(1510), \,\eta _c \eta , \,\chi _{c1} \eta , \nonumber \\&h_c \phi (1020), \,J/\psi h_1(1380)/f_1(1510),\nonumber \\&D_s^*D_{s0}(2317),\, D_s^*D_{s1}(2460)/D_{s1}(2536),\nonumber \\ \end{aligned}$$

(33)

where the $(\pi \pi )_S$ and $(KK)_S$ denote the S-wave $\pi \pi$ and $KK$ pairs, respectively.

The mass spectrum of the light scalar mesons is well understood in terms of diquark–antidiquark bound states, while the strong decays into two pseudoscalar mesons based on the quark rearrangement mechanism cannot lead to a satisfactory description of the experimental data. In Ref. [68, ’t Hooft et al. introduce the instanton-induced effective six-fermion Lagrangian, and they illustrate that such a Lagrangian leads to the tetraquark–$\bar{q}q$ mixing, therefore provides an additional amplitude which brings the strong decays of the light scalar mesons in good agreement with the experimental data. In the present work, we discuss the OZI super-allowed strong decays of the tetraquark states based on the quark rearrangement mechanism or fall-apart mechanism, as there is no instanton-induced effective six-fermion Lagrangian in the hidden-charm systems to describe the tetraquark–$\bar{q}q$ mixing beyond the usual QCD interactions. The present predictions can be confronted with the experimental data of BESIII, LHCb, and Belle-II in the future.

4 Conclusion

In this article, we study the $Z_c(4020)$, $Z_c(4025)$, $Y(4360)$, and $Y(4660)$ as the diquark–antidiquark type vector tetraquark states in detail with the QCD sum rules. We distinguish the charge conjugations of the interpolating currents, calculate the contributions of the vacuum condensates up to dimension-10 and discard the perturbative corrections in the operator product expansion, and we take into account the higher dimensional vacuum condensates consistently, as they play an important role in determining the Borel windows. Then we suggest the formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_c)^2}$ to estimate the energy scales of the QCD spectral densities of the hidden charmed tetraquark states, and we study the masses and pole residues of the $J^{PC}=1^{-\pm }$ tetraquark states in detail. The formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_c)^2}$ works well. The masses of the $c{\bar{c}}u{\bar{d}}$ ($1^{-\pm }$) tetraquark states disfavor assigning the $Z_c(4020)$, $Z_c(4025)$, and $Y(4360)$ as the $C-C\gamma _\mu$ type vector tetraquark states, and they favor assigning the $Z_c(4020)$, $Z_c(4025)$ as the diquark–antidiquark type $1^{+-}$ tetraquark states. While the masses of the $c{\bar{c}}s{\bar{s}}$ and $c{\bar{c}}(u{\bar{u}}+d{\bar{d}})/\sqrt{2}$ tetraquark states favor assigning the $Y(4660)$ as the $C-C\gamma _\mu$ type $1^{--}$ tetraquark state, more experimental data are still needed to distinguish the quark constituents. There are no candidates for the $C=+$ vector tetraquark states, the predictions can be confronted with the experimental data in the futures at the BESIII, LHCb, and Belle-II. The pole residues can be taken as basic input parameters to study relevant processes of the vector tetraquark states with the three-point QCD sum rules.

Appendix

We have the spectral densities $\rho _i(s)$ with $i=0$, 3, 4, 5, 6, 7, 8, 10 at the level of the quark–gluon degrees of freedom,

$$\begin{aligned}&\rho _{0}(s)=\frac{1}{3072\pi ^6}\int \mathrm{d}y\mathrm{d}z \, yz(1-y-z)^3\left( s-\overline{m}_c^2\right) ^2\nonumber \\&\qquad \qquad \quad \times \left( 35s^2-26s\overline{m}_c^2+3\overline{m}_c^2 \right) \nonumber \\&\qquad \qquad \quad -t\frac{m_c^2}{1536\pi ^6} \int \mathrm{d}y\mathrm{d}z \, (1-y-z)^3\left( s-\overline{m}_c^2\right) ^3 \nonumber \\&\qquad \qquad \quad +(1+t)\frac{m_s m_c}{512\pi ^6} \int \mathrm{d}y\mathrm{d}z \, (y+z) (1-y-z)^2\nonumber \\&\qquad \qquad \quad \times \left( s-\overline{m}_c^2\right) ^3,\end{aligned}$$

(34)

$$\begin{aligned}&\rho _{3}(s)=-(1+t)\frac{m_c\langle {\bar{s}}s\rangle }{64\pi ^4}\int \mathrm{d}y\mathrm{d}z \, (y+z)(1-y-z) \left( s-\overline{m}_c^2\right) ^2 \nonumber \\&\qquad \qquad +\frac{m_s\langle {\bar{s}}s\rangle }{32\pi ^4}\int \mathrm{d}y\mathrm{d}z \, yz\,(1-y-z)\left( 15s^2-16s\overline{m}_c^2+3 \overline{m}_c^4\right) \nonumber \\&\qquad \qquad +\frac{m_s m_c^2\langle {\bar{s}}s\rangle }{8\pi ^4}\int \mathrm{d}y\mathrm{d}z \left( s-\overline{m}_c^2\right) \nonumber \\&\qquad \qquad +t\frac{m_s \langle {\bar{s}}s\rangle }{32\pi ^4}\int \mathrm{d}y\mathrm{d}z \, yz \left( s-\overline{m}_c^2\right) ^2\nonumber \\&\qquad \qquad -t\frac{m_s m_c^2\langle {\bar{s}}s\rangle }{32\pi ^4} \int \mathrm{d}y\mathrm{d}z \,(1-y-z)\left( s-\overline{m}_c^2\right) , \end{aligned}$$

(35)

$$\begin{aligned}&\rho _{4}(s)=-\frac{m_c^2}{2304\pi ^4} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int \mathrm{d}y\mathrm{d}z \left( \frac{z}{y^2}+\frac{y}{z^2}\right) \nonumber \\&\qquad \qquad \quad \times (1-y-z)^3 \left\{ 8s-3\overline{m}_c^2+\overline{m}_c^4\delta \left( s-\overline{m}_c^2\right) \right\} \nonumber \\&\qquad \qquad \quad \!+\,t\frac{m_c^4}{4608\pi ^4}\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int \mathrm{d}y\mathrm{d}z \left( \frac{1}{y^3}\!+\!\frac{1}{z^3} \right) (1-y-z)^3 \nonumber \\&\qquad \qquad \quad \!-t\frac{m_c^2}{1536\pi ^4}\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int \mathrm{d}y\mathrm{d}z \left( \frac{1}{y^2}\!+\!\frac{1}{z^2} \right) \!\!\!\!\nonumber \\&\qquad \qquad \quad \times (1\!-\!y\!-\!z)^3 \left( s\!-\!\overline{m}_c^2\right) \nonumber \\&\qquad \qquad \quad +\frac{1}{1536\pi ^4}\left\langle \frac{\alpha _s GG}{\pi } \right\rangle \int \mathrm{d}y\mathrm{d}z \, (y\!+\!z) (1\!-\!y\!-\!z)^2 \nonumber \\&\qquad \qquad \quad \times s\left( 5s-4\overline{m}_c^2\right) \!\!\! \nonumber \\&\qquad \qquad \quad -t\frac{m_c^2}{1024\pi ^4}\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int \mathrm{d}y\mathrm{d}z \left( \frac{1}{y}\!+\!\frac{1}{z}\right) (1\!-\!y\!-\!z)^2\nonumber \\&\qquad \qquad \quad \times \left( s\!-\!\overline{m}_c^2\right) \nonumber \\&\qquad \qquad \quad +t\frac{m_c^2}{2304\pi ^4}\left\langle \frac{\alpha _s GG}{\pi } \right\rangle \nonumber \\&\qquad \qquad \quad \times \int \mathrm{d}y\mathrm{d}z \left\{ \frac{(1\!-\!y\!-\!z)^2}{yz}\!-\!\frac{(1\!-\!y\!-\!z)^3}{6yz}\right\} \left( s\!-\!\overline{m}_c^2 \right) ,\nonumber \\ \end{aligned}$$

(36)

$$\begin{aligned}&\rho _{5}(s)=(1+t)\frac{m_c\langle {\bar{s}}g_s\sigma Gs\rangle }{128\pi ^4}\int \mathrm{d}y\mathrm{d}z \, (y+z) \left( s-\overline{m}_c^2 \right) \nonumber \\&\qquad \qquad +\frac{m_c\langle {\bar{s}}g_s\sigma Gs\rangle }{128\pi ^4}\int \mathrm{d}y\mathrm{d}z \left( \frac{y}{z}+\frac{z}{y} \right) (1-y-z) \left( 2s-\overline{m}_c^2 \right) \nonumber \\&\qquad \qquad -t\frac{m_c\langle {\bar{s}}g_s\sigma Gs\rangle }{128\pi ^4}\int \mathrm{d}y\mathrm{d}z \, (1-y-z) \left( s-\overline{m}_c^2 \right) \nonumber \\&\qquad \qquad -t\frac{m_c\langle {\bar{s}}g_s\sigma Gs\rangle }{1152\pi ^4}\!\int \! \mathrm{d}y\mathrm{d}z \left( \frac{y}{z}+\frac{z}{y} \right) (1\!-\!y\!-\!z) \left( 5s\!-\!3\overline{m}_c^2 \right) \nonumber \\&\qquad \qquad -\frac{m_s\langle {\bar{s}}g_s\sigma Gs\rangle }{96\pi ^4}\int \mathrm{d}y\mathrm{d}z \, yz\left\{ 8s-3\overline{m}_c^2 +\overline{m}_c^4 \delta \left( s-\overline{m}_c^2 \right) \right\} \nonumber \\&\qquad \qquad -\frac{m_s m_c^2\langle {\bar{s}}g_s\sigma Gs\rangle }{32\pi ^4}\int _{y_i}^{y_f} \mathrm{d}y +t\frac{m_s m_c^2\langle {\bar{s}}g_s\sigma Gs\rangle }{192\pi ^4}\int \mathrm{d}y\mathrm{d}z \nonumber \\&\qquad \qquad -t\frac{m_s \langle {\bar{s}}g_s\sigma Gs\rangle }{64\pi ^4}\int _{y_i}^{y_f} \mathrm{d}y \, y(1-y) \left( s-\widetilde{m}_c^2 \right) \nonumber \\&\qquad \qquad +\frac{m_s m_c^2\langle {\bar{s}}g_s\sigma Gs\rangle }{128\pi ^4}\int \mathrm{d}y\mathrm{d}z \left( \frac{1}{y}+\frac{1}{z}\right) \nonumber \\&\qquad \qquad +t\frac{m_s\langle {\bar{s}}g_s\sigma Gs\rangle }{256\pi ^4}\int \mathrm{d}y\mathrm{d}z \, (y+z)\left( s-\overline{m}_c^2 \right) , \end{aligned}$$

(37)

$$\begin{aligned}&\rho _{6}(s)=-\frac{m_c^2\langle {\bar{s}}s\rangle ^2}{12\pi ^2}\int _{y_i}^{y_f}\mathrm{d}y -t\frac{ \langle {\bar{s}}s\rangle ^2}{24\pi ^2}\int _{y_i}^{y_f}\mathrm{d}y\,y(1-y) \left( s-\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad +\frac{g_s^2\langle {\bar{s}}s\rangle ^2}{648\pi ^4}\int \mathrm{d}y\mathrm{d}z\, yz \left\{ 8s-3\overline{m}_c^2 +\overline{m}_c^4\delta \left( s-\overline{m}_c^2 \right) \right\} \nonumber \\&\qquad \qquad -t\frac{g_s^2m_c^2\langle {\bar{s}}s\rangle ^2}{1296\pi ^4}\int \mathrm{d}y\mathrm{d}z -\frac{g_s^2\langle {\bar{s}}s\rangle ^2}{2592\pi ^4}\int \mathrm{d}y\mathrm{d}z\,(1-y-z)\nonumber \\&\qquad \qquad \times \left\{ \left( \frac{z}{y}+\frac{y}{z} \right) \times 3\left( 7s-4\overline{m}_c^2 \right) +\left( \frac{z}{y^2}+\frac{y}{z^2} \right) \right. \nonumber \\&\qquad \qquad \times \left. m_c^2\left[ 7+5\overline{m}_c^2\delta \left( s-\overline{m}_c^2 \right) \right] -(y+z)\left( 4s-3\overline{m}_c^2 \right) \right. \nonumber \\&\qquad \qquad \left. -\left( \frac{1}{y}+\frac{1}{z} \right) t\frac{3m_c^2}{2}\right\} -\frac{g_s^2\langle {\bar{s}}s\rangle ^2}{3888\pi ^4}\int \mathrm{d}y\mathrm{d}z\left\{ \left( \frac{z}{y}+\frac{y}{z} \right) \right. \nonumber \\&\qquad \qquad \left. \times 3\left( 2s-\overline{m}_c^2 \right) \right. \left. +\left( \frac{z}{y^2}+\frac{y}{z^2} \right) m_c^2\left[ 1+\overline{m}_c^2\delta \left( s-\overline{m}_c^2\right) \right] \right. \nonumber \\&\qquad \qquad \left. +(y\!+\!z)2\left[ 8s\!-\!3\overline{m}_c^2 +\overline{m}_c^4\delta \left( s-\overline{m}_c^2\right) \right] \right. \left. \!-\!\left( \!\frac{1}{y}\!+\!\frac{1}{z}\!\right) t\frac{3m_c^2}{2}\!\right\} \!,\nonumber \\ \end{aligned}$$

(38)

$$\begin{aligned}&\rho _7(s)=(1+t)\frac{m_c^3\langle {\bar{s}}s\rangle }{576\pi ^2} \left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \mathrm{d}y\mathrm{d}z\nonumber \\&\quad \qquad \qquad \times \left( \frac{y}{z^3}+\frac{z}{y^3}+ \frac{1}{y^2}+\frac{1}{z^2}\right) (1-y-z) \delta \left( s-\overline{m}_c^2\right) \nonumber \\&\quad \qquad \qquad -(1+t)\frac{m_c\langle {\bar{s}}s\rangle }{192\pi ^2} \left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \mathrm{d}y\mathrm{d}z \nonumber \\&\quad \qquad \qquad \times \left( \frac{y}{z^2}+\frac{z}{y^2}\right) (1-y-z) \nonumber \\&\quad \qquad \qquad -\frac{m_c\langle {\bar{s}}s\rangle }{64\pi ^2} \left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \mathrm{d}y\mathrm{d}z\left\{ 1+\frac{4\overline{m}_c^2}{9} \delta \left( s-\overline{m}_c^2\right) \right\} \nonumber \\&\quad \qquad \qquad -t\frac{m_c\langle {\bar{s}}s\rangle }{384\pi ^2} \left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \mathrm{d}y\mathrm{d}z\left( \frac{z}{y}+\frac{y}{z}\right) \nonumber \\&\quad \qquad \qquad -(1+t)\frac{m_c\langle {\bar{s}}s\rangle }{1152\pi ^2} \left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \mathrm{d}y\mathrm{d}z, \end{aligned}$$

(39)

$$\begin{aligned}&\rho _8(s)=\frac{m_c^2\langle {\bar{s}}s\rangle \langle {\bar{s}}g_s\sigma Gs\rangle }{24\pi ^2}\int _0^1 \mathrm{d}y \left( 1+\frac{\widetilde{m}_c^2}{T^2} \right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad \quad +t\frac{ \langle {\bar{s}}s\rangle \langle {\bar{s}}g_s\sigma Gs\rangle }{16\pi ^2}\int _{y_i}^{y_f} \mathrm{d}y\, y(1-y)\left\{ 1+\frac{\widetilde{m}_c^2}{3} \delta \left( s-\widetilde{m}_c^2\right) \right\} \nonumber \\&\qquad \qquad \quad -\frac{m_c^2\langle {\bar{s}}s\rangle \langle {\bar{s}}g_s\sigma Gs\rangle }{96\pi ^2}\int _0^1 \mathrm{d}y \left( \frac{1}{y}+\frac{1}{1-y} \right) \nonumber \\&\qquad \qquad \quad \times \delta \left( s-\widetilde{m}_c^2\right) -t\frac{\langle {\bar{s}}s\rangle \langle {\bar{s}}g_s\sigma Gs\rangle }{192\pi ^2}\int _{y_i}^{y_f}\mathrm{d}y, \end{aligned}$$

(40)

$$\begin{aligned}&\rho _{10}(s)=-\frac{m_c^2\langle {\bar{s}}g_s\sigma Gs\rangle ^2}{192\pi ^2T^6}\int _0^1 \mathrm{d}y \, \widetilde{m}_c^4 \, \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad \quad -t\frac{\langle {\bar{s}}g_s\sigma Gs\rangle ^2}{64\pi ^2}\int _0^1 \mathrm{d}y \, y(1-y)\left( 1+\frac{2 \widetilde{m}_c^2}{3T^2}+\frac{\widetilde{m}_c^4}{6T^4} \right) \nonumber \\&\qquad \qquad \quad \times \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad \quad +\frac{m_c^4\langle {\bar{s}}s\rangle ^2}{216T^4} \left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1 \mathrm{d}y \left\{ \frac{1}{y^3}+\frac{1}{(1-y)^3}\right\} \nonumber \\&\qquad \qquad \quad \times \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad \quad +t\frac{m_c^2\langle {\bar{s}}s\rangle ^2}{432T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1 \mathrm{d}y \left\{ \frac{1-y}{y^2}+\frac{y}{(1-y)^2}\right\} \nonumber \\&\qquad \qquad \quad \times \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad \quad -\frac{m_c^2\langle {\bar{s}}s\rangle ^2}{72T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1 \mathrm{d}y \left\{ \frac{1}{y^2}+\frac{1}{(1-y)^2}\right\} \nonumber \\&\qquad \qquad \quad \times \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad \quad +\frac{m_c^2\langle {\bar{s}}g_s\sigma Gs\rangle ^2}{384 \pi ^2T^4} \int _0^1 \mathrm{d}y \left( \frac{1}{y}+\frac{1}{1-y}\right) \widetilde{m}_c^2 \, \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad \quad +t\frac{ \langle {\bar{s}}g_s\sigma Gs\rangle ^2}{768\pi ^2 }\int _0^1 \mathrm{d}y \left( 1+\frac{\widetilde{m}_c^2}{T^2}\right) \delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad \quad \!-\frac{m_c^2\langle {\bar{s}} s\rangle ^2}{216 T^6}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _0^1 \mathrm{d}y \, \widetilde{m}_c^4 \, \delta \left( s\!-\!\widetilde{m}_c^2\right) \nonumber \\&\qquad \qquad \quad -\!t\frac{ \langle {\bar{s}} s\rangle ^2}{72}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \nonumber \\&\qquad \qquad \quad \times \int _0^1 \mathrm{d}y \,y(1-y)\left( 1+\frac{2\widetilde{m}_c^2}{3T^2} +\frac{\widetilde{m}_c^4}{6T^4} \right) \delta \left( s-\widetilde{m}_c^2\right) ,\nonumber \\ \end{aligned}$$

(41)

$\int \mathrm{d}y\mathrm{d}z=\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z$, $y_{f}=\frac{1+\sqrt{1-4m_c^2/s}}{2}$, $y_{i}=\frac{1-\sqrt{1-4m_c^2/s}}{2}$, $z_{i}=\frac{y m_c^2}{y s -m_c^2}$, $\overline{m}_c^2=\frac{(y+z)m_c^2}{yz}$, $\widetilde{m}_c^2=\frac{m_c^2}{y(1-y)}$, $\int _{y_i}^{y_f}\mathrm{d}y \rightarrow \int _{0}^{1}\mathrm{d}y$, $\int _{z_i}^{1-y}\mathrm{d}z \rightarrow \int _{0}^{1-y}\mathrm{d}z$ when the $\delta$ functions $\delta \left( s-\overline{m}_c^2\right)$ and $\delta \left( s-\widetilde{m}_c^2\right)$ appear.