Spherical top-hat collapse of a viscous unified dark fluid

Abstract

In this paper, we test the spherical collapse of a viscous unified dark fluid (VUDF) which has constant adiabatic sound speed and show the nonlinear collapse for VUDF, baryons, and dark matter, which are important in forming the large-scale structure of our Universe. By varying the values of the model parameters $\alpha$ and $\zeta _{0}$, we discuss their effects on the nonlinear collapse of the VUDF model, and we compare its result to the $\Lambda$CDM model. The results of the analysis show that, within the spherical top-hat collapse framework, larger values of $\alpha$ and smaller values of $\zeta _{0}$ make the structure formation earlier and faster, and the other collapse curves are almost distinguished with the curve of $\Lambda$CDM model if the bulk viscosity coefficient $\zeta _{0}$ is less than $10^{-3}$.

1 Introduction

As a competitive model to explain the lately accelerated expansion of universe, a unified dark fluid (UDF) model [1–15] was investigated extensively in the recent years. The striking features of the UDF model are that it combines cold dark matter and dark energy and that it behaves like the cold dark matter and the dark energy at an early epoch and a late time, respectively. Furthermore, it can match the image of the $\Lambda$CDM model very well on the background level. Among those UDF models, the same assumption for the model, the medium of universe as an idealized perfect fluid, was taken. This means that all components of the matter-energy in our universe are considered as a perfect fluid without viscosity. However, in recent years, more and more cosmological observations suggest that our universe is permeated by an imperfect fluid, in which the negative pressure, as was argued in [16, 17], with an effective pressure including bulk viscosity, can drive the present acceleration of universe. The first attempts at creating a viscosity theory of relativistic fluids were executed by Eckart [18] and Landau and Lifshitz [19] who considered only a first-order deviation from equilibrium. The general form of the bulk viscosity is chosen as a time-dependent function or a density-dependent function. In the literature, a density-dependent viscosity obeying $\zeta =\zeta _{0}\rho ^{m}$ coefficient is widely investigated, where the condition $\zeta _{0}>0$ ensures a positive entropy production in conformity with the second law of thermodynamics. For simplification, we will devote ourselves to studying the case $m=\frac{1}{2}$, a similar form as taken in Refs. [15, 20–22].

For any proposed cosmological model, if its cosmic observations cannot coincide with the theoretical calculations, it would be ruled out, and so is the VUDF model. As the large-scale structure formation originates from the primordial quantum perturbations of our universe, the nonlinear stages of the perturbations become very important during one investigation of the evolutions of density perturbations of the VUDF model. A fully nonlinear analysis is a cumbersome task usually handled by hydrodynamical/N-body numerical codes (see e.g. [23–26]). However, to the best of our knowledge, the hydrodynamical/N-body numerical simulation is very complicated and expensive.

In this paper we focus on the collapse of a spherically symmetric perturbation of the VUDF model, with a classical top-hat profile, instead of using the cumbersome hydrodynamical/N-body numerical simulation. We modify the pressure of UDF $p=\alpha \rho -A$ in Ref. [6] to the form $p=\alpha \rho -\zeta _{0}\rho -A$ to obtain the VUDF model. As mentioned in Ref. [27], one needs to avoid the averaging problem [28, 29] when studying the nonlinear perturbations. The problem comes from the fact that

$$\begin{aligned} \langle p\rangle =-\langle A/\rho ^\beta \rangle \ne -A/\langle \rho \rangle ^\beta =p(\langle \rho \rangle ), \end{aligned}$$

(1)

in the case of $\beta \ne 0$. However, for a model with a linear relation, $p=\alpha \rho -\zeta _{0}\rho -A$, it is not a problem. So it would be interesting to study the evolution of nonlinear perturbation in this VUDF model because of its escaping from the averaging problem. Avoiding the use of the hydrodynamical/N-body numerical simulation, we will research the large-scale structure formation in the framework of spherical top-hat collapse for the viscous unified dark fluid (VUDF).

The paper is organized as follows. In Sect. 2, a brief introduction of the VUDF with a constant adiabatic sound speed is given. Then we present some basic equations for the spherical top-hat collapse of a viscous fluid in Sect. 3. The method and main results are summarized in Sect. 4. The last section is for the conclusion.

2 Viscous unified dark fluid with constant adiabatic sound speed

In this section, we will give some basic equations of a VUDF model which has a constant adiabatic sound speed (CASS). In order to obtain the viscous unified dark fluid, we rewrite the pressure of the UDF $p=\alpha \rho -A$ in Ref. [6] into the form

$$\begin{aligned} p_{d}&= p-3H\zeta ; \end{aligned}$$

(2)

this expression includes the UDF model as a special case when $\zeta =0$, as for the case that $\zeta \ne 0$, when adopting the normal form $\zeta =\frac{\zeta _{0}}{\sqrt{3}}\rho ^{\frac{1}{2}}$, a similar form being taken in Refs. [15, 20–22]. We have for the pressure of the VUDF

$$\begin{aligned} p_{d}=\alpha \rho _{d}-\zeta _{0}\rho _{d}-A, \end{aligned}$$

(3)

where $A=\rho _{d0}(1+\alpha -\zeta _{0})(1-B_{s})$. Applying the energy conservation of the VUDF, one can deduce its energy density as being of the following form:

$$\begin{aligned} \rho _d&= \rho _{d0}\left\{ (1-B_s)+B_s a^{-3(1+\alpha -\zeta _{0})}\right\} , \end{aligned}$$

(4)

where the model parameters $B_s$, $\alpha$, and $\zeta _{0}$ are all in the range $[0,1]$. So one obtains the equation of state (EoS)

$$\begin{aligned} w_d=\frac{p_{d}}{\rho _{d}} =\alpha -\zeta _{0}-\frac{(1+\alpha -\zeta _{0})(1-B_s)}{(1-B_s)+B_s a^{-3(1+\alpha -\zeta _{0})}}, \end{aligned}$$

(5)

and the adiabatic sound speed

$$\begin{aligned} c_s^2=\left( \frac{\partial p_d}{\partial \rho _d}\right) _s=\frac{d p_d}{d\rho _d}=\rho _d\frac{dw_d}{d\rho _d}+w_d=\alpha -\zeta _{0}, \end{aligned}$$

(6)

where $A$, $\zeta _{0}$, and $w_d$ are the integration constant, bulk viscosity coefficient, and the equation of state (EoS) of the VUDF, respectively. Therefore, the Friedmann equation in a spatially flat FRW universe is given as

$$\begin{aligned} H^{2}&= H^{2}_{0}\left\{ (1-\Omega _{b}-\Omega _{r})\left[ (1-B_{s})+B_{s}a^{-3(1+\alpha -\zeta _{0})}\right] \right. \nonumber \\&\left. +\Omega _{b}a^{-3}+\Omega _{r}a^{-4}\right\} , \end{aligned}$$

(7)

where $H$ is the Hubble parameter and $H_{0}=100\text { h km s}^{-1}$ $\text { Mpc}^{-1}$ is its present value. The $\Omega _{i}$ ($i=b,r$) are dimensionless energy density parameters, where $b$ and $r$ stand for baryon and radiation.

3 Equations of spherical top-hat collapse of viscous fluid

The spherical collapse (SC) as a simple analytical model was first introduced by Gunn and Gutt [30] in order to calculate the evolution of the perturbations of in-falling material into a bound system, which provides a way to glimpse into the nonlinear regime of perturbation theory. Usually, the SC model is used to investigate a spherically symmetric perturbation which is embedded in a static, expanding or collapsing homogeneous background. In this paper we focus on the collapse of a spherically symmetric perturbation in a homogeneous expanding background, with a classical top-hat profile which has a constant density [31] in the perturbed region. With the assumption of a top-hat profile, one maintains the simplified spherical collapse model as regards the uniformity of the perturbation throughout the collapse, which makes its evolution only time-dependent. So we do not need to worry about the gradients through the collapse.

In the spherical top-hat collapse (SC-TH) model, the background evolution equations are still in the following form:

$$\begin{aligned} \dot{\rho }&= -3H(\rho +p), \end{aligned}$$

(8)

$$\begin{aligned} \frac{\ddot{a}}{a}&= -\frac{4\pi G}{3}\sum _i(\rho _i+3p_i), \end{aligned}$$

(9)

where $H=\dot{a}/a$ is the Hubble parameter. For the perturbed region, the basic equations which depend on local quantities can be written as

$$\begin{aligned} \dot{\rho }_c&= -3 h(\rho _c+p_c), \end{aligned}$$

(10)

$$\begin{aligned} \frac{\ddot{r}}{r}&= -\frac{4\pi G}{3}\sum _i(\rho _{c_i}+3p_{c_i}). \end{aligned}$$

(11)

Here the perturbed quantities $\rho _c$ and $p_c$ are defined as $\rho _c=\rho +\delta \rho$, $p_c=p+\delta p$; and $h=\dot{r}/r$ and $r$ are the local expansion rate and the local-scale factor respectively, and furthermore $h$ relates to the local expansion rate in the STHC model by [32, 33]

$$\begin{aligned} h=H+\frac{\theta }{3a}, \end{aligned}$$

(12)

where $\theta \equiv \nabla \cdot \overrightarrow{v}$ is the divergence of the peculiar velocity.

So, the equations of the density contrast $\delta _i=(\delta \rho /\rho )_i$ and $\theta$ are [31, 32]

$$\begin{aligned} \dot{\delta }_i&= -3H\left( c^2_{e_i}-w_i\right) \delta _i-\left[ 1+w_i+\left( 1+c^2_{e_i}\right) \delta _i\right] \frac{\theta }{a}, \end{aligned}$$

(13)

$$\begin{aligned} \dot{\theta }&= -H\theta -\frac{\theta ^2}{3a}-4\pi Ga\sum _i\rho _i\delta _i\left( 1+3c^2_{e_i}\right) , \end{aligned}$$

(14)

where the effective sound speed is $c^2_{e_i}=(\delta p/\delta \rho )_i$, where $i$ stands for the different energy components. Equations (13) and (14) can be rewritten into the form in regard to the scale factor $a$:

$$\begin{aligned} \delta '_i&= -\frac{3}{a}\left( c^2_{e_i}-w_i\right) \delta _i-\left[ 1+w_i+\left( 1+c^2_{e_i}\right) \delta _i\right] \frac{\theta }{a^2H}, \end{aligned}$$

(15)

$$\begin{aligned} \theta '&= -\frac{\theta }{a}-\frac{\theta ^2}{3a^2H}-\frac{3H}{2}\sum _i\Omega _i\delta _i\left( 1+3c^2_{e_i}\right) , \end{aligned}$$

(16)

where we have used the definition $\Omega _i=8\pi G\rho _i/3H^2$.

From the above equations, one can find that the $w_c$ and $c^2_e$ are important quantities. The definition of the EoS $w_c$ [31] is

$$\begin{aligned} w_c=\frac{p+\delta p}{\rho +\delta \rho }=\frac{w}{1+\delta }+c^2_e\frac{\delta }{1+\delta }. \end{aligned}$$

(17)

The effective sound speed $c^2_e$ of the CASS model is given as

$$\begin{aligned} c^2_{e}=\frac{\delta p}{\delta \rho }=\frac{p_c-p}{\rho _c-\rho }. \end{aligned}$$

(18)

So, substituting the relation $p=\alpha \rho -\zeta _{0}\rho -A$ into the above equation, one has

$$\begin{aligned} c^2_{e}=\frac{[(\alpha -\zeta _{0})\rho _c]-A-[(\alpha -\zeta _{0})\rho -A]}{\rho _c-\rho }=\alpha -\zeta _{0}.\nonumber \\ \end{aligned}$$

(19)

4 The method and results

In this section, we will use the spherical collapse model to investigate the nonlinear evolution of the VUDF perturbations. As the baryon and VUDF are the possible components responsible for formatting the large-scale structure, we will firstly consider these two components, where the results of some model parameters come from Ref. [6]: $\Omega _{d}=0.956$, $H_0=71.341 \text { km s}^{-1}\text { Mpc}^{-1}$, and $\Omega _{b}=0.044$. With the aid of the software Mathematica and setting the initial conditions (ICs) $\delta _{d}$ and $\delta _{b}$ at the redshift $z=1000$ as in Ref. [31], we solve the differential equations of the perturbations.

In order to explore the influence of $\alpha$ on the spherical collapse of the baryon and unified dark fluid, we immobilize $\delta _{d}(z=1000)=3.5\times 10^{-3}$, $\delta _{b}(z=1000)=10^{-5}$, $\zeta _{0}=0$, and $B_s= 0.229$, but we change the model parameter to $\alpha =0, 10^{-3}, 10^{-2}$, and $10^{-1}$, respectively. We obtain the same calculated results as Table 1 in Ref. [34], where the redshift $z_{ta}$ is for the turnaround redshift when the collapse is beginning. From Table 1, one can conclude that the perturbations collapse earlier and faster for larger values of $\alpha$ and larger values of $c^2_{e}=\alpha$.

Table 1 Models for the STHC model, where the values of $\alpha$ are small positive values due to the constraint from the background evolution history. The redshift $z_{ta}$ denotes the turnaround redshift when the perturbed region begins to collapse

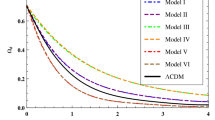
In the following, we will show the influence of the bulk viscosity coefficient $\zeta _{0}$ on the evolution of the density perturbations of baryon and VUDF. Here we alter the values of $\zeta _{0}$ for the different models, which correspond to $\alpha =10^{-1}, 10^{-2}, 10^{-3},$ and $0$, respectively. For the viscous unified dark fluid model, the $\Lambda$CDM model is recovered when the model parameters $\zeta _{0}=0$ and $B_{s}=0$ are taken. In order to compare the VUDF model with the $\Lambda$CDM model, we plot collapse curves of these two models in the same figure. The corresponding evolutions of the density perturbations are shown in Figs. 1, 2, 3, and 4. Moreover, dark matter is regained if the model parameters $B_{s}=1$ and $\alpha =0$ are respected; therefore, we plot the nonlinear and linear perturbations evolution curves of dark matter in Fig. 5. From the first four figures, one can see that the smaller value of $\alpha$ is taken, the more inconspicuous influence on the collapse is obtained, for example in Fig. 4, when $\alpha =0$, one is almost unable to distinguish the five curves. Observing Figs. 1, 2, 3, 4, and 5, the horizon line denotes the limit of a linear perturbation, i.e. $\delta =1$, and the vertical parts of the curved lines denote the collapse of the perturbed regions; therefore, one can see that the smaller value of the bulk viscosity coefficient $\zeta _{0}$ can result in earlier collapse, that is to say, a larger value of the bulk viscosity coefficient $\zeta _{0}$ can make the collapse later, and these results are compatible with the well-known convention that the value of bulk viscosity coefficient $\zeta _{0}$ should not be too large. Furthermore, one finds that when the bulk viscosity coefficient $\zeta _{0}$ is less than $10^{-3}$, the other collapse curves almost overlap with the curve of the $\Lambda$CDM model.

Fig. 1

The evolutions of the density perturbations with respect to the redshift for the models $\alpha =10^{-1}$. The top and bottom panels are for baryons and VUDF, respectively. Here the solid, dashed, dotted, and green curved lines are for the models $\zeta _{0}=10^{-1}, 10^{-2}, 10^{-3}, 0$, respectively; beyond that, the red dashed curve stands for the $\Lambda$CDM model. The horizon line denotes the limit of a linear perturbation, i.e. $\delta =1$. The vertical parts of the curved lines denote the collapse of the perturbed regions

Fig. 2

The evolutions of the density perturbations with respect to the redshift for the models $\alpha =10^{-2}$. The top and bottom panels are for baryons and VUDF, respectively. Here the solid, dashed, dotted, and green curved lines are for the models $\zeta _{0}=10^{-2}, 10^{-3}, 10^{-4}, 0$, respectively; beyond that, the red dashed curve stands for the $\Lambda$CDM model. The horizon line denotes the limit of a linear perturbation, i.e. $\delta =1$. The vertical parts of the curved lines denote the collapse of the perturbed regions

Fig. 3

The evolutions of density perturbations with respect to the redshift for the models $\alpha =10^{-3}$. The top and bottom panels are for baryons and VUDF, respectively. Here the solid, dashed, dotted, and green curved lines are for the models $\zeta _{0}=10^{-2}, 10^{-3}, 10^{-4}, 0$, respectively; beyond that, the red dashed curve stands for the $\Lambda$CDM model. The horizon line denotes the limit of a linear perturbation, i.e. $\delta =1$. The vertical parts of the curved lines denote the collapse of the perturbed regions

Fig. 4

The evolutions of density perturbations with respect to the redshift for the models $\alpha =0$. The top and bottom panels are for baryons and VUDF, respectively. Here the solid, dashed, dotted, and green curved lines are for the models $\zeta _{0}=10^{-3}, 10^{-4}, 10^{-5}, 0$ respectively; beyond that, the red dashed curve stands for the $\Lambda$CDM model. The horizon line denotes the limit of a linear perturbation, i.e. $\delta =1$. The vertical parts of the curved lines denote the collapse of the perturbed regions

Fig. 5

The evolutions of density perturbations with respect to the redshift for the VUDF model and the $\Lambda$CDM model. The top and bottom panels are for the nonlinear matter perturbation and the linear matter perturbation, respectively. Here the solid, dashed, dotted, and green curved lines are for the models $\zeta _{0}=10^{-2}, 10^{-3}, 10^{-4}, 0$; beyond that, the red dashed curve stands for the $\Lambda$CDM model. The horizon line denotes the limit of a linear perturbation, i.e. $\delta =1$. The vertical parts of the curved lines denote the collapse of the perturbed regions

It is time to show the influence of $\zeta _{0}$ on the evolution of the equation of state (EoS) of the VUDF $w_{d}$ and the EoS of the collapse region $w_{c}$. Observing the evolving curves of $w_{c}$ in Figs. 6, 7, 8, and 9, one can easily conclude that higher values of $\zeta _{0}$ result in values of $w_{c}$ closer to and higher than $w_{c}=0$ during the collapse as shown in Figs. 6 and 7, and they result in values of $w_{c}$ closer to and lower than $w_{c}=0$ during the collapse as shown in Figs. 8 and 10. But the result is values of $w_{c}$ almost overlapping, as shown in Fig. 9. However, the effects of $\zeta _{0}$ on the evolution of the equation for $w_{d}$ is very different comparing to the results above. Apart from the almost distinguishable influence of $\zeta _{0}$ on $w_{d}$ as shown in Figs. 7, 8, and 9, we know that a smaller $\zeta _{0}$ makes the curves of $w_{d}$ higher as shown in Fig. 6. Based on the discussion above, we draw the conclusion that the influence of $\zeta _{0}$ on the evolution of $w_{d}$ and $w_{c}$ is enhanced on increasing the values of $\alpha$. Apart from that, from Figs. 6, 7, 8, 9, and 10, we easily conclude that, whatever the value of parameters $\alpha$ and $\zeta _{0}$ are, the evolution curves of $w_{d}$ for the VUDF model and the $\Lambda$CDM model are very different. However, for the evolution curves of $w_{c}$, the curves of the VUDF model (when the value of $\zeta _{0}$ is less than $10^{-3}$) and the $\Lambda$CDM model match at the late time, and as the value of $\alpha$ is larger, the superposition happens earlier.

Fig. 6

The evolutions for the equation of state $w$ with respect to the redshift $z$ for different models $\alpha =10^{-1}$. The top and bottom panels are for $w_c$ and $w_d$, respectively. Here the solid, dashed, dotted, and green curved lines are for $\zeta _{0}=10^{-1}, 10^{-2}, 10^{-3}, 0$, respectively; beyond that, the red dashed curve stands for the $\Lambda$CDM model

Fig. 7

The evolutions for the equation of state with respect to the redshift $z$ for different models $\alpha =10^{-2}$. The top and bottom panels are for $w_c$ and $w_d$, respectively. Here the solid, dashed, dotted, and green curved lines are for $\zeta _{0}=10^{-2}, 10^{-3}, 10^{-4}, 0$, respectively; beyond that, the red dashed curve stands for the $\Lambda$CDM model

Fig. 8

The evolutions for the equation of state with respect to the redshift $z$ for different models $\alpha =10^{-3}$. The top and bottom panels are for $w_c$ and $w_d$, respectively. Here the solid, dashed, dotted, and green curved lines are for $\zeta _{0}=10^{-2}, 10^{-3}, 10^{-4}, 0$, respectively; beyond that, the red dashed curve stands for the $\Lambda$CDM model

Fig. 9

The evolutions for the equation of state with respect to the redshift $z$ for different models $\alpha =0$. The top and bottom panels are for $w_c$ and $w_d$, respectively. Here the solid, dashed, dotted, and green curved lines are for $\zeta _{0}=10^{-3}, 10^{-4}, 10^{-5}, 0$, respectively; beyond that, the red dashed curve stands for the $\Lambda$CDM model

Fig. 10

The evolutions for the equation of state $w$ with respect to the redshift $z$ for the VUDF model and $\Lambda$CDM model. The top and bottom panels are for $w_c$ and $w_m$, respectively. Here the solid, dashed, dotted, and green curved lines are for the models $\zeta _{0}=10^{-2}, 10^{-3}, 10^{-4}, 0$; beyond that, the red dashed curve stands for the $\Lambda$CDM model

Through the calculation and analysis above, for the VUDF model, it is possible to format the large-scale structure. Also, it is obvious that the model parameters $\zeta _{0}$ and $\alpha$ have influence on the density perturbations evolutions.

5 Conclusion

In this paper, we investigated the density perturbations of a VUDF model with a constant adiabatic sound speed in the framework of spherical top-hat collapse, and the results showed that it is possible to form large-scale structure in the VUDF model. We studied their influence on the evolutions of the perturbations through varying the values of $\zeta _{0}$ and $\alpha$. Through the calculation and analysis, we concluded that smaller values of $\zeta _{0}$ and larger values of $\alpha$ can make the density perturbations collapse earlier and faster, and that the other collapse curves almost overlap with the curve of $\Lambda$CDM if the bulk viscosity coefficient $\zeta _{0}$ is less than $10^{-3}$. Furthermore, we also conclude that the influence of $\zeta _{0}$ on the evolution of $w_{d}$ and $w_{c}$ is enhanced with increasing values of $\alpha$. In the following work, we will try to apply the spherical collapse to other cosmological models and compare the simulated results with the observed large-scale structure of the universe.