1 Introduction

The idea of extra dimensions offers the possibility of explaining the hierarchy between the Planck scale \(M_\mathrm{Pl}\simeq 10^{18}\;\hbox {GeV}\) and the electroweak scale \(m_\mathrm{W}\simeq 10^2\;\hbox {GeV}\); therefore it has received a lot of attention during the last decade. Randall and Sundrum proposed a very elegant model (RS1) to solve the hierarchy problem [1] and also an attractive alternative (RS2) for the compactification of the extra dimension [2]. Both models suffer from the presence of infinitesimally thin structures, so-called D3 branes. In addition the RS1 requires the presence of a brane with negative tension. There were many attempts to regularize thin branes of RS1 by certain configurations of a scalar field with localized energy density. Unfortunately, it turns out that periodicity constrains the dynamics of those models so strongly that only trivial (constant) configurations of the scalar field are allowed; see [3] and [4]. Therefore, here we are going to limit ourself to the case of an uncompactified extra dimension, à la RS2. We will consider a generalized version of the RS2, allowing for different cosmological constants on both sides of the brane. In this case a nontrivial profile of the scalar field is allowed and a thick (smooth) brane could be adopted to regularize the singular thin brane. There have been many studies devoted to thick branes with different motivations and setups [4–18]; for a review see for example [19] and references therein. In order to obtain a desired (warped) form of solutions for the Einstein equations, both in the RS1 and the RS2 model, one has to impose certain relations between the brane tension and the cosmological constants. Here we are going to prove that under certain mild assumptions, the relation between the brane tension and the cosmological constants obtained in the brane limit of the thick-brane scenario does not depend on the detailed shape of the scalar field profile.

The paper is organized as follows. The generalized RS2 model is defined in Sect. 2. Section 3 contains a discussion of the thick-brane version of the generalized RS2. In Sect. 4 we show that the RS2 relation between the brane tension \(\lambda \) and cosmological constants \(\Lambda _\pm \) does not depend on the details of the thick-brane profile. Section 5 summarizes our findings.

2 RS2 generalization

We will consider the following action, which is an extension of the Randall–Sundrum model with a single brane (RS2) [2]Footnote 1:

$$\begin{aligned} S&= \int d^5x\sqrt{-g}\left( 2M_*^{3}R-\Lambda _+\Theta (y-y_0)\right. \nonumber \\&\quad \left. -\Lambda _-\Theta (-y+y_0)-\lambda \delta (y-y_0)\right) \!, \end{aligned}$$
(2.1)

where \(\Lambda _+\) and \(\Lambda _-\) are 5D cosmological constants for \(y>y_0\) and \(y<y_0\), respectively, whereas \(y_0\) is the brane location and \(\lambda \) represents the brane tension. In the above action \(M_*\) is the 5D Planck mass. In our convention capital Roman indices will refer to 5D objects, i.e., \(M,N,\ldots =0,1,2,3,5\), while Greek indices will label four-dimensional (4D) objects, i.e., \(\mu ,\nu ,\ldots =0,1,2,3\). In (2.1) \(\Theta \) is the Heaviside theta function and \(\delta \) is the Dirac delta function. For simplicity we will choose \(y_0=0\).

We are going to look for solutions of the Einstein equations assuming the following form of the 5D metric:

$$\begin{aligned} \mathrm{d}s^2=e^{2A(y)}\eta _{\mu \nu }\mathrm{d}x^\mu \mathrm{d}x^\nu +\mathrm{d}y^2. \end{aligned}$$
(2.2)

Then the Einstein equations following from the action (2.1) reduce to

$$\begin{aligned}&6A^{\prime 2}=-\frac{1}{4M_*^{3}}\left( \Lambda _+\Theta (y)+\Lambda _-\Theta (-y)\right) , \end{aligned}$$
(2.3)
$$\begin{aligned}&3A^{\prime \prime }\!+\!6A^{\prime 2}\!=\!-\frac{1}{4M_*^{3}}\left( \Lambda _+\Theta (y)\!+\!\Lambda _-\Theta (-y)\!+\!\lambda \delta (y)\right) . \nonumber \\ \end{aligned}$$
(2.4)

The solution of (2.3) is given by

$$\begin{aligned} A(y)= - |y| k_\pm \qquad \mathrm{for} \qquad y\gtrless 0, \end{aligned}$$
(2.5)

where \( k_\pm \equiv \sqrt{-\frac{1}{24M_*^{3}}\Lambda _\pm }\) can be related to the AdS curvatures \(R_\pm \) for \(y\gtrless 0\) as \( k_\pm \propto 1/R_\pm \). Now one can calculate \(A^\prime \) and \(A^{\prime \prime }\) from the above expression as

$$\begin{aligned} A^\prime (y)\!=\! \mp k_\pm \;\; \mathrm{for} \;\; y\gtrless 0 \quad \,\mathrm{and} \quad \,A^{\prime \prime }(y)\!=\!-( k_+\!+\! k_-)\delta (y). \nonumber \\ \end{aligned}$$
(2.6)

The discontinuity of \(A^\prime (y)\) at \(y=0\) results in the following jump:

$$\begin{aligned} \left[ A^\prime \right] _0=-\frac{\lambda }{12M_*^{3}}, \end{aligned}$$
(2.7)

where \([A^\prime ]_0\equiv A^\prime (0+\epsilon )-A^\prime (0-\epsilon )\), and \(\epsilon \rightarrow 0\). From the Einstein equations (2.3) and (2.4), we have

$$\begin{aligned} A^{\prime \prime }(y)=-\frac{\lambda }{12M_*^{3}}\delta (y). \end{aligned}$$
(2.8)

Comparing (2.8) and the second equation of (2.6) yields

$$\begin{aligned} \lambda =\sqrt{6 M_*^{3}}\left( \sqrt{-\Lambda _+}+\sqrt{-\Lambda _-}\right) , \end{aligned}$$
(2.9)

which is an analog of the Randall–Sundrum relation between the bulk cosmological constant and the brane tension [1, 2]. It is important to note that the relation (2.9) is necessary in order to recover the 4D Poincaré invariance on the brane.

As we have checked by explicit calculation the 4D effective gravity on the brane could be recovered with the Planck mass given by

$$\begin{aligned} M^{2}_\mathrm{Pl}=\frac{M_*^3}{2k_+}+\frac{M_*^3}{2k_-}. \end{aligned}$$
(2.10)

We have also verified that the above solutions of the Einstein equations are stable against small perturbations of the metric. Our findings concerning the asymmetric version of the RS2 with singular brane confirm results obtained in [20]. Some of the aspects of asymmetric singular-brane worlds are discussed in [21–24].

3 Thick-brane version of the generalized RS2

In this section we will extend the solution found in the previous section for a singular D3-brane to a thick- (smooth-) brane scenario in which the thick brane is dynamically generated by a scalar field. The action for a 5D scalar field minimally coupled to the Einstein–Hilbert gravity is

$$\begin{aligned} S=\int \mathrm{d}x^5 \sqrt{-g}\left\{ 2M_*^{3}R-\frac{1}{2}g^{MN}\nabla _{M}\phi \nabla _{N}\phi -V(\phi )\right\} , \end{aligned}$$
(3.1)

and we assume the 5D metric to be of the form

$$\begin{aligned} \mathrm{d}s^2=e^{2A(y)}\eta _{\mu \nu }\mathrm{d}x^\mu \mathrm{d}x^\nu +\mathrm{d}y^2. \end{aligned}$$
(3.2)

The Einstein equations and the equation of motion for \(\phi \), resulting from the action (3.1), are

$$\begin{aligned}&R_{MN}-\frac{1}{2}g_{MN}R=\frac{1}{4M_*^{3}}T_{MN},\end{aligned}$$
(3.3)
$$\begin{aligned}&\nabla ^{2}\phi -\frac{dV}{d\phi }=0, \end{aligned}$$
(3.4)

where \(\nabla ^2\) is the 5D covariant d’Alembertian operator, while the energy-momentum tensor \(T_{MN}\) for the scalar field \(\phi (y)\) is

$$\begin{aligned} T_{MN}=\nabla _{M}\phi \nabla _{N}\phi -g_{MN}\left( \frac{1}{2}(\nabla \phi )^{2}+V(\phi )\right) . \end{aligned}$$
(3.5)

From the Einstein equations (3.3) and (3.4), one gets the following equations of motion for the metric (3.2):

$$\begin{aligned}&24M_*^{3}(A^{\prime })^{2}=\frac{1}{2}(\phi ^{\prime })^{2}-V(\phi ),\end{aligned}$$
(3.6)
$$\begin{aligned}&12M_*^{3}A^{\prime \prime }+24M_*^{3}(A^{\prime })^{2}=-\frac{1}{2}(\phi ^{\prime })^{2}-V(\phi ),\end{aligned}$$
(3.7)
$$\begin{aligned}&\phi ^{\prime \prime }+4A^{\prime }\phi ^{\prime }-\frac{dV}{d\phi }=0. \end{aligned}$$
(3.8)

We assume that the scalar potential \(V(\phi )\) could be expressed in terms of a superpotential [4–6] \(W(\phi )\) as follows:

$$\begin{aligned} V(\phi )=\frac{1}{2}\left( \frac{\partial W(\phi )}{\partial \phi }\right) ^{2}-\frac{1}{6M_*^{3}}W(\phi )^{2}, \end{aligned}$$
(3.9)

where \(W(\phi )\) satisfies the following relations:

$$\begin{aligned} \phi ^{\prime }=\frac{\partial W(\phi )}{\partial \phi } \quad \text {and}\quad A^{\prime }=-\frac{1}{12M_*^{3}} W(\phi ). \quad \quad \end{aligned}$$
(3.10)

Although the use of this method is motivated by supergravity, no supersymmetry is involved in our setup. This method is elegant and very efficient; in particular, it reduces the system of second order differential equations (3.6)–(3.8) to first order ordinary differential equations.

We are interested in the case for which the scalar field \(\phi (y)\) is given by a kink-like profile,Footnote 2 i.e.,

$$\begin{aligned} \phi (y)= \frac{\kappa }{\sqrt{\beta }}\tanh (\beta y), \end{aligned}$$
(3.11)

where \(\beta \) is the thickness regulator and \(\kappa \) parameterizes the tension of the brane in the so-called brane limit: \(\beta \rightarrow \infty \). The energy density (\(T_{00}\)) implied by \(\phi (y)\) is localized near \(y=0\) with the corresponding width controlled by \(\beta \). We will find solutions which mimic a positive-tension brane along with two different cosmological constants on either side of the brane. If the scalar field \(\phi (y)\) is known, then the superpotential \(W(\phi )\) can be obtained from (3.10) as

$$\begin{aligned} \phi ^{\prime }(y)&=\frac{\partial W(\phi )}{\partial \phi }=\frac{\partial W(\phi (y))}{\partial y}\frac{\partial y}{\partial \phi (y)}= \frac{W^{\prime }(y)}{\phi ^\prime (y)},\end{aligned}$$
(3.12)
$$\begin{aligned} W(y)&=\int \limits _{y_0}^y (\phi ^{\prime }(y))^{2}\mathrm{d}y+W_{0}, \end{aligned}$$
(3.13)

where \(W_0\) is a constant of integration. It is important to note that in deriving the above relation it is assumed that \(\phi (y)\) must be an invertible function of \(y\), such that \(W(\phi )\) can be represented as \(W(y)\). Now with the scalar field (3.11) the superpotential \(W(\phi )\) could be explicitly obtained as a function of \(y\):

$$\begin{aligned} W(y)=&\kappa ^2\left\{ \tanh (\beta (y))-\frac{1}{3}\tanh ^{3}(\beta (y))\right\} +W_{0}. \end{aligned}$$
(3.14)

The integration constant \(W_0\) can be fixed by initial conditions imposed upon \(A^\prime (y)\), e.g., such that \(A'(y_\mathrm{max})=0)\) for a given \(y_\mathrm{max}\). The non-zero value of \(W_0\) turns out to be essential to reproduce, in the brane limit, the generalized RS2 model presented in the previous section, whereas for \(W_0=0\) the solution for \(A(y)\) is symmetric under \(y\leftrightarrow -y\) and it corresponds to the standard RS2 in the brane limit [5, 6]. It is instructive to write down explicitly the brane-limit results for the thick-brane scenario in order to determine necessary relations that must be satisfied to reproduce the RS2 relations (2.9) in the brane limit. As we will show below there is a direct relation between \(W_0\ne 0\) and the fact that \(\Lambda _+\ne \Lambda _-\).

Let us consider only the scalar field part of the action:

$$\begin{aligned} S_{\phi }&=\int \mathrm{d}x^5 \sqrt{-g}\left\{ -\frac{1}{2}g^{MN}\nabla _{M}\phi \nabla _{N}\phi -V(\phi )\right\} \nonumber \\&=\int \mathrm{d}x^5 \sqrt{-g}\left\{ -\left( \frac{\partial W(\phi )}{\partial \phi }\right) ^{2}+\frac{1}{6M_*^{3}}W^{2}(\phi ) \right\} \nonumber \\&=\int \mathrm{d}x^5 \sqrt{-g}\left\{ \frac{-\beta \kappa ^2}{\cosh ^4(\beta ( y))} +\frac{1}{6M_*^{3}}\right. \nonumber \\&\quad \left. \times \left[ \kappa ^2\left( \tanh (\beta ( y))-\frac{1}{3}\tanh ^{3}(\beta ( y))\right) +W_{0} \right] ^{2}\right\} . \end{aligned}$$
(3.15)

In the brane limit, i.e., \(\beta \rightarrow \infty \) we have

$$\begin{aligned} \lim _{\beta \rightarrow \infty }\left\{ \frac{\beta }{\cosh ^4(\beta ( y))}\right\} =\frac{4}{3}\delta (y), \end{aligned}$$

such that the scalar action (3.15) can be written as

$$\begin{aligned} S_{\phi }&=\int \mathrm{d}x^5 \sqrt{-g}\left\{ -\frac{4}{3}\kappa ^2\delta (y)-\Lambda _+\Theta (y) - \Lambda _-\Theta (-y) \right\} . \end{aligned}$$
(3.16)

Here \(\Lambda _\pm \) are cosmological constants in the bulk for \(y\gtrless 0\):

$$\begin{aligned} \Lambda _\pm&= \lim _{\beta \rightarrow \infty }\left[ \!-\!\frac{1}{6M_*^{3}} \left\{ \pm \kappa ^2\left( \tanh (\beta ( y))\!-\!\frac{1}{3}\tanh ^{3}(\beta ( y))\right) \right. \right. \nonumber \\&\left. \left. +W_{0} \right\} ^{2}\right] , \nonumber \\&=-\frac{1}{6M_*^{3}} \left( \pm \frac{2}{3}\kappa ^2 \!+\!W_{0}\right) ^{2} \!=\!-\frac{1}{6 M_*^{3}} \left( \frac{\lambda }{2} \pm W_{0}\right) ^{2} \quad y\gtrless 0, \nonumber \\ \end{aligned}$$
(3.17)

and \(\lambda \equiv \frac{4}{3}\kappa ^2\) corresponds to the brane tension. Hereafter, we will consider the case \(-\Lambda _+>-\Lambda _-\), which implies \(W_0>0\). It is also important to note that (3.17) implies that the bulk cosmological constants \(\Lambda _\pm \) are negative on either side leading to anti-de Sitter vacua or in the case with \( W_{0}=\lambda /2\) corresponding to a Minkowski geometry in that region of space. Equation (3.17) implies that in order to reproduce the generalized RS2 scenario defined by a given \(M_*\), \(\lambda \) and \(\Lambda _\pm \), the following constraints on the parameters (\(\kappa \), \(W_0\)) of the thick-brane model must hold:

$$\begin{aligned} \kappa ^2&= \frac{3}{4} \lambda , \end{aligned}$$
(3.18)
$$\begin{aligned} W_0&= \sqrt{\frac{3}{2}M_*^{3}}\left( \sqrt{-\Lambda _+}-\sqrt{-\Lambda _-}\right) . \end{aligned}$$
(3.19)

For consistency of the above choice for \(W_0\), the following inequality must hold:

$$\begin{aligned} 0 < W_0 < \frac{\lambda }{2}. \end{aligned}$$
(3.20)

Therefore, only scenarios with limited splitting between cosmological constants could be realized:

$$\begin{aligned} \sqrt{6M_*^{3}}\left( \sqrt{-\Lambda _+}-\sqrt{-\Lambda _-}\right) <\lambda . \end{aligned}$$
(3.21)

Then, for \(W_0\) in the limit (3.20), (3.17) implies that

$$\begin{aligned} \lambda = \sqrt{6M_*^{3}}\left( \sqrt{-\Lambda _+}+\sqrt{-\Lambda _-}\right) \!, \end{aligned}$$
(3.22)

which is identical to the generalized RS2 relation (2.9). Note that for the \(Z_2\) symmetric case (the standard RS2 model) for which \(\Lambda _+=\Lambda _-=\Lambda _B\), we recover the RS2 relation between the brane tension and bulk cosmological constant \(\lambda =\sqrt{-24M_*^{3}\Lambda _B}\) [1, 2] and \(W_0=0\).

It is straightforward to calculate the warp function \(A(y)\) by integrating the second equation in (3.10) w.r.t. \(y\). The result reads

$$\begin{aligned} A(y)\!=\!&-\frac{\kappa ^2}{72M_*^{3}\beta }\left( \tanh ^{2}(\beta y)\!+\!\ln \cosh ^{4}(\beta y)\right) -\frac{W_0}{12M_*^{3}}y. \end{aligned}$$
(3.23)

The integration constant above was fixed by the condition \(A(0)=0\). As we have shown in (3.19) \(W_0\) is fixed uniquely at a non-zero value; then, as a consequence, in the smooth case the warp function \(A(y)\) will not have a maximum on the brane location, i.e., \(y=0\) but it will be shifted to a position \(y_\mathrm{max}\), for instance for \(M_*=1\), \(\kappa =1\), and \(W_0=0.5M_*^3\),

$$\begin{aligned} y_\mathrm{max} \sim -\frac{0.6}{\beta }. \end{aligned}$$
(3.24)

It is worth noticing that even though \(A'(0)\ne 0\), nevertheless the maximum of \(A(y)\) approaches the brane location, i.e., \(y_\mathrm{max}\rightarrow 0\) as \(\beta \rightarrow \infty \), which is manifested from the above equation.

Note that far away from the thick brane the warp function approaches the generalized RS2 form as presented in Sect. 2,

$$\begin{aligned} A(y)&\approx -k_\pm \vert y\vert , \quad \vert y\vert \rightarrow \infty , \end{aligned}$$
(3.25)

where

$$\begin{aligned} k_\pm =\frac{1}{24M_*^{3}}\lambda \pm \frac{W_0}{12M_*^{3}}, \end{aligned}$$

It is also important to note that one obtains the same behavior of \(A(y)\) (3.25), for all values of \(y\) in the brane limit when \(\beta \rightarrow \infty \), i.e.,

$$\begin{aligned} A(y)\approx -k_\pm \vert y\vert , \quad \beta \rightarrow \infty \mathrm{for}y\gtrless 0. \end{aligned}$$

Since \(\phi (y)\) is invertible therefore we can write the superpotential \(W(\phi )\) and the scalar potential \(V(\phi )\) as follows:

$$\begin{aligned} W(\phi )&= \kappa \sqrt{\beta }\phi \left( 1-\frac{\beta }{3\kappa ^2}\phi ^2\right) +W_0, \end{aligned}$$
(3.26)
$$\begin{aligned} V(\phi )&= \frac{\beta ^3}{2\kappa ^2}\left( \phi ^2-\frac{\kappa ^2}{\beta }\right) ^2 -\frac{1}{54M_*^{3}}\frac{\beta ^3}{\kappa ^2}\phi ^2\left( \phi ^2-3\frac{\kappa ^2}{\beta }\right) ^2 \nonumber \\&+\frac{1}{9M_*^{3}}\frac{\beta ^{3/2}}{\kappa }\phi \left( \phi ^2-3\frac{\kappa ^2}{\beta }\right) W_0-\frac{1}{6M_*^{3}}W_0^2. \nonumber \\ \end{aligned}$$
(3.27)

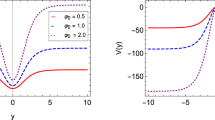
Note that the constant term of superpotential \(W_0\), in Eq. (3.26), plays the most crucial role in producing the asymmetry in the bulk cosmological constants and then in the warp function \(A(y)\) on the left and the right of the (thick) brane. In the left panel of Fig. 1 we have shown \(y\)-dependent shapes of \(A(y)\), \(W(y)\), \(\phi (y)\) and \(T_{00}(y)\), while in the right one \(W(\phi )\) and \(V(\phi )\) are plotted as a function of \(\phi \).

Fig. 1
figure 1

This left graph shows the behavior of \(A(y)\), \(W(y)\), \(\phi (y)\) and \(T_{00}(y)\) as a function of \(y\), whereas, the right graph presents the superpotential \(W(\phi )\) and the potential \(V(\phi )\) as a function of the scalar field \(\phi \) for \(W_0=0.5 M_*^4\) and \(M_*=\beta =\kappa =1\)

Full size image

For the thick-brane scenario one can show (following e.g. [4]) that the 4D effective gravity on the thick brane could be recovered and the background solutions found above are stable. Here we will only discuss the behavior of the zero mode of tensor perturbations which corresponds to the 4D graviton and the Schrödinger-like potential in the generalized RS2 case with thick brane.

In order to illustrate stability of our solutions for the Einstein equations let us perturb the metric (3.2) such that

$$\begin{aligned} \mathrm{d}s^{2}&=e^{2A(y)}(\eta _{\mu \nu }+H_{\mu \nu })\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }+\mathrm{d}y^{2}, \end{aligned}$$
(3.28)

where \(H_{\mu \nu }=H_{\mu \nu }(x,y)\) is the transverse and traceless tensor fluctuation, i.e.,

$$\begin{aligned} \partial ^\mu H_{\mu \nu }=H^{\mu }_{\mu }=0. \end{aligned}$$
(3.29)

One can find the following form of the linearized field equation for the tensor mode:

$$\begin{aligned} \left( \partial _{5}^{2}+4A^{\prime }\partial _{5}+e^{-2A}\Box \right) H_{\mu \nu }&=0, \end{aligned}$$
(3.30)

where \(\partial _5\equiv \partial /\partial y\) and \(\Box \) is the 4D d’Alembertian operator. The zero-mode solution (corresponding to \(\Box H_{\mu \nu }=0\)) of the above equation represents the 4D graviton while the non-zero modes (corresponding to \(\Box H_{\mu \nu } = m^2 H_{\mu \nu } \ne 0\)) are the Kaluza–Klein (KK) graviton excitations.

In order to gain more intuition and understanding of the tensor mode equation of motion (3.30), it is convenient to change the variables such that we can get rid of the exponential factor in front of the d’Alembertian and the single derivative term with \(A^{\prime }\), so that we convert the above equation into the standard Schrödinger-like form. We can achieve this in two steps; first by changing coordinates such that the metric becomes conformally flat:

$$\begin{aligned} \mathrm{d}s^{2}&=e^{2A(z)}\left( \eta _{\mu \nu }\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }+\mathrm{d}z^{2}\right) , \end{aligned}$$
(3.31)

with \(z\) defined through the differential equation: \(\mathrm{d}z=e^{-A(y)}\mathrm{d}y\). In the new coordinates the (3.30) takes the form

$$\begin{aligned} \left( \partial _{z}^{2}+3\dot{A}(z)\partial _{z}+\Box \right) H_{\mu \nu }&=0, \end{aligned}$$
(3.32)

where \(dot\) over \(A\) represents a derivative with respect to \(z\) coordinate. Now we can perform the second step removing the single derivative term in (3.32) by the following redefinition of the tensor fluctuation:

$$\begin{aligned} H_{\mu \nu }(x,z)&=e^{-3A(z)/2}\tilde{H}_{\mu \nu }(x,z). \end{aligned}$$
(3.33)

Hence the (3.32) will take the form of the Schrödinger equation,

$$\begin{aligned} \left( \partial _{z}^{2}-\frac{9}{4}\dot{A}^{2}(z)-\frac{3}{2}\ddot{A}(z)+\Box \right) \tilde{H}_{\mu \nu }(x,z)&=0. \end{aligned}$$
(3.34)

We can decompose the \(\tilde{H}_{\mu \nu }(x,z)\) into the \(x\) and \(z\) dependent parts as \(\tilde{H}_{\mu \nu }(x,z)=\hat{H}_{\mu \nu }(x)\psi (z)\). Here \(\hat{H}_{\mu \nu }(x)\propto e^{ipx}\) is a \(z\)-independent plane wave solution such that \(\Box \hat{H}_{\mu \nu }(x)=m^2\hat{H}_{\mu \nu }(x)\), with \(-p^2=m^2\) being the 4D KK mass of the tensor mode. Then the above equation takes the form

$$\begin{aligned} \bigg (-\partial _{z}^{2}+\mathcal{V}(z)\bigg )\psi (z) = m^{2}\psi (z), \end{aligned}$$
(3.35)

where \(\mathcal{V}(z)\) is the Schrödinger-like potential,

$$\begin{aligned} \mathcal{V}(z) =\frac{9}{4}\dot{A}^{2}(z)+\frac{3}{2}\ddot{A}(z). \end{aligned}$$
(3.36)

Note that we can rewrite the Schrödinger-like equation (3.35) in supersymmetric quantum mechanics form as

$$\begin{aligned} \mathcal{Q}^{\dagger }\mathcal{Q}\psi =\left( -\partial _{z}-\frac{3}{2}\dot{A}\right) \left( \partial _{z}-\frac{3}{2}\dot{A}\right) \psi =m^{2}\psi . \end{aligned}$$
(3.37)

The zero-mode (\(m^2=0\)) profile, \(\psi _0(z)\), corresponds to the graviton in the 4D effective theory. The stability with respect to the tensor fluctuations of the background solution is guaranteed by the positivity of the operator \(\mathcal{Q}^{\dagger }\mathcal{Q}\) in the supersymmetric quantum mechanics version of the equation of motion (3.37) as it forbids the existence of any tachyonic mode with negative mass square, \(m^{2}<0\).Footnote 3 So, in that case, the perturbation is not growing in time, hence the background solution is stable.

The zero-mode wave function \(\psi _0(z)\) can be obtained by noticing that

$$\begin{aligned} \mathcal{Q}\psi _0&=\left( \partial _{z}-\frac{3}{2}\dot{A}\right) \psi _0=0, \end{aligned}$$
(3.38)

which implies that

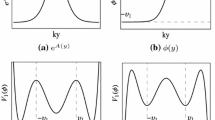
$$\begin{aligned} \psi _0(z)&=e^{\frac{3}{2}A(z)} . \end{aligned}$$
(3.39)

In Fig. 2 we have plotted the zero mode of tensor perturbations \(\psi _0(z)=e^{\frac{3}{2}A(z)}\) given by (3.39) and \(\mathcal{V}(z)\) for the warp function \(A[y(z)]\) (3.23).

Fig. 2
figure 2

This graph shows the behavior of the zero mode for tensor perturbations \(\psi (z)\) and the Schrödinger-like potential \(\mathcal{V}(z)\) as a function of \(z\). The solid lines correspond to the symmetric case \(W_0=0\), whereas the dashed lines refer to the asymmetric case with \(W_0=0.5 M_*^4\) for \(M_*=\beta =1\) and \(\kappa =5\)

Full size image

One can make the following comments resulting from the profile of the zero mode for tensor perturbations \(\psi _0(z)\) and the Schrödinger-like potential \(\mathcal{V}(z)\) shown in Fig. 2:

  • The zero mode \(\psi _0(z)\) implies that

    $$\begin{aligned} \int \mathrm{d}z \psi _0^{2}(z) = \int \mathrm{d}z e^{3A(z)} = \int \mathrm{d}y e^{2A(y)} < \infty , \end{aligned}$$
    (3.40)

    therefore \(\psi _0(z)\) is normalizable and it turns out that the effective 4D Planck mass \(M^{2}_\mathrm{Pl}\) is finite, hence the effective 4D gravity can be reproduced for the thick-brane case.

  • As \(\mathcal{V}(z)\rightarrow 0\) as \(|z|\rightarrow \infty \), therefore the KK-mass spectrum is continuous without a gap and it starts from \(m=0\).

  • The (asymmetric) volcano-like shape of \(\mathcal{V}(z)\) in Fig. 2 suggests that at large \(z\) the wave function’s massive KK modes should have a plane wave behavior.

  • The presence of the large barriers near the thick brane (\(z=0\)) implies that corrections to the Newton’s law due to continuum spectrum of the KK modes will not be large [9, 24].

4 Generalized thick branes

In this section we will consider a general case for the background scalar field. We are going to show that even without an a priori defined shape of the scalar field profile, the thin-brane generalized RS2 relation (2.9) between the brane tension \(\lambda \) and the bulk cosmological constants \(\Lambda _\pm \) is reproduced in the brane limit under certain mild assumptions. In other words the relation is independent of the function adopted to regularize a thin brane. For this purpose we consider the following general form of the scalar background field:

$$\begin{aligned} \phi (y) = \frac{\phi _0 (\beta y)}{\sqrt{\beta }} , \end{aligned}$$
(4.1)

where \(\beta \) will turn out to be the thickness controlling parameter. We assume that \(\phi _0 (\beta y)\) is monotonic, and \((\sqrt{\beta }\phi _0' (\beta y))^2\) is an integrable function of \(y\).Footnote 4 We use the superpotential method described in the previous section. It is worth to note here that the method is equivalent to the standard approach (i.e. solving the Einstein equations) as long as the solutions for scalar field have monotonic profile. Let us consider the scalar field action

$$\begin{aligned} S_\phi&\!=\!\int \mathrm{d}x^5 \sqrt{-g}\left\{ -\frac{1}{2}g^{MN}\nabla _{M}\phi \nabla _{N}\phi -V(\phi )\right\} \nonumber \\&\!=\!\int \mathrm{d}x^5 \sqrt{-g}\left\{ -\left( \frac{\partial W(\phi )}{\partial \phi }\right) ^{2}+\frac{1}{6M_*^{3}}W^{2}(\phi ) \right\} \nonumber \\&\!=\!\int d^5 x \sqrt{- g} \left\{ \!-\! (\phi ')^2 \!+\! \frac{1}{6 M_*^{3}} \left( \int \limits _0^y (\phi '( \bar{y}))^2 d\bar{y} \!+\! W_0 \right) ^2 \right\} , \end{aligned}$$
(4.2)

where \(V(\phi )\) and \(W(\phi )\) are obtained from (3.9) and (3.10), respectively. Since \(W_0\) is an arbitrary integration constant, the lower integration limit could be chosen at \(\bar{y}=0\) without compromising generality. After using (4.1) and changing variables from \(\tilde{y}\rightarrow \beta \bar{y}\) one gets

$$\begin{aligned} S_\phi&= \int d^5x \sqrt{- g} \left\{ - \beta (\phi _0' (\beta y))^2\nonumber \right. \\&\quad + \left. \frac{1}{6 M_*^{3}} \left( \int \limits _0^{\beta y} (\phi _0' (\tilde{y}))^2 d\tilde{y} + W_0 \right) ^2 \right\} . \end{aligned}$$
(4.3)

From the above scalar field action, one finds that, in the brane limit, i.e., \(\beta \rightarrow \infty \):

  • The integrand \(\beta (\phi _0' (\beta y))^2\) converges to zero everywhere except \(y=0\) (as the function is integrable) therefore the first term above approaches \(- \lambda \delta (y)\), with

    $$\begin{aligned} \lambda = \int \limits _{- \infty }^{+ \infty } (\phi _0' (\tilde{y}))^2 d\tilde{y}, \end{aligned}$$

    where \(\delta (y)\) is the Dirac delta function.

  • The second term converges to a sum of contributions to bulk cosmological constants \(- \Lambda _+\Theta (y) - \Lambda _-\Theta (-y)\), where

    $$\begin{aligned} \Lambda _+&= -\frac{1}{6M_*^{3}}\left( \int \limits _0^{+\infty } (\phi _0'(\tilde{y}))^2 d\tilde{y} + W_0 \right) ^2, \end{aligned}$$
    (4.4)
    $$\begin{aligned} \Lambda _-&= -\frac{1}{6M_*^{3}}\left( -\int \limits _{-\infty }^0 (\phi _0'(\tilde{y}))^2 d\tilde{y} + W_0 \right) ^2. \end{aligned}$$
    (4.5)

Equations (4.4)–(4.5) imply that in order to reproduce the generalized RS2 relation (2.9) the following inequality must hold:

$$\begin{aligned} \sqrt{6M_*^{3}}\left( \sqrt{-\Lambda _+}-\sqrt{-\Lambda _-} \right) < \lambda . \end{aligned}$$
(4.6)

Note that this is the same condition as the one that was limiting the splitting between the cosmological constants which was obtained in Sect. 3. Therefore we conclude that regardless of what the choice is of the scalars’ profile, only those thin-brane models could be obtained in the brane limit for which (4.6) is satisfied.

It is easy to see that if \(W_0\) is chosen as

$$\begin{aligned} W_0&= \sqrt{\frac{3}{2} M_*^{3}}\left( \sqrt{-\Lambda _+}-\sqrt{-\Lambda _-} \right) \nonumber \\&\quad + \frac{1}{2} \left( \,\,\int \limits _{-\infty }^0 (\phi _0' (y))^2 \mathrm{d}y - \int \limits _0^{+\infty } (\phi _0' (y))^2 \mathrm{d}y \right) , \nonumber \\ \end{aligned}$$
(4.7)

then indeed

$$\begin{aligned} \lambda = \sqrt{6M_*^{3}}\left( \sqrt{-\Lambda _+}+\sqrt{-\Lambda _-} \right) . \end{aligned}$$
(4.8)

Thus we recover the result (2.9) for our generalized RS2 model. It is worth to rephrase the above result as follows. For any given thin-brane model to be reproduced in the brane limit and any profile of the scalar field \(\phi _0(y)\) (monotonic with \((\phi _0'(y))^2\) integrable), (4.7) provides the choice of the integration constant \(W_0\) which guarantees that the condition (2.9) holds.

In the case of the kink-like profile considered in Sect. 3, \((\phi _0' (y))^2\) was an even function of \(y\); therefore \(W_0\) reduces to the value adopted in (3.19). Of course, if we limit ourself to the \(Z_2\)-symmetric case, \(W_0\) must vanish as in [5].

5 Summary

We have discussed a thick-brane version of the Randall–Sundrum model 2 in which we allow for different cosmological constants on two sides of the brane. The Einstein equations have been solved and stability of the solution has been illustrated. The thin-brane limit of the model have been discussed. The properties of the thick-brane solution have been considered in detail. It has been shown that, under mild assumptions, the relation between cosmological constants and the brane tension of the Randall–Sundrum model 2 could be obtained in the brane limit of our model by an appropriate choice of integrating constant (which defines the scalar potential) independently of the particular profile of the scalar field.

Note added: After this paper has appeared, another interesting study on the same subject has been publicized [25].