Different approaches to calculate the $K^{\pm }\rightarrow \pi ^{\pm }\pi ^0e^+e^-$ decay width

Abstract

The rare $K^\pm \rightarrow \pi ^\pm \pi ^0 e^+e^-$ decay, currently under analysis by the NA62 Collaboration, is considered. We have followed two theoretical approaches to calculate the differential decay width—in the kaon rest frame, where we use Cabibbo–Maksymowicz variables, and in the center-of-mass system of the lepton pair. The latter essentially simplifies the computations. A comparison between the two approaches has been performed. We have also found the dependencies of the differential decay rate as a function of the virtual photon and dipion system masses.

1 Introduction

For many years the radiative kaon decay $K^\pm \rightarrow \pi ^\pm \pi ^0\gamma$ has been considered as a good tool for studying the low energy structure of QCD. The amplitude of this process consists of two parts: a long distance contribution called inner Bremsstrahlung (IB) and a direct emission (DE) part. The IB contribution is associated with the $K^\pm \rightarrow \pi ^{\pm }\pi ^0$ decay according to Low’s theorem [1], and DE can be calculated in the framework of the Chiral Perturbation Theory (ChPT) [2, 3]. In its turn, the DE part is decomposed into electric and magnetic parts. Despite the fact that the $K^\pm \rightarrow \pi ^{\pm }\pi ^0$ decay is suppressed by the $\Delta {I}=1/2$ rule, the Bremsstrahlung contribution is still much larger than DE.

For the above mentioned radiative process DE is the region of relatively hard photons and large angles between pion and photon. The following variables are usually adopted [4, 5]: the charged pion kinetic energy in the kaon rest frame $T_c$; the Lorentz invariant variable $W^2=\frac{(p_1q)(p_Kq)}{m^2m_K^2}$, where $p_1,p_K,q$ are charged pion, kaon, and photon 4-momenta and $m,m_K$—masses of charged pion and kaon. These variables enable one to make a distinction between DE and IB contributions by means of the $W^2$-dependence of the decay width [5].

As the DE piece is almost two orders of magnitude smaller than the Bremsstrahlung contribution [6], the correct consideration of interference terms between IB and DE becomes crucial. Recently, the NA48/2 Collaboration has measured precisely the magnetic contribution and for the first time has found a non-vanishing contribution for the interference between the DE and IB parts of the $K^\pm \rightarrow \pi ^{\pm }\pi ^0\gamma$ decay channel [4]. These results have been obtained due to an accurate Dalitz plot analysis by using ($T_c,W^2$) variables in the kaon rest frame. The NA48/2 Collaboration has also shown that the main contribution in DE, which comes from the magnetic part, is more than one order of magnitude larger than the electric contribution for the $K^\pm \rightarrow \pi ^{\pm }\pi ^0\gamma$.

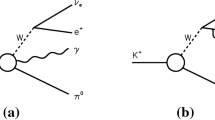
At present the NA62 Collaboration at CERN SPS is analyzing the experimental data on the radiative decay with a virtual photon that has not been observed up to now:

$$\begin{aligned} K^\pm (P_K)\!\rightarrow \!\pi ^\pm \pi ^0\gamma ^*(q)\!\rightarrow \!\pi ^\pm (p_1)\pi ^0(p_2) e^+(k_1)e^-(k_2).\nonumber \\ \end{aligned}$$

(1)

The advantage of this decay in comparison with the radiative decay with a real photon for the DE component extraction is obvious: the photon virtuality ($q^2$) allows one to analyze the additional kinematical region which is absent in the case of real photons (Fig. 1).

Fig. 1

The first two diagrams represent the inner Bremsstrahlung contribution. The third diagram corresponds to the direct emission

The solid theoretical base for this decay was developed in [7], where the DE contribution was calculated up to the next-to-leading order (up to $O(p^4)$) in ChPT.

The essential step has been done recently [8]. The authors have rewritten the matrix element and phase space in terms of five independent variables relevant to the decay with a real photon and have investigated the IB and DE contributions in different kinematical regions.

Keeping in mind the importance of the correct theoretical description of the decay (1) and the necessity of taking into account all possible effects in view of relative smallness of the DE contribution, we have slightly revised the theoretical approach [8] to the $K^{\pm }\rightarrow \pi ^{\pm }\pi ^0e^+e^-$ decay, recalculating the decay width by using the Cabibbo–Maksymowicz variables [9].

As the next step, we have obtained the expression for the differential decay width of $K^\pm \rightarrow \pi ^\pm \pi ^0 e^+e^-$ in the center-of-mass system (c.m.s.) of the lepton pair. Such an approach simplifies the calculations and makes the exploration of the rare process (1) more obvious. Applying the obtained formulas, we calculate the contribution of IB and DE to the differential decay rate as a function of the virtual photon mass $q^2$ and dipion mass $s_\pi$. As a result we have performed a comparison between the two approaches in different frames of the $K^\pm \rightarrow \pi ^\pm \pi ^0 e^+e^-$ decay.

2 Decay width

The invariant amplitude of the decay (1) can be parameterized as a product of leptonic and hadronic currents due to the covariance

$$\begin{aligned} A=\frac{e}{q^2}j^{\mu }(k_1,k_2)J_{\mu }(p_1,p_2,q) \end{aligned}$$

(2)

where $p_1,p_2$ are the 4-momenta of charged and neutral pions, $k_1,k_2$ the leptons’ 4-momenta, and $q = k_1 + k_2$ is the momentum of the virtual photon. The leptonic current is

$$\begin{aligned} j^{\mu }(k_1,k_2)=\bar{u}(k_2)\gamma ^{\mu }v(k_1), \end{aligned}$$

(3)

whereas the hadronic current is represented in terms of two electric form factors, $F_{1,2}$, and the magnetic one, $F_3$:

$$\begin{aligned} J_{\mu }(p_1,p_2,q)=F_1p_{1\mu }+F_2p_{2\mu } +F_3\epsilon ^{\mu \nu \alpha \beta }p_{1\nu }p_{2\mu }q_{\beta }. \end{aligned}$$

(4)

The decay width is given by the standard expression:

$$\begin{aligned} \mathrm{d}\Gamma =\frac{1}{2M_k}|A|^2 \mathrm{d}\Phi . \end{aligned}$$

(5)

The invariant phase space for the four-body decay is usually defined as

$$\begin{aligned} \mathrm{d}\Phi&= (2\pi )^4\delta (P_k-p_1-p_2-k_1-k_2)\nonumber \\&\times \frac{\mathrm{d}^3p_1}{2(2\pi )^3E_1} \frac{\mathrm{d}^3p_2}{2(2\pi )^3E_2} \frac{\mathrm{d}^3k_1}{2(2\pi )^3\varepsilon _1} \frac{\mathrm{d}^3k_2}{2(2\pi )^3\varepsilon _2}. \end{aligned}$$

(6)

The square of the leptonic current summed over spins is given as follows:

$$\begin{aligned} t^{\mu \nu }&= \sum _\mathrm{{spins}}{j^{\mu }j^{\nu }}=4(k_1^{\nu }k_2^{\mu }+ k_2^{\nu }k_1^{\mu }- g^{\mu \nu }(k_1k_2+m_e^2))\nonumber \\&= 2(q_{\mu }q_{\nu }-k_{\mu }k_{\nu }-q^2g^{\mu \nu }), \end{aligned}$$

(7)

where $k=k_1-k_2$ is the difference of leptons momenta, $m_e,m,m_0$ are electron, charged, and neutral pion masses, respectively.

Introducing the relevant variables for the dipion as $P=p_1+p_2$ and $Q=p_1-p_2$ and convoluting expression (7) with the square of the hadronic current (4), we obtain the following expression for the squared amplitude:

$$\begin{aligned} |A|^2&= \frac{e^2}{q^4}(|A_E|^2+|A_M|^2+A_{EM});\nonumber \\ |A_E|^2&= (-4m^2q^2+(qP+qQ)^2-(kP+kQ)^2)|F_1|^2 \nonumber \\&+ (-4m_0^2q^2+(qP-qQ)^2-(kP-kQ)^2)|F_2|^2\nonumber \\&+(F_1F_2^*+F_1^*F_2)(-q^2(P^2-Q^2)+(qP)^2\nonumber \\&+(kQ)^2-(qQ)^2-(kP)^2);\nonumber \\ |A_M|^2\!&= \!|F_3|^2 \{m_e^2[(16m^2m_0^2\!-\!(P^2\!-\!Q^2)^2)q^2\nonumber \\&-\,4m^2((qP)^2\!+\!(qQ)^2))\nonumber \\&-\,4m_0^2((qP)^2-(qQ)^2))\!+\!2(P^2\!-\!Q^2)((qP)^2\!-\!(qQ)^2)]\nonumber \\&+\frac{1}{4}(kP+kQ)^2((qp-qQ)^2-4m_0^2q^2)) \nonumber \\&+\frac{1}{4}(kP-kQ)^2((qP+qQ)^2-4m^2q^2)\nonumber \\&+2((kP)^2\!-\!(kQ)^2) (q^2P^2\!-\!q^2Q^2\!-\!(qP)^2\!+\!(qQ)^2)\};\nonumber \\ A_{EM}&= \left( \left( kP+kQ)(F_1^*F_3+F_1F_3^*) \right. \right. \nonumber \\&\left. \left. +(kP-kQ)(F_2^*F_3+F_2F_3^*)\right. \right) \epsilon ^{\mu \nu \rho \sigma }k_{\mu }q_{\nu }P_{\rho }Q_{\sigma }. \end{aligned}$$

(8)

These formulas¹ are in accordance with expressions (19) from [8]. The only difference is that we take into account the charged and neutral pion mass difference in (8).

The electric form factors can be decomposed into Bremsstrahlung and direct emission pieces: $F_i=F_i^\mathrm{B} +F_i^{\mathrm{{DE}}}$, while the magnetic form factor consists of direct emission only, $F_3=F_3^{\mathrm{{DE}}}$.

Taking into consideration Low’s theorem, the Bremsstrahlung part can be written in terms of the matrix element for the kaon decay into two pions $M(K^+\rightarrow \pi ^+\pi ^0)$ and the sum of amplitudes corresponding to radiation of the virtual photon by the $K^{\pm }$-meson or charged pion:

$$\begin{aligned}&M(K^+\rightarrow \pi ^+\pi ^0 \gamma ^{*})_B= e M(K^+\rightarrow \pi ^+\pi ^0) \nonumber \\&\quad \times \left( - \frac{\epsilon _{\mu }P^{\mu }_k}{(P_k\cdot q) - \frac{q^2}{2}} + \frac{\epsilon _{\mu }p^{\mu }_1}{(p_1 \cdot q)+\frac{q^2}{2}}\right) . \end{aligned}$$

(9)

Comparing this expression with Eq. (4) for the hadronic current, one immediately obtains relations between the lowest order $O(p^2)$ contribution in electric form factors $F_1^\mathrm{B},F_2^\mathrm{B}$ and decay amplitude $M(K^+\rightarrow \pi ^+\pi ^0)$ [8]:

$$\begin{aligned} F_1^\mathrm{B}&= \frac{2ie(qP-qQ)}{(q^2+qQ+qP)(q^2+2qP)}M(K^+\rightarrow \pi ^+\pi ^0),\nonumber \\ F_2^\mathrm{B}&= \frac{-2ie}{q^2+2qP}M(K^+\rightarrow \pi ^+\pi ^0). \end{aligned}$$

(10)

As is mentioned above, the matrix element of the $K^+\rightarrow \pi ^+\pi ^0$ decay and the higher order terms $O(p^4)$ in the form factors caused by direct emission can be calculated in ChPT [7, 8]:

$$\begin{aligned}&M(K^+\rightarrow \pi ^+\pi ^0)\nonumber \\&\quad =\left( \frac{5}{3}G_{27}f_\pi (m_k^2-m^2)-f_\pi \delta {m^2} \left( G_8+\frac{3G_{27}}{2}\right) \right) e^{i\delta ^2_0}\nonumber \\&\quad =|M(K^+\rightarrow \pi ^+\pi ^0)|e^{i\delta ^2_0},\nonumber \\&F_1^{\mathrm{{DE}}}=-\frac{ieG_8e^{\delta ^1_1}}{f_\pi }\left( (qP-qQ)N_E^0+ \frac{4q^2N_E^1}{3}+4q^2L_9\right) ,\nonumber \\&F_2^{\mathrm{{DE}}}=\frac{ieG_8 e^{\delta ^1_1}}{f_\pi } \left( (qP+qQ)N_E^0-\frac{2q^2N_E^{(2)}}{3}\right) ,\nonumber \\&F_3^{\mathrm{{DE}}}=-\frac{2eG_8 e^{\delta ^1_1}}{f_\pi }N_M^0,\nonumber \\&\delta {m^2}=m^2-m_0^2. \end{aligned}$$

(11)

Here $\delta ^2_0$ and $\delta ^1_1$ are the strong phases associated with the interactions of the pions in the final state. In calculations we have used the values of constants from Ref. [8].

These equations allow us to calculate the differential decay width of the rare $K^{\pm }\rightarrow \pi ^{\pm }\pi ^0e^+e^-$ process [7].

On the other hand, to describe the kaon decays to four particles in the final state, it is enough to use five independent variables as was shown for the $K^{\pm }\rightarrow \pi ^+ \pi ^- e^{\pm }\nu$ ($K_{e4}$) decay many years ago [9, 10].

Similarly to the $K_{e4}$ channel, we introduce five independent variables which describe completely the decay (1)—dipion and dilepton invariant masses, $s_{\pi }=(p_1+p_2)^2$ and $s_e=q^2=(k_1+k_2)^2$, and three angles: $\theta _{\pi }$—the angle of the $\pi ^{\pm }$ in the ($\pi ^{\pm }\pi ^0$) c.m.s. with respect to the dipion flight direction; $\theta _e$—the angle of the $e^+$ in the ($e^+e^-$) c.m.s. with respect to the dilepton flight direction and $\varphi$—the angle between dipion and dilepton planes.

Applying Lorentz transformations, one can express the covariant scalar products in formulas (8) in terms of these variables:

$$\begin{aligned}&qP=\frac{m_k^2-s_{\pi }-s_e}{2}; \nonumber \\&qQ= (qP) \cdot \frac{\delta m^2}{s_{\pi }} + \frac{\beta _{\pi } \lambda ^{\frac{1}{2}}(s_{\pi },m^2,m_{K}^2)}{2} \cos {\theta _{\pi }};\nonumber \\&kP=\frac{1}{2} \beta _{e}\lambda ^{\frac{1}{2}}(s_{\pi },m_K^2,q^2) \cos {\theta _{e}}; \end{aligned}$$

(12)

$$\begin{aligned}&kQ=\beta _e \cos {\theta _e}\left[ \frac{\delta m^2}{s_{\pi }} \frac{\lambda ^{\frac{1}{2}}(s_{\pi },m_K^2,q^2)}{2} +(qP)\beta _{\pi } \cos {\theta _{\pi }}\right] \nonumber \\&\quad \qquad \quad -\beta _{\pi } \beta _e(q^2 s_{\pi })^{\frac{1}{2}} \sin {\theta _e} \sin {\theta _{\pi }} \cos {\varphi } \end{aligned}$$

(13)

$$\begin{aligned}&\beta _{\pi }=\frac{\lambda ^{\frac{1}{2}}(s_{\pi },m^2,m_0^2)}{s_{\pi }}; \quad \beta _e=\sqrt{1-\frac{4m_e^2}{s_e}};\nonumber \\&\quad \lambda (x,y,z)=x^2+y^2+z^2-2xy-2xz-2yz. \end{aligned}$$

(14)

Rewriting the invariant phase space (6) in terms of the variables introduced above, we obtain the following:

$$\begin{aligned} \mathrm{d}\Phi&= \frac{1}{4(4\pi )^6}\sqrt{1-\frac{4m_e^2}{s_e}} \sqrt{1-\frac{(m+m_0)^2}{s_\pi }}\nonumber \\&\times \sqrt{1-\frac{(m-m_0)^2}{s_\pi }} \sqrt{1-\frac{(\sqrt{s_\pi }+\sqrt{s_e})^2}{m_k^2}}\nonumber \\&\times \sqrt{1-\frac{(\sqrt{s_\pi }-\sqrt{s_e})^2}{m_k^2}} \mathrm{d}s_{\pi }\mathrm{d}s_e\mathrm{d}\cos {\theta _{\pi }}\mathrm{d}\cos {\theta _e}\mathrm{d}\varphi . \nonumber \\ \end{aligned}$$

(15)

Let us note that the relations (14) and expression (15) for the phase space coincide with the relevant formulas in Ref. [8] if one rewrites them in terms of the corresponding variables.²

3 The decay width calculation in the dilepton center-of-mass system

In the dilepton center-of-mass system ($\vec q=\vec k_1+\vec k_2=0$) the virtual photon 4-momentum is $q=(\omega ,0,0,0)$ and we have $k=\omega (0,v\vec {n})$; $\omega$ is the virtual photon energy, $\vec {n}$ is the unit vector and $v=\sqrt{1-\frac{4m_e^2}{\omega ^2}}$ is the lepton velocity. The lepton tensor $t_{\mu \nu }$ in (7) has the property $t_{00}=t_{0k}$ $(k=1,2,3)$, which essentially simplifies the expression for the product of the lepton and hadron currents:

$$\begin{aligned} J_{\mu }J_{\nu }t_{\mu \nu }=s_e \left( |\vec {J}|^2 - (\vec {J}\vec {v})^2 \right) = s_e\left( |\vec {J}|^2 - v^2(\vec {J}\vec {n})^2 \right) .\nonumber \\ \end{aligned}$$

(16)

The square of the matrix element reads

$$\begin{aligned} \sum _{\lambda } |A|^2=\frac{2e^2}{s_e} \left( |\vec {J}|^2 - \frac{(\vec {J}\vec {q})(\vec {J}\vec {q})}{s_e} \right) . \end{aligned}$$

(17)

Integrating this expression over the solid angle from the phase space (15), one obtains

$$\begin{aligned}&\sum _{\lambda } \int |A|^2 \mathrm{d}\Omega _q=\frac{2\pi e^2}{s_e} |\vec {J}|^2 \left( 1-\frac{k^2}{3q^2}\right) \nonumber \\&\quad =\frac{8\pi e^2}{s_e}|\vec {J}|^2\left( 1-\frac{v^2}{3}\right) . \end{aligned}$$

(18)

The square of the hadron current is a function of the pion three-dimensional momenta $\vec {p_1},\vec {p_2}$ in the dilepton c.m.s.:

$$\begin{aligned} |\vec {J}|^2&= \vec {p_1}^{2}|F_1|^2+ \vec {p_2}^{2}|F_2|^2+2(\vec {p_1}\vec {p_2}) ReF_1F_2^{*}\nonumber \\&+ s_e(\vec {p_1}^2\vec {p_2}^2-(\vec {p_1}\vec {p_2})^2)|F_3|^2. \end{aligned}$$

(19)

To proceed, we divide the pions momenta into longitudinal and transverse parts. Using the Lorentz transformations, we express them in terms of the pion momentum $p^{*}$ in the dipion c.m.s.:

$$\begin{aligned}&p_{1L}=\gamma p^{*} \cos \theta +\beta E_1^{*},\nonumber \\&p_{2L}=-\gamma p^{*} \cos \theta +\beta E_2^{*}, \nonumber \\&|\vec {p_{1\perp }}|=|\vec {p_{2\perp }}|=p^{*}\sin \theta , \end{aligned}$$

(20)

where $\theta$ is the angle between the charged pion in the dipion c.m.s. and the dipion flight direction, $\gamma =\frac{M^2_K-s_{\pi }-s_e}{2\sqrt{s_{\pi }s_e}}$ is the relevant Lorentz factor, and $\beta =\sqrt{\gamma ^2-1}$. Now gathering the appropriate expressions, we obtain

$$\begin{aligned}&\mathrm{d} \Gamma =\frac{{\alpha }^2}{4(4\pi )^3 M_K s_e} ( |F_1|^2 {\vec {p_1}}^2 + |F_2|^2 {\vec {p_2}}^2\nonumber \\&\qquad \quad + 2 (\vec {p_1}\cdot \vec {p_2}) Re(F_1F^{*}_2)\nonumber \\&\qquad \quad + s_e [ {\vec {p_1}}^2 {\vec {p_2}}^2 - (\vec {p_1}\cdot \vec {p_2})^2 ] |F_3|^2 )\nonumber \\&\qquad \quad \times \left( 1-\frac{v^3}{3}\right) \mathrm{d} s_{\pi } \mathrm{d}s_e \mathrm{d}\cos \theta ;\nonumber \\&F^\mathrm{B}_1 =\frac{2 i (\gamma E^{*}_2 - \beta p^{*} \cos {\theta }}{(\gamma E^{*}_1 + \beta p^{*}\cos \theta + \omega /2)(M_K^2-s_{\pi })}\nonumber \\&\qquad \quad \times |M(K^{\pm }\rightarrow \pi ^{\pm }\pi ^0)|e^{i{\delta }^2_0};\nonumber \\&F^\mathrm{B}_2 =\frac{2 i}{(M_K^2-s_{\pi })}\times |M(K^{\pm }\rightarrow \pi ^{\pm }\pi ^0)|e^{i{\delta }^2_0};\nonumber \\&F^{\mathrm{{DE}}}_1 =\frac{2 i G_8}{f_{\pi }}e^{i{\delta }^1_1} \left( N^0_E \omega (\gamma E^{*}_2 - \beta p^{*} \cos \theta )\right. \nonumber \\&\left. \quad \quad \quad +\frac{2}{3} {\omega }^2 N^1_E + 2 q^2 L_9 \right) ;\nonumber \\&F^{\mathrm{{DE}}}_2=\frac{2 i G_8}{f_{\pi }}e^{i{\delta }^1_1} \left( N^0_E \omega (\gamma E^{*}_1 + \beta p^{*}\cos \theta ) +\frac{1}{3} {\omega }^2 N^2_E \right) ;\nonumber \\&F^{\mathrm{{DE}}}_3=\frac{2 e G_8}{f_{\pi }}e^{i{\delta }^1_1}N^0_M. \end{aligned}$$

(21)

These formulas allow us to calculate the differential decay width of the rare process (1) using the minimum set of variables ($s_e,s_\pi ,\theta$).

4 Numerical calculations and comparison of different approaches

First of all we have calculated the contribution of the inner Bremsstrahlung and the full decay width in the frameworks of the two approaches above mentioned. For these calculations we have used the set of constants from Ref. [8], the full kaon width and branching ratio to the hadronic decay $K^\pm \rightarrow \pi ^\pm \pi ^0$ from [6]. The full width of the $K^\pm \rightarrow \pi ^\pm \pi ^0 e^+e^-$ decay is $\Gamma ^{\mathrm{{full}}}=2.231\times 10^{-22}$ MeV, whereas the Bremsstrahlung contribution gives $\Gamma ^{\mathrm{{IB}}}=2.181\times 10^{-22}$ MeV. The branching ratio of the decay under consideration is BR$(K^+\rightarrow \pi ^+\pi ^0e^+e^-)=419.33\times 10^{-8}$. The calculations in two different approaches, the present one and that from Ref. [8], give the same numbers. The computations using the dilepton c.m.s. (21) have an obvious advantage in comparison with the kaon rest system (14)—we need only three integrations for the full decay width calculation instead of the five integrals in Ref. [8].

The dependence of the decay width on invariant masses of dilepton and dipion systems calculated by our formulas (21) has been compared with the MC generator implemented by using the CERNLIB library [11], where the square of the matrix element (8) has been used. The result is shown in Fig. 2. As is seen, the agreement is excellent.

Fig. 2

Comparison of the full differential decay width with respect to invariants $q^2$ and $S_{\pi }$, obtained by theoretical calculation in the lepton pair c.m.s. (solid curve) and with the MC generator in the kaon rest frame formulation (dots are given with their statistical errors)

Looking at the comparison between $\frac{\mathrm{d}\Gamma ^{\mathrm{{IB}}}}{\mathrm{d}q^2} (\frac{\mathrm{d}\Gamma ^{\mathrm{{IB}}}}{\mathrm{d}s_{\pi }})$ and $\frac{\mathrm{d}\Gamma ^\mathrm{full}}{\mathrm{d}q^2} (\frac{\mathrm{d}\Gamma ^\mathrm{full}}{\mathrm{d}s_{\pi }})$, shown in Fig. 3, one can see that the difference between them due to the direct emission contribution is small and it is evident at large values of $q^2$ and in the region of small values of $s_{\pi }$.

Fig. 3

Comparison between the decay width of IB contribution (solid line) and the full decay width (dashed line) with respect to the invariant masses of the dilepton and dipion systems

The direct emission contribution in the full decay width of the $K^{\pm }\rightarrow \pi ^{\pm }\pi ^0e^+e^-$ is ${\sim }2.3~\%$, whereas in the case of the $K^{\pm }\rightarrow \pi ^{\pm }\pi ^0\gamma$ it is ${\sim }3.32~\%$ [4].

We took the values of the $N^0_E$ and $N^0_M$ constants in (21) from the experimental study of the $K^{\pm }\rightarrow \pi ^{\pm }\pi ^0\gamma$ by the NA48/2 Collaboration [4] and implemented them in the DE piece computation.

5 Summary

The general expression for the differential width of the $K^\pm \rightarrow \pi ^\pm \pi ^0e^+e^-$ decay has been investigated in the kaon rest frame and the dilepton c.m.s. Previously we had calculated the differential decay width in terms of the Cabibbo–Maksymowicz variables. We had also used the decay amplitude in the c.m.s. of the lepton pair, which is more convenient for computations. By means of these expressions, we have calculated the branching ratio of the $K^\pm \rightarrow \pi ^\pm \pi ^0 e^+e^-$ channel and obtained the dependencies of the differential width on virtual photon mass $q^2$ and the invariant mass of pion pair $s_\pi$ for inner Bremsstrahlung and full decay widths. The comparison between the approaches discussed is presented by using the dependence of the decay width on the invariant masses $s_{\pi }$ and $q^2$.