1 Introduction

As is well known, our current universe is flat and undergoing a phase of accelerated expansion, which is supported by the recent observational data sets [1, 2]. In principle, this phenomenon can be explained by either dark energy (see Ref. [3] for reviews) which constitutes about three-fourths of the whole matter budget of our universe according to the recent WMAP data [4] and Planck data [5]. This phenomenon would be due to an exotic component with large negative pressure, or else would be described by modified theories of gravity [6–11]. Alternative to dark energy, modified theories of gravity are extremely attractive; a new modified gravity theory, namely the so-called \(f(T)\) theory, has been proposed recently to drive the current accelerated expansion without invoking dark energy [12–16]. It is a generalized version of the so-called teleparallel gravity originally proposed by Einstein [17]. Moreover, the modified Gauss–Bonnet gravity, i.e., \(f(G)\) gravity, where \(f(G)\) is a general function of the Gauss–Bonnet (GB) term, was studied in [18–22]. At present specific models of \(f(G)\) gravity have been proposed to account for the late-time cosmic acceleration [22–24]. Recently the energy conditions in \(f(G)\) gravity have been also discussed [25], but they are only adapted to \(f(G)\) gravity without coupling between matter and geometry. \(f(G)\) gravity models with curvature–matter coupling have been proposed, and some relevant issues, such as the energy conditions, the stability criterion, and the conditions for late-time cosmic accelerated expansion, have been studied in [26].

In addition, another interesting alternative modified theory of gravity is \(f(R)\) gravity (see, for instance, Ref. [27] for reviews). Here \(f(R)\) is an arbitrary function of the Ricci scalar \(R\). Cosmic acceleration can be explained by \(f(R)\) gravity [28], and the conditions of viable cosmological models have been derived in [29–34]. A general model of \(f(R)\) gravity has been proposed in Ref. [35], which contains a non-minimal coupling between geometry and matter. This coupling term can be considered as a gravitational source to explain the current acceleration of the universe. As a result of the coupling the motion of the massive particles is non-geodesic, and an extra force, orthogonal to the four-velocity, arises. Different forms for the Lagrangian density of matter \(L_{m}\), and the resulting extra force, were considered in [36], and it was shown that more natural forms for \(L_{m}\) do not imply the vanishing of the extra force. The implications of the non-minimal coupling on the stellar equilibrium were investigated in [37, 38], where constraints on the coupling were also obtained. An inequality which expresses a necessary and sufficient condition to avoid the Dolgov–Kawasaki instability for the model was derived in [39–45]. However, a more general model, in which the coupling style is arbitrary and the Lagrangian density of matter only appears in the coupling term, has been proposed in Ref. [46], i.e., the so-called the generalized \(f(R)\) gravity with arbitrary coupling between matter and geometry. In this class of models the energy-momentum tensor of the matter is generally not conserved, and the matter–geometry coupling can induce a supplementary acceleration of the test particles. The first law and the generalized second law of thermodynamics for the generalized \(f(R)\) gravity with curvature–matter coupling have been studied in the spatially homogeneous, isotropic FRW universe [47]. Moreover, the energy conditions and the Dolgov–Kawasaki criterion for the model have been derived in Refs. [48, 49], which are quite general and can degenerate to the well-known energy conditions in GR and \(f(R)\) gravity with non-minimal coupling and non-coupling as special cases.

On the other hand, it is well known that gravity is the only dominant long-range interaction, and we do not fully understand the character of gravity on a cosmological scale yet. Therefore, alternative theories of gravity were proposed such as the Kaluza–Klein (KK) theory [50–54], which was initiated by the motivation of unifying the gravitation field and the electromagnetic field in a 5D metric. Since the fifth dimension is supposed to be a compact \(S^{1}\) circle with an extremely tiny radius, it would actually yield no observable effect. Recently a new model of modified KK cosmology was studied in [55], where the universe in turns inflates, decelerates, and then accelerates, in early times, radiation-dominated era, and matter-dominated era, respectively, which shows that the results meet the observational facts roughly. In addition, the Brans–Dicke (BD) theory of gravity, introduced in [56] to match the Mach principle, was extended to 5D spacetime, which can naturally predict the cosmic acceleration without the requirement of a time-varying BD parameter \(\omega \) [57] or a fabricated potential in its 4D counterpart [58, 59]. Recently, the 5D \(f(R)\) theories of gravity without coupling were studied in [60], in which the fifth dimension is supposed to be a small unobservable compact ring \(S^{1}\) so that a Killing vector field would arise naturally in the low energy environment. The 5D theories can be reduced to their 4D formalism by using the Killing reduction. Thus, a natural question we may ask is whether the generalized \(f(R)\) gravity with curvature–matter coupling can be extended to 5D spacetime, as well as what effects in the 4D sensational world arise when this 5D generalized \(f(R)\) gravity is reduced to the 4D spacetime, which are our motivations and purposes in this paper. The research results show that the extension of the 4D generalized \(f(R)\) gravity to 5D spacetime can be realized by assuming a hypersurface-orthogonal space-like Killing vector field in 5D spacetime. The evolutionary trajectories of the scale factor \(a(t)\), the deceleration parameter \(q(t)\), and the scalar field \(\epsilon (t),\phi (t)\) of the specific models can be illustrated in the reduced 4D spacetime, which shows that this type of models can explain the current accelerated expansion of our universe.

This paper is organized as follows. In Sect. 2, we will study the generalized \(f(R)\) gravity with curvature–matter coupling in 5D spacetime by using Killing reduction, which can be set up as a 4D formalism with coupling with two scalar fields. In Sect. 3, we will discuss the reduced generalized \(f(R)\) model in the homogeneous and isotropic universe with the 4D FRW metric. In Sect. 4, the accelerated universe in reduced generalized \(f(R)\) gravity will be investigated by a numerical analysis of the evolutionary trajectories of the scale factor \(a(t)\), the deceleration parameter \(q(t)\), and the scalar field \(\epsilon (t),\phi (t)\). In the two sections, the corresponding results for the special cases will be discussed. The conclusions of our work will be given in the last section.

2 Killing reduction of 5D generalized \(f(R)\) gravity

The action of 5D \(f(R)\) gravity [60] is

$$\begin{aligned} S=\int {\mathcal {L}}^{(5)}\sqrt{-g}\hbox {d}^{5}x= \int \left[ \frac{1}{2\kappa }f(R)+L_{m}\right] \sqrt{-g}\hbox {d}^{5}x, \end{aligned}$$
(1)

in which \(\kappa =8\pi G^{(5)}/c^{4},G^{(5)}\) is the gravitational constant in the 5D spacetime, and \(L_{m}\) represents the Lagrangian density of matter.

In the following, we consider the generalized \(f(R)\) gravity studied in [46–49], in which the coupling style between matter and geometry is arbitrary and the Lagrangian density of matter only appears in coupling term. Now, its action can be extended from 4D to 5D spacetime as follows:

$$\begin{aligned} S&= \int {\mathcal {L}}^{(5)}\sqrt{-g}\hbox {d}^{5}x\nonumber \\&= \int \left[ \frac{1}{2\kappa }f_{1}(R)+B(L_{m})f_{2}(R)\right] \sqrt{-g}\hbox {d}^{5}x, \end{aligned}$$
(2)

where \(f_{i}(R)(i=1,2)\) and \(B(L_{m})\) are arbitrary functions of the Ricci scalar \(R\) and the Lagrangian density of matter, respectively. It follows that when \(f_{2}(R)=1\) and \(B(L_{m})=L_{m}\), Eq. (2) can be reduced to Eq. (1).

Varying the action (2) with respect to the metric \(g^{ab}\) of 5D spacetime yields the field equation

$$\begin{aligned}&F_{1}(R)R_{ab}-\frac{1}{2}f_{1}(R)g_{ab}+(g_{ab} \Box -\nabla _{a}\nabla _{b})F_{1}(R)\nonumber \\&\quad =\kappa \{-2B(L_{m})F_{2}(R)R_{ab} -2(g_{ab}\Box -\nabla _{a}\nabla _{b})\nonumber \\&\qquad \times B(L_{m})F_{2}(R) -f_{2}(R)\left[ K(L_{m})L_{m}-B(L_{m})\right] g_{ab}\nonumber \\&\qquad +f_{2}(R)K(L_{m})T_{ab}\}, \end{aligned}$$
(3)

where \(T_{ab}=\frac{-2}{\sqrt{-g}}\frac{\delta S_{m}}{\delta g^{ab}}\) is the energy-momentum tensor for matter fields, \(\Box =g^{ab}\nabla _{a}\nabla _{b}\), \(F_{i}(R)=\hbox {d}f_{i}(R)/\hbox {d}R (i=1,2)\) and \(K(L_{m})=\hbox {d}B(L_{m})/\hbox {d}L_{m}\), respectively. Note that \(R\), \(R_{ab}\), and \(T_{ab}\) represent quantities in the 5D spacetime. By contraction of Eq. (3) with \(g^{ab}\), we obtain the dynamical equation for \(F_{1}(R)+2\kappa B(L_{m})F_{2}(R)\):

$$\begin{aligned}&\nabla ^{a}\nabla _{a}\left[ F_{1}(R)+2\kappa B(L_{m})F_{2}(R)\right] \nonumber \\&\quad =\frac{1}{4}\left\{ \frac{5}{2}f_{1}(R)-RF_{1}(R) -2\kappa B(L_{m})F_{2}(R)R \right. \nonumber \\&\qquad -5\kappa f_{2}(R)\left[ K(L_{m})L_{m}-B(L_{m})\right] \nonumber \\&\qquad \left. +\kappa f_{2}(R)K(L_{m})T^{(5)}\right\} , \end{aligned}$$
(4)

in which \(g_{ab}g^{ab}=5\) instead of 4. By using the field equation, the Ricci tensor \(R^{(5)}_{ab}\) is given by

$$\begin{aligned} R^{(5)}_{ab}&= \frac{1}{f'_{1}+2\kappa Bf'_{2}}\left\{ \frac{1}{2}g_{ab}f_{1}-\kappa f_{2}(B'L_{m}-B)g_{ab}\right. \nonumber \\&\left. +\kappa f_{2}B'T^{(5)}_{ab}-(g_{ab}\Box - \nabla _{a}\nabla _{b})f'_{1}\right. \nonumber \\&\left. -2\kappa (g_{ab}\Box -\nabla _{a}\nabla _{b})(Bf'_{2})\right\} . \end{aligned}$$
(5)

For convenience, \(f_{i}=f_{i}(R)(i=1,2)\), \(B=B(L_{m})\), and the prime denotes differentiation with respect to the Ricci scalar \(R\) and the Lagrangian density \(L_{m}\), respectively.

Below, following the idea of [60], the structure of the 5D spacetime is considered by assuming that the 5D spacetime possesses a Killing vector field \(\eta ^{a}\) which represents the fifth dimension and is everywhere space-like. Hence, the 5D metric can be expressed as

$$\begin{aligned} g_{ab}=h_{ab}+\epsilon ^{-1}\eta _{a}\eta _{b}, \end{aligned}$$
(6)

where \(h_{ab}\) is the metric in the usual 4D universe and \(\epsilon =\eta ^{a}\eta _{a}\). We choose a coordinate system \(\{x^{\mu },x^{5}\}\), \(\mu =0,1,2,3\), adapted to the congruence of \(\eta ^{a}\), i.e., \((\frac{\partial }{\partial x^{5}})^{a}=\eta ^{a}\). In the case where \(\eta ^{a}\) is not hypersurface orthogonal (\(\eta _{\mu }\ne 0\)), \(\eta _{\mu }\) will behave as the electromagnetic 4-potential in the reduced 4D theory. Since we are concerned mainly with the cosmological effect of the reduced model, to simplify the discussion, we will consider only the case where \(\eta ^{a}\) is hypersurface orthogonal. Thus, the line element of \(g_{ab}\) reads \(\hbox {d}s^{2}=g_{\mu \nu }\hbox {d}x^{\mu }\hbox {d}x^{\nu }+\epsilon \hbox {d}x^{5}\hbox {d}x^{5}\). Through Killing reduction [61, 62], the Ricci tensor \(R^{(4)}_{ab}\) of the 4-metric \(h_{ab}\) and the scalar field \(\epsilon \) are related to the Ricci tensor \(R^{(5)}_{ab}\) of \(g_{ab}\) by

$$\begin{aligned} R^{(4)}_{ab}=\frac{1}{2}\epsilon ^{-1}D_{a}D_{b} \epsilon -\frac{1}{4}\epsilon ^{-2}(D_{a}\epsilon )D_{b} \epsilon +h^{m}_{a}h^{n}_{b}R^{(5)}_{mn}, \end{aligned}$$
(7)

and

$$\begin{aligned} D^{2}\epsilon =\frac{1}{2}\epsilon ^{-1}(D^{a} \epsilon )D_{a}\epsilon -2R^{(5)}_{ab}\eta ^{a}\eta ^{b}, \end{aligned}$$
(8)

where \(D_{a}\) is the covariant derivative on 4D spacetime, which satisfies all the conditions of a derivative operator. Furthermore, the stress-energy tensor in (3) is regarded to be the one for a perfect fluid in 5D spacetime, with the form

$$\begin{aligned} T^{(5)}_{ab}&= L^{-1}\epsilon ^{-\frac{1}{2}} \left[ \left( \rho +\frac{P}{c^{2}}\right) U_{a}U_{b}+Pg_{ab}\right] \nonumber \\&= L^{-1}\epsilon ^{-\frac{1}{2}}\left[ T^{(4)}_{ab}+P\epsilon ^{-1}\eta _{a}\eta _{b}\right] , \end{aligned}$$
(9)

in which \(\rho \) and \(P\) are the 4D energy density and the hydrostatic pressure, respectively, \(L\) is the coordinate scale of the fifth dimension. Using the field equation (3), and Eqs. (6) and (7), we can obtain the 4D field equation for \(h_{ab}\), thus,

$$\begin{aligned} G^{(4)}_{ab}&= \frac{1}{2}\epsilon ^{-1}(D_{a}D_{b}\epsilon -h_{ab}D^{c}D_{c}\epsilon ) \nonumber \\&-\frac{1}{4}\epsilon ^{-2}\left[ (D_{a}\epsilon )D_{b}\epsilon -h_{ab}(D^{c}\epsilon )D_{c}\epsilon \right] \nonumber \\&+\frac{1}{f'_{1}+2\kappa Bf'_{2}}\left\{ \frac{1}{2}h_{ab}\left[ f_{1}-(f'_{1}+2\kappa Bf'_{2})R\right. \right. \nonumber \\&\left. -2\kappa f_{2}(B'L_{m}-B)\right] +(D_{a}D_{b}-h_{ab}D^{c}D_{c})f'_{1}\nonumber \\&\left. +2\kappa (D_{a}D_{b}-h_{ab}D^{c}D_{c})(Bf'_{2})- \frac{1}{2}\epsilon ^{-1}h_{ab}(D^{c}\epsilon ) \right. \nonumber \\&\left. \times D_{c}f'_{1} - \kappa h_{ab}\epsilon ^{-1}(D^{c}\epsilon )D_{c}(Bf'_{2}) \right. \nonumber \\&\left. + \kappa f_{2}B'L^{-1}\epsilon ^{-\frac{1}{2}}T^{(4)}_{ab}\right\} . \end{aligned}$$
(10)

By using Eq. (8), we obtain the dynamical equation of \(\epsilon \):

$$\begin{aligned} D^{a}D_{a}\epsilon&= \frac{1}{2}\epsilon ^{-1}(D^{a} \epsilon )D_{a}\epsilon -\frac{1}{f'_{1}+2\kappa Bf'_{2}}\left\{ \frac{\epsilon }{2}\left[ -\frac{1}{2}f_{1}\right. \right. \nonumber \\&\left. +\kappa f_{2}(B'L_{m}-B) +(f'_{1}+2\kappa Bf'_{2})R\right] \nonumber \\&\left. +(D^{a}\epsilon )D_{a}f'_{1}+2\kappa (D^{a}\epsilon )D_{a}(Bf'_{2})\right. \nonumber \\&\left. -\kappa f_{2}B'L^{-1}\epsilon ^{\frac{1}{2}}\left( \frac{1}{2}T^{(4)}-\frac{3}{2}P\right) \right\} . \end{aligned}$$
(11)

The dynamical equation of \(f'_{1}+2\kappa Bf'_{2}\) is

$$\begin{aligned}&D^{a}D_{a}(f'_{1}+2\kappa Bf'_{2})=\frac{1}{4}\left\{ \frac{5}{2}f_{1}-Rf'_{1}-2\kappa Bf'_{2}R \right. \nonumber \\&\quad \left. -5\kappa f_{2}(B'L_{m}-B) +\kappa f_{2}B'L^{-1}\epsilon ^{-\frac{1}{2}}(T^{(4)}+P)\right\} \nonumber \\&\quad -\frac{1}{2}\epsilon ^{-1}(D^{c}\epsilon )D_{c}f'_{1} -\kappa \epsilon ^{-1}(D^{c}\epsilon )D_{c}(Bf'_{2}). \end{aligned}$$
(12)

Equations (10)–(12) are just the 4D gravitational field equations.

3 The reduced generalized \(f(R)\) gravity in FRW universe

The 4D spatially homogeneous and isotropic FRW universe is considered and described by the metric

$$\begin{aligned} \hbox {d}s^{2}=-\hbox {d}t^{2}+a(t)^{2} \left( \frac{\mathrm{d}r^{2}}{1-kr^{2}}+r^{2}\mathrm{d}\Omega ^{2}_{2}\right) , \end{aligned}$$
(13)

where \(a(t)\) is the scale factor of the universe with \(t\) being the cosmic time and \(\hbox {d}\Omega ^{2}_{2}\) is the metric of the 2D sphere with unit radius; the spatial curvature constant \(k\) takes the values \(+1,0,-1\) according to a closed, flat, and open universe, respectively. Below, we only consider the spatially flat case, i.e., \(k=0\). Thus the two components of the field equation (10) are

$$\begin{aligned}&3\left( \frac{\dot{a}}{a}\right) ^{2}=-\frac{3}{2}\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }-3\frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi } -\frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi }+\frac{1}{\phi }\nonumber \\&\quad \times \left\{ \frac{8\pi G}{c^{2}}\cdot f_{2}B'\epsilon ^{-\frac{1}{2}}\rho \!+\!\frac{1}{2}\left[ 2\kappa f_{2}\left( B'L_{m}-B\right) \!+\!R\phi \!-\!f_{1}\right] \!\right\} ,\nonumber \\ \end{aligned}$$
(14)

and

$$\begin{aligned}&-\left( 2\frac{\ddot{a}}{a}+\frac{\dot{a}^{2}}{a^{2}}\right) = \frac{1}{2}\frac{\ddot{\epsilon }}{\epsilon }+ \frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon } -\frac{1}{4}\frac{\dot{\epsilon }^{2}}{\epsilon ^{2}}+ \frac{\ddot{\phi }}{\phi }+2\frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi } \nonumber \\&\quad +\frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi } +\frac{1}{2\phi }\left[ f_{1} -R\phi -2\kappa f_{2}(B'L_{m}-B)\right] \nonumber \\&\quad +\frac{8\pi G}{c^{4}}\cdot \frac{f_{2}B'\epsilon ^{-\frac{1}{2}}}{\phi }P, \end{aligned}$$
(15)

where \(\phi \equiv f'_{1}+2\kappa Bf'_{2}\). Furthermore, the dynamical equations of \(\epsilon \), \(\phi \), and the scale factor \(a(t)\) can be obtained by means of the above equations as well as Eqs. (11) and (12):

$$\begin{aligned}&\frac{\ddot{\epsilon }}{\epsilon }=-3 \frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }+\frac{1}{2}\frac{\dot{\epsilon }^{2}}{\epsilon ^{2}} -\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi } \nonumber \\&\qquad \quad + \frac{1}{2\phi }\left[ -\frac{1}{2}f_{1}+R\phi +\kappa f_{2}(B'L_{m}-B)\right] \nonumber \\&\qquad \quad +\frac{8\pi G}{c^{2}}\cdot \frac{f_{2}B'\epsilon ^{-\frac{1}{2}}}{\phi }\cdot \frac{\rho }{2}, \end{aligned}$$
(16)
$$\begin{aligned}&\frac{\ddot{\phi }}{\phi }=-3 \frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi }- \frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi } \nonumber \\&\qquad \quad -\frac{1}{4\phi } \left[ \frac{5}{2}f_{1}-R\phi -5\kappa f_{2}(B'L_{m}-B) \right] \nonumber \\&\qquad \quad +\frac{8\pi G}{c^{2}}\cdot \frac{f_{2}B'\epsilon ^{-\frac{1}{2}}}{\phi }\cdot \left( \frac{\rho }{4}-\frac{P}{c^{2}}\right) , \end{aligned}$$
(17)
$$\begin{aligned}&\frac{\ddot{a}}{a}=\frac{\dot{a}^{2}}{a^{2}}+\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }+2\frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi } +\frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi }+\frac{1}{4\phi } \left[ \frac{3}{2}f_{1}-R\phi \right. \nonumber \\&\quad \left. +3\kappa f_{2}(B'L_{m}-B)\right] -\frac{8\pi G}{c^{2}}\cdot \frac{f_{2}B'\epsilon ^{-\frac{1}{2}}}{\phi }\cdot \frac{3\rho }{4}. \end{aligned}$$
(18)

These are the reduced 4D gravitational field equations from the generalized \(f(R)\) gravity with curvature–matter coupling in 5D spacetime, which is abbreviated as FGCMC hereafter.

Now some comments on Eqs. (16)–(18) are given.

  1. 1.

    Let \(B(L_{m})=L_{m}\) and \(f_{2}(R)\) be rescaled as \(1+\lambda f_{2}(R)\), then Eqs. (16)–(18) can be changed into

    $$\begin{aligned}&\frac{\ddot{\epsilon }}{\epsilon }=-3\frac{\dot{a}}{a} \frac{\dot{\epsilon }}{\epsilon }+\frac{1}{2} \frac{\dot{\epsilon }^{2}}{\epsilon ^{2}} -\frac{\dot{\epsilon }}{\epsilon } \frac{\dot{\phi }}{\phi }+\frac{1}{2\phi } \left[ -\frac{1}{2}f_{1}+R\phi \right] \nonumber \\&\qquad \quad +\frac{8\pi G}{c^{2}}\cdot \frac{(1+\lambda f_{2}) \cdot \epsilon ^{-\frac{1}{2}}}{\phi }\cdot \frac{\rho }{2}, \end{aligned}$$
    (19)
    $$\begin{aligned}&\frac{\ddot{\phi }}{\phi }=-3\frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi }-\frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi } -\frac{1}{4\phi }\left[ \frac{5}{2}f_{1}-R\phi \right] \nonumber \\&\qquad \quad +\frac{8\pi G}{c^{2}}\cdot \frac{(1+\lambda f_{2}) \cdot \epsilon ^{-\frac{1}{2}}}{\phi }\cdot \left( \frac{\rho }{4}-\frac{P}{c^{2}}\right) , \end{aligned}$$
    (20)
    $$\begin{aligned}&\frac{\ddot{a}}{a}=\frac{\dot{a}^{2}}{a^{2}}+\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }+2\frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi } +\frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi }+\frac{1}{4\phi } \left[ \frac{3}{2}f_{1}-R\phi \right] \nonumber \\&\qquad \quad -\frac{8\pi G}{c^{2}}\cdot \frac{(1+\lambda f_{2}) \cdot \epsilon ^{-\frac{1}{2}}}{\phi }\cdot \frac{3\rho }{4}. \end{aligned}$$
    (21)

    Here \(\phi =f'_{1}+2\kappa \lambda L_{m}f'_{2}\). Evidently, Eqs. (19)–(21) are just the reduced 4D gravitational field equations from the 5D \(f(R)\) gravity with non-minimal coupling, FGNMC for short.

  2. 2.

    By setting \(B(L_{m})=L_{m}\), \(f_{2}(R)=1\), which results in \(\phi =f'_{1}\), in the case of the corresponding results for Eqs. (16)–(18) we have

    $$\begin{aligned}&\frac{\ddot{\epsilon }}{\epsilon }=-3\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }+\frac{1}{2}\frac{\dot{\epsilon }^{2}}{\epsilon ^{2}} -\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi } \nonumber \\&\qquad \quad +\frac{1}{2\phi }\left[ -\frac{1}{2}f_{1}+R\phi \right] +\frac{8\pi G}{c^{2}}\cdot \frac{\epsilon ^{-\frac{1}{2}}}{\phi }\cdot \frac{\rho }{2}, \end{aligned}$$
    (22)
    $$\begin{aligned}&\frac{\ddot{\phi }}{\phi }=-3\frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi }-\frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi } \nonumber \\&\qquad \quad -\frac{1}{4\phi }\left[ \frac{5}{2}f_{1}-R\phi \right] +\frac{8\pi G}{c^{2}}\cdot \frac{\epsilon ^{-\frac{1}{2}}}{\phi }\cdot \left( \frac{\rho }{4}-\frac{P}{c^{2}}\right) , \end{aligned}$$
    (23)
    $$\begin{aligned}&\frac{\ddot{a}}{a}=\frac{\dot{a}^{2}}{a^{2}}+\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }+2\frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi } +\frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi }\nonumber \\&\qquad \quad +\frac{1}{4\phi } \left[ \frac{3}{2}f_{1}-R\phi \right] -\frac{8\pi G}{c^{2}}\cdot \frac{\epsilon ^{-\frac{1}{2}}}{\phi }\cdot \frac{3\rho }{4}. \end{aligned}$$
    (24)

    The above equations are just the reduced ones from 5D pure \(f(R)\) gravity with no coupling, FGNC for short, which are consistent with the ones in Ref. [60].

  3. 3.

    If \(B(L_{m})=L_{m}\), \(f_{2}(R)=1\) and \(f_{1}(R)=R\), we have \(\phi =1\). Thus, Eqs. (16)–(18) become

    $$\begin{aligned}&\frac{\ddot{\epsilon }}{\epsilon }=-3\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }+\frac{1}{2}\frac{\dot{\epsilon }^{2}}{\epsilon ^{2}} +\frac{R}{4} +\frac{8\pi G}{c^{2}}\cdot \frac{\epsilon ^{-\frac{1}{2}}\rho }{2}, \end{aligned}$$
    (25)
    $$\begin{aligned}&\frac{\ddot{a}}{a}=\frac{\dot{a}^{2}}{a^{2}}+\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon } +\frac{R}{8}-\frac{8\pi G}{c^{2}}\cdot \frac{3\epsilon ^{-\frac{1}{2}}\rho }{4}, \end{aligned}$$
    (26)

    which are just the reduced 4D gravitational field equations from 5D Einstein gravity (EG).

It follows that Eqs. (16)–(18) are quite general and can give the corresponding results for Einstein gravity, and \(f(R)\) gravity with no-coupling and non-minimal coupling in 5D spacetime as special cases.

4 The accelerated universe for the reduced generalized \(f(R)\) gravity

Now, we consider a specific type of \(f(R)\) models, \(f_{1}(R)=f_{2}(R)=\alpha R^{m}\) (\(m\ne 1\)), and we choose \(B(L_{m})=L_{m}=-\rho \) in order to further study the evolutionary characters of some cosmological quantities such as the scale factor \(a(t)\), the deceleration parameter \(q(t)\) etc. According to \( \phi \equiv f'_{1}+2\kappa Bf'_{2}=\alpha m(1-2\kappa \rho )R^{m-1}\), we obtain \(R=\left[ \frac{\phi }{\alpha m(1-2\kappa \rho )}\right] ^\frac{1}{m-1}\), \(f_{1}(R)=f_{2}(R)=\frac{\phi }{m(1-2\kappa \rho )} \left[ \frac{\phi }{\alpha m(1-2\kappa \rho )}\right] ^\frac{1}{m-1}\), where \(\alpha \) is a dimensional constant. Furthermore, we consider the present epoch of the universe to be matter dominated and choose \(p=0\) and \(\rho =\rho _{0}(\frac{a_{0}}{a})^{3}\); thus the three cosmological evolution equations from the combination of Eqs. (16)–(18) are

$$\begin{aligned}&\frac{\ddot{\epsilon }}{\epsilon }=-3\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }+\frac{1}{2}\frac{\dot{\epsilon }^{2}}{\epsilon ^{2}} -\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi } \nonumber \\&\quad -\left[ \frac{\phi }{\alpha m\left( 1-2\kappa \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}\right) }\right] ^\frac{1}{m-1} \nonumber \\&\quad \times \left[ \frac{1-2m\left( 1-2\kappa \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}\right) -2\epsilon ^{-\frac{1}{2}}\cdot c^{2}\kappa L^{-1}\cdot \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}}{4m\left( 1-2\kappa \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}\right) }\right] ,\nonumber \\ \end{aligned}$$
(27)
$$\begin{aligned}&\frac{\ddot{\phi }}{\phi }=-3\frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi }-\frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi } \nonumber \\&\quad -\left[ \frac{\phi }{\alpha m\left( 1-2\kappa \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}\right) }\right] ^\frac{1}{m-1} \nonumber \\&\quad \times \left[ \frac{5-2m\left( 1-2\kappa \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}\right) -2\epsilon ^{-\frac{1}{2}}\cdot c^{2}\kappa L^{-1}\cdot \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}}{8m\left( 1-2\kappa \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}\right) }\right] ,\nonumber \\ \end{aligned}$$
(28)
$$\begin{aligned}&\frac{\ddot{a}}{a}=\left( \frac{\dot{a}}{a}\right) ^{2}+\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }+2\frac{\dot{a}}{a}\frac{\dot{\phi }}{\phi } +\frac{1}{2}\frac{\dot{\epsilon }}{\epsilon }\frac{\dot{\phi }}{\phi } \nonumber \\&\quad +\left[ \frac{\phi }{\alpha m\left( 1-2\kappa \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}\right) }\right] ^\frac{1}{m-1} \nonumber \\&\quad \times \left[ \frac{3-2m\left( 1-2\kappa \rho _{0} \left( \frac{a_{0}}{a}\right) ^{3}\right) -6\epsilon ^{-\frac{1}{2}}\cdot c^{2}\kappa L^{-1}\cdot \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}}{8m\left( 1-2\kappa \rho _{0}\left( \frac{a_{0}}{a}\right) ^{3}\right) }\right] .\nonumber \\ \end{aligned}$$
(29)

It is worth stressing that for the above derivations we have taken \(G=6.67\times 10^{-11}~\hbox {kg}^{-1}\,\hbox {m}^{3}\,\hbox {s}^{-2}\), \(\rho _{0}=(3.8\pm 0.2)\times 10^{-28}~\hbox {kg~m}^{-3}\), \(H_{0}=(2.3\pm 0.1)\times 10^{-18}~\hbox {s}^{-1}\) [63] and \(G^{(5)}=G\cdot L=6.67\times 10^{-44}~\hbox {kg}^{-1}~\hbox {m}^{4}~\hbox {s}^{-2}\) (note \(L=10^{-34}~\hbox {m}\)). For the numerical simulation, \(a_{0}\) and \(\epsilon _{0}\) themselves have no direct physical meaning, therefore they can be simply fixed as 1 with no dimension. Thus, we can directly determine the value of \({\dot{a}}_{0}\) by the present value of the Hubble parameter \(H_{0}=(\frac{\dot{a}}{a})_{t_{0}}\). Furthermore, we adopt the idea in the dynamical compactification model of KK cosmology [64], i.e., the extra dimensions contract while the four visible dimensions expand in order to assume that the present universe satisfies [57]

$$\begin{aligned} a^{3}(t)\epsilon ^{\frac{n}{2}}(t)=\hbox {constant}, \end{aligned}$$
(30)

where \(n\) is a positive number. Hence, we have \(\frac{\dot{\epsilon }}{\epsilon }=-\frac{6}{n}H\). In addition, in the spirit of the literature [60], we expect \(\epsilon ^{-\frac{1}{2}}\phi ^{\frac{1}{m-1}}\sim 1\), at least for the present period, which results in \(\phi _{0}=1\) with no dimension and \(\left( \frac{\dot{\phi }}{\phi }\right) _{t_{0}}=\frac{m-1}{2}\left( \frac{\dot{\epsilon }}{\epsilon } \right) _{t_{0}}\). It follows that the initial conditions mentioned above in summary are

$$\begin{aligned}&a_{0}=\epsilon _{0}={\phi }_{0}=1, {{\dot{a}}}_{0}=H_{0},\nonumber \\&\quad {{\dot{\epsilon }}}_{0}=- \frac{6}{n}H_{0}, {{\dot{\phi }}}_{0}=\frac{3(1-m)}{n}H_{0}. \end{aligned}$$
(31)

By complicated calculations the 5D curvature scalar can be given as

$$\begin{aligned} R=6\left( \frac{\ddot{a}}{a}+\frac{{\dot{a}}^{2}}{a^{2}}\right) + \frac{\ddot{\epsilon }}{\epsilon } -\frac{1}{2}\left( \frac{\dot{\epsilon }}{\epsilon }\right) ^{2} +3\frac{\dot{a}}{a}\frac{\dot{\epsilon }}{\epsilon }. \end{aligned}$$
(32)

Substituting Eq. (27) into (32), we can obtain

$$\begin{aligned}&\left[ \frac{1}{\alpha m\left( 1-2\kappa \rho \right) }\right] ^\frac{1}{m-1}=\frac{24m}{2m+1}\nonumber \\&\quad \times \left[ 1-q_{0}+\frac{3\left( 1-m\right) }{n^{2}}\right] H^{2}_{0}, \end{aligned}$$
(33)

where the deceleration parameter \(q\equiv -\frac{\ddot{a}a}{\dot{a}^{2}}=-\frac{1}{H^{2}}\frac{\ddot{a}}{a}\), and \(q_{0}\) is its present value. By virtue of (33) and (29), the relationship between the parameters \(m\) and \(n\) can be obtained as follows:

$$\begin{aligned}&6m^{2}(n-3)+m\{27+n\left[ 3+n(2-4q_{0})\right] \}\nonumber \\&\quad +n^{2}(4q_{0}-5)-9=0. \end{aligned}$$
(34)

Similar to the above discussions, we find that in the reduced FGNMC model the relationship between the parameters \(m\) and \(n\) is the same as Eq. (34), but different from the one in the FGNC model, which is given by

$$\begin{aligned} 4mn^{2}q_{0}-4n^{2}q_{0}+5n^{2}-2mn^{2}-18m+9=0. \end{aligned}$$
(35)

Evidently, it is just the same as Eq. (26) in Ref. [60]. For the sake of comparison we have listed the related quantities for the FGCMC, FGNMC, FGNC, and EG models in Table 1, from which it is easy to find that there is no need to constrain the value of the parameter \(m\) in Einstein gravity in the reduced 4D spacetime.

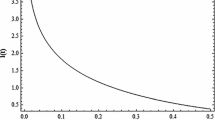
Table 1 The related quantities to the FGCMC, FGNMC, FGNC, and EG models
Full size table

As is well known, one necessary and sufficient condition for the present accelerated expansion of the universe is that the deceleration parameter satisfies the condition \(q_{0}<0\), and according to the present observation the allowed range for \(q_{0}\) is \(q_{0}=(-0.57\pm 0.10)\) [63]. Now we use this criterion to determine the allowed ranges for the parameters \(m\) and \(n\). For Eq. (34) it is not difficult to find that it has two sets of solutions for positive and negative values of \(m\), respectively, but Eq. (35) only has one, due to \(n>0\). This is illustrated in Figs. 1 and 2, respectively. From the figures, it is evident that there do exist suitable values of the parameters \(m\) and \(n\), which are just the shaded parts surrounded by the two curves in Figs. 1 and 2. It follows that in the reduced 4D spacetime the present cosmic acceleration can be explained by our model rather than dark energy.

Fig. 1
figure 1

The constraints on the parameters \(m\) and \(n\) of the FGCMC or FGNMC models with \(q_{0}\in (-0.67,-0.47)\). The solid line shows the case of \(q_{0}=-0.47\) and the dotted line shows the case of \(q_{0}=-0.67\) in each figure. a The positive solution of \(m\) and b corresponds to the negative solution of \(m\)

Full size image
Fig. 2
figure 2

The constraints on the parameters \(m\) and \(n\) of FGNC model with \(q_{0}\in (-0.67,-0.47)\). The solid line shows the case of \(q_{0}=-0.47\) and the dotted line shows the case of \(q_{0}=-0.67\)

Full size image

In addition, to illustrate the evolutionary characters of some cosmological quantities such as the scale factor \(a(t)\), the deceleration parameter \(q(t)\), and the scalar field \(\epsilon (t)\), \(\phi (t)\), around the present epoch in these models, we would here choose some specific values of \(m\) and \(n\) in the admissible range. For example, we choose \(m=1.3\) with \(n=8\), which results in \(\left[ \frac{1}{\alpha m\left( 1-2\kappa \rho \right) }\right] ^\frac{1}{m-1}\approx 13.75H_{0}^{2}\) in the reduced FGCMC model. Thus, by using Eqs. (27)–(29) and the initial values, the evolutionary trajectories of \(a(t),q(t),\epsilon (t)\), and \(\phi (t)\) can be plotted in Figs. 3 and 4.

Fig. 3
figure 3

a, b Respectively, the evolutionary trajectories of the scale factor \(a(t)\) and the deceleration parameter \(q(t)\). Here we have the current values \(\rho _{0}=3.8\times 10^{-28}~\hbox {kg}~\hbox {m}^{-3}\), \(H_{0}=2.3\times 10^{-18}\hbox {s}^{-1}\), and \(a_{0}=\epsilon _{0}=\phi _{0}=1\), and \(t=0\) corresponds to today

Full size image
Fig. 4
figure 4

a, b Respectively, the evolutionary trajectories of the scalar field \(\phi (t)\) and \(\epsilon (t)\) with the same parameters and current values as those in Fig. 3

Full size image

Similarly, we plot the evolutionary trajectories of the reduced FGNMC, FGNC models as well as EG model in Figs. 3 and 4. By analysis we can find the present deceleration parameter \(q_{0}=-0.6\), which is consistent with observations [63]. Moreover, the values of the scalar factor \(a(t)\) would be increasing slowly from the past to the future in Fig. 3(a), besides the one in the EG model which has a rapid increase at \(t=(13.8+3.0)~\hbox {Gyr}\) if the age of the universe is taken as \(13.8~\hbox {Gyr}\) [5]. In Fig. 3b, each of the deceleration parameters \(q(t)\) in the FGCMC, FGNMC, and FGNC models smoothly rolls from a positive value to a negative one in the recent past. After each of the \(q(t)\) reaches the minimal value, it rolls back again and becomes positive, which means that the universe will become decelerating in the future rather than be endlessly accelerating. \(q(t)\) in the EG model also changes from a positive value to a negative one, but reaches the minimal value sharply; then it has a linear increase to a constant acceleration, which suggests that the universe will be moving at a constant acceleration. The scalar field \(\phi (t)\) increases to a maximum value in the past near the present in the FGCMC and FGNMC models, but it goes to a maximum value for the present period in the FGNC model. In addition, \(\phi (t)\) is constant in the EG model; \(\epsilon (t)\) of the four models would decrease from a large value in the past and increase slowly in the future in Fig. 4, but a severe change will happen once again at \(t=(13.8+3.0)~\hbox {Gyr}\) in the EG model.

In general, the evolutionary trajectories of the scale factor \(a(t)\), the deceleration parameter \(q(t)\) and the scalar field \(\epsilon (t),\phi (t)\) in the reduced FGCMC, FGNMC, FGNC, and EG models are able to explain the accelerated expansion of the universe without introducing dark energy. Obviously, the results discussed in FGNC model are agree with Ref. [60]. However, the reduced EG model will be facing a dramatic change of the universe in the next three billion years, and then it will be endlessly accelerating at a constant acceleration.

On the other hand, by taking the negative solutions of \(m\) in Eq. (34), we find that the present value in the evolutionary trajectory of \(q(t)\) is always inconsistent with observations so that we have failing negative solutions of \(m\).

5 Conclusions

In this paper we have established the 5D generalized \(f(R)\) gravity with curvature–matter coupling (FGCMC) by assuming that there is a hypersurface-orthogonal space-like Killing vector field in the underlying 5D spacetime. This theory is an extension of the original 4D generalized \(f(R)\) gravity to the 5D spacetime, and it is quite general and can give the corresponding results for Einstein gravity (EG), and \(f(R)\) gravity with both no-coupling (FGNC), and non-minimal coupling (FGNMC) in 5D spacetime as special cases. It follows that we have given some new results besides previous ones given by Ref. [60]. Moreover, by using the approach of a Killing reduction the 5D generalized FGCMC can be reduced to the 4D theory. Furthermore, in order to get some insight into the effects of this theory on the 4D spacetime, by taking the specific type of models with \(f_{1}(R)=f_{2}(R)=\alpha R^{m}\) and \(B(L_{m})=L_{m}=-\rho \), not only have we listed the related quantities corresponding to the different gravity models such as FGCMC, FGNMC, FGNC, as well as EG in Table 1, but also we have illustrated the constraints on the model parameters \(m,n\) and the evolutionary trajectories of the scale factor \(a(t)\), the deceleration parameter \(q(t)\), and the scalar field \(\epsilon (t)\), \(\phi (t)\) in the reduced 4D spacetime in Figs. 1, 2, 3, and 4, respectively. The research results show that there do exist suitable values of the parameters \(m\) and \(n\), which means that the 5D generalized FGCMC, FGNMC, and FGNC can account for the present accelerated expansion of the universe. Meanwhile, the evolutionary laws of the scale factor \(a(t)\), the deceleration parameter \(q(t)\), and the scalar field \(\epsilon (t),\phi (t)\) in the reduced FGCMC, FGNMC, FGNC, and EG models are consistent with what is observed. They show the consistency between our results and the observations, and they would explain the current accelerated expansion of our universe without introducing dark energy. However, the reduced EG model will be facing a dramatic change of the universe in the next three billion years, which would be endlessly accelerating at a constant acceleration. Also, it is worth of notice that in these models both expansion and contraction of the extra dimension could result in the present accelerated expansion of other spatial dimensions. Hence it is reasonable to infer that the present accelerated expansion of spatial dimensions might show a basic characteristic of the 5D spacetimes.