Inner-most stable circular orbits in extremal and non-extremal Kerr–Taub-NUT spacetimes

Abstract

We study causal geodesics in the equatorial plane of the extremal Kerr–Taub-NUT spacetime, focusing on the inner-most stable circular orbit (ISCO), and we compare its behavior with extant results for the ISCO in the extremal Kerr spacetime. Calculations of the radii of the direct ISCO, its Kepler frequency, and the rotational velocity show that the ISCO coincides with the horizon in the exactly extremal situation. We also study geodesics in the strong non-extremal limit, i.e., in the limit of a vanishing Kerr parameter (i.e., for Taub-NUT and massless Taub-NUT spacetimes as special cases of this spacetime). It is shown that the radius of the direct ISCO increases with NUT charge in Taub-NUT spacetime. As a corollary, it is shown that there is no stable circular orbit in massless NUT spacetimes for timelike geodesics.

1 Introduction

It is perhaps Lynden-Bell and Nouri-Zonoz [1] who are the first to motivate investigation on the observational possibilities for (gravito)magnetic monopoles. It has been claimed that signatures of such spacetimes might be found in the spectra of supernovae, quasars, or active galactic nuclei. The authors of [2] have recently brought this into focus, by a careful and detailed analysis of geodesics in such spacetimes. Note that (gravito)magnetic monopole spacetimes with angular momentum admit relativistic thin accretion disks of a black hole in a galaxy or quasars [3]. This provides a strong motivation for studying geodesics in such spacetimes because they will affect accretion in such spacetimes from massive stars, and might offer novel observational prospects.

We know that the marginally stable orbit [also called Inner-most stable circular orbit (ISCO)] plays an important role in the accretion disk theory. That fact is important for spectral analysis of X-ray sources [4, 5]. The circular orbits with $r > r_\mathrm{ISCO}$ turn out to be stable, while those with $r < r_\mathrm{ISCO}$ are not. Basically, accretion flows of almost free matter (stresses are insignificant in comparison with gravity or centrifugal effects) resemble almost circular motion for $r > r_\mathrm{ISCO}$, and almost radial free-fall for $r < r_\mathrm{ISCO}$. In the case of thin disks, this transition in the character of the flow is expected to produce an effective inner truncation radius in the disk. The exceptional stability of the inner radius of the X-ray binary LMC X-3 [6] provides considerable evidence for such a connection and, hence, for the existence of the ISCO. The transition of the flow at the ISCO may also show up in the observed variability pattern, if variability is modulated by the orbital motion [5]. One may expect that the there will be no variability observed with frequencies $\Omega > \Omega _\mathrm{ISCO}$, i.e., higher than the Keplerian orbital frequency at ISCO, or that the quality factor for variability, $Q\sim \frac{\Omega }{\Delta \Omega }$ will significantly drop at $\Omega _\mathrm{ISCO}$. Several variants of this idea have been discussed in the following references [7, 8].

The Taub-NUT geometry [9, 10] possesses gravitomagnetic monopoles. Basically, this spacetime is a stationary and spherically symmetric vacuum solution of Einstein equation. As already mentioned, the authors of Ref. [2] have made a complete classification of geodesics in Taub-NUT spacetimes and describe elaborately the ‘full’ set of orbits for massive test particles. However, there is no specific discussion on the various innermost stable orbits in such spacetimes for null as well as timelike geodesics. This is the gap in the literature which we wish to fill in this paper. Our focus here is the three parameter Taub-NUT version of the Kerr spacetime which has angular momentum, mass, and the NUT parameter ($n$, the gravitomagnetic monopole strength), and which is a stationary, axisymmetric vacuum solution of the Einstein equation. The geodesics and the orbits of the charged particles in Kerr–Taub-NUT (KTN) spacetimes have also been discussed by Miller [11]. Abdujabbarov et al. [12] discuss some aspects of these geodesics in KTN spacetime, although the black hole solution remains a bit in doubt. Liu et al. [3] have also obtained the geodesic equations but there are no discussions of the ISCOs in KTN spacetime. We know that ISCO plays many important roles in astrophysics as well as in gravitational physics; hence the strong physical motivation to study them.

The presence of a NUT parameter lends the Taub-NUT spacetime a peculiar character and renders the NUT charge into a quasi-topological parameter. For example in the case of maximally rotating Kerr spacetime (extremal Kerr) where we can see that the timelike circular geodesics and null circular geodesics coalesce into a zero energy trajectory. This result and also the geodesics of the extremal Kerr spacetime have been elaborately described in Ref. [13]. They show that the ISCOs of the extremal Kerr spacetime for null geodesics and timelike geodesics coincide on the horizon (at $r=M$) which means that the geodesic on the horizon must coincide with the principal null geodesic generator. This is a very peculiar feature of extremal spacetimes.

In the case of the non-extremal Kerr spacetime Chandrasekhar [14] presents complete and detailed discussion on timelike and null geodesics (including ISCOs and other circular orbits). However, in that reference, subtleties associated with the extremal limit and special features of the precisely extremal Kerr spacetime have not been probed thoroughly. Likewise, the behavior of geodesics, especially those close to the horizon (in the equatorial plane, where subtleties regarding geodesic incompleteness [2] can be avoided) have not been considered in any detail.

We wish to investigate in this paper the differences of ISCOs in KTN spacetimes due to the inclusion of the NUT parameter in Kerr spacetime. While centering on the set of ISCOs, we also probe the Keplerian orbital frequencies and other important astronomical observables (namely, angular momentum ($L$), energy ($E$), rotational velocity ($v^{(\phi )}$) etc.), relevant for accretion disk physics, in the KTN and Taub-NUT spacetimes; these have not been investigated extensively in the extant literature. The presence of the NUT parameter in the metric always throws up some interesting phenomena in these particular spacetimes (KTN and Taub-NUT), arising primarily from their topological properties, which we wish to bring out here in the context of our investigation on the ISCOs. E.g., while it has been demonstrated in Ref. [2] that the orbital precession of spinless test particles in Taub-NUT geodesics vanishes, investigation by P. Majumdar and me has shown that in both the massive and massless Taub-NUT spacetimes spinning gyroscopes exhibit non-trivial frame-dragging (Lense–Thirring) precession [15]. Even though we do not discuss inertial frame-dragging in detail in this paper, this does provide a theoretical motivation as well to probe ISCOs in KTN spacetimes, following well-established techniques [14].

A word about our rationale for explicitly restricting ourselves to causal geodesics on the equatorial plane: these geodesics are able to avoid issues involving geodesic incompleteness exhibited in the spacetimes for other polar planes. Since there is a good deal of discussion of these issues elsewhere (see [2] for a competent review), we prefer to avoid them and concentrate instead on other issues of interest.

The paper is organized as follows: in Sect. 2 we discuss the KTN metric and its geodesics on the equatorial plane of precisely extremal spacetime. We discuss ISCOs and other astronomical observables for the null geodesics and timelike geodesics in the Sects. 3 and 4, respectively. In each section of Sects. 3 and 4, there are two subsections in which we derive the radii of ISCOs and some other important astronomical observables (like $L, E, v^{(\phi )}, \Omega$) for Taub-NUT and massless Taub-NUT spacetimes as the special cases of KTN spacetimes. We end in Sect. 5 with a summary and an outlook for future work.

2 Kerr–Taub-NUT metric

The KTN spacetime is a geometrically stationary, axisymmetric vacuum solution of Einstein equation with Kerr parameter $(a)$ and NUT charge or dual mass $(n)$. This dual mass is an intrinsic feature of general relativity. If the NUT charge [9, 10] vanishes, the solution reduces to the Kerr geometry [16]. The KTN metric, represented here in Schwarzschild-like coordinates [11], is

$$\begin{aligned} \mathrm{d}s^2&= -\frac{\Delta }{p^2}(\mathrm{d}t-A \mathrm{d}\phi )^2+\frac{p^2}{\Delta }\mathrm{d}r^2+p^2 \mathrm{d}\theta ^2\nonumber \\&+\frac{1}{p^2}\sin ^2\theta (a\mathrm{d}t-B\mathrm{d}\phi )^2 \end{aligned}$$

(1)

with

$$\begin{aligned} \begin{aligned} \Delta&=r^2-2Mr+a^2-n^2, p^2=r^2+(n+a\cos \theta )^2,\\ A&=a \sin ^2\theta -2n\cos \theta , B=r^2+a^2+n^2. \end{aligned} \end{aligned}$$

(2)

At first, we want to study the geodesic motions in the equatorial plane of the KTN spacetimes. So, the line element of the KTN spacetime at the equator will be

$$\begin{aligned} \mathrm{d}s_e^2&= -\frac{r^2-2Mr-n^2}{p_e^2}\mathrm{d}t^2-\frac{4a(Mr+n^2)}{p_e^2}\mathrm{d}\phi \mathrm{d}t\nonumber \\&+\frac{B^2-a^2\Delta }{p_e^2}\mathrm{d}\phi ^2+\frac{p_e^2}{\Delta }\mathrm{d}r^2 \end{aligned}$$

(3)

where

$$\begin{aligned} p_e^2=r^2+n^2. \end{aligned}$$

(4)

From the above metric we can easily derive the velocity components (for $\theta =\frac{\pi }{2}$ and $\dot{\theta }=0$) of the massive test particle [17]

$$\begin{aligned}&\dot{t}=\frac{1}{p^2}\left[ \frac{B}{\Delta }P(r)+aO(\theta )\right] \!,\end{aligned}$$

(5)

$$\begin{aligned}&\dot{\phi }=\frac{1}{p^2}\left[ \frac{a}{\Delta }P(r)+O(\theta )\right] \!,\end{aligned}$$

(6)

$$\begin{aligned}&\dot{r}^2=\frac{\Delta }{p^2}\left[ k+\frac{1}{p^2}\left( \frac{P^2}{\Delta }-O^2\right) \right] \end{aligned}$$

(7)

where

$$\begin{aligned}&P(r)=BE-La,\end{aligned}$$

(8)

$$\begin{aligned}&O(\theta )=L-aE=x. \end{aligned}$$

(9)

We may set without loss of generality,

$$\begin{aligned} k&= -1 \,\, \text {for timelike geodesics,}\nonumber \\&= 0 \,\, \text {for nulllike geodesics;} \end{aligned}$$

(10)

$L$ is the specific angular momentum or angular momentum per unit mass of the test particle and $E$ is to be interpreted as the specific energy or energy per unit mass of the test particle for the timelike geodesics $k=-1$.

3 ISCOs for the null geodesics in Kerr–Taub-NUT spacetimes

In this section, we derive the radii of ISCOs and other important astronomical quantities for null geodesics $(k=0)$ in the two spacetimes, one is KTN spacetimes and the other is Taub-NUT spacetimes.

As we have noted, $k=0$ for null geodesics and the radial equation (7) becomes

$$\begin{aligned} \dot{r}^2=E^2+2(L-aE)^2\frac{(Mr+n^2)}{(r^2+n^2)^2}-\frac{(L^2-a^2E^2)}{(r^2+n^2)}.\quad \end{aligned}$$

(11)

It will be more convenient to distinguish the geodesics by the impact parameter

$$\begin{aligned} D=\frac{L}{E}, \end{aligned}$$

(12)

rather than $L$.

We first observe the geodesics with the impact parameter

$$\begin{aligned} D=a \,\,\, \text {or}\,\,\, L=aE. \end{aligned}$$

(13)

Thus, in this case, Eqs. (5), (6), and (11) reduce to

$$\begin{aligned}&\dot{r}=\pm E,\end{aligned}$$

(14)

$$\begin{aligned}&\dot{t}=\frac{(r^2+n^2+a^2)}{\Delta }E \end{aligned}$$

(15)

and

$$\begin{aligned}&\dot{\phi }=\frac{a}{\Delta }E. \end{aligned}$$

(16)

The radial coordinate is described uniformly with respect to the affine parameter while the equations governing $t$ and $\phi$ are

$$\begin{aligned} \frac{\mathrm{d}t}{\mathrm{d}r}=\pm \frac{(r^2+n^2+a^2)}{\Delta } \end{aligned}$$

and

$$\begin{aligned} \frac{\mathrm{d}\phi }{\mathrm{d}r}=\pm \frac{a}{\Delta }. \end{aligned}$$

(17)

The solutions of these equations are

$$\begin{aligned} \pm t&= r+\frac{r_+^2+a^2+n^2}{r_+-r_-}\ln \left( \frac{r}{r_+}-1\right) \nonumber \\&-\frac{r_-^2+a^2+n^2}{r_+-r_-}\ln \left( \frac{r}{r_-}-1\right) ,\end{aligned}$$

(18)

$$\begin{aligned} \pm \phi&= \frac{a}{r_+-r_-}\ln \left( \frac{r}{r_+}-1\right) -\frac{a}{r_+-r_-}\ln \left( \frac{r}{r_-}-1\right) .\nonumber \\ \end{aligned}$$

(19)

These solutions exhibit the characteristic behaviors of $t$ and $\phi$ of tending to $\pm \infty$ as the horizons at $r_+$ and $r_-$ are approached. The coordinate $\phi$, like the coordinate $t$, is not a ‘good’ coordinate for describing what really happens with respect to a co-moving observer: a trajectory approaching the horizon (at $r_+$ or $r_-$) will spiral round the spacetime an infinite number of times even as it will take an infinite coordinate time $t$ to cross the horizon and neither will it associate with the experience of the co-moving observer.

The null geodesics which are described by Eq. (17) are the members of the principal null congruences and these are confined in the equatorial plane.

In general it is clear that there is a critical value of the impact parameter $D=D_c$ for which the geodesic equations allow an unstable circular orbit of radius $r_c$. In the case of $D<D_c$, only one kind of orbits is possible.

It will be arriving from infinity and cross both horizons and terminate into the singularity. For $D>D_c$, we can get two types of orbits:

• (a) arriving from infinity, have perihelion distances greater than $r_c$, terminate into the singularity at $r=0$ and $\theta =\frac{\pi }{2}$;

• (b) arriving from infinity, have aphelion distances less than $r_c$, terminate into the singularity at $r=0$ and $\theta =\frac{\pi }{2}$. For $n=0$, we can recover the results in the case of the Kerr geometry (see Eq. 77 of [14]).

The equations determining the radius ($r_c$) of the stable circular ‘photon orbit’ are (Eq. 11)

$$\begin{aligned} E^2+2(L-aE)^2\frac{(Mr_c+n^2)}{(r_c^2+n^2)^2}-\frac{(L^2-a^2E^2)}{(r_c^2+n^2)}=0\nonumber \\ \end{aligned}$$

(20)

and

$$\begin{aligned}&-(L-aE)^2\frac{(3Mr_c^2+4r_cn^2-Mn^2)}{(r_c^2+n^2)^3}\nonumber \\&\quad +\frac{r_c(L^2-a^2E^2)}{(r_c^2+n^2)^2}=0. \end{aligned}$$

(21)

Substituting $D=\frac{L}{E}$ in the above equations (20, 21), we get from Eq. (21)

$$\begin{aligned} \frac{D_c-a}{D_c+a}=\frac{r_c(r_c^2+n^2)}{r_c(3Mr_c+4n^2)-Mn^2}. \end{aligned}$$

(22)

Letting

$$\begin{aligned} y=D_c+a, \end{aligned}$$

(23)

and substituting it in Eq. (22) we get

$$\begin{aligned} y=2a\left[ 1-\frac{r_c(r_c^2+n^2)}{r_c(3Mr_c+4n^2)-Mn^2}\right] ^{-1}. \end{aligned}$$

(24)

Therefore, the critical value of the impact parameter $D_c$ in KTN spacetime is

$$\begin{aligned} D_c=2a\left[ 1-\frac{r_c(r_c^2+n^2)}{r_c(3Mr_c+4n^2)-Mn^2}\right] ^{-1}-a. \end{aligned}$$

(25)

To get the value of $r_c$ we have to take Eq. (20) which reduces to

$$\begin{aligned} 1+2(D_c-a)^2\frac{(Mr_c+n^2)}{(r_c^2+n^2)^2}-\frac{(D_c^2-a^2)}{(r_c^2+n^2)}=0. \end{aligned}$$

(26)

Substituting the value of

$$\begin{aligned} D_c=y-a=2a\left[ 1+\frac{r_c(r_c^2+n^2)}{r_c(3Mr_c+4n^2)-Mn^2}\right] -a\nonumber \\ \end{aligned}$$

(27)

(neglecting the higher order terms of $r_c$, we have $r_c<n$ and $r_c<M$) in Eq. (26) we get the equation to determine the radius ($r_c$) of the stable circular photon orbit:

$$\begin{aligned}&(9-4a_M^2)r_{cM}^4+4(6n_M^2-a_M^2)r_{cM}^3\nonumber \\&\quad +2n_M^2(8n_M^2-6a_M^2-3)r_{cM}^2\nonumber \\&\quad +4n_M^2(a_M^2-2n_M^2)r_{cM}+n_M^4=0 \end{aligned}$$

(28)

where the lower index ‘M’ of a particular parameter represents that the parameter is divided by ‘M’ (such as $a_M=\frac{a}{M}$). For $r_c<n$ we get the solution of $r_c$,

$$\begin{aligned} r_{cM}&= \frac{n_M}{6(a_M^2-6n_M^2)}\left[ (U-18Vn_M^2+3n_M^2V)^{\frac{1}{3}}\right. \nonumber \\&\left. +W(U-18Vn_M^2+3n_M^2V)^{-\frac{1}{3}}\right. \nonumber \\&\left. +n_M(8n_M^2-6a_M^2-3)\right] \end{aligned}$$

(29)

where the values of $U, \, V, \, W$ are given in the footnote¹. Here, the expression of $r_{cM}$ is the radius of the ISCO as it is the smallest positive real root of the ISCO equation (28).

Extremal case We know that in KTN spacetime, the horizons are at

$$\begin{aligned} r_{\pm }=M \pm \sqrt{M^2+n^2-a^2}, \end{aligned}$$

(30)

where $r_+$ and $r_-$ define the event horizon and the Cauchy horizon, respectively. In the case of an extremal KTN spacetime,

$$\begin{aligned}&r_+=r_-\nonumber \\&\text {or} \quad a^2 = M^2+n^2. \end{aligned}$$

(31)

Therefore, the horizon of extremal KTN spacetime is at

$$\begin{aligned} r=M. \end{aligned}$$

(32)

Now, we can substitute the value of Eq. (22) in Eq. (20) (also we take $a^2=M^2+n^2$) and get the result that the equation for determining the radius $(r_c)$ of the stable circular photon orbit is

$$\begin{aligned}&r_c^2(r_c^2-3Mr_c-3n^2)^2-4(M^2+n^2)r_c^2(Mr_c+2n^2)\nonumber \\&\quad +2Mn^2r_c(r_c^2-3Mr_c-n^2+2M^2)+M^2n^4=0.\quad \quad \end{aligned}$$

(33)

Interestingly, the solution of this sixth order non-trivial equation is

$$\begin{aligned} r_c=M. \end{aligned}$$

(34)

This is the radius of the ISCO as it is the smallest positive real root of the ISCO equation (33). It means that the radius of the ISCO ($r_c$) coincides with the horizon in extremal KTN spacetime for null geodesics. This is the same thing as happens in an extremal Kerr spacetime also. In an extremal Kerr spacetime, the direct ISCO coincides with the horizon at $r=M$ for null geodesic. Now, we can calculate the critical value of the impact parameter in the extremal KTN spacetime:

$$\begin{aligned} D_c=M\frac{3M^2+5n^2}{M^2+3n^2}. \end{aligned}$$

(35)

The physical significance of the impact parameter $D_c$ and the ISCO have already been discussed in detail. Now, we can give our attention to the Taub-NUT spacetime, which is quite interesting.

3.1 ISCOs in Taub-NUT spacetimes

The Taub-NUT spacetime is a stationary and spherically symmetric vacuum solution of Einstein equation [18]. Now, we shall discuss the very special case in which we set $a=0$; the angular momentum of the spacetime vanishes. We note that for $a=0$, the primary metric (Eq. 1) of the KTN spacetime reduces to the Taub-NUT metric in which the constant is set as $C=0$. If we take the Taub-NUT metric in a more general form, it would be

$$\begin{aligned} \mathrm{d}s^2&= -f(r)\left[ \mathrm{d}t-2n(\cos \theta +C)\mathrm{d}\phi \right] ^2+\frac{1}{f(r)}\mathrm{d}r^2\\&+ (r^2+n^2)(\mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2) \end{aligned}$$

where $C$ is an arbitrary real constant. If we take $C=0$ for the above metric, the form of Taub-NUT metric is the same as the metric (1) of ‘KTN spacetimes with $a=0$’. Physically, $C=0$ leads to the only possibility for the NUT solutions to have a finite total angular momentum. After noting the above points, we write the line element of the Taub-NUT spacetimes at the equator as

$$\begin{aligned} \mathrm{d}s_e^2&= -\frac{r^2-2Mr-n^2}{r^2+n^2}\mathrm{d}t^2+\frac{r^2+n^2}{r^2-2Mr-n^2}\mathrm{d}r^2\nonumber \\&+(r^2+n^2)\mathrm{d}\phi ^2. \end{aligned}$$

(36)

To determine the radius $(r_{cn})$ of the stable circular photon orbit, we put $a=0$ in Eq. (33) and we get the following:

$$\begin{aligned}&r_{cn}^2(r_{cn}^2-3Mr_{cn}-3n^2)^2+2Mn^2r_{cn} (r_{cn}^2-3Mr_{cn}-3n^2)\nonumber \\&\quad +M^2n^4=0\nonumber \\&\text {or}\nonumber \\&r_{cn}^3-3Mr_{cn}^2-3n^2r_{cn}+Mn^2=0. \end{aligned}$$

(37)

Solving the above equation we get

$$\begin{aligned}&r_{cn}=M+2(M^2+n^2)^{1/2}\cos \left[ \frac{1}{3}\tan ^{-1}\left( \frac{n}{M}\right) \right] ,\end{aligned}$$

(38)

$$\begin{aligned}&\text {or}\quad \nonumber \\&r_{Mcn}=1+2(1+n_M^2)^{1/2}\cos \left[ \frac{1}{3}\tan ^{-1}\left( n_M\right) \right] . \end{aligned}$$

(39)

This is the radius of the ISCO as it is the smallest positive real root of the ISCO equation (37). For $n_M=\frac{n}{M}=0$, we can recover $r_c=3M$ of Schwarzschild spacetime. We know that the position of the event horizon in Taub-NUT spacetime is

$$\begin{aligned}&r_+=M+\sqrt{M^2+n^2},\end{aligned}$$

(40)

$$\begin{aligned}&\text {or}\quad \nonumber \\&r_{+M}=1+\sqrt{1+n^2}. \end{aligned}$$

(41)

It seems that the position of the ISCO ($r_{cn}$) could be in timelike, nulllike or spacelike surfaces depending on the value of NUT charge ($n_M$) in Taub-NUT spacetime. But this never occurs. We cannot get any solution of $n_M$ for $r_{Mcn}=r_{+M}$. If we plot (Fig. 1) $r_{Mcn}$ (green) and $r_{+M}$ (red) vs. $n_M$ we can see that $r_{Mcn}$ and $r_{+M}$ are continuously increasing for $n_M\ge 0$. They cannot intersect each other in any point. So, we can conclude that ISCO could not be on the horizon for any value of $n_M$. Thus, a photon orbit is always in the timelike region for any real value of $n_M$ in Taub-NUT spacetime.

Fig. 1

Plot of $r_{Mcn}$ (green) and $r_{+M}$ (red) vs. $n_M$

3.2 ISCOs in massless Taub-NUT spacetimes

The NUT spacetime for the mass $M=0$ is also well defined (see, for example, the appendix of [19]). So, we can also determine the radius $(r_{0cn})$ of the stable circular photon orbit for massless Taub-NUT spacetimes. This turns out to be

$$\begin{aligned} r_{0cn}=\sqrt{3}n. \end{aligned}$$

(42)

We note that the horizons of massless Taub-NUT spacetime are at $r=\pm n$ [15]. So, the ISCO of this spacetime for null geodesic is always outside the horizon, by which we mean in the timelike surface. Here, it should also be highlighted that in the case of Taub-NUT spacetime the horizons are at

$$\begin{aligned} r_{\pm }=M \pm \sqrt{M^2+n^2} \end{aligned}$$

(43)

as $a=0$. We can see that one horizon is located at $r_+>2M$ and the other at $-|n|<r_-<0$.

Thus there are mainly two important features of the Taub-NUT and massless Taub-NUT spacetime, one is that the second horizon is at a negative value of the radial Schwarzschild coordinate and another is that the both spacetimes possess the quasi-regular singularity [20]. But the presence of the Kerr parameter $(a)$ leads to the naked singularity in the non-extremal KTN spacetime as well as the non-extremal Kerr spacetime. In these cases, both horizons are located at imaginary distances. This means that we can observe the singularity from infinity. So this is called a naked singularity. But in the Taub-NUT spacetime the absence of the Kerr parameter never leads to any of the horizons at an imaginary distance. So, there could not be any naked singularity in Taub-NUT and massless Taub-NUT spacetime. The absence of the Kerr parameter also leads to the non-existence of any extremal case for Taub-NUT spacetime as the horizons of Taub-NUT spacetime cannot act as the actual horizons like the horizons of our other well-known spacetimes (such as the Kerr and Reissner–Nordström geometries). In the extremal KTN spacetime, the horizon is located at $r=M$, which is the same as the Kerr spacetime. We note that the NUT charge has not any effect on determining the ISCO in extremal KTN spacetime as the Kerr parameter takes it highest value $a=\sqrt{M^2+n^2}$, but the ISCO radius (Eq. 29) in non-extremal KTN spacetime depends on the NUT charge.

4 ISCOs for the timelike geodesics in Kerr–Taub-NUT spacetimes

For timelike geodesics, Eqs. (5) and (6) for $\dot{\phi }$ and $\dot{t}$ remain unchanged; but Eq. (7) is reduced to

$$\begin{aligned} (r^2+n^2)\dot{r}^2&= 2(L-aE)^2\frac{Mr+n^2}{r^2+n^2}\nonumber \\&+E^2(r^2+n^2)-(L^2-a^2E^2)-\Delta . \end{aligned}$$

(44)

The circular and associated orbits We now turn to a consideration of the radial equation (44) in general. With the reciprocal radius $u(=\frac{1}{r})$ as the independent variable and substituting $L-aE=x$, the equation takes the form

$$\begin{aligned}&(1+n^2u^2)^2\dot{u}^2 u^{-4}\nonumber \\&\quad =2x^2u^3(M+n^2u)+(1+n^2u^2)[E^2(1+n^2u^2)\nonumber \\&\qquad -(1+a^2u^2-n^2u^2-2Mu)-u^2(x^2+2aEx)].\quad \end{aligned}$$

(45)

Like the Schwarzschild, Reissner–Nordström and Kerr geometries, the circular orbits play an important role in the classification of the orbits. Besides, they are useful for some special features of the spacetimes, after all; the reason for studying the geodesics. When the values of $L$ and $E$ are completely arbitrary, the quartic polynomial of the right hand side of Eq. (45) will have a triple root. For the conditions for the occurrence of the triple root from Eq. (45) we get

$$\begin{aligned}&2x^2u^3(M+n^2u)+(1+n^2u^2) [E^2(1+n^2u^2)\nonumber \\&\quad -(1+a^2u^2-n^2u^2-2Mu)-u^2(x^2+2aEx)]=0\nonumber \\ \end{aligned}$$

(46)

and

$$\begin{aligned}&3Mx^2u^2\!+\!M(1\!+\!3n^2u^2)\!+\!u(2E^2n^2\!-\!a^2)\!-\!u(x^2\!+\!2aEx)\nonumber \\&\quad +\,2n^2u^3(x^2-2aEx+E^2n^2+n^2-a^2)=0. \end{aligned}$$

(47)

Equations (46) and (47) can be combined to give

$$\begin{aligned} E^2=1-Mu+\frac{Mx^2u^3(1-n^2u^2)+2x^2n^2u^4}{(1+n^2u^2)^2} \end{aligned}$$

(48)

and

$$\begin{aligned}&2aExu(1+n^2u^2)\nonumber \\&\quad =[x^2u^2(3M+3n^2u-Mn^2u^2)-ux^2]\nonumber \\&\qquad -(1+n^2u^2)[(a^2-2n^2)u-M(1-n^2u^2)]. \end{aligned}$$

(49)

By eliminating $E$ between these equations we get the following quadratic equation. For $x$

$$\begin{aligned}&x^4u^2[(u(3M+3n^2u-Mn^2u^2)-1)^2\nonumber \\&\quad -\,4a^2u^3(M(1-n^2u^2)+2n^2u)]\nonumber \\&\quad -\,2x^2u(1+n^2u^2)[(u(3M+3n^2u-Mn^2u^2) -1)\nonumber \\&\quad \times ((a^2\!-\!2n^2)u\!-\!M(1\!-\!n^2u^2)) \!-\!2a^2u(1\!+\!n^2u^2)(Mu\!-\!1)]\nonumber \\&\quad +\,(1+n^2u^2)^2[(a^2-2n^2)u-M(1-n^2u^2)]^2=0. \end{aligned}$$

(50)

The discriminant ‘$\frac{1}{4}(b^2-4ac)$’ of this equation is

$$\begin{aligned} 4a^2u^3(1+n^2u^2)^2[M(1-n^2u^2)+2n^2u]\Delta _u^2 \end{aligned}$$

(51)

where

$$\begin{aligned} \Delta _u=[1-2Mu+(a^2-n^2)u^2]. \end{aligned}$$

(52)

The solution of Eq. (50) is

$$\begin{aligned} u^2x^2&= (1+n^2u^2)\frac{Q_{\pm }\Delta _u-Q_+Q_-}{Q_+Q_-}\nonumber \\&= \frac{(1+n^2u^2)}{Q_{\mp }}(\Delta _u-Q_{\mp }) \end{aligned}$$

(53)

where

$$\begin{aligned}&Q_+Q_-=[(u(3M+3n^2u-Mn^2u^2)-1)^2\nonumber \\&-4a^2u^3(M(1-n^2u^2)+2n^2u)],\end{aligned}$$

(54)

$$\begin{aligned}&Q_{\pm }=1-u(3M+3n^2u-Mn^2u^2)\nonumber \\&\pm 2a\sqrt{u^3[M(1-n^2u^2)+2n^2u]}. \end{aligned}$$

(55)

We verify that

$$\begin{aligned} \Delta _u-Q_{\mp }=u\left[ a\sqrt{u}\pm \sqrt{M(1-n^2u^2)+2n^2u}\right] ^2. \end{aligned}$$

(56)

Thus, the solution of the $x$ takes the simple form

$$\begin{aligned} x=-\sqrt{\frac{1+n^2u^2}{uQ_{\mp }}}\left[ a\sqrt{u}\pm \sqrt{M(1-n^2u^2)+2n^2u}\right] \!.\quad \quad \end{aligned}$$

(57)

It will appear presently that the upper sign in the foregoing equation applies to the retrograde orbits, while the lower sign applies to the direct orbits. We adhere to this convention in this whole section. Substituting the value of $x$ in Eq. (48), we get

$$\begin{aligned} E&= \frac{1}{\sqrt{(1+n^2u^2)Q_{\mp }}}\left[ 1-2Mu-n^2u^2\right. \nonumber \\&\left. \mp a\sqrt{u^3[M(1-n^2u^2)+2n^2u]}\right] \end{aligned}$$

(58)

and the value of $L$ which is associated with $E$ is

$$\begin{aligned}&L=aE+x=\mp \sqrt{\frac{M(1-n^2u^2)+2n^2u}{u(1+n^2u^2)Q_{\mp }}}\nonumber \\&\quad \times \left[ 1+(a^2+n^2)u^2\pm 2a(M+n^2u)\sqrt{\frac{u^3}{M(1-n^2u^2)+2n^2u}}\right] .\nonumber \\ \end{aligned}$$

(59)

As the manner of derivation makes explicit, $E$ and $L$ given by Eqs. (58) and (59) are energy and angular momentum per unit mass, of a particle describing a circular orbit of reciprocal radius $u$. The angular velocity $\Omega$ follows from the equation

$$\begin{aligned} \Omega =\frac{\dot{\phi }}{\dot{t}}=\frac{\mathrm{d}\phi }{\mathrm{d}t}=\frac{aP+O\Delta }{BP+aO\Delta } =\frac{a(BE-La)+x\Delta }{B(BE-La)+ax\Delta }.\nonumber \\ \end{aligned}$$

(60)

Substituting the values of $x$, $L$, and $E$ in the above equation we get the angular velocity of a chargeless massive test particle which is moving in a particular orbit of radius $R(=\frac{1}{u})$ in KTN spacetime:

$$\begin{aligned} \Omega _\mathrm{KTN}=\frac{\sqrt{u^3[M(1-n^2u^2)+2n^2u]}}{1+n^2u^2 \mp a\sqrt{u^3[M(1-n^2u^2)+2n^2u]}}. \end{aligned}$$

(61)

Generally, $\Omega _\mathrm{KTN}$ is also called the Kepler frequency in KTN spacetime.

The time period $(T)$ of a massive chargeless test particle which is rotating in an orbit of radius $R(=\frac{1}{u})$ can also be determined from the Kepler frequency by the simple relation between $\Omega$ and $T$:

$$\begin{aligned} T=\frac{2\pi }{\Omega _\mathrm{KTN}}. \end{aligned}$$

(62)

For $n=0$, we can easily get the Kepler frequency in Kerr spacetime:

$$\begin{aligned} \Omega _{K}=\frac{\sqrt{Mu^3}}{1\mp a\sqrt{Mu^3}}=\frac{M^{\frac{1}{2}}}{R^{\frac{3}{2}}\mp aM^{\frac{1}{2}}}. \end{aligned}$$

(63)

It is already noted that the upper sign is applicable for the retrograde orbits and the lower sign is applicable for the direct orbits.

The rotational velocity $v^{(\phi )}$ of a chargeless massive test particle could be determined by the following equation:

$$\begin{aligned} v^{(\phi )}=e^{\psi -\nu }(\Omega -\omega ) \end{aligned}$$

(64)

where $\psi$, $\nu$, and $\omega$ are defined from the general axisymmetric metric [14]

$$\begin{aligned} \mathrm{d}s^2&= -e^{2\nu }(\mathrm{d}t)^2+e^{2\psi }(\mathrm{d}\phi -\omega \mathrm{d}t)^2\nonumber \\&+\,e^{2\mu _2}(\mathrm{d}x^2)^2+e^{2\mu _3}(\mathrm{d}x^3)^2. \end{aligned}$$

(65)

In the above metric $\psi$, $\nu$, $\omega$, $\mu _2$ and $\mu _3$ are the functions of $x^2$ and $x^3$. In our case (for KTN spacetimes),

$$\begin{aligned}&e^{2\psi }=\frac{B^2-a^2\Delta }{p_e^2}\nonumber \\&\omega =\frac{2a(Mr+n^2)}{B^2-a^2\Delta }\nonumber \\&e^{2\nu }=\frac{1}{p_e^2}\left[ (r^2-2Mr-n^2)+\frac{4a^2(Mr+n^2)^2}{B^2-a^2\Delta }\right] . \end{aligned}$$

(66)

Now, substituting the above values in Eq. (64), we get the rotational velocity of a chargeless massive test particle which is moving in a particular orbit of radius $R(=\frac{1}{u})$ in KTN spacetime:

$$\begin{aligned}&v^{(\phi )}_\mathrm{KTN} =\frac{(B^2-a^2\Delta )(\Omega -\omega )}{[(r^2-2Mr-n^2) (B^2-a^2\Delta )+4a^2(Mr+n^2)^2]^{\frac{1}{2}}}\nonumber \\&\quad =\frac{(B^2-a^2\Delta )(\Omega -\omega )}{(r^2+n^2)\sqrt{\Delta }}\nonumber \\&\quad =\frac{\mp \sqrt{u[M(1-n^2u^2)+2n^2u]}[1+(a^2\!+\!n^2)u^2]-2au^2(M+n^2u)}{\sqrt{\Delta _u}[1+n^2u^2\mp a\sqrt{u^3[M(1-n^2u^2)+2n^2u]}]}.\nonumber \\ \end{aligned}$$

(67)

Here, a point, considered as describing a circular orbit (with the proper circumference $\pi e^{\psi }$) with an angular velocity $\Omega$ (also called Kepler frequency) in the chosen coordinate frame, will be assigned an angular velocity,

$$\begin{aligned} e^{\psi -\nu }(\Omega -\omega ), \end{aligned}$$

(68)

in the local inertial frame. Accordingly, a point which is considered as at rest in the local inertial frame (i.e., velocity components $u^{(1)} =u^{(2)}=u^{(3)}=0$), will be assigned an angular velocity $\omega$ in the coordinate frame. On this account the non-vanishing of $\omega$ is said to describe ‘dragging of inertial frame’. In the weak gravity regime,

$$\begin{aligned} \omega \sim \frac{2J}{r^3}, \end{aligned}$$

(69)

where $J$ is the angular momentum of the spacetime. For the exact calculation of $\omega$ in the strong gravity regime, see Chakraborty and Majumdar [15].

We note that the effective potential expression of a massive test particle plays many interesting roles in gravitational physics and also in astrophysics. Here, we need this potential at this moment to determine the radius of the ISCO in KTN spacetime. We know that

$$\begin{aligned} \frac{E^2-1}{2}=\frac{1}{2}\dot{r}^2+V_\mathrm{eff}(r,E,L) \end{aligned}$$

(70)

where the effective potential governing the radial motion is

$$\begin{aligned} V_\mathrm{eff}(r,E,L)\!=\!\frac{1}{2}\left[ (E^2-1)-\frac{P^2-(r^2+n^2+O^2)\Delta }{(r^2+n^2)^2}\right] .\nonumber \\ \end{aligned}$$

(71)

For $n=0$, the effective potential reduces to Eq. (15.20) of [4]. This is applicable to the Kerr geometry. An important difference is that the potentials are energy and angular momentum dependent in stationary spacetimes, i.e., Kerr, KTN etc. This has not happened in the static spacetimes, i.e., Schwarzschild, Reissner–Nordström etc. In the static spacetimes the effective potential is only depends on radial coordinate $r$, not depends on $L$ and $E$. This difference arises due to the involvement of ‘rotational motion’ in stationary spacetimes. For example, particles that fall from infinity rotating in the same direction as the spacetime (positive values of $L$) move in a different effective potential than initially counterrotating particles (negative values of $L$). These differences reflect, in part, the rotational frame dragging of the spinning spacetime and the test particles are dragged by its rotation.

Many interesting properties of the orbits of particles in the equatorial plane could be explored with the radial equation (71) and the equations of the other components (which are already discussed) of the four velocity. We could calculate the radii of circular orbits, the shape of bound orbits etc. These are all different, depending upon whether the particle is rotating with the black hole (corotating) or in the opposite direction (counterrotating). For instance, in the geometry of an extremal Kerr black hole $(a=M)$, there is a corotating stable circular particle orbit at $r=M$ (direct ISCO) and a counterrotating stable circular orbit at $r=9M$ (retrograde ISCO). However, as we already mentioned, for an introductory discussion it seems appropriate not to stress all these interesting properties but rather to focus on the one property which is most important for astrophysics, mainly for the accretion mechanism—the binding energy of the inner-most stable circular particle orbit (ISCO).

For a particle to describe a circular orbit at radius $r=R$, its initial radial velocity must vanish. Imposing this condition we get from Eq. (70)

$$\begin{aligned} \frac{E^2-1}{2}=V_\mathrm{eff}(R,E,L). \end{aligned}$$

(72)

To stay in a circular orbit the radial acceleration must also vanish. Thus, differentiating Eq. (70) with respect to $r$ leads to the condition

$$\begin{aligned} \frac{\partial V_\mathrm{eff}(r,E,L)}{\partial r}|_{r=R}=0. \end{aligned}$$

(73)

Stable orbits are ones for which small radial displacements away from $R$ oscillate about it rather than accelerate away from it. Just as in newtonian mechanics, this is the condition that the effective potential must be a minimum:

$$\begin{aligned} \frac{\partial ^2 V_\mathrm{eff}(r,E,L)}{\partial r^2}|_{r=R}>0. \end{aligned}$$

(74)

Equations (72–74) determine the ranges of $E,\, L, \,R$ allowed for stable circular orbits in the KTN spacetime. At the ISCO, the one just on the verge of being unstable—(Eq. 74) becomes an equality. The last three equations are solved to obtain the values of $E,\, L, \,R=r_\mathrm{ISCO}$ that characterize the orbit. Equations (72) and (73) have already been solved for KTN spacetime at the very beginning of this section as Eqs. (46) and (47) to obtain the exact expressions of $E$ and $L$. Now, we obtain the following from Eq. (74):

$$\begin{aligned}&(r^2+n^2)[(a^2+2aEx)(3r^2-n^2)-2Mr^3\nonumber \\&\quad +6Mrn^2-6n^2r^2+2n^4]\nonumber \\&\quad +3x^2(r^4-4Mr^3-6r^2n^2+4Mrn^2+n^4)=0. \end{aligned}$$

(75)

Substituting the values of $Ex$ and $x^2$ in terms of $r=R$ in the above equation we get

$$\begin{aligned}&2M^2R(2n^2R^2-3n^4-3R^4)+M\left[ (R^6-n^6)\right. \nonumber \\&\quad \left. -15R^2n^2(R^2-n^2)+a^2(n^4+6n^2R^2-3R^4)\right] \nonumber \\&\quad \mp 8a\left[ MR(R^2-n^2)+2n^2R^2\right] ^{\frac{3}{2}}-8n^2R^3(a^2+2n^2)=0.\nonumber \\ \end{aligned}$$

(76)

This is the equation to obtain the radius of the ISCO in non-extremal KTN spacetime for timelike geodesic. Solving the above equation, we can determine the radius of the inner-most stable circular orbit in the non-extremal KTN spacetime. But this equation cannot be solved analytically as it is actually a twelfth order equation. So, we determine the radius of ISCO in extremal KTN spacetime. For that we can substitute

$$\begin{aligned} a^2=M^2+n^2 \end{aligned}$$

(77)

in the above equation. Defining

$$\begin{aligned} R_M=\frac{R}{M} , \,\,\, n_M=\frac{n}{M}, \,\,\, a_M=\frac{a}{M}=\sqrt{1+n_M^2}, \end{aligned}$$

(78)

we can rewrite the extremal ISCO equation in KTN spacetime as

$$\begin{aligned}&2R_M(2n_M^2R_M^2-3n_M^4-3R_M^4)+\left[ (R_M^6-n_M^6)\right. \nonumber \\&\left. -15R_M^2n_M^2(R_M^2\!-\!n_M^2)\!+\!(1\!+\!n_M^2)(n_M^4\!+\!6n_M^2R_M^2\!-\!3R_M^4)\right] \nonumber \\&+8\sqrt{1+n_M^2}\left[ R_M(R_M^2-n_M^2)+2n_M^2R_M^2\right] ^{\frac{3}{2}}\nonumber \\&-8n_M^2R_M^3(1+3n_M^2)=0. \end{aligned}$$

(79)

Interestingly, the solution of the above non-trivial equation is

$$\begin{aligned} R_M=1 \,\,\, \text {or,} \,\,\, R=M. \end{aligned}$$

(80)

This is the radius of the ISCO as it is the smallest positive real root of the ISCO equation (79). So, in extremal KTN spacetime, the direct ISCO radius does not depend on the value of NUT charge. ISCO radius is completely determined by the ADM mass of the spacetime. We note that the horizon in extremal KTN spacetime is at $R=M$. So, we can say that if $R=M$, the direct ISCO is on the horizon in extremal KTN spacetime. It is also further observed that the timelike circular geodesics and null circular geodesics coalesce into a single zero energy trajectory (both are on $R=M$)

$$\begin{aligned} E=0. \end{aligned}$$

(81)

Thus, the geodesic on the horizon must coincide with the principal null geodesic generator. The existence of a timelike circular orbit turning into the null geodesic generator on the event horizon (nulllike) is a peculiar feature of extremal KTN spacetime. It is not only that the energy $(E=0)$ vanishes on the ISCO in KTN spacetime but angular momentum $(L=0)$ also vanishes on that. The same thing also happens in the case of the Kerr geometry.

Substituting $n=0$, we can recover the expressions of $\Omega$, $v^{(\phi )}$ in Kerr spacetimes. These have already been described by Chandrasekhar [14] in detail. The ISCO equation in Kerr spacetime is

$$\begin{aligned} R^2-6MR\mp 8a\sqrt{MR}-3a^2=0. \end{aligned}$$

(82)

For extremal Kerr spacetime we can put $a=M$ in the above equation, and solving the above equation we get

$$\begin{aligned}&R_\mathrm{directISCO}=M,\nonumber \\&R_\mathrm{retrogradeISCO}=9M. \end{aligned}$$

(83)

Table 1 Comparison between radius of the horizon ($r_{Mhor}$) and radius of the ISCO $(r_{Misco})$ at Taub-NUT spacetimes

4.1 ISCOs in Taub-NUT spacetimes

To get various useful expressions in Taub-NUT spacetimes, we should first take $a=0$. We do not want to reiterate the whole process for Taub-NUT spacetimes. This is the same as in the previous section in which we have done this in detail for KTN spacetimes. The energy per unit mass $(E_{TN})$ and the angular momentum per unit mass $(L_{TN})$ of a chargeless massive test particle which is moving in a particular orbit of radius $r=\frac{1}{u}$ in Taub-NUT spacetime will be

$$\begin{aligned} E_{TN}=\frac{(1-2Mu-n^2u^2)}{\sqrt{(1+n^2u^2)Q_{TN}}} \end{aligned}$$

(84)

and

$$\begin{aligned} L_{TN}=\sqrt{\frac{(1+n^2u^2)[M(1-n^2u^2)+2n^2u]}{uQ_{TN}}} \end{aligned}$$

(85)

where

$$\begin{aligned} Q_{TN}=1-u(3M+3n^2u-Mn^2u^2). \end{aligned}$$

(86)

Now, we can find the angular velocity $\Omega _{TN}$ of a chargeless massive test particle which is moving in a particular orbit of radius $r=\frac{1}{u}$ at Taub-NUT spacetime:

$$\begin{aligned} \Omega _{TN}=\frac{\sqrt{u^3[M(1-n^2u^2)+2n^2u]}}{(1+n^2u^2)}. \end{aligned}$$

(87)

For $n=0$, we can recover the well-known Kepler frequency for a non-rotating star whose geometry is described by Schwarzschild metric. The Kepler frequency, which is a very useful parameter in relativistic astrophysics, is defined as (substituting $n=0$ in Eq. (87))

$$\begin{aligned} \Omega _\mathrm{Kep}^2=Mu^3=\frac{M}{R^3} \end{aligned}$$

(88)

where $M$ is the mass of the star, $R$ is the distance of the planet from the center of the star, and $\Omega _\mathrm{Kep}$ is the uniform angular velocity of the planet, moving in a circular orbit of radius $R$ around the star.

The rotational velocity $v^{(\phi )}_{TN}$ of a chargeless massive test particle which is moving in a particular orbit of radius $r=\frac{1}{u}$ at Taub-NUT spacetime:

$$\begin{aligned} v^{(\phi )}_{TN}=\sqrt{\frac{u[M(1-n^2u^2)+2n^2u]}{\Delta _u}}. \end{aligned}$$

(89)

Finally, the direct ISCO equation in Taub-NUT spacetimes can be expressed as

$$\begin{aligned}&2r_M(2n_M^2r_M^2-3n_M^4-3r_M^4)\nonumber \\&\quad +\left[ (r_M^6-n_M^6)-15r_M^2n_M^2(r_M^2-n_M^2)\right] -16n_M^4r_M^3=0.\nonumber \\ \end{aligned}$$

(90)

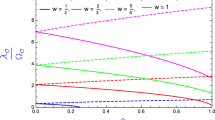
It is a sixth order equation, which is very difficult to solve analytically. Thus, we plot the values of $n_M$ vs. $r_M$.

Fig. 2

Plot of radius of direct ISCO $r_{Misco}$ (along $y$ axis) vs. NUT charge $n_M$ (along $x$ axis)

We can see from the plots (Fig. 2) and also from Table 1 that in a Taub-NUT spacetime, the radius of direct ISCO is increasing with the increasing of the NUT charge. We do not see this special feature in the case of extremal KTN spacetimes.

Even though we can also solve the ISCO equation in Taub-NUT spacetimes with the assumption $r_M>n_M$. In this case Eq. (90) reduces to

$$\begin{aligned} r_M^3-6r_M^2-15r_Mn_M^2-16n_M^4=0. \end{aligned}$$

(91)

Solving the above equation, we get

$$\begin{aligned} r_M|_{r>n}=2+\frac{1}{\alpha ^{\frac{1}{3}}}[\alpha ^{\frac{2}{3}}+5n_M^2+4] \end{aligned}$$

(92)

where

$$\begin{aligned} \alpha =8n_M^4+15n_M^2+8+n_M^2\sqrt{64n_M^4+115n_M^2+53}. \end{aligned}$$

(93)

The value of $r_M$ determines the radius of direct ISCO in Taub-NUT spacetime for timelike geodesic in the case of the radius of the Taub-NUT spacetime is much greater than the value of the NUT charge $n_M<r_M$.

For, $n_M=0$, we can recover $r_M=6$ as the radius of ISCO in Schwarzschild spacetime.

We can make the further assumption of $r<n$, which helps to reduce Eq. (90) to

$$\begin{aligned} 16r_M^3-15r_M^2+6r_M+n_M^2=0. \end{aligned}$$

(94)

Solving this equation we get

$$\begin{aligned} r_M|_{r<n}=\frac{5}{16}+\frac{1}{16\beta }[\beta ^{\frac{2}{3}}-7] \end{aligned}$$

(95)

where

$$\begin{aligned} \beta =16\sqrt{64n_M^4+115n_M^2+53}-128n_M^2-115. \end{aligned}$$

(96)

The value of $r_M$ determines the radius of direct ISCO in Taub-NUT spacetime for timelike geodesic in case of the radius of the Taub-NUT spacetime is much less than the value of the NUT charge $n_M>r_M$.

4.2 ISCOs in massless NUT spacetimes

In massless NUT spacetimes, the energy of a chargeless massive test particle which is moving in a particular orbit of radius $r=\frac{1}{u}$ is

$$\begin{aligned} E_{0TN}=\frac{(1-n^2u^2)}{\sqrt{(1+n^2u^2)(1-3n^2u^2)}} \end{aligned}$$

(97)

and the angular momentum of this particle will be

$$\begin{aligned} L_{0TN}=\sqrt{\frac{2n^2(1+n^2u^2)}{(1-3n^2u^2)}}, \end{aligned}$$

(98)

due to

$$\begin{aligned} Q_{0TN}=(1-3n^2u^2). \end{aligned}$$

(99)

Now, we can find the Kepler frequency $\Omega _{0TN}$ of a chargeless massive test particle which is moving in a particular orbit of radius $r=\frac{1}{u}$ at massless NUT spacetime:

$$\begin{aligned} \Omega _{0TN}=\frac{\sqrt{2}nu^2}{(1+n^2u^2)} \end{aligned}$$

(100)

and the rotational velocity $v^{(\phi )}_{0TN}$ of this test particle at massless NUT spacetime will be

$$\begin{aligned} v^{(\phi )}_{0TN}=nu\sqrt{\frac{2}{(1-n^2u^2)}}. \end{aligned}$$

(101)

The expressions of all astronomical observables are valid for $\frac{1}{u}=r>\sqrt{3}n$ as $L$ and $E$ would be complex for $r<\sqrt{3}n$ and diverge for $r=\sqrt{3}n$. Finally, the direct ISCO equation in massless NUT spacetimes can be expressed as

$$\begin{aligned} 16n^4r^3=0. \end{aligned}$$

(102)

As $n\ne 0$, we get

$$\begin{aligned} r=0. \end{aligned}$$

(103)

This means that the inner-most stable circular orbit is in the center of the massless NUT spacetime. This is unphysical, because, in the classification of Ellis and Schmidt [20, 21] the singularity of the Taub-NUT spacetime has been termed a quasi-regular singularity, since the curvature remains finite (see also [22, 23]). As $r=n$ has the singularity in the massless Taub-NUT spacetime, all geodesics are terminated at $r=n$ [2] before reaching $r=0$, which may be regarded as a spacelike surface. So, we cannot go beyond $r<n$ to determine ISCO. Apparently, the curvature of the Taub-NUT spacetime shows that $r=n$ is not a singular surface but in reality, $\theta =0, \pi$ are the singularities in the Taub-NUT spacetimes, as the curvature diverges for $\theta =0$ and $\pi$ [24]. Thus, the final conclusion is that there is not any physically reliable inner-most stable circular orbit in massless NUT spacetime for timelike geodesic.

5 Summary and discussion

In this paper we have calculated the radius of the innermost-stable circular orbit (ISCO) exactly for extremal KTN, Taub-NUT, massless Taub-NUT spacetimes. We also calculated some other important astronomical observables (i.e., $L, E, v^{(\phi )}, \Omega _\mathrm{Kep}$) for KTN (non-extremal and extremal both), Taub-NUT and massless Taub-NUT spacetimes. All the ISCOs of the non-extremal KTN, Taub-NUT and massless Taub-NUT lie on the timelike surface but the ISCOs of the extremal KTN spacetime (both for nulllike and timelike geodesics) lie on the horizons, i.e., on the lightlike surface. We cannot solve the ISCO equation of the non-extremal KTN spacetime analytically. However, one can see intuitively from the ISCO equation that the ISCO must belong to the timelike region, i.e., $r_\mathrm{ISCO}>r_+$ where $r_+=M+\sqrt{M^2+n^2-a^2}$. The Kerr parameter ($a_k$) of the extremal Kerr metric can take the highest value as $a_K=M$, but it takes $a_\mathrm{KTN}=\sqrt{M^2+n^2}$ in the case of an extremal KTN spacetime. So, the highest angular momentum of a Kerr spacetime is $J_K=M^2$ but it will be $J_\mathrm{KTN}=M\sqrt{M^2+n^2}$ in the case of extremal KTN spacetime. Thus, the ratio between these two is

$$\begin{aligned} \frac{J_K}{J_\mathrm{KTN}}=\frac{a_K}{a_\mathrm{KTN}}=\frac{M}{\sqrt{M^2+n^2}} . \end{aligned}$$

(104)

But the interesting thing is that the radii of the ISCOs in extremal KTN spacetime are the same as $R=M$. Thus,

$$\begin{aligned} \frac{r_\mathrm{KISCO}}{r_\mathrm{KTNISCO}}=1. \end{aligned}$$

(105)

It is quite remarkable that the NUT charge which appears in the expression of maximal angular momentum ($J$) has no effect for determining the radius of the ISCO in extremal KTN spacetimes. So, the radius of the ISCO is independent of NUT charge $n$. We know that the radius of the ISCO in extremal Kerr spacetime is $M$ [14] for both null and timelike geodesics. It is expected that if a new parameter appears in Kerr geometry, the ISCO should be altered away from $M$. But this is not happening in extremal KTN spacetime though the Kerr metric is modified with a new parameter $n$ as KTN spacetime. This non-dependence of ISCO behavior in the extremal case is somewhat mysterious. The NUT parameter in an extremal KTN spacetime behaves like a shield, so that the ISCO could not go away from the horizon. Another interesting thing is that the geodesic on the horizon coincides with the principal null geodesic generator for both extremal Kerr and extremal KTN spacetimes.

In the very non-extremal spacetime, when the Kerr parameter vanishes, i.e., in the case of the Taub-NUT spacetime, the ISCO is shifted to $M+2(M^2+n^2)^{1/2}\cos \left[ \frac{1}{3}\tan ^{-1} \left( \frac{n}{M}\right) \right]$ for null geodesics. For timelike geodesics, the ISCO of Taub-NUT spacetime is also shifted from null surface (in the case of extremal KTN spacetime) to timelike surface. The amount of this shifting is discussed in detail in the Sects. 3.1 and 4.1 of Sects. 3 and 4. Another thing is that the massless NUT spacetime does not hold any inner stable circular orbit for timelike geodesics. But it holds an ISCO at $\sqrt{3}n$ (which is outside the horizon) for null geodesics.

There are additional avenues of further work currently being investigated for an understanding of the thin disk accretion mechanism in KTN spacetime, applicable to some special candidates (like, supernovae, quasars, or active galactic nuclei etc.) which are of astrophysical importance. One could also investigate the exact Lense–Thirring precession rate of a test particle which is rotating on the ISCO in strong gravity regime of extremal KTN spacetimes. This is very important in the accretion mechanism as the accretion disk is mainly formed near the ISCO which lies in the strong gravity regime. Chakraborty and Majumdar [15] derived the exact Lense–Thirring (LT) precession rates in the KTN, Taub-NUT and massless Taub-NUT spacetimes, but their formula is valid only in a timelike spacetime; it is not valid on the horizon, i.e., on a null surface. Thus, it is not possible to derive the exact LT precession rate on the ISCO of extremal KTN spacetime by that formula. But it would be quite helpful for understanding the accretion mechanism in the future.