Abstract
Differential cross sections of charged particles in inelastic pp collisions as a function of p T have been measured at \(\sqrt{s} = 0.9,\ 2.76\ \text{and}\ 7\ \text{TeV}\) at the LHC. The p T spectra are compared to NLO-pQCD calculations. Though the differential cross section for an individual \(\sqrt{s}\) cannot be described by NLO-pQCD, the relative increase of cross section with \(\sqrt{s}\) is in agreement with NLO-pQCD. Based on these measurements and observations, procedures are discussed to construct pp reference spectra at \(\sqrt{s} = 2.76\ \text{and}\ 5.02~\text{TeV}\) up to p T=50 GeV/c as required for the calculation of the nuclear modification factor in nucleus–nucleus and proton–nucleus collisions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The measurement of charged particle production in proton–proton collisions at high energy gives insight into the dynamics of soft and hard interactions. Hard parton–parton scattering processes with large momentum transfer are quantitatively described by perturbative Quantum Chromodynamics (pQCD). Measurements at high transverse momenta (p T) at LHC-energies can help to constrain parton distribution and fragmentation functions in current next-to-Leading-Order (NLO) pQCD calculations [1] of charged particle production. As data at various \(\sqrt{s}\) become available at the LHC, a systematic comparison with current NLO-pQCD calculations over a large span of \(\sqrt{s}\) is now possible. However, most particles are produced at low momentum, where particle production is dominated by soft interactions and only phenomenological approaches can be applied (e.g. PYTHIA [2–4], PHOJET [5]) to describe the data. A systematic comparison to data at different values of \(\sqrt{s}\) is an essential ingredient to tune these Monte Carlo event generators.
Furthermore, the measurement of charged particle transverse momentum spectra in pp collisions serves as a crucial reference for particle spectra in Pb–Pb collisions. To quantify final state effects due to the creation of a hot and dense deconfined matter, commonly referred to as the Quark–Gluon Plasma (QGP), p T spectra in the two collision systems are compared. The observed suppression [6] in central Pb–Pb collisions at LHC-energies at high p T relative to an independent superposition of pp collisions is generally attributed to energy loss of the partons as they propagate through the hot and dense QCD medium. To enable this comparison a pp reference p T spectrum at the same \(\sqrt{s}\) with the same p T coverage has to be provided. Similarly, a pp reference spectrum is also needed for p–Pb collisions to investigate possible initial-state effects in the collision.
In this paper we present a measurement of primary charged particle transverse momentum spectra in pp collisions at \(\sqrt{s} = 0.9,\ 2.76 \ \mbox{and}\ 7\ \text{TeV}\). Primary charged particles are considered here as all charged particles produced in the collision and their decay products, except for particles from weak decays of strange hadrons. The measurement is performed in the pseudorapidity range |η|<0.8 for particles with p T>0.15 GeV/c. Reference spectra for comparison with Pb–Pb spectra at \(\sqrt {s_{\mathrm{NN}}} = 2.76\ \mbox{TeV}\) and p–Pb spectra at \(\sqrt{s_{\mathrm {NN}}} = 5.02\ \mbox{TeV}\) in the corresponding p T range up to p T=50 GeV/c are constructed.
2 Experiment and data analysis
The data were collected by the ALICE apparatus [7] at the CERN-LHC in 2009–2011. The analysis is based on tracking information from the Inner Tracking System (ITS) and the Time Projection Chamber (TPC), both located in the central barrel of the experiment. The minimum-bias interaction trigger was derived using signals from the forward scintillators (VZERO), and the two innermost layers of the ITS, the Silicon Pixel Detector (SPD). Details of the experimental setup used in this analysis are discussed in [8].
The events are selected based on the minimum-bias trigger MBOR requiring at least one hit in the SPD or VZERO detectors, which are required to be in coincidence with two beam bunches crossing in the ALICE interaction region. In addition, an offline event selection is applied to reject beam induced (beam-gas, beam-halo) background. The VZERO counters are used to remove these beam-gas or beam-halo events by requiring their timing signals to be in coincidence with particles produced in the collision. The background events are also removed by exploiting the correlation between the number of the SPD hits and the number of the SPD tracklets (short track segments reconstructed in the SPD and pointing to the interaction vertex). The beam-gas or beam-halo events typically have a large number of hits in the SPD compared to the number of reconstructed tracklets; this is used to reject background events. In total 6.8 M, 65 M and 150 M pp events at \(\sqrt{s}=0.9,\ 2.76\ \mbox{and}\ 7\ \text{TeV}\) fulfill the \(\rm {MB_{{OR}}}\) trigger and offline selection criteria. The typical luminosity for these data taking was about 1029 s−1 cm−2. The average number of interactions per bunch crossing varied from 0.05 to 0.1.
In this analysis the focus is on inelastic (INEL) pp events originating from single-diffractive, double-diffractive and non-diffractive processes. The INEL events are selected with an efficiency \(\varepsilon _{\mathrm{MB}_{\mathrm{OR}}}\) of \(91^{+3.2}_{-1.0}~\%\), \(88.1^{+5.9}_{-3.5}~\%\) and \(85.2^{+6.2}_{-3.0}~\%\) for the three energies. The trigger efficiencies are determined [9] based on detector simulations with PYTHIA6 [2–4] and PHOJET [5] event generators.
The primary event vertex is determined based on ITS and TPC information. If no vertex is found using tracks in the ITS and the TPC, it is reconstructed from tracklets in the SPD only. Tracks or tracklets are extrapolated to the experimental collision region utilizing the averaged measured beam intersection profile in the x–y plane perpendicular to the beam axis.
An event is accepted if the z-coordinate of the vertex is within ±10 cm of the center of the interaction region along the beam direction. This corresponds to about 1.6 standard deviations from the mean of the reconstructed event vertex distribution for all three energies. In this range, the vertex reconstruction efficiency is independent of z. The event vertex reconstruction is fully efficient for events with at least one track in the pseudorapidity range |η|<1.4 for all three energies.
Only tracks within a pseudorapidity range of |η|<0.8 and transverse momenta p T>0.15 GeV/c are selected. A set of standard cuts based on the number of space points and the quality of the track fit in ITS and TPC is applied to the reconstructed tracks [10].
Efficiency and purity of the primary charged particle selection are estimated using simulations with PYTHIA6 [2–4] and GEANT3 [11] for particle transport and detector response. The overall p T-dependent efficiency (tracking efficiency × acceptance) is 40–73 %, 36–68 % and 40–73 % at \(\sqrt{s}=0.9,\ 2.76\ \mbox{and}\ 7\ \text{TeV}\). At \(\sqrt{s}=2.76~\text{TeV}\) the overall efficiency is lower than at \(\sqrt {s}=0.9\ \text{and}\ 7\ \text{TeV}\) due to the smaller number of operational channels in the SPD. Contamination of secondary tracks which passed all selection criteria amounts to 7 % at p T=0.15 GeV/c and decreases to ∼0.6 % for p T>4 GeV/c. In addition, the contribution from secondary tracks originating from weak decays of strange hadrons was scaled up by a factor of 1–1.5 (p T-dependent) to match the contribution in data. The secondary tracks were subtracted bin-by-bin from the p T spectra.
The p T resolution is estimated from the space point residuals of the track fit. It is verified by the width of the invariant mass peaks of Λ, \(\overline{\varLambda}\) and \(\mathrm{K}^{0}_{\mathrm{{s}}}\), reconstructed from their decays into two charged particles. The relative p T resolution is 3.5 %, 5.5 % and 9 % at the highest p T of 20, 32 and 50 GeV/c at \(\sqrt{s}=0.9,\ 2.76\ \text{and}\ 7~\text{TeV}\), respectively. From invariant mass distributions M inv(p T) of Λ and \(\mathrm{K}^{0}_{\mathrm{{s}}}\), the relative uncertainty on the p T resolution is estimated to be ≈20 % for all three energies. To account for the finite p T resolution of tracks, correction factors to the spectrum for p T>10 GeV/c are derived using an unfolding procedure. The determination of the correction factors is based on measured tracks without involving simulation. The choice of the unfolding procedure is based on the observation that p T smearing has a small influence on the measured spectrum. As input to the procedure a power-law parametrization of the measured p T spectrum for p T>10 GeV/c is used. This parametrization is folded with the p T resolution obtained for a given p T from the measured track covariance matrix. The p T dependent correction factors are extracted from the ratio of the input to the folded parametrization and are applied (bin-by-bin) to the measured p T spectrum. It was checked that the derived correction factors are the same when replacing the measured with the corrected p T distribution in the unfolding procedure. The correction factors depend on \(\sqrt{s}\) due to the change of the spectral shape and reach 2 %, 4 % and 6.5 % at \(\sqrt{s}=0.9,~2.76~\text{and}~7~\text{TeV}\) for the highest p T. The systematic uncertainty of the momentum scale is |Δ(p T)/p T|<0.01 at p T=50 GeV/c, as determined from the mass difference between Λ and \(\overline{\varLambda}\) and the ratio of positively to negatively charged tracks, assuming charge symmetry at high p T.
A summary of the systematic uncertainties is given in Table 1. The systematic uncertainties on the event selection are determined by changing the lower and upper limits on the z-coordinate of the vertex. Track selection criteria [10] are varied to determine the corresponding systematic uncertainties resulting in a maximal contribution of 4.3–5.5 % for p T<0.6 GeV/c. The systematic uncertainties on the tracking efficiency are estimated from the difference between data and simulation in the TPC-ITS track matching efficiency. The systematic uncertainties related to the p T resolution correction are derived from the unfolding procedure including a relative uncertainty on the p T resolution, and reach maximum values at the highest p T covered. The systematic uncertainties on the material budget (∼11.5 % X 0 [12], where X 0 is the radiation length) are estimated by changing the material density (conservatively) by ±10 % in the simulation, contributing mostly at p T<0.2 GeV/c. To assess the systematic uncertainties on the tracking efficiency related to the primary particle composition the relative abundance of π, K, p was varied by 30 % in the simulation; they contribute mostly at p T<0.5 GeV/c. The Monte Carlo (MC) event generator dependence was studied using PHOJET as a comparison, with the largest contribution at p T<0.2 GeV/c. The yield of secondary particles from decays of strange hadrons has been varied by 30 % to determine the corresponding uncertainty of maximum 0.3 % at p T≈1 GeV/c. The total p T dependent systematic uncertainties for the three energies amount to 6.7–8.2 %, 6.4–8.0 % and 6.6–7.9 % and are shown in the bottom panel of Fig. 1. They are dominated by the systematic uncertainties on the tracking efficiency. There are also comparable contributions related to the track selection (p T<0.6 GeV/c) and p T resolution correction at the highest p T covered. The systematic uncertainties on the normalization are related to the minimum bias nucleon–nucleon cross section (\(\sigma^{\mathrm {NN}}_{\mathrm{MB}}\)) determination [9] and amount to +5.1/−4.0 %, ±1.9 % and ±3.6 % for pp at \(\sqrt{s}=0.9~\mbox{TeV},\ 2.76~\text{TeV}\ \mbox{and}\ 7~\text{TeV}\), respectively.
Top: Differential cross section of charged particles in INEL pp collisions at \(\sqrt{s} = 0.9,\ 2.76\ \text{and}\ 7~\text{TeV}\) as a function of p T compared to a NLO-pQCD calculation [1] at the same energy. Only statistical uncertainties are shown. Bottom: Systematic uncertainties as a function of p T for all three energies. The uncertainty on the normalization (compare Table 1) of the spectra is not included (Color figure online)
The differential cross section d2 σ ch/dη dp T is calculated as \(\mathrm{d}^{2}\sigma_{\mathrm{ch}} / {\mathrm{d}}\eta\,\mathrm {d}p_{\mathrm{T}} = \sigma_{\mathrm{MB}_{\mathrm {OR}}}^{\mathrm{NN}} \times\mathrm{d}^{2} {N}^{\mathrm {MB}_{\mathrm{OR}}}_{\mathrm{{ch}}} / {\mathrm{{d}}} \eta \,{\mathrm{{d}}}p_{\mathrm{T}}\) with \(\mathrm{{d}}^{2} {{N}}^{\mathrm{{MB_{\mathrm{{OR}}}}}}_{\mathrm {{ch}}} / {\mathrm{{d}}} \eta\,{\mathrm{{d}}}p_{\mathrm{T}}\) being the per event differential yield of charged particles in minimum bias collisions. \(\sigma_{\mathrm{MB}_{\mathrm{OR}}}^{\mathrm{{NN}}}\) is determined based on van-der-Meer scans [9] as \(\sigma_{\mathrm{MB}_{\mathrm{OR}}}^{\mathrm{NN}} = 55.4 \pm1.0\) (62.2±2.2) mb at \(\sqrt{s}=2.76~(7)~\mbox{TeV}\). At \(\sqrt{s}=0.9~\mbox{TeV}\) van-der-Meer scans were not performed and \(\sigma_{\mathrm{MB}_{\mathrm{OR}}}^{\mathrm {{NN}}}=47.8^{+2.5}_{-3.0}~\mbox{mb}\) is obtained based on detector simulations using the INEL cross section \(\sigma^{\mathrm{{NN}}}_{\mathrm{{INEL}}}=52.5^{+2}_{-3.3}~\mbox{mb}\) [9]. \(\sigma^{\mathrm{{NN}}}_{\mathrm{{INEL}}}\) includes the UA5 measurement [13] and re-analysis of the extrapolation to low diffractive masses [14].
3 Results
The differential cross section in INEL pp collisions as a function of p T is shown in Fig. 1 for all three measured collision energies. At high p T a clear evolution of the slope from \(\sqrt {s}= 0.9\ \mbox{to}\ 7~\text{TeV}\) can be observed. A NLO-pQCD calculation [1] for p T>3 GeV/c is compared to the spectra. The calculation shows a similar evolution of the high-p T dependence with \(\sqrt{s}\) but overpredicts the data by a factor two [12, 15]. The low systematic uncertainties demonstrate the accuracy of the measurements for all energies over the full p T range.
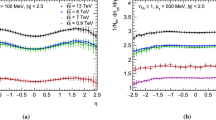
Though the p T dependence of the cross section for a single \(\sqrt{s}\) is not well described by NLO-pQCD, the relative dependence on p T of cross sections of two collision energies is described much better. Figure 2 shows the ratio between the differential cross section in INEL pp collisions at \(\sqrt{s} = 2.76\ \mbox{to}\ 7~\mbox{TeV},\ 0.9\ \mbox{to}\ 2.76~\mbox{TeV}\ \mbox{and}\ 0.9\ \mbox{to}\ 7~\mbox{TeV}\) as a function of p T in comparison to the same ratio calculated with NLO-pQCD. The total p T dependent systematic uncertainties on the ratios are evaluated taking into account correlated contributions, and amount to 8.1–9.8 %, 7.8–9.8 % and 7.9–9.9 % for 0.9 TeV/2.76 TeV, 0.9 TeV/7 TeV and 2.76 TeV/7 TeV. The corresponding normalization uncertainties amount to +5.4 %/−4.4 %, +6.2 %/−5.4 % and ±4.1 %, and are calculated assuming that the normalization uncertainties on the p T spectra (Table 1) are uncorrelated. In all three ratios good agreement between data and NLO-pQCD calculations is found, which can be seen in the double ratio of data and NLO-pQCD for the three energy ratios in the lower panel of Fig. 2.
Top: Ratio of differential cross sections of charged particles in INEL pp collisions at different collision energies as a function of p T. Gray boxes denote p T dependent systematic uncertainties. Normalization uncertainties are not shown (see text for details). The histograms show the same ratio determined from NLO calculations. Bottom: Ratio of data and NLO calculations derived from upper panel. A variation of the renormalization and factorization scale of the NLO calculation gives a systematic uncertainty on the double ratio of 0.5–23.6 % for 0.9 TeV/2.76 TeV, 1.0–37.8 % for 0.9 TeV/7 TeV and 2.4–12.3 % for 2.76 TeV/7 TeV (Color figure online)
4 Construction of a pp reference for \(\sqrt{s} = 2.76\ \mbox{TeV}\)
For the determination of the nuclear modification factor
in heavy-ion collisions a well described pp reference \(\mathrm{d}^{2} \sigma_{\mathrm {ch}}^{\mathrm{pp}} / {\mathrm{d}} \eta\,{\mathrm{d}}p_{\mathrm{T}}\) at the same center-of-mass energy up to high p T is essential. \({N}_{\mathrm{ch}}^{\mathrm{AA}}\) describes the charged particle yield per event in nucleus–nucleus collisions and 〈T AA〉 is the average nuclear overlap function [6, 10]. The statistics in the measurement of \(\mathrm{d}^{2} \sigma_{\mathrm {ch}}^{\mathrm{pp}} / {\mathrm{d}} \eta\,{\mathrm{d}}p_{\mathrm{T}}\) for \(\sqrt{s} = 2.76\ \mbox{TeV}\) reported in this paper allows p T=32 GeV/c to be reached. In order to extrapolate to higher p T, the measured cross section needs to be parametrized.
As can be seen in Fig. 1 for p T>10 GeV/c the pp spectrum at \(\sqrt{s} = 2.76\ \mbox{TeV}\) shows a clear power-law dependence on p T. To constrain the parametrization better by including data points at lower p T, \(\mathrm{d}^{2} \sigma_{\mathrm{ch}}^{\mathrm{pp}} / {\mathrm{d}} \eta\,{\mathrm{d}}p_{\mathrm{T}}\) has been parametrized by a so-called modified Hagedorn function [16]
where m T denotes the transverse mass \(m_{\mathrm{T}} = \sqrt{m_{0}^{2} + p_{\mathrm{T}}^{2}}\), with m 0=140 MeV/c assumed for all tracks. For small p T, the term \((1+ \frac {p_{\mathrm{T}}}{p_{\mathrm{T,0}}} )^{-n}\) behaves like an exponential function with an inverse slope parameter of \(p_{\mathrm{T,0}}/n\) while for large p T the Hagedorn function behaves like a power-law function.
To determine the extrapolation to high p T, \(\mathrm {d}^{2} \sigma_{\mathrm{ch}}^{\mathrm{pp}} / {\mathrm{d}} \eta \,{\mathrm{d}}p_{\mathrm{T}}\) is parametrized for p T>5 GeV/c. For 5 GeV/c<p T<10 GeV/c the exponential part of the Hagedorn function acts as a correction term to the power-law part in the function.
Figure 3 shows the differential cross section in INEL pp collisions as a function of p T for \(\sqrt{s} = 2.76~\mbox{TeV}\) together with the parametrization for p T>5 GeV/c. The ratio between data and parametrization in the lower panel demonstrates the good agreement of the parametrization with the data. The gray band indicates the total p T dependent systematic uncertainty of the measured spectrum as presented in Table 1.
Top: Differential cross section of charged particles in INEL pp collisions at \(\sqrt{s} = 2.76\ \mbox{TeV}\) as a function of p T together with the parametrization (p T>5 GeV/c) described in the text. Bottom: Ratio of data to parametrization. The gray band indicates the total p T dependent systematic uncertainty of the data, open circles show data points only used for the evaluation of the systematic uncertainty of the parametrization (Color figure online)
To estimate the systematic uncertainty of the parametrization and extrapolation, the lower boundary of the fit range of the Hagedorn parametrization is varied between p T=3 GeV/c and p T=7 GeV/c, while the upper boundary is fixed to the highest data point measured at p T=32 GeV/c. Together with the systematic uncertainties on the measured differential cross section as shown in Table 1 this results in a total systematic uncertainty on the reference at \(\sqrt{s} = 2.76\ \mbox{TeV}\) of 6.4 % for low p T up to 19 % at p T=50 GeV/c.
The final pp reference for the determination of R AA at \(\sqrt{s} = 2.76\ \mbox{TeV}\) is constructed from the measured data points up to p T=5 GeV/c and the parametrization for p T>5 GeV/c. Statistical uncertainties in the extrapolated part of the reference are obtained from the covariance matrix of the parametrization. The systematic uncertainties on the spectrum are propagated to the reference by application of the full extrapolation procedure using the measured data points shifted up and down by the total systematic uncertainty.
This reference is compared to alternative measurements and approaches. Figure 4 shows the ratio between alternative pp references and the reference at \(\sqrt{s} = 2.76\ \mbox{TeV}\) presented in this paper. Above p T=20 GeV/c, all references agree within the systematic uncertainties. Simulations with the PYTHIA8 generator [17] agree with the new reference for p T>15 GeV/c. Below p T=20 GeV/c, the shape of the PYTHIA8 spectrum is similar to the measured reference. A pp reference presented by the CMS collaboration [18] agrees best for p T<6 GeV/c. The overall normalization systematic uncertainties ±1.9 % (±6 %) for ALICE (CMS) are not included in the comparison. A reference based on an interpolation between measured yields at \(\sqrt {s} = 0.9\ \text{and}\ 7~\text{TeV}\) as discussed in [6] does not agree with the new reference for p T>6 GeV/c. Finally a scaling of the measured differential cross section in INEL pp collisions at \(\sqrt{s} = 7\ \mbox{TeV}\) with the ratio of pQCD calculations (as shown in Fig. 2)
agrees well in shape and normalization with the measured data over a wide range in p T. The systematic uncertainty of the new reference is indicated in Fig. 4 as a gray band for comparison.
Ratio of alternative references to the new constructed pp reference at \(\sqrt{s} = 2.76\ \mbox{TeV}\) as discussed in the text. The gray band indicates the total p T dependent systematic uncertainty as discussed in the text. The overall normalization systematic uncertainties ±1.9 % (±6 %) for ALICE (CMS) are not shown (Color figure online)
5 Construction of a pp reference for \(\sqrt{s} = 5.02\ \mbox{TeV}\)
Similar to R AA, a nuclear modification factor R pA in proton-lead collisions has been studied [19] at \(\sqrt{s} = 5.02\ \mbox{TeV}\). No measured pp reference is available at this collision energy. Due to the asymmetric p–Pb collision system, the η coverage of the detector is shifted with respect to the symmetric pp or Pb–Pb collisions. To obtain a maximum overlap between the pp and p–Pb systems, a pp reference is needed for |η|<0.3. To construct the pp reference at this energy, different methods for three p T-ranges are combined.
0.15<p T<5 GeV/c: As NLO-pQCD becomes unreliable for small p T, the measured differential cross sections for pp collisions of \(\sqrt{s} = 2.76\ \mbox{and}\ 7~\text{TeV}\) are interpolated for a given p T, assuming a power-law behavior of the \(\sqrt{s}\) dependence of the cross section. Here the maximum relative systematic uncertainty of the underlying measurements has been assigned as systematic uncertainty.
5<p T<20 GeV/c: The measured differential cross section for pp collisions at \(\sqrt{s} = 7\ \mbox{TeV}\) is scaled to \(\sqrt{s} = 5.02\ \mbox{TeV}\) using the NLO-pQCD calculations (Eq. (3)). Systematic uncertainties are determined by taking into account differences to an interpolated reference as well as to a scaled reference using μ=p T/2 and μ=2p T as alternative choices for the renormalization and factorization scales.
p T>20 GeV/c: The NLO-scaled reference is parametrized in the range 20<p T<50 GeV/c by a power-law function and the parametrization is used.
The constructed pp reference for \(\sqrt{s} = 5.02\ \mbox{TeV}\) is shown in Fig. 5 together with the reference for \(\sqrt{s}=2.76~\mbox{TeV}\) discussed above. For p T>20 GeV/c the data points show the NLO-scaled reference which is parametrized by a power-law function (line) to obtain the final reference at \(\sqrt {s} = 5.02\ \mbox{TeV}\). In the bottom part of the figure a comparison of the NLO-scaled reference and the parametrization is shown.
Top: Constructed pp references for \(\sqrt{s} = 2.76\ \text{and} \ \sqrt{s} = 5.02\ \mbox{TeV}\). Bottom: Comparison of NLO-scaled reference and parametrization. The parametrization is used for p T>20 GeV/c. The gray band indicates the total p T dependent systematic uncertainty as discussed in the text (Color figure online)
6 Summary
Differential cross sections of charged particles in inelastic pp collisions as a function of p T have been presented for \(\sqrt{s} = 0.9,\ 2.76\ \text{and}\ 7~\text{TeV}\). Comparisons of the p T spectra with NLO-pQCD calculations show that the cross section for an individual value of \(\sqrt{s}\) cannot be described by the calculation. The relative increase of cross section with \(\sqrt{s}\) is well described by NLO-pQCD, however. The systematic comparison of the energy dependence can help to tune the model dependent ingredients in the calculation. Utilizing these observations and measurements procedures are discussed to construct pp reference spectra at \(\sqrt{s} = 2.76\) (|η|<0.8) and 5.02 TeV (|η|<0.3) in the corresponding p T range of charged particle p T spectra in Pb–Pb and p–Pb collisions measured by the ALICE experiment. The reference spectra are used for the calculation of the nuclear modification factors R AA [10] and R pA [19]. The systematic uncertainties related to the pp reference were significantly reduced with respect to the previous measurement by using the p T distribution measured in pp collisions at \(\sqrt{s}=2.76~\mbox{TeV}\).
References
R. Sassot, P. Zurita, M. Stratmann, Inclusive hadron production in the CERN-LHC era. Phys. Rev. D 82, 074011 (2010). arXiv:1008.0540. doi:10.1103/PhysRevD.82.074011
T. Sjostrand, High-energy physics event generation with PYTHIA 5.7 and JETSET 7.4. Comput. Phys. Commun. 82, 74 (1994). doi:10.1016/0010-4655(94)90132-5
T. Sjostrand, S. Mrenna, P.Z. Skands, PYTHIA 6.4 physics and manual. J. High Energy Phys. 0605, 026 (2006). arXiv:hep-ph/0603175. doi:10.1088/1126-6708/2006/05/026
P.Z. Skands, The Perugia tunes. arXiv:0905.3418
R. Engel, J. Ranft, S. Roesler, Hard diffraction in hadron hadron interactions and in photoproduction. Phys. Rev. D 52, 1459 (1995). arXiv:hep-ph/9502319. doi:10.1103/PhysRevD.52.1459
K. Aamodt (ALICE Collaboration), Suppression of charged particle production at large transverse momentum in central Pb–Pb collisions at \(\sqrt{s_{\mathrm{NN}}} = 2.76\ \mbox{TeV}\). Phys. Lett. B 696, 30 (2011). arXiv:1012.1004. doi:10.1016/j.physletb.2010.12.020
K. Aamodt et al. (ALICE Collaboration), The ALICE experiment at the CERN LHC. J. Instrum. 3, S08002 (2008). doi:10.1088/1748-0221/3/08/S08002
K. Aamodt et al. (ALICE Collaboration), Transverse momentum spectra of charged particles in proton–proton collisions at \(\sqrt{s} = 900\ \mbox{GeV}\) with ALICE at the LHC. Phys. Lett. B 693, 53 (2010). arXiv:1007.0719. doi:10.1016/j.physletb.2010.08.026
B. Abelev et al. (ALICE Collaboration), Measurement of inelastic, single- and double-diffraction cross sections in proton–proton collisions at the LHC with ALICE. Eur. Phys. J. C 73, 2456 (2013). arXiv:1208.4968. doi:10.1140/epjc/s10052-013-2456-0
B. Abelev et al. (ALICE Collaboration), Centrality dependence of charged particle production at large transverse momentum in Pb–Pb collisions at \(\sqrt{s_{\mathrm{NN}}} = 2.76\ \mbox{TeV}\). Phys. Lett. B 720, 52 (2013). arXiv:1208.2711. doi:10.1016/j.physletb.2013.01.051
R. Brun et al., GEANT: Detector Description and Simulation Tool, CERN Program Library Long Writeup W5013 (CERN, Geneva, 1994)
B. Abelev et al. (ALICE Collaboration), Neutral pion and η meson production in proton–proton collisions at \(\sqrt{s}=0.9\ \mbox{TeV}\ \mbox{and}\ \sqrt{s}=7\ \mbox{TeV}\). Phys. Lett. B 717, 162 (2012). arXiv:1205.5724
R. Ansorge et al. (UA5 Collaboration), Diffraction dissociation at the CERN pulsed collider at cm energies of 900 GeV and 200 GeV. Z. Phys. C 33, 175 (1986). doi:10.1007/BF01411134
M. Poghosyan, Two remarks about UA5 published data on general characteristics of \(p\bar{p}\) collisions at \(\sqrt{s} = 900\ \mbox{GeV}\). arXiv:1005.1806
S. Chatrchyan et al. (CMS Collaboration), Charged particle transverse momentum spectra in pp collisions at \(\sqrt{s} = 0.9\ \mbox{and}\ 7\ \text{TeV}\). J. High Energy Phys. 1108, 086 (2011). arXiv:1104.3547
R. Hagedorn, Multiplicities, p T distributions and the expected hadron → quark–gluon phase transition. CERN-TH-3684, 1983
T. Sjostrand, S. Mrenna, P.Z. Skands, A brief introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852 (2008). arXiv:0710.3820. doi:10.1016/j.cpc.2008.01.036
S. Chatrchyan et al. (CMS Collaboration), Study of high-p T charged particle suppression in PbPb compared to pp collisions at \(\sqrt{s_{\mathrm{NN}}}=2.76\ \mbox{TeV}\). Eur. Phys. J. C 72, 1945 (2012). arXiv:1202.2554. doi:10.1140/epjc/s10052-012-1945-x
B. Abelev et al. (ALICE Collaboration), Transverse momentum distribution and nuclear modification factor of charged particles in p–Pb collisions at \(\sqrt{s_{\mathrm{NN}}}=5.02\ \mbox{TeV}\). Phys. Rev. Lett. 110, 082302 (2013). arXiv:1210.4520. doi:10.1103/PhysRevLett.110.082302
Acknowledgements
The ALICE collaboration would like to thank all its engineers and technicians for their invaluable contributions to the construction of the experiment and the CERN accelerator teams for the outstanding performance of the LHC complex.
The ALICE collaboration acknowledges the following funding agencies for their support in building and running the ALICE detector:
State Committee of Science, World Federation of Scientists (WFS) and Swiss Fonds Kidagan, Armenia;
Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Financiadora de Estudos e Projetos (FINEP), Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP);
National Natural Science Foundation of China (NSFC), the Chinese Ministry of Education (CMOE) and the Ministry of Science and Technology of China (MSTC);
Ministry of Education and Youth of the Czech Republic;
Danish Natural Science Research Council, the Carlsberg Foundation and the Danish National Research Foundation;
The European Research Council under the European Community’s Seventh Framework Programme;
Helsinki Institute of Physics and the Academy of Finland;
French CNRS-IN2P3, the ‘Region Pays de Loire’, ‘Region Alsace’, ‘Region Auvergne’ and CEA, France;
German BMBF and the Helmholtz Association;
General Secretariat for Research and Technology, Ministry of Development, Greece;
Hungarian OTKA and National Office for Research and Technology (NKTH);
Department of Atomic Energy and Department of Science and Technology of the Government of India;
Istituto Nazionale di Fisica Nucleare (INFN) and Centro Fermi—Museo Storico della Fisica e Centro Studi e Ricerche “Enrico Fermi”, Italy;
MEXT Grant-in-Aid for Specially Promoted Research, Japan;
Joint Institute for Nuclear Research, Dubna;
National Research Foundation of Korea (NRF);
CONACYT, DGAPA, México, ALFA-EC and the EPLANET Program (European Particle Physics Latin American Network);
Stichting voor Fundamenteel Onderzoek der Materie (FOM) and the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO), Netherlands;
Research Council of Norway (NFR);
Polish Ministry of Science and Higher Education;
National Authority for Scientific Research—NASR (Autoritatea Naţională pentru Cercetare Ştiinţifică—ANCS);
Ministry of Education and Science of Russian Federation, Russian Academy of Sciences, Russian Federal Agency of Atomic Energy, Russian Federal Agency for Science and Innovations and The Russian Foundation for Basic Research;
Ministry of Education of Slovakia;
Department of Science and Technology, South Africa;
CIEMAT, EELA, Ministerio de Economía y Competitividad (MINECO) of Spain, Xunta de Galicia (Consellería de Educación), CEADEN, Cubaenergía, Cuba, and IAEA (International Atomic Energy Agency);
Swedish Research Council (VR) and Knut & Alice Wallenberg Foundation (KAW);
Ukraine Ministry of Education and Science;
United Kingdom Science and Technology Facilities Council (STFC);
The United States Department of Energy, the United States National Science Foundation, the State of Texas, and the State of Ohio.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Consortia
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
The ALICE Collaboration., Abelev, B., Adam, J. et al. Energy dependence of the transverse momentum distributions of charged particles in pp collisions measured by ALICE. Eur. Phys. J. C 73, 2662 (2013). https://doi.org/10.1140/epjc/s10052-013-2662-9
Received:
Revised:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-013-2662-9