Novel discrete symmetries in the general supersymmetric quantum mechanical model

Abstract

In addition to the usual supersymmetric (SUSY) continuous symmetry transformations for the general SUSY quantum mechanical model, we show the existence of a set of novel discrete symmetry transformations for the Lagrangian of the above SUSY quantum mechanical model. Out of all these discrete symmetry transformations, a unique discrete transformation corresponds to the Hodge duality operation of differential geometry and the above SUSY continuous symmetry transformations (and their anticommutator) provide the physical realizations of the de Rham cohomological operators of differential geometry. Thus, we provide a concrete proof of our earlier conjecture that any arbitrary SUSY quantum mechanical model is an example of a Hodge theory where the cohomological operators find their physical realizations in the language of symmetry transformations of this theory. Possible physical implications of our present study are pointed out, too.

Appendix: On the derivation of 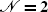SUSY algebra

The whole of algebraic structures in Sect. 6 are based on the basic SUSY algebra $Q^{2} = \bar{Q}^{2} = 0, \{Q, \bar{Q}\} = H, [H, Q] = [H, \bar{Q}] = 0$ which is satisfied on the on-shell. To corroborate this statement, first of all, auxiliary variable A in the Lagrangian (10) is replaced by (−W′) due to the equation of motion A=−W′ (which emerges from (10) itself). Furthermore, the symmetry transformations s ₁ and s ₂ (cf. (11)) are modified a bit by the overall constant factors. Thus, we have the following different looking Lagrangian:

$$\begin{aligned} L_0 = \frac{1}{2} {\dot{x}}^2 + i\bar{\psi}\dot{\psi}- \frac {1}{2} \bigl(W'\bigr)^2 + W'' \bar{\psi}\psi, \end{aligned}$$

(A.1)

which remains invariant under the following transformations:

$$\begin{aligned} \begin{aligned} & s_1 x = -\frac{1}{\sqrt{2}}i \psi, \qquad s_1 \bar{\psi}= \frac{1}{\sqrt{2}}\bigl(\dot{x} - iW'\bigr), \qquad s_1 \psi = 0, \\ & s_2 x = + \frac{1}{\sqrt{2}}i \bar{\psi}, \qquad s_2 \psi = - \frac{1}{\sqrt{2}} \bigl(\dot{x} + iW'\bigr),\\ & s_2 \bar{\psi}= 0. \end{aligned} \end{aligned}$$

(A.2)

The above transformations are nilpotent of order two (i.e. $s_{1}^{2} = s_{2}^{2} = 0$) only when the equations of motion $\dot{\psi}- i W'' \psi = 0, \dot {\bar{\psi}} + i W'' \bar{\psi}= 0$ are used. It can be checked that $s_{1} L_{0} = d/dt (W^{\prime}\psi/ \sqrt{2} )$ and $s_{2} L_{0} = d/dt (i \bar{\psi}\dot{x}/ \sqrt{2} )$. Hence, the action integral S=∫dtL ₀ remains invariant under s ₁ and s ₂.

The conserved Noether charges, which emerge corresponding to (A.2), are

$$\begin{aligned} Q = -\frac{1}{\sqrt{2}} \bigl(i\dot{x} + W' \bigr) \psi, \qquad \bar{Q} = +\frac{1}{\sqrt{2}} \bar{\psi}\bigl(i\dot{x} - W' \bigr). \end{aligned}$$

(A.3)

These charges are same as quoted in (15) except the fact that A has been replaced by (−W′) (due to the equation of motion from the Lagrangian (10)) and the constant factors $(\mp 1/\sqrt{2})$ have been included for the algebraic convenience. It can be readily checked that the above charges are the generator for the transformations (A.2) because we have the following relationships:

$$\begin{aligned} s_1 \varPhi = \pm i [\varPhi, Q ]_\pm, \qquad s_2 \varPhi = \pm i [\varPhi, \bar{Q} ]_\pm, \end{aligned}$$

(A.4)

where the generic variable Φ corresponds to the variables $x, \psi, \bar{\psi}$ and the subscripts (±) on square brackets stand for the (anti)commutator depending on the generic variable Φ being (fermionic) bosonic in nature. The (±) signs, in front of the brackets, are also chosen judiciously (see, e.g. [21] for details).

The structure of the specific SUSY algebra now follows when we exploit the basic relationship (A.4). In other words, we observe the following:

$$\begin{aligned} \begin{aligned} & s_1 Q = i \{Q, Q \} = 0\quad \Longrightarrow\quad Q^2 = 0, \\ & s_1 \bar{Q} = i \{\bar{Q}, \bar{Q} \} = 0\quad \Longrightarrow\quad \bar{Q}^2 = 0, \\ & s_1 \bar{Q} = i \{\bar{Q}, Q \} = iH \quad\Longrightarrow\quad \{\bar{Q}, Q \} = H, \\ & s_2 Q = i \{Q, \bar{Q} \} = iH \quad\Longrightarrow\quad \{Q, \bar{Q} \} = H, \end{aligned} \end{aligned}$$

(A.5)

where H is the Hamiltonian (corresponding to the Lagrangian (A.1)). The explicit form of H can be mathematically expressed as

$$\begin{aligned} H =& \frac{1}{2} {\dot{x}}^2 + \frac {1}{2} \bigl(W'\bigr)^2 - W'' \bar{\psi}\psi \\ \equiv & \frac{1}{2} p^2 + \frac {1}{2} \bigl(W'\bigr)^2 - W'' \bar{\psi}\psi, \end{aligned}$$

(A.6)

where $p = \dot{x}$ is the momentum corresponding to the variable x. We also lay emphasis on the fact that we have exploited the inputs from equations of motion $\dot{\psi}- i W'' \psi = 0, \dot {\bar{\psi}} + i W'' \bar{\psi}= 0$ in the derivation of H from the Legendre transformation $H = \dot{x} p + \dot{\psi}\varPi_{\psi}+ \dot{\bar{\psi}} \varPi_{\bar{\psi}} - L$ where $\varPi_{\psi}= - i \bar{\psi}$ and $\varPi_{\bar{\psi}} = 0$. The derivation of specific SUSY algebra (cf. (A.5)) is very straightforward because we have used only (A.2) and (A.3) in the calculation of l.h.s. of (A.5) from which, the results of the r.h.s. (i.e. specific SUSY algebra) trivially ensue.

We end this appendix with the remarks that the specific SUSY algebra $Q^{2} = \bar{Q}^{2} = 0, \{Q, \bar{Q}\} = H$, listed in (A.5), is valid only on the on-shell where the validity of the Euler–Lagrange equations of motion is taken into account. Furthermore, it may be trivially noted that, for the choices W′=ωx and W′=ωf(x) in the Lagrangian (A.1), we obtain the Lagrangians for the SUSY harmonic oscillator and its generalization in [5]. For the description of the motion of a charged particle in the X−Y plane under the influence of a magnetic field along the Z-direction, the choice for W′ could be found in the standard books on SUSY quantum mechanics and relevant literature (see, e.g. [2, 3]).