Search for physics beyond the standard model in events with τ leptons, jets, and large transverse momentum imbalance in pp collisions at $\sqrt{s}=7\ \mathrm{TeV}$

Abstract

A search for physics beyond the standard model is performed with events having one or more hadronically decaying τ leptons, highly energetic jets, and large transverse momentum imbalance. The data sample corresponds to an integrated luminosity of 4.98 fb⁻¹ of proton-proton collisions at $\sqrt{s}=7 ~\text {TeV}$ collected with the CMS detector at the LHC in 2011. The number of observed events is consistent with predictions for standard model processes. Lower limits on the mass of the gluino in supersymmetric models are determined.

1 Introduction

The standard model (SM) of particle physics has been successful in explaining a wide variety of data. In spite of this, the SM is incomplete. For example, it possesses a divergence in the Higgs sector [1] and has no cold dark matter (DM) candidate [2]. Many models of physics beyond the SM (BSM) have been proposed in order to address these problems.

DM particles, if produced in proton-proton collisions at the CERN Large Hadron Collider (LHC), would escape detection and result in a significant transverse momentum (p _T) imbalance in the detector. Additionally, cascade decays of heavy colored particles to final states with a high multiplicity of energetic jets and τ leptons appear very naturally in many BSM physics scenarios. Hence, events with multiple τ lepton candidates, large jet multiplicity, and significant transverse momentum imbalance, represent a distinct signature of new physics. In this paper, focus is placed on final states with hadronically decaying τ leptons. In what follows, the visible part of a hadronically decaying τ lepton will be referred to as τ _h.

In certain models of supersymmetry (SUSY), the lightest supersymmetric particle (LSP) is a candidate for DM. It has been appreciated for some time that the DM relic density may be sensitive to coannihilation processes involving the LSP and the next-to-lightest supersymmetric particle (NLSP). Coannihilation is characterized by a mass difference (ΔM) between the NLSP and the LSP of approximately 5–15 GeV [3–6]. This small mass difference would be necessary to allow the NLSP to coannihilate with the LSP in the early universe, leading to the dark matter abundance that is currently observed [7]. If the supersymmetric partner of the τ lepton, the stau ($\widetilde{ \tau }$), is the NLSP, and if the $\widetilde{ \tau }$ decays primarily to a τ lepton and the LSP, small values of ΔM would lead to final states with low-energy τ leptons (p _T∼ΔM) [8]. Decays of colored SUSY particles can produce the $\widetilde{ \tau }$ via chargino ($\widetilde{\chi} ^{\pm}$) or neutralino ($\widetilde{\chi}^{0}$) intermediate states (e.g., $\widetilde{\chi}^{0}_{2} \to\tau \widetilde{ \tau } \to \tau\tau \widetilde{\chi}^{0}_{1}$), resulting in final states with at least one τ _h.

We present a search for BSM particles in events with exactly one τ _h lepton and jets (single-τ _h final state), and in events with jets and two or more τ _h leptons (multiple-τ _h final state). These two topologies provide complementary sensitivity to models with a wide range of ΔM values. For example, in the case of very small values of ΔM (∼5 GeV), the low-energy τ _h cannot be effectively detected and the search for new physics in the single-τ _h final state has better sensitivity. The analysis is performed using proton-proton collision data at $\sqrt {s} = 7 ~\text{TeV}$ collected with the Compact Muon Solenoid (CMS) detector [9] at the LHC in 2011. The data sample corresponds to an integrated luminosity of 4.98±0.11 fb⁻¹. The search is characterized by methods that determine the backgrounds directly from data, to reduce the reliance on simulation. To illustrate the sensitivity of this search to BSM processes, the constrained minimal supersymmetric extension of the standard model, or minimal supergravity, is chosen as the benchmark [3, 10, 11]; we denote this benchmark as “CMSSM”. An interpretation of the results in the context of simplified model spectra (SMS) [12, 13] is also presented. The ATLAS collaboration has published a result on a search for one or more hadronically decaying tau leptons, highly energetic jets, and a large transverse momentum imbalance probing minimal Gauge Mediated Symmetry Breaking (GMSB) models [14].

2 The CMS detector

The central feature of the CMS apparatus is a superconducting solenoid, of 6 m inner diameter, providing a magnetic field of 3.8 T. Within the field volume are a silicon pixel and strip tracker, a crystal electromagnetic calorimeter (ECAL), which includes a silicon sensor preshower detector in front of the ECAL endcaps, and a brass-scintillator hadron calorimeter. Muons are measured in gas-ionization detectors embedded in the steel return yoke. In addition to the barrel and endcap detectors, CMS has extensive forward calorimetry.

The inner tracker measures charged particles within |η|<2.5 and provides an impact parameter resolution of about 15 μm and a p _T resolution of about 1.5 % for 100 GeV particles. Collision events are selected with a first-level trigger based on fast electronics, and a higher-level trigger that runs a version of the offline reconstruction program optimized for speed.

The CMS experiment uses a right-handed coordinate system, with the origin at the nominal interaction point, the x axis pointing to the center of the LHC ring, the y axis pointing up (perpendicular to the plane of the LHC ring), and the z axis along the counterclockwise beam direction. The polar angle θ is measured from the positive z axis and the azimuthal angle in the x–y plane. The pseudorapidity is given by η=−ln[tan(θ/2)].

3 Object reconstruction and identification

Jets in the detector are reconstructed using particle-flow (PF) objects [15]. In the PF approach, information from all subdetectors is combined to reconstruct and identify final-state particles (muons, electrons, photons, and charged and neutral hadrons) produced in the collision. The anti-k _T clustering algorithm [16] with a distance parameter R=0.5 is used for jet clustering. Jets are required to satisfy criteria designed to identify anomalous behavior in the calorimeters, and to be well separated from any identified τ lepton.

Validation and efficiency studies are performed utilizing events with a τ _h lepton and a light-lepton ℓ, with ℓ representing an electron (e) or muon (μ). Muons are reconstructed using the tracker and muon chambers. Selection requirements based on the minimum number of hits in the silicon tracker, pixel detector, and muon chambers are applied to suppress muon backgrounds from decays-in-flight of pions or kaons [17]. Electrons are reconstructed by combining tracks with ECAL clusters. Requirements are imposed to distinguish between prompt and non-prompt electrons, where the latter can arise from charged pion decay or photon conversion [18]. The light-lepton candidates are required to satisfy both track and ECAL isolation requirements. The track isolation variable is defined as the sum of the p _T of the tracks, as measured by the tracking system, within an isolation cone of radius $\Delta R = \sqrt{(\Delta\eta)^{2} + (\Delta\phi)^{2}}=0.4$ centered on the light-lepton track. The ECAL isolation variable is based on the amount of energy deposited in the ECAL within the same isolation cone. In both cases the contribution from the light-lepton candidate is removed from the sum.

Reconstruction of hadronically decaying τ leptons is performed using the hadron-plus-strips (HPS) algorithm [19], designed to optimize the performance of τ _h reconstruction by considering specific τ _h decay modes. To suppress backgrounds in which light-quark or gluon jets mimic hadronic τ decays, a τ _h candidate is required to be spatially isolated from other energy deposits in the calorimeter. Charged hadrons and photons not considered in the reconstruction of the τ _h decay mode are used to calculate the isolation. Additionally, τ _h candidates are required to be distinguished from electrons and muons in the event. In this analysis, two HPS isolation definitions are used. The τ _h isolation definition used for single-τ _h final states rejects a τ _h candidate if one or more charged hadrons with p _T>1.0 GeV or one or more photons with transverse energy E _T>1.5 GeV is found within an isolation cone of radius ΔR=0.5. The τ _h isolation definition used for multiple-τ _h final states rejects a τ _h candidate if one or more charged hadrons with p _T>1.5 GeV or one or more photons with transverse energy E _T>2.0 GeV is found within an isolation cone of radius ΔR=0.3. The isolation criteria used for the multiple-τ _h final state increases the signal-to-background ratio while reducing the rate of τ _h misidentification. This affects the yield of events with light-quark or gluon jets that are misidentified as τ _h leptons, which depends on the square of the misidentification rate. Here a final state with exactly two τ _h candidates is considered since events with more than two τ _h candidates are only a small fraction (<1 %) of events.

The missing transverse momentum is defined as:

(1)

where the sum runs over all the jets with $p_{\mathrm {T}} ^{\text{jet}} > 30 ~\text{GeV}$ inside the fiducial detector volume of |η|<5. The vector is the negative of the vector sum in Eq. (1). The observable $H_{\mathrm{T}} = \sum {\boldsymbol{p}}_{\mathrm{T}} ^{\text{jet}}$ is used to estimate the overall energy scale of the event. For the single-τ _h final state, H _T is calculated using jets with p _T>50 GeV and will be referred to as $H_{\mathrm {T}} ^{50}$. For the multiple-τ _h final state, H _T is calculated using jets with p _T>30 GeV and will be referred to as $H_{\mathrm {T}} ^{30}$. In both instances of the H _T calculation, we consider all jets in |η|<5 (the fiducial detector limit). The use of a lower p _T threshold for the jets in the multiple-τ _h final state increases the efficiency of signal events without significantly increasing the background.

4 Signal and background samples

The major sources of SM background are top-quark pair ($\mathrm {t}\overline{\mathrm {t}}$) events and events with a W or Z boson accompanied by jets. Both $\mathrm {t}\overline{\mathrm {t}}$ and W+jets events can have genuine τ _h leptons, large genuine from W boson decays, and jets that can be misidentified as a τ _h. Similarly, Z+jets events with Z(→νν) and with one or more jets misidentified as a τ _h lepton provide a source of background. Z+jets events with Z(→νν) present a background because of the genuine τ _h leptons and the genuine from the neutrinos in the τ _h decay. QCD multijet events can become a background when a mismeasured jet gives rise to large and jets are misidentified as τ _h leptons.

Data are compared with predictions obtained from samples of Monte Carlo (MC) simulated events. Signal and background MC samples are produced with the pythia 6.4.22 [20] and MadGraph [21] generators using the Z2 tune [22] and the NLO CTEQ6L1 parton distribution function (PDF) set [23]. The τ lepton decays are simulated with the Tauola [24] program. The generated events are processed with a detailed simulation of the CMS apparatus using the Geant4 package [25]. The MC yields are normalized to the integrated luminosity of the data using next-to-leading order (NLO) cross sections [26–31]. For the 2011 LHC running conditions, the mean number of interactions in a single beam crossing is ∼10. The effect of multiple interactions per bunch crossing (pileup) is taken into account by superimposing MC minimum-bias events so that the probability distribution for overlapping pp collisions in the simulation matches the measured distribution.

5 Event selection

Events for both the single- and multiple-τ _h final states are selected using a trigger that requires . This trigger allows us to maintain sensitivity in regions where the p _T value of the τ _h is small (p _T∼15 GeV). This trigger efficiency, for an offline selection requirement of , is 98.9 %. For the τ _h efficiency and validation studies, samples are chosen using triggers that require the presence of both a τ _h candidate and a muon.

The τ _h candidates must satisfy p _T>15 GeV and |η|<2.1. For the single-τ _h final state we require that no additional light leptons be present in the event. This requirement suppresses background from $\mathrm {t}\overline{\mathrm {t}}$, W+jets, and Z+jets events. For the multiple-τ _h final state there is no requirement placed on the number of light leptons.

For the single-τ _h final state, we define a baseline event selection $H_{\mathrm{T}} ^{50} > 350 ~\text{GeV}$ and . The sample obtained with the baseline selection is used to validate the background predictions. The signal region (SR) for the single-τ _h final state is defined by $H_{\mathrm{T}} ^{50} > 600 ~\text {GeV}$ and .

For the multiple-τ _h final state, the SR is defined by and by the requirement that there be at least two jets with p _T>100 GeV and |η|<3.0. QCD multijet events are rejected by requiring the azimuthal difference between the second leading jet in p _T and to satisfy Finally, events are required to contain at least one τ _h τ _h pair separated by ΔR(τ _h,i ,τ _h,j )>0.3.

6 Background estimate

The background contributions are categorized differently for the single- and multiple-τ _h final states. For the single-τ _h final state, the background contributions are divided into events containing a genuine τ _h and events where a jet is misidentified as a τ _h. For the multiple-τ _h final state, the main background contribution arises from misidentified τ _h leptons. We identify the different sources of background individually using dedicated data control regions (CR).

6.1 Estimate of backgrounds in the single-τ _h final state

In the single-τ _h final state, the largest background contribution comes from W + jets events that contain a genuine τ _h lepton. The other significant contribution arises from QCD multijet events in which a jet is misidentified as a τ _h. The W+jets background contribution is estimated using a sample of W+jets events with W→μν. The QCD multijet background is determined by selecting a QCD-dominated CR and evaluating the τ _h misidentification rate.

6.1.1 Estimate of the W + jets background in the single-τ _h final state

To evaluate the W+jets background, we exploit the similarity between W decays to a muon and to a tau lepton and select a sample of W+jets events with W(→μν). This sample will be referred to as the muon control sample. To select the muon control sample, events are required to contain exactly one muon and no reconstructed τ _h or electron. To emulate the τ _h acceptance, the muon is required to satisfy |η|<2.1. The yields in the muon control sample are corrected for muon reconstruction ($\varepsilon_{\mu}^{\text{reco}}$) and isolation efficiency ($\varepsilon_{\mu}^{\text{iso}}$). The muon reconstruction efficiency is derived from data using a sample of Z + jets events and parameterized as a function of p _T and η. The muon isolation criteria help to distinguish between muons from the decay of the W boson and muons from semileptonic decays of c and b quarks. The isolation efficiency is parameterized as a function of the separation from the nearest jet and the momentum of the jet. A correction factor ($P^{ \mathrm{W} }_{\mu}$) is applied to the muons in the muon control sample to account for muons that do not come from a τ-lepton decay. This correction factor depends on the p _T of the muon and the value in the event and is derived from a simulated sample of W+jets events.

As the muons in the muon control sample are selected to mimic a τ _h, a correction is applied to emulate the probability to reconstruct and identify a τ _h lepton. The reconstruction and identification efficiency $\varepsilon_{\tau }^{\text{reco}}$ is parameterized as a function of the p _T of the τ _h candidate and as a function of the total number N of charged particles and photons in the isolation cone [Fig. 1(a)]. Corrections are also applied to account for the hadronic branching fraction ($f_{\tau}^{\text{bf(hadr)}}$) of a τ lepton. Except for the $f_{\tau}^{\text{bf(hadr)}}$ the values of the correction factors differ in each event. The corrections are combined to define an overall event weight, defined as:

$$ f^\text{corr}_\text{event} = \frac{P_{\mu}^{ \mathrm {W} } \times \varepsilon_{\tau} \times f_{\tau}^{\text{bf(hadr)}}}{\varepsilon _{\mu}^{\text{reco}} \times\varepsilon_{\mu}^{\text{iso}}}. $$

(2)

Fig. 1

(a) Dependence of the τ _h reconstruction efficiency $\epsilon_{\tau}^{\text{reco}}$ on the number of additional particles N in the isolation cone in bins of τ _h lepton p _T for the single-τ _h final state, where N is the total number of the photons and charged hadrons in the isolation cone, and (b) dependence of τ _h response on $p_{\mathrm{T}} ^{\tau , \text{gen}}$. Both distributions are derived from a simulated sample of W(→τν)+jets events

A τ _h response template is derived from simulated events. The response template is given by the ratio of the reconstructed energy of the τ _h to the true generator-level energy. The τ _h response depends on the transverse momentum of the generated τ lepton [Fig. 1(b)] and on the number of reconstructed primary vertices in the event. The muon p _T spectrum is smeared as a function of p _T and the number of primary vertices to mimic the p _T distribution of the τ _h.

Fully simulated W+jets events are used to verify the procedure. Figure 2 shows the $H_{\mathrm{T}} ^{50}$ and distributions from simulated W+jets events for the single-τ _h final state. These events satisfy the baseline selection described in Sect. 5. The reconstructed τ _h is required to match a hadronically decaying generated tau lepton, to ensure that only the genuine tau background is addressed in this check. The event yield and distributions are compared with the prediction from the simulated muon control sample and agree within statistical uncertainties, thus verifying the closure of the method in MC simulation. Hence, the predicted $H_{\mathrm{T}} ^{50}$ and distributions from the muon control sample can be taken to describe a τ _h sample within statistical uncertainties.

Fig. 2

Distributions of (a) $H_{\mathrm{T}} ^{50}$ and (b)  for the genuine τ _h estimate in simulated W+jets events for the single-τ _h final state. The black triangles show the results for events that satisfy the baseline selection and that contain a reconstructed τ _h matched to the visible part of a generated, hadronically decaying τ lepton. The filled green areas show the prediction obtained from the simulated muon control sample. The hatched areas are the total uncertainty on the prediction (Color figure online)

The muon control sample consists primarily of W+jets events, but also contains $\mathrm {t}\overline {\mathrm {t}}$ events in which one W boson decays into a muon while the other W boson decays either into an unidentified τ lepton or into a light lepton that is not reconstructed. Any isolated muons produced through the decay of b or c quarks can also contribute to the muon control sample. SM processes containing a Z boson or two W bosons can also contribute to the muon control sample if one of the two decay muons is not reconstructed.

The true event yields of each process as determined from simulation are summarized in Table 1 for the baseline and SR selections. For both selections the number of predicted events with a genuine τ _h lepton is seen to agree with the true number of events. The value of $\varepsilon_{\tau}^{\text{reco}}$ that is used to calculate the predicted rate is measured in a sample of W+jets and is different from the value that would be measured in a sample of $\mathrm {t}\overline{\mathrm {t}}$ events. This leads to an overestimation of the $\mathrm {t}\overline{\mathrm {t}}$ contribution. A systematic uncertainty is assigned to account for this overestimation.

Table 1 The selected and predicted background contributions for simulated events with a genuine τ _h passing the baseline and signal selection in the single-τ _h final state. The reconstructed τ _h is required to match the visible part of the generated, hadronically decaying τ-lepton. The predictions are derived from the muon control sample

6.1.2 Estimate of the QCD multijet background in the single-τ _h final state

To estimate the background where a jet is misidentified as a τ _h lepton, a QCD-dominated control sample is obtained by selecting events with $H_{\mathrm{T}} ^{50} > 350 ~\text{GeV}$ and . The control sample is selected using a prescaled H _T trigger with criteria that lead to a sample where about 99 % of the events arise from QCD multijet production. The probability for a jet to be misidentified as a τ _h lepton is measured by determining the fraction of jets from the single-τ _h control sample that pass the τ _h identification criteria. Jets considered in the calculation of the misidentification rate satisfy the requirements p _T>5 GeV and |η|<2.5. The misidentification rates f _i for each jet i depend on η and p _T and are used to determine an overall weight, which is applied to each event. The event weights are defined as:

$$ w^{\text{corr}}_{\text{event}} = 1 - \prod_i^n (1-f_i), $$

(3)

where n is the number of jets. The measured misidentification rates shown in Fig. 3(a) are applied to data events in the region with $H_{\mathrm{T}} ^{50}>350 ~\text {GeV}$ and with $H_{\mathrm{T}} ^{50}>600$ for two regions of : and . These four regions are dominated by QCD multijet events. The results for data and simulation, as well as the predicted fraction of QCD multijet events, are shown in Table 2. The ratio of selected events over predicted events is statistically compatible with one and stable over the range of . Figure 3(b) shows the distributions of predicted and selected events for simulated QCD multijet events with $H_{\mathrm {T}} ^{50}>350 ~\text{GeV}$. The two distributions agree over the whole range of .

Fig. 3

(a) The rate of jet misidentification as a τ _h lepton in simulation (triangular symbols) and data (circular symbols) as a function of $p_{\mathrm{T}} ^{\text{jet}}$ for events with $H_{\mathrm{T}} ^{50}>350 ~\text{GeV}$ and ; (b) The distribution estimated in simulated events with $H_{\mathrm{T}} ^{50}>350 ~\text {GeV}$, where the triangular symbols represent events that pass the baseline selection, the filled blue area shows the predicted events, and the hatched area shows the total uncertainty on the prediction. These distributions correspond to the single-τ _h final state (Color figure online)

Table 2 The percentage of QCD multijet events in the binned samples for different QCD multijet dominated regions in the single-τ _h final state

6.2 Estimate of backgrounds in the multiple-τ _h final state

The estimate of the SM background contributions to the SR sample for multiple-τ _h events is based on the number of observed events in CRs. The events in each CR are selected with similar selection requirements to those used in the SR, but are enriched with events from the background process in question. Correction factors and selection efficiencies are measured in those CRs and used to extrapolate to the SR. We use the observed jet multiplicity in each CR along with the measured rate at which a jet is misidentified as a τ _h to calculate the yield in the SR. The following equation is used to estimate each background contribution B:

$$ N_{\mathrm{B}}^\mathrm{SR} = N_{\mathrm{B}}^\mathrm{CR}\bigl[ \alpha _{\tau\tau}{\mathcal{P}} (0) + \alpha_{\tau j}{\mathcal{P}} (1) + \alpha_{jj}{\mathcal{P}} (2)\bigr], $$

(4)

where $N_{\mathrm{B}}^{\mathrm{SR}}$ is the predicted rate in the SR, $N_{\mathrm{B}}^{\mathrm{CR}}$ is the observed number of events in the CR, and α _xy is the correction factor for acceptance and efficiency for events in the CR with true physics objects “x” and “y”. Here the physics object can be a τ _h or a quark or gluon jet. Since the dominant SM backgrounds contribute to the SR when jets are misidentified as τ _h lepton, the background estimation strategy outlined in Eq. (4) relies on the determination of the event probability ${\mathcal{P}} (m)$ for at least “m” jets to be misidentified as a τ _h, where ${\mathcal{P}} (m)$ is the product of three factors: (i) the probability P(N) for an event to contain N jets, (ii) the number of possible ways for exactly n jets to pass the τ _h identification criteria given N possible jets C(N,n)=N!/n!(N−n)!, and (iii) the probability f for a single jet to be misidentified as a τ _h. The ${\mathcal{P}} (m)$ terms are given by:

$$ {\mathcal{P}} (m)=\sum_{N=m}^{\infty}P(N)\sum _{n=m}^{N}C(N,n)f^{n}(1-f)^{N-n}. $$

(5)

Equation (5) would be identical to Eq. (3) if used in the case of the single-τ _h final state. Equation (4) is used to estimate the $\mathrm {t}\overline{\mathrm {t}}$, W+jets, and Z+jets background contributions to the SR. The P(N) terms are determined from data using the jet multiplicity distribution in each CR, while the f terms are measured for each background process by determining the fraction of jets in each CR that pass the τ _h identification criteria. Since the QCD multijet contribution to the SR for the multiple-τ _h final state is negligible according to simulation, a data-to-MC scale factor is used to correct the QCD multijet prediction from simulation. In the sections that follow, the selections used to define high purity CRs are outlined and the correction factors α _xy used in Eq. (4) are defined. The fraction of events with two τ _h leptons is denoted A _ττ , the fraction with one τ _h lepton and one jet misidentified as a τ _h lepton is denoted A _τj , and the fraction with two jets misidentified as τ _h leptons is denoted A _jj .

6.2.1 Estimate of the $\mathrm {t}\overline{\mathrm {t}}$ event background to the multiple-τ _h final state

To estimate the contribution of $\mathrm {t}\overline{\mathrm {t}}$ events to the multiple-τ _h SR, a CR is selected by removing the τ _h isolation requirement and by requiring the presence of at least two b-quark jets (b jets), identified using the track-counting-high-efficiency (TCHE) algorithm at the medium working point [32]. Because QCD multijet, W+jets, Z(→ττ)+jets and Z(→νν)+jets events are unlikely to contain two b jets, this requirement provides a sample in which about 99 % of the events are $\mathrm {t}\overline{\mathrm {t}}$ events, according to simulation. Figure 4(a) shows the p _T distribution of τ _h leptons in the $\mathrm {t}\overline {\mathrm {t}}$ CR for data and simulation.

Fig. 4

Data-to-MC comparison for the multiple-τ _h final state: (a) the p _T distribution of the τ _h candidate in the $\mathrm {t}\overline{\mathrm {t}}$ CR; (b)  distribution in the Z(→μμ)+jets CR; (c)  distribution in the W+jets CR; and (d)  distribution with the requirement . The bottom panes show the ratio between data and background while the hatched area depicts the total uncertainty on the MC

According to simulation, the fraction of events in the $\mathrm {t}\overline{\mathrm {t}}$ control sample that contains one genuine τ _h is A _τj =0.166±0.011, while the fraction without a genuine τ _h is A _jj =0.834±0.025. The genuine τ _h τ _h contribution is negligible (A _ττ ∼0) according to simulation. Incomplete knowledge of the genuine τ _h τ _h contribution is included as a source of systematic uncertainty in the $\mathrm {t}\overline{\mathrm {t}}$ background prediction. Therefore, α _τj in Eq. (4) is given by $A_{\tau j}{\varepsilon_{\tau}^{\text{iso}}}/{P(\text{2 $\mathrm {b}$\ jets})}$, where $\varepsilon_{\tau}^{\text{iso}}$ is the probability for a τ _h lepton to pass the isolation requirement, while α _jj is given by A _jj /P(2 b jets). The probability $P(\text{2 $\mathrm {b}$\ jets})$ to identify two or more b jets is determined by the b jet identification efficiency factor [32]. The number of $\mathrm {t}\overline{\mathrm {t}}$ events in the SR is calculated as:

$$ N_{ \mathrm {t}\overline{\mathrm {t}} }^\mathrm{SR} = \frac{N^\mathrm{CR}_{t \overline{t}}}{P(\text{2 $\mathrm {b}$\ jets})}\bigl[ A_{\tau j} \varepsilon_{\tau}^{\text{iso}}{\mathcal{P}} (1) + A_{j j}{ \mathcal{P}} (2) \bigr]. $$

(6)

The probability for a jet in a $\mathrm {t}\overline {\mathrm {t}}$ event to be misidentified as a τ _h lepton has an average measured value of f=0.022±0.004. Cross checks are made to validate the use of the b-jet identification efficiency as measured in Ref. [32] for this analysis. The estimated $\mathrm {t}\overline{\mathrm {t}}$ contribution in the SR is determined to be $N_{ \mathrm {t}\overline{\mathrm {t}} }^{\mathrm{SR}} = 2.03 \pm0.36$.

6.2.2 Estimate of the Z(→νν)+jets event background to the multiple-τ _h final state

The contribution of Z(→νν)+jets events to the multiple-τ _h SR is evaluated by selecting a sample of Z(→μμ)+jets events and treating the muons as neutrinos. The sample is collected using a trigger designed to select a muon and a τ _h. Jet selection criteria similar to those used for the SR sample are imposed. In addition, we require two muons passing the criteria outlined in Sect. 3. The control sample has a purity of about 99 % as estimated from simulation. The distribution for events in this CR is shown in Fig. 4(b). The Z(→νν)+jets background is estimated by interpreting the p _T of the pair of muons as . In order to predict the Z(→νν)+jets rate in the SR, the Z(→μμ)+jets sample is corrected for the ratio of the branching fractions R=B(Z→νν)/B(Z→μμ), for trigger efficiencies, for the geometric acceptance A _μ as measured from simulation, and for the reconstruction efficiency $\varepsilon_{\mu}^{\text{reco}}$ as measured from data. Therefore, α _jj in Eq. (4) is given by:

(7)

Since there is no prompt production of a genuine τ _h in the Z(→μμ)+jets sample, α _τj =0 and α _ττ =0. The Z(→νν)+jets contribution to the SR is calculated as:

(8)

where is the trigger efficiency and $\varepsilon^{\text{Trigger}}_{\mu\tau}$ the μτ _h trigger efficiency. The efficiency for the signal selection () is determined by calculating the fraction of the observed events in the CR that have . The muon identification efficiency ε _μ is measured using a “tag-and-probe” method. The probability for a jet to be misidentified as a τ _h lepton has a measured value of f=0.016±0.002. The estimated Z(→νν)+jets contribution to the SR is determined to be $N_{ \mathrm {Z} (\to\nu\nu )}^{\mathrm{SR}} = 0.03 \pm0.02$.

6.2.3 Estimate of the Z(→ττ)+jets event background to the multiple-τ _h final state

The contribution from Z→ττ events is determined with the Z(→μμ)+jets CR sample used to estimate the background from Z(→νν)+jets, with the muons treated as τ _h leptons. The α _xy factors are more difficult to estimate for Z→ττ events since there are several ways in which Z→ττ events can contribute to the SR: (i) both τ _h leptons pass the kinematic acceptance and identification criteria; (ii) both τ _h leptons pass the kinematic acceptance criteria, but only one passes the identification criteria; (iii) one τ _h fails the kinematic acceptance criteria, while the other τ _h passes both the kinematic acceptance and identification criteria; or (iv) both τ _h leptons fail the kinematic acceptance criteria. The Z(→ττ)+jets contribution to the SR is calculated as:

$$ \begin{aligned}[b] N_{ \mathrm {Z} \to\tau\tau}^\mathrm{SR} &= N^\mathrm{CR}_{ \mathrm {Z} \to\mu\mu}R \biggl[ \frac{A_{\tau}^{2}\varepsilon_{\tau}^{2}}{A_{\mu}^{2}\varepsilon _{\mu}^{\text{reco 2}}} + \frac{2A_{\tau}^{2}\varepsilon_{\tau}(1-\varepsilon_{\tau })}{A_{\mu}^{2}\varepsilon_{\mu}^{\text{reco 2}}}{\mathcal{P}} (1) \\ &\quad {}+\frac{2A_{\tau}(1-A_{\tau})\varepsilon_{\tau}}{A_{\mu }^{2}\varepsilon_{\mu}^{\text{reco 2}}}{\mathcal{P}} (1) + \frac{(1-A_{\tau})^{2}}{A_{\mu}^{2}\varepsilon_{\mu}^{\text{reco 2}}}{\mathcal{P}} (2) \biggr], \end{aligned} $$

(9)

where R is given by:

(10)

A _τ is the τ _h acceptance, ε _τ is the τ _h identification efficiency in this control sample, and f=0.016±0.002. The estimated Z (→ττ) + jets contribution to the SR is determined to be $N_{{ \mathrm {Z} } (\to\tau\tau )}^{\mathrm{SR}} = 0.21 \pm0.13$.

6.2.4 Estimate of the W + jets event background to the multiple-τ _h final state

To select the W+jets CR, the τ _h isolation requirement, which discriminates between a τ _h lepton and other jets, is removed from the SR selection requirements. However, the lack of the τ _h isolation requirement increases the contribution from other backgrounds as most of the backgrounds arise because jets are misidentified as a τ _h lepton. To minimize the contribution from $\mathrm {t}\overline{\mathrm {t}}$ production, events are required to have no jets identified as a b jet. This requirement reduces the contamination from $\mathrm {t}\overline{\mathrm {t}}$ events to around 5 %. The purity of the W+jets CR is approximately 65 %. Figure 4(c) shows the distribution, defined as the magnitude of the negative of the vector sum of the transverse momentum of all PF objects in the event, for events in the W+jets CR. The contributions of QCD multijet, $\mathrm {t}\overline{\mathrm {t}}$, and Z(→νν)+jets events are subtracted in order to determine the number of W+jets events in the CR. The predicted rates for QCD multijet, $\mathrm {t}\overline{\mathrm {t}}$, and Z(→νν)+jets events are determined by extrapolating from their corresponding CRs. Since there is no genuine multiple-τ _h production in W+jets, α _ττ =0. According to simulation, the fraction of events in the CR with one genuine τ _h is A _τj =0.149±0.016, while the fraction of events without a genuine τ _h is A _jj =0.851±0.038. Therefore, α _τj in Eq. (4) is given by $A_{\tau j}{\varepsilon_{\tau}^{\text{iso}}}/{P(\text{0 $\mathrm {b}$\ jets})}$, where $\varepsilon_{\tau}^{\text{iso}}$ is the probability for a τ _h to pass the isolation requirement and $P(\text{0 $\mathrm {b}$\ jets})$ is the probability to not have any light-quark or gluon jet misidentified as a b jet. Similarly, α _jj is given by ${A_{jj}}/{P(\text{0 $\mathrm {b}$\ jets})}$. The contribution of W+jets events to the SR is then calculated as:

$$ N_{W+\text{jets}}^\mathrm{SR} = \frac{N^{\text{After subtraction}}_{ \mathrm{W} +\textrm {jets}}}{P(\text{0 $\mathrm {b}$\ jets})} \bigl[ A_{\tau j} \varepsilon _{\tau}^{\text {iso}}{\mathcal{P}} (1) + A_{jj}{ \mathcal{P}} (2) \bigr]. $$

(11)

The average rate at which jets are misidentified as a τ _h lepton is measured to be 0.019±0.001. The rate f _b at which light-quark jets or gluon jets are misidentified as a b jet is used to determine $P(\text{0 $\mathrm {b}$\ jets})$. The estimated W+jets contribution to the SR is determined to be $N_{ \mathrm{W} + \textrm{jets}}^{\mathrm{SR}} = 5.20 \pm0.63$.

6.2.5 Estimate of the QCD multijet event background to the multiple-τ _h final state

QCD multijet events contribute to the multiple-τ _h SR when mismeasurements of jet energies lead to large values of and when jets are misidentified as τ _h candidates. By removing the τ _h isolation criteria and inverting the requirement, a QCD CR sample with about 99 % purity is obtained. Figure 4(d) shows the expected and observed distributions for this sample. A scale factor is obtained from this CR and used to correct the signal prediction for QCD multijet events in simulation. The estimated contribution to the SR from QCD multijet events is determined to be $N_{\mathrm{QCD}}^{\mathrm{SR}} = 0.02 \pm0.02$.

7 Systematic uncertainties

Systematic uncertainties are taken into account for both signal and background events and are described separately. Both the signal and background are affected by the systematic uncertainty in the identification of the τ _h candidate. The systematic uncertainty for τ _h identification is obtained using a Z→ττ enhanced region and by correcting this cross section by that measured for $\mathrm {Z} \to{\rm ee}$ and Z→μμ events. This uncertainty is validated on a control sample of Z→ττ events. The level of agreement between data and simulation is found to be at the level of 7 %. Further validation of the performance of τ _h identification in a SUSY-like environment is performed by selecting a W(→τν→τ _h νν) +jets CR with large hadronic activity (H _T) and large transverse momentum imbalance (). The level of agreement between the predicted rate for W(→τν→τ _h νν) events and the observed number of events is within 7 % and is determined as a function of H _T and .

7.1 Systematic uncertainties on background events

The principal sources of systematic uncertainty on the background predictions arise from the correction factors, the finite number of events in the CRs, the measured rates at which jets are misidentified as a τ _h lepton, and the level of agreement between the observed and predicted numbers of events in CRs.

The contributions to the uncertainties on the correction factors are different for each background category. The dominant effect is due to the uncertainty in the τ _h identification efficiency. In the multiple-τ _h final state, uncertainties in the jet-energy scale (JES) [33] and the τ _h-energy scale (TES) [34] are used to evaluate how changes in H _T, , and jet kinematics affect the correction factors. The systematic uncertainty on the correction factors due to the JES and TES is at most ∼3 % for all backgrounds. Smaller contributions to the uncertainties in the correction factors arise from the muon reconstruction and isolation efficiency (<1 %), the uncertainty in the branching fractions (≪1 %), and the uncertainties in trigger efficiency (1 %).

The systematic uncertainties on the measured rates for jet misidentification as a τ _h lepton are dominated by the size of the jet sample used to measure these rates and range from 2 % for the single-τ _h final state to 5.6–10 % for the multiple-τ _h final state. The level of agreement between the observed and predicted number of events in MC studies of the CRs is used to assign an additional systematic uncertainty and ranges from 2 % for the single-τ _h final state to 3 % for the multiple-τ _h final state. Finally, the systematic uncertainty arising from statistical uncertainties on the number of events in the CRs ranges from 2–5 % for the multiple-τ _h final state to 3–10 % for the single-τ _h final state.

7.2 Systematic uncertainties on signal events

The main sources of systematic uncertainties in the SR are due to trigger efficiencies, identification efficiencies, the energy, and momentum scales, the luminosity measurement and PDFs. The uncertainty on the luminosity measurement is 2.2 % [35]. Systematic uncertainties on the triggers (2.5 %) are measured using a sample in which around 99 % of the events are $\mathrm {t}\overline{\mathrm {t}}$ events, which have a similar topology to events in the SR samples. The systematic uncertainties on the TES and JES (3.0 %) yield an uncertainty on the signal acceptance of 2.3 %. The uncertainty on the scale depends on the uncertainty of the JES (2–5 % depending on the η and p _T values of the jet) and on the unclustered energy scale (10 %). Unclustered energy is defined as the energy found “outside” any reconstructed lepton or jet with p _T>10 GeV. The unclustered energy scale uncertainty has a negligible systematic uncertainty on the signal acceptance. The systematic uncertainty due to imprecise knowledge of the PDFs (11 %) is determined by comparing the CTEQ6.6L [36], MSTW 2008 NLO [37], and NNPDF2.1 [38] PDFs with the default PDF [39]. The systematic uncertainty due to the imprecise modeling of the initial-state and final-state radiation [40] is negligible (≪1 %). The systematic uncertainties associated with event pileup are also negligible. Uncertainties on the theoretical cross sections are evaluated by varying the PDFs and by changing the renormalization and factorization scales by a factor of two [26–31].

8 Results

For the single-τ _h final state, the number of background events containing a genuine τ _h, as well as the number of background events containing a misidentified τ _h, are estimated with data. The results for the baseline and the full selection are listed in Table 3. Figure 5 shows the $H_{\mathrm {T}} ^{50}$ and distributions of data and the different background predictions. The observed number of events in data is in agreement with the SM predictions.

Fig. 5

Distributions of (a) $H_{\mathrm{T}} ^{50}$, and (b) for the single-τ _h final state. The points with errors represent data that satisfy the baseline selection while the filled green (light) and filled blue (dark) areas shows the predicted backgrounds due to events containing a genuine τ _h and a misidentified τ _h, respectively. The hatched area shows the total uncertainty on the prediction (Color figure online)

Table 3 Number of data and estimated background events with statistical and systematic uncertainties, respectively, in the single-τ _h final state

The largest sources of background for the multiple-τ _h final state are from $\mathrm {t}\overline {\mathrm {t}}$ and W+jets events. A counting experiment is performed and the background predictions from data are compared with the observed number of events. Table 4 lists these background predictions and the observed number of events in the SR. Figure 6 shows the $H_{\mathrm{T}} ^{30}$ as well as the M _eff distributions in the SR, where M _eff is the sum . The background distributions in Fig. 6 are taken from simulation and normalized over the full spectrum. The estimated number of events due to the SM background processes is in agreement with the number of observed events in the SR.

Fig. 6

Stacked distributions of (a) $H_{\mathrm {T}} ^{30}$, and (b) M _eff in the SR for the multiple-τ _h final state. The background distributions are taken from MC events that are normalized to the predictions based on data over the full region. The shapes obtained from MC simulation are used for illustrative purposes only

Table 4 Number of data and estimated background events with statistical and systematic uncertainties, respectively, in the multiple-τ _h final state

9 Limits on new physics

The observed numbers of events in the single-τ _h and multiple-τ _h final states do not reveal any evidence of physics beyond the standard model. Exclusion limits are set using the CL_s [41] criterion in the context of the CMSSM [42]. The CMSSM parameter space with tanβ=40, A ₀=−500 GeV, μ>0, and M _t=173.2 GeV is chosen as a possible scenario with a light $\widetilde{ \tau }$ and a value of ΔM≤20 GeV. The excluded regions are shown for the single-τ _h and multiple-τ _h final states in Figs. 7(a) and 7(b), respectively. The limits are set using a simple counting experiment. Systematic uncertainties are treated as nuisance parameters and marginalized, and contamination from signal events in the control samples is taken into account. In the CLs method, both the background-only as well as the signal + background hypothesis are used to derive the confidence levels CL_s and the resulting limits and the uncertainty bands on the exclusion contours. In the case of very small values of ΔM(∼5 GeV), the lower-energy τ _h cannot be effectively detected and only the energetic τ _h from the decay of the neutralino can be observed. The search for new physics with a single τ lepton has a better sensitivity in this case. The single-τ _h and multiple-τ _h topologies thus have complementary sensitivity and together provide coverage for models with a wide range of ΔM values.

Fig. 7

95 % CL exclusion limits in the CMSSM plane at tanβ=40 for: (a) Single-τ _h final state, and (b) multiple-τ _h final state. In the figures shown, the solid red line (Obs. Limit) denotes the experimental limit while the dotted red lines (Obs. ±σ (theory)) represent the uncertainty on the experimental limit due to uncertainties on the theoretical cross sections. The blue band (Exp. ±σ) represents the expected uncertainties. The contours of constant squark and gluino mass are in units of  GeV (Color figure online)

Using the limits set by the single-τ _h analysis, a common gaugino mass m _1/2 of <495 GeV is excluded at 95 % Confidence Level (CL) for a common scalar mass m ₀ of <440 GeV. For the multiple-τ _h analysis, m _1/2<465 GeV is excluded at 95 % CL for m ₀=440 GeV. A gluino with mass <1.15 TeV is excluded at 95 % CL for m ₀<440 GeV. It can be noted that the single-τ _h analysis shows better sensitivity for small values of ΔM, which is near the boundary of $\widetilde { \tau } = \mathrm{LSP}$.

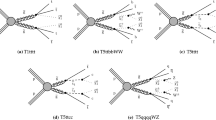
The results for the multiple-τ _h final states are also interpreted in the context of SMS [13]. The ττ SMS scenario (T3tauh) is studied where gluinos are produced in pairs and subsequently decay to τ lepton pairs and an LSP via a neutralino ($\widetilde{\mathrm{g}} \to \mathrm {q} \overline{\mathrm {q}} \widetilde {\chi}^{0}_{2}$; $\widetilde{\chi }^{0}_{2} \to\tau\overline{\tau} \to\tau\tau \widetilde{\chi}^{0}_{1}$). The diagram for the T3tauh model is given in Fig. 8. A gluino mass of <740 GeV is excluded at 95 % CL for LSP masses up to 205 GeV (here, the mass of $\widetilde{\chi}^{0}_{2}$ is the average of the masses of the gluino and the LSP). Figure 9(a) shows the 95 % CL exclusion region obtained for T3tauh. The limits on the mass of the gluino and LSP are shown with a solid red line.

Fig. 8

Diagram for the T3tauh SMS model

Fig. 9

Exclusion limits for the multiple-τ _h final state: (a) 95 % CL exclusion region obtained for the T3tauh model, where the solid red line represents the limits on the mass of the gluino and the LSP; (b) 95 % CL cross section upper limits as a function of gluino mass in the GMSB scenario. In this figure σ ^prod represents the cross section for the production of a pair of gluinos with subsequent decay into τ lepton pairs at a 100 % branching fraction (Color figure online)

In the simplified GMSB scenario, the $\widetilde{ \tau }$ is the NLSP and decays to a τ lepton and a gravitino $\widetilde{ \mathrm {G} }$, with a mass of the order of ∼ keV [43–45] ($\widetilde{\chi}^{0}_{2} \to\tau \widetilde{ \tau } \to\tau\tau \widetilde{ \mathrm {G} }$). The topology for this simplified GMSB scenario is similar to that of T3tauh except for the assumption that both the gluinos decay to τ-lepton pairs with a branching fraction of 100 %. Therefore, the results are also interpreted in the simplified GMSB scenario using the T3tauh scenario. The signal acceptance is corrected to account for the final state containing up to four τ leptons. A gluino with mass <860 GeV is excluded at 95 % CL. Figure 9(b) shows the exclusion limits for the simplified GMSB scenario as a function of the gluino mass.

Since the SMS topologies considered in this paper are characterized by two τ leptons in the final state, we do not present SMS limits for the single-τ _h final state.

10 Summary

A search for physics beyond the standard model with one or more hadronically decaying τ leptons, highly energetic jets, and large transverse momentum imbalance in the final state is presented. The data sample corresponds to an integrated luminosity of 4.98±0.11 fb⁻¹ of pp collisions at $\sqrt{s}=7 ~\text{TeV}$ collected with the CMS detector. The final number of events selected in data is consistent with the predictions for standard model processes. We set upper limits on the cross sections for the CMSSM, GMSB, and SMS scenarios. Within the CMSSM framework at tanβ=40, a gaugino mass m _1/2<495 GeV is excluded at 95 % CL for scalar masses m ₀<440 GeV. This result sets a lower limit on the mass of the gluino at 1.15 TeV with 95 % CL in this region. In the multiple-τ _h final state, a gluino with a mass less than 740 GeV is excluded for the T3tauh simplified model while a gluino with a mass less than 860 GeV is excluded for the simplified GMSB scenario at 95 % CL.