A study of measurement precision of the Higgs boson branching ratios at the International Linear Collider

Abstract

Precise measurement of the Higgs boson couplings is an important task for International Linear Collider (ILC) experiments and will clarify the understanding of the particle mass generation mechanism. In particular, high precision measurement of Higgs branching ratios plays a key role in the search for the origin of the Yukawa and Higgs interactions. In this study, the measurement accuracies of Higgs boson branching ratios to b and c quarks and gluons were evaluated using a full detector simulation based on the International Large Detector, and assuming a Higgs mass of 120 GeV/c ². We analyze two center-of-mass (CM) energies, 250 and 350 GeV, close to the e ⁺ e ⁻→ZH and $e^{+}e^{-}\to t\bar{t}$ production thresholds. At both energies, an integrated luminosity of 250 fb⁻¹ and an electron (positron) beam polarization of −80 % (+30 %) were assumed. We obtain the following measurement accuracies for the product of the Higgs production cross section and the branching ratio of the Higgs into $b\bar{b}$, $c\bar{c}$, and gg: 1.0 %, 6.9 %, and 8.5 % at a CM energy of 250 GeV and 1.0 %, 6.2 %, and 7.3 % at 350 GeV. (After writing our article, Large Hadron Collider experiments reported the observation of a new resonance around the mass of 125 GeV/c ² (ATLAS Collaboration, arXiv:1207.7214v1 [hep-ex]; CMS Collaboration, arXiv:1207.7235v1 [hep-ex]). Considering the small difference in branching ratios of the Higgs at masses of 120 and 125 GeV/c ², our results are not significantly affected by this mass difference.)

1 Introduction

The Higgs boson is a spin-zero particle responsible for the mass generation of elementary particles. In the Standard Model (SM), the Yukawa couplings of the Higgs boson to the fermion fields are given by the ratio of the respective fermion masses to the vacuum expectation value of the Higgs doublet. This relation may however be modified in theories beyond the SM [1]. The Higgs boson has been searched for over many years at several experiments [2–5] and a precise study of Higgs boson properties is a primary target of the future high energy collider, International Linear Collider (ILC).

Precise measurements of the Higgs decay branching ratios (BRs) are crucial to confirm the mass-coupling relation in SM or to search for physics beyond the SM [6–9]. In experiments at the Large Hadron Collider (LHC) [4, 5], it is not easy to measure the BRs of Higgs to quarks and gluons due to the large QCD backgrounds in hadron collisions. In contrast, precise measurements of BRs are anticipated at e ⁺ e ⁻ linear collider experiments, owing to the cleaner experimental conditions, well-defined initial states and beam polarizations [10, 11].

Studies of the measurement of Higgs BRs at linear colliders have been performed at several center-of-mass (CM) energies employing fast detector simulations [12–14], predicting BR precisions ranging from a few percent to for hadronic decay channels. These measurements require good jet energy resolution and efficient quark flavor tagging however the performance of such tools is difficult to simulate reliably in fast simulation tools. A detailed and realistic detector model and sophisticated reconstruction tools are required to make reliable prediction for the achievable precision of such measurements.

Full simulation studies of BRs measurements of Higgs to $b\bar{b}$, $c\bar{c}$ and gg have been reported using the ILD [10] and SiD [11, 15] detector models at a CM energy of 250 GeV. The SiD study was based on a neural net based cut analysis, while the ILD study performed only a simple cut based analysis on a few decay modes. This paper is an extension of the ILD analysis including all possible detection channels and employing a template fitting technique for an improved sensitivity. The study also includes an analysis at a CM energy of 350 GeV, suitable for a simultaneous study of the top pair production near threshold and Higgs properties.

After describing the detector model and reconstruction tools in Sect. 2, the event selection is described in the Sect. 3 and the determination of branching ratio by a template fitting method is discussed in Sect. 4. The conclusion is given in Sect. 5.

2 Higgs physics at the ILC

2.1 ILC experiment and Higgs production

The ILC is a proposed electron-positron (e ⁻ e ⁺) linear collider at an initial CM energy ($\sqrt{s}$) up to 500 GeV, extendable to 1 TeV. The production cross section of the Higgs boson is shown in Fig. 1(a) as a function of the CM energy for a Higgs mass of 120 GeV/c ². At low CM energies, the Higgs boson is produced primarily through the Higgs-strahlung process e ⁺ e ⁻→ZH, which has a maximum cross section at around 250 GeV, when the effect of initial state radiation is considered. At $\sqrt{s}=350~\mathrm{GeV}$, the total cross section is reduced, although the contribution of the W/Z fusion process is greater than that at 250 GeV.

Fig. 1

(a) Production cross section of Higgs boson at a Higgs mass of 120 GeV/c ² through the Higgs-strahlung (ZH) (solid) and all $f\bar{f}H$ (dashed) processes assuming the −80 % electron and +30 % positron beam polarization. The cross section was calculated by Whizard [16, 17], including the effects of initial state radiation. (b) SM Higgs branching ratios as a function of Higgs mass, as calculated by PYTHIA [18]

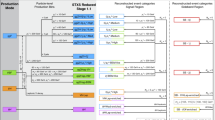
The decay BRs of the Higgs boson in the SM are shown as a function of its mass in Fig. 1(b). For a Higgs mass around 120 GeV/c ², its main decay channel is to $b\bar{b}$ and other hadronic decay channels are also sizable. Higgs analysis modes are categorized in terms of the three Z boson decay channels: $Z\to\nu\bar{\nu}$ (neutrino), $q\bar{q}$ (hadronic), and ℓ ⁺ ℓ ⁻ (leptonic), as shown in Fig. 2. We assume polarizations of −80 % (+30 %) for the initial electrons (positrons), which enhances the Higgs production cross section by 50 % with respect to the case with unpolarized beams.

Fig. 2

Higgs boson production diagrams categorized according to the final states: (a) neutrino ($\nu\bar{\nu}H$), (b) hadronic ($q\bar {q}H$), and (c) leptonic (ℓ ⁺ ℓ ⁻ H) channels. Each channel is produced mainly through the Higgs-strahlung (ZH) process at low CM energies, although the neutrino (charged lepton) channels also include contributions from WW (ZZ) fusion

2.2 ILD concept

We used the ILD model for this study. The ILD is equipped with a highly segmented calorimeter and a hybrid tracking system consisting of gaseous, silicon-strip, and silicon-pixel trackers. They provide an excellent jet energy resolution by the use of particle flow analysis, as well as excellent momentum resolution and vertex flavor tagging capability, necessary for the precision measurement of multi-jet final states in the ILC energy region.

All sub-detector components of the ILD are shown in Fig. 3. The ILD consists of a silicon-pixel vertex detector (VTX), silicon inner and outer detectors (SIT, SET, ETD), a time projection chamber (TPC), high-granularity electromagnetic and hadron calorimeters (ECAL, HCAL), a super-conducting solenoid providing a 3.5 T magnetic field, and an iron return yoke with a muon detector. Additional silicon trackers and beam/luminosity calorimeters are installed in the forward region.

Fig. 3

A schematic view of the ILD detector

The VTX system consists of three double layers of silicon pixel sensors with a 2.8 μm point resolution located at radii between 16 mm and 60 mm, with a total radiation length of 0.74 %. The impact parameter resolution (σ _IP ) of the VTX system is 5 μm⊕10 μm⋅GeV/c/psin^3/2 θ. The TPC occupies a volume up to a radius of 1.8 m, with a half-length of 2.3 m along the beam axis, providing a stand-alone momentum resolution of $\sigma_{1/P_{T}} \sim 9 \times10^{-5}~\mathrm{GeV}^{-1}$. The SIT and SET are placed at the inner and outer sides of the TPC, providing a point resolution of 7 (50) μm in the R−ϕ (z) direction. The overall momentum resolution of the tracking system ($\sigma_{1/P_{T}}$) is 2×10⁻⁵ GeV⁻¹⊕1×10⁻³/P _T sinθ in the momentum range 1-200 GeV [10]. The ECAL consists of tungsten absorber layer (total thickness of 24 X ₀) with a highly segmented (5×5 mm²) readouts. The HCAL consists of steel absorber layers (total thickness 5.5 λ _I ) with a 3×3 cm² scintillator tile readout. Using the ILD particle flow algorithm package, PandoraPFA [19], a dijet energy resolution of $25~\%/\sqrt{E~(\mathrm{GeV})}$ has been achieved for a 45 GeV dijet [10].

2.3 Analysis framework and Monte Carlo samples

Monte Carlo (MC) generator samples for the physics study were produced using Whizard. Fragmentation and hadronization processes were simulated by PYTHIA. The SM Higgs branching ratios in PYTHIA are 65.7 %, 3.6 %, and 5.5 % for $b\bar{b}$, $c\bar{c}$, and gg, respectively. The generated particles were passed through the Geant4 [20] based detector simulator Mokka [21] using the ILD model. The simulated hits were digitized by the MarlinReco package [22], which was also used to reconstruct tracks of charged particles. The individual particles are reconstructed following particle flow concept using the PandoraPFA package. The size of the simulated Higgs signal samples were 500 fb⁻¹ for both CM energies of both 250 and 350 GeV. Samples were scaled to obtain results corresponding to an integrated luminosity of 250 fb⁻¹.

The major SM background processes for the e ⁺ e ⁻→ZH analysis are e ⁺ e ⁻→ZZ and W ⁺ W ⁻; thus we considered final sample states of ${\nu}{\bar{\nu}}{q}{\bar {q}}$, νℓqq, ${\ell}{\ell}{q}{\bar{q}}$, ννℓℓ, $q\bar{q}q\bar{q}$ and ℓℓℓℓ. In addition, the $q\bar{q}$ and $t\bar{t}$ backgrounds were also considered for the neutrino and hadronic channels. $t\bar{t}$ background was only used for $\sqrt{s}=350~\mathrm{GeV}$ generated setting a top mass of 174.9 GeV/c ² and taking into account the cross section enhancement due to QCD corrections at the top pair threshold [23]. In the leptonic channel, most of the multi-jet backgrounds are very effectively suppressed once dilepton identification is required: in this channel only the ${\ell}{\ell}{q}{\bar{q}}$ and νℓqq backgrounds were considered.

We used the 250 GeV samples produced for the ILD letter of intent (LOI) studies [10]; thus, their beam parameters correspond to those defined in the ILC Reference Design Report [24]. On the other hand, the 350 GeV samples were produced for this study using the SB2009 [25] beam parameter. The instantaneous luminosities are 0.75 (1)×(10³⁴ cm⁻² s⁻¹) for 250 (350) GeV, which yield integrated luminosities of 188 (250) fb⁻¹ in 300 days of operation at design performance.

3 Event reconstruction and background suppression

Depending on the Z decay mode, the analysis channels are categorized as neutrino (dijet), hadronic (four-jets) or leptonic channels (dileptons+dijets), each of which are described in the following subsections.

3.1 Neutrino channel ($\nu\bar{\nu}H$)

For neutrino channel analysis, particles in the event are first forcibly clustered into two jets by the Durham jet-finding algorithm. After this dijet clustering, selection cuts are applied to reduce backgrounds as shown in Table 1. At a CM energy of 250 GeV, the Higgs is produced almost at rest since it is close to the production threshold, whereas it is boosted at 350 GeV. The cut conditions are therefore optimized to obtain the best signal significance at each energy. In this channel, the Z boson decays invisibly ($\nu\bar{\nu}$), so the ${\nu}{\bar{\nu}}{q}{\bar{q}}$ and νℓqq processes are the major SM backgrounds. To reduce them, a cut on the missing mass (M _miss ) was applied. Although this cut decreases the Higgs signal from the WW fusion process, the νℓqq, ${\ell}{\ell}{q}{\bar{q}}$ and $q\bar {q}q\bar{q}$ backgrounds are effectively reduced. The $q\bar{q}$ background was reduced by the following cuts on kinematical variables: the transverse visible momentum (P _t ), longitudinal visible momentum (P _l ), and maximum track momentum (P _max ). The ℓℓℓℓ background is strongly reduced by a cut on the number of charged tracks in an event (N _chd ). In addition, the νℓqq background reduction is further reduced by cuts on Y ₁₂ and Y ₂₃, where Y ₁₂ and Y ₂₃ are the maximum and the minimum y values (scaled jet masses) required to cluster the event into two jets.

Table 1 Summary of the $\nu\bar{\nu}H$ channel background reduction assuming with P(e ⁻,e ⁺)=(−0.8,+0.3)

The background reductions for each cut are summarized in Table 1 for each CM energy. After all selection criteria were met, a likelihood ratio (LR) cut was applied to improve the background reduction. The LR was defined using the following variables: M _miss , the number of reconstructed particles (N _PFO ), Y ₁₂, P _max , P _ℓ , and M _jj . The likelihood cut values were optimized to maximize the signal significance, giving LR>0.165 (0.395) at the CM energies of 250 (350) GeV. The signal significance $S/\sqrt{S+B}$ and signal efficiency after all background reductions are also listed in Table 1, where S and B are the numbers of Higgs signal and background events, respectively. The major remaining backgrounds are νℓqq (60 %), ${\nu }{\bar{\nu}}{q}{\bar{q}}$ (20 %), and $q\bar{q}$ (10 %) at both 250 and 350 GeV.

3.2 Hadronic channel ($q\bar{q}H$)

For the analysis in the hadronic channel, particles in the event are first forcibly clustered into four jets with Durham algorithm. These jets were then paired into Higgs and Z candidate dijets that minimize the following χ ²:

$$ \chi^{2} = \biggl(\frac{M_{j_{1}j_{2}}-M_{Z}}{\sigma_{Z}} \biggr)^2+ \biggl( \frac{M_{j_{3}j_{4}}-M_{H}}{\sigma_{H}} \biggr)^2, $$

(1)

where $M_{j_{1}j_{2}/j_{3}j_{4}}$ represent the dijet invariant masses paired from the four jets (j ₁₋₄), and M _Z/H are the Z and Higgs masses. Here σ _Z =4.7 GeV and σ _H =4.4 GeV were used for $\sqrt{s}=250~\mathrm{GeV}$ and σ _Z/H =3.8 GeV for $\sqrt{s}=350~\mathrm{GeV}$. These resolutions were determined from the dijet mass distribution reconstructed using the true MC information, as shown in Fig. 4. After the jet pairing, background reduction cuts were applied.

Fig. 4

Reconstructed Z and Higgs dijet mass distribution with true MC jet combination at $\sqrt{s}=250~\mathrm{GeV}$

To select the four-jet-like events, cuts on the number of charged tracks N _charged and jet clustering parameter Y ₃₄ were applied. Y ₃₄ is the minimum scaled jet mass y required for four-jet clustering. The leptonic backgrounds (ℓℓℓℓ, ${\ell}{\ell }{q}{\bar{q}}$) are effectively reduced by these conditions. In addition, cuts on the thrust and thrust angle were applied to reduce the ZZ background, utilizing the difference between the event shape of the signal (isotropic) and ZZ, $q\bar{q}$ (back-to-back). The numbers of $q\bar{q}q\bar{q}$ and $q\bar{q}$ background events were reduced by a cut on the angle between the Higgs candidate jets (θ _H ). The WW and ZZ backgrounds are further suppressed by cuts on the results of a kinematical constrained fit to the four-jet system, performed as follows: each jet was parameterized by $E_{j_{i}}$, θ _i , and ϕ _i (i=1–4) and fitted with constraints on the total energy ($\sum_{i} E_{j_{i}} =\sqrt{s}$), the total momentum ($\sum_{i} \mathbf{P}_{j_{i}} = 0$), and Higgs and Z mass difference ($M_{j_{1}j_{2}}-M_{j_{3}j_{4}}=M_{H}-M_{Z}$), where $E_{j_{i}}$, $P_{j_{i}}$, θ _i , and ϕ _i are the energy, momentum, and theta and phi angles of the i-th jet, respectively. After these cuts were applied, an additional cut was applied on a LR derived from the following input variables: thrust, cosθ _thrust , minimum angle between all jets (θ _min ), number of particles in Higgs candidate jets, fitted Z mass, and fitted Higgs mass. The likelihood cut position was selected to maximize the signal significance: LR>0.375 at 250 GeV and LR>0.15 at 350 GeV. All background reduction cuts are summarized in Table 2. The composition of the remaining background after all cuts is 80 % $q\bar{q}q\bar{q}$ and 20 % $q\bar{q}$ at 250 GeV and 60 % $q\bar{q}q\bar{q}$, 30 % $q\bar{q}$ and 10 % $t\bar{t}$ at 350 GeV.

Table 2 Summary of $q\bar{q}H$ channel background reduction assuming with P(e ⁻,e ⁺)=(−0.8,+0.3)

3.3 Leptonic channel (ℓ ⁺ ℓ ⁻ H)

For the analysis of leptonic channel analysis, we considered the cases where the lepton is either an electron or muon. We considered only the ℓℓqq and ℓνqq background processes. First, the following cuts were applied to selected isolated leptons:

• Lepton isolation: E _cone <20 GeV,

• Lepton track momentum:

  

where E _cone is the energy sum for particles within 10 degrees of the lepton. Prompt leptons have a smaller E _cone than leptons produced in heavy quark decays. Electrons and muons were identified as follows:

• Electron ID: $\frac{E_{ECAL}}{E_{Total}}>0.9$, $0.7 < \frac{E_{Total}}{P}<1.2$

• Muon ID: $\frac{E_{ECAL}}{E_{Total}}<0.5$, $\frac{E_{Total}}{P}<0.4$,

where E _ECAL , E _Total and P denote the ECAL energy associated with a track, total energy deposited in the ECAL and HCAL, and track momentum, respectively. If more than two isolated electron or muon candidates were identified, the pair whose invariant mass is closest to Z is selected.

After the dilepton identification, forced two-jets clustering is applied to the remaining particles and the following selection was applied. First, a dilepton mass (M _ℓℓ ) cut, which should be consistent with the Z mass, was applied: 70<M _ℓℓ <110 GeV for electrons and 70<M _ℓℓ <100 GeV for muons. Because the ZZ or WW backgrounds are boosted to the forward region compared to the signal, a cut was applied on the polar angle of the Z momentum: |cosθ _Z |<0.8. Finally, cuts on dijet mass (M _jj ) and the mass recoil to the lepton pair (M _rec ) were applied to select the Higgs signal: 100<M _jj <140 GeV and 70<M _rec <140 GeV for electrons; 115<M _jj <140 GeV and 70<M _rec <140 GeV for muons. The background reduction procedures for the leptonic channel are summarized in Table 3. After all cuts were applied, the background was dominated by ${\ell }{\ell}{q}{\bar{q}}$.

Table 3 Summary of background reduction in the eeH and μμH channels assuming with P(e ⁻,e ⁺)=(−0.8,+0.3)

4 Branching ratio measurement

After the event selection, the measurement accuracies of the Higgs BRs to $b\bar{b}$, $c\bar{c}$, and gg were evaluated on the basis of template fitting to the flavor likeness of the Higgs dijets, calculated by the LCFIVertexing package [26]. The probabilities of b and c quarks for each jet [b _i , c _i  (i=1,2)] were calculated by LCFIVertex using neural networks trained on $Z \to q\bar{q}$ samples generated at the Z-pole. An additional c probability (bc _1,2) was also calculated, whose neural-net is trained using only the $Z\to b\bar{b}$ sample as background. For Higgs dijets, we define the flavor likeness X (X=b, c, bc) as follows from the x _i [x _i =b _i , c _i , bc _i  (i=1,2)] flavor probability of each jet:

$$ X = \frac{x_{1}x_{2}}{x_{1}x_{2}+(1-x_{1})(1-x_{2})}. $$

(2)

The flavor tagging performance in the $ZZ \to\nu\bar{\nu}q\bar{q}$ sample at $\sqrt{s} = 250$ and 350 GeV is shown in Fig. 5. The $ZZ\to\nu\bar{\nu}q\bar{q}$ samples are compared for each CM energy because they form the same final state as $Z\to q\bar{q}$, which was used to train the flavor tagging neural networks.

Fig. 5

Flavor tagging performance at CM energies of 250 and 350 GeV in the $ZZ \to\nu\bar{\nu}q\bar{q}$ sample. The horizontal axis shows the efficiency for b/c jets; vertical axis shows the purity of tagged b/c jets

Figure 5 shows that no significant difference in the flavor tagging performance at $\sqrt{s} = 250$ and 350 GeV is observed for any of the flavors.

To evaluate the measurement accuracy of the BRs, the b-, c-, and bc-likenesses of the selected events were binned in a three-dimensional histogram and fitted with those of the template samples, which consist of $H\to b\bar{b}$, $c\bar{c}$, and gg and other background processes. Figure 6 shows the three-dimensional histogram projected to the two-dimensional b- and c-likeness axes for the hadronic channel. The probability of entries in each template sample bin is expected to be given by the Poisson statistics:

$$ P_{ijk} = \frac{\mu^{n}e^{-\mu}}{n!}\quad \bigl(n\equiv N^{data}_{ijk},\mu \equiv N^{template}_{ijk} \bigr), $$

(3)

where P _ijk and $N^{data}_{ijk}$ are the probability of entries and the number of data entries at the (i,j,k) bin, respectively. $N^{template}_{ijk}$ is given by

$$ N^{template}_{ijk} = \sum_{s=b\bar{b},c\bar{c},gg} r_{s}\cdot N^{s}_{ijk} + N_{ijk}^{bkg}, $$

(4)

where $N^{s}_{ijk}$ is the number of entries at the (i,j,k) bin in each $H\to b\bar{b}$, $c\bar{c}$, and gg template; $N^{bkg}_{ijk}$ is the number of entries in the background template sample, which is the sum of the SM background events and the Higgs-to-nonhadronic decay events. $r_{b\bar{b}}$, $r_{c\bar{c}}$, and r _gg are the parameters to be determined by template fitting. They are defined as the Higgs branching ratios to $H\to b\bar{b}$, $c\bar{c}$ and gg, respectively, normalized SM BRs,

$$ r_{s} = \frac{\sigma\cdot \mathit{BR} (H\to s )}{\sigma^{SM} \cdot \mathit{BR} (H\to s )^{SM}}\ (s=b\bar{b},c \bar{c},gg). $$

(5)

Here σ is the measured Higgs production cross section and σ ^SM and BR(H→s)^SM are respectively the cross section and branching ratio in the SM. From Eq. (5), the measurement accuracies of σ⋅BR are obtained as follows;

$$\frac{\Delta (\sigma\cdot \mathit{BR})}{\sigma\cdot \mathit{BR}}(H\to s) = \frac{\Delta r_{s}}{r_{s}}\ (s = b\bar{b},c\bar{c},gg). $$

The r _s values were determined by a binned log likelihood fit, where each bin probability is given by Eq. (3). On the basis of the three-dimensional (3D) histogram, 5000 toy MC events were generated using the Poisson distribution function for each bin, which were then fitted to obtain $r_{b\bar{b}}$, $r_{c\bar{c}}$, and r _gg . The number of bins in the 3D histogram were optimized to minimize the statistical fluctuation in the fitted results caused by bins with low-statistic. Bins with fewer than one entry were not used for the fitting. The distributions of $r_{b\bar{b}}$, $r_{c\bar{c}}$, and r _gg from the template fitting of 5000 toy MC events are shown in Fig. 7. The error in r _s is determined by Gaussian fittings to these distributions, the results of which are shown in Tables 4 and 5 for CM energies of 250 and 350 GeV.

Fig. 6

Two-dimensional projections of three-dimensional template for b-likeness vs. c-likeness

Fig. 7

Typical examples of (a) $r_{b\bar{b}}$, (b) $r_{c\bar{c}}$, and (c) r _gg distributions

Table 4 Summary of template fitting results r _s and accuracies of (σ⋅BR) and BR after correcting σ for an accuracy of 2.5 % at $\sqrt{s}=250~\mathrm{GeV}$ assuming with P(e ⁻,e ⁺)=(−0.8,+0.3)

Table 5 Summary of template fitting results r _s and accuracies of (σ⋅BR) and BR after correcting σ for an accuracy of 3.5 % at $\sqrt{s}=350~\mathrm{GeV}$ assuming with P(e ⁻,e ⁺)=(−0.8,+0.3)

The tables also show the accuracies after correction of the total cross section. From a study of the recoil mass in the process of e ⁺ e ⁻→eeH and μμH, the accuracy of the total cross section (Δσ/σ) was estimated to be 2.5 % at 250 GeV [10, 27]. For 350 GeV, we assumed an accuracy of 3.5 % because the recoil mass measurement relies on the ZH process, whose cross section is inversely proportional to the square of the CM energy; thus, the accuracy of the total cross section measurement would be inversely proportional to the CM energy.

From Tables 4 and 5, we see that the Higgs cross section times branching ratio can be measured with a precision of around 1 % for $H\to b\bar{b}$ and 7 to 9 % for $H \to c\bar{c}$ and gg. The measurement is approximately 10–20 % better at 350 GeV than at 250 GeV. The instantaneous luminosity at 350 GeV is 25 % greater than that at 250 GeV according to the ILC beam parameters used in this study. Thus, for an equal running time, measurements at 350 GeV will give about 20–30 % better accuracy than those at 250 GeV. On the other hand, the accuracy of the BR to $b\bar{b}$, $\Delta \mathit{BR}/\mathit{BR}(H\to b\bar{b})$, is limited by the uncertainty on the total cross section; measurement at 250 GeV therefore gives better results than that at 350 GeV. In the other decay channels, comparable BR measurements are possible if the same integrated luminosities are assumed.

5 Conclusion

The accuracies at which the Higgs branching ratios $H\to b\bar{b}$, $c\bar{c}$, and gg can be measured were evaluated at $\sqrt {s}=250~\mathrm{GeV}$ and 350 GeV. In terms of signal significance, $\sqrt{s}=350~\mathrm{GeV}$ yields better background suppression than $\sqrt{s}=250~\mathrm{GeV}$ in each channel. The combined results for the measurement accuracies of the Higgs cross section times BRs (Δ(σ⋅BR)/σ⋅BR) to $H\to b\bar{b}$, $c\bar {c}$, and gg are 1.0 %, 6.9 %, and 8.5 % at CM energies of 250 GeV and 1.0 %, 6.2 %, and 7.3 % at 350 GeV, assuming the same integrated luminosity of 250 fb⁻¹.

At the ILC, the total Higgs cross-section σ is measured using the Z recoil mass process. Assuming that Δσ/σ=2.5 % for 250 GeV and assuming it is 3.5 % at 350 GeV, Higgs BRs (ΔBR/BR) to $b\bar{b}$, $c\bar{c}$, and gg are derived as 2.7 %, 7.3 %, and 8.9 % at CM energies of 250 GeV and as 3.6 %, 7.2 %, and 8.1 % at 350 GeV.

We therefore conclude that, assuming equal integrated luminosities at the two CM energies, the Higgs cross section times BR (BR×σ) can be measured better at 350 GeV than at 250 GeV owing to the higher S/N at the higher energy. However, when the accuracy of the total cross section measurement by recoil mass measurement is considered, the $H\to b\bar{b}$ BR can be measured better at 250 GeV.