Associated production of charged Higgs bosons and top quarks with POWHEG

Abstract

The associated production of charged Higgs bosons and top quarks at hadron colliders is an important discovery channel to establish the existence of a non-minimal Higgs sector. Here, we present details of a next-to-leading order (NLO) calculation of this process using the Catani–Seymour dipole formalism and describe its implementation in POWHEG, which allows to match NLO calculations to parton showers. Numerical predictions are presented using the PYTHIA parton shower and are compared to those obtained previously at fixed order, to a leading order calculation matched to the PYTHIA parton shower, and to a different NLO calculation matched to the HERWIG parton shower with MC@NLO. We also present numerical predictions and theoretical uncertainties for various Two Higgs Doublet Models at the Tevatron and LHC.

1 Introduction

One of the most important current goals in high-energy physics is the discovery of the mechanism of electroweak symmetry breaking. While this can be achieved, as in the Standard Model (SM), with a single Higgs doublet field, giving rise to only one physical neutral Higgs boson, more complex Higgs sectors are very well possible and in some scenarios even necessary. E.g., in the Minimal Supersymmetric SM, which represents one of the most promising theories to explain the large hierarchy between the electroweak and gravitational scales, a second complex Higgs doublet is required by supersymmetry with the consequence that also charged Higgs bosons should exist.

At hadron colliders, the production mechanism of a charged Higgs boson depends strongly on its mass. If it is sufficiently light, it will be dominantly produced in decays of top quarks, which are themselves copiously pair produced via the strong interaction. Experimental searches in this channel have been performed at the Tevatron by both the CDF [1] and D0 [2] collaborations and have led to limits on the top-quark branching fraction and charged Higgs-boson mass as a function of tanβ, the ratio of the two Higgs vacuum expectation values (VEVs), for various Two Higgs Doublet Models (2HDMs). However, if the charged Higgs boson is heavier than the top quark, it is dominantly produced in association with top quarks with a semi-weak production cross section. The D0 collaboration have searched for charged Higgs bosons decaying into top and bottom quarks in the mass range from 180 to 300 GeV and found no candidates [3]. At the LHC, the ATLAS (and CMS) collaborations have already excluded top-quark branching ratios to charged Higgs bosons with masses of 90 (80) to 160 (140) GeV and bottom quarks above 0.03−0.10 (0.25−0.28) using 1.03 fb⁻¹ (36 pb⁻¹) of data taken at $\sqrt{S}=7~\mathrm{TeV}$ [4, 5]. At 14 TeV and with an integrated luminosity of 30 fb⁻¹, the discovery reach may be extended to masses of about 600 GeV using also the decay into tau leptons and neutrinos [6, 7]. It may then also become possible to determine the spin and couplings of the charged Higgs boson, thereby identifying the type of the 2HDM realized in Nature. Searches for pair-produced charged Higgs bosons decaying into tau leptons and neutrinos, second generation quarks and W-bosons and light neutral Higgs bosons have been performed at LEP and have led to mass limits of m _H >76.7 (78.6) GeV for all values of tanβ in Type-I [8] (Type-II [9]) 2HDMs, where only one (both) Higgs doublet(s) couple to the SM fermions. Indirect constraints from flavor-changing neutral currents (FCNCs) such as b→sγ can be considerably stronger, e.g. m _H >295 GeV for tanβ≥2 in the absence of other new physics sources [10].

In this paper, we concentrate on the associated production of top quarks and charged Higgs bosons at hadron colliders, which is of particular phenomenological importance for a wide range of masses and models. Conversely, s-channel single, pair, and associated production of charged Higgs bosons with W-bosons are less favorable in most models. Isolation of this signal within large SM backgrounds, e.g. from top-quark pair and W-boson associated production, and an accurate determination of the model parameters require precise predictions that go beyond the next-to-leading order (NLO) accuracy in perturbative QCD obtained previously [11–13]. We therefore present here details of our re-calculation of this process at NLO using the Catani–Seymour (CS) dipole subtraction formalism [14, 15]. The virtual loop and unsubtracted real emission corrections are then matched with a parton shower (PS) valid to all orders in the soft-collinear region using the POWHEG method [16, 17] in the POWHEG BOX framework [18]. A similar calculation has been presented using the Frixione–Kunszt–Signer (FKS) subtraction formalism [19] and matching to the HERWIG PS with the MC@NLO method [20]. Other new physics processes recently implemented in MC@NLO include, e.g., the hadroproduction of additional neutral gauge bosons [21]. Unlike MC@NLO, POWHEG produces events with positive weight, which is important when the experimental analysis is performed via trained multivariate techniques. POWHEG can be easily interfaced to both HERWIG [22] and PYTHIA [23] and thus does not depend on the Monte Carlo (MC) program used for subsequent showering.

The remainder of this paper is organized as follows: In Sect. 2, we present details of our NLO calculation of top-quark and charged Higgs-boson production. We emphasize the renormalization of wave functions, masses, and couplings, in particular the one of the bottom Yukawa coupling, in the virtual loop amplitudes as well as the isolation and cancellation of soft and collinear divergences with the Catani–Seymour dipole formalism in the real emission amplitudes. The implementation in POWHEG is described in Sect. 3. As the associated production of top quarks with charged Higgs bosons is very similar to the one with W-bosons [24], we concentrate here on the differences of the two channels. We also emphasize the non-trivial separation of the associated production from top-quark pair production with subsequent top-quark decay in scenarios, where the charged Higgs boson is lighter than the top quark, using three methods: removing completely doubly resonant diagrams, subtracting them locally in phase space, or including everything, so that top-quark pair production with the subsequent decay of an on-shell top quark into a charged Higgs boson is effectively included at leading order (LO). In Sect. 4, we present a detailed numerical comparison of the new POWHEG implementation to the pure NLO calculation without PS [12], to a tree-level calculation matched to the PYTHIA parton shower [25], and to the MC@NLO implementation with the HERWIG PS [20]. We also give numerical predictions and theoretical uncertainties for various 2HDMs at the Tevatron and LHC. Our conclusions are summarized in Sect. 5.

2 NLO calculation

2.1 Organization of the calculation

At tree level and in the five-flavor scheme with active bottom (b) quarks as well as gluons (g) in protons and antiprotons, the production of charged Higgs bosons (H ⁻) in association with top quarks (t) occurs at hadron colliders via the process b(p ₁)+g(p ₂)→H ⁻(k ₁)+t(k ₂) through the s- and t-channel diagrams shown in Fig. 1. The massive top quark is represented by a double line, whereas the bottom quark is treated as massless and represented by a single line. The Born matrix elements can then be given in terms of the Mandelstam variables

(1)

(2)

(3)

A NLO calculation in a four-flavor scheme, where the bottom quark is treated as massive and generated by the splitting of an initial gluon, has been presented elsewhere [26], but the effect of the bottom mass through the parton densities was subsequently found to be strongly suppressed compared to its impact on the bottom Yukawa coupling [27]. The four-momenta of the participating particles have been ordered in accordance with the POWHEG scheme, where the initial-state particles with four-momenta p ₁ and p ₂ are followed by the four-momentum k ₁ of the final-state massive colorless particle and then the four-momentum k ₂ of the outgoing massive colored particle. The additional radiation of a massless particle (gluon or light quark), which occurs at NLO in real emission diagrams, is assigned the last four-momentum k ₃.

Fig. 1

Tree-level diagrams for the associated production of charged Higgs bosons and top quarks at hadron colliders in the s-channel $\mathcal{S}$ and the t-channel $\mathcal{T}$

The hadronic cross section

(4)

is obtained as usual as a convolution of the parton density functions (PDFs) $f_{a/A,\,b/B}(x_{a,b},\mu_{F}^{2})$ with the partonic cross section

$$ \sigma\bigl(p_1,p_2;\mu_F^2 \bigr) = \sigma^{LO}(p_1,p_2)+ \sigma^{NLO}\bigl(p_1,p_2;\mu_F^2 \bigr) $$

(5)

with partonic center-of-mass energy s=x _a x _b S, S being the hadronic center-of-mass energy. Its LO contribution

$$ \sigma^{LO}(p_1,p_2) = {1\over2s} \int \mathrm{d} \varPhi^{(2)} \overline{|\mathcal{M}_{\mathrm{Born}}|^2} $$

(6)

is obtained from the spin- and color-averaged squared Born matrix elements $\overline{|\mathcal{M}_{\mathrm{Born}}|^{2}}$ through integration over the two-particle phase space dΦ ⁽²⁾ and flux normalization.

2.2 Virtual corrections and renormalization scheme

Like the LO partonic cross section σ ^LO, its NLO correction

(7)

has a two-body final-state contribution

(8)

which consists of the virtual cross section dσ ^V, i.e. the spin- and color-averaged interference of the Born diagrams with their one-loop corrections, and the Born cross section dσ ^LO convolved with a subtraction term I, which can be written as ₂〈H,t;b,g|I(ϵ)|H,t;b,g〉₂ and which removes the infrared singularities present in the virtual corrections. The three-body final-state contribution σ ^NLO{3} and the finite remainders σ ^NLO{2}(x,…) of the initial-state singular terms will be described in the third part of this section.

The ultraviolet divergences contained in the virtual cross section dσ ^V have been made explicit using dimensional regularization with D=4−2ϵ dimensions and are canceled against counterterms originating from multiplicative renormalization of the parameters in the Lagrangian. In particular, the wave functions for the external gluons, bottom and top quarks are renormalized in the $\overline{\mathrm{MS}}$ scheme with

(9)

(10)

where Δ _UV =1/ϵ−γ _E +ln4π, γ _E is the Euler constant, N _C =3 and N _F =6 are the total numbers of colors and quark flavors, respectively, and $C_{F} = (N_{C}^{2}-1)/(2 N_{C})$. The counterterm for the strong coupling constant $\alpha_{S}=g_{S}^{2}/(4\pi)$

$$ {\delta g_S\over g_S} = -\frac{\alpha_S(\mu_R^2)}{8 \pi} \biggl[ \Delta_{UV} \biggl( \frac{11}{3} N_C - \frac{2}{3} N_F \biggr) - \frac{2}{3} \ln \frac {\mu^2_R}{m_t^2} \biggr], $$

(11)

is computed in the $\overline{\mathrm{MS}}$ scheme using massless quarks, but decoupling explicitly the heavy top quark with mass m _t from the running of α _S  [28]. The top-quark mass entering in the kinematics and propagators is renormalized in the on-shell scheme,

$$ \frac{\delta m_t^{\mathrm{OS}} }{m_t} = -\frac{\alpha_S(\mu ^2_R)}{4 \pi } 3 C_F \biggl( \Delta_{UV} +\frac{4}{3} +\ln\frac{\mu^2_R}{m_t^2} \biggr). $$

(12)

On the other hand, we perform the renormalization of both the bottom and top Yukawa couplings in the $\overline{\mathrm{MS}}$ scheme,

$$ \frac{\delta y_{b,t}}{y_{b,t}(\mu^2_R)} = - \frac{\alpha_S (\mu ^2_R)}{ 4 \pi} 3 C_F \Delta_{UV} . $$

(13)

This enables us to factorize the charged Higgs-boson coupling at LO and NLO, making the QCD correction (K) factors independent of the 2HDM and value of tanβ under study. In particular, in (13) we do not subtract the mass logarithm, but rather resume it using the running quark masses

$$ \bar{m}_Q(\mu_R) = \bar{m}_Q(M_Q) \frac{c ( \alpha_s(\mu_R)/\pi)}{c ( \alpha_s(M_Q)/\pi)} $$

(14)

in the Yukawa couplings, where

$$ c(x) = \biggl( \frac{23}{6}x \biggr)^{12/23} \bigl(1+1.175x+1.501x^2 \bigr) $$

(15)

for m _b <μ _R <m _t and

$$ c(x) = \biggl( \frac{7}{2}x \biggr)^{4/7} \bigl(1+1.398x+1.793 x^2\bigr) $$

(16)

for μ _R >m _b,t  [29]. The starting values of the $\overline{\mathrm{MS}}$ masses are obtained from the on-shell masses M _Q through the relation

$$ \bar{m}_Q(M_Q) = \frac{M_Q}{1+\frac{4}{3} \frac{\alpha_S(M_Q)}{\pi } + K_Q \bigl( \frac{\alpha_s(M_Q)}{\pi} \bigr)^2} $$

(17)

with K _b ≈12.4 and K _t ≈10.9 [30, 31].

After the renormalization of the ultraviolet singularities has been performed as described above, the virtual cross section contains only infrared poles. These are removed with the second term in (8), i.e. by convolving the Born cross section with the subtraction term [14, 15]

(18)

where in our case I ₂(ϵ,μ ²;{k ₂,m _t })=0, since there are no QCD dipoles with a final-state emitter and a final-state spectator. The dipoles depending on one initial-state parton (a=b,g) with four-momentum p _i (i=1,2) are

(19)

where T _a,t denotes the color matrix associated to the emission of a gluon from the parton a or the top quark t, the dimensional regularization scale μ is identified with the renormalization scale μ _R , and s _ta =s _at =2p _i k ₂. The kernels

(20)

(21)

(22)

consist of the singular terms

(23)

with $Q^{2}_{ta} = Q^{2}_{at} = s_{ta} + m_{t}^{2} + m_{a}^{2}$ and the non-singular terms

(24)

(25)

(26)

The constant κ in (19) is a free parameter, which distributes non-singular contributions between the different terms in (7). The choice κ=2/3 considerably simplifies the gluon kernel. For massive quarks, one has in addition

$$ \varGamma_t(\mu,m_t;\epsilon) = C_F \biggl( \frac{1}{\epsilon}+\frac {1}{2}\ln\frac{m_t^2}{\mu^2}-2 \biggr), $$

(27)

while

(28)

and

$$ \begin{aligned} &K_q = \biggl( \frac{7}{2}-\frac{\pi^2}{6} \biggr) C_F , \\ &K_g = \biggl( \frac{67}{18} - \frac{\pi^2}{6} \biggr)N_C -\frac {10}{9}T_R N_f \end{aligned} $$

(29)

with T _R =1/2 and N _f =5 the number of light quark flavors. The last term in (18)

(30)

depends on both initial-state partons. Since the process we are interested in involves only three colored particles at the Born level, the color algebra can be performed in closed form. To be concrete, we have

(31)

(32)

(33)

(34)

2.3 Real corrections

The second term in (7)

(35)

includes the spin- and color-averaged squared real emission matrix elements $\overline{|\mathcal{M}_{3,ij}(k_{1},k_{2},k_{3};p_{1}, p_{2})|^{2}}$ with three-particle final states and the corresponding unintegrated QCD dipoles $\mathcal {D}$, which compensate the integrated dipoles I in the previous section. Both terms are integrated numerically over the three-particle differential phase space dΦ ⁽³⁾.

The real emission processes can be grouped into the four classes

• (a) b(p ₁)+g(p ₂)→H ⁻(k ₁)+t(k ₂)+g(k ₃),

• (b) $g(p_{1})+g(p_{2}) \rightarrow H^{-}(k_{1})+t(k_{2})+\bar{b}(k_{3})$,

• (c) $b(p_{1})+q/\bar{q}(p_{2})\rightarrow H^{-}(k_{1})+t(k_{2})+q/\bar {q}(k_{3})$, and

• (d) $q(p_{1})+\bar{q}(p_{2}) \rightarrow H^{-}(k_{1})+t(k_{2})+\bar{b}(k_{3})$,

where the second process (b) can be obtained from the first one (a) by crossing the four-momenta k ₃ and −p ₁ and multiplying the squared matrix element by a factor of (−1) to take into account the crossing of a fermion line. The processes in the two other classes (c) and (d) can interfere when q=b, but these contributions are numerically negligible due to the comparatively small bottom quark parton distribution function. Process (d) is furthermore convergent for q=u,d,s and c.

The sum over the dipoles in (35) includes initial-state emitters ab with both initial- and final-state spectators c ($\mathcal {D}^{ab,c}$ and $\mathcal{D}^{ab}_{c}$) and the final-state emitter ab with initial-state spectators c ($\mathcal{D}_{ab}^{c}$). For the three divergent processes, we have

(36)

(37)

(38)

Denoting by a the original parton before emission, b the spectator, and i the emitted particle, the dipole for initial-state emitters and initial-state spectators is given by

(39)

where the momentum of the intermediate initial-state parton $\tilde {ai}$ is $\tilde{p}^{\mu}_{ai}= x_{i,ab} p_{a}^{\mu}$ with x _i,ab =(p _a p _b −k _i p _a −k _i p _b )/(p _a p _b ), the momentum p _b is unchanged, and the final-state momenta k _j with j=1,2 are shifted to

$$ \tilde{k}_{j}^{\mu} = k_{j}^{\mu}- \frac{2 k_j \cdot(K+\tilde{K})}{ (K+\tilde{K})^2}(K+\tilde{K})^{\mu}+ \frac{2 k_j \cdot K}{K^2} \tilde{K}^{\mu} $$

(40)

with $K^{\mu}= p_{a}^{\mu}+p_{b}^{\mu}-k_{i}^{\mu}$ and $\tilde{K}^{\mu }=\tilde{p}_{ai}^{\mu}+ p_{b}^{\mu}$. The necessary splitting functions V ^ai,b for {ai,b}={qg,g;gg,q;gq,g;qq,q} can be found in Ref. [14]. The dipole for initial-state emitters and a final-state spectator, which is in our case the top quark t, is given by

(41)

where the momentum of the intermediate initial-state parton $\tilde {ai}$ is $\tilde{p}_{ai}^{\mu} = x_{it,a} p_{a}^{\mu}$ with x _it,a =(p _a k _i +p _a p _t −k _i p _t )/(p _a k _i +p _a p _t ), the momentum p _b is unchanged, and the momentum of the final-state top quark p _t is shifted to $\tilde{p}_{t}^{\mu} = k_{i}^{\mu} + p_{t}^{\mu}-(1-x_{it,a})p_{a}^{\mu }$. The necessary splitting functions $\mathbf{V}^{ai}_{t}$ for {ai,t}={qg,t;gg,t;gq,t;qq,t} can be found in Ref. [15]. Finally, the dipole for final-state emitter (the top quark t) and initial-state spectator a is given by

(42)

where the momentum of the initial parton a is shifted to $\tilde {p}_{a}^{\mu} = x_{it,a}p_{a}^{\mu}$ with x _it,a =(p _a k _i +p _a p _t −k _i p _t )/(p _a k _i +p _a p _t ), the momentum p _b is unchanged, and the momentum of the intermediate final-state top quark p _t is $\tilde{p}_{it}^{\mu} = k_{i}^{\mu} + p_{t}^{\mu}- (1-x_{it,a}) p_{a}^{\mu}$. The required splitting function $\mathbf {V}^{a}_{gt}$ can again be found in Ref. [15].

The last terms in (7) are finite remainders from the cancellation of the ϵ-poles of the initial-state collinear counterterms. Their general expressions read

(43)

and similarly for (a↔b) and (p ₁↔p ₂). The color-charge operators K and P are explicitly given in Ref. [15].

3 POWHEG implementation

The calculation in the previous section has been performed using the Catani–Seymour dipole formalism for massive partons [14, 15]. For the implementation of our NLO calculation in the POWHEG Monte Carlo program, we need to retain only the Born process, the finite terms of the virtual contributions, and the real emission parts of our calculation, since all necessary soft and collinear counterterms and finite remnants are calculated automatically by the POWHEG BOX in the FKS scheme [19]. Soft and collinear radiation is then added to all orders using the Sudakov form factor. In this section, we briefly describe the three relevant contributions, following closely the presentation in Ref. [18], and address the non-trivial separation of the associated production of charged Higgs bosons and top quarks from top-quark pair production with subsequent top-quark decay in scenarios, where the charged Higgs boson is lighter than the top quark.

3.1 Born process

In the POWHEG formalism, a process is defined by its particle content. Each particle is encoded via the Particle Data Group numbering scheme [32] except for gluons, which are assigned the value zero. The order of the final-state particles has to be respected. Colorless particles are listed first, then heavy colored particles, and finally massless colored particles. The Born processes (two with respect to the different bg and gb initial states) are defined with $\mathtt{flst\_nborn}=2$ and are listed as

$$ \bigl(bg \rightarrow H^-t\bigr) = [5,0,-37,6 ] $$

(44)

and

$$ \bigl(gb \rightarrow H^-t\bigr) = [0,5,-37,6 ] $$

(45)

in the subroutine init_processes.

In the subroutine born_phsp, the integration variables xborn(i) for the Born phase space are generated between zero and one. The hadronic cross section is then obtained from the differential partonic cross section dσ via the integration (see (4))

(46)

where f _i/I is the PDF of parton i inside hadron I with momentum fraction x _i and where we have performed the change of variables

$$ y= \ln\frac{x_a}{\sqrt{x_a x_b}} \quad\mbox{and}\quad \tau= x_a x_b. $$

(47)

The integration limits are given in Table 1. The Jacobian for the change of integration variables from xborn(i) to (τ,y,t)

$$ \Delta_{jac}= (\tau_{\max}-\tau_{\min}) \times(y_{\max}-y_{\min})\times(t_{\max}-t_{\min}) $$

(48)

has to be multiplied with 2π for the integration over the azimuthal angle ϕ, which is randomly generated by POWHEG. The different kinematical variables can then be constructed in the center-of-mass reference frame as well as in the laboratory frame via boosts. The renormalization scale μ _R and factorization scale μ _F are set in the subroutine set_fac_ren_scales according to the usual convention

$$ \mu_R=\mu_F= \frac{m_t+m_H}{k}, $$

(49)

where k is to be varied around two for uncertainty studies. Both the born_phsp and the set_fac_ren_scales subroutines can be found in the file Born_phsp.f.

Table 1 Integration limits for the hadronic cross section

All other routines relevant to the Born process are contained in the file Born.f. The subroutine setborn contains the factors for the color-correlated Born amplitudes, which are related to the Born process through the color factors quoted in (31) and (32). The subroutine borncolor_lh contains the color flow of the Born term in the large-N _C limit shown in Fig. 2. The routine compborn contains the spin-correlated Born matrix element

$$ \mathcal{M}^{\mu\nu}_{\mathrm{Born}} = - \bigl( \mathcal{S}^{\mu } \mathcal{S}^{\nu}+\mathcal{S}^{\mu} \mathcal{T}^{\nu}+ \mathcal{T}^{\mu}\mathcal{S}^{\nu}+ \mathcal{T}^{\mu} \mathcal{T}^{\nu} \bigr) $$

(50)

before summing over the initial gluon polarizations as well as

$$ \mathcal{M}_{\mathrm{Born}}= - g_{\mu\nu}\mathcal{M}^{\mu\nu }_{\mathrm{Born}}, $$

(51)

where g _μν is the metric tensor.

Fig. 2

Color flow in the Born contribution [5,0,−37,6] and for switched incoming partons [0,5,−37,6]

3.2 Virtual loop corrections

The renormalized virtual cross section is defined in dimensional regularization and in the POWHEG convention by

$$ \mathcal{V}= \frac{(4 \pi)^{\epsilon}}{\varGamma (1-\epsilon)} \biggl( \frac{\mu_R^2}{Q^2} \biggr)^{\epsilon} \frac{\alpha_s}{2 \pi} \biggl[ \biggl(\frac {C_2}{\epsilon^2}+ \frac{C_1}{\epsilon} \biggr)|\mathcal{M}_{\mathrm{Born}}|^2 + \mathcal{V}_{\mathrm{fin}} \biggr], $$

(52)

where $|\mathcal{M}_{\mathrm{Born}}|^{2}$ is now the squared Born matrix element computed in D=4−2ϵ dimensions and where the remaining double and simple infrared poles are proportional to

(53)

(54)

The POWHEG implementation needs then only the finite coefficient $\mathcal{V}_{\mathrm{fin}}$, which has been organized into terms stemming from scalar 2-, 3- and 4-point integral functions B ₀, C ₀ and D ₀ plus remaining terms and can be found in the file virtual.f. Non-divergent C ₀-functions and Euler dilogarithms are computed using routines contained in the file loopfun.f.

3.3 Real emission corrections

In the subroutine init_processes, the index of the first colored light parton in the final state is defined, which is in our case the additional jet from the real emission ($\mathtt{flst\_lightpart}=5$). All $\mathtt{flst\_ nreal}= 30$ real emission processes are then assigned a number according to the list given in Table 2. The expressions of the squared real emission matrix elements are given in the file real_ampsq.f.

Table 2 Process numbers of the different real emissions. Here q=d,u,s,c

3.4 Separation of associated production and pair production of top quarks

If the charged Higgs-boson mass m _H is lower than the top-quark mass m _t , the antitop propagator of the real emission amplitudes shown in Fig. 3 can go on shell, resulting in a drastic increase of the total cross section. In other words, the prevalent production mechanism becomes the on-shell production of a $t\bar{t}$ pair, followed by the decay of the antitop quark into a charged Higgs boson. The corresponding Feynman graphs contribute to top-antitop production at LO with the charged Higgs boson being produced in top-quark decays, but also to tH ⁻ production at NLO. The relevant NLO processes are free from collinear and soft singularities.

Fig. 3

Real emission contributions in the gluon–gluon and quark–antiquark channels with an antitop propagator that can go on shell

At this point the problem arises how to separate the two production mechanisms. In the literature two methods have been proposed: Diagram Removal (DR) and Diagram Subtraction (DS) [33]. Both remove the top-quark resonance from the cross section, but the procedure for combining top-pair production with the associated production is not completely clear. If we separate the amplitudes of a real emission process with colliding partons a and b into contributions $\mathcal{M}_{ab}^{t \bar{t}}$, which proceed through $t\bar {t}$-production, and contributions $\mathcal{M}_{ab}^{tH^{-}}$ which do not,

$$ \mathcal{M}_{ab}= \mathcal{M}_{ab}^{t \bar{t}} + \mathcal{M}_{ab}^{tH^-}, $$

(55)

squaring the amplitudes gives rise to three different quantities:

(56)

The term $\mathcal{D}_{ab}$ contains neither collinear nor soft singularities, while the interference term $\mathcal{I}_{ab}$ contains integrable infrared singularities. These terms are therefore sometimes referred to as subleading with respect to those in $\mathcal{S}_{ab}$, which contains all infrared singularities and must be regularized, e.g., via the subtraction formalism. DR requires removing $t\bar{t}$ production at the amplitude level. The only contributing element is then $\mathcal{S}_{ab}$. Since it contains all divergences, the dipoles used in the m _H >m _t case remain valid. In the DS scheme, one subtracts from the cross section the quantity

$$ \mathrm{d} \sigma^{\mathrm{sub}}_{H^-t}=\frac{f_{\mathrm{BW}}(m_{H^-\bar {b}})}{f_{\mathrm{BW}}(m_t)} \bigl\vert\tilde{ \mathcal{A}}^{(t\bar{t})}\bigr\vert^2 $$

(57)

locally in phase space. The momenta are reorganized so as to put the $\bar{t}$ quark on its mass shell. Although gauge invariant, this procedure is still somewhat arbitrary. We therefore introduce here a third option, where nothing is removed or subtracted from the associated production, but simply the full production cross section is retained. Once a sample of events is generated, one can then still decide to remove events near the resonance region and replace them with events obtained, for example, with a full NLO implementation of $t\bar{t}$ production.

In our POWHEG code, we implemented all three methods described above. DR is the simplest case. If the flag DR is set to one in the file powheg.input, the resonant diagrams of Fig. 3 are simply not included. For the other two procedures, i.e. DS and keeping the full cross section, DR should be set to zero. The s-channel propagators of the $\bar{t}$ quark in the real amplitudes are then replaced by a Breit–Wigner form. Setting the flag DS to one turns on diagram subtraction. If neither DS nor DR are set to one, the full cross section is computed. In this case it is, however, hard to probe the $\bar{t}$ pole with sufficient accuracy in the Monte Carlo integration. An additional flag sepresonant is therefore introduced that, when set to one, causes POWHEG to treat the resonant contributions as a regular remnant. This is possible since they do not require subtractions. A specific routine for the generation of the phase space of the regular remnant ensures that appropriate importance sampling is used in the $\bar{t}$ resonant region.

While with the DR or the full scheme the fraction of negative weights is very small, this is not the case in the DS scheme. Here the real cross section can become negative in certain kinematic regions, so that POWHEG must then be run with the flag withnegweights set to one. Negatively weighted events are then kept, but are hard to interpret, since they correspond to the subtraction of an ad hoc quantity from the cross section.

Removing diagrams at the amplitude level causes the loss of gauge invariance. A considerable part of Ref. [33] has been dedicated to the analysis of the corresponding impact on Wt production. There, different gauges were considered for the gluon propagator, and differences at the per-mille level were found. Note, however, that gauge invariance is not only spoiled through the gluon propagator, but also when the polarization sum

$$ P^{\mu\nu}(k)= \sum_{\lambda= 1,2} \epsilon^{\mu}(k,\lambda) \epsilon^{\nu}(k,\lambda) $$

(58)

of external gluons is replaced by

$$ P^{\mu\nu}(k)= -g^{\mu\nu} $$

(59)

for simplicity. Here, k ^μ is the four-momentum, λ is the polarization, and ϵ ^μ(k,λ) is the polarization vector of the external gluon. Equation (59) includes not only physical transverse, but also non-physical gluon polarizations that must be canceled by ghost contributions. Removing individual diagrams then causes the loss of gauge invariance. We therefore abandon the use of the simple polarization sum, (59), and sum instead only over physical states with

$$ P^{\mu\nu}(k) = -g^{\mu\nu} - \frac{1}{ (k \cdot\eta )^2} \bigl[ \eta^2 k^{\mu} k^{\nu} - k \cdot\eta\bigl( k^{\mu} \eta^{\nu} + \eta^{\mu} k^{\nu} \bigr) \bigr], $$

(60)

where η ^μ is an arbitrary four-vector transverse to the polarization vector ϵ ^μ. When calculating a gauge invariant quantity, the η-dependence would drop out, but this will not be the case in DR as argued above. For the channels with two external gluons and incoming four-momenta p ₁ and p ₂, we choose for the polarization vectors

$$ \eta_1 = p_2 \quad \mbox{and}\quad \eta_2 = p_1. $$

(61)

4 Numerical results

4.1 QCD input

For the parton density functions (PDFs) in the external hadrons, we use the set CT10 obtained in the latest global fit by the CTEQ collaboration [34]. It has been performed at NLO in the $\overline{\mathrm{MS}}$ factorization scheme with n _f =5 active flavors as required by our calculation. The employed value of α _s (M _Z )=0.118, close to the world average, is equivalent to setting the QCD scale parameter $\varLambda_{\overline {\mathrm{MS}}}^{n_{f}= 5}$ to 226.2 MeV as in the previous fits. We also adopt their value for the bottom quark mass of m _b =4.75 GeV and for the top-quark mass of m _t =172 GeV and not the newest average value of m _t =173.2 GeV obtained in direct top observation at the Tevatron [35], as the former value corresponds nicely to the one in the MC@NLO publication [20] that we will compare with later in this section. For the sake of easier comparisons we also adopt the default scale choice μ _F =μ _R =(m _H +m _t )/2 as in the MC@NLO study. We use the versions HERWIG 6.5.10 and PYTHIA 6.4.21 with stable top quarks and Higgs bosons and no kinematic cuts to simplify the analysis. Multiparticle interactions were neglected. For a discussion of the numerical impact of the bottom mass in the PDFs we refer the reader to Ref. [27].

4.2 Two Higgs doublet models

New particles with masses in the TeV range that couple to quarks at tree level can strongly modify the predictions for Flavor-Changing Neutral Current (FCNC) processes, since these are absent at tree level in the SM. Thus all extensions of the SM, including the 2HDMs, must avoid conflicts with the strict limits on FCNCs, such as the electroweak precision observable $R_{b}=\varGamma(Z\to b\bar{b})/\varGamma(Z\to\mathrm{hadrons})$ or the branching ratio BR(B→X _s γ). In 2HDMs, tree-level FCNCs are traditionally avoided by imposing the hypothesis of Natural Flavor Conservation (NFC), which allows only one Higgs field to couple to a given quark species due to the presence of a flavor-blind Peccei–Quinn U(1) symmetry or its discrete subgroup Z ₂ [36]. Alternatively, all flavor-violating couplings can be linked to the known structure of Yukawa couplings and thus the Cabibbo–Kobayashi–Maskawa (CKM) matrix under the hypothesis of Minimal Flavor Violation (MFV) [37]. Both hypotheses have recently been compared with the result that the latter appears to be more stable under quantum corrections, but that the two hypotheses are largely equivalent at tree level [38].

In a general 2HDM, one introduces two complex SU(2)-doublet scalar fields

$$ \varPhi_i = \left( \begin{array}{c} \phi_i^+\\ (v_i+\phi_i^{0,r}+i\phi^{0,i}_i)/\sqrt{2} \end{array} \right) \quad\mbox{with}\ i=1,2, $$

(62)

where the Vacuum Expectation Values (VEVs) v _1,2 of the two doublets are constrained by the W-boson mass through $v^{2}=v_{1}^{2}+v_{2}^{2}=4m_{W}^{2}/g^{2}=(246~\mathrm{GeV})^{2}$ [39]. The physical charged Higgs bosons are superpositions of the charged degrees of freedom of the two doublets,

(63)

and the tangent of the mixing angle tanβ=v ₂/v ₁, determined by the ratio of the two VEVs, is a free parameter of the model, along with the mass of the charged Higgs bosons m _H . The allowed range of tanβ can be constrained by the perturbativity of the bottom- and top-quark Yukawa couplings (y _t,b ≤1) to 1≤tanβ≤41. Note that in the Minimal Supersymmetric SM (MSSM) m _H >m _W at tree level. The possible assignments of the Higgs doublet couplings to charged leptons, up- and down-type quarks satisfying NFC are summarized in Table 3.

Table 3 Couplings of the two Higgs doublets Φ _1,2 to up-type quarks (u), down-type quarks (d), and charged leptons (l) in 2HDMs satisfying Natural Flavor Conservation [41]

In the Type-I 2HDM, only Φ ₂ couples to the fermions in exactly the same way as in the minimal Higgs model, while Φ ₁ couples to the weak gauge bosons [40]. The Feynman rules for the charged Higgs-boson couplings to quarks in this model, with all particles incoming, are

(64)

where V _ij is the CKM matrix and $P_{L,R}=(1\mp\gamma_{5})/\sqrt {2}$ project out left- and right handed quark eigenstates. As can be seen from Table 3, these couplings are the same in the lepton-specific 2HDM.

In the Type-II 2HDM, Φ ₂ couples to up-type quarks and Φ ₁ to down-type quarks and charged leptons. The Feynman rules for charged Higgs-boson couplings to quarks in this model, with all particles incoming, are

(65)

As can again be seen from Table 3, they are identical to those in the flipped 2HDM [41].

Since the NFC and MFV hypotheses allow for the possibility that the two Higgs doublets couple to quarks with arbitrary coefficients $A_{u,d}^{i}$, there exists also the possibility of a more general 2HDM, sometimes called Type-III 2HDM [42]. In this case, the Feynman rules for the charged Higgs-boson couplings to quarks, with all particles incoming, are

(66)

where the family-dependent couplings $A_{u,d}^{i}$ read

(67)

Under the assumption that no new sources of CP violation apart from the complex phase in the CKM matrix are present, the coefficients A _u,d and ϵ _u,d are real. The case ϵ _u,d =0 corresponds to the NFC situation, in which the Yukawa matrices of both Higgs doublets are aligned in flavor space. LEP measurements of R _b constrain |A _u | to values below 0.3 and 0.5 (0.78 and 1.35) for m _H =100 and 400 GeV at 1σ (2σ), when A _d =0. For opposite (same) signs of A _u and A _d , the average of BABAR, Belle and CLEO measurements of BR(B→X _s γ) allow for one (two) region(s) of A _d for given values of A _u and m _H . For A _u =0.3 and m _H =100 GeV, both A _d ∈[0;1] and [16;18] are allowed, while for A _u =0.3 and m _H =400 GeV, both A _d ∈[0;2.5] and [50;56] are allowed at 2σ [42]. Since general color-singlet Higgs-boson couplings and (theoretically possible) color-octet Higgs bosons induce different QCD corrections, we will not study these scenarios numerically. In the literature, one may also find Type-III 2HDMs where no flavor symmetry is imposed and FCNCs are avoided by other methods, e.g. by the small mass of first and second generation quarks [43]. These models then allow for the couplings of charged Higgs bosons to bottom and charm quarks, which induces a phenomenology that is different from the one studied in this paper.

4.3 Predictions for various 2HDMs

The calculation presented in the previous sections was performed in a generic way, which makes it possible to use the result for various models with charged Higgs bosons. Out of the models mentioned in the last section, our calculation is in particular valid for the Type-I and Type-II 2HDMs. In this subsection, we perform a numerical analysis for a set of typical collider scenarios for these 2HDMs. As in these models the scattering matrix element is directly proportional to the Higgs-top-bottom quark coupling even at NLO, the type of the model has no influence on kinematic distributions apart from their normalization to the total cross section.

We therefore concentrate here on the total cross sections and on the uncertainties both from the variation of the renormalization and factorization scales and from the parton distribution functions. For a better comparison, we analyze the total cross sections and their uncertainties by choosing the same values for the mass of the charged Higgs boson and for tanβ in all scenarios, i.e. m _H =300 GeV and tanβ=10. All relevant values are summarized in Table 4.

Table 4 Total cross sections (in pb) for different 2HDMs at the Tevatron and at the LHC at leading order (LO) and at next-to-leading order (NLO) including the scale and PDF uncertainties. All scenarios assume the same parameters for better comparison, i.e. m _H =300 GeV and tanβ=10

In all scenarios, both at the Tevatron and at the LHC, the next-to-leading order correction is substantial, ranging from 57 % at the Tevatron in the Type-I 2HDM to 38 % at the LHC in the same model. Apart from enhancing the total cross section, including the NLO correction reduces the theoretical error defined as the scale uncertainty of the cross section. The scale uncertainty is obtained by varying both the renormalization and factorization scales simultaneously in the interval

$$ \frac{m_t+m_H}{4} < \mu< m_t+m_H . $$

(68)

At leading order, the strong scale dependence comes from the strong coupling constant and from the Yukawa coupling in the tree-level amplitude. Including higher-order corrections, this uncertainty is dramatically reduced in some scenarios.

Another large source of error stems from the parton distribution functions. We use the CT10 NLO PDF set with its error PDF sets to determine the error coming from the uncertainty contained in determining the parton content of the colliding hadrons. The process considered here is extremely sensitive to the gluon distribution function through having a gluon in the initial state and through having a heavy-quark initial state, which is radiatively generated from the gluon PDF. Moreover, the production of a heavy Higgs boson in association with a top quark probes the higher x content of the initial-state (anti-)proton. The values of Bjorken-x probed can be expressed as

$$ x_a x_b = \frac{(k_1+k_2)^2}{s} > \frac{(m_t+m_H)^2}{s}, $$

(69)

which at the Tevatron leads to typical values of x∼0.3. This is exactly the region where the gluon PDF is poorly known, which translates into large PDF uncertainties on the cross section at the Tevatron. At the LHC, the Bjorken-x probed is x∼0.1, and the PDF uncertainties are therefore much smaller.

4.4 Checks of the NLO calculation and comparisons with POWHEG

As a check of the numerical implementation of our analytical results, we have compared our complete NLO calculation obtained with the Catani–Seymour dipole formalism with the one performed previously with a phase-space slicing method using a single invariant-mass cutoff [12], which had in turn been found to agree with a calculation using a two (soft and collinear) cutoff phase-space slicing method [11]. We found good agreement for all differential and total cross sections studied, but refrain from showing the corresponding figures here, since the fixed-order results are well-known.

For the remainder of the analysis, we will constrain ourselves to the Type-II 2HDM, as the kinematic distributions have the same features in both Type-I and Type-II 2HDMs. In all of our discussion, we consider three collider scenarios:

• Tevatron, $\sqrt{S}=1.96~\mathrm{TeV}$,

• LHC, $\sqrt{S}=7~\mathrm{TeV}$, and

• LHC, $\sqrt{S}=14~\mathrm{TeV}$.

Moreover, in the comparison of our NLO calculation with our implementation of its relevant parts in the POWHEG BOX, we assume m _H =300 GeV and tanβ=10. The results are shown in Fig. 4 for the Tevatron with $\sqrt{S}=1.96~\mathrm{TeV}$ and Figs. 5 and 6 for the LHC with a center-of-mass energy of $\sqrt{S}=7\ \mathrm{and}\ 14~\mathrm{TeV}$, respectively.

Fig. 4

Distributions in transverse momentum p _T (top left) and rapidity y (top right) of the charged Higgs boson, p _T (center left) and y (center right) of the top quark, as well as p _T (bottom left) and azimuthal opening angle Δϕ (bottom right) of the tH ⁻ system produced at the Tevatron with $\sqrt{S}=1.96~\mathrm{TeV}$. We compare the NLO predictions without (blue) and with matching to the PYTHIA (black) and HERWIG (red) parton showers using POWHEG in the Type-II 2HDM with tanβ=10 and m _H =300 GeV (Color figure online)

Fig. 5

Same as Fig. 4 at the LHC with $\sqrt{S}=7~\mathrm{TeV}$ (Color figure online)

Fig. 6

Same as Fig. 4 at the LHC with $\sqrt{S}=14~\mathrm{TeV}$ (Color figure online)

If we concentrate first on the transverse-momentum (p _T , left) and rapidity (y, right) distributions of the charged Higgs boson (top) and top quark (center) individually, we observe good agreement in absolute normalization and shape for all three collider scenarios, independently if a parton shower is matched to the NLO calculation or not. This corresponds to the well-known fact that these distributions are largely insensitive to soft or collinear radiation, in particular from the initial state, and this can therefore be seen as a further consistency test of our calculations. Soft radiation becomes relevant in all three collider scenarios when we consider the azimuthal opening angle of the top-Higgs pair (bottom right), where the singularity occurring at NLO in back-to-back kinematics at Δϕ=π is regularized and resumed by the parton showers. This holds also for the p _T -distribution of the top-Higgs pair (bottom left), which diverges perturbatively at p _T =0 GeV and even turns negative at the LHC.

An advantage of the POWHEG method is that it can also provide events including first radiation only in the form of an event file according to the Les Houches format (LHEF), making them independent of the parton shower. We therefore compare in Figs. 7, 8 and 9 the distributions obtained from these files to those obtained with NLO accuracy for the same set of parameters as in Figs. 4–6. As one can clearly see, they lie within the NLO scale uncertainty band, showing that the difference comes from terms beyond NLO accuracy. This provides a good consistency check of the matching procedure.

Fig. 7

Distributions in transverse momentum p _T (top left) and rapidity y (top right) of the charged Higgs boson, p _T (center left) and y (center right) of the top quark, as well as p _T (bottom left) and azimuthal opening angle Δϕ (bottom right) of the tH ⁻ system produced at the Tevatron with $\sqrt{S}=1.96~\mathrm{TeV}$. We compare the NLO scale uncertainty band (blue) the POWHEG result including first radiation only (red) (Color figure online)

Fig. 8

Same as Fig. 7 at the LHC with $\sqrt{S}=7~\mathrm{TeV}$ (Color figure online)

Fig. 9

Same as Fig. 7 at the LHC with $\sqrt{S}=14~\mathrm{TeV}$ (Color figure online)

4.5 POWHEG predictions with HERWIG and PYTHIA parton showers

In Figs. 4–6, we also show two different predictions with POWHEG coupled either to the angularly ordered HERWIG or to the virtuality-ordered PYTHIA parton shower. The agreement of the HERWIG and PYTHIA results is in general very good. They differ only slightly in the p _T distributions of the top-Higgs pair, where the PYTHIA p _T -distribution is a little bit harder, in particular at the Tevatron.

4.6 POWHEG comparison with MATCHIG

As described in Sect. 2, the production of charged Higgs bosons and top quarks proceeds at LO through the process bg→H ⁻ t, while at NLO the process $gg\to H^{-}t\bar{b}$ appears. The latter implies the creation of a virtual initial b-quark, which may either occur in the perturbative part of the calculation or is resumed into a b-quark PDF. In the full NLO calculation, the separation is achieved through the factorization procedure and induces a dependence on the factorization scale μ _F .

Before schemes to match parton showers with full NLO calculations were developed, the importance of the contribution of this particular two-to-three process and the perturbative origin of the b-quark density had already been recognized [25]. It had been proposed to supplement the LO calculation by this particular two-to-three process and to remove the overlap by subtracting the doubly counted (DC) term

(70)

where $f_{b'}(x,\mu_{F}^{2})$ is the LO b-quark density given by

$$ f_{b'}\bigl(x,\mu_F^2\bigr) \simeq {\alpha_s\over2\pi} \ln{\mu_F^2\over m_b^2} \int{\mathrm{d}z\over z} P_{qg}(z) f_{g} \biggl( {x\over z},\mu_F^2 \biggr) $$

(71)

with P _qg (z) the g→q splitting function, $f_{g}(x,\mu_{F}^{2})$ the gluon PDF, and z the longitudinal gluon momentum fraction taken by the b-quark. The two-to-three and double-counting processes had been implemented in an addition to PYTHIA called MATCHIG.

With our full NLO calculation matched to PYTHIA within the POWHEG BOX, it is now possible to compare the two approaches numerically. The results are shown in Fig. 10. Since the normalization of the MATCHIG prediction is still effectively of LO, we have normalized all distributions to their respective total cross sections in order to emphasize the shapes of the distributions. One observes that when both the MATCHIG (black) and POWHEG (red) predictions are matched to the PYTHIA parton shower, there is very little difference, even at low p _T and large Δϕ of the top-Higgs pair. Only at large p _T and small Δϕ the differences become sizable, which can be attributed to the fact that MATCHIG includes only one of the four classes of real emission processes, while our POWHEG prediction includes also the quark-initiated real emission processes. Let us emphasize again that while the spectra are already quite well described with MATCHIG, their normalization is only accurate to LO and not NLO as in POWHEG.

Fig. 10

Distributions in transverse momentum p _T (top left) and rapidity y (top right) of the charged Higgs boson, p _T (center left) and y (center right) of the top quark, as well as p _T (bottom left) and azimuthal opening angle Δϕ (bottom right) of the tH ⁻ system produced at the LHC with $\sqrt{S}=7~\mathrm{TeV}$. We compare the tree-level predictions matched to PYTHIA using MATCHIG (black) with our NLO calculation matched to PYTHIA (red) and HERWIG (blue) using POWHEG. All distributions have been normalized to the respective total cross sections (Color figure online)

4.7 Comparison with MC@NLO

In a recent publication, two of us and a number of other authors have matched a NLO calculation performed with the FKS subtraction formalism to the HERWIG PS with the MC@NLO method [20]. It is therefore mandatory that we compare in this paper this previous work with our new POWHEG implementation, which we do in Fig. 11. Note that here we employ a value of tanβ=30 as in the MC@NLO publication. In both calculations, we use the HERWIG PS in order to emphasize possible differences in the matching methods and not those in the parton shower. We also normalize the differential cross sections again to the total cross section for a better comparison of the shapes of the distributions.

Fig. 11

Distributions in transverse momentum p _T (top left) and rapidity y (top right) of the charged Higgs boson, p _T (center left) and y (center right) of the top quark, as well as p _T (bottom left) and azimuthal opening angle Δϕ (bottom right) of the tH ⁻ system produced at the LHC with $\sqrt{S}=14~\mathrm{TeV}$. We compare the NLO predictions with matching to the HERWIG parton showers using POWHEG (red) and MC@NLO (black) in the Type-II 2HDM with tanβ=30 and m _H =300 GeV. All distributions have been normalized to the respective total cross sections (Color figure online)

As in the other comparisons, the rapidity distributions of the charged Higgs boson (top right) and the top quark (center right) show little variation, confirming the consistency of the two calculations. However, the corresponding p _T -spectra (top and center left) are slightly harder with the MC@NLO matching than in POWHEG. This behavior is known from other processes [24, 44]. It is less pronounced in the p _T -distribution of the top-Higgs pair, shown on a logarithmic scale (bottom left). Since we are using the HERWIG PS, the rise at small azimuthal angle Δϕ (bottom right) is not very strong with MC@NLO and only slightly more so with POWHEG. In total, all of these differences are similarly small in the production of a top quark with a W-boson [24] and with a charged Higgs boson at the LHC.

4.8 Diagram removal, diagram subtraction, and no subtraction

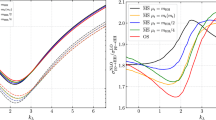
If the charged Higgs boson was lighter than the top quark, it would dominantly be created in top-pair production and the decay of an (anti-)top quark into it. As discussed above, one must then find a suitable definition to separate this process from the associated top-Higgs production discussed in this paper. In addition to the Diagram Removal (DR) and Diagram Subtraction (DS) methods discussed above, we introduce here also the option of not removing or subtracting anything from the associated production, but simply retaining the total production cross section, which then allows for the removal of fully simulated events near the resonance region and replacing them with events obtained, e.g., with a full NLO implementation of $t\bar{t}$ production. The results are shown in Fig. 12.

Fig. 12

Distributions in transverse momentum p _T (top left) and rapidity y (top right) of the charged Higgs boson, p _T (center left) and y (center right) of the top quark, as well as p _T (bottom left) and azimuthal opening angle Δϕ (bottom right) of the tH ⁻ system produced at the LHC with $\sqrt{S}=14~\mathrm{TeV}$. We compare the NLO predictions matched to the HERWIG parton shower using POWHEG with Diagram Removal (red), Diagram Subtraction (black), and without removing or subtracting anything (blue) in the Type-II 2HDM with tanβ=30 and m _H =100 GeV. All distributions have been normalized to the respective total cross sections (Color figure online)

The rapidity distributions of the charged Higgs boson (top right) and top quark (center right) show again little sensitivity to the different theoretical approaches. However, the p _T -distribution of the charged Higgs boson (top left) is somewhat softer and the one of the top quark (center left) considerably harder without removal or subtraction, as the difference describes the distributions of the lighter decay product and the heavier decaying particle, respectively. The p _T -distribution of the top-Higgs pair (bottom left) is significantly harder (note again the logarithmic scale) and its maximum moves from p _T = 20 to 70 GeV, indicating that the transverse momentum of the pair is balanced by a hard object, i.e. the fast additional b-quark jet, in the other hemisphere. This also allows the top-Higgs pair to move closer together in azimuthal angle (bottom right).

The theoretical pros and cons and the numerical differences of Diagram Removal and Diagram Subtraction have been discussed extensively above and also elsewhere [20]. It is clear from Fig. 12 that the numerical difference of DR vs. DS is much less pronounced than the difference of both with respect to no removal or subtraction at all. We emphasize that the total cross section is continuous across the m _H =m _t threshold in all three schemes (see also Ref. [27]).

The differences of POWHEG and MC@NLO are small for m _H <m _t in both the DR and DS schemes, as can be seen when comparing Figs. 13 and 14. This coincides nicely with our observation above that these differences should be as small as in the associated production of W-bosons and top quarks [24].

Fig. 13

Same as Fig. 11, but for a light charged Higgs boson of mass m _H =100 GeV and using the DR method (Color figure online)

Fig. 14

Same as Fig. 11, but for a light charged Higgs boson of mass m _H =100 GeV and using the DS method (Color figure online)

5 Conclusion

In this paper, we presented a new NLO calculation of the associated production of charged Higgs bosons and top quarks at hadron colliders using the Catani–Seymour dipole subtraction formalism and matched it to parton showers with the POWHEG method. We discussed the different types of 2HDM as well as the corresponding current experimental constraints and provided, for specific benchmark values of the charged Higgs-boson mass and the ratio of the two Higgs VEVs tanβ, the central values, scale, and PDF uncertainties of the total cross sections at the Tevatron and LHC in tabular form for future reference. As expected, the scale uncertainty was considerably reduced from up to ±100 % at LO to less than ±15 % at NLO. However, the PDF uncertainty, estimated with the CT10 set of global analyses, remained quite substantial, in particular at the Tevatron, where high momentum fractions of the gluons and b-quarks in the protons and antiprotons are probed.

For the differential cross sections, we established good numerical agreement of our full NLO calculation with previous calculations. We then performed detailed comparisons of our new POWHEG implementation with the purely perturbative result, with PYTHIA or HERWIG parton showers, with a LO calculation matched to the PYTHIA parton shower using MATCHIG, and with a NLO calculation matched to the HERWIG parton shower using MC@NLO.

While the transverse-momentum distributions and the relatively central rapidity distributions of the charged Higgs boson and top quark individually showed little sensitivity to the existence and type of parton showers, the transverse-momentum distribution of the top-Higgs pair depended quite strongly on the different theoretical approaches as expected. This was also true for the distribution in the azimuthal angle of the top-Higgs pair. For scenarios in which the charged Higgs boson is lighter than the top quark, we implemented in POWHEG in addition to the previously proposed Diagram Removal and Diagram Subtraction schemes the possibility to retain the full cross section and replace the simulated events in the resonance region with a full NLO Monte Carlo for top-quark pair production.

It will now be very interesting to observe the impact of our work on the experimental search for charged Higgs bosons. The numerical code and technical support is, of course, available from the authors.