1 Geometry, interactions, and emergent behaviour in complex systems

The role of self-organised criticality (SOC) has been increasingly recognised in various complex systems, from brain functioning to social and geophysical phenomena [1] as a mechanism enabling robust functioning and emergent properties at a larger scale that reside on collective dynamic behaviours; for a recent review of general features of complex systems, see [2,3,4,5]. These are nonlinear dynamical systems repeatedly driven by environmental forces that self-organise towards an attractor with a stationary state characterised by avalanches, long-range correlations, and scale invariance. These stationary out-of-equilibrium critical states enable the system’s response to driving forces at all scales, thus providing robust functioning and stability. Critical dynamics out of equilibrium is currently an active research field. Two challenging issues are the impact of a dynamically changing environment and underlying complex geometry [1].

Besides numerical simulations, the renormalisation-group (RG) theory with scaling concepts and methodologies based on quantum and statistical field theory for equilibrium phase transitions are extended to non-equilibrium dynamics and SOC; see recent reviews [6, 7] and references there. The described models with SOC behaviours [7] demonstrate the field-theory methodologies as powerful tools to characterise collective fluctuations in stationary states of complex systems that are driven out of equilibrium. Beyond external and internal noise terms, this methodology properly considers the dynamical environment, which can critically impact the intrinsic SOC dynamics [8]. Another promising way to understand the role of the complex systems’ coupling to the environment can be built by the use of quantum formalism; a representative example is the study of adaptive complex systems [9], where the formal theory leads to a requirement that the emergent “quantum” potential needs to be effectively balanced by the environmental coupling. It should be noted that the RG theory is based on continuous field models. For example, studies [8, 10, 11] of SOC are based on continuous versions of the original discrete sandpile automata (SPA) model, incorporating its essential intrinsic anisotropy of diffusion on otherwise homogeneous space. However, considering more complex underlying geometries [12] within the RG theory [13, 14], in particular, those enabling geometry-embedded higher order interactions [15,16,17,18], remains a challenging problem. Here, we aim to highlight the interplay of higher order geometry and emergent SOC behaviour in complex systems.

Three types of underlying geometry that can shape the collective dynamics and SOC can be recognised as networks with fixed, co-evolving, and temporal structures. The dynamical units associated with the network’s nodes interact via the network-provided connections of different orders. As explained below, this separation is conditional in real-world systems, relating the time-scale of the network’s evolution vs the dynamics of interacting units on it.

Fixed geometry network substrates extend the idea of physics models, e.g., spins at sites of a regular 2D- or 3D-lattice to a more complex structure described by the network or simplical complex measures; see more details below. The dynamical units associated with the network’s nodes and interacting through the local or nonlocal structure may have identical dynamics, i.e., as phase oscillators [19, 20] or spins on simplicial complexes [21]; another option often used in the agent-based modelling is that each unit has individual dynamics and parameters characteristic of each agent associated with a given node [22]. The temporal evolution of each unit is subject to interactions (of different orders), driving fields, and constraints by the surrounding geometry. It can be described by a set of update rules, as in the case of cellular automata or spin kinetics or by solving differential equations with identical, for example, in the case of phase oscillators, or individual forms and parameters, as in the case of agent-based models.

Co-evolving networks represent structural patterns that appear through the dynamics of interacting units and develop over time. They can be visualised as mathematical graphs, similar to the networks of users mentioned above, or by bipartite graphs, for example, in blog data, where indirect interactions among users (as one partition) are effectuated over another partition as posted subjects of communications. In this case, graph mapping enables advanced graph theory methods to quantitatively study the structure of these dynamical patterns and how they change over time. However, the co-evolutionary mechanisms are more subtle, involving collective dynamics with SOC signatures; see, for example, [22] and references there. The geometry emerges from the dynamics of interacting units, meanwhile, the currently existing structure facilitates the diffusion (of information, knowledge, emotion) to spread further. Unsurprisingly, in cooperative users’ activities, such as collective knowledge building [23, 24], some stable network structures emerge in the other partition. For example, they represent the network of emergent knowledge (of subjects) in the case of knowledge-creation dynamics in Mathematics data or a stable “social graph” emerges among users of Ubuntu Chats that persists over the years, satisfying the social ’weak ties’ hypothesis; see [25] and references there. Evolutionary processes, where the respective time-scale is system characteristic, comprise one of the fundamental features of complexity [3]. In this context, the network mappings of the brain represent different types of functional patterns rather than a fixed structure graph; for a recent survey, see [26]. A more detailed description of the human connectome is given in Sect. 1.1.

Time-varying geometries represent another category of structures compared to the above-discussed cases; they exhibit partial or global reconstruction, which is virtually independent of the processes of dynamical units at their nodes but occurs at the time-scale of these processes. The structural changes cause nonlocal effects that can be examined directly in real and phase space or indirectly by their impact on the dynamics. This issue deserves more attention, particularly in higher order networks. In analogy to methods of programmable self-assembly of materials [27], local reconstruction due to, for example, built-in defects in the simplicial complexes architecture [28] can cause a collapse of hierarchical structure at a larger scale.

This perspective paper focuses on the interplay of higher order geometry features and SOC dynamics. In this context, the time-scale of the structural evolution is particularly relevant, given the critical requirement of the time-scale separation between the internal dynamics and driving for the occurrence of SOC. In the following, we describe the concepts of SOC and higher order geometry with simplicial complexes and survey current research trends. As a representative example, a more detailed study is presented considering spin-reversal dynamics on a structure of geometrically assembled triangles, where the competing pairwise and triangle-embedded interactions lead to emergent SOC behaviours. The paper ends with a brief discussion with a summary of open questions and research directions.

1.1 Collective dynamics and self-organised criticality in complex systems

As stated above, the term SOC refers to out-of-equilibrium critical behaviour occurring in a steady state near an attractor of intrinsic nonlinear dynamics without apparent phase transition. For a more recent review, see [29,30,31] and references there. Such attractors are reached by the system’s response to repeated driving by external forces when the driving rate is slow compared to the time-scales of the intrinsic dynamics. Self-organised dynamics possess characteristic self-similarity manifested in avalanching behaviours, temporal correlations, and scaling, adequately described by theoretical concepts [8] and numerical methods [32].

Ever since Bak and coworkers introduced it and defined the paradigmatic SPA model [33, 34], the idea of self-organised dynamics was utilised to understand mechanisms underlying complexity [1, 35, 36]. Signatures of SOC are increasingly found in many complex systems across the scales in physics [30]—from nano assemblies to rainfalls [37], geophysics and solar activity [38], and biology [39, 40]. Furthermore, collective dynamics based on social cooperation represents a specific type of SOC behaviour evidenced by empirical data analysis, for example, in human activity devoted to collective knowledge creation [24] but also in schooling fish [41]. Further examples include bio-social epidemic processes [42, 43], socio-technological [44, 45], and socio-economical systems [46]. In addition to characteristic avalanches superimposed to cyclical trends [47], monitoring changes in the co-evolving network geometry serves as a “blueprint” of complexity in social dynamics [25].

Understanding brain functions and mechanisms of brain disorders in neurology [48,49,50] represent the most challenging issues in the science of complexity and their applications, in particular, in the era of artificial intelligence [51]. In this context, network mapping [52] and the complexity of the brain dynamics as an SOC system of firing neurons are central questions both in theoretical and experimental research [53,54,55]. There is increasing experimental evidence of SOC signatures in brain dynamics [55] on the one hand and higher order brain functional connectivity across spatiotemporal scales [56] on the other. Theoretical studies aim to reveal the background mechanisms and role of SOC in the brain’s evolutionary development towards robustness and functional efficiency [54]. Recent studies in references [57,58,59,60] and others have revealed the structure of higher order connections in the human connectome, providing a new perspective for investigating their impact on brain dynamics and SOC. The whole brain computational connectomics [61] and imaging techniques monitoring different brain functions, for example, attention [62] and cognition [63] or pain processing [64], reveal multiple scales interplay between integration and segregation processes that involve many distinct brain regions and variable communications among them. Therefore, information about the architecture of these distributed neuronal processes can be gained by modelling brain dynamics and identifying temporal variations of local order in the corresponding brain networks; see a recent survey in [65]. Among phenomenological models, synchronisation processes of Kuramoto phase oscillators are often studied on brain networks. In this picture, “the human brain is a complex system comprising subregions that dynamically exchange information between its various parts through synchronisation” persisting in a natural metastable at the edge of synchrony [66]. These studies gain some importance in quantifying brain dynamics in various psychiatric illnesses and brain disorders implicating altered metastability [66, 67]. Mathematically, it was shown[68] that the structure of the brain network does not permit a stable full synchronisation. Potential mechanisms for maintaining partial synchrony through negative pairwise couplings, characterised by co-evolving clusters of weakly synchronised nodes, are demonstrated in the human connectome, as illustrated in Fig. 1; the core network, which consists of links forming simplexes of all sizes attached to eight brain hubs, was considered [69].

Fig. 1
figure 1

The pattern of phase evolution at negative pairwise coupling with partially synchronised groups of nodes (brain regions) in the core network of the human connectome; see text. Each line marked with a different colour represents the evolutionary path of an individual oscillator. Data are from [69]

Full size image

1.2 Higher order connectivity and dynamics on simplicial complexes

In networks mapping functional connections in many complex systems, hidden geometry of higher order relations occurs [70]. They can be revealed by advanced mathematical techniques beyond standard graph theory [71], such as the algebraic topology of graphs [72]. They are described by aggregates of simplexes (simplicial complexes) [73] and multigraphs. For example, in social graphs [17], Human connectome [57,58,59,60], etc., such structures naturally evolved with the self-organised dynamics. Meanwhile, in materials design [74], such complex structures often emerge from self-assembly processes, particularly those based on preformatted building blocks, e.g., groups of nanoparticles [75]. Such higher order geometries provide a basis for multiple interactions that play their role in the dynamics and determine the system’s collective behaviours. Therefore, studies of the impact of higher order geometries on the dynamics are vital for understanding the mechanisms underlying dynamic critical behaviours and can be used to estimate the predictability limits [76] in the system’s evolution. The interplay of the dynamics and higher order structures can be also utilised to design new methodologies of network control [77].

Recently, attention has been devoted to the dynamics of units associated with the nodes in simplicial complexes with a fixed structure [15]. Below, we describe some key features of such geometries and embedded higher order interactions in the case of spin-reversal dynamics and synchronisation among phase oscillators. For this type of study, an underlying simplicial complex is grown, i.e., using a model; depending on the research aims, several generative models of simplicial complexes with different emergent structures are known in the literature [28, 78, 80, 81]. Alternatively, a real-world network, e.g., human connectome [69], can be considered, and methods of Q-analysis [82] applied to determine its detailed architecture [57].

Growth of simplicial complexes Here, we briefly describe the model introduced in [78], where the rules for the attachment of simplexes are motivated by cooperative self-assembly of nanostructured materials. For demonstration purposes, an online applet for the simplexes self-assembly with varied parameters is available [79]. Specifically, starting with a single simplex of the order \(q_{\max }\), at each growth step \(t_g\), a new simplex is added, such that it shares one of its faces of the order \(q=0,1\cdots q_{\max }-1\), i.e., a node, an edge, triangle, etc., with an existing simplex, randomly selected in the structure; the attaching probability is given by

$$\begin{aligned} P(q_{\max },q;t_g)= \frac{c_q(t_g)e^{-\nu (q_{\max }-q)}}{\sum _{q=0}^{q_{\max }}c_q(t_g)e^{-\nu (q_{\max }-q)}}, \end{aligned}$$
(1)

where \(c_q(t_g)\) stands for the number of geometrically compatible locations that are found in the existing structure at the growth step \(t_g\). The parameter \(\nu \) represents the chemical affinity of the existing structure towards adding of \(q_{\max }-q\) new nodes. Thus, simplicial complexes with a sparse architecture are grown when \(\nu <0\), representing a “tree of cliques” that predominantly share a single node, whereas the structure becomes increasingly more compact with increasing \(\nu >0\), where sharing larger faces is more probable. When \(\nu =0\), the process is controlled by strictly geometrical rules. We note that the spectral dimension of the Laplacian operator associated with the adjacency matrix of the underlying graph, i.e., 1-skeleton of a simplicial complex is another measure of its architecture that determines the nature of collective dynamics on it [83, 84]. The graphs of complexes grown at different chemical affinity are characterised by the spectral dimension that varies from the random-tree dimension at \(\nu <0\) through \(d_s\sim 2\) at \(\nu =0\), and continuously increasing with \(\nu >0\) and the dimension of simplexes; see detailed analysis in [85]. The size of the newly added simplex is fixed a priori or drawn from a given size distribution; see the original reference [78] for representative examples of complexes grown at different chemical affinities, and their higher order structures determined by Q-analysis. In self-assembly, the distances between building simplexes are equal to zero; consequently, these simplicial complexes are 1-hyperbolic [86]; furthermore, the size of the largest clique determines the dimension of the simplicial complex [78]. An example with self-assembled triangles is shown in Fig. 2, exhibiting several branches of triangles attached to each other through shared nodes and edges. A representative structure of the assembled triangles based on geometrical attachment rules is used in Sect. 2.

Fig. 2
figure 2

Close-up view of the simplicial complex of triangles self-assembled under chemical affinity and geometric compatibility rules in (1) with \(\nu =5\); different colours indicate mesoscopic communities, interconnected through hub nodes

Full size image

In the remaining part of this section, we give an insight into how the structure of simplicial complexes yields the geometry-embedded interactions in the more general cases and how they are taken into account in numerical simulations of two fundamental processes leading to collective phenomena: phase synchronisation and spin dynamics.

Spin dynamics on simplicial complexes We consider the case where Ising spin \(S_i=\pm 1\) is attached to each node, and interactions among spins enabled by the simplexes and their faces of different sizes \(k^\prime =2, 3 \cdots q_{\max }+1\), up to the order \(q_{\max }\) of the simplicial complex in question. Given the pairwise adjacency matrix, as is usually the case with real-world network data, all simplexes and their faces can be identified by Q-analysis, as stated above. Alternatively, in the self-assembly model described above, by monitoring all added simplexes, we keep track of the identity of the nodes that make them. In this way, we can produce a unique list of simplexes of all sizes \(k^\prime \); then, we can write the Hamiltonian with all possible geometry-embedded interactions in that simplicial complex as follows [1]:

$$\begin{aligned} {\mathcal {H}}= & {} -\sum _{k^{\prime }=2}^k\sum _{(i_1,\ldots i_{k^{\prime }})\in {\mathcal {L}}_{k^{\prime }}}J_{i_1,i_2,\ldots i_{k^{\prime }}}S_{i_1}S_{i_2}\cdots S_{i_{k^{\prime }}}\nonumber \\{} & {} -h\sum _iS_i \ . \end{aligned}$$
(2)

Here, h is the external magnetic field and \(J_{i_1,i_2,\ldots i_{k^{\prime }}}\) stands for the interaction tensor of the order \(k^{\prime }\), whose elements differ from zero when the indexes \((i_1,i_2,\ldots i_{k^{\prime }})\) match one of the simplexes in the list \({\mathcal {L}}_{k^{\prime }}\) of simplexes of the size \(k^\prime \), and zero otherwise. For example, \(J_{i_1,i_2}\) is nonzero when the indexes correspond to the nonzero elements of the network’s adjacency matrix; similarly, the nonzero values of \(J_{i_1,i_2,j_3}\) correspond to all triangles in the structure, and so on. As usual in studies of spin systems with pairwise interactions, the sign and strength of interactions and potential disorder, as well as the presence of given higher order interactions, are determined considering the physics of the problem and the study objectives. In Sect. 2, we present a detailed analysis of the field-driven spin-reversal dynamics on a simplicial complex assembled of triangles.

Synchronisation on simplicial complexes In most studied Kuramoto model that we present here, 1-dimensional phase oscillators \(\theta _i\) are associated with the nodes \(i=1,2 \cdots N\) of the simplicial complex, and the geometry-embedded interactions are provided by simplexes of different orders \(q=0,1,\cdots q_{\max }\); see review in [15]. For the synchronisation of topological signals associated with faces of simplexes, see recent work in [88] and references there. Then, the evolution of phases of all nodes is obtained by solving the differential equations interconnected via interaction tensors, as described below. For this purpose, for each interaction order q, we prepare a unique list \({\mathcal {L}}_i^{q}\) of the simplexes of the order q that contain the considered node i. Then, the generalised equation of motion can be written as

$$\begin{aligned} \frac{\textrm{d}\theta _i}{\textrm{d}t}= & {} \omega _i -\sum _{q=1}^{q_{\max }} \frac{K_q}{qk_i^{(q)}} \sum _{(j_1,j_2\cdots j_q)\in {\mathcal {L}}_q^{i}}\nonumber \\{} & {} \times B_{i,j_1,j_2\cdots j_q}\sin \left( q\theta _i-\sum _{m=1}^q\theta _{j_m}\right) , \ \end{aligned}$$
(3)

where \(\omega _i\) is the node’s internal frequency and the interaction tensor \(B_{i,j_1,j_2\cdots j_q}=1\) when the set of indexes \((i,j_1,j_2\cdots j_q)\) matches one of the entries in the list \({\mathcal {L}}_i^{q}\) of simplexes of the order q, and zero otherwise; the number of such simplexes is the node’s i generalised degree \(k_q^{(i)}\). Note that the coupling function in (3) satisfies general conditions for the diffusive-like, non-invasive, and natural coupling [15]. The corresponding interaction constants \(K_q\) are varied to explore the system’s transition to the synchronised states; see for example, [89, 90], for the case of high-dimensional simplicial complexes with the pairwise and triangle-embedded interactions. It has been recognised that higher order interactions cause new collective dynamics phenomena; for example, triangle-embedded interactions induce the broadening of the hysteresis loop and an abrupt desynchronisation transition [19]. Studies [84, 90] have demonstrated the relevance of the architecture of simplicial complexes to synchronisation, quantified by varied spectral dimensions. Moreover, spectral analysis and eigenvector localisation have recently been explored to predict cluster synchronisation in theoretical [20] and experimental studies [91, 92]. We note that, in systems with coupled oscillators, the occurrence of complete synchrony and SOC states are two alternative behaviours. A potential phase transition between these phases can occur when the coupling and driving parameters are varied, as demonstrated in [93] for the system of integrate-and-fire oscillators under nonlinear driving on a compact lattice. In the present context, the network structures that do not support a stable synchronised state, for example, those with the spectral dimension \(d_s\gtrsim 2\), are candidates for self-organised cluster synchronisation. The self-organising properties of synchronisation and the role of higher order interactions in these processes remain for future investigation.

2 Hysteresis-loop self-organised criticality with triangle-embedded interactions

As mentioned above, this section presents a more detailed analysis of a representative example of spin-reversal dynamics, demonstrating the emergence of SOC due to the complex geometry of the underlying simplicial complex with higher order interactions. Using the self-assembly model described above, we grow a simplicial complex of triangles, taking \(\nu =0\). Hence, the probability in Eq. (1) of sharing faces of the order \(q=0\) (nodes) and \(q=1\) (edges) is governed by strictly geometric compatibility rules. Specifically, about 21% of edges and 33% of single-node faces are shared among two or more triangles in this type of structure. Moreover, as shown in [87], the underlying graph exhibits the assortative nodes’ correlations and broad distributions of the generalised degree (the number of edges and triangles per node, which behave statistically similar in this case). The degree distribution shows a power-law decay with an exponent \(\gamma \ge 3\) for a segment of intermediate degrees, excluding the nodes with extensive connectivity (hubs). These structures have the spectral dimension [85] close to \(d_s\simeq 2.1\). During the assembly process, we enumerate edges and triangles listing the nodes that make them; such lists comprise the corresponding adjacency tensors \({\mathcal {L}}_2\) and \({\mathcal {L}}_3\) for the geometry-embedded interactions among spins indicated in Eq. (2).

The process of spin-reversal is driven by the slow ramping of the magnetic field h along the hysteresis loop. The spins are situated at nodes of a large complex of self-assembled triangles; cf. Fig. 2. Therefore, we have two types of geometry-embedded interactions in the Hamiltonian (2), specifically

$$\begin{aligned} {\mathcal {H}}= & {} (\kappa -1)\sum _{(i,j)\in {\mathcal {L}}_2}J_{ij}S_iS_j -\kappa \sum _{(i,j,k)\in {\mathcal {L}}_3}J_{ijk}S_iS_jS_k\nonumber \\{} & {} - h\sum _iS_i \ , \end{aligned}$$
(4)

where \({\mathcal {L}}_2\) and \({\mathcal {L}}_3\) stand for unique lists of the network’s edges and triangles, respectively. For this study, we set \(J_{ij}=-J_2\) fixing the antiferromagnetic pairwise interactions among all implicated pairs of spins, and \(J_{ijk}=J_3\); a parameter \(\kappa \in [0,1]\) is added to balance their respective contributions. As shown below, we can differentiate the ferromagnetic and \(J_{ijk}=-J_3\) for antiferromagnetic triangle-embedded interactions; see also [87]. As usual, the dimensionless units can apply; thus, we set \(J_2=1\) and \(J_3=1\). Moreover, the magnetisation (in Bohr magnetons \(\mu _B\)) is determined as \(M=(N_+ -N_-)/N \in [-1,1]\) by the balance of the respective up and down oriented spins \(N_+\) and \(N_-\) with respect to their number N. The external field (in the units \(\mu _B\)), \(h\in [-h_{\max },+h_{\max }]\), where \(h_{\max }\) is related to the maximum number of neighbours of the vertices, is varied in a quasistatic manner, as explained below.

Starting with a uniform state of all spins \(\{S_i=-1\}\) and \(h=-h_{\max }\), the spin-reversal process is driven by slow field ramping \(h\rightarrow h+\delta h\) along an ascending branch of the hysteresis and then reversing the field to close the loop. As it is a widely accepted approach in the study of Barkhausen noise in disordered magnetic systems a zero-temperature dynamics is applied; see, for example, [94] and references therein. In particular, the spin \(S_i\) at the node i flips to align along the external field which can balance the local field due to the neighbouring spins, i.e., when \(h_i^\textrm{loc}S_i <0\). Here, \(h_i^\textrm{loc}= (\kappa -1)\sum _{j\in {\mathcal {L}}_2^i}J_{ij}S_j -\kappa \sum _{(j,k)\in {\mathcal {L}}_3^i}J_{ijk}S_jS_k- h\) is the local field acting on the spin at node i at a current value of the external field h and the summation indicates the corresponding subsets of the edges \({\mathcal {L}}_2^i\) and triangles \({\mathcal {L}}_3^i\) that contain the node i. Thus, the spin-flip at node i causes changes in the local fields of its neighbours, which can satisfy the condition to flip, and so on, resulting in an avalanche. The avalanche stops when no more spins satisfy the above condition to flip. The boundary between the domain of flipped and unflipped spins defines the position of the domain wall at a given value of the external field. When the avalanche stops, the external field is changed again by \(\delta h\) (adiabatic driving). We note that spin frustration [95] with the antiferromagnetic pairwise interaction among spins on a triangle prevents all three spin pairs from simultaneously ordering with the field; thus, some spins may flip back, even though the above condition is fulfilled. To avoid frequent back-and-forth flips of the same spin at a given field value, flips with a probability \(p\lesssim 1\) are adopted. Moreover, without the magnetic disorder, the field ramping parameter \(\delta h=1\) is the lowest value that may move the domain wall [1, 87].

In the simulations, a time step t consists of a parallel update of all spins in the network. At each time step during the spin-activity avalanches, we sample the current value of the external field h, the total number of flipped spins \(n_t\), and the number of spins ordered with the field (unnormalised magnetisation) \(M_t=n_t^{+}-n_t^{-}\). Here, our focus is on the distributions of avalanches. The results are shown in Fig. 3 for three representative values of the parameter \(\kappa \), in particular, \(\kappa =0\), describing purely antiferromagnetic pairwise \(-J_2\) interactions, \(\kappa =1\), corresponding to the case where only triangle-embedded interactions \(J_3\) are present, and the case \(\kappa =0.5\), where these two interaction types are well balanced. (See Ref. [87] for the analysis of hysteresis-loop shape and temporal correlations of the signals \(\{n_t\}\).)

Fig. 3
figure 3

Top panels: cumulative distributions of the avalanche size (black circles) and duration (red squares) averaged over the entire hysteresis loop for \(\kappa =\) 0.0, 0.5, and 1.0, as indicated. For the case \(\kappa =0.5\), the distributions for \(J_3<0\) are shown; see text for a detailed description of fits. Lower panels: Hysteresis loops corresponding to the values of \(\kappa \) in the panel above; forward/backward branch shown in black/red; full and dotted lines for \(\kappa =0.5\) and \(\kappa =1\) are for \(J_3>0\) and \(J_3<0\), respectively

Full size image

As this figure shows, the spin-activity avalanches appear in different sizes and durations that can be described by a cumulative distribution function having a power-law segment and an exponential cut-off

$$\begin{aligned} P_c(X)=AX^{-\tau _X-1}e^{-X/X_0}, \end{aligned}$$
(5)

where X stands for the size s (the number of spin flips) and the duration T (measured by the number of time steps from the field rump till the activity stops). In the critical dynamics where the scaling exists, the corresponding scaling exponents obey the relation \(\gamma _{sT}=\frac{\tau _T-1}{\tau _s-1}\), where \(\gamma _{sT}\) scales the average size of the avalanches of a given duration T, i.e., \(<s>_T\sim T^{\gamma _{sT}}\). In Fig. 3, we show the results for the distributions of size and duration of the spin-activity avalanches for the case of purely pairwise antiferromagnetic coupling, \(\kappa =0\), purely triangular ferromagnetic coupling, \(\kappa =1\), and the intermediate case with balanced pairwise and triangular interactions, \(\kappa =0.5\). The hysteresis loops showing the magnetisation vs external field are given in the corresponding lower panel. As Fig. 3 shows, the distributions of spin-activity avalanches are exhibiting a power-law decay with an exponential cut-off according to Eq. (5); however, two sets of scaling exponents apply. In particular, when \(\kappa =0\), corresponding to strictly pairwise antiferromagnetic interactions, large avalanches decay with the exponents \(\tau _s-1=0.526\pm 0.018\) and \(\tau _T-1=0.993\pm 0.023\), close to the mean-field SOC [96]. Whereas, the exponents found by fitting the corresponding curves in the case of \(\kappa =1\) are lower, \(\tau _s-1=0.326\pm 0.013\) and \(\tau _T-1=0.49\pm 0.021\). We note that these exponents are numerically close to the ones in the universality class of directed percolation cellular automata [97]. Other options are discussed below.

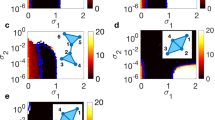
To demonstrate the multifractal properties of these magnetisation reversal processes, we exploit the underlying scale invariance of the fluctuation function \(F_r(n)\) as a function of the time segment n and determine the spectrum of generalised Hurst exponents \(H_r\). Here, we analyse the time series of the number of spin flips \(\{n_t\}\) along the entire hysteresis loop. \(T_{\max }\) is the time-series length. In particular, following the procedure for the de-trended multifractal analysis described in [98, 99], the profile \(Y(i) =\sum _{t=1}^i(n_t-\langle n_t\rangle ) \) of the considered time series is determined. The profile is then divided into \(2N_s=2\textrm{int}(T_{\max }/n)\) non-overlapping segments of the length n, starting from the beginning of the series, and then, the process is repeated starting from the end. At each segment \(\mu =1,2\cdots N_s\), the local trend \(y_\mu (i)\) is determined, and the standard deviation around it is computed as \(F(\mu ,n) =\left\{ \frac{1}{n}\sum _{i=1}^n[Y((\mu -1)n+i)-y_\mu (i)]^2\right\} ^{1/2} \), and similarly, \(F(\mu ,n) =\{\frac{1}{n}\sum _{i=1}^n[Y(N-(\mu -N_s)n+i)-y_\mu (i)]^2\}^{1/2}\) for \(\mu =N_s+1,\cdots 2N_s\). Then, the rth-order fluctuation function for the segment of the length n is obtained and averaged over all such segments as

$$\begin{aligned} F_{r}(n)=\left\{ \frac{1}{2N_s}\sum _{\mu =1}^{2N_s} \left[ F^2(\mu ,n)\right] ^{ {r}/2}\right\} ^{1/ {r}} \sim n^{H_{r}} . \end{aligned}$$
(6)

For varying the parameter \(r\in [-4.5,4.5]\), we explore the scale-invariant parts of the fluctuation function \(F_r(n)\) against n, where the segment length is varied in the range \(n\in [2,\textrm{int}(T_{\max }/4)]\), cf. Fig. 4. In this way, the segments of the signal representing small and large fluctuations, respectively, are enhanced in different ways to maintain the self-similarity of the whole time series. Here, a generalised Hurst exponent \(H_ {r}\) depends on the amplification factor r, suggesting that the small fluctuations (amplified when \( r<0\)) along the signal have different scaling properties than the large fluctuations (\(r>0\)). Having the spectrum of the generalised Hurst exponents \(H_r\), we determine other multifractal measures; see, for example, reference [98]. Specifically, we obtain \(\tau _r=rH_r-1\), which is related to the standard (box probability) measure, and the singularity spectrum \(\Psi (\alpha )=r\alpha -\tau _r\), where \(\alpha = \textrm{d}\tau /\textrm{d}r\); in this context, different \(\alpha \) values indicate variations in the power-law singularities along the considered time series. In the inset to Fig. 4, we show how the shape of the singularity spectrum changes when the balance between antiferromagnetic pairwise and triangle-embedded interactions is varied via the parameter \(\kappa \).

Fig. 4
figure 4

The fluctuation function \(F_r(n)\) vs time interval length n for \(r\in [-4.5,+4.5]\) (every second line is shown for better vision), for the case \(\kappa =0.5\) of balanced antiferromagnetic pairwise and ferromagnetic triangle-based interactions, using the whole loop signal. Inset: the singularity spectrum \(\Psi (\alpha )\) vs \(\alpha \) for three cases the parameter \(\kappa \), as indicated in the legend

Full size image

3 Discussion and future directions

In this paper, we have given a survey of recent research activities aiming at understanding the role of higher order connectivity in functional complex systems. Our leading idea concerns the intricate interdependences of the higher order structures and the out-of-equilibrium self-organised critical dynamics as a plausible mechanism for emerging new properties at a larger scale, the central paradigm of physical complexity. Having briefly described both issues, we have mentioned an increasing number of studies that evidence the occurrence of higher order (hidden) structures and signatures of SOC in many complex systems across the scales. We have highlighted the most striking example, mapping the brain structure and its dynamics, which has considerable influence on the science of complexity theory and practice, as well as the applications in artificial intelligence. Furthermore, we highlighted the relevance of different time-scales in the light of the structure–dynamics interdependences. In this context, the time-scale separation between the intrinsic dynamics and driving is required for the nonlinear systems to evolve towards SOC attractors. In addition, we stress the relevance of the time-scale of changes in the underlying geometry evolution as compared to the SOC dynamics; they can be characterised by the appropriate graph or simplicial complex measures. In this regard, we differentiate two limiting cases, particularly structures co-evolving with the intrinsic dynamics and the quenched structure, whose evolution time exceeds both time-scales relevant to the SOC. We referred to several pertinent examples of both groups of systems studied in the literature. Another interesting, much less understood case concerns the underlying geometry reconstruction at an intermediate time-scale between the intrinsic dynamics and driving. It can occur virtually independent from the dynamics of the actual units comprising the system, for example, reconstructions via built-in temporal defects, or can have a hidden connection with the driving forces. We have briefly described two currently most studied dynamic models—synchronisation of phase oscillators and zero-temperature spin dynamics on simplicial complexes of a fixed architecture, which provides geometry-embedded higher order interactions. A more detailed study of the spin-reversal dynamics with the competing geometry-embedded interactions leading to SOC behaviour is given as an illustrative example.

In the studied example with Ising spins on an assembly of triangles, we have shown that the spin-reversal zero-temperature dynamics with competing interactions of different orders when driven by avalanches-adapted field changes lead to self-organised critical dynamics on the hysteresis loop. We observe two different universality classes of SOC that are associated with the order of the primary spin interactions. Here, we emphasise that the system with triangle-embedded interactions without background pairwise couplings evolves towards the SOC state in a new universality class, compared to the one induced by the pairwise interactions. Specifically, for \(\kappa =1\) where only triangle-based interactions are present, the exponents found by fitting the corresponding curves are \(\tau _s-1=0.326\pm 0.013\), and \(\tau _T-1=0.49\pm 0.021\), which are close to the exact exponents of SOC in the directed sandpile automata \(\tau _s =4/3\) and \(\tau _T=3/2\), derived in [97]. In contrast, numerically determined exponents \(\tau _s-1=0.526\pm 0.018\) and \(\tau _T-1=0.993\pm 0.023\) close to the mean-field SOC [96], i.e., \(\tau _s =3/2\) and \(\tau _T=2\), are found in the limit \(\kappa =0\), where only the antiferromagnetic pairwise interactions are present. It is worth emphasising that the observed critical behaviour occurs over the entire hysteresis loop, not for a specific (critical) value of the field. The physical principles leading to such self-organised hysteresis loop criticality were first discussed in [100], pointing out the role of frustrated spin–glass interactions in the infinite-range Sherrington–Kirkpatrick model. In the present context, a similar role can be attributed to the long-range effects of frustrated antiferromagnetic interactions and non-locality of higher order couplings on triangles in conjunction with complex network topology.

To understand the impact of geometry on the nature of these dynamic critical states, we refer to the theoretical concepts regarding the equivalence between the zero-temperature Ising spin dynamics and the directed percolation cellular automata [103]. Furthermore, we recall that spin-reversal avalanches triggered by the external field change propagate as a directed branching process, where the actual architecture of triangles determines the underlying branching tree. In particular, for fractal networks, where the average branching number saturates for significant distances, the study [101] utilising spanning trees based on the betweenness centrality of edges reveals that the probability of cluster size s (mass when the box length \(\ell _B\rightarrow \infty \)) scales with the exponent \(\tau _s=\gamma /(\gamma -1)\); the exponent \(\gamma \) is related to the degree distribution, i.e., the number of edges per node). Then, we can compute the corresponding duration exponent \(\tau _T\) from the scaling relation [102] \(\tau _s=2-1/\tau _T\), which gives \(\tau _T=(\gamma -1)/(\gamma -2)\). We note that the generalised degree distribution for the network of finite size, considered in the above numerical simulations, has an intermediate scale-free segment compatible with the exponent \(\gamma \sim 3.8\pm 0.4\), excluding the hub nodes; meanwhile, s smaller exponent applies for the low-degree nodes. It is relevant to mention that, in this particular case, the number of triangles per node scales similarly to the number of edges. Apart from the structure of potential branches, a crucial difference regarding the nature of avalanche branching occurs due to the spin frustration effects in the limit \(\kappa =0\). In this case, each triangle contains at least one frustrated spin, which prevents propagation of the local order set by the current value of the external field. The situation corresponds to a critical branching process, where the average branching number remains constant, which leads to the mean-field SOC according to the original work in [96]. On the other side, for triangle-based interactions only (\(\kappa =1\)), no spin frustration occurs. Multiplicative branching processes are enabled by the network’s fractality, leading to the exponents as above, but now the structure is related to the architecture of triangles [87]. Given the well-known equivalence of the (zero-temperature) Ising model dynamics with the Domany–Kinzel cellular automata for directed percolation [103], as well as the related directed sandpile automata with probabilistic toppling [102], we note that the numerical values of the exponents, in this case, are close to the ones of the directed percolation, which are known with more significant numerical precision, i.e., \(\tau _s=1.32059\), \(\tau _t=1.47244\), and the anisotropy exponent \(\zeta =0.63261\)); see [102] and references there. The presented numerical work provides sufficient evidence for two different classes of SOC universality on the hysteresis loop of these complex structures, whose geometry also plays a role. It remains for further investigation whether a distinct class of SOC could be observed when studying simplexes of larger sizes and the interactions embedded in them, as opposed to pairwise antiferromagnetic coupling, where we always expect the mean-field SOC.

In conclusion, the presented survey and the numerically studied example of the hysteresis-loop criticality in a simplicial complex with geometry-embedded interactions highlight the relevance of self-organised dynamics in functional complex systems and the critical role of geometry in the emergence of this type of collective behaviour. In this regard, our results suggest that triangle-embedded interactions play the primary role in critical dynamics beyond standard pairwise interactions in systems with higher order geometry. These studies call for more theoretical investigations, i.e., by the renormalisation-group methodology, to confirm the existence of different fixed points representing the classes of emergent non-equilibrium critical dynamics and their stability. To this end, equivalent continuous models that consider features of complex geometry (at the local-to-mesoscopic scale) that are relevant to emergent critical dynamics need to be developed, which creates a challenging theoretical problem. We mention some ideas from the physics of hierarchical spin glasses [104, 105], mapping directed cellular automata onto zero-temperature Ising model [103], SOC models with quenched disorder noise with specific correlations [8, 11], topological defects, and the use of tropical geometry [106] that may serve as an inspiring point in this direction. Another interesting open problem regards the potentials of quantum formalism, such as in reference [9], to elucidate the interplay of geometry and time-varying driving forces in the occurrence of self-organised critical states. On the other side, several open questions remain accessible to numerical modelling and empirical data analysis using the theoretical concept of self-organised critical behaviour [1]. Some examples include the geometry reconstruction associated with the avalanche driving rate, the role of extended defects, and the occurrence of different types of SOC in systems with “meaningful” interactions among social subjects in contrast to the physics laboratory systems and others. Considering natural complex systems, these theoretical concepts linking higher order connectivity and self-organised critical dynamics expand our possibilities for designing robust functional materials and revealing relevant patterns from higher order network data. In particular, these ideas may further help explain observations of brain processes and differentiate brain disorders. Furthermore, we expect that they can improve our understanding of temporal regularities associated with higher order interactions in economic systems and predictions of global trends in social dynamics.

One of the critical ingredients of the developed framework that we highlighted and detailed here is the interplay between self-organised critical dynamics and higher order connectivity networks. Not only does it reveal new lines of theoretical research, but it also offers a fresh perspective for data analysis based on these scientific concepts. Namely, self-organised criticality as an active mechanism in the evolution of a complex system manifests itself in characteristic patterns of spatiotemporal correlations that a perceptive analysis of data can reveal and thus enable the use of appropriate theory for further predictions (in contrast to considering an ever-increasing amount of data as uncorrelated sets). Such a combined analysis would allow a deeper understanding of the functional characteristics of many complex systems, for example, the brain, which may allow a more critical approach in designing AI algorithms that utilise brain functions and various medical implications.