Universal Pareto laws in agent-based exchange models: debt and varying initial-money distributions

Abstract

We examine by Monte-Carlo simulations the behavior of a kinetic exchange-trading model for various initial distributions of money in the system of agents. Our goal is to analyze the characteristics of the Pareto laws for the long-time money distribution, in both closed and open systems. We consider three different initial distributions for these two situations. We first briefly summarize the concepts and results of some agent-based money-exchange models. Then, via employing the Monte-Carlo computer simulations, for both types of systems we obtain the long-time money distributions for the initially homogeneous or constant, for positive random, and finally, for both positive and negative random distributions of money among the agents. We conclude that the Pareto laws and their exponents remained nearly the same in all these situations showing little sensitivity to the initial conditions imposed.

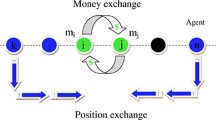
Graphic abstract

Appendix A: Auxiliary figures

Here, we present some supplementary plots supporting the claims of the main text (see Figs. 5, 6, 7, 8, 9, 10, 11).

Fig. 5

Money distribution f(x) for the simulated 1D traps-free exchange model. Inset: a log–log plot of the same f(x) yielding the Pareto exponent $-(1+\alpha ) = -2.0$

Fig. 6

Money distributions f(x) for randomly distributed and homogeneous initial amounts of positive money (green squares/rhombuses and red circles, correspondingly). The inset shows the initial money amounts for each site of the lattice. In our simulations, each agent positioned at each site of the 1D lattice acquires a certain random amount of money at the start of the simulation procedure. Each simulation run these numbers are chosen anew so that a statistical ensemble for later averaging of the results is being created

Fig. 7

Money distribution $f_{\pm }(x)$ for randomly distributed initial amounts of positive and negative money (see the legend for notations), used as the starting conditions in simulations. Parameters: $L=L_0$, $R=R_0$, and $t=t_0$

Fig. 8

Long-time money distribution for a closed system with debt shown for different lengths of simulations, see the legend. Other parameters are the same as in Fig. 2

Fig. 9

Money distributions $f_{+}(x)$ for random initial conditions, shown for two densities of the trapping sites $\rho$ (see the legend). As a reference, the results for a homogeneous money distribution from Fig. 6 are also shown

Fig. 10

The same quantities as in Fig. 8 but for an open system with positive and negative money and in the presence of traps, computed for different trajectory lengths (see the legend for the values of parameters)

Fig. 11

Evolution of money in a system with variable density of traps and with both positive- and negative-money agents. Other parameters are the same as in Fig. 4