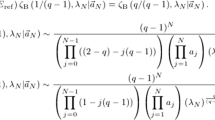Abstract
We study the energy and the entropies of N independent harmonic oscillators in the microcanonical and the canonical ensembles in the Tsallis classical and the Tsallis quantum statistics of entropic parameter q, where N is the number of the oscillators and the value of q is larger than one. The energy and the entropies are represented with the physical temperature, and the well-known expressions are obtained for the energy and the Rényi entropy. The difference between the microcanonical and the canonical ensembles is the existence of the condition for N and q in the canonical ensemble: \(N(q-1)<1\). The condition does not appear in the microcanonical ensemble.The entropies are q-dependent in the canonical ensemble, and are not q-dependent in the microcanonical ensemble. For \(N(q-1)<1\), this difference in entropy is quite small, and the entropy in the canonical ensemble does not differ from the entropy in the microcanonical ensemble substantially.
Graphic abstract



Similar content being viewed by others
Data availability statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This study is theoretical, and the graphs were drawn with the equations given in this paper.].
References
C. Tsallis, Introduction to nonextensive statistical mechanics (Springer Science + Business Media, LLC, 2010)
M. Ishihara, Thermodynamics of the independent harmonic oscillators with different frequencies in the Tsallis statistics in the high physical temperature approximation. Eur. Phys. J. B. 95, 53 (2022)
C. Tsallis, R.S. Mendes, A.R. Plastino, The role of constraints within generalized nonextensive statistics. Physica A 261, 534 (1998)
A.S. Parvan, Rényi statistics in equilibrium mechanics. Phys. Lett. A 374, 1951 (2010)
S. Kalyana Rama, Tsallis statistics: averages and a physical interpretation of the Lagrange multiplier \(\beta \), Phys. Lett. A 276, 103 (2000)
S. Abe, S. Martinez, F. Pennini, A. Plastino, Nonextensive thermodynamic relations. Phys. Lett. A 281, 126 (2001)
S. Abe, Heat and entropy in nonextensive thermodynamics: transmutation from Tsallis theory to Rényi-entropy-based theory. Physica A 300, 417 (2001)
H.H. Aragão-Rêgo, D.J. Soares, L.S. Lucena, L.R. da Silva, E.K. Lenzi, and Kwok Sau Fa, Bose–Einstein and Fermi–Dirac distributions in nonextensive Tsallis statistics: an exact study. Physica A 317, 199 (2003)
E. Ruthotto, Physical temperature and the meaning of the \(q\) parameter in Tsallis statistics. arXiv:cond-mat/0310413
R. Toral, On the definition of physical temperature and pressure for nonextensive thermodynamics. Physica A 317, 209 (2003)
H. Suyari, The unique non self-referential \(q\)-canonical distribution and the physical temperature derived from the maximum entropy principle in Tsallis statistics. Prog. Theor. Phys. Suppl. 162, 79 (2006)
M. Ishihara, Phase transition for the system of finite volume in the \(\phi ^4\) theory in the Tsallis nonextensive statistics. Int. J. Mod. Phys. A 33, 1850067 (2018)
M. Ishihara, Momentum distribution and correlation for a free scalar field in the Tsallis nonextensive statistics based on density operator. Eur. Phys. J. A 54, 164 (2018)
M. Ishihara, Thermodynamic relations and fluctuations in the Tsallis statistics. arXiv:2104.11427v2
S. Abe, Stability of Tsallis entropy and instabilities of Rényi and normalized Tsallis entropies: a basis for q-exponential distributions. Phys. Rev. E 66, 046134 (2002)
L.G. Moyano, C. Tsallis, M. Gell-Mann, Numerical indications of a \(q\)-generalized central limit theorem. Europhys. Lett. 73, 813 (2006)
E. Vives, A. Plane, Is Tsallis thermodynamics nonextensive? Phys. Rev. Lett. 88, 020601 (2002)
A. Boumali, The one-dimensional thermal properties for the relativistic harmonic oscillators. arXiv:1409.6205v1
A. Boer, Study of second order phase transitions in the 2D Ising model using Tsallis statistics. Bull. Transilvania Univ. Braşov 3(52), 209 (2010)
S.N.M. Ruijsenaars, On Barnes multiple zeta and gamma functions. Adv. Math. 156, 107 (2000)
K. Kirsten, “Basic zeta functions and some applications in physics”, from A Window into Zeta and Modular Physics, Editors K. Kirsten and F. Williams, MSRI Pub. 57, 101, Cambridge University Press, Cambridge (2010)
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares no competing interest.
Appendix A: Hurwitz zeta function and Barnes zeta function
Appendix A: Hurwitz zeta function and Barnes zeta function
In this appendix, we give the approximate expressions of Hurwitz and Barnes zeta functions. The derivation is also given in the appendices A and B of the reference [2] .
The Hurwitz zeta function \(\zeta _{\textrm{H}}\) is defined by
In this appendix, we treat the case of \(s>1\) and \(\alpha >0\).
Applying the Euler–Maclaurin formula, we have
where \(B_k\) is Bernoulli number. The Hurwitz zeta function can be expressed in the other forms [18]. From Eq. (A.2), we find that \(\zeta _{\textrm{H}}(1+z, \alpha )\) for \(\alpha \gg 1\) behaves as
The Barnes zeta function [20, 21] is defined by
where \(s>N\), \(\alpha > 0\), and \(\omega _j > 0\). The Barnes zeta function for sufficiently large \(\alpha \) has the following relation
This relation is derived with Eq. (A.3). Using the recurrence relation, Eq. (A.5), we have the following approximate expression of \(\zeta _{\textrm{B}}\) for \(\alpha \gg 1\):
In the present case, \(\mathbf {\omega }_N\) is set to \(\mathbf {\omega }_N = (1,1,\ldots ,1)\). For simplicity, we use the following notation for the Barns zeta function \(\zeta _{\textrm{B}}\) with \(\mathbf {\omega }_N = (1,1,\ldots ,1)\):
The approximate expression of \(\zeta _{\textrm{B}}(1+z, \alpha ; N)\) for \(\alpha \gg 1\) is
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ishihara, M. Thermodynamic quantities of independent harmonic oscillators in microcanonical and canonical ensembles in the Tsallis statistics. Eur. Phys. J. B 96, 13 (2023). https://doi.org/10.1140/epjb/s10051-023-00481-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjb/s10051-023-00481-7