Skip to main content
SpringerLink
Log in

Breather-impurity interactions and modulational instability in a quantum 2D Klein–Gordon chain

  • Regular Article - A: Solid State and Materials
  • Published:
The European Physical Journal B Aims and scope Submit manuscript

Abstract

We study the breather-impurity interactions and modulational instability in a quantum 2D Klein–Gordon chain. By using the second quantification operators, we transform classical Hamiltonian into its quantum version, through Glauber’s coherent state representation in addition to the multiple-scale method, the 2D nonlinear Schrödinger equation (NLSE) is obtained. This NLSE is analytically solved by adopting the Rayleigh–Ritz variational method. Around impurity’s critical mass, we prove the existence of resonant structure. This critical mass is observed when plotting the frequency spectrum under the effect of the impurity mass and harmonic force constants. The effects of impurity mass and the harmonic force constants are found in the amplitude frequency spectra. When the breather interacts with the impurity, the system exhibit different scenario that are: barrier, well, excitation and chaotic all related to the trapping phenomenon. The modulational instability (MI) which helps to confirm the existence of breather is investigated. We have shown that impurity strength increases the instability regions, and the MI growth rate can be dramatically affected by the impurity mass around the critical value.

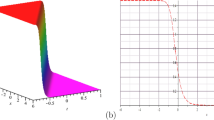
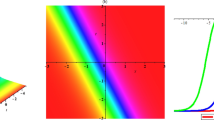
Graphic abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data Availability

This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The authors declare that all data supporting the findings of this study are available within the article.]

References

  1. A.A. Ovshinnikov, Localized long-lived vibrational states in molecular crystals. Sov. Phys. JETP 30, 147 (1970)

    ADS  Google Scholar 

  2. A.M. Kosevitch, A.S. Kovalev, Selflocalization of vibrations in a one-dimensional anharmonic chain. Sov. Phys. JETP 67, 1793 (1974)

    Google Scholar 

  3. A.A. Sukhorukov, Y.S. Kivshar, H.S. Eisenberg, Y. Silberberg, Spatial optical solitons in waveguide arrays. IEEE J. Quant. Electron. 39, 31 (2003)

    Article  ADS  Google Scholar 

  4. H.S. Eisenberg, R. Morandotti, Y. Silberberg, J.M. Arnold, G. Pennelli, J.S. Aitchison, Optical discrete solitons in waveguide arrays. I. Soliton formation. J. Opt. Soc. Am. B 19, 2938 (2002)

    Article  ADS  Google Scholar 

  5. A. Trombettoni, A. Smerzi, Discrete solitons and breathers with dilute Bose–Einstein condensates. Phys. Rev. Lett. 86, 2353 (2001)

    Article  ADS  Google Scholar 

  6. L. Yakusevich, Nonlinear physics of dna, wiley series in nonlinear sciences (Wiley, Weinheim, 2004)

    Book  Google Scholar 

  7. A. Alvarez, F.R. Romero, J.F.R. Archilla, J. Cuevas, P.V. Larsen, Breather trapping and breather transmission in a DNA model with an interface. Eur. Phys. J. B 51, 119 (2006)

    Article  ADS  Google Scholar 

  8. M. Gueron, M. Kochoyan, J.-L. Leroy, A single mode of DNA base-pair opening drives imino proton exchange. Nature 328, 89 (1987)

    Article  ADS  Google Scholar 

  9. T. Dauxois, M. Peyrard, C.R. Willis, Discreteness effects on the formation and propagation of breathers in nonlinear Klein–Gordon equations. Phys. Rev. E 48, 4768 (1993)

    Article  ADS  Google Scholar 

  10. F. Yoshida, T. Nakayama, T. Sakuma, Computer-simulated scattering of lattice solitons from impurity at free boundary. J. Phys. Soc. Jpn. 40, 901 (1976)

    Article  ADS  Google Scholar 

  11. F. Yoshida, T. Sakuma, Computer-simulated scattering of lattice solitons from a mass interface in a one-dimensional nonlinear lattice. J. Phys. Soc. Jpn. 42, 1412 (1977)

    Article  ADS  Google Scholar 

  12. A. Nakamaura, S. Takeno, Scattering of a soliton by an impurity atom in the Toda Lattice and Localized Modes. Prog. Theor. Phys. 58, 1074 (1977)

    Article  ADS  Google Scholar 

  13. N. Yajima, Scattering of lattice solitons from a mass impurity. Phys. Scr. 20, 431 (1979)

    Article  ADS  Google Scholar 

  14. F. Zhang, Y.S. Kivshar, L. Vázquez, Resonant soli ton-impurity interactions. Phys. Rev. Let. 67, 1177 (1991)

    Article  ADS  Google Scholar 

  15. F. Zhang, Y.S. Kivshar, L. Vázquez, Resonant kink-impurity interactions in the Sine–Gordon model. Phys. Rev. A 45, 6019 (1992)

    Article  ADS  Google Scholar 

  16. F. Zhang, Y.S. Kivshar, L. Vázquez, Resonant kink-impurity interactions in the phi 4 model. Phys. Rev. A 46, 5214 (1992)

    Article  ADS  Google Scholar 

  17. F. Zhang, Breather scattering by impurities in the Sine–Gordon model. Phys. Rev. E 58, 2558 (1998)

    Article  ADS  Google Scholar 

  18. B.A. Malomed, D.K. Campbell, N. Knowles, R. Flesch, Phys. Lett. A 178, 271 (1993)

    Article  ADS  Google Scholar 

  19. O.M. Braun, Y.S. Kivshar, Nonlinear dynamics of the Frenkel–Kontorova model with impurities. Phys. Rev. B 43, 1060 (1991)

    Article  ADS  Google Scholar 

  20. K. Forinash, M. Peyrard, B. Malomed, Interaction of discrete breathers with impurity modes. Phys. Rev. E 49, 3400 (1994)

    Article  ADS  Google Scholar 

  21. Q. Luo, Local vibrational mode of an impurity in a monatomic linear chain under open and periodic boundary conditions. Eur. J. Phys. 37, 065501 (2016)

    Article  MATH  Google Scholar 

  22. K. Keiler, P. Schmelcher, Interaction-induced single-impurity tunneling in a binary mixture of trapped ultracold bosons. Phys. Rev. A 100, 043516 (2019)

    Article  ADS  Google Scholar 

  23. T. Dauxois, M. Peyrard, C.R. Willis, Localized breather-like solution in a discrete Klein-Gordon model and application to DNA. Phys. D 57(3), 267 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  24. P.T. Dinda, M. Remoissenet, Breather compactons in nonlinear Klein–Gordon systems. Phys. Rev. E 60(5), 6218 (1999)

    Article  ADS  Google Scholar 

  25. J.C. Comte, Exact discrete breather compactons in nonlinear Klein–Gordon lattices. Phys. Rev. E 65(6), 067601 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  26. J. Cuevas, F. Palmero, J.F.R. Archilla, F.R. Romero, Moving discrete breathers in a Klein–Gordon chain with impurity. Phys. A 35(49), 10519 (2002)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. J. Cuevas, P.G. Kevrekidis, Breather statics and dynamics in Klein–Gordon chains with a bend. Phys. Rev. E 69, 056609 (2004)

    Article  ADS  MathSciNet  Google Scholar 

  28. L. Yang, T. Yi, Bright and dark small amplitude nonlinear localized modes in a quantum one-dimensional Klein–Gordon chain. Chin. Phys. B 17(10), 3841 (2008)

    Article  ADS  Google Scholar 

  29. D.J. Li, W.X. Mi, K. Deng, Y. Tang, Quantum solitons and localized modes in a one-dimensional lattice chain with nonlinear substrate potential. Commun. Theor. Phys. 45, 869 (2006)

    Article  ADS  Google Scholar 

  30. X. Quan, Q. Tian, Two-dimensional discrete gap breathers in a two-dimensional discrete diatomic kleingordon lattice. Chin. Phys. Lett. 26, 070501 (2009)

    Article  Google Scholar 

  31. D. Bambusi, S. Paleari, T. Penati, Existence and continuous approximation of small amplitude breathers in 1D and 2D Klein–Gordon lattices. Appl. Anal. Int. J. 89(9), 1313–1334 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  32. Z.I. Djoufack, F. Kenmogne, J.P. Nguenang, A. Kenfack-Jiotsa, Dynamics of solitons with periodic loops intrinsic localized modes and modulational instability in a quantum 2D nonlinear square Klein–Gordon chain. Chaos Solitons Fract. 142, 110403 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  33. T.B. Benjamin, J. Feir, the disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 27, 417 (1967)

    Article  ADS  MATH  Google Scholar 

  34. M. Peyrard, A.R. Bishop, Statistical mechanics of a nonlinear model for DNA denaturation. Phys. Rev. Lett. 62, 2755 (1989)

    Article  ADS  Google Scholar 

  35. Y.S. Kivshar, M. Peyrard, Modulational instabilities in discrete lattices. Phys. Rev. A 46, 3198 (1992)

    Article  ADS  Google Scholar 

  36. Y.S. Kivshar, Localized modes in a chain with nonlinear on-site potential. Phys. Lett. A 173, 172 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  37. T. Dauxois, M. Peyrard, Energy localization in nonlinear lattices. Phys. Rev. Lett. 70, 3935 (1993)

    Article  ADS  Google Scholar 

  38. I. Daumont, T. Dauxois, M. Peyrard, Modulational instability: first step towards energy localization in nonlinear lattices. Nonlinearity 10, 617–630 (1997)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. F. Baronio, S. Chen, P. Grelu, S. Wabnitz, M. Conforti, Baseband modulation instability as the origin of rogue waves. Phys. Rev. A 91, 033804 (2015)

    Article  ADS  Google Scholar 

  40. G. Gor, T. Macrì, A. Trombettoni, Modulational instabilities in lattices with powerlaw hoppings and interactions. Phys. Rev. E 87, 032905 (2013)

    Article  ADS  Google Scholar 

  41. L. Wang, Y.-J. Zhu, F.-H. Qi, M. Li, R. Guo, Modulational instability, higher-order localized wave structures, and nonlinear wave interactions for a nonautonomous Lenells–Fokas equation in inhomogeneous fibers. Chaos 25, 063111 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  42. L. Wang, J.-H. Zhang, Z.-Q. Wang, C. Liu, M. Li, F.-H. Qi, R. Guo, Breather–Tosoliton transitions, nonlinear wave interactions, and modulational instability in a higher-order generalized nonlinear Schrödinger equation. Phys. Rev. E 93, 012214 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  43. L. Wang, J.-H. Zhang, C. Liu, M. Li, F.-H. Qi, Breather transition dynamics, Peregrine combs and walls, and modulation instability in a variable-coefficient nonlinear Schrödinger equation with higher-order effects. Phys. Rev. E 93, 062217 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  44. B. Tang, K. Deng, Discrete breathers and modulational instability in a discrete \({\phi ^{4}}\) nonlinear lattice with next-nearest-neighbor couplings. Nonlinear Dyn. 88(4), 2417–2426 (2017)

    Article  MathSciNet  Google Scholar 

  45. R.J. Glauber, Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766 (1963)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  46. W.-M. Zhang, D.H. Feng, R. Gilmore, Coherent states. Rev. Mod. Phys. 62(4) (1990)

  47. R. J. Glauber, Quantum theory of parametric amplification ii, in quantum theory of optical coherence: selected papers and lectures. Wiley-VCH Verlag GmbH and Co. KGaA, Weinheim (2006). https://doi.org/10.1002/9783527610075.ch7

  48. H. Smith, Introduction to Quantum Mechanics (World Scientific, Singapore, 1991), p. 108

    Book  Google Scholar 

  49. A.I. Butt, J.A.D. Wattis, Discrete breathers in a two dimensional Fermi Pasta Ulam lattice. J. Phys. A Math. Gen. 39, 4955 (2006)

  50. Z.I. Djoufack, E. Tala-Tebue, J.P. Nguenang, A. Kenfack-Jiotsa, Radial solitons and modulational instability in two-dimensional Ablowitz–Ladik equation for certain applications in nonlinear optics. Optik 225, 165639 (2021)

    Article  ADS  Google Scholar 

  51. M. Remoissenet, Low-amplitude breather and envelope solitons in quasi-one-dimensional physical models. Phys. Rev. B 33, 2386 (1986)

    Article  ADS  Google Scholar 

  52. G. Schneider, C.E. Wayne, Counter-propagating waves on fluid surfacesand the continuum limit of the Fermi-Pasta-Ulam model. In: International Conference on Differential Equations, World Scientific, River Edge, NJ, pp. 390 (2000)

  53. R.H. Goodman, P.J. Holmes, M.I. Weinstein, Strong NLS soliton-defect interactions. Physica D 192, 215–248 (2004)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  54. F. Reika, O. Masahito, O. Tohru, Nonlinear Schrödinger equation with a point defect, Science Direct, 837-845 (2008)

  55. J.H. Li, K.S. Chiang, K.W. Chow, Modulation instabilities in two-core optical fiers. J. Opt. Soc. Am. B 28(7), 1693 (2011)

    Article  ADS  Google Scholar 

  56. A. Govindarajan, B.A. Malomed, A. Mahalingam, A. Uthayakumar, Modulational instability in linearly coupled asymmetric dual-core fibers. Appl. Sci. 7, 645 (2017)

    Article  Google Scholar 

Download references

Acknowledgements

Zacharie Isidore Djoufack acknowledges the African Institute for Mathematical Sciences (AIMS) South Africa for research facilities.

Author information

Authors and Affiliations

  1. Pure Physics Laboratory: Group of Nonlinear physics and Complex systems, Department of Physics, University of Douala, P.O. Box 24157, Douala, Cameroon

    R. Abouem A. Ribama & J. P. Nguenang

  2. Unité de Recherche d’Automatique et Informatique Apliquée (UR-AIA), Fotso Victor University Institute of Technology, University of Dschang, P.O. Box 134, Bandjoun, Cameroon

    Z. I. Djoufack

  3. The African Institute for Mathematical Sciences (AIMS), 6 Melrose Road, Muizenberg, Cape Town, 7945, South Africa

    Z. I. Djoufack

Authors
  1. R. Abouem A. Ribama
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Z. I. Djoufack
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. P. Nguenang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Z. I. Djoufack.

Ethics declarations

Author contribution statement

RAAR: design, calculations, simulations, writing; ZID: design, conception, calculations, simulations, writing, reading, revision; JPN: design, conception, reading, revision and supervision.

Appendix

Appendix

$$\begin{aligned}&u^2_{l,n}=\frac{\hbar }{2m\omega _0}\left( b^{\dagger }_{l,n}b^{\dagger }_{l,n} +b^{\dagger }_{l,n}b_{l,n}+b_{l,n}b^{\dagger }_{l,n}+b_{l,n}b_{l,n}\right) \nonumber \\&P^2_{l,n}=-\frac{\hbar {m\omega _0}}{2}\left( b^{\dagger }_{l,n}b^{\dagger }_{l,n} -b^{\dagger }_{l,n}b_{l,n}-b_{l,n}b^{\dagger }_{l,n}+b_{l,n}b_{l,n}\right) \nonumber \\&u^2_{l-1,n}=\frac{\hbar }{2m\omega _0}\left( b^{\dagger }_{l-1,n}b^{\dagger }_{l-1,n}\right. \nonumber \\&\qquad \left. +b^{\dagger }_{l-1,n}b_{l-1,n}+b_{l-1,n}b^{\dagger }_{l-1,n}+b_{l-1,n}b_{l-1,n}\right) \nonumber \\&u^2_{l,n-1}=\frac{\hbar }{2m\omega _0}\left( b^{\dagger }_{l,n-1}b^{\dagger }_{l,n-1}\right. \nonumber \\&\qquad \left. +b^{\dagger }_{l,n-1}b_{l,n-1}+b_{l,n-1}b^{\dagger }_{l,n-1}+b_{l,n-1}b_{l,n-1}\right) \end{aligned}$$
(54)
$$\begin{aligned}&u^4_{l,n}=\left( \frac{\hbar }{2m\omega _0}\right) ^2\left( b^{\dagger }_{l,n}b^{\dagger }_{l,n} +b^{\dagger }_{l,n}b_{l,n}+b_{l,n}b^{\dagger }_{l,n}+b_{l,n}b_{l,n}\right) \nonumber \\&\qquad \left( b^{\dagger }_{l,n}b^{\dagger }_{l,n}+b^{\dagger }_{l,n}b_{l,n} +b_{l,n}b^{\dagger }_{l,n}+b_{l,n}b_{l,n}\right) \nonumber \\&\quad =\left( \frac{\hbar }{2m\omega _0}\right) ^2(b^{\dagger }_{l,n} b^{\dagger }_{l,n}b^{\dagger }_{l,n}b^{\dagger }_{l,n} +b^{\dagger }_{l,n}b^{\dagger }_{l,n}b^{\dagger }_{l,n}b_{l,n}\nonumber \\&\qquad +b^{\dagger }_{l,n}b^{\dagger }_{l,n}b_{l,n}b^{\dagger }_{l,n} +b^{\dagger }_{l,n}b^{\dagger }_{l,n}b_{l,n}b_{l,n} +b^{\dagger }_{l,n}b_{l,n}b^{\dagger }_{l,n}b^{\dagger }_{l,n}\nonumber \\&\qquad +b^{\dagger }_{l,n}b_{l,n}b^{\dagger }_{l,n}b_{l,n}+b^{\dagger }_{l,n} b_{l,n}b_{l,n}b^{\dagger }_{l,n}+b^{\dagger }_{l,n}b_{l,n}b_{l,n}b_{l,n}\nonumber \\&\qquad +b_{l,n}b^{\dagger }_{l,n}b^{\dagger }_{l,n}b^{\dagger }_{l,n} +b_{l,n}b^{\dagger }_{l,n}b^{\dagger }_{l,n}b_{l,n}\nonumber \\&\qquad +b_{l,n}b^{\dagger }_{l,n}b_{l,n}b^{\dagger }_{l,n}\nonumber \\&\qquad +b_{l,n}b^{\dagger }_{l,n}b_{l,n}b_{l,n} +b_{l,n}b_{l,n}b^{\dagger }_{l,n}b^{\dagger }_{l,n}+b_{l,n}b_{l,n}b^{\dagger }_{l,n}b_{l,n}\nonumber \\&\qquad +b_{l,n}b_{l,n}b_{l,n}b^{\dagger }_{l,n}+b_{l,n}b_{l,n}b_{l,n}b_{l,n}) \end{aligned}$$
(55)
$$\begin{aligned}&u_{l,n}u_{l-1,n}=\left( \frac{\hbar }{2m\omega _0}\right) (b^{\dagger }_{l,n}+b_{l,n}) (b^{\dagger }_{l-1,n}+b_{l-1,n})\nonumber \\&\quad =\left( \frac{\hbar }{2m\omega _0}\right) (b^{\dagger }_{l,n}b^{\dagger }_{l-1,n}\nonumber \\&\qquad +b^{\dagger }_{l,n}b_{l-1,n}+b_{l,n}b^{\dagger }_{l-1,n}+b_{l,n}b_{l-1,n}) \end{aligned}$$
(56)
$$\begin{aligned}&u_{l,n}u_{l,n-1}=\left( \frac{\hbar }{2m\omega _0}\right) (b^{\dagger }_{l,n}+b_{l,n}) (b^{\dagger }_{l,n-1}+b_{l,n-1})\nonumber \\&\quad =\left( \frac{\hbar }{2m\omega _0}\right) (b^{\dagger }_{l,n}b^{\dagger }_{l,n-1}\nonumber \\&\qquad +b^{\dagger }_{l,n}b_{l,n-1}+b_{l,n}b^{\dagger }_{l,n-1}+b_{l,n}b_{l,n-1}) \end{aligned}$$
(57)
$$\begin{aligned}&u^2_{l-1,n}-2u_{l,n}u_{l-1,n}=\left( \frac{\hbar }{2\omega _0}\right) (b^{\dagger }_{l-1,n}b^{\dagger }_{l-1,n}\nonumber \\&\qquad +b^{\dagger }_{l-1,n}b_{l-1,n}+b_{l-1,n}b_{l-1,n}-2b^{\dagger }_{l,n}b^{\dagger }_{l-1,n}\nonumber \\&\qquad -2b^{\dagger }_{l,n}b_{l-1,n}-2b_{l,n}b^{\dagger }_{l-1,n}\nonumber \\&\qquad -2b_{l,n}b_{l-1,n}+b_{l-1,n}b^{\dagger }_{l-1,n}) \end{aligned}$$
(58)
$$\begin{aligned}&u^2_{l,n-1}-2u_{l,n}u_{l,n-1}=\left( \frac{\hbar }{2m\omega _0}\right) (b^{\dagger }_{l,n-1}b^{\dagger }_{l,n-1}\nonumber \\&\qquad +b^{\dagger }_{l,n-1}b_{l,n-1} +b_{l,n-1}b_{l,n-1}-2b^{\dagger }_{l,n}b^{\dagger }_{l,n-1}\nonumber \\&\qquad -2b^{\dagger }_{l,n}b_{l,n-1}-2b_{l,n}b^{\dagger }_{l,n-1}\nonumber \\&\qquad -2b_{l,n}b_{l,n-1}+b_{l,n-1}b^{\dagger }_{l,n-1}). \end{aligned}$$
(59)

Inserting (54), (55), (56), (57), (58) and (59) into (1), we have:

$$\begin{aligned}&{H_{eff}}= \sum _{l}\sum _{n}\frac{\hbar \omega _{0}}{4}\Big (b_{l,n}^{\dagger }b_{l,n}+ b_{l,n}b_{l,n}^{\dagger }\Big )\nonumber \\&\quad + \sum _{l}\sum _{n}\frac{\hbar c_{x}}{4m\omega _{0}}\Big [b_{l,n}^{\dagger }b_{l,n}+b_{l,n}b_{l,n}^{\dagger }+ b_{l-1,n}^{\dagger }b_{l-1,n}\nonumber \\&\quad + b_{l-1,n}b_{l-1,n}^{\dagger }-2 b_{l,n}^{\dagger }b_{l-1,n}-2b_{l,n}b_{l-1,n}^{\dagger }\Big ]\nonumber \\&\quad + \sum _{l}\sum _{n}\frac{\hbar c_{y}}{4m\omega _{0}}\Big [b_{l,n}^{\dagger }b_{l,n}+ b_{l,n}b_{l,n}^{\dagger }+ b_{l,n-1}^{\dagger }b_{l,n-1} \nonumber \\&\quad +b_{l,n-1}b_{l,n-1}^{\dagger }-2 b_{l,n}^{\dagger }b_{l,n-1}-2b_{l,n}b_{l,n-1}^{\dagger }\Big ]\nonumber \\&\quad + \sum _{l}\sum _{n}\frac{\hbar k_{2}}{4m\omega _{0}}\Big (b_{l,n}^{\dagger }b_{l,n}+ b_{l,n}b_{l,n}^{\dagger }\Big )\nonumber \\&\quad +\sum _{l}\sum _{n}\frac{k_{4}}{4} \Big (\frac{\hbar }{2m\omega _{0}}\Big )^{2}\Big [6b_{l,n}^{\dagger }b_{l,n}^{\dagger }b_{l,n}b_{l,n}+ 12b_{l,n}^{\dagger }b_{l,n}+3\Big ]\nonumber \\&H^{'}=-\sum _{l}\sum _{n}\frac{\hbar \omega _{0}}{4}\Big (b_{l,n}^{\dagger }b_{l,n}^{\dagger }+ b_{l,n}b_{l,n}\Big )\nonumber \\&\quad + \sum _{l}\sum _{n}\frac{\hbar k_{2}}{4m\omega _{0}}\Big (b_{l,n}^{\dagger }b_{l,n}^{\dagger }+ b_{l,n}b_{l,n}\Big )\nonumber \\&\quad +\sum _{l}\sum _{n}\frac{k_{4}}{4} \Big (\frac{\hbar }{2m\omega _{0}}\Big )^{2}\Big [b_{l,n}^{\dagger } b_{l,n}^{\dagger }b_{l,n}^{\dagger }b_{l,n}^{\dagger }\nonumber \\&\quad +b_{l,n}^{\dagger }b_{l,n}^{\dagger }b_{l,n}^{\dagger }b_{l,n} +b_{l,n}^{\dagger }b_{l,n}^{\dagger }b_{l,n}b_{l,n}^{\dagger } +b_{l,n}b_{l,n}b_{l,n}b_{l,n}\nonumber \\&\quad +b_{l,n}b_{l,n}b_{l,n}^{\dagger }b_{l,n}+b_{l,n}b_{l,n}b_{l,n}b_{l,n}^{\dagger } +b_{l,n}^{\dagger }b_{l,n}b_{l,n}^{\dagger }b_{l,n}^{\dagger }\nonumber \\&\quad +b_{l,n}^{\dagger }b_{l,n}b_{l,n}b_{l,n} +b_{l,n}b_{l,n}^{\dagger }b_{l,n}^{\dagger }b_{l,n}^{\dagger } +b_{l,n}b_{l,n}^{\dagger }b_{l,n}b_{l,n}\Big ]\nonumber \\&\quad +\sum _{l}\sum _{n}\frac{\hbar c_{x}}{4m\omega _{0}}\Big [b_{l,n}^{\dagger }b_{l,n}^{\dagger }+ b_{l,n}b_{l,n}+ b_{l-1,n}^{\dagger }b_{l-1,n}^{\dagger } \nonumber \\&\quad + b_{l-1,n}b_{l-1,n}-b_{l-1,n}^{\dagger }b_{l,n}^{\dagger }-b_{l-1,n}b_{l,n}\nonumber \\&\quad -b_{l,n}^{\dagger }b_{l-1,n}^{\dagger }-b_{l,n}b_{l-1,n}\Big ]\nonumber \\&\quad +\sum _{l}\sum _{n}\frac{\hbar c_{y}}{4m\omega _{0}}\Big [b_{l,n}^{\dagger }b_{l,n}^{\dagger }\nonumber \\&\quad + b_{l,n}b_{l,n}+ b_{l,n-1}^{\dagger }b_{l,n-1}^{\dagger }\nonumber \\&\quad +b_{l,n-1}b_{l,n-1}-b_{l,n-1}^{\dagger }b_{l,n}^{\dagger }-b_{l,n-1}b_{l,n}\nonumber \\&\quad -b_{l,n}^{\dagger }b_{l,n-1}^{\dagger }-b_{l,n}b_{l,n-1}\Big ]\nonumber \\&\quad i\frac{d\langle b_{l, n}\rangle }{dt}=\langle [b_{l, n}, H_{eff}]\rangle \end{aligned}$$
(60)
$$\begin{aligned}&{[}b_{l,n},H_{eff}]=\sum _{l}\sum _{n}\frac{\hbar {\omega _0}}{4}[b_{l,n}, b^{\dagger }_{l,n}b_{l,n}+b_{l,n}b^{\dagger }_{l,n}]\nonumber \\&\quad +\sum _{l}\sum _{n} \frac{\hbar {c_x}}{4m\omega _0}[b_{l,n},b^{\dagger }_{l,n}b_{l,n}+b_{l,n}b^{\dagger }_{l,n}]\nonumber \\&\quad +\sum _{l}\sum _{n}\frac{\hbar {c_x}}{4m\omega _0}[b_{l,n},b^{\dagger }_{l-1,n} b_{l-1,n}+b_{l-1,n}b^{\dagger }_{l-1,n}]\nonumber \\&\quad -\sum _{l}\sum _{n} \frac{\hbar {c_x}}{4m\omega _0}[b_{l,n},2(b^{\dagger }_{l,n}b_{l-1,n}+b_{l,n}b^{\dagger }_{l-1,n})]\nonumber \\&\quad +\sum _{l}\sum _{n}\frac{\hbar {c_y}}{4m\omega _0}[b_{l,n}, b^{\dagger }_{l,n}b_{l,n}+b_{l,n}b^{\dagger }_{l,n}]\nonumber \\&\quad +\sum _{l}\sum _{n} \frac{\hbar {c_y}}{4m\omega _0}[b_{l,n},b^{\dagger }_{l,n-1}b_{l,n-1} +b_{l,n-1}b^{\dagger }_{l,n-1}]\nonumber \\&\quad -\sum _{l}\sum _{n}\frac{\hbar {c_y}}{4m\omega _0}[b_{l,n},2(b^{\dagger }_{l,n}b_{l,n-1} +b_{l,n}b^{\dagger }_{l,n-1})]\nonumber \\&\quad +\sum _{l}\sum _{n}\frac{k_2\hbar }{4m\omega _0} [b_{l,n},b^{\dagger }_{l,n}b_{l,n}+b_{l,n}b^{\dagger }_{l,n}]\nonumber \\&\quad +\sum _{l}\sum _{n}\frac{k_4}{4}\left( \frac{\hbar }{2m\omega _0}\right) ^2[b_{l,n}, 6b^{\dagger }_{l,n}b^{\dagger }_{l,n}b_{l,n}b_{l,n}]\nonumber \\&\quad +\sum _{l}\sum _{n}\frac{k_4}{4}\left( \frac{\hbar }{2m\omega _0}\right) ^2 \left( [b_{l,n},12b^{\dagger }_{l,n}b_{l,n}]+[b_{l,n},3]\right) \end{aligned}$$
(61)
$$\begin{aligned}&i\hbar \frac{\partial {b_{l,n}}}{\partial {t}} =\hbar \bigg [\frac{\omega _0}{2}b_{l,n}+\frac{c_x}{m\omega _0}b_{l,n}\nonumber \\&\quad +\frac{c_y}{m\omega _0}b_{l,n}+3k_4\hbar \left( \frac{1}{2m\omega _0}\right) ^2b_{l,n}\nonumber \\&\quad +\frac{k_2}{2m\omega _0}b_{l,n}\nonumber \\&\quad -\frac{c_x}{2m\omega _0}(b_{l,n+1}-b_{l,n-1}) -\frac{c_y}{2m\omega _0}(b_{l+1,n}-b_{l-1,n})\nonumber \\&\quad +3k_4\hbar \left( \frac{1}{2m\omega _0}\right) ^2b^{\dagger }_{l,n}b_{l,n}b_{l,n}\bigg ] \end{aligned}$$
(62)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ribama, R.A.A., Djoufack, Z.I. & Nguenang, J.P. Breather-impurity interactions and modulational instability in a quantum 2D Klein–Gordon chain. Eur. Phys. J. B 95, 86 (2022). https://doi.org/10.1140/epjb/s10051-022-00337-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjb/s10051-022-00337-6

Search

Navigation