Oscillations of photonic heat current through parallel-coupled double circular mesoscopic Josephson junction devices

Abstract

The parallel-coupled double circular mesoscopic Josephson junction devices connecting to two photon reservoirs are investigated, and the time-dependent photonic heat current formula is derived. The time-oscillating structures of heat current are contributed by the superposition of heat current branches with frequencies $0,\pm \omega _i,\pm 2\omega _i$ ($i=1,2$). The frequency ratio $\omega _{2}/\omega _{1}$ of field-induced oscillation branches dominates the current evolution structure. The main oscillation wave package can be superposed by multiple resonant peaks as the two frequencies do not match entirely. As magnetic fluxes $\Phi _{i}$ possess the relation $\Phi _{2}=m\Phi _{1}$, the dc photonic heat current versus $\Phi _{1}$ exhibits maximum values with equal height located at $\Phi _{1}=n\Phi _{0}$, where m, n are integers, and $\Phi _0$ is the flux quantum. The main peaks are split to form multi-peak structure, and the number of split resonant peaks in a period $\Phi _0$ is equal to m. The detailed behavior is intimately ascribed to whether m being odd or even.

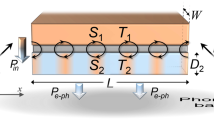
Graphic abstract

Appendices

Appendix A

In the derivation of Eq. (6), the Keldysh Green’s function of two times t and $t^\prime$ defined as

$$\begin{aligned} \langle \langle {\hat{I}}_{j}(t){\hat{a}}^\dag _{\gamma k}(t^\prime )\rangle \rangle ^<=-\frac{i}{\hbar }\langle {\hat{a}}^\dag _{\gamma k}(t^\prime ){\hat{I}}_{j}(t)\rangle \end{aligned}$$

(A1)

is involved in the current formula. The photon operator ${\hat{a}}_{\gamma k}(t)$ describing the terminal photons coupled with CMJDs is determined by the equation of motion (EOM). Through algebraic evaluation and ensemble average, we express the EOM of terminal photon operator as the integration equation, and we obtain integration form of retarded Green’s function $\langle \langle {\hat{I}}_{j}(t),{\hat{a}}^\dag _{\gamma k}(t^\prime )\rangle \rangle ^r$. The Keldysh Green’s function $\langle \langle {\hat{I}}_{j}(t){\hat{a}}^\dag _{\gamma k}(t^\prime )\rangle \rangle ^<$ is given by the connection of Langreth’s relation [40]. This procedure of treatment results in the heat current formula displayed in Eq. (6).

The retarded (advanced) Green’s function for the current operators in the CMJDs is defined as

$$\begin{aligned} \langle \langle {\hat{I}}_{j}(t),{\hat{I}}_{j^\prime }(t^\prime )\rangle \rangle ^{r(a)}=\mp \frac{i}{\hbar }\theta (\pm t\mp t^\prime )\langle [{\hat{I}}_{j}(t),{\hat{I}}_{j^\prime }(t^\prime )]\rangle .\ \ \ \end{aligned}$$

(A2)

The Keldysh Green’s functions of the current operators in the CMJDs are defined by

$$\begin{aligned} \langle \langle {\hat{I}}_{j}(t),{\hat{I}}_{j^\prime }(t^\prime )\rangle \rangle ^{<}=-\frac{i}{\hbar }\langle {\hat{I}}_{j^\prime }(t^\prime ){\hat{I}}_{j}(t)\rangle , \end{aligned}$$

(A3)

and

$$\begin{aligned} \langle \langle {\hat{I}}_{j}(t),{\hat{I}}_{j^\prime }(t^\prime )\rangle \rangle ^{>}=-\frac{i}{\hbar }\langle {\hat{I}}_{j}(t){\hat{I}}_{j^\prime }(t^\prime )\rangle . \end{aligned}$$

(A4)

We derive the retarded Green’s function by employing EOM approach. Substituting the total Hamiltonian into the Heisenberg equation $i\hbar \frac{d }{d t}{\hat{b}}_j(t)=[{\hat{b}}_j, H]$, by subtle algebra evaluations, we have

$$\begin{aligned} i\hbar \frac{d }{d t}{\hat{b}}_j(t)= & {} {\hat{\zeta }}_j(t)+E_{C_j}({\hat{b}}_j-{\hat{b}}_j^\dag )\nonumber \\+ & {} \sum _{\gamma }I_{0j}M_{\gamma j}{\hat{i}}_{\gamma } +\mathcal { M}_{ij}I_{0j}{\hat{I}}_i, \end{aligned}$$

(A5)

for $i\ne j$, and $i,j=1,2$. We have defined ${\hat{\zeta }}_j(t) = E_{J_j}\sin ({\hat{z}}_j)+2E_{L_j}\sin (2{\hat{z}}_j)$, ${\hat{z}}_j={\hat{\theta }}_{_j}+ \omega _j t$, ${\hat{\theta }}_{j}={\hat{b}}_j+{\hat{b}}^{\dag }_j$, $E_{C_j}=\frac{e^2}{C_j}$, $E_{L_j}=L_jI_{C_j}^{2}/4$. There exits the relation ${\hat{\zeta }}_j^{\dag }(t)={\hat{\zeta }}_j(t)$. The term ${\mathcal {M}}_{ij}I_{0j}{\hat{I}}_i$ describes the coupling of two CMJDs through mutual inductance ${\mathcal {M}}_{ij}$, where ${\hat{I}}_i=I_{0i}\big ({\hat{b}}_i+{\hat{b}}^{\dag }_i\big )$. Making complex conjugation over the EOM of ${\hat{b}}_j(t)$, we can write out the EOM for the operator ${\hat{b}}_j^{\dag }(t)$. The retarded Green’s function $\langle \langle {\hat{b}}_i(t),{\hat{b}}^\dag _i(t^\prime )\rangle \rangle ^r$, for instance, is defined by

$$\begin{aligned} \langle \langle {\hat{b}}_i(t),{\hat{b}}^\dag _i(t^\prime )\rangle \rangle ^r=-\frac{i}{\hbar }\theta ( t- t^\prime )\langle [{\hat{b}}_i(t),{\hat{b}}^\dag _i(t^\prime )]\rangle . \end{aligned}$$

(A6)

Employing the EOMs for operators ${\hat{b}}_i(t)$ and ${\hat{b}}_i^{\dag }(t)$, we can derive the EOMs for the retarded Green’s functions. Making Fourier transformation over times t and $t^\prime$, we transfer the EOMs into algebraic equations for $\langle \langle {\hat{b}}_{i}(\epsilon ),{\hat{b}}_{i^\prime }(\epsilon ^\prime )\rangle \rangle ^{r}, \ \langle \langle {\hat{b}}_{i}(\epsilon ),{\hat{b}}_{i^\prime }^\dag (\epsilon ^\prime )\rangle \rangle ^{r}, \ \ \langle \langle {\hat{b}}_{i}^\dag (\epsilon ),{\hat{b}}_{i^\prime }(\epsilon ^\prime )\rangle \rangle ^{r}, \langle \langle {\hat{b}}_{i}^\dag (\epsilon ),{\hat{b}}_{i^\prime }^\dag (\epsilon ^\prime )\rangle \rangle ^{r}\$. Therefore, to find the heat current Eq. (8), one has to derive each Greens function of operators ${\hat{b}}_{i}(\epsilon )$ and ${\hat{b}}_{i}^\dag (\epsilon )$. The retarded Green’s functions of a CMJD are coupled with the others, and we solve them self-consistently. Here, we present only one algebraic EOM in the same CMJD as example

$$\begin{aligned}&\langle \langle {\hat{b}}_i(\epsilon ),{\hat{b}}^\dag _i(\epsilon ^\prime )\rangle \rangle ^r ={\widetilde{\Theta }}_i(\epsilon ) \Big \{ 2\pi \hbar \delta (\epsilon -\epsilon ^\prime )\nonumber \\&\quad + \Big [1-{\bar{G}}^r_{C_i}(\epsilon ) \big [\chi ^r_{ii}(\epsilon ) -E_{C_i} \big ]\Big ] \langle \langle {\hat{\zeta }}_i(\epsilon ),{\hat{b}}_i^\dag (\epsilon ^\prime )\rangle \rangle ^r\nonumber \\&\quad +\Big [ \big [\chi ^r_{ij}(\epsilon ) +{\mathcal {M}}_{ji}I_{0i}I_{0j} \big ]\nonumber \\&\quad -{\bar{G}}^r_{C_i}(\epsilon ) \big [\chi ^r_{ii}(\epsilon ) -E_{C_i} \big ]\big [\chi ^r_{ij}(\epsilon )^* +{\mathcal {M}}_{ji}I_{0i}I_{0j} \big ] \Big ]\nonumber \\&\quad \times \langle \langle \big ({\hat{b}}_j(\epsilon )+{\hat{b}}^{\dag }_j(\epsilon )\big ),{\hat{b}}_i^\dag (\epsilon ^\prime )\rangle \rangle ^r \Big \},\nonumber \\ \end{aligned}$$

(A7)

where the subscribes $i\ne j$. In the equation above, we have defined the function ${\widetilde{\Theta }}_i(\epsilon )$ by the following form:

$$\begin{aligned} {\widetilde{\Theta }}_i(\epsilon )=\frac{{\widetilde{G}}^r_{C_i}(\epsilon )}{1+{\bar{G}}^r_{C_i}(\epsilon )\mid \big [\chi ^r_{ii}(\epsilon ) -E_{C_i} \big ]\mid ^2 {\widetilde{G}}^r_{C_i}(\epsilon ) }, \end{aligned}$$

(A8)

where

$$\begin{aligned} {\widetilde{G}}^r_{C_i}(\epsilon ) =\frac{1}{\epsilon -E_{C_i}-\chi ^r_{ii}(\epsilon )}, \ \ {\bar{G}}^r_{C_i}(\epsilon ) =\frac{1}{\epsilon +E_{C_i}+\chi ^r_{ii}(\epsilon )^*}, \end{aligned}$$

and

$$\begin{aligned} \chi ^r_{ij^\prime }(\epsilon )=\sum _{\gamma k }M_{\gamma i}M_{\gamma j^\prime } \kappa _{\gamma }^2I_{0i}I_{0j^\prime }\Delta {\mathcal {G}}^r_{\gamma k}(\epsilon ), \end{aligned}$$

(A9)

where $\Delta {\mathcal {G}}^r_{\gamma k}(\epsilon )={\mathcal {G}}^r_{\gamma k}(\epsilon ) -\bar{{\mathcal {G}}}^r_{\gamma k}(\epsilon )$. The retarded and advanced Green’s functions of photons in the Fourier transformed version are ${\mathcal {G}}_{\gamma k}^{r(a)}(\epsilon )=1/[ \epsilon -\hbar \omega _{\gamma k}\pm i\eta ]$. The corresponding Green’s functions of anti-particle are given by $\bar{{\mathcal {G}}}_{\gamma k}^{r(a)}(\epsilon ) =1/[\epsilon +\hbar \omega _{\gamma k}\pm i\eta ]$.

Appendix B

We evaluate the Green’s functions through the procedure similar to the mean-field theory by decoupling the higher order Green’s functions of ${\hat{b}}_i(\epsilon )$ and ${\hat{b}}_i^\dag (\epsilon )$ in the EOMs. This treatment can be performed by taking the approximation for Green’s functions as $\langle \langle {\hat{\zeta }}_i(\epsilon ),{\hat{b}}_i^\dag (\epsilon ^\prime )\rangle \rangle ^r\approx \langle \langle {\hat{\zeta }}_i(\epsilon ),{\hat{b}}_i^\dag (\epsilon ^\prime )\rangle \rangle _0^r$ in Eq. (A7). The notation “$\langle \langle ..,..\rangle \rangle _0^r$” indicates taking ensemble average over the state of oscillator. We take the quantum state of an oscillator as the base state of CMJD by $\mid n \rangle =\frac{({\hat{b}}_i^{\dag })^n}{\sqrt{n!}}\mid 0 \rangle$. We expand ${\hat{\zeta }}_i(t)$ in series of operators ${\hat{b}}_{\gamma }(\epsilon )$ and ${\hat{b}}_{\gamma }^\dag (\epsilon )$, and consider the ensemble average in the linear LC oscillator of the device with Hamiltonian $H_{0i}=\hbar \omega _{0i}({\hat{b}}_i^\dag {\hat{b}}_i+\frac{1}{2})$. The ensemble average of an arbitrary quantum operator [29] ${\hat{A}}$ is given by

$$\begin{aligned} \langle {\hat{A}}\rangle =\Delta _{0i}\sum _{n=0}^{\infty }\langle n\mid e^{-\beta _{0i}\hbar \omega _{0i}n}{\hat{A}}\mid n\rangle , \end{aligned}$$

(B1)

where $\Delta _{0i}=1-e^{-\beta _{0i}\hbar \omega _{0i}}$, and $\beta _{0i}=1/(k_BT_{0i})$. In Heisenberg representation, the boson operators ${\hat{b}}_i$ and ${\hat{b}}_i^{\dag }$ vary with time t as ${\hat{b}}(t)={\hat{b}}_i e^{-i\omega _{0i}t},\ \ {\hat{b}}_i^{\dag }(t)={\hat{b}}^{\dag }e^{i\omega _{0i}t}.$ As the operator $e^{- u_i {\hat{b}}_i}$ acts on the number state, we have

$$\begin{aligned} e^{- u_i{\hat{b}}_i}\mid n\rangle =\sum _{\ell =0}^{n}\frac{(-u_i)^{\ell }}{\ell !}\sqrt{\frac{n!}{(n-\ell )!}}\mid n-\ell \rangle , \end{aligned}$$

(B2)

where $u_i$ is a complex as $u_i=ie^{-i\omega _{0i}t}$.

In the derivation of Green’s function matrices of Eq. (10), the function ${\varvec{G}}^{r}_{\zeta }(\epsilon ,\epsilon ')$ is presented, which is a diagonal matrix associated with the CMJDs and time-oscillation effect defined by

$$\begin{aligned} {\varvec{G}}^{X}_{\zeta }(\epsilon ,\epsilon ') =\left( \begin{array}{cc} G^X_{\zeta _1}(\epsilon ,\epsilon '),&{} 0\\ 0,&{} G^X_{\zeta _2}(\epsilon ,\epsilon ') \end{array} \right) , \end{aligned}$$

where $X\in \{r,a,<,>\}$. The elements are defined by

$$\begin{aligned} G^{X}_{\zeta _j}(\epsilon ,\epsilon ^\prime )=\langle \langle {\hat{\zeta }}_j(\epsilon ),{\hat{b}}_j^\dag (\epsilon ^\prime )\rangle \rangle ^{X} +\langle \langle {\hat{\zeta }}_j(\epsilon ),{\hat{b}}_j(\epsilon ^\prime )\rangle \rangle ^{X},\ \ \ \end{aligned}$$

(B3)

for $j=1,2$. The function ${\hat{\zeta }}_j(\epsilon )$ is the Fourier transformed version of the operator ${\hat{\zeta }}_j(t)$ defined in Eq. (A5). Through evaluating over the expectation values, and making rearrangement over the summation, we obtain $G^{X}_{\zeta _i}(\epsilon ,\epsilon ^\prime ) =\Delta _{0i} \Delta {\mathcal {G}}^X_{0i}(\epsilon ^\prime ) X_i( {\bar{\epsilon }}),$ where ${\bar{\epsilon }} =\epsilon -\epsilon ^\prime$, $\Delta {\mathcal {G}}^X_{0i}(\epsilon )={\mathcal {G}}^X_{0i}(\epsilon ) -\bar{{\mathcal {G}}}^X_{0i}(\epsilon )$. We have defined the function $X_i( {\bar{\epsilon }})$ in above formula by

$$\begin{aligned} X_i( {\bar{\epsilon }})= \sum _{n=0}^{\infty }\sum _{\ell =0}^{n} \frac{(-1)^{\ell }}{(\ell !)^2}\frac{n!}{(n-\ell )!}e^{-\beta \hbar \omega _{0i}n} {\widetilde{W}}^{(i)}_{\ell +1}({\bar{\epsilon }}), \end{aligned}$$

(B4)

where

$$\begin{aligned} {\widetilde{W}}^{(i)}_{\ell }({\bar{\epsilon }})=(2\pi \hbar )\frac{1}{2}\big \{E_{J_i}e^{-\frac{1}{2}}[\delta ({\bar{\epsilon }}+\hbar \omega _i) +\delta ({\bar{\epsilon }}-\hbar \omega _i)]\nonumber \\ +E_{L_i}e^{-2}4^{\ell }[\delta ({\bar{\epsilon }}+2\hbar \omega _i) +\delta ({\bar{\epsilon }}-2\hbar \omega _i)]\big \}.\ \ \ \end{aligned}$$

(B5)

In the derivation of heat current, we encounter the retarded and advanced Green’s functions of photons in the Fourier transformed version ${\mathcal {G}}_{\gamma k}^{r(a)}(\epsilon )$. The corresponding Keldysh Green’s functions of photons are expressed by

$$\begin{aligned} {\mathcal {G}}^<_{\gamma k}(\epsilon )= & {} -i2\pi \delta (\epsilon -\hbar \omega _{\gamma k})n_\gamma (\epsilon ),\nonumber \\ \ {\mathcal {G}}^>_{\gamma k}(\epsilon )= & {} -i2\pi \delta (\epsilon -\hbar \omega _{\gamma k}) [n_\gamma (\epsilon )+1]. \end{aligned}$$

(B6)

The corresponding Green’s functions of anti-particle are given by

$$\begin{aligned} \bar{{\mathcal {G}}}^<_{\gamma k}(\epsilon )= & {} -i2\pi \delta (\epsilon +\hbar \omega _{\gamma k})n_\gamma (\epsilon ),\nonumber \\ \bar{{\mathcal {G}}}^>_{\gamma k}(\epsilon )= & {} -i2\pi \delta (\epsilon +\hbar \omega _{\gamma k})[n_\gamma (\epsilon )+1]. \end{aligned}$$

(B7)

The retarded Green’s function matrices ${\varvec{G}}^{r}_A(\epsilon )$, ${\varvec{G}}^{r}_B(\epsilon )$ in Eq. (10) are given by

$$\begin{aligned} {\varvec{G}}^{r}_A(\epsilon )= & {} \frac{2\epsilon }{ \Xi (\epsilon )} \left( \begin{array}{cc} \varepsilon _2(\epsilon ), &{} \sigma _{12}(\epsilon ) \\ \sigma _{21}(\epsilon ) ,&{}\varepsilon _1(\epsilon ) \end{array} \right) , \end{aligned}$$

(B8)

$$\begin{aligned} {\varvec{G}}^{r}_B(\epsilon )= & {} \frac{ 4 }{\Xi (\epsilon )} \left( \begin{array}{cc} E_{C_1}\varepsilon _2(\epsilon ) ,&{} E_{C_2}\sigma _{12}(\epsilon )\\ E_{C_1} \sigma _{21}(\epsilon ) ,&{}E_{C_2}\varepsilon _1(\epsilon ) \end{array} \right) , \end{aligned}$$

(B9)

where $\Xi (\epsilon )= \varepsilon _1(\epsilon ) \varepsilon _2(\epsilon )- \sigma _{21}(\epsilon )\sigma _{12}(\epsilon )$, and

$$\begin{aligned} \sigma _{ji}(\epsilon )= & {} 2\big [ 2E_{C_j}Re\chi ^r_{ji}(\epsilon )+2E_{C_j}\mathcal { M}_{ij}I_{0j}I_{0i}+i\epsilon Im\chi ^r_{ji}(\epsilon )\big ],\ \ \\ \varepsilon _j(\epsilon )= & {} \epsilon ^2-4E_{C_j}Re\chi ^r_{jj}(\epsilon )-2i\epsilon Im \chi ^r_{jj}(\epsilon ), \ \ \ \ (i\ne j). \end{aligned}$$

The functions $\chi _{ij}^{X}(\epsilon )$ describing the properties of photon reservoirs are defined by

$$\begin{aligned} \chi _{ij}^{X}(\epsilon )=\sum _{\gamma k } \kappa _{\gamma }^2 U_{\gamma ,ij}\Delta {\mathcal {G}}^{X}_{\gamma k}(\epsilon ),\ \ X\in \{r,a,>,<\}, \end{aligned}$$

(B10)

where $\Delta {\mathcal {G}}^{X}_{\gamma k}(\epsilon )= {\mathcal {G}}^{X}_{\gamma k}(\epsilon )-\bar{{\mathcal {G}}}^{X}_{\gamma k}(\epsilon )$. Due to the symmetric and asymmetric relations $Re\chi ^r_{ji}(\epsilon )=Re\chi ^r_{ji}(-\epsilon )$, and $Im \chi ^r_{ji}(\epsilon )=- Im \chi ^r_{ji}(-\epsilon )$, we have $\sigma _{ji}(\epsilon )=\sigma _{ji}(-\epsilon )$, and $\varepsilon _j(\epsilon )=\varepsilon _j(-\epsilon )$.

In Eq. (B3), ${\mathcal {G}}^X_{0i}(\epsilon )$ signifies the retarded (advanced), and Keldysh Green’s functions of free bosons in the ith CMJD denoted by ${\mathcal {G}}^{r(a)}_{0i}(\epsilon )=1/(\epsilon -\hbar \omega _{0i}\pm i\eta ) ,\$ and

$$\begin{aligned} {\mathcal {G}}^<_{0i}(\epsilon )= & {} -i2\pi \delta (\epsilon -\hbar \omega _{0i})n_{0i}(\epsilon ), \nonumber \\ {\mathcal {G}}^>_{0i}(\epsilon )= & {} -i2\pi \delta (\epsilon -\hbar \omega _{0i})[n_{0i}(\epsilon )+1]. \end{aligned}$$

(B11)

The expression $\bar{{\mathcal {G}}}^X_{0i}(\epsilon )$ indicates corresponding retarded (advanced), and Keldysh functions of free anti-bosons in the ith CMJD given by $\bar{{\mathcal {G}}}^{r(a)}_{0i}(\epsilon )= 1/(\epsilon +\hbar \omega _{0i}\pm i\eta )$, and

$$\begin{aligned} \bar{{\mathcal {G}}}^<_{0i}(\epsilon )= & {} -i2\pi \delta (\epsilon +\hbar \omega _{0i})n_{0i}(\epsilon ),\nonumber \\ \bar{{\mathcal {G}}}^>_{0i}(\epsilon )= & {} -i2\pi \delta (\epsilon +\hbar \omega _{0i})[n_{0i}(\epsilon )+1]; \end{aligned}$$

(B12)

$n_{0i}(\epsilon )$ is the distribution function of free bosons in the ith CMJD.

The Keldysh self-energy matrices $\varvec{\Sigma }_{A(B)}^{>,<}(\epsilon )$ in Eqs. (12) and (13) are explicitly given by

$$\begin{aligned} \varvec{\Sigma }_A^{>,<}(\epsilon )= & {} \left( \begin{array}{cc} \chi _{11}^{>,<}(\epsilon ) ,&{} \chi _{12}^{>,<}(\epsilon ) \\ \chi _{21}^{>,<}(\epsilon ),&{} \chi _{22}^{>,<}(\epsilon ) \end{array} \right) ,\ \ \ \end{aligned}$$

(B13)

$$\begin{aligned} \varvec{\Sigma }^{>,<}_B(\epsilon )= & {} \frac{\epsilon }{2} \left( \begin{array}{cc} \chi ^{>,<}_{11}(\epsilon )/E_{C_1},&{} \chi ^{>,<}_{12}(\epsilon ) /E_{C_1} \\ \chi ^{>,<}_{21}(\epsilon ) /E_{C_2},&{} \chi ^{>,<}_{22}(\epsilon )/E_{C_2} \end{array} \right) .\ \ \ \ \ \ \end{aligned}$$

(B14)

There exists the relation

$$\begin{aligned} \chi ^r_{ij}(\epsilon )-\chi _{ij}^a(\epsilon )=\chi _{ij}^{> }(\epsilon )- \chi _{ij}^{< }(\epsilon ) =-i\Gamma _{ij}(\epsilon ), \end{aligned}$$

(B15)

where $Im\chi ^r_{ij}(\epsilon )=-\frac{1}{2}\Gamma _{ij}(\epsilon )$, and $\Gamma _{ij}(\epsilon )=\sum _{\gamma }\Gamma _{\gamma ,ij}(\epsilon )$ are the elements of $\varvec{ \Gamma }_{\gamma }(\epsilon )$ .

The advanced Green’s function matrices ${\varvec{G}}^{a}_A(\epsilon )$, ${\varvec{G}}^{a}_B(\epsilon )$ and ${\varvec{G}}^{a}_{\zeta }(\epsilon ,\epsilon ')$ are obtained by taking complex conjugation over corresponding retarded Green’s function matrices as ${\varvec{G}}^{a}_A(\epsilon )={\varvec{G}}^{r}_A(\epsilon )^\dag , \ {\varvec{G}}^{a}_B(\epsilon )={\varvec{G}}^{r}_B(\epsilon )^\dag , \ {\varvec{G}}^{a}_{\zeta }(\epsilon ,\epsilon ')={\varvec{G}}^{r}_{\zeta }(\epsilon ,\epsilon ')^\dag .$ The imaginary part of retarded Green’s function matrix is determined by $Im {\varvec{G}}^{r}(\epsilon ',\epsilon ) =\frac{1}{2i}\big [ {\varvec{G}}^{r}(\epsilon ',\epsilon ) -{\varvec{G}}^{a}(\epsilon ',\epsilon )\big ]$.

Appendix C

The matrix ${\varvec{W}}_{\gamma }(\epsilon )$ in Eq. (18) is defined by

$$\begin{aligned} {\varvec{W}}_{\gamma }(\epsilon ) =\left( \begin{array}{cc} U_{\gamma , 11}\epsilon /E_{C_1},&{} U_{\gamma ,12}\epsilon /E_{C_1} \\ U_{\gamma ,21}\epsilon /E_{C_2},&{} U_{\gamma ,22}\epsilon /E_{C_2} \end{array} \right) . \end{aligned}$$

The functions involved in Eq. (20 ) are given by

$$\begin{aligned}&P^{(i)}_{\gamma }( \epsilon ,\epsilon ^\prime ) =\xi _i(\epsilon )Re \gamma _i(\epsilon ^\prime ) + \Delta _{0i}Re\big [\Delta {\mathcal {G}}^r_{0i} (\epsilon ) \big ] \nonumber \\&\quad \times Re \widetilde{\varvec{{\mathcal {T}}}}^B_{\gamma \gamma ,ii }(\epsilon ^\prime ),\ \ \ \ \ \ \end{aligned}$$

(C1)

$$\begin{aligned}&O^{(i)}_{\gamma }( \epsilon ,\epsilon ^\prime )=\Delta _{0i}Re\big [\Delta {\mathcal {G}}^r_{0i} (\epsilon )\big ]\Big (Re \gamma _i(\epsilon ^\prime ) + \frac{1}{2} Im \widetilde{\varvec{{\mathcal {T}}}}^B_{\gamma \gamma ,ii }(\epsilon ^\prime )\Big )\nonumber \\&\quad +\frac{1}{2}\xi _i(\epsilon ) Im \gamma _i(\epsilon ^\prime ),\ \ \ \ \ \ \end{aligned}$$

(C2)

$$\begin{aligned}&\gamma _i(\epsilon ^\prime )=\varphi _i^2{\varvec{G}}^{r}_{B,ii}(\epsilon ^\prime )+\varphi _i\varphi _{i^\prime }{\varvec{G}}^{r}_{B,i^\prime i}(\epsilon ^\prime ), \ \ (i\ne i^\prime ). \end{aligned}$$

(C3)

The transmission coefficients $\sum _i\widetilde{\varvec{{\mathcal {T}}}}^A_{\gamma \beta ,ii }(\epsilon )$ and $\sum _i\widetilde{\varvec{{\mathcal {T}}}}^B_{\gamma \beta ,ii }(\epsilon )$ are derived from $\varvec{{\mathcal {T}}}^A_{\gamma \beta }(\epsilon )$ and $\varvec{{\mathcal {T}}}^B_{\gamma \beta }(\epsilon ,\epsilon ^\prime )$ defined by Eqs. (15) and (16). Substituting corresponding quantities and accomplishing the evaluations, we obtain the transmission coefficient $\sum _i\widetilde{\varvec{{\mathcal {T}}}}^A_{\gamma \beta ,ii }(\epsilon )$ expressed as the form

$$\begin{aligned}&\sum _i\widetilde{\varvec{{\mathcal {T}}}}^A_{\gamma \beta ,ii }(\epsilon ) = \Psi _{\beta }(\epsilon )\frac{ 2\kappa \epsilon ^3 }{\mid \Xi (\epsilon )\mid ^2} \sum _i\Big \{ \varphi ^2_i\varphi ^2_{i} \mid \varepsilon _{i^\prime }(\epsilon )\mid ^2\nonumber \\&\quad +3 \varphi _i^3\varphi _{i^\prime } Re\big \{\varepsilon _{i^\prime }(\epsilon )\sigma _{ii^\prime }(\epsilon )^* \big \} + \varphi _{i}^2\varphi _{i^\prime }^2\Big (2\mid \sigma _{ii^\prime }\mid ^2\nonumber \\&\quad +Re[\varepsilon _i\varepsilon _{i^\prime }^*] \Big ) + \varphi _{i}\varphi _{i^\prime }^3 Re\big \{\varepsilon _{i}(\epsilon )\sigma _{i^\prime i}(\epsilon )^* \big \} \Big \}.\ \ \end{aligned}$$

(C4)

The real and imaginary parts of $\widetilde{\varvec{{\mathcal {T}}}}^B_{\gamma \gamma ,ii }(\epsilon )$ are concretely determined by

$$\begin{aligned}&Re \widetilde{\varvec{{\mathcal {T}}}}^B_{\gamma \gamma ,ii }(\epsilon ) = \kappa \Psi _{\beta }(\epsilon )\epsilon ^2\frac{ 4 E_{C} }{\mid \Xi (\epsilon )\mid ^2} \Big \{ \varphi ^2_i\varphi ^2_{i} \mid \varepsilon _{i^\prime }(\epsilon )\mid ^2\nonumber \\&\quad +3 \varphi _i^3\varphi _{i^\prime } Re\big \{\varepsilon _{i^\prime }(\epsilon )\sigma _{ii^\prime }(\epsilon )^* \big \} + \varphi _{i}^2\varphi _{i^\prime }^2\Big (2\mid \sigma _{ii^\prime }\mid ^2\nonumber \\&\quad +Re[\varepsilon _i\varepsilon _{i^\prime }^*] \Big ) + \varphi _{i}\varphi _{i^\prime }^3 Re\big \{\varepsilon _{i}(\epsilon )\sigma _{i^\prime i}(\epsilon )^* \big \} \Big \},\ \nonumber \\ \end{aligned}$$

(C5)

$$\begin{aligned}&Im \widetilde{\varvec{{\mathcal {T}}}}^B_{\gamma \beta ,ii }(\epsilon ) = \kappa \Psi _{\beta }(\epsilon )\epsilon ^2\frac{ 4 E_{C} }{\mid \Xi (\epsilon )\mid ^2} \Big \{ \varphi _{i}^2\varphi _{i^\prime }^2 Im[\varepsilon _i\varepsilon _{i^\prime }^*]\ \ \nonumber \\&\quad + \varphi _{i}\varphi _{i^\prime }^3 Im\big \{\varepsilon _{i}(\epsilon )\sigma _{i^\prime i}(\epsilon )^* \big \} -\varphi _{i^\prime }\varphi _{i}^3 Im\big \{\varepsilon _{i^\prime }(\epsilon )\sigma _{i i^\prime }(\epsilon )^* \big \} \Big \},\nonumber \\ \end{aligned}$$

(C6)

where $\kappa = \frac{2}{\hbar R_{\gamma }} M_0^2I_{0}^2$. The contribution of magnetic fluxes $\Phi _j$ to the heat current is ascribed to the function $\varphi _j$ defined by $\varphi _j= \sqrt{ \mid \cos (\pi \Phi _j/\Phi _0)\mid ^{3/2}}.$ Both of the real and imaginary parts of the function $\widetilde{\varvec{{\mathcal {T}}}}^B_{\gamma \beta ,ii }(\epsilon )$ contribute to the time-dependent heat current.