Barrier escape from a truncated quartic potential driven by correlated Lévy noises with opposite correlation

Abstract

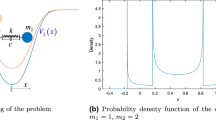
Within the numerical simulation method applied to the Langevin equation, the escape problem of particle moving in the truncated quartic potential driven by two types of correlated Lévy noise, i.e., Ornstein–Uhlenbeck Lévy noise and harmonic velocity Lévy noise, is studied. The dependence of the escape rate on the noise intensity parameter, the Lévy index, the noise correlation, and the particle mass is discussed. Results reveal that the correlation, especially the strong correlation, makes the power-law exponent $\alpha (\mu )$ and the inverse coefficient $\text {lnc}(\mu )$ present significantly different dependences on the Lévy index $\mu$. Especially, because of the distinctly opposite correlation properties of these two noises, the escape rate shows entirely opposite phenomena, i.e., the escape rate of the particles driven by the Ornstein–Uhlenbeck Lévy noise decreases with correlation increasing, whereas the escape rate of the particles driven by the harmonic velocity Lévy noise increases instead. Since the particle becomes heavy with m increasing, for the two types of correlated Lévy flight, the escape rates both decrease monotonically with particle mass increasing.

Appendices

Appendix A: Numerical algorithm of OULN

The OULN $\xi (t)$ can be generated from the generalized OULP, the detailed introduction of the numerical algorithm is presented in our previous work [33]. Here we present a brief introduction.

Solving Eq. (1) by an inverse Laplace transform, we have

$$\begin{aligned} \xi (t)=e^{-\frac{t}{\tau _c}}\xi (0)+\frac{1}{\tau _c}\int _{0}^{t}e^{\frac{s-t}{\tau _c}}L(s)\,ds \end{aligned}$$

(A1)

and

$$\begin{aligned} \xi (t+\Delta {t})=e^{-\frac{\Delta {t}}{\tau _c}}\xi (t)+\frac{1}{\tau _c}e^{-\frac{t+\Delta {t}}{\tau _c}}\int _{t}^{t+\Delta {t}}e^{\frac{s}{\tau _c}}L(s)\,ds.\nonumber \\ \end{aligned}$$

(A2)

Introducing $y=\frac{1}{\tau _c}e^{-\frac{t+\Delta {t}}{\tau _c}}\int _{t}^{t+\Delta {t}}e^{\frac{s}{\tau _c}}L(s)\,ds$, we have a characteristic function P(k),

$$\begin{aligned} P(k)= & {} \left<e^{-iky}\right> \nonumber \\= & {} \left<e^{-ik[\frac{1}{\tau _c}e^{-\frac{t+\Delta {t}}{\tau _c}}\int _{t}^{t+\Delta {t}}e^{\frac{s}{\tau _c}}L(s)\,ds]}\right> \nonumber \\= & {} e^{-\frac{D|k|^\mu }{\mu \tau _c^{\mu -1}}(1-e^{-\frac{\mu \Delta {t}}{\tau _c}})}. \end{aligned}$$

(A3)

Hence, we have

$$\begin{aligned} \xi (t+\Delta {t})=e^{-\frac{\Delta {t}}{\tau _c}}\xi (t)+\left[ {\frac{D}{\mu \tau _c^{\mu -1}}(1-e^{-\frac{\mu \Delta {t}}{\tau _c}})}\right] ^{\frac{1}{\mu }}L_{\mu },\nonumber \\ \end{aligned}$$

(A4)

in which $L_{\mu }$ is a symmetric Lévy $\mu$-stable random number [46,47,48],

$$\begin{aligned} L_{\mu }=\left( -\frac{\ln u\cos {\phi }}{\cos [(1-\mu )\phi ]}\right) ^{(1-\frac{1}{\mu })}\frac{\sin (\mu \phi )}{\cos \phi }, \end{aligned}$$

(A5)

in which $\phi = \pi (\nu -1/2)$ and $u,\nu \in (0,1)$ are independent uniform random numbers.

Finally, the numerical simulation of the Langevin equation (10) is

$$\begin{aligned} x(t+\Delta {t})= & {} x(t)+v(t)\Delta {t}, \end{aligned}$$

(A6)

$$\begin{aligned} v(t+\Delta {t})= & {} v(t)-\gamma _0 v(t)\Delta {t}-\gamma _2 v^3(t)\Delta {t}\nonumber \\&+f(x(t))\Delta {t}+\xi (t)\Delta {t}. \end{aligned}$$

(A7)

Appendix B: Numerical algorithm of HVLN

The numerical algorithm of the Langevin equation driven by HVLN can be executed by the following process. Combining Eqs. (7), (8), and (10), we have

$$\begin{aligned} {\dot{x}}= & {} v, \nonumber \\ {\dot{v}}= & {} -\gamma v+f(x(t))+u(t), \nonumber \\ {\dot{\varepsilon }}(t)= & {} u(t), \nonumber \\ {\dot{u}}(t)+ & {} \Gamma u(t)+\Omega ^2 \varepsilon (t)=L(t), \end{aligned}$$

(B1)

and the numerical calculations can be executed by

$$\begin{aligned} x(t+\Delta {t})= & {} x(t)+v(t)\Delta {t}, \nonumber \\ v(t+\Delta {t})= & {} v(t)-\gamma v(t)\Delta {t}+f(x(t))\Delta {t}+u(t)\Delta {t}, \nonumber \\ \varepsilon (t+\Delta t)= & {} \varepsilon (t)+u(t)\Delta t, \nonumber \\ u(t+\Delta t)= & {} u(t)-\Gamma u(t)\Delta t+\Omega ^2 \varepsilon (t) \Delta (t)+(D \Delta t)^{\frac{1}{\mu }}L_{\mu },\nonumber \\ \end{aligned}$$

(B2)

in which $L_{\mu }$ is generated from Eq. (A5).