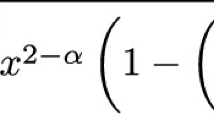Distributions of historic market data: relaxation and correlations

Abstract

We investigate relaxation and correlations in a class of mean-reverting models for stochastic variances. We derive closed-form expressions for the correlation functions and leverage for a general form of the stochastic term. We also discuss correlation functions and leverage for three specific models— multiplicative, Heston (Cox-Ingersoll-Ross) and combined multiplicative-Heston—whose steady-state probability density functions are Gamma, Inverse Gamma and Beta Prime respectively, the latter two exhibiting “fat” tails. For the Heston model, we apply the eigenvalue analysis of the Fokker-Planck equation to derive the correlation function—in agreement with the general analysis— and to identify a series of time scales, which are observable in relaxation of cumulants on approach to the steady state. We test our findings on a very large set of historic financial markets data.

Graphic abstract

Appendices

A Correlation function of multi-day realized variance

In Sect. 2 we argued that for the mean-reverting models, (2), the correlation function of stochastic variance is given, per (9), by ${\text {corr}}[v_t v_{t+\tau }] =e^{-\gamma \tau }$. The problem with this prediction is relating ${\text {corr}}[v_t v_{t+\tau }]$ to actual market quantities. For daily returns it is given by the l.h.s. of (13), however its fit with the $e^{-\gamma \tau }$ in Fig. 1 is rather poor. The latter may be attributed to that continuous, mean-reverting models of stochastic variance are not a good match for daily returns. On the other hand, they may be more appropriate for multi-day returns [12, 23]. Unfortunately, the relationship between multi-day realized² and stochastic variances is complicated, per (11), and so is determining dependence on $\tau$ in presence of two time scales, t and $\gamma$.

Consequently, we surmised, per (15), that the correlation function of multi-day realized variance is expressed by a pure exponent, ${\text {corr}}[\mathrm {d}x_t^2 \mathrm {d}x_{t+\tau }^2] \approx e^{-\gamma _1 \tau }$. We fitted ${\text {corr}}[\mathrm {d}x_t^2 \mathrm {d}x_{t+\tau }^2]$ with $a e^{-\gamma _1 \tau }$ for multi-day S&P returns (DJIA is very similar) and summarized our empirical findings, including $r^2$ statistics, in Table 3. In Fig. 5 we show exponential fit of $\gamma _1$ itself as a function of days of accumulation. In Fig. 6 we show sample $a e^{-\gamma _1 \tau }$ fits for 21, 28, 105, 112, 189 and 196 days of accumulation with parameter values from Table 3. At present, we do not have plausible interpretation of our empirical findings.

B Correlations and relaxation in Heston (Cox-Ingersoll-Ross) model

1.1 B.1 Eigenvalue solution of Fokker-Planck equation

We have previously investigated correlations and relaxation in multiplicative model [6]. Here we will apply the same approach to Heston (Cox-Ingersoll-Ross) model. To remain consistent with notations of [6], we replace $v_t$ with x (not to confuse with stock returns), drop superfluous indices and write the model as

$$\begin{aligned} \mathrm {d}x = -\gamma (x - \theta )\mathrm {d}t + \kappa \sqrt{x}\mathrm {d}W \end{aligned}$$

(34)

Obviously, via rescaling $x/\theta \rightarrow x$ and $\kappa \sqrt{\theta } \rightarrow \kappa$, this equation can be reduced to that with the unity mean

$$\begin{aligned} \mathrm {d}x = -\gamma (x -1)\mathrm {d}t + \kappa \sqrt{x}\mathrm {d}W \end{aligned}$$

(35)

For now, however, we will proceed with (34).

The Fokker-Planck equation for this process is given by

$$\begin{aligned} \frac{\partial P(x,t)}{\partial t}=\gamma \frac{\partial (x-\theta ) P(x,t)}{\partial x} +\frac{\kappa ^2}{2}\frac{\partial ^2 x P(x,t)}{\partial x^2} \end{aligned}$$

(36)

To find correlations and relaxation, we use an eigenvalue approach [2] to solving it. Namely, we seek the solution in the following form:

$$\begin{aligned} P(x,t)=P_0 (x)+P(\lambda ; x)e^{-\lambda t} \end{aligned}$$

(37)

where $\lambda >0$ and $P_0(x)$ is a Ga steady-state distribution of (34)

$$\begin{aligned} P_0(x)=\frac{e^{-\frac{2\gamma x}{\kappa ^2} }{\left( \frac{2\gamma x}{\kappa ^2}\right) }^{\frac{2\gamma \theta }{\kappa ^2}-1}}{\frac{\kappa ^2}{2\gamma }\varGamma \left( \frac{2\gamma \theta }{\kappa ^2}\right) }, \quad \frac{2\gamma \theta }{\kappa ^2} > 1 \end{aligned}$$

(38)

where the latter assures that $P_0(0)=0$. $P(\lambda ; x)e^{-\lambda t}$ describe relaxation to the steady state and we should also have $P(\lambda ; 0)=0$

Substitution of (37) into (36) yields

$$\begin{aligned} \frac{\kappa ^2}{2}(x P(\lambda ; x))^{\prime \prime }+\gamma ((x-\theta )P(\lambda ; x))^{\prime }+\lambda P(\lambda ; x)=0 \end{aligned}$$

(39)

which has two solutions

$$\begin{aligned} P_1(\lambda ; x) \propto e^{-\frac{2x\gamma }{\kappa ^2}} U \left( 1-\frac{2\gamma \theta }{\kappa ^2}-\frac{\lambda }{\gamma },2 -\frac{2\gamma \theta }{\kappa ^2},\frac{2x\gamma }{\kappa ^2}\right) \end{aligned}$$

(40)

and

$$\begin{aligned} P_2(\lambda ; x) \propto e^{-\frac{2x\gamma }{\kappa ^2}} {\mathbf {L}}^{\left( 1-\frac{2\gamma \theta }{\kappa ^2}\right) }_{\left( \frac{2\gamma \theta }{\kappa ^2}+\frac{\lambda }{\gamma }-1\right) } \left( \frac{2x\gamma }{\kappa ^2}\right) \end{aligned}$$

(41)

where U is Tricomi’s confluent hypergeometric function and L is Laguerre polynomial function. Condition $P(\lambda ; 0)=0$ cannot be satisfied by $P_2(\lambda ; x)$ and for $P_1(\lambda ; x)$ it leads to quantization of $\lambda$, $\lambda _n=n\gamma$, where $n>0$ is an integer. Consequently, the eigenfunctions of (39) are given by

$$\begin{aligned} P_1(\lambda _n ; x)&\equiv P_n(x)\propto e^{-\frac{2x\gamma }{\kappa ^2}} U\nonumber \\&\quad \left( 1-\frac{2\gamma \theta }{\kappa ^2}-n,2 -\frac{2\gamma \theta }{\kappa ^2},\frac{2x\gamma }{\kappa ^2}\right) , \quad \lambda _n=n\gamma \end{aligned}$$

(42)

Table 4 MLE-obtained parameters and KS values for fitting distribution function of relaxation times for $\gamma =10^{-1}$ and several values of $\kappa ^2$

Fig. 9

Fits of the distribution of relaxation times from Table 4 for $\kappa ^{2}=10^{-4}$ (top) and $\kappa ^{2}=0.5\times 10^{-1}$ (bottom)

Fig. 10

On log-log scale, dependence of the mean, variance and third cumulant of the relaxation time distribution on $\gamma$ for $\kappa ^2=10^{-2}$ (left) and $\kappa ^2=5 \times 10^{-3}$ (middle) for $\gamma$ varying between $10^{-2}$ and 1. For $\gamma =10^{-1}$ dependence on $\kappa$ which varies between $10^{-4}$ and 0.1 (right)

The correlation function can be found as [2]

$$\begin{aligned} \langle \delta x(t+\tau )\delta x(t)\rangle =\sum _{n} g_n^2 e^{-\lambda _n \tau } \end{aligned}$$

(43)

where

$$\begin{aligned} g_n \propto \int xP(\lambda _n;x)\mathrm {d}x=\int \delta xP(\lambda _n;x)\mathrm {d}x \end{aligned}$$

(44)

Using (42), we find

$$\begin{aligned} g_n \propto \frac{\kappa ^4\varGamma \left( 1+\frac{2\gamma \theta }{\kappa ^2}\right) }{4\gamma ^2\varGamma (2-n)} \end{aligned}$$

(45)

Clearly, the only non-zero $g_n$ is $g_1$. Using normalization condition [2]

$$\begin{aligned} \int _{0}^{\infty } \frac{P_1^2(\lambda _1;x)}{P_0(x)}\mathrm {d}x=1 \end{aligned}$$

(46)

We find

$$\begin{aligned} P_1(\lambda _1;x)=\frac{e^{-\frac{2x\gamma }{\kappa ^2}}(x-\theta ) \left( \frac{2x\gamma }{\kappa ^2}\right) ^{1+\frac{2 \theta \gamma }{\kappa ^2}}}{x^2 \sqrt{\varGamma \left( 1+\frac{2\gamma \theta }{\kappa ^2}\right) } \sqrt{\varGamma \left( \frac{2\gamma \theta }{\kappa ^2}\right) }} \end{aligned}$$

(47)

so that

$$\begin{aligned} g_1= \int _{0}^{\infty } P_1(\lambda _1;x) x \mathrm {d}x=\sqrt{\frac{\theta \kappa ^2}{2\gamma }} \end{aligned}$$

(48)

and

$$\begin{aligned} \langle \delta x(t+\tau )\delta x(t)\rangle =\theta ^2+ \frac{\theta \kappa ^2}{2\gamma }e^{-\gamma \tau } \end{aligned}$$

(49)

that is

$$\begin{aligned} \frac{\langle \delta x(t+\tau )\delta x(t)\rangle -\langle \delta x(t)\rangle ^2}{\langle \delta x(t)\rangle ^2} =\frac{\kappa ^2}{2\gamma \theta }e^{-\gamma \tau } \end{aligned}$$

(50)

which is the same result as we already found in (30). The value of eigenvalue approach, however, is to establish multiple relaxation (time) scales, which we address next.

1.2 B.2 Cumulant relaxation

As is for multiplicative model, the easiest way to observe multiple relaxation times predicted using eigenvalue method, is through relaxation of cumulants [6]. As was observed in B.1, the mean can always be set to unity, $\theta =1$, and in what follows we will use (35). We will also use two sets of initial conditions, $x(0)=0$ and $x(0)=1$. For the former, the expressions for the mean and the cumulants are given by

$$\begin{aligned} x(0)&=0: \quad \langle x\rangle =1-e^{-\gamma t}, \\ \kappa _n&=\left( \frac{\kappa ^2}{\gamma }\right) ^{n-1} \frac{(n-1)!}{2^{n-1}} e^{-n\gamma t}(e^{\gamma t} - 1)^n \end{aligned}$$

and in particular

$$\begin{aligned} x(0)&=0: \quad \kappa _2=\frac{\kappa ^2}{2\gamma }(1-2 e^{-\gamma t}+e^{-2\gamma t}),\\ \kappa _3&=\frac{\kappa ^4}{2\gamma ^2}(1-3 e^{-\gamma t}+3 e^{-2\gamma t}- e^{-3\gamma t}) \end{aligned}$$

For the latter, we have

$$\begin{aligned} x(0)&=1: \quad \langle x\rangle =1, \\ \kappa _n&=\left( \frac{\kappa ^2}{\gamma }\right) ^{n-1} \frac{(n-1)!}{2^{n-1}} e^{-n\gamma t}(e^{\gamma t} - 1)^{n-1} (e^{\gamma t} +(n-1)) \end{aligned}$$

and in particular

$$\begin{aligned} x(0)&=1: \quad \kappa _2=\frac{\kappa ^2}{2\gamma }(1 - e^{-2t\gamma }), \\ \kappa _3&=\frac{\kappa ^4}{2\gamma ^2} (1 - 3 e^{-2\gamma t} + 2 e^{-3\gamma t}) \end{aligned}$$

The behavior of the mean starting with $x(0)=0$ is shown in Fig. 7 and the behavior of the mean and cumulants $\kappa _2$ and $\kappa _3$ starting with $x(0)=1$ in Fig. 8. Time series of various durations were used, as well as different values of $\kappa ^2$. Clearly, theory describes the mean and cumulants approach to equilibrium values very well.

1.3 B.3 Distribution of relaxation times

In the same manner as was done for multiplicative model [6], we investigate the distribution of relaxations times. Namely, we generate a time series (35) and observe how quickly its distribution approaches the steady-state distribution (38). The relaxation time is determined by saturation of the Kolmogorov-Smirnov (KS) statistic for comparison between numerical and theoretical distribution to its lowest value. We generated $10^5$ relaxation times and studies their distribution function. We fitted with Normal (N), Lognormal (LN), InverseGamma (IGa), Gamma (Ga), Weibull (Wbl) and Inverse Gaussian (IG) distributions using maximum likelihood estimation (MLE) and evaluated KS statistics for this fits (lower KS numbers indicate better fits.) The results are summarized in Table 4 and fits, for the same $\gamma$ as in Table 4 and two values of $\kappa ^2$ from it, are shown in Fig. 9.

As was the case with the multiplicative model, IG distribution

$$\begin{aligned} IG(a\gamma ^{-1},b\gamma ^{-1};x)=\sqrt{\frac{b}{2\pi \gamma x^3}} {\text {exp}}\left[ -\frac{b\gamma (x-a\gamma ^{-1})^2}{2a^2x}\right] \end{aligned}$$

(51)

provided by far the best fit. It should be noted that for (51), cumulants $\kappa _n \propto \gamma ^{-n}$ and are independent of the coefficient $\kappa$. Figure 10 shows excellent agreement with numerical results.