Description of Shapiro steps on the potential energy surface of a Frenkel–Kontorova model Part I: The chain in a variable box

Abstract

We explain the vibrations of a Frenkel–Kontorova (FK) model under Shapiro steps by the action of an external alternating force. We demonstrate Shapiro steps for a case with soft ‘springs’ between an 8-particles FK chain. Shapiro steps start with a single jump over the highest $\hbox {SP}_4$ in the global valley through the PES. They finish with doubled, and again doubled oscillations. We study in this part I a traditional FK model with periodic boundary conditions.

1 Introduction

Shapiro steps are reported in the observation of different experiments [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. We concentrate here on the emergence of such steps in calculations with the FK model with periodic boundary conditions (PBC) [16,17,18,19,20]. This paper can be seen as a deeper explanation on recent results [21, 22], but mainly it is devoted to the aim to understand what happens under a Shapiro step inside the FK chain. How does the chain in the mountains of the potential energy surface (PES) moves if it slides downhill the effective PES? To the best of our knowledge, we think that the question was never treated in the past. Usually, the average velocities of the chain are studied. To look inside the FK chain, we use in this work the PES of the chain [23,24,25], as well as the tool of the highest Lyaponov Exponent [26].

The FK model describes the situation of a chain of particles with harmonic spring forces in between. It is embedded in a site-up potential, and additionally it suffers from a tilting force of ‘direct current’ (dc) and/or ‘alternating current’ (ac) character. Here we specialize in the spring force to a soft value [21], in comparison to the site-up potential, in contrast to our former references [23,24,25]. The competition between the collective behavior of softly correlated particles and the influence of the environment on individual particles is important for many-particle problems.

The periodic substrate potential is assumed to be a sinusoidal curve. Other forms are possible [16] but not treated here. The chain is really of finite length. We search the form of the movement of a 1D FK chain through a site-up potential. The winding number is the relation, the misfit, between the original spring distances, $a_o$, and the periodicity, $a_s$, of the site-up potential. We discuss an example of ‘soft’ springs with winding number 1/2 being the ratio of the two periodicities of the problem.

Overall, we treat here the PES for N particles of the chain and search for a global valley through the ‘mountains’ of the N-dimensional PES for a sliding of the chain over the site-up potential. The method corresponds to studies of chemical reactions through the PES of a molecule. We use the ansatz of a Langevin equation [21].

We find that the chain does not move as an inelastic, solid body along the site-up potential with translational symmetry of the chain. The motion of the chain goes on by steps of the periodicity $a_s$ with internal compression and/or stretchings of the chain. This we can here illustrate.

In Sect. 2, we introduce the FK—in a variable box—model used in this paper. In Sect. 3, the case of the spring potential with N = 8 chain length [21] and $k=1/4 v$ soft springs is discussed. In the main Sect. 4, we calculate and discuss a Langevin equation where the Shapiro steps emerge. To detect all possible such steps, we use the highest Lyapunov exponent which is explained in Sect. 4.2. Finally, we give some conclusions.

2 The FK model

$\mathbf{u}=(u_1,...,u_N)$ represents the position of N discrete particles of a chain. We treat a finite chain. The positions $u_i$ are on a 1D axis. It holds $u_i < u_{i+1}$ for the ordered chain. The chain without the site-up potential, and without the external force, has the equilibrium distance, $a_o$. The current end points of the chain determine the current average distance ${\tilde{a}}_o=(u_N-u_1)/(N-1)$. In the past traditionally, the so called periodic boundary conditions (PBC) of the kind $u_{N+1}=u_1+N\,a_o$, with $a_o$ equilibrium constant of the chain, and $u_{0}=u_N-N\,a_o$ [21] using two ghostly particles $u_0$ and $u_{N+1}$ are used.

The harmonic spring potential is the sum of all particles and it results in the harmonic energy of nearest neighbor potentials, and a variable box potential representing the PBC

$$\begin{aligned} S_{box}(\mathbf{u})&= \frac{k}{2}(\sum _{i=1}^{N-1} (u_{i+1}-u_i-a_o)^2 \nonumber \\&\quad + (u_1 -u_N +(N-1)\ a_0)^2 ) . \end{aligned}$$

(1)

The last summand is the contribution to the PBC; its form leads to a simple gradient. The PES for the variable changes of the $u_i$ is the Frenkel–Kontorova model ‘in a variable box’ (FKivb)

$$\begin{aligned} V(\mathbf{u}) = P(\mathbf{u}) + S_{box}(\mathbf{u}) \end{aligned}$$

(2)

where the site-up P is the potential [21]

$$\begin{aligned} P(\mathbf{u}) = \frac{v}{(2\pi )^2} \sum _{i=1}^N (1 - Cos(2\pi \,u_i/a_s)) . \end{aligned}$$

(3)

In numerical tests, we scale the $a_s$-constant of the P-potential to 1 for computational simplicity. We fix the potential constants $v=4$ and $k=1$ and use a short chain with $N=8$ particles [21]. We treat a special case of the FKivb model with $a_o=a_s/2$ with the commensurate misfit, 1/2, between the two potentials.

Because $v>0$, and $a_o\ne a_s$, the on-site potential will modulate the chain if an external further force is applied. We use a linear force. We name the resulting PES an effective PES

$$\begin{aligned} V_{eff}(\mathbf{u})= V(\mathbf{u}) - F \ (l_1,..,l_N)^T \cdot \mathbf{u} . \end{aligned}$$

(4)

The multiplication point between the N-dimensional normalized force vector $(l_1,..,l_N)^T$ and the N-variable u means the scalar product. F is the factor for the amount of the external force. The new term is named dc driving [17, 27] (for direct current) if F is fixed. If the amount of the force alternates in time then one names it ac driving [28] (for alternate current) with

$$\begin{aligned} F=F_{dc}+F_{ac}\,sin(2\pi \,\nu _o\,t) \end{aligned}$$

(5)

with a frequency $\nu _o$, and a ‘time’ variable, t, which will also be used for the step length below in a Langevin equation. The force tilts the former on-site potential for particle $u_i$ with the incline $F\, l_i, \ i=1,...,N$. The extremal points of the effective PES, $V_{eff}$, minimums and SPs, move if F increases. A corresponding curve is described by a Newton trajectory (NT) [29,30,31,32].

3 The overdamped Langevin equation

The components of the gradient of the effective PES are

$$\begin{aligned} g_{eff\,i}= k\,( 2\ u_{i} - u_{i+1} - u_{i-1}) +v\, sin(u_{i}) -F\,l_i \ \end{aligned}$$

(6)

for $i=1,...,N$. For $i=0$ and $i=N+1$ here emerge additional particles which are connected over the PBC. They form the movable ‘box’ of this FK model, see Sect. 2. If we put the gradient to zero, we get the ansatz of the NT theory [23]. In contrast, one can put the gradient into a steepest descent equation, the overdamped Langevin equation [21]

$$\begin{aligned} \eta \ \dot{\mathbf{u}}= - \mathbf{g}_{eff}(\mathbf{u},t) . \end{aligned}$$

(7)

A ‘time’, t, comes into the effective gradient by the external ac-force, Eq. (5). Every time step is depicted by ‘Node’ in the corresponding figures. We use the damping factor $\eta =100$ throughout. Because of the damping, the ‘velocity’ $\dot{\mathbf{u}}$ in Eq. (7) has to be treated carefully. It describes the steepest descent along $\mathbf{g}_{eff}$ in small steps. It is a mathematical tool for the description of an abstract sliding along the tilted site-up potential. Nevertheless, the abstract velocity also originates the Shapiro steps being the yield of many former references [16, 17, 21, 22, 33], to name just a few. In former works, the unspecific washboard force [6] $l_i=1/\sqrt{N}$ for all i is usually used.

Be $F_c$ the critical force. If $F>F_c$, then a really amount emerges in the Langevin equation, for the velocity of a change of the chain. F is then the tilting force which causes the depinning of the chain and which causes the sliding downhill the effective PES.

What happens with the ‘variable’ ac force?

Fig. 1

Schematic pathway of an ac-driven Langevin particle on a tilted PES

$F_{ac}\, sin(2\pi \, \nu _o\, t)$ is alternating, and for $F_{dc}$ near $F_c$ critical, it can be that the sum of both overcomes $F_c$, or again is below $F_c$, if t goes on. In Fig. 1 we give a schematic picture of a Langevin ac-driven particle. A harmonic potential in x direction is tilted in y direction, where a sliding also goes on for every external force. If additionally the ac-vibration is applied then the particle ‘vibrates’ on the downhill path over the x direction. In this way, we have to imagine the case of a Shapiro-step of the ac-driven FK model. Anywhere in the PES mountains of the chain the frequency of the ac driving finds left and right walls for a downhill vibration of parts of the chain.

3.1 Lyapunov exponents

To understand the global behavior of the solutions of the Langevin equation, one studies the action of the phase flow on certain partial sets of the phase space R$^N$. Usually, the flow is not to grasp analytically, but the vector field, $\mathbf{g}_{eff}$, of Eq.(7) is the velocity field of the phase flow. The divergence, $div \,\mathbf{g}_{eff}$, then determines the velocity by which the value of an infinitesimal volume element changes at u(t), under the action of the flow. If $\mathbf{u}(t)$ is a region of R$^N$, v(t) is its volume, and s(t) is its border then one gets after a Liouville theorem [34]

$$\begin{aligned} \frac{\mathrm{d}\,v(t)}{\mathrm{d}t} = \int _{s(t)} div \, \mathbf{g}_{eff}(\mathbf{u}) d\mathbf{u} . \end{aligned}$$

(8)

If one approximates $div \, \mathbf{g}_{eff}(\mathbf{u})$ to be nearly constant then one would get $v(t)=v(0) e^{t\,div\,\mathbf{g}_{eff} }.$ The divergence of the effective gradient is the sum of the diagonal of the Hessian of the PES. If the sum is less than zero, then we name the system dissipative. If one concentrates on the largest eigenvalue of the Hessian, one can use this Lyapunov exponent for a quantity which characterizes the rate of separation of two trajectories which are infinitesimally close at an initial point of time. We treat, of course, the Eq. (7). They form a dynamical system of N first-order ordinary differential equations. One assumes a rate by

$$\begin{aligned} |\delta \mathbf{u}(t)| \approx e^{\lambda t} |\delta \mathbf{u_o}(t)| . \end{aligned}$$

(9)

Of course, if the Lyapunov exponent $\lambda <0$ one can expect some sort of order for different trajectories. The more negative $\lambda <0$ is the more regular movement is to expect. Usually, for general dynamical systems, the rate depends on the initial points. However, here, we have a dissipative system where the start only determines some transient steps.

Lyapunov exponents are a tool for detecting chaos [35]. They provide a computable, quantitative measure of the degree of stochasticity of solutions for large times, t. We use the works of Benettin et al.  [36], and Wolf et al.  [26] for an application to the FKivb model. It is based on a Gram-Schmidt method. We use the algebraic formulation of the model from which the Jacobian matrix is derived. A set of N infinitesimal perturbations is generated (one for each direction of the phase space) and the Jacobian matrix is used to estimate locally the divergence or the convergence of the flow. To dimension, N, of Eq. (7) we form N further vectors, $\mathbf{y}_i$, $i=1,...,N$, the components of which are set at start to $y_{i,j}=\delta _{i,j}=0$ for $i \ne j$ and $y_{i,i}=\delta _{i,i}=1$. Therefore, to say, every $\mathbf{y}_i$ represents one dimension of the chain, thus one particle. Using the Hessian of the PES, note that for the FK model holds $\mathbf{H}_{eff}=\mathbf{H}$, we treat the extension of the Langevin Eq. (7) by the $N^2$ additional equations

$$\begin{aligned} \dot{\mathbf{Y}} =\mathbf{H}(\mathbf{u}(t)) \ \mathbf{Y} . \end{aligned}$$

(10)

This is a so-called linearization of Eq. (7) with respect to a solution $\mathbf{u}(t)$. The Hessian matrix is the Jacobian matrix of the gradient, and the $\mathbf{y}_i$ are treated as a small deviation of the trajectory $\mathbf{u}(t)$. The Hessian matrix in Eq. (10) is a linear evolution operator in the tangent space of the $\mathbf{y}_i$ vectors. For large t, the limit

$$\begin{aligned} \Lambda = \lim _{t\rightarrow \infty } \frac{1}{2 t} log(\mathbf{Y}(t)\, \mathbf{Y}^T(t)) \end{aligned}$$

(11)

defines a matrix, if it exists [37]. The eigenvalues of matrix $\Lambda$ are the Lyapunov exponents. Using a proposal of Refs. [26, 38], one can orthonormalize the $\mathbf{y}_i$ vectors in every t-step and thus one can automatically get the eigenvalues. In our case, the set of Lyapunov exponents will be the same for almost all start structures of the chain.

Fig. 2

The first Lyapunov exponent, $\lambda$, for increasing external force, $F_{dc}$, with $F_{ac} =0.2$ and $\nu _o=0.2$ fixed. The biggest spike around $F_{dc}=0.22$ depicts the first, the main Shapiro step. Further steps are numbered with increasing $F_{dc}$

We fix $F_{ac}=0.2$, and $\nu _o=0.2$. For a step length of 0.01 in t and 100 000 steps for the common system (7) and (10) (in $N\,(N+1)$ dimensions), we calculate for a series of $F_{dc}$ values in the range from $F_c$ to 1.0 the Lyapunov exponents, with steps of $\Delta F_{dc}=0.001$. We represent the first Lyapunov exponent, named $\lambda$, for increasing $F_{dc}$ in Fig. 2. Compare the analogous former result [21].

We will treat the regions of the spikes of Fig. 2: every spike ‘houses’ one Shapiro step of the FKivb model. The deeper the value of $\lambda$, the more ‘stable’ is the oscillation of the chain on its way downhill the tilted site-up potential. Note: all interesting aspects concern the sliding region of the external force. There is no kind of ‘steady state’ as it is pretended [33]. At least, we find a kind of steady flow.

4 The PES of the FKivb chain N = 8, v = 4, k = 1

4.1 The first Shapiro step for the periodic movements of 2$\pi$ along the site-up potential

In the range of $F_{dc} \in [0.16,\,0.3]$, one meets the first Shapiro step, compare Fig. 1 a) of Ref.  [21]. We use the fixed ac-force $F_{ac}=0.2$ and $\nu _o=0.2$.

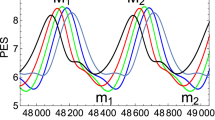
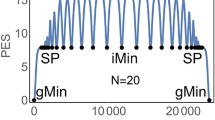
We draw in Fig. 3 the energy profile of the PES only, over a trajectory, thus the tilting energy is suppressed. The additional part of the external energy is projected out of the representation. This delivers a good imagination of the movement of the chain on the sliding downhill pathway. The profile shows periodic, regular, and short oscillations of a stable kind. For the cases of $F_{dc}$ in the full range of the Shapiro step, we find the same frequency of the profile: it is locked. We emphasize a cycle of 1 000 time steps of the profile. The time steps are depicted by ‘Node’. It is done in Fig. 3 by the blue profile for $F_{dc}=0.17$, and by the green profile for the larger $F_{dc}=0.28$. An animation for the front part of the $F_{dc}$ of Shapiro step 1 is given in the Supplementary data.

Fig. 3

Energy profiles (PES only, without the effective part) of 1000 t-steps of two Langevin trajectories at the Shapiro step 1. The colors are $F_{dc}=0.17$ blue, and $F_{dc}=0.28$ green. Four turning points of the blue profile are depicted by $M_i$ for maximal TPs, or by $m_i$ for minimal TPs. One double-cycle of 1000 nodes of the profile corresponds to a double-step of the chain by one period over the site-up potential, see Fig. 4. For comparison, the ac-oscillation is schematically shown by the red curve. Its scale is adapted to the PES scale

The turning points (TP) of the blue profile are depicted by $M_i$ for the upper ones, and by $m_i$ for the lower ones. One full cycle over 4 TPs makes a movement of the chain by one site-up well further, a step of $2\pi$ along the site-up potential, see Fig. 4. Two full cycles of the ac-force are used here. A trajectory in the region of the first Shapiro step explores the PES of the chain in an impressive kind: the upper TPs on the PES cross the ‘global’ $\hbox {SP}_4$ where half of the particles at the same time turn over their next tops of the site-up potential. It happens just in time with the maximal external force, compare the red help curve in Fig. 3. In every substep from $m_i$ to $M_i$, $i=1,2$, four alternating particles climb over the next tops of the site-up potential, and on the other side they form the next, complementary global minimums of the chain.

Fig. 4

Structures of the chain for the four turning points of the blue profile of the Langevin trajectory of Fig. 3. They form the corner stones of a full cycle of the moving chain with a 2$\pi$ step along the site-up potential. The lower TPs cross the two different structures of the global minimum of the chain. The upper TPs cross the two different structures of the $\hbox {SP}_4$. The particles are artificially lifted on the potential to guide the eye. The real chain is on a straight line. Only the distances can change

Fig. 5

Structures of the chain for the six turning points of the green profile of the Langevin trajectory of Fig. 3. They are a full cycle of the moving chain with a 2$\pi$ step along the site-up potential. Internally happens a substep with a forward- and a backward oscillation between $m_1$ and $m_3$

The two upper $\hbox {SP}_4$ are mirror pictures, vice versa, thus they are equal in energy. One can imagine that particle 5 plays the role of a reflection point to obtain the other version. However, this is only an abstract picture, because it would change the numbering of the particles. Note that the two $\hbox {SP}_4$ are the tops of the global valley through the PES. One can imagine still SPs with higher index, however, they do then not belong to the interesting valley through the PES for a movement of the chain.

The lower TPs cross the two global minimums of the chain. The two global minimums, on the other hand, are of the same energy, but they are not mirror pictures, vice versa. Internally, the structures of all four stationary points have a mirror symmetry with the reflection point at the half of the central bond, between particles 4 and 5.

The oscillation fits into the ‘global’ valley over the two high $\hbox {SP}_4$ structures. The corresponding times for an increase or a decrease of the pathways on the PES are perfectly synchronized with the ac-oscillation. Note that the chain behaves not as a fixed body like former workers had assumed [33, 39]. No, it moves in contrast like an accordion with internally changing distances. At minimum $m_1$, we have ${{\tilde{a}}}_o > a_o$, at $\hbox {SP}_4$ it is ${{\tilde{a}}}_o = a_o$, but at minimum $m_2$, we have ${{\tilde{a}}}_o < a_o$.

On the frequency itself: In the program, we use a t-step length of 1/$\eta$=0.01, and $\nu _o=0.2$, thus a cycle of 500 t-steps is one period of the ac-force. 1 000 steps correspond in Fig. 3 to a double-cycle in the ac-force (5) of $sin(4 \pi )$. 500 steps of the ac excitation make the cycle from $m_1$ to $M_1$, but the next 500 steps finish the cycle over $m_2$ to $M_2$. Then, the next double-cycle starts. The maxima of the profile correspond to the maxima of the ac-force, and the minima of the profile correspond to the minima of the ac-force. The Shapiro step needs such a lockstep of the sliding and the ac-force (5).

How can the equal frequency be realized under a different external force, $F_{dc}$? We can study this by the behavior of the green profile being at the end of the step interval of $F_{dc}$. The sliding still goes over the global $\hbox {SP}_4$ of the chain in the substep from $m_1$ to $M_1$. Thus, the quite rigid box condition (1) prevents any other lower SPs of a lower index than four [23,24,25], compare also part II of this series [40]. We try to understand how the period of the sliding acts. We are in the region of a larger $0.28=F_{dc}>F_c=0.255$ of a sliding. However, the negative part of the ac-force, of $F_{ac}\ sin(2\pi \nu _o t)$, can cause the sum of both parts become smaller than $F_c$. Then, the chain is pinned in the current well of the PES. The Langevin trajectory searches the minimum of the well, but the ac-force continuously changes. It causes an internal oscillation of the chain just in time with the ac-force, so that we can overcome the next $\hbox {SP}_4$ for the next cycle at the suitable time step. Note that the lower TPs at the $m_i$ structures now do not cross the global minimums of the chain. The larger $F_{dc}$ in this case may cause an earlier crossing of the region of the $\hbox {SP}_4$, at $M_1$, then the internal vibration will consume the additional time so that the next crossing of the $\hbox {SP}_4$ region at $M_3$ is again in time with the maximum of the external ac-oscillation, compare Fig. 5. Then, a next cycle will start.

One can ask how the large interval of $F_{dc}$ values of the main Shapiro step will come to its end? A profile is shown for the region between the intervals of the first and the second Shapiro step, at $F_{dc}=0.304$ in Fig. 6. The vibration ‘continuously’ degenerates.

Fig. 6

Accidental section of an energy profile (PES only) of a Langevin trajectory between the first and the second Shapiro steps, at $F_{dc}=0.304$. A periodic oscillation does not emerge

Fig. 7

Energy profiles (PES only) of a cycle of 500 t-steps of two Langevin trajectories at the second Shapiro step. The colors are: $F_{dc}=0.317$ blue, and $F_{dc}=0.388$ green. One cycle of the profile of 500 nodes corresponds to a step of the chain by one period over the site-up potential, see Fig. 8

Fig. 8

The turning points of the blue profile of a Langevin trajectory of Fig. 7 form a full cycle of the moving chain with 2$\pi$ along the site-up potential

Fig. 9

The six turning points of the green profile of a Langevin trajectory of Fig. 7 form the full cycle of the moving chain with 2$\pi$ along the site-up potential

4.2 A second Shapiro step

This step includes the interval $F_{dc}\in [0.315,\,0.4]$. We use a fixed ac-force $F_{ac}=0.2$ and $\nu _o=0.2$. The profile in Fig. 7 again shows periodic, and regular oscillations of a stable kind. For the cases of $F_{dc}$ in the range of the Shapiro step, we find the same frequency of the profile: it is locked. We emphasize a cycle over 1 000 time steps of the profile. It is done in Fig. 7 by the blue profile for $F_{dc}=0.317$, and by the green profile for $F_{dc}=0.388$. Note the equal frequencies of the curves in Fig. 7. The turning points of the blue profile are depicted with $M_i$ for upper, and $m_i$ for lower ones. One full cycle over four turning points makes a movement of the chain by one site-up well further, a step of $2\pi$ along the site-up potential. It looks like the first Shapiro step, however, now only 500 time steps form one cycle. Thus, the velocity is doubled by which the chain slides downhill, in comparison to step one. The TPs are depicted in Fig. 8.

Again the question emerges, how can the equal frequency of the step be realized under a different external force, $F_{dc}$? Similarly, we look at the behavior of the green profile being at the end of the step interval of $F_{dc}$. The sliding again goes over the global $\hbox {SP}_4$ of the chain in the substeps over the $M_i$. But an internal oscillation of the chain just in time with the ac-force realizes that it is overcoming the next $\hbox {SP}_4$ for the next cycle at the suitable time step.

Good to see by the structures, in Fig. 9, is that some parts of the chain do a back-step in their site-up wells if the ac part of the force is in a pinned region. Though a half-loop of the Langevin trajectory is there in the pinned region of the energy, it does not converge to a fixed structure because the trajectory escapes for the next $F>F_c$ from the pinned region and slides into the next well. The steady change of the external force, F, by the ac-part is necessary for a Shapiro step. For a pure dc-force one has the theorem that if ${\dot{u}}_i(0)>0$, for $i=1,...,N$, then it holds in the sliding case ${\dot{u}}_i(t)>0$ for all $t>0$ [41]. Then, all particles move forward only.

4.3 A third Shapiro step

The next Shapiro step of the movement of 2$\pi$ along the site-up potential is in the range of $F_{dc} \in [0.435, 0.45]$. We again use the fixed ac-force $F_{ac}=0.2$ and frequency $\nu _o=0.2$. The profile in Fig. 10 shows periodic, regular, and short oscillations of a stable kind. We emphasize 1 000 nodes being the time steps. An animation for the final part of the $F_{dc}$ is given in the Supplementary data.

Fig. 10

Energy profiles (PES only) of a double-cycle of 500 t-steps of a Langevin trajectory at the Shapiro step 3 at $F_{dc}=0.44$. One cycle of the profile corresponds to a step of the chain by one period over the site-up potential, see Fig. 11

Fig. 11

The six turning points of the profile of a Langevin curve of Fig. 10 form 1+1/2 cycles of the moving chain along the site-up potential

The resulting force, F, is now throughout over $F_c$, The turning points of the profiles are again depicted with $M_i$ for upper, and $m_i$ for lower ones. Corresponding structures of the chain for the points $M_i$ or $m_i$, are shown in Fig. 11.

A full cycle over six turning points causes a movement of the chain by one and a half site-up well further. Such a cycle consists of three nearly equal subcycles.

A cycle of 500 steps in Fig. 10 corresponds to 3 subcycles in the ac-force (5) of $sin(2 \pi )$.

4.4 Shapiro step 4

At $F_{dc} =0.565$ is a small region of a periodic oscillation with 8 TPs, over a time interval of 500 time steps. We represent one profile in Fig. 12.

Fig. 12

Energy profile (PES only) of 500 t-steps of a cycle of the Langevin trajectory of Shapiro step 4

A cycle of 500 steps in Fig. 12 corresponds to 4 subcycles in the ac-force (5) of $sin(2 \pi )$.

4.5 A fractional Shapiro step

We treat the external excitation with $F_{dc}=0.308$ between the first and the second Shapiro step [21], compare Fig. 2. It was named in former treatments as Shapiro step with number 3/2. It results in a periodic oscillation with one cycle over 1 000 t-steps, and an oscillation number of 8 TPs all in all. It causes a movement of the chain over 3$\pi$ along the site-up potential. Three subcycles move 1$\pi$ further along the TPs $\hbox {M}_1$ to $\hbox {M}_3$, but one subcycle is a back-movement, from $M_4$ to $m_4$. In Fig. 13, we show the energy profile of a cycle.

Fig. 13

Energy profile (PES only) of a cycle of 1 000 t-steps of a Langevin trajectory at Shapiro step 3/2 with $F_{dc}=0.306$

5 Discussion

Shapiro steps concern the average velocity of the trajectory of the Langevin equation. This velocity is locked on a step. Note that there is no such construct like a ‘steady state’ as it is often claimed in former papers [16, 33]. The Langevin trajectory goes downhill the effective PES without forming a stable orbit.

In the case of a linear chain treated here, there is no possibility that a single particle moves. The interaction of the particles in the chain leads to collective states like antikinks or kinks. Here, the box-potential makes that ‘fourfold’ antikinks or kinks move along the chain from a zero level minimum over the $\hbox {SP}_4$ to the next zero level minimum. However, no real dynamics is treated. We only study the damped steepest descent on the tilted effective PES.

References  [16, 17, 21, 22, 33] pretend a translational symmetry

$$\begin{aligned} u_l(t)+2\pi =u_{l+i}(t+s) \end{aligned}$$

(12)

with an integer index, i. It means that the chain acts like a single body [39]. The chain is an ordered chain of N particles where every particle has its own, fixed number, l. The imagination of a symmetry like in Eq. (12) may lead to the picture of a rigid chain with a fixed $a_0$ distance. Already with the first Shapiro step one can observe that this picture is not correct. Thus, assertion (12) is not correct. What the box condition of the spring part of the potential energy, Eq.(5), enforces here is a fourfold symmetry of the chain: any two consecutive particles behave like the next two, or the two before. This property does not hold for a chain with free boundaries [40]. In contrast, we found that for an FK chain with free boundaries the results of the FK model with the periodic boundary conditions are not transferable. Surprisingly, the sequence of the Shapiro steps becomes inverse, see the accompanying paper, part II of this series [40].

6 Conclusion

In the depinned case of the FKivb chain, the solution of the Langevin equation is, in principle, a boring affair: it slides downhill, and slides, and slides down to minus infinity. However, an interesting fact is the possibility of regular, equal vibrations over certain intervals of the $F_{dc}$ force. Thus, the frequency, as well as the average velocity of the chain, are locked. There emerge Shapiro steps which one can compare with experimental results [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15].

It is a matter of fact, that we confirm the reported properties of FKivb chains under ($dc+ac$)-force in the past [16, 17, 21, 22], to name but few. Like the integer and fractional steps, the Farey-steps [18, 34], the changeability of ac-frequency, or of the site-up potential, and others. Here, we demonstrate the kind of oscillation which the FKivb chain undergoes at a Shapiro step. The chain ‘breathes’ as a whole, it is compressed, or stretched into the two wells of the two different global minimums, but the barrier in between is formed by the two $\hbox {SP}_4$-structures, see Fig. 4 as the prototype.

Different values of the parameter $F_{dc}$ on one and the same Shapiro step are balanced by different ‘back’-oscillations of subloops of the oscillation. The oscillation frequency itself is locked, just in time with the ac-frequency.

For Shapiro step 1, we obtain an oscillation of the chain, compare Fig. 4, exactly in time with the ac-frequency. The movement leads over the profile between global minimums and the two $\hbox {SP}_4$. The corresponding pathway goes in the SP region along a highly symmetric ridge. This is enforced by the box-potential which prevents an outbreak to lower index SPs, compare part II of this series [40]. If the dc-amount in the interval of the Shapiro step increases, we find a balance of the additional force by an internal back-vibration of the chain. In sum, the same frequency happens again.

For Shapiro step 2, we get a shorter oscillation cycle to one half of number one. But the character of the oscillation is the same. And so on for the still higher steps.