Kinematic interaction and condensation factor in two-dimensional quantum Heisenberg ferromagnet

Abstract

We investigate the influences of Dyson’s kinematic and dynamic interaction on the physical properties of two-dimensional quantum Heisenberg ferromagnet with O(3) rotational symmetry. It is found that the repulsive potential led by dynamic interaction modifies the third large term with $T^{3}$ in the low-temperature series of specific heat. Under mean-field approximation, the kinematic interaction transforms the occupation-number configuration into a coherent-state configuration and significantly improves the result of modified spin wave theory in the high-temperature limit. In the low-temperature limit, the kinematic-interaction contribution to specific heat is negligibly small. For finite-size systems, it is found that a crossover temperature can be used to characterize the transition to a single-domain-type magnet. In the thermodynamic limit, the condensation factor (the number of zero-mode magnons) dominates the isothermal compressibility of magnon gas although there is not a real phase transition at finite temperatures. The asymptotic behavior of static structure factor depends on the relative size of the spin-wave wavelength with respect to the correlation length.

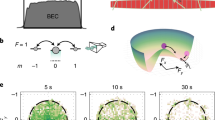
Graphic abstract

Appendices

Appendix A: Properties of $f_{L}(x)$

Equation (6) in the text defines function $f_{L}(x)$ with non-negative integer L

$$\begin{aligned} f_{L}(x) = e^{-x} \sum _{n=L+1}^{\infty } \frac{ x^{n} }{\Gamma (n+1)} \end{aligned}$$

(A.1)

where, $\Gamma (z)$ is the Gamma-function. The n-order derivative of $f_{L}(x)$ with respect to x satisfies the following recurrence relation

$$\begin{aligned} \frac{ \partial ^n f_{L}(x) }{ \partial x^n} = \sum _{j=0}^{n} \frac{n!}{j!(n-j)!}(-1)^{n-j}f_{L-j}(x) \end{aligned}$$

(A.2)

Appendix B: Coherent state configuration

In the occupation-number configuration, the trace in the partition function can be rewritten as

$$\begin{aligned} Z_\mathrm{mf}= & {} \sum _{ \{n_k\} }{\langle {\{n_k\}}|} \sqrt{ \hat{P}_\mathrm{mf} } e^{-\beta \hat{H}_0 } \sqrt{ \hat{P}_\mathrm{mf}} {|{\{n_k\}}\rangle } \nonumber \\= & {} \sum _{ \{\Omega _k\} } {\langle { \{\Omega _k\} }|} e^{-\beta \hat{H}_0 } {|{ \{\Omega _k\} }\rangle } \end{aligned}$$

(B.1)

The new states read as

$$\begin{aligned} {|{ \{\Omega _k\} }\rangle } = \sqrt{ \hat{P}_\mathrm{mf}} \sum _{ \{n_k\} } \prod _{k} {|{n_k}\rangle } = \prod _{k} {|{\Omega _k}\rangle } \end{aligned}$$

(B.2)

where

$$\begin{aligned} {|{\Omega _k}\rangle } = e^{\frac{C}{2} } \sum _{n_k=0}^{\infty }(1+D)^{\frac{1}{2}n_k} {|{n_k}\rangle } \ \end{aligned}$$

(B.3)

with $-1< D <0$. The absent normalization factor $A_k$ in the above expression can be determined from $\left\langle \Omega _k|\Omega _k\right\rangle =1$ and leads to

$$\begin{aligned} A_k = e^{ -\frac{C}{2} } \sqrt{|D|} \end{aligned}$$

(B.4)

It is noticed that the kinematic interaction under mean-field approximation maps the occupation-number configuration onto a coherent-state configuration. The mean-field approximation completely suppresses the fluctuations in momentum space, which corresponds to a common chemical potential shared by all $\mathbf {k}$-states.

Appendix C: Solution to the saddle-point equations

In deducing the saddle-point Eq. (22), the following relation is used

$$\begin{aligned} \frac{ \partial n }{ \partial \Delta } = \frac{ \partial n }{ \partial D} \frac{ \partial D }{ \partial \Delta } \end{aligned}$$

(C.1)

where,

$$\begin{aligned} \frac{ \partial n }{ \partial D} = \frac{1}{N}\sum _{k} \frac{1}{ \left[ e^{\beta \epsilon _k} - (1+D)\right] ^2} \end{aligned}$$

(C.2)

$\frac{ \partial D }{ \partial \Delta }$ is the first-order partial derivative of D with respect to $\Delta$ and explicitly written as

$$\begin{aligned} \frac{ \partial D }{ \partial \Delta } \!=\! \frac{ e^{-\Delta } }{L!} \frac{ 1-f_{L-1}(\Delta ) }{[1-f_{L}(\Delta )]^2} \left( \Delta \!-\! L\frac{1-f_L(\Delta )}{1-f_{L\!-\!1}(\Delta ) }\right) \Delta ^{L-1}\nonumber \\ \end{aligned}$$

(C.3)

Since the expression in the round bracket is never equal to zero, equation $\frac{ \partial D }{ \partial \Delta }=0$ has the unique solution $\Delta = 0$ while $L>1$.

Appendix D: Density of state

Using the following equation

$$\begin{aligned} \rho (x) = \frac{1}{N} \sum _{\mathbf {k} } \delta (x-\gamma _{ \mathbf {k} }) = \frac{2}{\pi ^2} K( \sqrt{1-x^2} ) \end{aligned}$$

(D.1)

where K(x) is the complete elliptic function of the first kind [18]. The density of state reads

$$\begin{aligned} g_2 (x)= & {} \frac{1}{N}\sum _{ \mathbf {k} }\delta (x-\epsilon _k) \nonumber \\= & {} \frac{4}{\pi ^2}\frac{1}{ \epsilon _\mathrm{max} } K\left( 2\sqrt{ \frac{x}{\epsilon _\mathrm{max}} -\frac{x^2}{\epsilon _\mathrm{max}^2} }\right) \end{aligned}$$

(D.2)

One can expand K(x) in terms of small x as

$$\begin{aligned} K(x) = \frac{\pi }{2} \sum _{n=0}^{\infty } \left[ \frac{ (2n-1)!! }{ (2n)!! }\right] ^{2} x^{2n} \end{aligned}$$

(D.3)

and obtain Eq. (38) in the text.

Appendix E: Magnetic susceptibility

The correlation function with $i\ne j$ can be written as

$$\begin{aligned} \left\langle \mathbf {S}_i\cdot \mathbf {S}_j \right\rangle =\left\{ \frac{1}{N}\sum _{k}e^{i\mathbf {k}\cdot (\mathbf {r}_j-\mathbf {r}_i)}\tilde{n}_k \right\} ^2,\quad i\ne j \end{aligned}$$

(E.1)

For the case with $i= j$, $\mathbf {S}_i\cdot \mathbf {S}_j =S(S+1)$. The magnetic susceptibility reads

$$\begin{aligned} \chi= & {} \frac{g^2\mu _\mathrm{B}^2}{k_\mathrm{B}T}\sum _{i,j}\left\langle \mathbf {S}_i^{z}\cdot \mathbf {S}_j^{z} \right\rangle \nonumber \\= & {} \frac{g^2\mu _\mathrm{B}^2}{3k_\mathrm{B}T}\sum _{i,j}\left\langle \mathbf {S}_i\cdot \mathbf {S}_j \right\rangle \nonumber \\= & {} \frac{g^2\mu _\mathrm{B}^2}{3k_\mathrm{B}T} \frac{1}{N} \sum _{k} \tilde{n}_k \left( 1 + \tilde{n}_k \right) \end{aligned}$$

(E.2)

The second expression uses the symmetrization of correlation function for the Heisenberg systems with O(3) symmetry.

Appendix F: Integral formula used in calculating the static structure factor

According to the integral formula

$$\begin{aligned} \int _{0}^{\pi } \frac{ {\mathrm{d}}{\theta } }{a+b\cos \theta } = \frac{\pi }{\sqrt{a^2-b^2}}, a>b>0 \end{aligned}$$

(F.1)

the equation (85) reduces to

$$\begin{aligned} I = \int _{ (2\xi )^{2} }^{ k_c^2+(2\xi )^{2} } \frac{ {\mathrm{d}}{y} }{y\sqrt{a+by+cy^2} } \end{aligned}$$

(F.2)

where

$$\begin{aligned} a= & {} q^4 + q^2\xi ^{-2},\\ b= & {} -2q^2,\\ c= & {} 1, \end{aligned}$$

Introducing the following parameter

$$\begin{aligned} \Delta = 4ac - b^2 = 4q^2\xi ^{-2} \end{aligned}$$

and using the integral formula

$$\begin{aligned} \int \frac{ {\mathrm{d}}{y} }{y\sqrt{a+by+cy^2} }= & {} -\frac{1}{ \sqrt{a} } \mathrm {arcsinh}\left( \frac{2a+bx}{x\sqrt{\Delta }}\right) , \nonumber \\&a>0, ~~ \Delta >0 \end{aligned}$$

(F.3)

we obtain the expression (86) in the text.