Cross sections and gamma cascades in $^{77}$Ge needed for background reduction in $0\nu \beta \beta$ experiments on $^{76}$Ge

Abstract

The compound nucleus model is employed to calculate neutron capture on $^{76}$Ge and the consecutive $\gamma$ decay. Total, inelastic and capture cross sections are compared to experiments in order to restrict model parameters. The respective $\gamma$ cascades are analyzed for possible background suppression schemes in future $0\nu \beta \beta$ decay searches with germanium detectors. Neutron energies in the range from 0.2 keV to 5 MeV are investigated. The spin dependence of the $\gamma$ cascades is proposed to be employed for determining the spin of thermal resonances.

1 Introduction

As time goes by, the famous Shakespearean Question “to be or not to be” has changed in physics towards the question “neutrino and/or anti-neutrino” [1]. In case the neutrino is of Majorana type, i.e., if the neutrino is its own anti-particle, this would constitute the second violation of the Standard Model of Particle Physics by the neutrino after establishing its finite mass. The neutrinoless double beta ($0\nu \beta \beta$) decay is one of the most sensitive probes of physics beyond the Standard Model. Presently, the most practical experimental access to learn about the neutrino’s nature seems to be the study of $0\nu \beta \beta$ decay. The $0\nu \beta \beta$ decay is a second order process violating lepton number conservation by 2 units, since 2 neutrons within a nucleus decay into 2 protons and 2 electrons only. Thus, major consequences might arise from its observation, e.g., for the understanding of the cosmic evolution, in particular it could help to explain the observed matter-anti-matter asymmetry in the universe [2].

Following the propositions by Maria Göppert-Mayer [3] and Wendell H. Furry [4] on double beta decay in the Thirties, a pioneering experiment on $0\nu \beta \beta$ decay on $^{76}$Ge was achieved in 1967 [5]. The 17 cm$^3$ Ge(Li) detector contained about $\sim$90 g of $^{76}$Ge and with an exposure of $\mathcal {E}$ $=7.3\times 10^{-3}$ kg$\cdot$yr the experiment gave the limit $T^{0\nu }_{1/2}$ $>3.1\times 10^{20}$ yr at 68 % confidence level (CL). The background rate in the region of interest at $Q_{\beta \beta }$ $=2039$ keV was at a level of $1.1\times 10^3$cts/(keV$\cdot$kg$\cdot$yr).

Out of 35 $0\nu \beta \beta$ candidates, several isotopes have been investigated [6] meanwhile. The most promising ones due to advanced experimental techniques, apart from $^{76}$Ge, are $^{136}$Xe and $^{130}$Te yielding the most stringent limits. The Cuore cryo-experiment [7] on $^{130}$Te yielded a Bayesian limit of $T^{0\nu }_{1/2}$ $>2.2\times 10^{25}$ yr at a 90 % credibility interval (CI). The corresponding median exclusion sensitivity of ${{{\mathcal {S}}}}^{0\nu }_{1/2}$ $>2.8\times 10^{25}$ yr at 90 % CI. KamLAND-Zen[8] is a scintillator based $0\nu \beta \beta$ experiment on $^{136}$Xe. Its latest result yielded $T^{0\nu }_{1/2}$ $>2.1\times 10^{26}$ yr at 90 % confidence level (CL) with a corresponding sensitivity of ${{{\mathcal {S}}}}^{0\nu }_{1/2}$ $>1.5\times 10^{26}$ yr (90 % CL). The $0\nu \beta \beta$ experiment Gerda at the Gran Sasso underground laboratories (Lngs) [9] of the Istituto Nazionale di Fisica Nucleare (INFN), Italy, is the only one of the leading $0\nu \beta \beta$ experiments where half life $T^{0\nu }_{1/2}$ and sensitivity ${{{\mathcal {S}}}}^{0\nu }_{1/2}$ are equal. This resulted from the fact, that this $^{76}$Ge experiment remained “background free” as the bare germanium detectors are suspended in liquid argon (LAr) with minimal structural material in its direct vicinity. Gerda has been completed in 2020 with a total $\mathcal {E}$ $=127.2$ kg$\cdot$yr [10]. The experiment resulted in a limit for the half life $T^{0\nu }_{1/2}$ $>1.8\times 10^{26}$ yr at 90 % CL in the frequentist approach. A Bayesian limit of $T^{0\nu }_{1/2}$ $>1.4\times 10^{26}$ yr at 90 % CI was achieved. For recent reviews see Refs. [6, 11].

The main advantage of the “background free” regime is the proportionality of ${{{\mathcal {S}}}}^{0\nu }_{1/2}\propto {\mathcal {E}}$, while background contributions B in the region of interest reduce the sensitivity to ${{{\mathcal {S}}}}^{0\nu }_{1/2}\propto \sqrt{{\mathcal {E}}/B}$ [11,12,13]. Increasing the limit $T^{0\nu }_{1/2}$ from the first $0\nu \beta \beta$ experiment to Gerda by a factor 5.81$\times 10^5$ was not only due to the increase in $\mathcal {E}$ (factor 1.74$\times 10^4$) by itself, but definitively due to the reduction in background; the ratio of the two factors amounts to 33.3. Gerda’s concept, i.e., being “background free”, will be applied to its follow-up experiment Legend aiming towards ${\mathcal {S}}\sim 10^{28}$ yr by enlarging the active mass towards the tonne-scale [14, 15]. For the higher ${{{\mathcal {S}}}}^{0\nu }_{1/2}$, the “background free” condition will be even more important than for the previous experiments. One of the possible obstacles in larger and more sensitive setups are cosmogenic neutrons producing the unstable isotope $^{77}$Ge. The single-$\beta$ decay of $^{77}$Ge (Q = 2703 keV) might obscure the neutrinoless double-$\beta$ decay signal of $^{76}$Ge at $Q_{\beta \beta }$ = 2039 keV due to the high energy range.

Despite the cosmic muons are reduced in intensity by the Gran Sasso mountain (3500 m.w.e.), the remaining muons may interact with material in the vicinity of the germanium detectors and produce hadronic showers with up to 30 neutrons or spallation products. The structural materials in Gerda had been reduced substantially by immersing the germanium crystals directly into the cryo-liquid argon. Passing muons and charged reactions products are detected and vetoed by the water Cherenkov detectors within the water tank [16,17,18] or the instrumentation of the liquid argon [13, 19]. High energetic neutrons are likely to produce charged reaction products and thus may be vetoed. However, neutrons in the MeV range remain mostly undetected by the veto-systems and are possibly being captured by $^{76}$Ge. Due to the water shielding of Gerda[13, 20] most of the neutrons from the natural decay chains located in the surrounding rock are thermalized and absorbed outside the central detector array of the germanium detectors. Simulations [21] have shown that neutrons with energies up to 1 MeV may be captured by $^{76}$Ge in the Gerda setup.

The first round of simulations [21] was based on Geant4 [22] employing cross sections compiled by ENDF [23]. Some resonances at 0.5, 5 and 9 keV, respectively, can be recognized in their simulations; furthermore, in the neutron energy range from 140 to 500 keV neutron capture occurs at a quite sizeable rate (Fig. 4 of Ref. [21]). The new data on thermal neutron capture [24, 25] exhibit discrepancies to the ENDF data. Still, these simulations show the need for calculations of cross sections of neutron and $\gamma$ emission in the range from a few keV up to a few MeV.

In Gerda so far contributions by neutron capture had been negligible, however, for experiments more sensitive by two orders of magnitudes the beta decay of $^{77}$Ge may cause background even at underground laboratories located deeper than Gran Sasso. Since the Legend-design is based on principles developped by Gerda, data from the latter are used to test further trigger and rejection schemes. The decay of the isomer $^{77m}$Ge can be tagged by $\gamma$s from the $^{77}$As decay; the decay of $^{77}$Ge from its ground state will be more difficult to detect directly. Thus, a good understanding of the population of all the intermediate states in $^{77}$Ge and their $\gamma$ decay is of great importance for designing background reduction schemes in hardware and in software for the upcoming germanium $0\nu \beta \beta$ experiments.

The present work aims at calculations based on the statistical Hauser-Feshbach (HF) model in order to reliably calculate the population of the intermediate compound-nucleus (CN) states and the production cross sections for $^{77}$Ge final states in the MeV range, i.e., for the $^{77}$Ge ground state and $^{77m}$Ge isomer at 160 keV. While the HF model is not valid in the resonance region, the calulations at low energies will concentrate on relative intensities of the $\gamma$ decay. Characteristics of the $\gamma$ emission spectra might further facilitate identification of the capture process depending on details of future setups. Section 2 briefly presents the model and its parameters, Sect. 3 compares the predictions to cross section data for the verification of the parameters chosen and Sect. 4 presents the resulting $\gamma$ spectra with concluding remarks in Sect. 5.

2 The Hauser-Feshbach model

In order to calculate neutron induced reaction cross sections statistical model calculations of Hauser-Feshbach type [26] are the appropriate tools. The code Maurina has been developed by M. Uhl to contain all the necessary parts [27]. It has recently been used to determine the $\gamma$ cascades in gadolinium isotopes [28]. For the present $^{76}$Ge calculations the maximum neutron energy $E_n^{max}$ is set to 5.0 MeV in the laboratory, which corresponds to 4.934 MeV in the center-of-mass system. Due to this energy limit only $^{77}$Ge and $^{76}$Ge nuclei are involved. The $^{76}$Ge(n,$\alpha$)$^{73}$Zn reaction would be possible, if not the Q-value of 1.974 MeV increased by the Coulomb barrier presents an effective threshold of 5.042 MeV. $E_n^{max}=5$ MeV corresponds to an excitation energy $E_x\cong 11$ MeV in $^{77}$Ge. Thus, up to this energy only neutron and $\gamma$ decay are relevant, simplifying the parameter search and reducing possible ambiguities. HF calculations provide valid cross sections in the region above the resonances. However, they may be used at low energies when investigating the spin dependence of the decay $\gamma$s.

Consequently, the quantities Maurina needs to calculate are firstly the energy E and $\ell$-dependent transmission coefficients $T_\ell (E)$ for neutrons to form the intermediate compound nucleus $^{77\star }$Ge($E_x$) starting from the ground state of $^{76}$Ge. These intermediate states at excitation energy $E_x$ then decay only via $\gamma$s to $^{77m}$Ge or $^{77}$Ge, and/or via neutron emission to $^{76}$Ge, respectively. The transmission coefficients $T_{XL}(\varepsilon _\gamma )$ for $\gamma$s are derived from the respective strength functions (see Ref. [28]). Secondly, the experimentally known levels with energy $E_x$, spin and parity $J^\pi$ must be entered as well as the parameters for the level densities $\rho (E_x,J^\pi )$ at higher excitation energies. At these low energies neither isospin quantum numbers must be considered nor competing pre-compound processes must be taken into account as the latter are below 1 %. Width-fluctuation corrections for low energies [29] are considered. Direct contributions to inelastic scattering are accounted for within the DWBA approach.

Only for the excitation function of the neutron capture reaction the calculations are expanded to $E_n\sim 8$ MeV for the comparison with available data. In this case the nuclei $^{77,76,75}$Ge, $^{76}$Ga and $^{73}$Zn are populated. Thus in this expanded range, also proton and $\alpha$ particle transmission coefficients are needed.

2.1 The optical model potentials

The particle potentials are standard spherical optical model potentials as shown in Table 1 to be used for the calculation of the transmission coefficients $T_\ell (E)$.

These are mostly global potentials valid for larger ranges of mass and energy. Only N9 is limited to $E^{max}_{N9}=5$ MeV, whereas the energy range of N8 starts at $E^{min}_{N8}=7$ MeV. Some have been modified for use in evaluations of other reactions.

Table 1 Optical model potentials for the particle transmission coefficients

2.2 The photon strength functions

The photon strength functions $f_{XL}(\varepsilon _\gamma )$ are related to the transmission coefficients $T_{XL}(\varepsilon _\gamma )$ for multipole type XL via

$$\begin{aligned} T_{XL}(\varepsilon _\gamma ) = 2\pi \ \varepsilon _\gamma ^{2L+1}\ f_{XL}(\varepsilon _\gamma ) \end{aligned}$$

(1)

where the $\gamma$-transition energy is denoted by $\varepsilon _\gamma$.

Maurina considers the six strength functions $f_{XL}$ for M1, E1, E2, M2, E3, and M3 radiation. For the first three types the strength functions are modeled by resonances formed by up to 3 Lorentzians as specified in detail in Table 2. The latter three are taken from the single particle model with 1 Weisskopf unit. At these low neutron energies $f_{E1}$ is the dominant one.

Table 2 Lorentzians for $^{76}$Ge and $^{77}$Ge determining the photon strength functions $f_{XL}(\varepsilon _\gamma )$. The E1 strength of $^{76}$Ge is parameterized either by 3 Lorentzians (3 SLO, ‘elbe2’) or by one (1 SLO), the standard Giant Dipole Resonance (GDR)

Fig. 1

The E1 photon strength function in $^{76}$Ge as described by the simple GDR parameterization (1 SLO) is shown in comparison to the fit (3 SLO) to the data from Ref. [38]

The E1 photon strength function $f_{E1}$ in $^{76}$Ge has been determined at the ELBE facility [38]. $f_{E1}$ is not well reproduced by a simple Giant Dipole Resonance (GDR, 1 SLO in Fig. 1) with parameters from global analyses based on photonuclear reactions [39,40,41]. Using 3 Standard Lorentz functions (3 SLO) a reasonable reproduction can be achieved (green line in Fig. 1 and green dot-dashed line in Fig. 2, ‘elbe1’). However, this function lacks strength above 10 MeV excitation in $^{76}$Ge. Thus, another strength function is tried (red line in Fig. 2, ‘elbe2’) in order to account also for the dominant part of the GDR strength. These strength functions of $^{76}$Ge have no influence on the neutron capture cross sections $\sigma _{\textrm{n}\gamma }$ below $E_n=10$ MeV. For $^{77}$Ge there are no experimental data and therefore a $f_{E1}$ (cyan dashed line) is constructed resembling the 3 SLO type of function for $^{76}$Ge guided by the established mass dependence of resonance parameters of GDRs focusing on E1(2). This $f_{E1}$ of $^{77}$Ge is relevant up to 11 MeV of excitation and has definitively a strong influence on $\sigma _{\textrm{n}\gamma }$.

Fig. 2

The E1 photon strength function in $^{76}$Ge and $^{77}$Ge including 1 or 3 Lorentzians (SLO) using parameters of Table 2. The latter (cyan dashed line) is reduced by a factor 0.1

2.3 The experimental levels

The experimental levels with their energies, spins, parities and branching ratios have been taken from the library RIPL [42]. Up to ten branching ratios for each level can be given to Maurina. In case the compilation did not provide any experimental branching, these are taken from calculations using the strength functions mentioned above.

Fig. 3

Binned experimental levels (open squares) of $^{76}$Ge in comparison to the level densities calculated by Maurina for the back-shifted Fermi Gas and constant-temperature model are shown in the lower panel. The upper panel shows the fraction of positive parity states per bin. A bin width of 100 keV was chosen. $E_c$ defines the continuum edge. The parameters a, $\Delta$, $U_\textrm{o}$ and T are discussed in Sect. 2.4

Fig. 4

Binned experimental levels of $^{77}$Ge, notation as in Fig. 3

The energies and parities of experimentally known levels have been binned by 100 keV into the respective distributions shown in Fig. 3 and 4. In $^{76}$Ge there are 104 states listed up to $E_x=4.939$ MeV, however, only the first 44 have been accepted to form a complete set. For the higher ones RIPL provides suggestions for the spins of states, for others only the energy is given; some levels might have been missed by experiments. Thus, the continuum edge is set at $E_c=3.390$ MeV (blue arrow in Fig. 3), i.e., above $E_c$ level densities and spin distributions are employed as described in the next subsection.

In $^{77}$Ge there are 63 levels known up to $E_x=3.560$ MeV, however, only the first 25 represent a complete set resulting in $E_c=1.560$ MeV.

The upper parts in Figs. 3 and 4 display the fraction of positive parity states as function of excitation energy. It is noted that the positive parity states are strongly favored in $^{77}$Ge.

2.4 The level densities

Level densities must be employed for excitation energies larger than $E_c$, where the experimental information on levels starts to be incomplete. Two models are compared to the binned experimental data: (i) The constant temperature model [43, 44] is used with the parameters $U_\textrm{o}$ and T given by RIPL [42] resulting from a fit up to $E_c$, and (ii) the classical back-shifted Fermi-Gas (FG) model [45] is used with parameters a and $\Delta$. The moment of inertia for a rigid body system is assumed.

For $^{76}$Ge no parameterization for the FG model is given in the literature. Employing the systematics derived by Egidy [46, 47] one obtains $a=9.328$ and $\Delta =0.961$. A slight adjustment in $\Delta$ is needed for a decent fit below $E_c$ (dashed red line in Fig. 3). Taking parameters from a fit to the level densities derived in a $^{70}$Zn($^7$Li,Xp)$^{76}$Ge experiment by Voinov [48] a different parameter set is obtained, however, giving similar results up to $E_x=5$ MeV (full red line in Fig. 3). The results from the constant temperature model are shown by black long-dashed lines.

Figure 4 compares the calculations for $^{77}$Ge with the experimentally known levels employing the parameter sets for the FG model from Plyaskin [49, 50], Dilg [51] and Egidy [46, 47], respectively. It is realized that only the Plyaskin parameterization describes the data below $E_c$, while the other two fall below by about one order of magnitude.

The numbers in the upper panel of Figs. 3 and 4 represent the respective counts for positive and negative parity levels in those nuclei. In the calculations the parity fractions can be kept constant ($\pi ^c$) or may decay exponentially with energy (green line, $\pi ^d$) towards 0.5.

3 Neutron cross sections

This work focuses on the $\gamma$ decay after neutron capture on $^{76}$Ge at low energies. For the present HF calculations, the level densities by Plyaskin [49, 50] for $^{77}$Ge and by Voinov [48] for $^{76}$Ge, respectively, are employed for excitation energies above $E_c$. The photon strength functions (3 SLO) were parameterized as given in Table 2. The neutron potential N5 is chosen for the standard model calculations. The numerical values for the neutron cross sections shown below have been mostly obtained from the EXFOR data base [52].

3.1 The total neutron cross sections

The total cross section is calculated for several potentials available in Maurina (see Table 1) as function of incoming neutron energy and displayed in Fig. 5.

The same data set of neutron total cross sections have been published twice by Musaelyan et al.: (i) in 1983 the data (after binning) were presented at the Kiev conference [53, 54] (their Fig. 1) and published in a report [55] and (ii) in 1992 the data are plotted binned and renormalized in Fig. 1 of Ref. [56, 57]. This normalization factor seems to be around 1.3.

The data cover just a small region in energy and scatter strongly. They are not well suited to select a specific potential as the potential differences are more pronounced at higher energies (see inset of Fig. 5).

Fig. 5

Total cross sections calculated with potentials given in Table 1 are compared to the same experimental data, however, analyzed separately by the two original authors (see text)

3.2 Inelastic neutron scattering

Inelastic scattering cross sections on $^{76}$Ge have been measured recently by Rouki et al.[58] and Crider et al.[59].

Fig. 6

Inelastic cross sections calculated with potential N5 for exclusive (red) and inclusive (blue) population of the first 5 excited states compared to the data of Ref. [58] (exclusive, squares) and Ref. [60] (inclusive, triangles). The vertical lines indicate the energies of the excited states

In Fig. 4 of Ref. [58] a comparison with older data [60,61,62,63] is provided for the inclusive reaction $^{76}$Ge(n,n’$\gamma$) populating the first excited state of $^{76}$Ge at 563 keV.

The inelastic cross sections for the first five excited states are plotted in Fig. 6 using the exclusive data from Ref. [58]. For the first two states also the inclusive data of Ref. [60] are given. The data compare well with the Maurina calculations using the neutron potential N5.

Fig. 7

Inelastic cross sections for exclusive population of the first excited state (Ref. [58]) compared to the calculations with different neutron potentials

To demonstrate the influence of the neutron potential on the inelastic cross sections the results of various potentials are compared to the first (Fig. 7) and fourth (Fig. 8) excited state. The spread of the calculations was to be expected. Overall the N5 potential gives the best results. The potentials N7 and N9 overshoot the data and the other potentials N2, N5 and N8 considerably. In contrast, N22 falls too low. It might be recognized already in the inset of Fig. 5 where N22 behaves quite differently at low energies when compared to the others.

Fig. 8

Same as Fig. 7, but for the fourth excited state

The state at 3952 keV in $^{76}$Ge features 5 $\gamma$-decay branches, one $\gamma$ has the energy of 2040.7 keV with a partial width of 4 %. This energy is rather close to the $Q_{\beta \beta }$-value of the $0\nu \beta \beta$ decay in $^{76}$Ge, and thus might be a background contribution. Since there has been some discussion about this state [58, 59], the inclusive inelastic cross section is calculated for a selected number of potentials. The inclusive cross section has been chosen since the information on states in this excitation energy range is not complete (note, that $E_c=3390$ keV has been set). Furthermore, the spin of the 3952 keV state may equal $J^\pi =1$ or 2 without parity information. The cross sections calculated for $J^\pi =1^+$ are smaller (dot-dashed lines in Fig. 9) by about 30 % than those for $J^\pi =2^+$ (full lines). Similar to Fig. 8, the potentials N7 and N9 overshoot the data and the other potentials N2, N5 and N8 considerably.

Fig. 9

The inclusive cross section for the seventieth excited state at 3952 keV for $J^\pi =1^+$ (dot-dashed lines) and $J^\pi =2^+$ (full lines) compared to data from Crider [59]

Most of the strength is concentrated in the neutron energy range 4 to 6 MeV. A conservative estimate for the contribution of the 2040.7 keV $\gamma$ starts from the N5 prediction with $J^\pi =2^+$, i.e., $\sigma \sim$10 mb, and due to its partial width resulting in $\sigma _\gamma ^\star =0.4$ mb. The $J^\pi =1^+$ assumption would result in $\sigma _\gamma ^\star =0.3$ mb. These numbers are on average a factor 2 larger than the numbers extracted by Ref. [59]. Assuming negative parity for the two states results in 7 % lower cross sections. Two more $\gamma$s in the vicinity of $Q_{\beta \beta }$ have been observed by Ref. [59], however, their spin is not known making a calculation unattractive. Due to the uncertainties mentioned above one cannot conclude firmly about the spin and parity of the state at 3952 keV from the present calculations.

3.3 Neutron capture

The neutron capture reaction has been measured at thermal energies and up to the MeV range via activation or time-of-flight [24, 25, 64,65,66,67,68].

These data are compared to the cross sections obtained from Maurina with the neutron potentials N2, N5 and N8 in Figs. 10 and 11. The color code in Fig. 10 distinguishes the cross sections to the ground state (red), the isomeric state (blue) and the sum of both (black); the line style distinguishes the three neutron potentials. The 20 % feeding of the ground state by the internal transition is not considered in the calculations. One recognizes in linear and logarithmic scale that the data are reasonably well described over most of the region spanning about 2 orders of magnitude; above 4 MeV the calculations for the ground state transitions overshot the data by up to a factor $\sim$2 while those for the isomeric state still fit the data reasonably well. In contrast to the inelastic scattering the three potentials give rather similar results for the capture reaction.

Figure 11 is adapted from Ref. [24] showing the thermal and epithermal cross sections. The region above the resonances ($\sim$30 keV) is well described by Maurina up to 1 MeV. The calculation definitively fails in the resonance region as this regime is beyond the scope of the Hauser-Feshbach model.

Fig. 10

The excitation function for neutron capture on $^{76}$Ge on a doubly logarithmic scale with an inset with linear scales. The data are from Refs. [64,65,66,67,68]

Fig. 11

Thermal and epithermal cross sections [24] in comparison to the predictions by Maurina with N5

Fig. 12

The ratio of isomeric to total cross section of Ref. [68] compared to predictions by Maurina

Fig. 13

The $\gamma$-cascades from $^{76}$Ge(n,$\gamma$)$^{77}$Ge employing the standard parameterization. Top: the total $\gamma$ spectrum in $^{77}$Ge and the running sum normalized to 1 (red line). Middle: the spectrum for the multiplicities M inversely stacked; the inset shows the distribution of multiplicity M. Bottom: the sequence of $\gamma$ quanta within the cascade inversely stacked. The color code is valid for the middle and bottom graph. 7+ indicates that all higher multiplicities have been added to $M=7$

Below 30 keV several resonances appear in the data of Ref. [24]. The $n\_$ ToF data [25] show resonances up to 50 keV, but do not show cross sections into the MeV range. Due to the overshoot of Maurina in the thermal region the respective Maxwell averaged cross sections are higher by about 50 %. The discrepancies between data and the ENDF evaluation demonstrate the need to repeat the simulations for neutron capture within the setup of Gerda.

Of paramount interest for the $0\nu \beta \beta$ experiments are the relative cross sections for population of the ground and isomeric state as different trigger schemes are needed for the filtering. Figure 12 shows the ratio $\sigma _m/\sigma _T$ of isomeric to total cross section [68] in comparison to the calculations for the three potentials N2, N5 and N8. Since these described the cross sections equally well, the ratios come also rather close. The largest difference is found around 3 MeV. Above 4 MeV the ratio falls below the data due to the larger ground state contributions.

Figures 2 displays a quite different behavior of the photon strength function $f_{E1}$ at photon energies below 11 MeV. To check the sensitivity of the cross section ratio $\sigma _m/\sigma _T$ on $f_{E1}$, $f_{E1}$(3 SLO) is replaced by $f_{E1}$(GDR), one derived from a simple Giant Dipole Resonance (see Table 2, GDR, dotted line in Fig. 12). The differences are small and comparable to those of the three potentials. Larger effects are achieved when the parity fraction of the continuum states are modified. The standard calculations use those shown in Fig. 4, whose positive parity fraction is parameterized as $f^+=0.95\times \exp {(-0.05/E_x)}$. Keeping $f^+$ constant at 0.5 (long dashes) or constant at 0.05 (dot-dashed) reduces the ratio strongly. Possible reasons for the discrepancies above 4 MeV might be missing information on discrete levels or a direct contribution. These findings are in contrast to the assumption $f^+=0.5$ taken in Ref. [48].

4 The $\gamma$ spectra after neutron capture

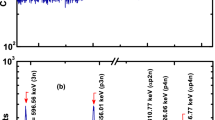
Up to neutron energies of $E_n=4$ MeV the excitation function calculated with the standard data set describes the capture data very well. Nevertheless, spectra at $E_n=200$ meV, 50 keV, 500 keV and 5 MeV will be shown for comparison of relative numbers. For each of these energies 10$^7$ $\gamma$ cascades are produced by a Monte Carlo procedure selecting the next lower state of the decay via the respective branching ratios. The populated compound nucleus decays via several $\gamma$s reaching finally either the isomeric or ground state of $^{77}$Ge. As first example, Fig. 13 shows the $\gamma$ spectrum for $E_n=200$ meV (top panel, blue line) with a binning of 1 keV. This energy is well within the resonance region and thus outside the range of the Hauser-Feshbach model, however, it is meant to show the characteristics for pure s-wave ($\ell =0$) capture. The transitions to the discrete levels are recognized on the high-energy side of the spectrum, those between them on the low-energy side. The central part of the spectrum is smooth due to continuum-continuum transitions and due to several $\gamma$s in the decay. More knowledge on discrete levels would reduce the purely smooth part of the spectrum. The red line gives the running sum normalized to 1. Figure 13 shows the $\gamma$s sorted by the multiplicity M of the cascade (middle panel) and by their sequence within the cascade (bottom panel). These two spectra are binned into 5 keV and plotted as stacked histograms in inverse order, i.e., highest number first. At this low neutron energy a maximum of 7 $\gamma$s have been seen, with a maximum of the distribution around 3 (see inset of middle panel). The ground state is populated dominantly directly and it is clearly the only one with $M=1$. The isomeric state is populated with $M=2$. The sequence spectra (bottom panel) show structures at the low energy part, but are smooth above photon energies of about 1.1 MeV except for the first photon. A selection of low lying states is directly populated by a high energetic photon.

Fig. 14

$\gamma$-cascades from $^{76}$Ge(n,$\gamma$)$^{77}$Ge, as in Fig. 13, but for an incident neutron energy of 5 MeV

4.1 The energy dependence

The spectra for $E_n=500$ keV are rather similar to those for $E_n=200$ meV. These (and others) can be found in the supplemental material [69].

At first sight also the spectra at $E_n=5$ MeV (Fig. 14) appear as stretched versions of those produced by keV neutrons. The multiplicity is slightly higher reaching up to $M=10$. In contrast, since the phase space is larger due to the higher excitation energy, the high energetic transitions of lower multipolarity are strongly favored. The direct population of low lying states occurs in such a way that they do not sit on a continuum any more. The ground state is populated purely by $M=1$ transitions in contrast to the $E_n=200$ meV case. Figure 14, bottom, shows that the first photons in the cascade having energies in excess of 9.5 MeV populate selected final states. The ground state, the 2$^{nd}$ and 3$^{rd}$ excited states are fed, but not the isomeric state. The relative strengths of the multiplicity and sequence distributions are a consequence of the phase space and the relative strengths of the $f_{XL}(\varepsilon _\gamma )$.

A close-up of the high-energy $\gamma$-region is given in Fig. 15 for neutron energies of $E_n=200$ meV, 50 keV and 500 keV showing the inversely stacked multiplicity histograms with same color coding as previously. For easier comparison the spectra are aligned in such a way that the ground state transitions for the two lower energies coincide with that for 500 keV. This figure confirms the dominant population of the ground state with $M=1$ and the recession of the upper continuum part with higher neutron energy.

Fig. 15

High energy part of $\gamma$-cascade spectra after neutron capture on $^{76}$Ge in dependence of the neutron energy $E_n$. The spectra for 200 meV and 50 keV have been aligned in such a way that the ground state transition appears at the same spot as that for 500 keV. Left column: transitions to the ground state; right column: transitions to the isomeric state at 160 keV. The color code indicates the multiplicity within the cascade (see Fig. 13 for the definition)

4.2 The spin dependence

Following the experience of gadolinium [28] the influence of the values for spin and parity of the intermediate compound nucleus state on the relative cross sections for capture to ground and isomeric state is investigated. Firstly, for a better understanding of the results the population of the involved states in the compound nucleus are shown in Fig. 16 for three energies, namely $E_n=0.5$ keV, 500 keV and 5 MeV, respectively. Note the enormous range of 43 orders of magnitude for the population of the intermediate CN state at low neutron energies. Therefore, a dominant population of $J^\pi$ $=1/2^+$ states after s-wave capture follows. Less staggering and fall-off are observed for the high energies. Setting a level of 1 mb, no state above $J^\pi$= 3/2 is reached at 0.5 keV neutron energy, with limits at 7/2 and 13/2 for 500 keV and 5 MeV, respectively. The left inset at the bottom shows a blow-up of the low-spin region, while the right inset gives the energy dependence for the lowest three spins reachable by s- and p-wave neutrons. The HF model shows a clear dominance for s-wave capture below about 100 keV.

Fig. 16

The population of the states with $J^\pi$ in the compound nucleus $^{77}$Ge after the $^{76}$Ge(n,$\gamma$)$^{77}$Ge reaction with neutron energies of $E_n=0.5$ keV, 500 keV and 5 MeV, respectively. Lines connect the data points to guide the eye. The left inset is a close-up of the low spin region. The right inset displays the populations as function of neutron energy $E_n$. The two gray lines show the 1 b and 1 mb level, respectively

Fig. 17

High energy part of $\gamma$-cascade spectra after neutron capture at $E_n=50$ keV in dependence of the spin $J^\pi$ of the compound nucleus. Left column: transitions to the ground state; right column: transitions to the isomeric state at 160 keV. The color code indicates the multiplicity within the cascade (see Fig. 13 for the definition)

The initial spin of the CN decides clearly the $\gamma$ decay pattern as shown in Fig. 17 for capture of 50 keV neutrons. For clarity only the upper ends of the spectra are shown. For the different transitions their strengths vary with changing conditions of CN spin or final state. No $M=1$ is observed for $J^\pi$ $=1/2^+$ in the CN or any other spin in the CN reaching the isomeric state. In general, different multiplicities are observed in dependence of initial and final states. This neutron energy has been chosen as the $n\_$ ToF data show a strong resonance at 50 keV. Measuring the decay $\gamma$s with sufficient resolution would allow to determine spin and parity of this resonance.

5 Conclusion

Calculations based on the statistical Hauser-Feshbach model have been undertaken to support $0\nu \beta \beta$ experiments with (enriched in $^{76}$Ge) germanium detectors. The code Maurina provided cross sections for several reactions to verify and justify the input parameters and indicate possible dependencies. In general, the data are described rather well as, e.g., inelastic scattering. However, some of them, e.g., the total cross section, leave quite some room for interpretation. Improved total neutron cross section data at higher energies could easily restrict neutron potentials. To avoid further ambiguities in the reaction mechanism the calculations were carried out up to neutron energies of 5 MeV. Up to these energies only neutrons and $\gamma$s needed to be considered. More information on photon strength functions $f_{XL}(\varepsilon _\gamma )$ or levels and their spin and parity would facilitate further calculations, in particular for higher neutron energies.

The important outputs are $\gamma$ spectra in order to tune triggering schemes and selection criteria needed to suppress backgrounds due to background signals arising from neutron capture on $^{76}$Ge. As these criteria are different for the decay of the ground state and isomer of $^{77}$Ge an important feature has been the reproduction of the cross section ratio for the production of the two states. Up to neutron energies of 4 MeV a very good agreement was achieved; uncertainties in the cross sections are estimated to less than 20 %. Above 4 MeV the calculation falls below the data by about 20–40 %. Missing information on levels might be the cause or some direct reaction contributions. The cross-section ratio for populating ground and isomeric state is shown to depend strongly on the parity fraction in the compound nucleus. Further work is needed to verify that such ratios can be used for parity assignments in the compound nucleus at higher energies.

The spin dependence of the $\gamma$ spectra after capture has been shown in the resonance region where few $\ell$-waves contribute. Below 30 keV the Hauser-Feshbach model is not valid to produce absolute cross sections. However, the $\gamma$ decay and relative intensities may be obtained. This shows an alternative path to improve the knowledge about resonances.

For several neutron energies $10^7$ $\gamma$ cascades have been calculated to serve as input for Geant4-simulation of the Gerda and Legend experiment. These simulations [70] have proven that Legend can be carried out at the Lngs laboratory of INFN as this background contribution is estimated to be on the level of 4 % of the total background. Further simulations are expected to further improve the background reduction efficiency.