Fission valleys and favored isotopes emitted from $^{310}$126

Abstract

The decay channels for the superheavy nucleus $^{310}$126 are studied under the binary macroscopic–microscopic method. The macroscopic part is calculated as the heavy-light interacting charged liquid drops, linked through the finite range Yukawa-plus-exponential force. The microscopic energy is calculated based on the spheroidally deformed two-center shell model. The proton and neutron single-particle levels are introduced in the binary Strutinsky procedure. The resulting shell corrections are added to the macroscopic part to obtain the fission barriers. The dynamical part follows by introducing the Werner–Wheeler inertia. The final lifetimes are calculated for all possible isotopic channels around the most favored heavy-light fragment pairs.

1 Introduction

The possibility of superheavy existence was certified through experiments. The facilities at GSI-Darmstadt [1, 2], RIKEN [3] and earlier at the Lawrence Berkeley [4] or Flerov [5] Laboratories performed successful reactions towards the synthesis of such nuclei. Three possible stable elements have been predicted by theory. Calculations are published since the twentieth century [6,7,8,9], and later on in [10]. These three most promising stable elements obtained with macroscopic–microscopic, but also with self-consistent calculations are Z = 114, 120 and 126 [11, 12]. The last one, Z = 126, has been emphasized using zero-range Skyrme forces SkP and Ly7, and RMF interactions [13]. It can also be obtained with Woods–Saxon microscopic single particle potential in [14]. Its stability properties are closely related to different ways of decay. Generally, these are studied through the macroscopic–microscopic method, with more or less degrees of complexity. Fission of superheavy elements used, among others, the Modified Generalized Liquid Drop Model [15,16,17].

Alpha decay is supposed to be the preferred way of decay for Z = 126, and for superheavy nuclei in general. This direction is theoretically covered by many authors [18,19,20]. All these studies are based on different versions of the macroscopic–microscopic method, assigned with several deformation spaces of the initial nucleus. The number N = 184 is accepted up to now as being the most probable neutron closure, both by macroscopic–microscopic [21], and by self-consistent approaches [22]. Consequently, the various decay channels of $^{310}$126 are browsed. Generally, the alpha decay has been considered the main decay way from super-heavy nuclei until recent calculations changed this perspective [23]. Using the analytical superasymmetric fission model (ASAF), the calculated half-lives for emitted clusters for alpha and heavier ($^{80}$Ge, $^{84}$Se from $^{298}$114 for ex.) proved to be more favorable. Alpha-decay half-lives of superheavy nuclei are also presented in [24] with Woods–Saxon potential and in [25], with proximity potentials and deformed-spherical Coulomb potential. Logarithmic alpha-decay half-lives for Z = 126 are calculated also in [16] with the Generalized Liquid Drop Model. The proximity potential for deformed nuclei produced alpha-decay half-lives for a range of superheavy nuclei, including Z = 126, as the alpha decay chain from Z = 128 is studied in [26]. The range of the half-life logarithm for alpha-decay in Coulomb-plus-proximity potential model [19] spans from $-$ 7.4 to 12.3, as the neutron number decreases for Z = 126.

Fission valleys are emphasized around dynamically preferred pairs of heavy-light fragments. Then an examination around the specified isotope pairs is effected in order to detect the most promising neutron pairs around a given isotope pair. In Sect. 2, the binary theoretical method is presented, whereas Sect. 3 presents the results for the fission of $^{310}$126, with the most favored pairs of fragments versus the alpha decay, followed by conclusions.

2 Heavy-light fission fragment related macroscopic–microscopic method

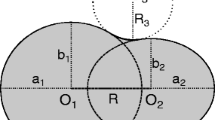
The theoretical method constructed here accounts for the description of two interacting nuclear systems, each corresponding to the heavy and light fragment. Fission-like configurations are considered, consisting in two partially overlapped spheroids. The shape evolves from the initiallly assumed sphere for $^{310}$126, up to two separated spheroids as the fragments split up. The particular characteristic of this binary method is that the total deformation energy is calculated for two fragments in interaction. The deformation space is formed of five free coordinates: the ratios of the spheroid semiaxes for the heavy $\chi _H=b_H/a_H$, and light fragment $\chi _L=b_L/a_L$, the small semiaxis of the emitted one $b_L$ and the distance between centers R. The origin of the coordinate system is taken at the center of the heavy fragment. Since the system is axially symmetric, cylindrical coordinates are employed, so that the center of the emitted fragment corresponds to $z=R$, and the separation plane between the two fragments situates at $z=z_s$.

As usual, there are two parts of the algorithm: the macroscopic term $E_{mac}$, calculated within a binary nuclear Yuakawa-plus-exponential potential $E_{YE}$, to which one adds the two interacting charged liquid drop repulsive potential $E_C$, as in [27], and the microscopic term $E_{sh}$ constructed as the shell correction energy based on the Strutinsky method [28]. The binary character of this method is given by the use of the deformed two-center shell model [29]. The two-center single-particle levels are introduced in the shell correction calculation at every point within the deformation space. Proton and neutron terms are finally summed up and $E_{sh}$ is obtained. The fission static barrier $E_b$ is calculated as the sum of the macroscopic and microscopic terms:

$$\begin{aligned} E_b=E_{mac}+E_{sh} \end{aligned}$$

(1)

2.1 The macroscopic energy adapted for fission-like configuration

In the general macroscopic formula for the energy, only two terms are deformation dependent: the nuclear surface tension $E_{YE}$ which maintain the nucleus together and the Coulomb one, $E_C$, which tends to separate the protons. One complies to the convention that for zero deformation (spherical shape), the deformed energy is zero. Then, the macroscopic deformed energy $E_{mac}$ for a charged liquid drop is:

$$\begin{aligned} E_{mac}=E_{YE}-E_C \end{aligned}$$

(2)

The surface energy depends on the area and shape of the nucleus, with a general formula function of the finite internuclear force of the Yukawa-plus-exponential type:

$$\begin{aligned} E_{YE}=\frac{V_0}{4\pi a^3} \int \int _{(vol)} \frac{\exp {(-r_{12}/a)}}{r_{12}/a} d^3r_1d^3r_2 \end{aligned}$$

(3)

with

$$\begin{aligned} V_0=\frac{a_2}{2\pi a r_0^2} \end{aligned}$$

(4)

where $a_2$ is the surface intensity, known from the basic $E_n \sim a_2 A^{2/3}$ surface dependence. The intergral is taken on the binary configuration, after Gauss–Ostrogradsky transformation; thus one has:

$$\begin{aligned} E_{YE}= & {} \frac{a_2}{8\pi ^2r_0^2a^4} \oint \oint _{surf}\nonumber \\{} & {} \left\{ \left[ \frac{r_{12}}{a} \left( \frac{r_{12}}{a}+2 \right) +2 \right] \exp {\left( -\frac{r_{12}}{a} \right) }-2 \right\} \nonumber \\{} & {} \frac{(dS_1r_{12})(dS_2r_{12})}{r_{12}^4/a^4} \end{aligned}$$

(5)

where $S_1$ and $S_2$ are taken over the surfaces of the heavy and light spheroids. When the differential surfaces $dS_i$ are expanded, one obtains expressions of the type:

$$\begin{aligned} E_{YE} \sim \frac{1}{4\pi r_0^2}c_sD_Y \end{aligned}$$

(6)

and when submitted to binary configurations, the Yukawa-plus-exponential energy reads:

$$\begin{aligned} E_{YE}=\frac{1}{4\pi r_0^2} \left[ c_{sH}D_{YH}+c_{sL}D_{YL}+2\left( c_{sH}c_{sL}\right) ^{1/2}D_{YHL}\right] \nonumber \\ \end{aligned}$$

(7)

The macroscopic parameters used to calculate the Yukawa-plus-exponential liquid-drop type energy are determined in [27] from experiments in ellastic scattering and nuclear masses. The finite range radius of the Yukawa force in Eq. (3) is a=0.68 fm. The effective surface energy constant upon the relative neutron-proton excess used in Eq. (7) is taken as:

$$\begin{aligned} c_{sH,L}=a_s \left[ 1-\kappa _s \left( \frac{N_{H,L}-Z_{H,L}}{A_{H,L}}\right) ^2 \right] \end{aligned}$$

(8)

where the surface energy constant $a_s=21.7$ MeV and the surface-asymmetry constant is $\kappa _s=3$. The last term in Eq. (7) represents the heavy-light interaction contribution. The terms belonging to the individual fragments and the interaction one are:

$$\begin{aligned} D_{YH}= & {} \int _0^{2\pi } d\phi \int _{-a_H}^{z_s} dz \int _{-a_H}^{z_s} E_{Y1}^{(H)}E_{Y2}^{(H)}Q^{(H)} dz^{\prime } \nonumber \\ D_{YL}= & {} \int _0^{2\pi } d\phi \int _{z_s}^{R+a_L} dz \int _{z_s}^{R+a_L} E_{Y1}^{(L)}E_{Y2}^{(L)}Q^{(L)} dz^{\prime } \nonumber \\ D_{YHL}= & {} \int _0^{2\pi } d\phi \int _{-a_H}^{z_s} dz \int _{z_s}^{R+a_L} E_{Y1}^{(HL)}E_{Y2}^{(HL)}Q^{(HL)} dz^{\prime } \nonumber \\ \end{aligned}$$

(9)

The integrands are entirely dependent on the geometry. The separated ones are:

$$\begin{aligned} E_{Y1}^{(H)}= & {} \rho _H^2(z)-\rho _H(z)\rho _H(z^{\prime })\cos \phi -0.5\left( z-z^{\prime }\right) \frac{d\rho _H^2(z)}{dz} \nonumber \\ E_{Y2}^{(H)}= & {} \rho _H^2(z^{\prime })-\rho _H(z)\rho _H(z^{\prime }) \cos \phi +0.5(z-z^{\prime } \frac{d\rho _H^2(z^{\prime })}{dz^{\prime }} \nonumber \\ E_{Y1}^{(L)}= & {} \rho _L^2(z)-\rho _L(z)\rho _L(z^{\prime }) \cos \phi -0.5\left( z-z^{\prime }\right) \frac{d\rho _L^2(z)}{dz} \nonumber \\ E_{Y2}^{(L)}= & {} \rho _L^2(z^{\prime })-\rho _L(z)\rho _L(z^{\prime }) \cos \phi +0.5\left( z-z^{\prime }\right) \frac{d\rho _L^2(z^{\prime })}{dz^{\prime }}\nonumber \\ \end{aligned}$$

(10)

and the interaction one:

$$\begin{aligned} E_{Y1}^{(HL)}= & {} \rho _H^2(z) - \rho _H(z)\rho _L(z^{\prime })\cos \phi -0.5\left( z-z^{\prime }\right) \frac{\rho _H^2(z)}{dz} \nonumber \\ E_{Y2}^{(HL)}= & {} \rho _L^2(z)-\rho _H(z)\rho _L(z^{\prime })\cos \phi +0.5\left( z-z^{\prime }\right) \frac{\rho _L^2(z^{\prime })}{dz^{\prime }}\nonumber \\ \end{aligned}$$

(11)

and:

$$\begin{aligned} Q^{(H,L)}=2-\left[ \left( \frac{\sigma _{H,L}}{a}\right) +2\frac{\sigma _{H,L}}{a}-2\right] \exp {\left( -\frac{\sigma _{H,L}}{a}\right) }\frac{1}{\sigma ^4_{H,L}}\nonumber \\ \end{aligned}$$

(12)

Here $\rho _{H,L}(z)$ is the surface shape equation for heavy (H) and light (L) fragment. Notice that the limit $z_s$ in the integral is the cutoff value between heavy and light fragment along the symmetry axis. The action range of the nuclear force is taken $a=0.68$ fm. $\sigma _{H,L}$ is also surface dependent.

The binary Coulomb energy treatment is almost the same. The basic formula:

$$\begin{aligned} E_C=\frac{\rho _e^2}{10} \oint \oint _{Sn} \frac{\left( \mathbf {r_s}\textbf{dS}\right) \left( |\mathbf {r_1}-\mathbf {r_s}|\mathbf {dS^{\prime }}\right) }{|\mathbf {r_1}-\mathbf {r_s}|} \end{aligned}$$

(13)

becomes:

$$\begin{aligned} E_C= & {} \frac{2 \pi }{3} \left\{ \rho _{eH}^2 \int _{-a_H}^{z_s}dz \int _{-a_H}^{z_s} dz^{\prime } G_H(z,z^{\prime }) \right. \nonumber \\{} & {} + \rho _{eL}^2 \int _{z_s}^{R+a_L} dz \int _{z_s}^{R+a_L} dz^{\prime } G_L (z,z^{\prime }) \nonumber \\{} & {} +\left. \rho _{eH}\rho _{eL} \int _{-a_H}^{z_s} dz \int _{z_s}^{R+a_L} dz^{\prime } G_{HL} (z,z^{\prime }) \right\} \end{aligned}$$

(14)

The integrands depend only on the heavy (H), light (L) or interaction (HL) surface geometry. The interaction term reads:

$$\begin{aligned} G_{HL}(z,z^{\prime })= & {} \left\{ \rho _H(z) \rho _L(z^{\prime }) \frac{K(k_{HL})-2D(k_{HL})}{3} \right. \nonumber \\{} & {} \cdot \left[ 2[(\rho _H^2(z) +\rho _L^2 (z^{\prime })] -\left( z-z^{\prime }\right) ^2 +1.5 \left( z-z^{\prime }\right) \right. \nonumber \\{} & {} \left. \left( \frac{d \rho _H ^2(z^{\prime })}{dz^{\prime }} - \frac{d \rho _L^2(z^{\prime })}{dz} \right) \right] \nonumber \\{} & {} \left. + K(k_{HL}) \left\{ \frac{\rho _H^2(z) \rho _L^2 (z^{\prime })}{3} \right. \right. \nonumber \\{} & {} +\left[ \rho _H^2(z) -0.5\left( z-z^{\prime }\right) \frac{\rho _H^2(z)}{dz} \right] \nonumber \\{} & {} \left. \left. \left[ \rho _L^2 (z^{\prime })+0.5\left( z-z^{\prime }\right) \frac{\rho _L^2 (z^{\prime })}{dz^{\prime }} \right] \right\} \right\} \end{aligned}$$

(15)

$G_L$ and $G_H$ are the geometry dependent integrands within the individual fragment terms for the Coulomb energy. Their expression depend only on the shape of the heavy or light fragment part of the partially overlapped configuration:

$$\begin{aligned} G_{H}(z,z^{\prime })= & {} \left\{ \rho _H(z) \rho _H(z^{\prime }) \frac{K(k_H)-2D(k_H)}{3} \cdot \right. \nonumber \\{} & {} \left[ 2[(\rho _H^2(z) +\rho _H^2 (z^{\prime })] -\left( z-z^{\prime }\right) ^2 +1.5 \left( z-z^{\prime }\right) \right. \nonumber \\{} & {} \left. \left( \frac{d \rho _H ^2(z^{\prime })}{dz^{\prime }} - \frac{d \rho _H^2(z)}{dz} \right) \right] \nonumber \\{} & {} \left. + K(k_{H}) \left\{ \frac{\rho _H^2(z) \rho _H^2 (z^{\prime })}{3}\right. \right. \nonumber \\{} & {} +\left[ \rho _H^2(z) -0.5\left( z-z^{\prime }\right) \frac{\rho _H^2(z)}{dz} \right] \nonumber \\{} & {} \left. \left. \left[ \rho _H^2 (z^{\prime })+0.5\left( z-z^{\prime }\right) \frac{\rho _H^2 (z^{\prime })}{dz^{\prime }} \right] \right\} \right\} \end{aligned}$$

(16)

where K and D are elliptic integrals of first and second degree. The light fragment term is obtained by replacing the index H with L. One should mention that both the Yukawa-plus-exponential surface and the Coulomb term contain the binary interaction energies.

2.2 The two-center Strutinsky corrections

The fission phenomenon is defined by pairs of fragments emerging from a parent nucleus. The way a certain pair is advantaged to be produced is determined by the dynamics of the process. It implies the shape of the potential barrier and the influence of the mass inertia. A low barrier is risen by the macroscopic part, but the differences are mainly influenced by the shell corrections. In order to have the proper quantitative impact due to a certain pair, one has to describe the appropriate shell corrections from the chosen mass division. This request can be fullfiled by the choice of a microscopic potential which relates to the particular binary configuration. Such a potential is formed by two Nilsson type quantum wells which partially overlap in connection to the geometrical configuration of two intersected spheroids [29]. Two-center shell models have also been developed using two Woods–Saxon type wells, taking advantage of a finite well beyond the Fermi level [30, 31]. This work uses two spheroidally deformed oscillators as the main part of the microscopic potential:

$$\begin{aligned}{} & {} V_{2-osc}(\rho ,z) \nonumber \\{} & {} = \left\{ \begin{array}{ll} \frac{1}{2}m_0 \left( \omega _{\rho _H}^2 \rho ^2+\omega _{zH}^2z^2\right) , &{} (\rho ,z<z_s) \in vol(A_H) \\ &{} \\ \frac{1}{2}m_0 \left[ \omega _{\rho _L}^2 \rho ^2 + \omega _{z_L}^2 (z-R)^2 \right] , &{} (\rho , z \ge z_s) \in vol(A_L) \end{array} \right. \nonumber \\ \end{aligned}$$

(17)

The ratio of the two frequencies $\omega _{\rho }/\omega _z$ is proportional to the spheroid semiaxes ratio of each fragment.

The two-center oscillator potential submits to the equipotentiality on the nuclear surface. For a sphere one has:

$$\begin{aligned} V_0=\frac{m_0\omega ^2R_i^2}{2} \end{aligned}$$

(18)

where $R_i$ is the radius of the parent nucleus, taken as $R_i=r_0A^{1/3}$. If one writes the same condition for the spheroid surface, one obtains:

$$\begin{aligned} \frac{m_0\omega _z^2a_{H,L}^2}{2}= & {} V_0 \nonumber \\ \frac{m_0 \omega _{\rho }^2b_{H,L}^2}{2}= & {} V_0 \end{aligned}$$

(19)

The frequencies are defined along the symmetry axis $\omega _z$ and perpendicular to it $\omega _{\rho }$ respectively. In this way the shapes of the fission fragment nuclei are coupled to the two-center potential via the two frequencies, through the relations:

$$\begin{aligned} \frac{\omega _z}{\omega _{\rho }}=\frac{b_{H,L}}{a_{H,L}} \end{aligned}$$

(20)

where $a_{H,L}$ is the small spheroid semiaxis and $b_{H,L}$ is the one along the symmetry axis.

The residual spin-orbit $V_{{\hat{l}}{\hat{s}}}(\rho ,z)$ and $V_{\hat{l^2}}(\rho ,z)$ are derived from the two-oscillator potential and adapted to the binary configuration:

$$\begin{aligned}{} & {} V_{{\hat{l}}{\hat{s}}}(\rho ,z) \nonumber \\{} & {} = \left\{ \begin{array}{cc} -\left\{ \displaystyle \frac{\hbar }{m_0 \omega _{0H}} \kappa _H(\rho ,z), (\nabla V_{2-osc} \times {\hat{p}}) {\hat{s}} \right\} , &{} vol(A_H) \\ -\left\{ \displaystyle \frac{\hbar }{m_0 \omega _{0L}} \kappa _L(\rho ,z), (\nabla V_{2-osc} \times {\hat{p}} ) {\hat{s}} \right\} , &{} vol(A_L) \end{array} \right. \nonumber \\ \end{aligned}$$

(21)

and similarly:

$$\begin{aligned}{} & {} V_{{\hat{l}}^2}(\rho ,z)\nonumber \\{} & {} = \left\{ \begin{array}{cc} -\left\{ \displaystyle \frac{\hbar }{m_0^2 \omega _{0H}^3} \kappa _H \mu _H(\rho ,z), (\nabla V_{2-osc} \times {\hat{p}})^2 \right\} , &{} vol(A_H) \\ -\left\{ \displaystyle \frac{\hbar }{m_0^2 \omega _{0L}^3} \kappa _L \mu _L (\rho ,z), (\nabla V_{2-osc} \times {\hat{p}})^2 \right\} , &{} vol(A_L) \end{array} \right. \nonumber \\ \end{aligned}$$

(22)

The microscopic potential is calculated to fulfill the possible demand that Z = 126, N = 184 form a structure of a doubly-magic nucleus. To this end, a study is performed so that the Strutinsky proton and neutron shell corrections have a local minimum at the spherical ground state. The way to fulfill this purpose is based on the variation of the residual spin-orbit and $l^2$ interaction strengths as parameters $\kappa$ and $\mu$ vary, in Eqs. (18, 19). The resulted values are: $\kappa _p=0.055$, $\mu _p=0.400$ for protons and $\kappa _n=0.045$, $\mu _n=0.427$ for neutrons. Since the strength intensities $\kappa$ and $\mu$ are z-dependent, the anticommutator is used in order to achieve self-adjointness. One has to mention the limit conditions for the ${\hat{l}}{\hat{s}}$ and $\hat{l^2}$ strength parameters: these quantities have to take values of $\kappa _0$ and $\mu _0$ of the initial parent and ($\kappa _{Hf}, \mu _{Hf}$), ($\kappa _{Lf}, \mu {Lf}$) for the final, separated nuclei configuration. To this end, a linear law of variation, geometry dependent, has been imposed:

$$\begin{aligned} \kappa _{H,L}= & {} \kappa _0+(\kappa _{Hf,Lf}-\kappa _0) \frac{R-R_i}{R_t-R_i} \nonumber \\ \mu _{H,L}= & {} \mu _0 +(\mu _{Hf,Lf} - \mu _0 ) \frac{R-R_i}{R_t-R_i} \end{aligned}$$

(23)

where $R_i$, $R_t$ are the initial and touching distances between centers. In this way the intensity strengths are dependent on the deformation at every point of the elongation, represented by the distance between centers R. At this point the deformed two-center Schroedinger equation reads:

$$\begin{aligned}{} & {} {}\left[ -\frac{\hbar ^2}{2m_0}\Delta +V_{2-osc}(\rho ,z)+V_{{\hat{l}}{\hat{s}}}(\rho ,z) +V_{\hat{l^2}}(\rho ,z) \right] \nonumber \\{} & {} \quad \Psi _{mn_{\rho }\nu }(\rho ,z,\phi ) =E_{mn_{\rho }\nu } \Psi _{mn_{\rho }\nu }(\rho ,z,\phi ) \end{aligned}$$

(24)

When solved only for the $V_{2-osc}(\rho ,z)$ potential, the equation produces the basis $\Psi _{m n_{\rho }\nu }^{(2-osc)}(\rho ,z,\phi )$ for further calculations:

$$\begin{aligned} \Psi _{m,n_{\rho },\nu }^{(2-osc)}(\phi ,\rho ,z) =\Phi _m(\phi )R_{n_{\rho }}^{|m|}(\rho ) Z_{\nu }(z) \end{aligned}$$

(25)

where the partial components read:

$$\begin{aligned}{} & {} \Phi _m(\phi ) = \frac{1}{\sqrt{2\pi }} \exp {(im \phi )}\nonumber \\{} & {} R_{n_{\rho }}^{|m|}(\rho ) = \left[ \frac{2 \Gamma (n_{\rho }+1)\alpha _H^2}{\Gamma (n_{\rho }+|m|+1)} \right] ^{1/2} \nonumber \\{} & {} \qquad \qquad \exp {\left( -\frac{\alpha _H^2 \rho ^2}{2} \right) } (\alpha _H^2\rho ^2)^{\frac{|m|}{2}} L_{n_{\rho }}^{|m|}(\alpha _H^2 \rho ^2) \nonumber \\{} & {} Z_{\nu }^{(H,L)}(z) \nonumber \\{} & {} = \left\{ \begin{array}{clc} C_{\nu _H}\exp {\left( -\frac{\alpha _H^2z^2}{2} \right) } H_{\nu _H}(-\alpha _Hz), &{} (z < z_s) \in vol(A_H) \nonumber \\ C_{\nu _L} \exp {\left[ -\frac{\alpha _L^2(z-R)^2}{2} \right] } H_{\nu _L}[\alpha _L(z-R)], &{} (z \ge z_s) \in vol(A_L) \end{array} \right. \nonumber \\ \end{aligned}$$

(26)

The function $L_{n_{\rho }}^{|m|}(x)$ is the Laguerre polynomial and $H_{\nu _{L,H}}(x)$ is the Hermite polynomial. They appear as the separated ordinary differential equations are solved along the $\rho$ and z directions respectively. The two coefficients, $\alpha _{\rho }$ and $\alpha _z$ are scaling factors for the two variables, $\rho$ and z. They should be different as the nuclei are deformed. Unfortunately, the total Schroedinger equation for the deformed two-center potential is not separable in $\rho$-direction if $\alpha _{\rho H}$ and $\alpha _{\rho L}$ are different. Their expression depend on the two orthogonal frequencies on the heavy and light fragment region:

$$\begin{aligned} \alpha _{\rho H}= & {} m_0\omega _{\rho H}/\hbar \nonumber \\ \alpha _{\rho L}= & {} m_0\omega _{\rho L}/\hbar \end{aligned}$$

(27)

so that $\alpha _{\rho }$ becomes z-dependent. Therefore one has to resort to an intermediary configuration, where $\alpha _{\rho H}=\alpha _{\rho L}$. This situation corresponds to a configuration of a sphere (heavy) intersected with a vertical spheroid, with the large semiaxis equal to the sphere radius. To obtain the energy (microscopic, deformed two-center potential) of the final configuration, one construct the differences between the intermediary and final (deformed) shape potentials as operators, followed by diagonalization. So the basis corresponds to the intermediary configuration with the same frequency along the $\rho$-direction, hence the same $\alpha _{\rho L}=\alpha _{\rho H}=\alpha _{\rho }$. For the axial part (z-direction) of the oscillator, the differential equation is solved for the two different frequencies, since one considers the whole z-range for every of the two $Z_{\nu }$-functions.

The spin-orbit and $\hat{l^2}$ contributions are obtained by constructing the matrices for $V_{{\hat{l}}{\hat{s}}}$ and $V_{\hat{l^2}}$ within the basis, followed by numerical diagonalization. The procedure provides the single-particle level schemes for protons and neutrons, which are furtheron introduced in the Strutinsky method. Only the main steps are presented here. The shell corrections $E_{sh}$ are calculated as the difference between the sum of the energy levels and a smoothed distribution energy ${\tilde{U}}$:

$$\begin{aligned} E_{sh}=\sum 2E_{\nu }-{\tilde{U}} \end{aligned}$$

(28)

The Strutinsky algorithm consists in calculating ${\tilde{U}}$ [28]. First one defines a smoothed level density ${\tilde{g}}(\epsilon )$, as:

$$\begin{aligned} {\tilde{g}}(\epsilon )= & {} \frac{1}{\gamma } \sum _i \left\{ \frac{1}{\sqrt{\pi }} \exp {\left[ -\left( \frac{\epsilon -\epsilon _i}{\gamma }\right) ^2 \right] } \right. \nonumber \\{} & {} \left. \sum _{k=0}^m a_{2k}H_{2k} \left( \frac{\epsilon -\epsilon _i}{\gamma } \right) \right\} \end{aligned}$$

(29)

where the smoothing interval is taken $\gamma \approx \hbar \omega _0$, the energy levels $\epsilon _i$ are taken up to three $\hbar \omega _0$ above the Fermi level and $H_i$ are the Hermite functions. The $\gamma$ interval for level smoothing is in fact not constant. Its value is determined by the so called plateau condition, which is obtained by performing all the Strutinsky algorithm, taking into account increasing $\gamma$ value and starting around a value of $\hbar \omega$. When the shell correction varies less than 1–2 percent, then one get the minimum necessary $\gamma$ value. The order of the correction m follows the same reasoning. As a particular case, for $^{310}$126, calculations proved that $m=3$ works well for all reactions, disregarding the mass asymmetry.

Then one considers the nucleon number conservation with the smoothed distribution in order to obtain the Fermi level ${\tilde{\lambda }}$ for this uniform distribution.

$$\begin{aligned} N_p=2 \int _{\infty } ^{{\tilde{\lambda }}} {\tilde{g}}(\epsilon )d\epsilon \end{aligned}$$

(30)

The final step is the calculation of the smoothed distribution energy ${\hat{U}}$:

$$\begin{aligned} {\tilde{U}}=2 \int _{- \infty }^{{\tilde{\lambda }}} {\tilde{g}}(\epsilon ) \epsilon d\epsilon \end{aligned}$$

(31)

The procedure is repeated separately for protons and neutrons and the two quantities are summed to produce the shell corrections for every step of the binary deformation. Finally the total deformation energy within the multidimensional space of configuration ($a_H, b_H; a_L, b_L; R$) is the sum of the macroscopic and microscopic terms:

$$\begin{aligned} E_b(a_H,b_H; a_L,b_L; R)= & {} E_{mac}(a_H,b_H; a_L,b_L;R) \nonumber \\{} & {} +E_{sh}(a_H,b_H;a_L,b_L;R). \end{aligned}$$

(32)

2.3 Mass inertia and dynamics

The Wentzel–Kramers–Brillouin (WKB) method is employed to calculate the fission barriers and halflives. The WKB formula implies the use of the nuclear mass to complete the dynamics. A lot of publications use only the reduced mass for simplicity. This work introduces the WKB mass inertia tensor calculated for the special binary space of deformation [32]. The mass tensor expresses the coupling between the free coordinates and their influence upon the total inertia. The coupled components are contracted along the distance between centers R, defining simple functions of dependence for the other coordinates, so that the total inertia $B_{b_L, \chi _H, \chi _L}(R)$ can be written as:

$$\begin{aligned} B_{b_L, \chi _H,\chi _L}(R)= & {} B_{b_L b_L}\left( \frac{db_L}{dR} \right) ^2 +2B_{b_L\chi _H}\frac{db_L}{dR}\frac{d\chi _H}{dR} \nonumber \\{} & {} +2B_{b_L\chi _L} \frac{db_L}{dR}\frac{d\chi _L}{dR} +2B_{b_LR}\frac{db_L}{dR} \nonumber \\{} & {} +B_{\chi _H\chi _H}\left( \frac{d\chi _H}{dR} \right) ^2 +2B_{\chi _H\chi _L}\frac{d\chi _H}{dR}\frac{d\chi _L}{dR}\nonumber \\{} & {} +2B_{\chi _HR}\frac{d\chi _H}{dR} +B_{\chi _L\chi _L}\left( \frac{d\chi _L}{dR}\right) ^2 \nonumber \\{} & {} +2B_{\chi _LR} \frac{d\chi _L}{dR} +B_{RR} \end{aligned}$$

(33)

where $\chi _L, \chi _H$ are the ratios $b_i/a_i$ of the spheroid semiaxes for the light and heavy fragment. Following the Wheeler assumption and respecting the binary character demands, the components of the inertia are calculated as:

$$\begin{aligned} B_{ij}{} & {} =\pi \sigma _m \int _{z_i}^{z_f}\rho _s^2(z,q) \left[ X_i(z)X_j(z) +\frac{1}{8}\rho _s^2(z,q) \right. \nonumber \\{} & {} \quad \left. \frac{\partial X_i}{\partial z}\frac{\partial X_j}{\partial z} \right] dz\nonumber \\ \end{aligned}$$

(34)

where q goes for all free coordinates and $\sigma _m$ is the nuclear mass density. The integrals are fragment dependent through geometry:

$$\begin{aligned} X_i^{(H)}(z)= & {} \frac{1}{\rho _s^2(z,q)}\frac{\partial }{\partial q_i} \int _{(z)_H}\rho _s^2 (z^{\prime },q)dz^{\prime } \nonumber \\ X_i^{(L)}(z)= & {} -\frac{1}{\rho _s^2(z,q)}\frac{\partial }{\partial q_i} \int _{(z)_L}\rho _s^2 (z^{\prime },q)dz^{\prime } \end{aligned}$$

(35)

The dynamics is finalized at this point and the penetrability $P_{fis}$ is obtained with the classic formulas:

$$\begin{aligned} P_{fis}=\exp {[-K_{fis}(b_L,\chi _H,\chi _L;R)]} \end{aligned}$$

(36)

and, following the WKB algorithm, the action intergral reads:

$$\begin{aligned}{} & {} K_{fis}(b_L,\chi _H,\chi _L;R)\nonumber \\{} & {} =\frac{2}{\hbar } \int _{(fis)} \left[ 2B_{b_L,\chi _H,\chi _L}(R)E_b(b_L,\chi _H,\chi _L;R) \right] ^{1/2}dR \end{aligned}$$

(37)

The halflife for every fragment pair is now calculated. After simple replacements one obtains:

$$\begin{aligned} \lg {(T_{fis})}=-20.54+\lg {[1+\exp {(2K_{fis})}]}-\lg {(2E_{zp})} \end{aligned}$$

(38)

where $E_{zp}$ is the zero point vibration energy, here taken as 0.7 MeV. The procedure is repeated for every heavy-light fission fragment pair. In this way the binary procedure is able to account for mass and charge asymmetry at the same time.

Fig. 1

Macroscopic deformation energy surface as a function of charge asymmetry $\eta _Z$ and reduced distance between centers for $^{310}$126. “Zero” macroscopic barrier is emphasized at Yb+Ba, as well as the Businaro–Gallone mountain

3 Discussion of the results

The binary procedure is applied to the decay of $^{310}$126 nucleus, as it is supposed to be doubly-magic, with Z = 126 and N = 184 being proton and neutron closures. In order to ensure this initial request, one keeps in mind that beyond Z = 20 the closures are decided by the spin-orbit potential. To this end, a study has been made by varying $\kappa _{p,n}$ and $\mu _{p,n}$ for $V_{{\hat{l}}{\hat{s}}}$ and $V_{\hat{l^2}}$, until a local minimum is reached. For values of $\kappa _p=0.055$ and $\mu _p=0.400$, a minimum of proton shell correction is reached at $-$ 6.384 MeV. For $\kappa _n=0.045$ and $\mu _n=0.427$, the neutron shell correction has a minimum of $-$ 6.718 MeV. Then the study continues with the macrosopic energy. The entire range of charge asymmetry has been calculated, so that all possible fission channels, from symmetry up to extreme asymmetry ($\alpha$-decay), are analyzed. Figures 1, 2 and 3 have been obtained from the calculation of the potential energy terms: macroscopic, macroscopic plus shell corrections, for the whole range of possible charge asymmetries. The main feature of the two-center macroscopic–microscopic model is the possibility to follow the evolution of a certain pair from the incipient stage-parent ground state, through the partially overlapping region, up to the final, separated fragments. Each path of Figs. 1, 2, 3 is formed by the deformation energy calculated for two intersected spheroids ($A_H,Z_H$), ($A_L,Z_L$), within the space of deformation: the distance between spheroid centers R (elongation equivalent), the ratio of the two semiaxes for the heavy and light fragment and the small semiaxis of the light fragment, namely 5 parameters. The last one allows the emitted fragment to emerge with a small semiaxis ranged between the radius of the parent and the value of the separated light spheroid. All parameters vary under the final assumption of taking the separated fragment deformation values at the end of the process. Each path is finally obtained after a grid-type minimization within the above mentioned space of deformation. The ratios of the semiaxes can vary between the parent deformation and final values of the heavy and light fragments.

Fig. 2

Total deformation energy (shell corrections included) of $^{310}$126 versus charge asymmetry $\eta _Z$ and reduced distance between centers. Potential valleys are carved at Dy+Nd, W+Te and asymmetric $\alpha$-decay

Fig. 3

Contour map of the various fission channels from $^{310}$126. Dy+Nd and W+Te are favored, as the exit point from the barrier is shortest. $\alpha$-valley is also emphasized

Fig. 4

Logarithm of penetrability for the fission channel $^{164}$Dy+$^{146}$Nd calculated with Werner–Wheeler mass inertia ($\lg {T_{WW}}$) and reduced mass $\lg {T_{\mu }}$. The introduction of inertia increase the penetrability with several orders of magnitude

Fig. 5

Logarithm of penetrability versus charge asymmetry $\eta _Z$, for Werner–Wheeler (continuous line) and reduced mass (dashed line) calculations. Differences are higher for more symmetric reactions. Even $\alpha$-decay displays 3 orders of magnitude difference when inertia is introduced

Fig. 6

Fission fragment mass distribution for $^{310}$126 for dynamical calculation with Werner–Wheeler mass tensor (full line) and with reduced mass calculation

Fig. 7

Logarithm of halflives versus charge asymmetry $\eta _Z$ for Werner–Wheeler (continuous line) and reduced mass (dashed line) calculations for all possible fission channels from $^{310}$126. Minima at Sm, Nd and Te are observed, together with $\alpha$-decay

Fig. 8

Logarithm of spontaneous fission lifetime versus neutron asymmetry for isotopes of Gd+Sm, for Werner–Wheeler (continuous line) and reduced mass (dashed line) calculations. $^{162}$Gd+$^{148}$Sm is the favoured reaction as spontaneous fission channel

The macroscopic Yukawa-plus-exponential energy evolution for the decay of $^{310}$126, from the inital ground state up to totally separated fragments and beyond, is presented in Fig. 1, as a function of the reduced distance between centers $(R-R_i)/(R_t-R_i)$ and charge asymmetry $\eta _Z = (Z_H-Z_L)/Z$. First observation is that for Z-symmetry region there are portions where the landscape is almost flat. For these reactions the Coulomb repulsion is maximal, overcoming the nuclear surface energy. In particular, the fission channel Yb+Ba has a macroscopic barrier height of 0.41 MeV. The Businaro–Gallone mountain is also visible for asymmetric reactions, near the alpha emission channel. Consequently, if it would be only for the macroscopic deformation energy, the superheavy nucleus would not survive. When shell corrections are added, there is a drastic change in the deformation energy landscape, as can be seen in Fig. 2. Valleys of deformation energy appear among the raised values against the ground state of $^{310}$126. Three paths are emphasized: quasi-symmetrical Dy+Nd, W+Te and the extreme asymmetrical alpha decay. The last one is effectively the start of the well known alpha chain from superheavy nuclei. To have a clearer picture of the length and height of the barriers, a contour map has been drawn in Fig. 3. The height of the symmetrical splitting is much lower than for larger charge asymmetry. Moreover, the exit point for quasi-symmetrical reactions takes place before the touching point. This behaviour, known for superheavy fission channels, can be explained by the formation of the single-particle structure of the fragments within the overlapping region. This effect, imposed via the shell corrections, is added to the very low values of the macrosopic deformation energy, and underlines the importance of taking a binary mode into account. One can observe that, from the statical point of view, Dy+Nd is a preferred way of decay, together with W+Te. Also the exit point beyond the touching configuration (reduced distance between centers = 1), is obvious for alpha decay channel $^{306}124+\alpha$.

Table 1 Logarithm of fission lifetime with reduced mass $lgT_{\mu }$ and Werner–Wheeler mass tensor $lgT_{WW}$ calculations for the Sm-valley emitted isotopes

In order to complete the dynamics, the mass inertia tensor is calculated. This work used the Werner–Wheeler (WW) procedure for irrotational flow [33]. The use of inertia tensor instead of the reduced mass gives a more realistic image of the process. The WKB penetrability for what seems the more promising fission channel, $^{164}$Dy+$^{146}$Nd, is displayed in Fig. 4. The logarithm of penetrability evolution against the reduced distance between centers is drawn for WW (continuous line) and for reduced mass ($\mu$) calculations. The exit point does not change its position, but the penetrability takes much higher values when the dynamic inertia is introduced. The difference emphasize the importance of taking into account the couplings between the deformation parameters. One can observe a difference which reaches almost ten orders of magnitude at the end of the process.

The whole picture of the difference between WW (continuous line) and $\mu$ type (dashed line) calculations is presented in Fig. 5, for all possible charge asymmetry values, for the fission reaction channels from $^{310}$126. The logarithm of penetrability is always higher whencalculated with the Werner–Wheeler inertia. The gap reaches several orders of magnitude especially as the charge asymmetry $\eta _Z$ is smaller. Peaks are registered for Sm, Nd and Te channels, as well as for alpha emission. Even for $\alpha$-decay, where sometimes the reduced mass $\mu$ is considered an acceptable approximation due to its small size and position near the parent surface, the difference goes up to five orders of magnitude.

Due to the results obtained in penetrability calculations, one can present the mass distribution of fragments for $^{310}$126, displayed in Fig. 6. The centroid of the mass distribution peaks at around 160 mass units. Local maxima are emphasized at (146,164) and (128,182) mass pairs. Also the alpha decay peak is visible for extremely asymmetric split, as expected. The picture suggest a browsing procedure over the fragment masses for the isotopes of Te, Nd and Sm as light fragments.

Fig. 9

Logarithm of spontaneous fission lifetime versus neutron asymmetry for isotopes of Dy+Nd, for Werner–Wheeler (continuous line) and reduced mass (dashed line) calculations. $^{164}$Dy+$^{146}$Nd is the favoured reaction as spontaneous fission channel for this charge splitting

The resulting logarithms of the spontaneous fission lifetimes for both type of calculations (WW and $\mu$) are shown in Fig. 7. WW-type results (continuous line) show smaller values for all reactions. A hint of influence for the WW-calculus is stressed when one compares the values for $\alpha$-decay and two of the minima in the symmetry region: values for $\mu$-calculations are almost equal for $\alpha$-emission and Te channel, and close to Sm and Nd emission. When WW-calculations are performed, the differences increase considerably. Quasi-symmetric channels Nd, Te lower their minima much beyond the $\alpha$-decay. Even the alpha decay lifetime is lowered by 5 orders of magnitude when obtained with WW-method.

Furtheron one considers the study of the most promising fission channels from $^{310}$126, namely Gd+Sm, Dy+Nd and W+Te. The previous results have been obtained for $^{150}$Sm, $^{146}$Nd and $^{128}$Te as light fragments. It is necessary to study the behaviour of these channels when the neutron asymmetry is changed. Different isotopes of the same channel are calculated. The first results for the logarithm of lifetime are displayed in Fig. 8 for Gd+Sm channel, against the neutron asymmetry $\eta _N = (N_{Gd}-N_{Sm})/N$, for WW (continuous line) and reduced mass $\mu$ (dashed line). The difference is maintained, WW-values are lower for all neutron asymmetry values. The $^{162}$Gd+$^{148}$Sm becomes the most preferable way of decay among the isotopic channels, when WW calculations are performed. One has to mention an abrupt rise after this neutron asymmetry value, due especially to the drastic change in shell corrections. The numerical results for Gd+Sm channels are summed up in Table 1. The logarithm of lifetime is presented for reduced mass calculation ($\lg {T_{\mu }}$) and Werner–Wheeler ($\lg {T_{WW}}$) one. The differences go up to 8 orders of magnitude. The lifetimes are expressed in seconds. Promising fission channels are the first five, culminating with $^{162}$Gd+$^{148}$Sm, having a $\lg {T_{WW}}$ of $-$ 0.884. The remarkable thing is that the minimum of $\lg {T_{\mu }}$ is at symmetrical neutron splitting. This behaviour underlines the importance of the mass inertia on the dynamics.

The same analysis is performed for the next possible minimum in lifetime, the Dy+Nd channel, displayed in Fig. 9. The previous results are obtained for $^{152}$Nd emission as the light fragment. Again, a entire range of neutron asymmetry is browsed for this fission channel. The neutron range has been covered from $^{154}$Nd to $^{138}$Nd emission. For the reduced mass calculations (dashed line), the very neutron-symmetric $^{156}$Dy+$^{154}$Nd has an overall minimum. One mention that in this $\mu$-case only the static barrier counts. When the WW-calculation is performed (continuous line), the minimum of the logarithm of lifetime shifts towards more pronounced neutron asymmetry, for $^{164}$Dy+$^{146}$Nd. The same abrupt change occurs after this minimum, towards higher values. The value for possible neutron splitting within the Dy+Nd channel are shown in Table 2. There are large differences between the $\lg {T_{\mu }}$ and $\lg {T_{WW}}$. It is also worth to mention that the overall minimum of lifetime shifts from $^{154}$Sm for $\mu$-type calculations to $^{148}$Sm for WW-calculations. A minimum value of $\lg {T_{WW}}$ is achieved at $-$ 1.325 for $^{164}$Dy+$^{146}$Nd fragment pair.

Table 2 Logarithm of fission lifetime with reduced mass $lgT_{\mu }$ and Werner–Wheeler mass tensor $lgT_{WW}$ calculations for the Nd-valley emitted isotopes

Fig. 10

Logarithm of spontaneous fission lifetime versus neutron asymmetry for isotopes of W+Te, for Werner–Wheeler (continuous line) and reduced mass (dashed line) calculations. $^{168}\hbox {W}+^{142}$Te has the lowest value for this fixed pair of proton division

Table 3 Logarithm of fission lifetime with reduced mass $lgT_{\mu }$ and Werner–Wheeler mass tensor $lgT_{WW}$ calculations for the Te-valley emitted isotopes

The last channel calculated for different neutron splittings is W+Te, which corresponds to the next minimum in $\lg {T}$ values. The results are shown in Fig. 10 for $\mu$-type (dashed-line) and WW-type (continuous line). A minimum is obtained for $^{168}\hbox {W}+^{142}$Te neutron division with Werner–Wheeler method, whereas a more neutron-symmetric reaction, $^{158}\hbox {W}+^{152}$Te has the lowest $\lg {T}$ value for $\mu$-type calculation. As the neutron asymmetry increase after $^{142}$Te, the lifetime also becomes larger. The nummerical results are shown in Table 3. As before, the reduced mass results $\lg {T_{\mu }}$ show an overall minimum at the most symmetrical neutron splitting, whereas the introduction of the WW-mass inertia shifts the minimum at $^{168}\hbox {W}+^{142}$Te pair, with almost 5 orders of magnitude smaller ($\lg {T_{WW}}=-3.724$) than the corresponding $\mu$-calculus. This fission channel displays a large number of negative values for the logarithm of lifetime. One mentions that for the $\alpha$-decay, one obtains a value of $\lg {T_{WW}^{(\alpha )}}=6.8$, so less favorable than quasi-symmetrical splitting.

4 Conclusions

A specialized binary macroscopic–microscopic procedure, based on the deformed two-center shell model and spheroidal free coordinates has been applied to the study of stability and decay of $^{310}$126 superheavy nucleus. This massive system has been shown to be stable for a certain set of values for the strengths of the proton and neutron spin-orbit potentials. The entire range of fission channels are calculated, covering the ($Z_H,Z_L$) range from alpha decay up to quasi-symmetric channels. The procedure has been applied for calculations with the reduced mass and with the Werner–Wheeler mass inertia. Three possible Z-splittings show local minima, within certain fission valleys, much lower than the alpha decay: Sm, Nd and Te accompanied fission. Different neutron splittings for each of these channels show that most favorable fragment pairs are $^{162}$Gd+$^{148}$Sm, $^{164}$Dy+$^{146}$Nd and $^{168}\hbox {W}+^{142}$Te, with lifetime values much lower than that of alpha decay.